Abstract
Quantum sensors based on spin defects in diamond have recently enabled detailed imaging of nanoscale magnetic patterns, such as chiral spin textures, two-dimensional ferromagnets, or superconducting vortices, based on a measurement of the static magnetic stray field. Here, we demonstrate a gradiometry technique that significantly enhances the measurement sensitivity of such static fields, leading to new opportunities in the imaging of weakly magnetic systems. Our method relies on the mechanical oscillation of a single nitrogen-vacancy center at the tip of a scanning diamond probe, which up-converts the local spatial gradients into ac magnetic fields enabling the use of sensitive ac quantum protocols. We show that gradiometry provides important advantages over static field imaging: (i) an order-of-magnitude better sensitivity, (ii) a more localized and sharper image, and (iii) a strong suppression of field drifts. We demonstrate the capabilities of gradiometry by imaging the nanotesla fields appearing above topographic defects and atomic steps in an antiferromagnet, direct currents in a graphene device, and para- and diamagnetic metals.
Similar content being viewed by others
Introduction
Nanoscale magnetic stray fields appearing at surfaces and interfaces of magnetically ordered materials provide important insight into the local spin structure. Such stray fields are present, for example, above magnetic domains and domain walls1, magnetic vortices2, spin spirals3, skyrmions4, or topographic steps and defects5, and often accompany other types of ordering, like ferroelectricity6. Similar stray fields also appear near flowing currents7,8 or materials with a magnetic susceptibility9. Therefore, stray field measurements are a general and versatile tool to study local material or device properties.
While the magnetic imaging of ferromagnetic and ferrimagnetic textures is well-established10,11,12, detection of the much weaker stray fields of, for example, antiferromagnets, multiferroics or nanoscale current distribution is a relatively new development. Quantum magnetometers based on single nitrogen-vacancy (NV) centers have recently led to exciting advances in this direction13,14,15,16,17,18,19. In their standard configuration, NV magnetometers image stray fields by scanning a sharp diamond probe over the sample surface and monitoring the static shift of the NV spin resonance frequency20,21. State-of-the-art scanning NV magnetometers reach a sensitivity to static fields of a few \(\,\mu {{{{{{{\rm{T}}}}}}}}/\sqrt{{{{{{{{\rm{Hz}}}}}}}}}\)16,22. This sensitivity is sufficient for imaging the domain structure of monolayer ferromagnets22,23,24 and uncompensated antiferromagnets14,15,16,17, however, it remains challenging to detect the even weaker stray fields of isolated magnetic defects, spin chains, or ideally compensated antiferromagnets. While higher sensitivities, on the order of \(50\,{{{{{{{\rm{nT}}}}}}}}/\sqrt{{{{{{{{\rm{Hz}}}}}}}}}\), have been demonstrated using dynamic (ac) detection of fields25,26, this approach is limited to the few systems whose magnetization can be modulated, like isolated spins27,28.
Here, we demonstrate a gradiometry technique for highly sensitive imaging of static magnetization patterns. Our method relies on up-conversion of the local spatial gradient into a time-varying magnetic field using mechanical oscillation of the sensor combined with sensitive ac quantum detection. This operating principle is well known from dynamic force microscopy29,30 and has recently been combined with scanning superconducting quantum interference devices31,32,33. While mechanical oscillation has been explored with NV centers in various forms21,34,35,36,37,38, it has not been realized for sensitive imaging of general two-dimensional magnetic samples. As a striking demonstration, we show that scanning gradiometry is able to resolve the nanotesla magnetic stray fields appearing above single atomic terraces in antiferromagnetic Cr2O3. Imaging of nanoscale current patterns, magnetic susceptibility in metals, and reconstruction of field maps from gradiometry data is also demonstrated.
Results
Gradiometry technique
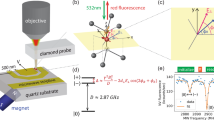
The operating principle of our gradiometry technique is shown in Fig. 1a. Our scanning magnetometer set-up consists of a sample plate that is scanned underneath a diamond probe containing a single NV center at the tip apex formed by ion implantation39. The diamond tip is attached to the prong of a quartz tuning fork (Fig. 1) providing atomic force microscopy (AFM) position feedback40. The microscope apparatus additionally includes an objective to optically polarize and readout the NV center spin state and a bond wire acting as a microwave antenna for spin manipulation (see Methods for details). In the conventional mode of operation, we record a spin resonance spectrum at each pixel location to build up a map of the sample’s static stray field16.
a Schematic of the scanning gradiometer. A single NV center located at the apex of a diamond tip is oscillated in shear-mode using a quartz tuning fork. The microwave pulse generation is synchronized, via a lock-in controller, with the electrical drive of the tuning fork. An objective located above the NV is used to apply laser pulses and collect the NV photo-luminescence. A three-axis piezo stage is used to position and scans the sample surface under the sensor. b Detail showing the orientations of sample, tip, NV center (purple), and direction of oscillation x(t). c Scanning electron micrograph of a quartz tuning fork and diamond tip (inset). Scale bars, 200 μm and 1 μm (inset).
To implement the gradiometer, we mechanically oscillate the NV in a plane parallel to the sample (shear-mode) by electrically driving the tuning fork at a fixed amplitude xosc ~ 10–70 nm. The NV center now experiences a time-dependent field given by
where B is the vector component of the sample’s stray field along the NV anisotropy axis (Methods), and where \(x(t)={x}_{0}+{x}_{{{{{{{{\rm{osc}}}}}}}}}\sin (2\pi {f}_{{{{{{{{\rm{TF}}}}}}}}}t)\) describes the mechanical oscillation around the center location x0 with frequency fTF. The amplitudes of the 0fTF, 1fTF, and 2fTF harmonics in leading orders of xosc are given by
and are therefore proportional to the static field, gradient, and second derivative, respectively. The series expansion in Eq. (2) is accurate for oscillation amplitudes xosc smaller than the scan height, typically d ~ 100 nm. Since the scan height sets the achievable spatial resolution7, the oscillation does not impair imaging resolution.
To detect the harmonics of B(t), we synchronize the mechanical oscillation with a suitable ac quantum sensing sequence41,42, shown in Fig. 2a. Quantum sensing sequences measure the quantum phase accumulated by the coherent precession of a superposition of spin states during an interaction time τ43. To measure the nfTF harmonic, we invert the spin precession n times during one mechanical oscillation period using microwave π-pulses (Carr-Purcell-Meiboom-Gill (CPMG-n) sequence43,44). The pulse protocols for the first (CPMG-1) and second (CPMG-2) signal harmonics are shown in Fig. 2a. The quantum phase accumulated for the first harmonic is given by
where γe = 2π × 28 GHz/T is the gyromagnetic ratio of the NV electronic spin and t0 = T/2 (see Fig. 2a). The derivation of Eq. (3) and general expressions for higher harmonics and for sequences that are off-centered with respect to the tuning fork oscillation (t0 ≠ T/2) are given in Supplementary Note 1. To determine ϕ experimentally, we measure the photo-luminescence (PL) intensity CΦ as a function of the phase Φ = x, y, −x, −y of the last microwave π/2 pulse (Fig. 2a). From the four PL signals CΦ we then extract the phase using the two-argument arc tangent (see Methods),
This four-phase readout technique has the advantage that the phase can be retrieved over the full 2π range with uniform sensitivity19,26. From ϕ(measured) and Eq. (3) we then compute the gradient field B1. Since we can only measure ϕ modulo 2π, a phase unwrapping step is necessary for large signals that exceed the range [−π; π)26. Additionally, the oscillation amplitude can be used as a control parameter (xosc < d) to dynamically set the maximum gradient before phase wrapping occurs.
a Timing diagram of sensor oscillation (red), resulting in magnetic field at the sensor location (black), microwave pulse sequences for first and second harmonic (blue and orange), laser pulses (green), and photodetector collection window (gray). Pulse indicators such as (π)x denote (angle)axis of the spin rotation. T = 1/fTF is the oscillation period, τ < T is the sensor interaction time, and t0 the trigger delay. We use a tuning fork with fTF ~ 32 kHz. Durations of pulses are ~2 μs (laser) and ~100 ns (microwave π-rotation). b Scheme for detecting the first harmonic signal over n oscillation periods in the regime τ ≫ T. Here, τ = nT and the number of π-pulses is 2n.
For NV centers with long coherence times (T2 ≫ T), the sensitivity can be improved further by accumulating phase over multiple oscillation periods using CPMG-2n sequences (Fig. 2b). The simplest way to meet the T2 ≫ T condition is to use a mechanical oscillator with a higher resonance frequency. Alternatively, as demonstrated in this work, a higher mechanical mode of the tuning fork can be employed45. High-frequency detection has the added advantage that the interval between π-pulses (given by 1/(2fTF)) becomes very short, which makes dynamical decoupling more efficient and in turn leads to improved sensitivity42,46. We demonstrate single and multi-period detection schemes with sensitivities of \(\sim \!\!120\,{{{{{{{\rm{nT}}}}}}}}/\sqrt{{{{{{{{\rm{Hz}}}}}}}}}\) and \(\sim\!\!100\,{{{{{{{\rm{nT}}}}}}}}/\sqrt{{{{{{{{\rm{Hz}}}}}}}}}\), respectively, that exceed our best dc sensitivities of \(\sim\!\!1-2\,\mu {{{{{{{\rm{T}}}}}}}}/\sqrt{{{{{{{{\rm{Hz}}}}}}}}}\) by one order of magnitude (Supplementary Notes 2 and 3).
Demonstration of scanning gradiometry
We begin measurements by calibrating the oscillation amplitude xosc and verifying Eqs. (2, 3). We characterize the gradiometry phase detection by parking the tip over a fixed position on a magnetic test sample and measuring the B1 and B2 signals as a function of the oscillation amplitude xosc (see Methods and Supplementary Note 4 for characterization and calibration details). Figure 3a confirms that the signals grow as B1 ∝ xosc and \({B}_{2}\propto {x}_{{{{{{{{\rm{osc}}}}}}}}}^{2}\), as expected from the Taylor expansion (Eq. 2). Further, to avoid mixing of mechanical and field harmonic signals through surface interactions, we retract the tip by ~20 nm from the contact point while measuring (Supplementary Note 5).
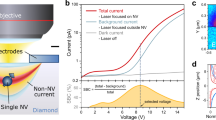
a Measured and unwrapped quantum phase ϕ(measured) plotted as a function of tip oscillation amplitude xosc for the first (blue) and second (orange) harmonic. Solid lines are ∝ xosc and \(\propto {x}_{{{{{{{{\rm{osc}}}}}}}}}^{2}\), respectively. The dashed line indicates maximum oscillation amplitude before the Taylor approximation breaks down due to the onset of spatial averaging. b Schematic of the bilayer graphene device (gray). A direct current of Idc ≈ 5.3 μA (white arrow) is applied between the indicated contacts (width ~400 nm). c, Static field map B0, gradient map B1, second derivative map B2 from the area indicated in b. Contours reflect the device layout. Dwell time is 30 s per pixel. Scale bar, 1 μm. d, Analytical spatial profiles for the z component of the magnetic field, gradient, and second derivative generated across the two contacts (dotted lines in c). The far-field decay with x is also indicated.
We establish two-dimensional imaging by detecting the stray field from a direct current flowing in a bilayer graphene device (Fig. 3b). This device provides an ideal test geometry because the magnetic stray field and gradient can be tuned and directly compared to the analytical model. Moreover, results can be benchmarked against those obtained by ac current driving26. Figure 3c presents gradiometry maps B1 and B2 and, for comparison, a static field map B0 recorded using a standard dc technique47 with no tuning fork oscillation. Note that all images are recorded with the same imaging time and pixel size. The figure immediately highlights several advantages of gradiometry versus static field imaging: First, the signal-to-noise ratio is strongly enhanced due to the more sensitive ac detection, despite a lower absolute signal. Second, magnetic drift throughout the imaging time (several hours) is present in the static image but suppressed in the gradiometry images. Magnetic drifts are suppressed for two reasons; they fluctuate at low frequencies far away from the detection frequency, and magnetic drift sources do not generate appreciable magnetic field gradients over the oscillation range (~100 nm). Numerically differentiating the static image to remove field drifts is not suitable as it introduces high-frequency noise (Supplementary Fig. 6c). Third, because gradient fields decay quickly with distance (B1 ∝ x−2 and B2 ∝ x−3 compared to B0 ∝ x−1, see Fig. 3d and Supplementary Note 6), they offer a higher apparent image resolution and are thus easier to interpret.
Imaging of antiferromagnetic surface texture
We now turn our attention to the imaging of stray fields above antiferromagnetic materials, focusing on the archetypical model system Cr2O3. Antiferromagnets represent a general class of weakly magnetic materials that are both challenging to the image by existing techniques48,49,50 and of key importance for understanding multiferroicity and topological magnetism in the context of antiferromagnetic spintronics51. Although antiferromagnets are nominally non-magnetic, weak stray fields can appear due to uncompensated moments at domain walls14,15,16, spin spirals13, topographic steps17, or surface roughness and defects. The latter is particularly difficult to detect, yet plays an important role in the pinning of domain walls17 and establishing an exchange bias at material interfaces52. Careful study of these weaker fields is therefore an important avenue for quantifying the interplay between surface roughness, stray field structure, local magnetization, and domain wall behavior.
In Fig. 4a we show a gradiometry image of a polished Cr2O3 single-crystal16. Cr2O3 has a layered structure of out-of-plane Cr3+ moments at the (0001) surface53,54 that lead to stray fields at topographic steps16,17. These stray fields are proportional to the step height. Indeed, Fig. 4a reveals a rich variety of magnetic anomalies on this surface, including two ~5 nm deep and ~200 nm wide topographic trenches introduced by polishing, a number of point defects, and general texture of the ~2 nm-rms surface roughness (see Supplementary Fig. 11 for topographic characterization). A quantitative calculation of the expected stray field maxima shows that the magnetic anomalies are well explained by the surface topography (Supplementary Note 7). Except for the trenches, these surface defects are not visible in the static field image (Fig. 4b). Note that it is possible to convert the gradiometry map into an improved static field map through integration and weighted averaging in k-space (Fig. 4c and Methods). See Supplementary Fig. 6 for the reverse process, where a B0 image is converted into a B1 image.
a Gradiometry map B1 of topographic defects from a polished Cr2O3 single crystal. Dwell time is 10 s per pixel and xosc = 23 nm. b Corresponding static field map B0. Dwell time is 1 s per pixel. c Improved static field map \({\tilde{B}}_{0}\) obtained from a weighted average of a and b (see Methods). The noise standard deviation is reduced from 1.8 μT (b) to 90 nT in the oscillation direction (x-direction) and 340 nT in the y-direction (c). The directional sensitivity could be avoided using tapping mode oscillation (see Methods). When normalized by measurement time, B1 is more sensitive than B0 by a factor larger than 8. d B1 image of the stray field generated by atomic steps on an as-grown Cr2O3(0001) surface. Two magnetic defects which produce much larger gradient signals are also visible. Inset is a detail of defects and atomic steps recorded with higher pixel resolution. The distance between steps is ca. 400 nm (arrow). Dwell time is 5 s per pixel. Scale bars in a–d 1 μm. e, f AFM line scans revealing mono- and diatomic steps with different terrace sizes. h is the distance between neighboring O-planes along the Cr2O3c-axis53,54. Insets show sketches of atomic steps and up–down ordering of Cr3+ moments (red, blue). Curved arrows are field lines. g–h Gradiometry line scans acquired over different areas on the as-grown Cr2O3 surface. The profiles are fitted to a stray field model involving atomic steps (solid lines). xosc = 46 nm in d, g, and h.
Next, we show that gradiometry is sufficiently sensitive to detect single atomic surface steps of the layered Cr2O3(0001) surface. Figure 4d displays a gradiometry image from a second Cr2O3 single crystal with an as-grown (unpolished) surface53. We observe a striking pattern of regular stripes separated by a few hundred nanometers and an approximate amplitude of B1 ~ 250 nT. The pattern extends over the entire crystal surface with different stripe separations and directions in different regions of the sample (Supplementary Fig. 12). By converting B1 measurements into local gradients we deduce height changes <1 nm (Supplementary Note 7), suggesting that the repeating striped patterns are caused by single (h = 0.227 nm), or multiple atomic step edges. To corroborate, we correlate the magnetic features to the AFM topography of the sample (Supplementary Fig. 12). Figure 4e, f show line cuts perpendicular to the stripe direction in two regions of the sample surface, and reveal the presence of both mono- and diatomic step edges. The gradiometry data (Fig. 4g, h), are well fitted by a simple model (see Methods), producing a fitted surface magnetization of σz = 2.1 ± 0.5 μB/nm2, in good agreement with earlier data14,16. Together, our findings unambiguously confirm the stepped growth of the Cr2O3(0001) surface54. To our knowledge, our work reports the first magnetic stray field imaging of atomic steps on an antiferromagnet. It opens a complementary path to existing atomic-scale techniques, such as spin-polarized scanning tunneling microscopy and magnetic exchange force microscopy55, without sharing the need for an ultra-high vacuum, a conducting surface, or cryogenic operation.
Imaging of magnetic susceptibility
We conclude our study by demonstrating nanoscale imaging of magnetic susceptibility. Susceptometry measurements are important for investigating, for example, the magnetic response of patterned metals and materials9,56, superconductors57 as well as para- and superparamagnetic nanoparticles58,59. Figure 5a shows a gradiometry map of a 50-nm-thick disc made from paramagnetic Pd placed in a bias field of Bext = 35 mT. Under the bias field, the disc develops a magnetization of M = χBext/μ0, where χPd is the magnetic susceptibility of the Pd film. A fit to the data (see Methods), shown in Fig. 5b, produces a susceptibility of χPd = (6.6 ± 0.2) × 10−4. This is slightly smaller than the value of pure Pd (χPd = 7.66 × 10−460). The decreased susceptibility may be attributed to either a finite-size effect61 or hydrogen adsorption62. Repeating the same experiment with Bi, a diamagnetic sample, produces an experimental value of χBi = −(1.7 ± 0.1) × 10−4(Fig. 5c, d), which matches the accepted room temperature value of χBi = − 1.67 × 10−460. Despite the ~4 × weaker susceptibility, the magnetic pattern is clearly visible and its sign is inverted compared to the paramagnetic Pd disc. Additionally, the apparent local structure at the center of the disc is explained by a variation in the film thickness (Supplementary Fig. 13). Together, Fig. 4a–d demonstrate the feasibility of extending sensitive dc susceptometry to the nanometer scale.
a Measured B1 image of a 2-μm-diameter paramagnetic Pd disc in a 35 mT bias field. b Calculated B1 image (best fit) of the Pd disc. c, d Corresponding measurement, and calculation for diamagnetic Bi in a bias field of 33 mT. Offsets of 51 nT and 38 nT due to the gradient of the external bias magnet are subtracted from a and c, respectively. See Methods for calculation and fit details. Scale bars, 1 μm.
Discussion
Our work demonstrates a simple yet powerful method for imaging static magnetization patterns with high sensitivity and spatial resolution. While we demonstrate scanning gradiometry on a layered antiferromagnet, extension to more challenging systems including perfectly compensated collinear antiferromagnets, screw and step dislocations5, or isolated magnetic defects is natural. In particular, the magnetic signal from an atomic step edge is equivalent to that of a one-dimensional spin chain with a linear magnetization density of σzh ≈ 0.5 μB/nm (Methods), demonstrating the feasibility of imaging generic 1D spin systems. Gradiometry is also well-positioned for imaging the internal structure of domain walls and skyrmions, and in particular, for quantifying their size and chirality16,63,64,65 (Supplementary Fig. 14). Finally, while we demonstrate gradiometry on magnetic fields, the technique can be extended to electric fields by orienting the external bias magnetic field perpendicular to the NV axis66,67,68. In particular, the dynamic mode of operation may alleviate charge screening that has previously limited scanning NV electrometry of dc electric field sources69. With the ability to image both magnetic and electric fields, one could imagine correlating antiferromagnetic and ferroelectric order in multiferroics51, providing a unique angle to investigate the magneto-electric coupling in these fascinating and technologically important materials.
Methods
Experimental set-up
All experiments were carried out at room temperature with two home-built scanning microscopes. Micro-positioning was carried out by closed-loop three-axis piezo stages (Physik Instrumente) and AFM feedback control was carried out by a lock-in amplifier (HF2LI, Zurich Instruments) and standard PID controls. PL of the NV centers was measured with avalanche photodiodes (APDs) (Excelitas) and data were collected by standard data acquisition cards (PCIe-6353, National Instruments). Direct currents sent through the bilayer graphene were created with an arbitrary waveform generator (DN2.663-04, Spectrum Instrumentation) and the current was measured with a trans-impedance amplifier (HF2TA, Zurich Instruments). Microwave pulses and sequences were created with a signal generator (Quicksyn FSW-0020, National Instruments) and modulated with an IQ mixer (Marki) and an arbitrary waveform generator (DN2.663-04, Spectrum Instrumentation, and HDAWG, Zurich Instruments). NV centers were illuminated at < 100 μW by a custom-designed 520 nm pulsed diode laser. Scanning NV tips were purchased from QZabre AG39. Three different NV tips were used throughout this study with standoff distances d between 70 and 130 nm (excluding the 20-nm retract distance). When imaging our samples, we typically measured for 5 to 30 seconds per pixel to achieve good signal-to-noise. We observed relatively small spatial drifts (typically <30-nm per day). As a result, we did not employ any drift correction techniques and we do not expect drifts to affect our results or scientific claims.
Magnetic samples
Bilayer graphene device
Standard microfabrication processes were used, including mechanical exfoliation and a dry transfer process for generating the hBN-bilayer-graphene-hBN stack, electron beam lithography, and plasma etching for creating the device geometry and physical vapor deposition for creating the metallic device contacts. Full details can be found in ref. 26.
Cr2O3 crystals
The mechanically polished and non-polished Cr2O3 bulk single crystals were provided by professor Manfred Fiebig. Both crystals have a (0001) surface orientation. Crystal growth and processing details can be found in refs. 16,53.
Pd and Bi discs
Metallic micro-discs were created using standard microfabrication processes. Discs were defined through electron beam lithography on spin-coated Si wafers. Chemical development of the spin-coated resist, followed by metal deposition of either 50-nm of Pd or Bi, and a lift-off process finished the fabrication.
Initialization and readout of NV spin state
A laser pulse of ~2 μs duration was used to polarize the NV center into the mS = 0 state. Then, the dc or ac quantum sensing measurement occurred on the mS = 0 to mS = −1 transition (see below). The readout of the NV’s spin state was performed by another ~2 μs long laser pulse, during which the photons emitted from the NV center were collected with the APD, binned as a function of time, and summed over a window (~300 ns) that optimized spin state-dependent PL contrast70.
DC sensing protocol
DC magnetic images were acquired with the pulsed ODMR method47. Measured magnetic resonance spectra were fitted for the center frequency fc of a Lorentzian function, \(L(f)=1-\epsilon {[(2\pi f-2\pi {f}_{c})/{\omega }_{L}]}^{2}+1{\left.\right]}^{-1}\), where ϵ is the spin contrast (in percent) and ωL is the width of the Lorentzian dip. In a 2D scan the magnetic field projected along the axis of the NV could be determined at each pixel using B(x, y) = 2π[fc(x, y) − f0]/γe where f0 is the resonance frequency far from the surface. For our diamond probes, the NV anisotropy axis was at an θ ~ 55∘ angle with respect to the out-of-plane direction (z-axis in Fig. 1). Therefore, B(x, y) corresponded to the vector field projection along this tilted direction.
AC sensing protocol
AC sensing used either a spin echo or dynamical decoupling sequence41,42. The NV spin state was initialized optically into the mS = 0 state followed by a microwave π/2-pulse to create a coherent superposition between the mS = 0 and mS = −1 states. The quantum phase ϕ accumulated between the two states during the coherent precession can be expressed as \(\phi =\int\nolimits_{0}^{\tau }{\gamma }_{{{{{{{{\rm{e}}}}}}}}}g(t)B(t)dt\) where g(t) is the modulation function43, B(t) is the magnetic field, τ is the interaction time (the time in between the first and last π/2-pulse), and where we use the rotating frame approximation. The modulation function alternates between ± 1 with each microwave π-pulse during the pulse sequence. While imaging with the gradiometry pulse sequences, 3π/2-pulses were sometimes used instead of the final π/2-pulses for the projective spin readout to reduce pulse imperfections caused by (ca. ± 100 kHz) drifts in the NV resonance frequency.
Calibration of tuning fork oscillation
We estimated the oscillation amplitude xosc and oscillation angle in the xy-plane, denoted by α, of the tuning forks with two different in-situ measurement techniques. The first method involved processing a static field map and a gradient field map acquired over the same region with a least-squares minimization scheme. By minimizing a cost function proportional to the pixel value differences between the B1 and numerically differentiated B0 images, estimates for xosc and α were determined. The second method involved stroboscopic imaging of the static field (B0) synchronized to the tuning fork oscillation. By measuring the time-tagged displacements of magnetic features recorded at different positions during the tuning fork oscillation, xosc and α could be estimated by fitting to the path taken by the NV. We found that xosc scaled linearly with the applied drive voltage for the voltages we used while imaging. Examples of these calibration methods are given in Supplementary Note 4.
Calibration of the trigger delay
In order to optimize the ac sensing sequences, and to distinguish between signals from the first and second derivatives (see Supplementary Note 1), a trigger delay (t0) calibration measurement must be made. The calibration measurement consisted of measuring the phase ϕ at a stationary point on the sample, while varying t0, thus producing a phase that oscillated as a function of t0. The chosen value of t0 was the value that maximized the measured phase. Examples of this calibration measurement, as well as the characterization of PL oscillation caused by the tuning fork motion, are shown in Supplementary Note 4.
Reconstruction of the static field map from the gradient map
A gradient map B1 can be used to reduce the noise and improve the image of a (less sensitive) static field map B0. While direct integration of B1 produces a B0 map32, a combination approach using B0 and B1 provides the best noise suppression across all spatial wavelengths, with no need for ad-hoc boundary conditions. Letting BT denote the true static magnetic field value, the experimentally measured B0 and B1 field maps are
where \(\frac{\partial }{\partial r}=\cos (\alpha )\frac{\partial }{\partial x}+\sin (\alpha )\frac{\partial }{\partial y}\) is the directional derivative and \({w}_{0} \sim {{{{{{{\mathcal{N}}}}}}}}(0,{\sigma }_{{B}_{0}}^{2})\) and \({w}_{1} \sim {{{{{{{\mathcal{N}}}}}}}}(0,{\sigma }_{{B}_{1}}^{2})\) are white noise added to each pixel (reflecting the Poissonian shot noise of the photo-detection). In k-space these equations can be transformed into
where \(\hat{X}\) denotes the Fourier transform of X, \({k}_{r}={k}_{x}\cos \alpha +{k}_{y}\sin \alpha\) is the dot product between the oscillation direction and the k-vector [kx, ky]. Integration in k-space introduces a k-dependent noise term in the gradient field map. In particular, the integrated gradient map has noise amplification near the line \({k}_{y}=-\cot (\alpha ){k}_{x}\) but has noise suppression far away from that line. Directional sensitivity could be avoided by oscillating the tuning fork in the z-direction (tapping mode), or by using an oscillator that supports orthogonal lateral modes. To circumvent this problem we average two k-space maps (Eq. (6)) with k-vector dependent weights that reflect the noise added by the integration process. The use of inverse variance weights additionally results in an image with the lowest possible variance. Thus, the optimal reconstructed static field map can be computed by taking the inverse Fourier transform of
where \({k}_{0}^{2}={\sigma }_{{B}_{1}}^{2}/({x}_{{{{{{{{\rm{osc}}}}}}}}}^{2}{\sigma }_{{B}_{0}}^{2})\) defines a cut-off wave vector determined by the oscillation amplitude and the noise variances \({\sigma }_{{B}_{0}}^{2}\) and \({\sigma }_{{B}_{1}}^{2}\). The corresponding cut-off wavelength λ = 2π/k0 reflects the spatial wavelength above (below) which the B0 (B1) field map is less noisy. It should also be noted that the k-space averaging process can be modified to include the B2 map, however, the B1 map provides the most significant improvement. Specifically, in Fig. 4c, xosc = 23 nm and α = 180∘ were used as reconstruction parameters (determined by the calibration in Supplementary Note 4). Note, since the gradient and k-space averaging are directional, the noise reduction is also directional (approximately 22 × in the x-direction and 5.6 × in the y-direction).
Stray fields from atomic step edges
For an atomic step edge propagating along the y-direction the stray field is modeled by two out-of-plane magnetic samples with different heights. Taking the analytical form (see ref. 63) for the stray fields above an edge at x = 0 as \({B}_{x}(x,z)=\frac{-{\mu }_{0}{\sigma }_{z}}{2\pi }\frac{z}{{x}^{2}+{z}^{2}}\), By = 0, and \({B}_{z}(x,z)=\frac{{\mu }_{0}{\sigma }_{z}}{2\pi }\frac{x}{{x}^{2}+{z}^{2}}\), where σz is the surface magnetization, we define the stray field produced by a small change in the height h as
with \({B}_{y}^{{{{{{{{\rm{step}}}}}}}}}=0\). The expressions are simplified in the limit of h ≪ d since the sub-nanometer atomic step edges are much smaller than typical standoff distances of d ~ 50 − 100 nm. We measure the gradient of the stray field along the oscillation direction, taken as the x-direction for simplicity. This leads to field gradients of
The fits in Fig. 4g, h are produced by projecting the field gradients onto the NV axis defined by \({{{{{{{\bf{e}}}}}}}}=[\sin \theta \cos \varphi ,\sin \theta \sin \varphi ,\cos \theta ]\) and summing over multiple steps. The line cuts are produced by rotating and plane averaging a 2D image (Supplementary Fig. 12). We account for the rotation angle in the xy-plane by introducing an additional image rotation angle \(\varphi ^{\prime}\). The experimentally measured B1 field is then fitted by
We set h = 0.227 nm and \(\varphi ^{\prime} =4{0}^{\circ }\) for the fit in Fig. 4g, h = 0.454 nm and \(\varphi ^{\prime} =2{3}^{\circ }\) for the fit in Fig. 4h and fixed xosc = 46 nm (determined by the tip calibration) in both fits. The standoff distance d, the surface magnetization σz, angles θ and φ and step edge locations are free parameters in the fit. Collectively, the fitted line scans give d = 89 ± 12 nm (including the 20 nm retract distance) and σz = 2.1 ± 0.5 μB/nm2, which is consistent with previous measurements on this sample16.
Note, Eq. (8) is functionally equivalent to the magnetic field from a one-dimensional ferromagnetic spin chain with a linear magnetization density of M1D = σzh. To demonstrate this, we calculate the stray field produced by a infinite line of magnetic dipoles along the line x = 0 and pointing in the x-direction as:
where r2 = x2 + y2 + d2.
Susceptibility fitting for Pd and Bi discs
Susceptibility fits followed the assumption that the stray field produced by a para- or diamagnetic sample is identical to that of a homogeneously magnetized body with a magnetization magnitude of M = χPd/BiBext/μ0 and a magnetization vector that is parallel to the external polarizing field. The stray field produced by this magnetization is B(r) = − μ0 ∇ ϕmag(r) where ϕmag(r) is the magnetic potential. We computed the stray field using the k-space method of ref. 71 and fitted the gradient image to the numerically computed gradient fields. In the fitting procedure we fixed xosc = 69 nm, α = 180∘ (determined by the tip calibration) and sample thickness t = 50 nm while the standoff distance d, magnetization magnitude M, angles θ and φ, circle radius and position are free parameters in the fit. The susceptibilities are computed as χPd/Bi = μ0M/Bext and the fitted magnetizations were MPd = 18.6 ± 0.6 A/m and MBi = −4.4 ± 0.4 A/m.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
References
Rondin, L. et al. Nanoscale magnetic field mapping with a single spin scanning probe magnetometer. Appl. Phys. Lett. 100, 153118 (2012).
Shinjo, T., Okuno, T., Hassdorf, R., Shigeto, K. & Ono, T. Magnetic vortex core observation in circular dots of permalloy. Science 289, 930–932 (2000).
Cox, D., Takei, W. & Shirane, G. A magnetic and neutron diffraction study of the Cr2O3-Fe2O3 system. J. Phys. Chem. Solids 24, 405–423 (1963).
Yu, X. et al. Real-space observation of a two-dimensional skyrmion crystal. Nature 465, 901–904 (2010).
Ravlić, R., Bode, M., Kubetzka, A. & Wiesendanger, R. Correlation of dislocation and domain structure of Cr(001) investigated by spin-polarized scanning tunneling microscopy. Phys. Rev. B 67, https://doi.org/10.1103/physrevb.67.174411 (2003).
Fiebig, M., Lottermoser, T., Frohlich, D., Goltsev, A. V. & Pisarev, R. V. Observation of coupled magnetic and electric domains. Nature 419, 818–820 (2002).
Chang, K., Eichler, A., Rhensius, J., Lorenzelli, L. & Degen, C. L. Nanoscale imaging of current density with a single-spin magnetometer. Nano Lett. 17, 2367 (2017).
Tetienne, J. P. et al. Quantum imaging of current flow in graphene. Sci. Adv. 3, e1602429 (2017).
Bluhm, H., Bert, J. A., Koshnick, N. C., Huber, M. E. & Moler, K. A. Spinlike susceptibility of metallic and insulating thin films at low temperature. Phys. Rev. Lett. 103, 026805 (2009).
Hopster, H. & (Eds.), H. P. O. Magnetic Microscopy of Nanostructures (Springer, Berlin, 2005).
Freeman, M. R. & Choi, B. C. Advances in magnetic microscopy. Science 294, 1484 (2001).
Hartmann, U. Magnetic force microscopy. Annu. Rev. Mater. Sci. 29, 53–87 (1999).
Gross, I. et al. Real-space imaging of non-collinear antiferromagnetic order with a single-spin magnetometer. Nature 549, 252 (2017).
Appel, P. et al. Nanomagnetism of magnetoelectric granular thin-film antiferromagnets. Nano Lett. 19, 1682–1687 (2019).
Wornle, M. S. et al. Current-induced fragmentation of antiferromagnetic domains. arXiv https://arxiv.org/abs/1912.05287 (2019).
Wornle, M. S. et al. Coexistence of Bloch and Neél walls in a collinear antiferromagnet. Phys. Rev. B 103, 094426 (2021).
Hedrich, N. et al. Nanoscale mechanics of antiferromagnetic domain walls. Nat. Phys. 17, 064007 (2021).
Jenkins, A. et al. Imaging the breakdown of ohmic transport in graphene. arXiv https://arxiv.org/abs/2002.05065 (2020).
Ku, M. J. H. et al. Imaging viscous flow of the Dirac fluid in graphene. Nature 583, 537–541 (2020).
Rondin, L. et al. Magnetometry with nitrogen-vacancy defects in diamond. Rep. Prog. Phys. 77, 056503 (2014).
Degen, C. L. Scanning magnetic field microscope with a diamond single-spin sensor. Appl. Phys. Lett. 92, 243111 (2008).
Sun, Q. et al. Magnetic domains and domain wall pinning in atomically thin CrBr3 revealed by nanoscale imaging. Nat. Commun. 12, 1989 (2021).
Thiel, L. et al. Probing magnetism in 2D materials at the nanoscale with single-spin microscopy. Science 364, 973 (2019).
Fabre, F. et al. Characterization of room-temperature in-plane magnetization in thin flakes of CrTe2 with a single-spin magnetometer. Phys. Rev. Mater. 5, 034008 (2021).
Vool, U. et al. Imaging phonon-mediated hydrodynamic flow in WTe2. Nat. Phys. 17, 1216 (2021).
Palm, M. et al. Imaging of submicroampere currents in bilayer graphene using a scanning diamond magnetometer. Phys. Rev. Appl. 17, https://doi.org/10.1103/physrevapplied.17.054008 (2022).
Rugar, D., Budakian, R., Mamin, H. J. & Chui, B. W. Single spin detection by magnetic resonance force microscopy. Nature 430, 329 (2004).
Grinolds, M. S. et al. Subnanometre resolution in three-dimensional magnetic resonance imaging of individual dark spins. Nat. Nano. 9, 279–284 (2014).
Hillenbrand, R., Stark, M. & Guckenberger, R. Higher-harmonics generation in tapping-mode atomic-force microscopy: insights into the tip-sample interaction. Appl. Phys. Lett. 76, 3478–3480 (2000).
Sahin, O., Quate, C., Solgaard, O. & Giessibl, F. Higher-harmonic force detection in dynamic force microscopy. Springer Handbook of Nanotechnol. 717–736 https://doi.org/10.1007/978-3-540-29857-1_26 (2007).
Uri, A. et al. Nanoscale imaging of equilibrium quantum Hall edge currents and of the magnetic monopole response in graphene. Nat. Phys. 16, 164–170 (2020).
Tschirhart, C. L. et al. Imaging orbital ferromagnetism in a Moiré chern insulator. Science 372, 1323–1327 (2021).
Wyss, M. et al. Magnetic thermal and topographic imaging with a nanometer-scale squid-on-lever scanning probe. Phys. Rev. Appl. 17, 034002 (2022).
Hong, S. et al. Coherent mechanical control of a single electronic spin. Nano Lett. 12, 3920–3924 (2012).
Kolkowitz, S. et al. Coherent sensing of a mechanical resonator with a single-spin qubit. Science 335, 1603–1606 (2012).
Teissier, J., Barfuss, A., Appel, P., Neu, E. & Maletinsky, P. Strain coupling of a nitrogen-vacancy center spin to a diamond mechanical oscillator. Phys. Rev. Lett. 113, 020503 (2014).
Esquinazi, P. D., Meijer, J. & Jelezko, F. Method and device for the determination of static electric and/or static magnetic fields and the topology of components by means of a sensor technology based on quantum effects. Patent Application DE102015016021A1 (2015).
Wood, A. A. et al. T2-limited sensing of static magnetic fields via fast rotation of quantum spins. Phys. Rev. B 98, 174114 (2018).
QZabre Ltd. https://qzabre.com.
Giessibl, F. J. High-speed force sensor for force microscopy and profilometry utilizing a quartz tuning fork. Appl. Phys. Lett. 73, 3956–3958 (1998).
Taylor, J. M. et al. High-sensitivity diamond magnetometer with nanoscale resolution. Nat. Phys. 4, 810 (2008).
Lange, G. D., Riste, D., Dobrovitski, V. V. & Hanson, R. Single-spin magnetometry with multipulse sensing sequences. Phys. Rev. Lett. 106, 080802 (2011).
Degen, C., Reinhard, F. & Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 89, 035002 (2017).
Meiboom, S. & Gill, D. Modified spin-echo method for measuring nuclear relaxation times. Rev. Sci. Instr. 29, 688 (1958).
Zeltzer, G. et al. Scanning optical homodyne detection of high-frequency picoscale resonances in cantilever and tuning fork sensors. Appl. Phys. Lett. 91, 173124 (2007).
Ryan, C. A., Hodges, J. S. & Cory, D. G. Robust decoupling techniques to extend quantum coherence in diamond. Phys. Rev. Lett. 105, 200402 (2010).
Dreau, A. et al. Avoiding power broadening in optically detected magnetic resonance of single NV defects for enhanced dc magnetic field sensitivity. Phys. Rev. B 84, 195204 (2011).
Fiebig, M., Fröhlich, D., Sluyterman v. L., G. & Pisarev, R. V. Domain topography of antiferromagnetic Cr2O3 by second-harmonic generation. Appl. Phys. Lett. 66, 2906–2908 (1995).
Scholl, A. et al. Observation of antiferromagnetic domains in epitaxial thin films. Science 287, 1014–1016 (2000).
Wu, N. et al. Imaging and control of surface magnetization domains in a magnetoelectric antiferromagnet. Phys. Rev. Lett. 106, https://doi.org/10.1103/physrevlett.106.087202 (2011).
Cheong, S. W., Fiebig, M., Wu, W., Chapon, L. & Kiryukhin, V. Seeing is believing: visualization of antiferromagnetic domains. npj Quantum Mater. 5, https://doi.org/10.1038/s41535-019-0204-x (2020).
Nogués, J., Moran, T. J., Lederman, D., Schuller, I. K. & Rao, K. V. Role of interfacial structure on exchange-biased FeF2-Fe. Phys. Rev. B 59, 6984–6993 (1999).
Fiebig, M. Nichtlineare spektroskopie und topografie an antiferromagnetischen domänen. PhD Thesis (1996).
He, X. et al. Robust isothermal electric control of exchange bias at room temperature. Nat. Mater. 9, 579–585 (2010).
Wiesendanger, R. Spin mapping at the nanoscale and atomic scale. Rev. Mod. Phys. 81, 1495–1550 (2009).
Gardner, B. W. et al. Scanning superconducting quantum interference device susceptometry. Rev. Sci. Instr. 72, 2361 (2001).
Low, D. et al. Scanning squid microscopy in a cryogen-free dilution refrigerator. Rev. Sci. Instr. 92, 083704 (2021).
Gould, M. et al. Room-temperature detection of a single 19 nm super-paramagnetic nanoparticle with an imaging magnetometer. Appl. Phys. Lett. 105, 072406 (2014).
Fescenko, I. et al. Diamond magnetic microscopy of malarial hemozoin nanocrystals. Phys. Rev. Appl. 11, 034029 (2019).
Lide, D. R. (ed.) CRC Handbook of Chemistry and Physics, 84th edn. J. Am. Chem. Soc. 126, 1586–1586 https://doi.org/10.1021/ja0336372 (2004).
Macfarlane, W. A. et al. Finite-size effects in the nuclear magnetic resonance of epitaxial palladium thin films. Phys. Rev. B 88, 144424 (2013).
Jamieson, H. C. & Manchester, F. D. The magnetic susceptibility of Pd, PdH and PdD between 4 and 300 K. J. Phys. F: Met. Phys. 2, 323–336 (1972).
Tetienne, J. P. et al. The nature of domain walls in ultrathin ferromagnets revealed by scanning nanomagnetometry. Nat. Commun. 6, 6733 (2015).
Dovzhenko, Y. et al. Magnetostatic twists in room-temperature skyrmions explored by nitrogen-vacancy center spin texture reconstruction. Nat. Commun. 9, 2712 (2018).
Velez, S. et al. Current-driven dynamics and ratchet effect of skyrmion bubbles in a ferrimagnetic insulator. Nat. Nanotechnol., in press (2022).
Dolde, F. et al. Electric-field sensing using single diamond spins. Nat. Phys. 7, 459–463 (2011).
Barson, M. S. J. et al. Nanoscale vector electric field imaging using a single electron spin. Nano Lett. 21, 2962–2967 (2021).
Bian, K. et al. Nanoscale electric-field imaging based on a quantum sensor and its charge-state control under ambient condition. Nat. Commun. 12, 2457 (2021).
Oberg, L. et al. Solution to electric field screening in diamond quantum electrometers. Phys. Rev. Appl. 14, 014085 (2020).
Schirhagl, R., Chang, K., Loretz, M. & Degen, C. L. Nitrogen-vacancy centers in diamond: nanoscale sensors for physics and biology. Annu. Rev. Phys. Chem. 65, 83 (2014).
Beardsley, I. A. Reconstruction of the magnetization in a thin film by a combination of Lorentz microscopy and external field measurements. IEEE Trans. Magn. 25, 671 (1989).
Acknowledgements
The authors thank P. Scheidegger, S. Diesch, S. Ernst, K. Herb, and M.S. Wörnle for fruitful discussions, J. Rhensius for help with the Pd and Bi micro-disc fabrication, and for the scanning electron micrograph in Fig. 1c, M. Giraldo and M. Fiebig for providing the Cr2O3 samples, P. Gambardella for helpful comments on the manuscript, and the staff of the FIRST lab cleanroom facility for technical support. This work was supported by the European Research Council through ERC CoG 817720 (IMAGINE), Swiss National Science Foundation (SNSF) Project Grant No. 200020_175600, the National Center of Competence in Research in Quantum Science and Technology (NCCR QSIT), and the Advancing Science and TEchnology thRough dIamond Quantum Sensing (ASTERIQS) program, Grant no. 820394, of the European Commission. M.T. acknowledges the Swiss National Science Foundation under Project no. 200021-188414.
Author information
Authors and Affiliations
Contributions
C.L.D., W.S.H., and M.L.P. conceived the idea and developed the theory. W.S.H., M.L.D., and M.L.P. implemented the scanning gradiometry technique, carried out the magnetometry experiments, and performed the data analysis. P.W. provided technical support with the magnetometry experiments. M.T. performed the atomic force microscopy of the unpolished Cr2O3 crystal. M.L.P. prepared the bilayer graphene sample. C.-H.L. prepared the Pd and Bi micro-discs. C.L.D. supervised the work. W.S.H. and C.L.D. wrote the manuscript. All authors discussed the results.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Huxter, W.S., Palm, M.L., Davis, M.L. et al. Scanning gradiometry with a single spin quantum magnetometer. Nat Commun 13, 3761 (2022). https://doi.org/10.1038/s41467-022-31454-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-31454-6
This article is cited by
-
Harnessing graph state resources for robust quantum magnetometry under noise
Scientific Reports (2024)
-
Quantum sensing of magnetic fields with molecular spins
npj Quantum Information (2024)
-
Imaging ferroelectric domains with a single-spin scanning quantum sensor
Nature Physics (2023)
-
Perspective: nanoscale electric sensing and imaging based on quantum sensors
Quantum Frontiers (2023)
-
Nanoscale electric field imaging with an ambient scanning quantum sensor microscope
npj Quantum Information (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.