Abstract
One of the open challenges of spintronics is to control the spin relaxation mechanisms. Layered metal-halide perovskites are an emerging class of semiconductors which possess a soft crystal lattice that strongly couples electronic and vibrational states and show promise for spintronic applications. Here, we investigate the impact of such strong coupling on the spin relaxation of excitons in the layered perovskite BA2FAPbI7 using a combination of cryogenic Faraday rotation and transient absorption spectroscopy. We report an unexpected increase of the spin lifetime by two orders of magnitude at 77 K under photoexcitation with photon energy in excess of the exciton absorption peak, and thus demonstrate optical control over the dominant spin relaxation mechanism. We attribute this control to strong coupling between excitons and optically excited phonons, which form polaronic states with reduced electron-hole wave function overlap that protect the exciton spin memory. Our insights highlight the special role of exciton-lattice interactions on the spin physics in the layered perovskites and provide a novel opportunity for optical spin control.
Similar content being viewed by others
Introduction
Materials for spintronics devices, which aim to utilise the spin degree of freedom for data storage and processing, require both efficient spin injection and long spin lifetimes1,2,3,4,5. However, traditionally, these two requirements are associated with quite different material properties. On the one hand, strong spin–orbit coupling (SOC) enables efficient spin-charge conversion6, while on the other hand, it typically increases the rate of spin relaxation7,8. Therefore, suppressing spin depolarisation in the presence of strong SOC is an ongoing challenge for semiconductor spintronics9 that could be addressed by metal halide perovskites10,11,12,13.
In contrast to conventional semiconductors, metal halide perovskites exhibit strong coupling between the electronic and vibrational degrees of freedom14,15. Studies have shown that dynamic strain fields arise in response to photoexcitation16, and that the low mean free path of phonons implies highly localised lattice vibrations17. Within the layered metal-halide perovskites, the term ‘exciton–polaron’ has been introduced to describe the coupling between excitons and lattice vibrations18,19,20,21, while further studies have indicated the formation of polaron states22 which are not well described by the Fröhlich Hamiltonian23 and may require a significantly more complex theoretical treatment24. For simplicity, in this paper, we refer to the former simply as excitons and the latter as polaronic states.
Layered metal-halide perovskites are quasi-2D self-assembled quantum wells of the form A2Bn-1PbI3n+1, where n is the number of lead-iodide unit cells between the organic spacer cations (A). These lead-iodide cages define the electronic orbitals and give rise to strong SOC25, which is typically utilised for spin-to-charge conversion within spintronic devices6. Reducing n, i.e. reducing the quantum-well width, has been shown to increase exciton–phonon coupling26,27. On the other hand, the small polar cations (B) are expected to increase the exciton–phonon coupling strength28, to couple their dipole moment to that of the excitons29, and to induce a localised dynamic disorder at elevated thermal energies when its rotational barrier is overcome17. These considerations suggest that exciton–phonon coupling may be strongest for bilayer (n = 2) perovskites—the narrowest wells containing intralayer cations.
While exciton–lattice coupling has received significant interest in these materials14,15,18,19,20,21,30,31, it remains an open question how it will impact the spin dynamics. Interestingly, it has been calculated that polaron formation in the presence of strong SOC and broken inversion symmetry32 significantly affects spin relaxation and transport efficiency33. Yet, while previous studies of spin relaxation within 2D perovskites11,34,35,36,37 have reported dependence on layer number32, excitation density38 and chemical composition39, the impact of strong exciton–phonon coupling on spin depolarisation is still unexplored.
Here, we employ a set of ultrafast optical spectroscopies from ambient to cryogenic temperatures and report that optical excitation with excess photon energy increases the cryogenic spin lifetime by two orders of magnitude due to a change in the dominant spin-relaxation mechanism. Using time-resolved Faraday rotation (FR) and transient absorption (TA) spectroscopy we propose that the ultrafast formation of polaronic states is the underlying mechanism that protects spin by reducing the rate of spin precession. Our results demonstrate that the strong electron-phonon coupling in 2D perovskites sets them apart as a unique material system in which the dominant spin-relaxation mechanism can be optically selected and a novel regime of polaronic spin dynamics can be studied. This unexpected ability to encode the photoexcitation energy into the spin lifetime can be a promising tool for future spintronic–photonic devices.
Results
Excitation-energy dependence of the spin lifetime
Polycrystalline films of the 2D-layered hybrid perovskite BA2FAPbI7, (BA = butylammonium, FA = formamidinium, Pb=lead, I = iodide), whose structure is sketched in Fig. 1a, are prepared by spin coating (see 'Methods') and optical measurements are then performed on multiple films to ensure consistency. Steady-state absorption and photoluminescence (PL) spectra are taken at room temperature and show a clear excitonic transition with no discernible contribution from 2D perovskites of n ≠ 2 (Fig. 1b and Supplementary Fig. 1).
a Sketch of the 2D perovskite BA2FAPbI7 structure and of lattice deformation associated with polaronic states. b Absorption (yellow line), and photoluminescence spectra (black line) of BA2FAPbI7 at 77 K. Spectra of the pump pulses used in TA and FR measurements are shown as red and blue shaded lines, respectively. c Experimental setup for FR measurements using a balanced photodetector (BPD). Probe photon energy is set to 1.91 eV, below the material absorption onset. d Temperature-dependent FR dynamics (spin polarisation as a function of time) following excitation with 2.17 eV and 2.43 eV pump photon energies at 77 K (solid lines) and at room temperature (dashed lines). All measurements had an exciton density smaller than 5 × 1016 cm–3 (see Supplementary Fig. S2). Lowering the temperature under 2.17 eV excitation decreases the spin lifetime, while under 2.43 eV excitation it leads to an increase.
We perform FR measurements, which track the decay of exciton spin polarisation, using pulses of 40 meV full-width-half-maximum bandwidth and 0.1 ps duration (Fig. 1b, c). Optical excitation using circularly polarised light generates excitonic states with polarised total angular momentum | ±1〉38. These states then depolarise via lattice and exciton interactions, with only the former being relevant at the low exciton densities corresponding to natural sunlight illumination levels. Therefore, we perform all measurements at low fluences (exciton density around 1016 cm–3) for which many body interactions do not play a significant role (see fluence-dependent data reported in Supplementary Fig. 2).
Motional narrowing type spin depolarisation, due to the exchange driven Maialle-Silva-Sham (MSS)40 or to the D’yakonov-Perel (DP)41 mechanism, has been reported within BA2FAPbI7 for moderate carrier densities following photoexcitation that is resonant with the lowest energy exciton34. In this regime, spin dephasing occurs due to precession around an effective magnetic field. As phonon scattering leads to random changes in the direction of the spin–orbit interaction, increased phonon scattering averages out spin dephasing and yields a longer spin lifetime42. To our knowledge, the spin dynamics that follow photoexcitation with excess energies beyond 50 meV have never been investigated, presumably because it is known that under low fluences excess energy is quickly dissipated through carrier-phonon scattering43,44,45. However, precisely because spin dephasing mechanisms are linked to phonons, the question of whether photoexcitation with excess energy leads to new lattice distortions that influence spin lifetimes is an intriguing one.
Figure 1d shows time-resolved FR of BA2FAPbI7 at room temperature (dashed lines) and at 77 K (solid lines) after photoexcitation either in resonance with the exciton (2.17 eV, red lines) or with excess energy (2.43 eV, blue lines). At room temperature, we observe bi-exponential depolarisation in both cases which is dominated by the long τ2 component of ~3 ps, with little dependence on pump photon energy. At 77 K, on the other hand, a striking difference is observed: excitation with 2.17 eV photons leads to a rapid spin decay with a monoexponential lifetime of ~0.3 ps, while excitation with 2.43 eV photons leads to a spin lifetime that is two orders of magnitude longer (~40 ps). This greater than 100-fold increase cannot be explained by increased phonon scattering within the motional narrowing regime, since the spin lifetime is significantly shorter at room temperature under the same 2.43 eV excitation. Therefore, we need to perform a more detailed investigation of the impact of phonons on spin relaxation.
Analysis of dominant spin-relaxation mechanisms
To isolate the effects of phonon scattering on the spin-relaxation dynamics, we perform temperature-dependent measurements. Figure 2a shows the FR at different temperatures following 2.17 eV excitation and reveals that the spin polarisation lifetime increases with temperature. Figure 2b shows the results of bi-exponential fits to this data and confirms that the spin relaxation is dominated by a motional narrowing contribution that leads to a short spin polarisation lifetime, τ1, when the phonons are frozen out.
a FR under 2.17 eV excitation and exciton density <3 × 1016 cm−3 (points) and fits to the bi-exponential decays (solid lines). b Time constants, τ1 and τ2, obtained from a fit to (a) with symbol transparency scaled to their relative amplitudes, and the full-width-half-maximum of the PL lineshape, ΓPL, plotted as a function of temperature (Supplementary Fig. 3). τ2 is scaled by 1/20 to plot it on the same scale. c FR with excitation energy of 2.43 eV and exciton density <0.67 × 1016 cm−3 (points) and fits to the tri-exponential decays (solid lines). d Time constants obtained from a fit to (c) with transparency scaled to amplitude (~33% amplitude of each component for all temperatures). Grey boxes in panels b and d indicate a new crystalline phase following a phase transition at 240 K (Supplementary Fig. S4).
Within a motional narrowing regime, an increase in the temperature can lead to both a higher momentum scattering rate, Γ and a faster spin precession, Ω(K), around an effective magnetic field if there is a non-zero average centre of mass wavevector (Supplementary Note 1). The temperature dependence of these two contributions determines the temperature dependence of the total spin-polarisation lifetime:
To determine the temperature dependence of Γ, we measure PL spectrum under 2.17 eV excitation as a function of temperature (Supplementary Fig. 3) and use the PL linewidth, ΓPL, to obtain Γ ∝ ΓPL (Supplementary Eq. (S11)). We find that both τ1 and ΓPL follow the same power-law dependence of τ1 ∝ ΓPL∝ T5/2 below 240 K (blue dots and black squares in Fig. 2b). This temperature dependence is consistent with that reported for 3D bulk perovskites46. Beyond 240 K (grey regions of Fig. 2b, d), the material undergoes a phase transition which may be linked to an order−disorder phase transition47 as seen in BA2PbI (Supplementary Fig. 4) that leads to a deviation from this power law. Such a linear proportionality between spin lifetime and the momentum scattering rate (Supplementary Fig. 5) suggests from Eq. (1) that the precession term, Ω(K), is nearly temperature-independent. This result is consistent with previous studies which have shown cooling through a vibrational manifold of distinct exciton states23,30,48,49, and have suggested a narrow spread of K-values such that that high-K excitons are unlikely to exist45. Interconversion within this manifold allows the average exciton energy to increase without a corresponding increase in exciton momentum. Alternatively, the temperature independence of Ω(K) can be explained by a zero average centre of mass wavevector.
We now consider the second contribution to the bi-exponential fit in Fig. 2a, which reveals a longer spin lifetime, τ2, that— contrary to τ1—decreases with increasing temperature. The amplitude of τ2 is zero below 180 K, Fig. 2b, but shows a greater contribution towards higher temperatures, indicating the onset of a new spin-relaxation mechanism as thermal phonons increase in number.
To investigate this new mechanism, we introduce optically excited phonons by repeating the FR temperature series with a photoexcitation energy of 2.43 eV. The spin polarisation now persists beyond 200 ps, with a lifetime that, again, decreases with increasing temperature, Fig. 2c. This agrees with the previous observation that there exist states, formed in the presence of phonons, for which phonon scattering instead induces depolarisation. We find that the kinetics require a tri-exponential fit to describe the decay, Fig. 2d. As hot-carrier relaxation takes place on ~0.4 ps timescales at low carrier densities43,44,45, the fast spin relaxation observed in Fig. 2a, b is expected to persist to some degree. Therefore, we constrain the first component of the triexponential fit to the same τ1 values found under 2.17 eV excitation and find that it accounts for about one-third of the amplitude at all temperatures. The third component τ3, yields a temperature-independent value of 2.9 ± 0.4 ps, which is consistent with the room-temperature spin lifetime, and could be attributed to some local heating of the lattice. Importantly, the second component, τ2, yields an inverse temperature dependence, with ~60 ps lifetime at 77 K, which cannot be explained by motional narrowing. A similar temperature dependence (although independent of pump energy) is observed for 3D perovskite structures50, with a spin-relaxation time of ~40 ps and τs ∝ T−3/2. We find excellent agreement with this dependence and note that, like in bulk perovskites50, this deviates from the τs ∝ T−7/2 expected by the Elliott–Yafet (EY) spin-relaxation mechanism (Supplementary Note 1).
Thus, we conclude that photoexcitation of BA2FAPbI7 with excess energy (Supplementary Fig. S6) generates new electronic states which are less susceptible to fast motional narrowing spin relaxation. Consequently, the dominant spin-relaxation mechanism changes to one which resembles that of the 3D perovskites50, and remains to be determined.
Coherent exciton–phonon coupling and polaron formation
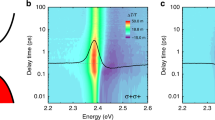
To examine the strong exciton–phonon coupling under excess excitation energy and the possible formation of polaronic states in BA2FAPbI7, we perform TA measurements. Figure 3a, b shows the TA maps at 77 K following photoexcitation at 2.17 eV and 2.43 eV, respectively. These maps are dominated by a positive ΔT/T bleach signal at 2.14 eV (red). When excess energy is provided by the excitation pulses (Fig. 3b), the positive ΔT/T peak is initially blue shifted and undergoes a rapid red shift over hot exciton cooling timescales of ~0.4 ps. Thus, we attribute it to hot-exciton cooling and the concomitant emission of phonons.
For both photoexcitation energies, we observe oscillations in the TA signal, with opposite phases on either side of the main photobleach peak (at 2.15 eV and 2.18 eV, see Supplementary Fig. 6). To extract the oscillatory component, we select the probe energy at which the oscillation amplitude is maximum and fit that trace using a combination of exponential and oscillatory components (see Supplementary Note 2 for details). The non-oscillatory components are subtracted from the raw data and the residual is shown in Fig. 3c, d for excitation energies of 2.17 and 2.43 eV, respectively. Similar oscillations were reported for a 2D perovskite variant in ref. 18 who attributed the effect to resonant impulsive stimulated Raman scattering (RISRS). We observe a cosine modulation of the TA signal which is consistent with both RISRS and displacive excitation of coherent phonons (DECP)51,52. DECP occurs when the equilibrium position of the ions experiences a sudden shift as they couple to the photoexcited charge distribution and gives rise to oscillations as the ions find their new minima52. Similar effects have been reported in the 3D perovskites53. This observation implies that photoexcitation drives crystalline distortion and indicates the presence of polaronic effects between the exciton and lattice. Interestingly, this implies that hot excitons can be generated by photoexcitation of vibronic sub-levels without increasing K, consistent with our observations and discussion of the motional narrowing spin relaxation, which implied either that high K excitons do not exist for the linear relationship that is observed between scattering rate and spin lifetime, or that there is no net transport.
The oscillations occur with a wavenumber of 53 cm−1 for both excitation energies (Supplementary Fig. 7), which is sufficiently low to fall within the bandwidth of the excitation pulses, and is similar in wavenumber to that reported for BA2PbI447. As such, the differences in spin lifetime when BA2FAPbI7 is optically excited with and without excess energy cannot be explained purely from these impulsively generated cage distortions. Correspondingly, this leaves phonons emitted during hot-exciton cooling and the delocalisation of hot-exciton wave functions as likely drivers that change the dominant spin-relaxation mechanism, from motional narrowing to one which resembles that observed in 3D bulk perovskites. Notably, these hot-exciton properties can explain the differences in the spin-relaxation dynamics that we observe at room temperature between the two photoexcitation energies, as shown in Fig. 1d. Here, both datasets contain a fast, motional narrowing spin depolarisation of ~0.5 ps. However, the amplitude of this decay is reduced under 2.43 eV photoexcitation when more delocalised hot excitons are formed, which indicates a decrease in the number of states that experience motional narrowing spin depolarisation.
In order to confirm that optical injection of phonons is responsible for the formation of a polaronic state that undergoes a different spin depolarisation mechanism, we perform FR at 77 K for different photoexcitation energies. Figure 4a shows that the spin lifetime τ2 increases as a function of the excess energy provided by the excitation photons. The contribution from the fast motional narrowing component, τ1 also decreases with excess energy. Together, these observations imply the formation of a new electronic state that requires additional energy to form, and which is dominated by a different spin-depolarisation mechanism. The formation of a polaronic state leads to a reduction in electron–hole wave function overlap, a process that relies on the availability of energy to overcome the Coulomb interaction.
We, therefore, propose that the formation of the polaronic state is a continuous that occurs across an activation barrier, a scheme of which is displayed in Fig. 4b. Photoexcitation at 2.17 eV fails to provide any excess energy to form polaronic states, and therefore only the spin-relaxation mechanism of the excitons is observed. By increasing the photoexcitation energy, an exploration of the excited state landscape is enabled, which slows down spin relaxation. The greater the excess energy, the greater the ‘transfer rate’ between exciton and polaronic states, and the greater the contribution from the polaronic population to the spin depolarisation time. In the limit of infinite excess energy, the observed spin depolarisation mechanism would become that of the polaronic states. As τ2 is our observable and as the starting population of excitons shows a 0.2 ps spin lifetime, we lack direct access to the transfer rate between excitons and polaronic states, since we always observe some spin relaxation while the excitons cross the activation barrier. This complicates the use of an Arrhenius plot to extract the activation barrier height, but we can extract an estimate of 18.4 meV, which is consistent with Fig. 2a (Supplementary Fig. 8). Incidentally, this discussion also explains the presence of the third component observed in Fig. 2d. Since spin relaxation is happening simultaneously along the formation of polaronic states, frustrated barrier crossings will lead to significant spin lifetime inhomogeneity with a transfer-rate-weighted-average lifetime between that of the excitons and that of the polaronic states.
Discussion
Consequently, we attribute the new, slow spin depolarisation mechanism to the formation of polaronic states, for which the spatial separation between electron and hole wave functions is increased40,54,55 and lattice symmetry modified. We propose that these changes will decrease the rate of spin precession that is expected within the MSS40 or D’yakonov–Perel mechanisms, respectively, which in turn allows a new depolarisation mechanism to dominate50. While the formation of polaronic states modifies many kinetics by also changing scattering rates, screening of the Frohlich interaction, and broadening the energy distribution, they do not impact the spin relaxation the way observed here (Supplementary Note 3). The requirement of excess excitation energy for the formation of polaronic states to occur can be attributed to the increased exciton delocalisation22 and the corresponding reduction in electron–hole wave function overlap of hot states, which are more similar to the conformation of the polaron state. Specifically, the polaron configuration requires excess energy to overcome the Coulombic electron–hole attraction. Due to the strong dependence of the optical properties on small changes to the organic cations29,31,48,56,57,58, our observations highlight the need for further studies of low-temperature spin depolarisation in the presence of strong exciton–phonon interactions within other layered perovskite variants.
Based on results from time-resolved Faraday rotation and transient absorption spectroscopy we have proposed that the formation of polaronic states radically modifies the dominant spin-relaxation mechanism in the n = 2 metal-halide perovskite BA2FAPbI7. We rationalise the change in dominant spin relaxation mechanism by a decrease in electron–hole wave function overlap55 or change in lattice symmetry which act to reduce the rate of motional narrowing spin precession40,54 that we observe for the exciton state. Consistent with other reports that contend exciton–phonon interactions21, we observe that the optical properties of the exciton transition are strongly coupled to a ≈50 cm−1 phonon mode51, with distinct exciton–lattice coupling9.
Our analysis of spin depolarisation as a function of temperature suggests that thermal energy is sufficient for the formation of polaronic states, which constitute a notable fraction of the photoexcited population at room temperature. Upon cooling to cryogenic temperatures, the proportion of thermally activated polaronic states quickly falls, while their spin lifetime increases. Therefore, by exciting far above the exciton resonance, low-temperature polaronic states with significantly longer spin depolarisation times can be generated. We have shown that the spin polarisation lifetime of these states decreases with increasing temperature, as is observed for free carriers in 3D perovskites. As this mechanism remains unclear, further low-temperature investigations should be performed to determine if there is a link to the rotation of the small intralayer organic cation. It has been shown that this cation gives rise to a dynamic disorder when the thermal rotation barrier is overcome17 and that the rotation time of this cation is inversely dependent on temperature, being very slow at low temperatures and ~3 ps at room temperature59 reminiscent of the spin depolarisation reported here and observed in the 3D perovskites. Recent theoretical calculations19 also suggest that the B-site cation plays a crucial role in polaron formation in 3D perovskites. These results demonstrate that the strong exciton–phonon coupling in 2D perovskites sets them apart as a unique material system which enables optical control over the dominant cryogenic spin-relaxation mechanism by manipulating the formation of polaronic states. Due to their inherent tunability, this material class provides a further means to control exciton and polaron spin transport and interaction mechanisms, which may hold promise for spintronic devices.
Methods
Sample preparation
Polycrystalline films of 2D halide perovskites were fabricated following the general formula of A2Bn−1PbnI 3n+1, where A = butylammonium, B = formamidinium, and n = 2. Lead iodide, butylammonium iodide, and formamidinium iodide are dissolved in dimethylformamide at 0.1 M concentration and ratio of 2:2:1. Glass coverslips were sonicated in first acetone, then isopropanol for 5 min, before 10 min of oxygen plasma etching. The precursor solution was then spin coated at 2000 r.p.m for 60 s, followed by annealing at 100 °C for 60 s inside the nitrogen filled glovebox. All chemicals were procured from Sigma-Aldrich.
Faraday rotation measurements
The transient Faraday rotation experiments were performed using a regenerative amplified Ti:Sapphire system operating at 2 kHz. The pump and probe beams were generated using homemade optical parametric amplifiers (OPA) both with 40 meV full-width-half-maximum bandwidth and 0.1 ps duration. A quarter waveplate immediately before the sample was used to circularly polarise the pump beam, while the probe is linearly polarised. The pump was chopped at 1 kHz, and the probe was detected using a pair of balanced photodiodes placed on a rotation mount after a Wollaston prism pair, such that by rotating the mount the linearly polarised probe can be perfectly split in half between the photodiodes at a negative pump-probe time delay. Finally, a lock-in amplifier was used to detect the difference between the signal at the photodiodes with the pump on and with the pump off, effectively measuring the rotation of the polarisation of the probe induced by the circularly polarised pump.
Transient absorption measurements
Transient absorption measurements are performed using a supercontinuum generated by tight focusing 800 nm pulses into a sapphire plate, and a narrowband pump from an OPA (tuned from 575 to 490 nm with 10 nm FWHM at 575 nm). The material is excited by the pump and the probe is passed through the excited region. The transmitted probe beam is dispersed in a monochromator and detected using a CCD array. The change in transmission, ΔT/T, is calculated as a function of wavelength and pump-probe delay using ΔT/T = (Ton − Toff)/Toff, where Toff and Ton are the transmission signals of the probe when the pump has been blocked or unblocked by an optical chopper. The pump-probe delay is increased up to 1.5 ns using an automated delay stage.
Data availability
The data that support the findings of this study are available on request from the corresponding authors (G.C. and F.D.). Source data are provided with this paper.
Code availability
No special code was developed to fit the experimental data.
References
Karimov, O. Z. et al. High temperature gate control of quantum well spin memory. Phys. Rev. Lett. 91, 246601 (2003).
Hall, K. C., Lau, W. H., Gündoǧdu, K., Flatté, M. E. & Boggess, T. F. Nonmagnetic semiconductor spin transistor. Appl. Phys. Lett. 83, 2937–2939 (2003).
Schliemann, J., Egues, J. C. & Loss, D. Nonballistic spin-field-effect transistor. Phys. Rev. Lett. 90, 4 (2003).
Meier, F. & Zakharchenya, B. P. Optical orientation. in Modern Problems in Condensed Matter Sciences. 536 (Elsevier Amsterdam, 1984).
Awschalom, D., Loss, D. & Samarth, N. Semiconductor Spintronics and Quantum Computation (Nanoscience and Technology) (Springer Berlin Heidelberg, 2002).
Sánchez, J. C. R. et al. Spin-to-charge conversion using Rashba coupling at the interface between non-magnetic materials. Nat. Commun. 4, 2944 (2013).
Manchon, A., Koo, H. C., Nitta, J., Frolov, S. M. & Duine, R. A. New perspectives for Rashba spin-orbit coupling. Nat. Mater. 14, 871–882 (2015).
Han, W., Kawakami, R. K., Gmitra, M. & Fabian, J. Graphene spintronics. Nat. Nanotechnol. 9, 794–807 (2014).
Fabian, J., Matos-Abiague, A., Ertler, C., Stano, P. & Žutić, I. Semiconductor spintronics. Acta Phys. Slov. 57, 565–907 (2007).
Wang, J. et al. Spin-optoelectronic devices based on hybrid organic-inorganic trihalide perovskites. Nat. Commun. 10, 129 (2019).
Lu, H. et al. Spin-dependent charge transport through 2D chiral hybrid lead-iodide perovskites. Sci. Adv. 5, eaay0571 (2019).
Zhang, C. et al. Magnetic field effects in hybrid perovskite devices. Nat. Phys. 11, 427–434 (2015).
Kim, Y. H. et al. Chiral-induced spin selectivity enables a room-temperature spin light-emitting diode. Science 371, 1129–1133 (2021).
Cinquanta, E. et al. Ultrafast THz probe of photoinduced polarons in lead-halide perovskites. Phys. Rev. Lett. 122, 166601 (2019).
Bretschneider, S. A. et al. Quantifying polaron formation and charge carrier cooling in lead-iodide perovskites. Adv. Mater. 30, 1707312 (2018).
Guzelturk, B. et al. Visualization of dynamic polaronic strain fields in hybrid lead halide perovskites. Nat. Mater. 20, 618–623 (2021).
Sharma, R. et al. Elucidating the atomistic origin of anharmonicity in tetragonal CH3NH3PbI3 with Raman scattering. Phys. Rev. Mater. 4(R), 092401 (2020).
Thouin, F. et al. Phonon coherences reveal the polaronic character of excitons in two-dimensional lead halide perovskites. Nat. Mater. 18, 349–356 (2019).
Duan, H. G. et al. Photoinduced vibrations drive ultrafast structural distortion in lead halide perovskite. J. Am. Chem. Soc. 142, 16569–16578 (2020).
Urban, J. M. et al. Revealing excitonic phonon coupling in (PEA)2 (MA)n-1PbnI3n+1 2D layered perovskites. J. Phys. Chem. Lett. 11, 5830–5835 (2020).
Thouin, F. et al. Electron-phonon couplings inherent in polarons drive exciton dynamics in two-dimensional metal-halide perovskites. Chem. Mater. 31, 7085–7091 (2019).
Esmaielpour, H. et al. Role of exciton binding energy on LO phonon broadening and polaron formation in (BA)2PbI4 Ruddlesden-Popper films. J. Phys. Chem. C. 124, 9496–9505 (2020).
Ram, A., Kandada, S. & Silva, C. Exciton polarons in two-dimensional hybrid metal-halide perovskites. J. Phys. Chem. Lett. 11, 3173–3184 (2020).
Hong Sio, W., Verdi, C., Poncé, S. & Giustino, F. Ab initio theory of polarons: formalism and applications. Phys. Rev. B 99, 235139 (2019).
Stoumpos, C. C. et al. Ruddlesden-Popper hybrid lead iodide perovskite 2D homologous semiconductors. Chem. Mater. 28, 2852–2867 (2016).
Long, H. et al. Exciton-phonon interaction in quasi-two dimensional layered (PEA)2(CsPbBr3)n -1PbBr4 perovskite. Nanoscale 11, 21867–21871 (2019).
Wang, S. et al. Temperature-dependent band gap in two-dimensional perovskites: thermal expansion interaction and electron-phonon interaction. J. Phys. Chem. Lett. 10, 2546–2553 (2019).
Zhang, Z., Fang, W. H., Tokina, M. V., Long, R. & Prezhdo, O. V. Rapid decoherence suppresses charge recombination in multi-layer 2D halide perovskites: time-domain ab initio analysis. Nano Lett. 18, 2459–2466 (2018).
Dou, Y., Wang, M., Zhang, J., Xu, H. & Hu, B. Identifying photoinduced dipolar polarization and orbit–orbit interaction between excitons in organic–inorganic hybrid perovskites. Adv. Funct. Mater. 30, 2003476 (2020).
Neutzner, S. et al. Exciton-polaron spectral structures in two-dimensional hybrid lead-halide perovskites. Phys. Rev. Mater. 2, 64605 (2018).
Seitz, M. et al. Exciton diffusion in two-dimensional metal-halide perovskites. Nat. Commun. 11, 2035 (2020).
Chen, X. et al. Impact of layer thickness on the charge carrier and spin coherence lifetime in two-dimensional layered perovskite single crystals. ACS Energy Lett. 3, 2273–2279 (2018).
Covaci, L. & Berciu, M. Polaron formation in the presence of Rashba spin-orbit coupling: Implications for spintronics. Phys. Rev. Lett. 102, 186403 (2009).
Todd, S. B. et al. Detection of Rashba spin splitting in 2D organic-inorganic perovskite via precessional carrier spin relaxation. APL Mater. 7, 081116 (2019).
Giovanni, D. et al. Coherent spin and quasiparticle dynamics in solution-processed layered 2D lead halide perovskites. Adv. Sci. 5, 1800664 (2018).
Zhai, Y. et al. Giant Rashba splitting in 2D organic-inorganic halide perovskites measured by transient spectroscopies. Sci. Adv. 3, e1700704 (2017).
Tao, W., Zhou, Q. & Zhu, H. Dynamic polaronic screening for anomalous exciton spin relaxation in two-dimensional lead halide perovskites. Sci. Adv. 6, eabb7132 (2020).
Bourelle, S. A. et al. How exciton interactions control spin-depolarization in layered hybrid perovskites. Nano Lett. 20, 5678–5685 (2020).
Long, G. et al. Spin control in reduced-dimensional chiral perovskites. Nat. Photonics 12, 528–533 (2018).
Maialle, M. Z., De Andrada, E., Silva, E. A. & Sham, L. J. Exciton spin dynamics in quantum wells. Phys. Rev. B 47, 15776–15788 (1993).
D’Yakonov, M. & Perel’, V. Spin orientation of electrons associated with the interband absorption of light in semiconductors. Sov. J. Exp. Theor. Phys. 33, 1053 (1971).
Žutić, I., Fabian, J. & Das Sarma, S. Spintronics: fundamentals and applications. Rev. Mod. Phys. 76, 323–410 (2004).
Abdel-Baki, K. et al. Exciton dynamics and non-linearities in two-dimensional hybrid organic perovskites. J. Appl. Phys. 119, 064301 (2016).
Yin, J. et al. Tuning hot carrier cooling dynamics by dielectric confinement in two-dimensional hybrid perovskite crystals. ACS Nano 13, 12621–12629 (2019).
Burgos-Caminal, A., Socie, E., Bouduban, M. E. F. & Moser, J.-E. Exciton and carrier dynamics in two-dimensional perovskites. J. Phys. Chem. Lett. 11, 7692–7701 (2020).
Wright, A. D. et al. Electron-phonon coupling in hybrid lead halide perovskites. Nat. Commun. 7, 11755 (2016).
Menahem, M. et al. Strongly anharmonic octahedral tilting in two-dimensional hybrid halide perovskites. ACS Nano 15, 10153–10162 (2021).
Straus, D. B. et al. Tailoring hot exciton dynamics in 2D hybrid perovskites through cation modification. ACS Nano 14, 3621–3629 (2020).
Straus, D. B. et al. Direct observation of electron-phonon coupling and slow vibrational relaxation in organic-inorganic hybrid perovskites. J. Am. Chem. Soc. 138, 13798–13801 (2016).
Odenthal, P. et al. Spin-polarized exciton quantum beating in hybrid organic-inorganic perovskites. Nat. Phys. 13, 894–899 (2017).
Merlin, R. Generating coherent THz phonons with light pulses. Solid State Commun. 102, 207–220 (1997).
Melnikov, A. A., Misochko, O. V. & Chekalin, S. V. Generation of coherent phonons in bismuth by ultrashort laser pulses in the visible and NIR: displacive versus impulsive excitation mechanism. Phys. Lett. A 375, 2017–2022 (2011).
Batignani, G. et al. Probing femtosecond lattice displacement upon photo-carrier generation in lead halide perovskite. Nat. Commun. 9, 1971 (2018).
He, J., Zhong, H. & Scholes, G. D. Electron-hole overlap dictates the hole spin relaxation rate in nanocrystal heterostructures. Phys. Rev. Lett. 105, 046601 (2010).
Ambrosio, F., Wiktor, J., De Angelis, F. & Pasquarello, A. Origin of low electron-hole recombination rate in metal halide perovskites. Energy Environ. Sci. 11, 101–105 (2018).
Ferreira, A. C. et al. Elastic softness of hybrid lead halide perovskites. Phys. Rev. Lett. 121, 085502 (2018).
Ni, L. et al. Real-time observation of exciton−phonon coupling dynamics in self-assembled hybrid perovskite quantum wells. ACS Nano 11, 10834–10843 (2017).
Fu, J. et al. Electronic states modulation by coherent optical phonons in 2D halide perovskites. Adv. Mater. 33, 2006233 (2021).
Bakulin, A. A. et al. Real-time observation of organic cation reorientation in methylammonium lead iodide perovskites. J. Phys. Chem. Lett. 6, 3663–3669 (2015).
Acknowledgements
S.A.B. acknowledges the support from the EPSRC Centre for Doctoral Training in Graphene Technology (EP/L016087/1). S.G. and G.C. acknowledge the Marie Curie actions (project H2020‐ MSCA‐IF‐2018-841356). T.W. and F.D. acknowledge funding from an EPSRC NI grant (EP/R044481/1). T.W. received funding from the European Union’s Horizon 2020 research and innovation programme under Marie Skłodowska-Curie grant agreement no. 838772 (LADIE). F.D. acknowledges a Winton Advanced Research Fellowship and funding from the DFG Emmy Noether Program. T.W.J.G. acknowledges funding from the Schiff Scholarship and support from the EPSRC Cambridge NanoDTC, EP/L015978/1. R.S. acknowledge funding and support from the SUNRISE project (EP/P032591/1) and Newton International Fellowship from The Royal Society. G.C. acknowledges support from the European Union Horizon 2020 Programme under Grant Agreement 881603 Graphene Core 3.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
S.A.B., F.C., S.G., G.C. and F.D. planned the experiments that were carried out by S.A.B., F.C., S.G., T.N. and T.W.J.G. Samples prepared by T.N. and R.S. F.D., T.W. and G.C. supervised the project. S.A.B., F.C. and S.G. performed data analysis. S.A.B. and F.C. wrote the manuscript with feedback from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bourelle, S.A., Camargo, F.V.A., Ghosh, S. et al. Optical control of exciton spin dynamics in layered metal halide perovskites via polaronic state formation. Nat Commun 13, 3320 (2022). https://doi.org/10.1038/s41467-022-30953-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-30953-w
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.