Abstract
Fe-bearing MgO [(Mg1−xFex)O] is considered a major constituent of terrestrial exoplanets. Crystallizing in the B1 structure in the Earth’s lower mantle, (Mg1−xFex)O undergoes a high-spin (S = 2) to low-spin (S = 0) transition at ∼45 GPa, accompanied by anomalous changes of this mineral’s physical properties, while the intermediate-spin (S = 1) state has not been observed. In this work, we investigate (Mg1−xFex)O (x ≤ 0.25) up to 1.8 TPa via first-principles calculations. Our calculations indicate that (Mg1−xFex)O undergoes a simultaneous structural and spin transition at ∼0.6 TPa, from the B1 phase low-spin state to the B2 phase intermediate-spin state, with Fe’s total electron spin S re-emerging from 0 to 1 at ultrahigh pressure. Upon further compression, an intermediate-to-low spin transition occurs in the B2 phase. Depending on the Fe concentration (x), metal–insulator transition and rhombohedral distortions can also occur in the B2 phase. These results suggest that Fe and spin transition may affect planetary interiors over a vast pressure range.
Similar content being viewed by others
Introduction
Fe-bearing MgO with the B1 (NaCl-type) structure, also known as ferropericlase (Mg1−xFex)O (0.1 < x < 0.2), is the second most abundant mineral in the Earth’s lower mantle (depth 660–2890 km, pressure range 23–135 GPa), constituting ~20 vol% of this region. Experiments and first-principles calculations have shown that B1 MgO remains stable up to ~0.5 TPa and transforms into the B2 (CsCl-type) structure upon further compression1,2,3,4,5,6,7,8,9,10,11,12,13,14. First-principles calculations have also predicted that B2 MgO remains dynamically stable up to at least ~4 TPa12,15,16. MgO has thus been considered a major constituent of terrestrial super-Earths (exoplanets with up to ~10 times of the Earth’s mass), where the interior pressure can reach to the tera-Pascal regime17,18.
With the abundance of Fe in the Earth interior, B1 MgO in the Earth’s lower mantle contains 10–20 mol% of Fe. Likewise, in terrestrial super-Earths, MgO is expected to contain considerable amount of Fe. With the incorporation of Fe, physical properties of the host mineral can be drastically changed. For example, in B1 (Mg1−xFex)O, Fe undergoes a pressure-induced spin transition (also referred to as spin crossover) from the high-spin (HS, S = 2) to the low-spin (LS, S = 0) state at ~45 GPa19,20,21; the intermediate-spin (IS, S = 1) state has never been observed in experiments and has been ruled out by first-principles calculations22. The HS–LS transition of B1 (Mg1−xFex)O is accompanied by anomalous changes of the structural, electronic, optical, magnetic, elastic, thermodynamic, and transport properties of this mineral23,24,25,26,27,28,29,30,31,32,33,34,35,36; it has also been suggested to change the iron diffusion and iron partitioning21,23,37,38,39, to control the structure of the large low velocity provinces40, and to generate the anti-correlation between bulk sound and shear velocities in the Earth’s lower mantle41. Recently, seismological expression of the spin transition of B1 (Mg1−xFex)O has also been reported42. Despite extensive studies on B1 (Mg1−xFex)O, B2 MgO, and the end member FeO (crystallizing in the B1 structure at pressure P ≲ 25 GPa, undergoing complicated structural transitions upon compression43,44,45,46, and stabilizing in the B2 structure at P ≳ 250 GPa47,48), effects of Fe and spin transition on the properties of B2 MgO and the B1–B2 transition remain unclear, especially for low Fe concentration (x ≤ 0.25) relevant to planetary interiors.
In this work, we study (Mg1−xFex)O at ultrahigh pressure using the local density approximation + self-consistent Hubbard U (LDA+Usc) method, with the Hubbard U parameters computed self-consistently. So far, LDA+Usc has been applied to various Fe-bearing minerals of geophysical and/or geochemical importance, including B1 (Mg1−xFex)O, Fe-bearing MgSiO3 perovskite (bridgmanite) and post-perovskite, ferromagnesite (Mg1−xFex)CO3, and the new hexagonal aluminous (NAL) phase22,49,50,51,52,53,54,55. Throughout these works, we have shown that spin-transition pressure determined by LDA+Usc is typically within 5–10 GPa around the experimental results, and the volume/elastic anomalies obtained by LDA+Usc are also in great agreement with experiments. With such accuracy, LDA+Usc has been established as a reliable approach to study Fe-bearing minerals at high pressure and is therefore adopted in this work. Further details of the computation and modeling are described in the Methods Section and Supplementary Information. To investigate the effects of Fe concentration, we perform calculations on (Mg1−xFex)O with x = 0.125 and 0.25 using 16 and 8-atom supercells, respectively (Fig. 1). For B2 IS (Mg0.75Fe0.25)O, we find ferromagnetic (FM) order more energetically favorable than antiferromagnetic (AFM) order; we therefore present the FM results in this paper.
Results and discussion
Self-consistent Hubbard U parameters
Within LDA+Usc, both the IS and LS states of B2 (Mg1−xFex)O can be obtained at ultrahigh pressure, while the HS state can only be obtained at P ≲ 0.29 TPa. The Hubbard Usc of Fe in (Mg0.875Fe0.125)O at various volume/pressure are shown in Fig. 2. Note that B2 (Mg0.875Fe0.125)O is stabilized via rhombohedral distortion (as further discussed in Figs. 3 and 4), hence referred to as rB2 hereafter. At ultrahigh pressure (0.5 < P < 1.8 TPa), as shown in Fig. 2b, Usc is mainly affected by pressure (increasing with P by ~2.5 eV) and marginally affected by the Fe spin state and crystal structure (by ~0.5 eV). In contrast, at P < 0.15 TPa, Fe spin/valence state affects Usc by up to ~2 eV, while pressure affects Usc by up to ~0.5 eV22,49,50,51,52,53,54.
Here, the intermediate-spin (IS, a–e) and low-spin (LS, f–j) states at volume V = 55.310 Å3/cell (6.914 Å3/f.u., pressure P ≈ 1.07 TPa) are shown. a, f FeO8 cubes in the supercell, with the Fe-O bond lengths (in Å) indicated by the numbers next to the oxygen atoms, and the lattice parameters (a and α) listed below; b, g phonon dispersion; c, h orbital occupation; d, i integrated local density of states (ILDOS) of the filled and empty t2g states; e, j total and projected DOS, with the Fermi energy set as the reference (0 eV). In panels a, d, f, and i, the [111] direction is pointing upward.
Here, the intermediate-spin (IS, a–e) and low-spin (LS, f–j) states at volume V = 55.310 Å3/cell (6.914 Å3/f.u., pressure P ≈ 1.07 TPa) are shown. a, f FeO8 dodecahedra in the supercell, with the Fe-O bond lengths (in Å) indicated by the numbers next to the oxygen atoms, and the lattice parameters (a and α) listed below; b, g phonon dispersion; c, h orbital occupation; d, i integrated local density of states (ILDOS) of the \(e^{\prime}\) and a1g bands; e, j total and projected DOS, with the Fermi level set as the reference (0 eV). In panels a, d, f, and (i), the [111] direction is pointing upward.
Soft phonons in cubic B2 (Mg0.875Fe0.125)O
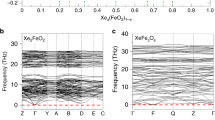
Fe spin states in B1 and B2 (Mg1−xFex)O exhibit distinct properties, due to the host minerals’ distinct crystal structures. In the B1 phase, Fe substitutes Mg in the 6-coordinate octahedral site (Fig. 1a, d), forming FeO6 octahedra (Supplementary Fig. 1a and Note 1). In FeO6 octahedra, the t2g orbitals have lower energy than the eg orbitals; the orbital configurations of HS and LS Fe2+ are \({t}_{2g}^{4}{e}_{g}^{2}\) and \({t}_{2g}^{6}{e}_{g}^{0}\), respectively (Supplementary Fig. 1b and Note 1). In the B2 phase, Fe substitutes Mg in the 8-coordinate site (Fig. 1b, e), forming FeO8 polyhedra (Fig. 1c, f). For cubic B2 (Mg1−xFex)O with x = 0.125, after structural optimization, FeO8 polyhedra remain cubic (Oh symmetry), with all eight Fe-O bonds in the same length. Expectedly, the Fe-O bonds of the IS state are slightly longer than those of the LS state (Fig. 3a, f). Remarkably, cubic B2 (Mg0.875Fe0.125)O is dynamically unstable, regardless of the Fe spin state, as indicated by the soft phonon modes (negative phonon frequencies) shown in Fig. 3b, g. Nevertheless, the electronic structure of cubic B2 (Mg0.875Fe0.125)O still provides valuable insights. In FeO8 cubes, the t2g orbitals have higher energy than the eg orbitals, and the orbital configurations of IS and LS Fe2+ are both \({e}_{g}^{4}{t}_{2g}^{2}\) (Fig. 3c, h). For the IS state, the eg orbitals are fully occupied, while the t2g orbitals are partially occupied by two spin-up electrons (Fig. 3c). A partially filled t2g band in the spin-up channel is thus formed, spanning across the Fermi energy (set as the reference, 0 eV) from −1.7 to 1.3 eV, as indicated by the density of states (DOS) shown in Fig. 3e. The t2g characteristic of the t2g band can be visualized via the integrated local density of states (ILDOS) over the energy intervals −1.7 < E < 0 and 0 < E < 1.3 eV for the filled and empty t2g states, respectively (Fig. 3d). For the LS state, the t2g orbitals are partially occupied by one spin-up and one spin-down electron (Fig. 3h), forming a partially filled t2g band in the interval of −1.2 < E < 1.6 eV (Fig. 3j). The ILDOS of the filled and empty t2g states (Fig. 3i) resemble those of the IS state (Fig. 3d). For both spin states, the completely filled eg bands are embedded in the oxygen band spanning over −20 ≲ E ≲ −4 eV (Fig. 3e, j). Evidently, the partially filled t2g band and thus the metallicity of cubic B2 (Mg0.875Fe0.125)O are the direct consequences of the cubic symmetry.
Rhombohedrally distorted rB2 (Mg0.875Fe0.125)O
Depending on the Fe spin state, dynamically unstable cubic B2 (Mg0.875Fe0.125)O is stabilized via rhombohedral compression or elongation. As shown in Fig. 4a/f, the IS/LS state is rhombohedrally compressed/elongated, with shortened/stretched Fe–O bonds along the [111] direction and rhombohedral angle α larger/smaller than 90∘. The resultant rB2 structures for both spin states are dynamically stable with no soft phonon mode (Fig. 4b, g). With rhombohedral distortion, the FeO8 cubes become FeO8 dodecahedra (D3d symmetry), and the three t2g orbitals split into a singlet (a1g), which is a \({d}_{{z}^{2}}\)-like orbital along the [111] direction, and a doublet (\(e^{\prime}_{g}\)). For the IS state, with shortened Fe-O bonds along the [111] direction, the a1g orbital has higher energy than the \(e^{\prime}_{g}\) orbitals; the four spin-up electrons occupy the eg and \(e^{\prime}_{g}\) orbitals, and the two spin-down electrons occupy the eg orbitals (Fig. 4c). With the splitting of t2g orbitals, an energy gap (~0.3 eV) is opened between the \(e^{\prime}_{g}\) and a1g bands, as indicated by the DOS (Fig. 4e). The \(e^{\prime}_{g}\) and a1g characteristics of these bands can be visualized via the ILDOS (Fig. 4d). For the LS state, with stretched Fe-O bonds along the [111] direction, the a1g orbital has lower energy than the \(e^{\prime}_{g}\) orbitals (Fig. 4h); the three spin-up and three spin-down electrons fully occupy the eg and a1g orbitals, with the \(e^{\prime}_{g}\) orbitals left unoccupied, resulting in a gap (~2.0 eV) between the a1g and \(e^{\prime}_{g}\) bands (Fig. 4j). The a1g and \(e^{\prime}_{g}\) characteristics of these two bands can also be visualized via the ILDOS (Fig. 4i). For both spin states, the completely filled eg bands are embedded in the oxygen bands spanning over −20 ≲ E ≲ −4 eV (Fig. 4e, j).
Cubic B2 (Mg0.75Fe0.25)O remaining stable
When the Fe concentration increases to x = 0.25, a three-dimensional (3D) network of corner-sharing FeO8 cubes is formed in B2 (Mg0.75Fe0.25)O (Fig. 1f), while for x ≤ 0.125, the FeO8 polyhedra are isolated/unconnected (Fig. 1c). For isolated FeO8 polyhedra, rhombohedral distortion is allowed and favored, as observed in rB2 (Mg0.875Fe0.125)O (Fig. 4). In contrast, connectivity of the 3D FeO8 network in B2 (Mg0.75Fe0.25)O suppresses the rhombohedral distortion and further stabilizes the cubic structure: Starting the structural optimization with rhombohedrally compressed/elongated rB2 IS/LS (Mg0.75Fe0.25)O, the crystal structure and FeO8 polyhedra resume cubic symmetry within a few steps. Within LDA+Usc, the LS state of cubic B2 (Mg0.75Fe0.25)O can be obtained throughout 0.2–1.8 TPa, while the IS state can only be obtained at P < 1.1 TPa and is subject to magnetic collapse: The total magnetization (M) decreases from 2μB/Fe to 0 in the region of 0.6 < P < 1.1 TPa and vanishes at P > 1.1 TPa (Fig. 5a). (Note: For x = 0.125, the IS state retains M = 2μB/Fe up to 1.8 TPa.) Regardless of the spin state and magnetization, cubic B2 (Mg0.75Fe0.25)O is dynamically stable with no soft phonon mode, even during the magnetic collapse (Fig. 5b–d). With FeO8 cubes (Oh symmetry), cubic B2 (Mg0.75Fe0.25)O and (Mg0.875Fe0.125)O have the same 3d orbital occupations and similar electronic structures. For cubic B2 IS (Mg0.75Fe0.25)O with M = 2μB/Fe (before the magnetic collapse), the spin-up t2g band spans across the Fermi energy (0 eV) while the spin-down t2g band lies above the Fermi energy (Fig. 5e), showing the same characteristic as cubic B2 IS (Mg0.875Fe0.125)O (Fig. 3e). Likewise, for cubic B2 LS (Mg0.75Fe0.25)O (Fig. 5g) and (Mg0.875Fe0.125)O (Fig. 3j), the t2g bands in both spin channels align, spanning across the Fermi energy. During the magnetic collapse (0 < M < 2μB/Fe), the t2g bands in the spin-up and spin-down channels are shifted upward and downward, respectively (Fig. 5f).
a Total magnetization (M); b–d phonon dispersion; e–g total and projected density of states (DOS), with the Fermi energy set as the reference (0 eV). Panel (a) indicates that the IS state retains M > 0 at P < 1.1 TPa. At P ≥ 1.1 TPa, only the nonmagnetic low-spin (LS) state (M = 0) can be obtained. Panels (d) and (g) thus also indicate the LS results.
Complicated transitions of (Mg1−xFex)O
To analyze the structural and spin transition of (Mg1−xFex)O, we compute the equations of state (EoS) of the B1 LS, (r)B2 IS, and (r)B2 LS states (Supplementary Fig. 2 and Note 2); the relative enthalpies (ΔH) of these states with respect to the (r)B2 IS state are plotted in Fig. 6. For x = 0.125 (Fig. 6a), (Mg0.875Fe0.125)O transforms from the B1 LS state into the rB2 IS state at 0.642 TPa. Upon further compression, the rB2 IS state undergoes a spin transition to the rB2 LS state at 1.348 TPa. Throughout these transitions, (Mg0.875Fe0.125)O remains insulating (see Supplementary Fig. 1 and Note 1 for the insulating B1 LS state). Remarkably, in the simultaneous structural (B1–rB2) and spin (LS–IS) transition at 0.642 TPa, Fe’s total electron spin S re-emerges from 0 to 1, opposite to the perception that S decreases upon compression. Furthermore, the IS state is energetically favorable over a wide pressure range (0.612–1.348 TPa), despite that IS state has never been observed in the Earth’s lower-mantle minerals, including B1 (Mg1−xFex)O, Fe-bearing MgSiO3 bridgmanite and post-perovskite, ferromagnesite (Mg1−xFex)CO3, and the NAL phase22,49,50,51,52,53,54. For x = 0.25 (Fig. 6b), a simultaneous structural, spin, and metal–insulator transition occurs at 0.539 TPa, from the insulating B1 LS state to the metallic B2 IS state (notice that S increases). Upon further compression, an IS–LS transition occurs in metallic B2 (Mg0.75Fe0.25)O at 0.855 TPa. From Fig. 6, effects of Fe concentration on the B1–(r)B2 transition pressure (\({P}_{T}^{B1/B2}\)) can also be inferred. For Fe-free MgO (x = 0), we find \({P}_{T}^{B1/B2}=0.535\) TPa (Supplementary Fig. 3 and Note 3), in agreement with other calculations3,4,5,6,7,8,9,10,11,12,13,14. As x increases, \({P}_{T}^{B1/B2}\) first increases to 0.642 TPa at x = 0.125 (Fig. 6a) and then decreases to 0.539 TPa at x = 0.25 (Fig. 6b), indicating a trend of decreasing \({P}_{T}^{B1/B2}\) in the region of 0.125 ≲ x ≤1, consistent with experiments: \({P}_{T}^{B1/B2}\) of FeO (~0.25 TPa)47,48 is much lower than that of MgO (~0.5 TPa)1,2,3,4. [Note: (1) For x = 0.25 (Fig. 6b), the EoS of the B2 IS state is fitted using the data points at P < 0.988 TPa (where M > 0). (2) To examine the robustness of the LDA+Usc results shown in Fig. 6, we perform extensive test calculations using various methods. Similar results are obtained, as shown in Supplementary Figs. 4, 5, and Note 4].
In the Earth’s mantle condition, Fe partitioning between B1 (Mg1−xFex)O, Fe-bearing MgSiO3 bridgmanite, and post-perovskite varies with pressure, temperature, and even the Fe valence/spin state21,23,37,38,39. Likewise, in exoplanet interiors, Fe concentration in B2 (Mg1−xFex)O may vary with the depth or the interior region, due to the variation of Fe partitioning between B2 (Mg1−xFex)O and other minerals phases, including post-perovskite and/or high-pressure silicates15,16. Evident by comparing Fig. 6a and b, spin, structural, and metal–insulator transition of B2 (Mg1−xFex)O can also be induced by the change of Fe concentration (x). In the depth/region with pressure of 0.642–0.855 TPa, if x increases from 0.125 to 0.25, a simultaneous structural and metal–insulator transition occurs [insulating rB2 IS (Mg0.875Fe0.125)O → metallic B2 IS (Mg0.75Fe0.25)O]; in the depth/region with pressure of 0.855–1.348 TPa, if x increases from 0.125 to 0.25, a simultaneous structural, spin, and metal–insulator transition occurs [insulating rB2 IS (Mg0.875Fe0.125)O → metallic B2 LS (Mg0.75Fe0.25)O]. Even in the depth/region of P > 1.348 TPa, where only LS Fe2+ exists, if x increases from 0.125 to 0.25, a simultaneous structural and metal–insulator transition occurs [insulating rB2 LS (Mg0.875Fe0.125)O → metallic B2 LS (Mg0.75Fe0.25)O]. On the other hand, if x decreases from 0.25 to 0.125, the aforementioned transitions would be reversed. Based on the above analysis, metal–insulator transition is always included in the composition-induced transitions of the B2 phase, suggesting that variation of Fe partitioning can significantly change the electrical and thermal transport properties of exoplanet interiors.
Implications of spin transition in the B2 phase
At temperature T ≠ 0, spin transition goes through a mixed-spin (MS) phase/state, in which different spin states coexist. For B2 (Mg1−xFex)O, only the IS and LS states are relevant. Within the thermodynamic model detailed in Supplementary Note 5, the LS fraction (nLS) in the MS phase can be written \({n}_{LS}=1/\left[1+3\exp ({{\Delta }}H/{k}_{B}Tx)\right]\), where ΔH ≡ HLS −HIS, and the IS fraction nIS = 1 −nLS. Despite that lattice vibration is not considered, the results obtained from this approach have been shown in great agreement with room-temperature experiments22,50,53,54,56. In Fig. 7, the LS and IS fractions, compression curves, and bulk modulus of B2 (Mg1−xFex)O at T = 300 K are shown. For x = 0.125, the IS–LS transition is smooth and spans over a wide pressure range (Fig. 7a), due to the small enthalpy difference (ΔH) between the rB2 IS and LS states (Fig. 6a). The compression curves V(P) of the MS, IS, and LS states are nearly the same (Fig. 7b); their difference is barely noticeable even by plotting the relative volume difference with respect to pure B2 MgO, namely, (V − VMgO)/VMgO (Fig. 7c). As a consequence, the bulk modulus K ≡ − V∂P/∂V barely changes during the spin transition (Fig. 7d). For x = 0.25, the spin transition is more abrupt (Fig. 7e), due to the larger ΔH between the B2 IS and LS states (Fig. 6b). With increased Fe concentration, the volume difference between the LS and IS states increases (Fig. 7f), resulting in prominent volume reduction (~0.5%) (Fig. 7g) and bulk modulus softening (~22%) (Fig. 7h). While the full elastic tensor (Cij) and shear modulus (G) are not computed, the volume and elastic anomalies shown in Fig. 7g and h clearly indicate anomalous softening of bulk sound velocity \({v}_{{{\Phi }}}=\sqrt{K/\rho }\) (ρ: density) and compressional wave velocity \({v}_{P}=\sqrt{\left(K+\frac{4}{3}G\right)/\rho }\). Furthermore, within the phonon gas model, lattice thermal conductivity \(\kappa \approx (1/3){C}_{V}{v}_{P}^{2}\tau\) (CV: heat capacity; τ: average phonon scattering time)57, suggesting that anomalous change of vP may play a role in the anomalous change of thermal conductivity. In the B1 phase, anomalous vΦ, vP20,28,29,30,31,32,33 and κ35,36 have all been observed. The volume/elastic anomalies accompanying the spin transition of the B2 phase may thus be a possible source of seismic and thermal anomalies in exoplanet interiors.
Experiments and computations have confirmed that HS–LS transitions in B1 (Mg1−xFex)O and ferromagnesite (Mg1−xFex)CO3 are accompanied by anomalous changes of major thermal properties, including thermal expansivity, heat capacity, Grüneisen parameter, thermal conductivity, and thermoelasticity20,28,29,30,31,32,33,35,36,55. As the temperature increases, the spin-transition pressure increases, and the transition is broadened29,55. Remarkably, for (Mg0.75Fe0.25)CO3, the anomalous increase of heat capacity retains its magnitude (~12%) without smearing out, even at high temperature55. Likewise, for the B2 phase, anomalous changes of thermal properties accompanying the spin transition can be expected. To investigate such anomalies at high P–T conditions, vibrational free energy must be included. Thermal calculations are thus highly desirable and will be left for future studies.
In summary, we have investigated (Mg1−xFex)O (x ≤ 0.25) at ultrahigh pressure up to 1.8 TPa via first-principles calculations. Our calculations indicate that Fe greatly affects the properties of (Mg1−xFex)O. For x = 0.125, insulating (Mg0.875Fe0.125)O undergoes a simultaneous structural and spin transition (B1 LS → rB2 IS) at 0.642 TPa, followed by a spin transition (rB2 IS–LS) at 1.348 TPa. For x = 0.25, (Mg0.75Fe0.25)O undergoes a simultaneous structural, spin, and metal–insulator transition (insulating B1 LS → metallic B2 IS) at 0.539 TPa, followed by a spin transition (metallic B2 IS–LS) at 0.855 TPa. Remarkably, Fe’s total electron spin S re-emerges from 0 to 1 in the B1–(r)B2 transition. In addition, structural, spin, and metal–insulator transitions of B2 (Mg1−xFex)O can also be induced by the change of Fe concentration (x). These results suggest that Fe and spin transition may greatly affect planetary interiors over a vast pressure range, considering the anomalous changes of elastic, transport, and thermal properties accompanying the spin and/or metal–insulator transition.
Methods
Computation
In this work, all major calculations are performed using the Quantum ESPRESSO codes58. We use ultrasoft pseudopotentials (USPPs) generated with the Vanderbilt method59. The valence electron configurations for the generations are 2s22p63s23p03d0, 3s23p63d6.54s14p0, and 2s22p43d0 for Mg, Fe, and O, respectively; the cutoff radii are 1.4, 1,8, and 1.0 a.u. for Mg, Fe, and O, respectively. The aforementioned USPPs of Mg and O have been used in refs. 15,16, and the USPP of Fe has been used in refs. 22,49,50,51,52,53,54. To properly treat the on-site Coulomb interaction of the Fe 3d electrons, we adopt the local density approximation + self-consistent Hubbard U (LDA+Usc) method, with the Hubbard U parameters computed self-consistently60,61,62,63. Briefly speaking, we start with an LDA+U calculation with a trial U (the “input Uin”) to obtain the desired spin state for (Mg1−xFex)O. For this LDA+Uin state, we compute the second derivative of the LDA energy with respect to the 3d electron occupation at the Fe site (d2ELDA/dn2) via a density functional perturbation theory (DFPT) approach63 implemented in Quantum ESPRESSO. This second derivative, d2ELDA/dn2, is considered as the “output Uout” and will be used as Uin in the next iteration. Such a procedure is repeated until self-consistency is achieved, namely, Uin = Uout ≡ Usc. Phonon calculations are performed using the Phonopy code64, which adopts the finite-displacement (frozen phonon) method. The third-order Birch–Murnaghan equation of state (3rd BM EoS) is used for the EoS fitting.
Thermodynamic model
In this work, analysis for the IS–LS transition in (r)B2 (Mg1−xFex)O at room temperature (300 K) is based on the thermodynamic model detailed in Supplementary Note 5. Plotted in Fig. 7, the IS/LS fractions and the EoS of the MS phase are given by Supplementary Eqs. 9 and 10, respectively.
Data availability
The authors declare that the main data supporting the findings of this study are contained within the paper and its associated Supplementary Information. Example input and output files of our calculations (using Quantum ESPRESSO) have been deposited at Zenodo (https://doi.org/10.5281/zenodo.6283200). All other relevant files are available from the corresponding author upon reasonable request.
Code availability
In this work, all major calculations are performed using the Quantum ESPRESSO (QE) codes, and phonon calculations are performed using Phonopy, as described in the Methods Section. Both QE and Phonopy are open-source packages; they can be downloaded for free from http://www.quantum-espresso.org/ and http://phonopy.github.io/phonopy/, respectively. Detailed information for the compilation and installation of these codes are contained in their own websites.
References
McWilliams, R. S. et al. Phase transformations and metallization of magnesium oxide at high pressure and temperature. Science 338, 1330 (2012).
Coppari, F. et al. Experimental evidence for a phase transition in magnesium oxide at exoplanet pressures. Nat. Geosci. 6, 926 (2013).
Miyanishi, K. et al. Laser-shock compression of magnesium oxide in the warm-dense-matter regime. Phys. Rev. E 92, 023103 (2015).
Root, S. et al. Shock response and phase transitions of MgO at planetary impact conditions. Phys. Rev. Lett. 115, 198501 (2015).
Karki, B. B. et al. Structure and elasticity of MgO at high pressure. Am. Mineral. 82, 51 (1997).
Mehl, M. J., Cohen, R. E. & Krakauer, H. Linearized augmented plane wave electronic structure calculations for MgO and CaO. J. Geophys. Res. 93, 8009 (1988).
Oganov, A. R., Gillan, M. J. & Price, G. D. Ab initio lattice dynamics and structural stability of MgO. J. Chem. Phys. 118, 10174 (2003).
Alfe, D. et al. Quantum Monte Carlo calculations of the structural properties and the B1-B2 phase transition of MgO. Phys. Rev. B 72, 014114 (2005).
Belonoshko, A. B., Arapan, S., Martonak, R. & Rosengren, A. MgO phase diagram from first principles in a wide pressure-temperature range. Phys. Rev. B 81, 054110 (2010).
Boates, B. & Bonev, S. A. Demixing instability in dense molten MgSiO3 and the phase siagram of MgO. Phys. Rev. Lett. 110, 135504 (2013).
Cebulla, D. & Redmer, R. Ab initio simulations of MgO under extreme conditions. Phys. Rev. B 89, 134107 (2014).
Taniuchi, T. & Tsuchiya, T. The melting points of MgO up to 4 TPa predicted based on ab initio thermodynamic integration molecular dynamics. J. Phys. Condens. Matter 30, 11400 (2018).
Bouchet, J. et al. Ab initio calculations of the B1-B2 phase transition in MgO. Phys. Rev. B 99, 094113 (2019).
Soubiran, F. & Militzer, B. Anharmonicity and phase diagram of magnesium oxide in the megabar regime. Phys. Rev. Lett. 125, 175701 (2020).
Umemoto, K., Wentzcovitch, R. M. & Allen, P. B. Dissociation of MgSiO3 in the cores of gas giants and terrestrial exoplanets. Science 311, 983 (2006).
Umemoto, K. et al. Phase transitions in MgSiO3 post-perovskite in super-Earth mantles. Earth Planet. Sci. Lett. 478, 40 (2017).
Duffy, T., Madhusudhan, N. & Lee, K. K. M. Mineralogy of super-Earth planets. In Treatise on Geophysics, 2nd edition, Vol. 2, pp. 149 (2015).
van den Berg, A. P., Yuen, D. A., Umemoto, K., Jacobs, M. H. G. & Wentzcovitch, R. M. Mass-dependent dynamics of terrestrial exoplanets using ab initio mineral properties. Icarus 317, 412 (2019).
Hsu, H., Umemoto, K., Wu, Z. & Wentzcovitch, R. M. Spin-state crossover of iron in lower-mantle minerals: Results of DFT.U investigations. Rev. Miner. Geochem. 71, 169 (2010).
Lin, J.-F., Speziale, S., Mao, Z. & Marquardt, H. Effects of the electronic spin transitions of iron in lower-mantle minerals: Implications for deep mantle geophysics and geochemistry. Rev. Geophys. 51, 244 (2013).
Badro, J. Spin transitions in mantle minerals. Annu. Rev. Earth Planet. Sci. 42, 231 (2014).
Hsu, H. & Wentzcovitch, R. M. First-principles study of intermediate-spin ferrous iron in the Earth’s lower mantle. Phys. Rev. B 90, 195205 (2014).
Badro, J. et al. Iron partitioning in Earthas mantle: toward a deep lower mantle discontinuity. Science 300, 789 (2003).
Lin, J.-F. et al. Spin transition of iron in magnesiowüstite in the Earthas lower mantle. Nature 436, 377 (2005).
Tsuchiya, T., Wentzcovitch, R. M., daSilva, C. R. S. & de Gironcoli, S. Spin transition in magnesiowüstite in Earth’s lower mantle. Phys. Rev. Lett. 96, 198501 (2006).
Goncharov, A. F., Struzhkin, V. V. & Jacobsen, S. D. Reduced radiative conductivity of low-Spin (Mg, Fe)O in the lower mantle. Science 312, 1205 (2006).
Lin, J.-F. et al. Spin transition zone in Earth’s lower mantle. Science 317, 1740 (2007).
Crowhurst, J., Brown, J. M., Goncharov, A. F. & Jacobsen, S. D. Elasticity of (Mg,Fe)O through the spin transition of iron in the lower mantle. Science 319, 451 (2008).
Wu, Z., Justo, J. F., daSilva, C. R. S., de Gironcoli, S. & Wentzcovitch, R. M. Anomalous thermodynamic properties in ferropericlase throughout its spin crossover transition. Phys. Rev. B 80, 014409 (2009).
Wentzcovitch, R. M. et al. Anomalous compressibility of ferropericlase throughout the iron spin cross-over. Proc. Natl Acad. Sci. USA 106, 8447 (2009).
Marquardt, H. et al. Elastic shear anisotropy of ferropericlase in Earthas lower mantle. Science 324, 224 (2009).
Antonangeli, D. et al. Spin crossover in ferropericlase at high pressure: a seismologically transparent transition? Science 331, 64 (2011).
Wu, Z., Justo, J. F. & Wentzcovitch, R. M. Elastic anomalies in a spin-crossover system: ferropericlase at lower mantle conditions. Phys. Rev. Lett. 110, 228501 (2013).
Holmström, E. & Stixrude, L. Spin crossover in ferropericlase from first-principles molecular dynamics. Phys. Rev. Lett. 114, 117202 (2015).
Ohta, K., Yagi, T., Hirose, K. & Ohishi, Y. Thermal conductivity of ferropericlase in the Earth’s lower mantle. Earth Planet. Sci. Lett. 465, 29 (2017).
Hsieh, W.-P., Deschamps, F., Okuchi, T. & Lin, J.-F. Effects of iron on the lattice thermal conductivity of Earth’s deep mantle and implications for mantle dynamics. Proc. Natl Acad. Sci. USA 115, 4099 (2018).
Kobayashi, Y. et al. Fe-Mg partitioning between (Mg,Fe)SiO3 post-perovskite, perovskite, and magnesiowüstite in the Earth’s lower mantle. Geophys. Res. Lett. 32, L19301 (2005).
Irifune, T. et al. Iron partitioning and density changes of pyrolite in Earthas lower mantle. Science 327, 193 (2010).
Piet, H. et al. Spin and valence dependence of iron partitioning in Earth’s deep mantle. Proc. Natl Acad. Sci. USA 113, 11127 (2016).
Huang, C., Leng, W. & Wu, Z. Iron-spin transition controls structure and stability of LLSVPs in the lower mantle. Earth Planet. Sci. Lett. 423, 173 (2015).
Wu, Z. & Wentzcovitch, R. M. Spin crossover in ferropericlase and velocity heterogeneities in the lower mantle. Proc. Natl Acad. Sci. USA 111, 10468 (2014).
Shephard, G. E. et al. Seismological expression of the iron spin crossover in ferropericlase in the Earth’s lower mantle. Nat. Commun. 12, 5905 (2021).
Ohta, K., Hirose, K., Shimizu, K. & Ohishi, Y. High-pressure experimental evidence for metal FeO with normal NiAs-type structure. Phys. Rev. B 82, 174120 (2010).
Ozawa, H. et al. Spin crossover, structural change, and metallization in NiAs-type FeO at high pressure. Phys. Rev. B 84, 134417 (2011).
Fischer, R. A. et al. Phase transition and metallization of FeO at high pressures and temperatures. Geophys. Rev. Lett. 38, L24301 (2011).
Hamada, M. et al. Magnetic and spin transitions in wüstite: a synchrotron Mössbauer spectroscopic study. Phys. Rev. B 93, 155165 (2016).
Ozawa, H., Takahashi, F., Hirose, K., Ohishi, Y. & Hirao, N. Phase transition of FeO and stratification in Earthas outer core. Science 334, 792 (2011).
Coppari, F. et al. Implications of the iron oxide phase transition on the interiors of rocky exoplanets. Nat. Geosci. 14, 121 (2021).
Hsu, H., Umemoto, K., Blaha, P. & Wentzcovitch, R. M. Spin states and hyperfine interactions of iron in (Mg,Fe)SiO3 perovskite under pressure. Earth Planet. Sci. Lett. 294, 19 (2010).
Hsu, H., Blaha, P., Cococcioni, M. & Wentzcovitch, R. M. Spin-state crossover and hyperfine interactions of ferric iron in MgSiO3 perovskite. Phys. Rev. Lett. 106, 118501 (2011).
Hsu, H., Yu, Y. G. & Wentzcovitch, R. M. Spin crossover of iron in aluminous MgSiO3 perovskite and post-perovskite. Earth Planet. Sci. Lett. 359-360, 34 (2012).
Yu, Y. G., Hsu, H., Cococcioni, M. & Wentzcovitch, R. M. Spin states and hyperfine interactions of iron incorporated in MgSiO3 post-perovskite. Earth Planet. Sci. Lett. 331-332, 1 (2012).
Hsu, H. & Huang, S.-C. Spin crossover and hyperfine interactions of iron in (Mg,Fe)CO3 ferromagnesite. Phys. Rev. B 94, 060404(R) (2016).
Hsu, H. First-principles study of iron spin crossover in the new hexagonal aluminous phase. Phys. Rev. B 95, 020406(R) (2017).
Hsu, H., Crisostomo, C., Wang, W. & Wu, Z. Anomalous thermal properties and spin crossover of ferromagnesite (Mg,Fe)CO3. Phys. Rev. B 103, 054401 (2021).
Hsu, H. & Huang, S.-C. Simultaneous metal-half-metal and spin transition in SrCoO3 under compression. Phys. Rev. Mater. 2, 111401(R) (2018).
Hofmeister, A. M. & Branlund, J. M. Thermal conductivity of the Earth. In Treatise on Geophysics, 2nd edition, Vol. 2, pp. 583 (2015).
Giannozzi, P. et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 29, 465901 (2017).
Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 41, 7892(R) (1990).
Cococcioni, M. & de Gironcoli, S. Linear response approach to the calculation of the effective interaction parameters in the LDA+U method. Phys. Rev. B 71, 035105 (2005).
Kulik, H. J., Cococcioni, M., Scherlis, D. A. & Marzari, N. Density functional theory in transition-metal chemistry: a self-consistent Hubbard U approach. Phys. Rev. Lett. 97, 103001 (2006).
Himmetoglu, B., Floris, A., de Gironcoli, S. & Cococcioni, M. Hubbard-corrected DFT energy functionals: the LDA+U description of correlated systems. Int. J. Quantum Chem. 114, 14 (2014).
Timrov, I., Marzari, N. & Cococcioni, M. Hubbard parameters from density-functional perturbation theory. Phys. Rev. B 98, 085127 (2018).
Togo, A. & Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 108, 1 (2015).
Acknowledgements
H.H. acknowledges support from the Ministry of Science and Technology of Taiwan under Grant Numbers MOST 107-2112-M-008-022-MY3, 107-2119-M-009-009-MY3, and 110-2112-M-008-033. K.U. acknowledges support from the JSPS Kakenhi Grant Numbers 17K05627 and 21K03698. Calculations were performed at National Center for High-performance Computing, Taiwan, and the Global Scientific Information and Computing Center at Tokyo Institute of Technology, Japan.
Author information
Authors and Affiliations
Contributions
Both authors designed and planned this research. K.U. initiated the work by performing preliminary calculations. H.H. performed the major calculations. Both authors analyzed the calculation results. H.H. wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Jung-Fu Lin and the anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
41467_2022_30100_MOESM1_ESM.pdf
Supplementary Information for “Structural transition and re-emergence of iron’s total electron spin in (Mg,Fe)O at ultrahigh pressure”
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hsu, H., Umemoto, K. Structural transition and re-emergence of iron's total electron spin in (Mg,Fe)O at ultrahigh pressure. Nat Commun 13, 2780 (2022). https://doi.org/10.1038/s41467-022-30100-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-30100-5
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.