Abstract
The microscopic origins of emergent behaviours in condensed matter systems are encoded in their excitations. In ordinary magnetic materials, single spin-flips give rise to collective dipolar magnetic excitations called magnons. Likewise, multiple spin-flips can give rise to multipolar magnetic excitations in magnetic materials with spin S ≥ 1. Unfortunately, since most experimental probes are governed by dipolar selection rules, collective multipolar excitations have generally remained elusive. For instance, only dipolar magnetic excitations have been observed in isotropic S = 1 Haldane spin systems. Here, we unveil a hidden quadrupolar constituent of the spin dynamics in antiferromagnetic S = 1 Haldane chain material Y2BaNiO5 using Ni L3-edge resonant inelastic x-ray scattering. Our results demonstrate that pure quadrupolar magnetic excitations can be probed without direct interactions with dipolar excitations or anisotropic perturbations. Originating from on-site double spin-flip processes, the quadrupolar magnetic excitations in Y2BaNiO5 show a remarkable dual nature of collective dispersion. While one component propagates as non-interacting entities, the other behaves as a bound quadrupolar magnetic wave. This result highlights the rich and largely unexplored physics of higher-order magnetic excitations.
Similar content being viewed by others
Introduction
The elementary excitation of a magnetically ordered material is a single dipolar spin-flip of an electron, delocalised coherently across the system in the form of a spin wave. The spin-wave quasiparticle, known as a magnon, carries a spin angular momentum of one unit and has well-defined experimental signatures. Collective dipolar magnetic excitations also appear in low-dimensional magnets that remain disordered to the lowest achievable temperatures because of quantum fluctuations. A paradigmatic example is the S = 1 antiferromagnetic Haldane spin chain, where magnetic order is suppressed in favour of a singlet ground state with nonlocal topological order1,2. Several theoretical and experimental works have established that a single spin-flip from this exotic ground state creates dipolar magnetic excitations that propagate along the chain above an energy gap of ΔH ~ 0.41J, the Haldane gap3,4,5,6,7,8.
Materials hosting 3d transition metal ions with a d2 or d8 configuration (such as Ni2+ for the latter) often possess strongly interacting spin-1 local magnetic moments with quantised spin projections Sz = −1, 0, 1. In addition to the usual single spin-flip excitations, it is possible to create quadrupolar magnetic excitations by changing the composite spin by two units. Such excitations can be conceived as flipping two of the constituent spin-1/2’s, as shown in Fig. 1a. Incidentally, quadrupolar magnetic waves arising from such transitions and carrying two units of angular momentum were predicted for S = 1 ferromagnetic chains as early as the 1970s9,10 and may play a role in the iron pnictide superconductors11. Since most probes are restricted by dipolar selection rules, however, such quadrupolar excitations have largely evaded detection except in rare situations where they are perturbed by anisotropic interactions, spin-orbit coupling, lattice vibrations, or large magnetic fields12,13,14,15,16,17. Quadrupolar magnetic excitations have never been observed in isotropic Haldane spin chains, even though dipolar magnetic excitations have been extensively studied3,4,5,6,7,8,18. It is then natural to wonder whether purely quadrupolar collective magnetic excitations exist in isotropic spin-1 systems.
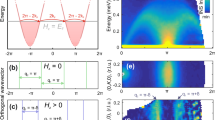
a Possible unpaired spin configurations in an S = 1 ion (Ni2+) and spin-flip transitions. b Process of probing single-site quadrupolar ΔStot = 2 excitations in L-edge RIXS. An L-edge RIXS process of a S = 1 3d8 ion (with two unpaired d electrons and ground state having Stot = 0) proceeds via creation of an intermediate 2p5 3d9 state. In this intermediate state, due to the strong spin-orbit coupling of 2p5 core-hole, the spin-angular momentum is not conserved leading to a valence orbital spin-flipped final state with Stot = 1. Additionally, due to the many-body core-valence Coulomb exchange interactions in the intermediate states, an additional available valence orbital spin-flip may occur thereby creating an excited final state with Stot = 221. The coloured (white) arrows represent the occupied (empty) spin states of the electrons involved in the scattering process. c A representative Haldane spin chain characterised by the topological non-local (string) order of alternating Sz = ±1 sites intervened by any number of Sz = 0 sites. Between neighbouring sites a pair of spin-1/2s form an antisymmetric singlet. Single-site single spin-flips give rise to dipolar singlet-triplet excitations while single-site double spin-flips give rise to quadrupolar excitations resulting in pairs of triplets. Single spin-flips at multiple sites give rise to two-magnons. d Schematic representation of dual nature of propagation of the pair of triplets formed after quadrupolar excitation.
Here, we uncover the presence of collective quadrupolar magnetic excitations in the isotropic S = 1 Haldane chain system Y2BaNiO5 using high energy-resolution Ni L3-edge resonant inelastic x-ray scattering (RIXS). Previous studies on nickelates have already shown that Ni L3-edge RIXS can probe dipolar magnons19,20. In addition, ref. 21 recently showed that double spin-flips are allowed at this edge through the combined many-body effect of core-valence exchange and core-hole spin-orbit interactions22,23 (Fig. 1b), making it the optimal tool for this study. Y2BaNiO5 is one of the best realisations of the isotropic Haldane spin chain material with intra-chain exchange J ~ 24 meV and negligibly small single-ion anisotropy ~0.035J, exchange-anisotropy ~0.011J, and inter-chain exchange ~0.0005J6,24. This aspect allows us to describe the system completely using a simple Heisenberg model, and emphasises the relevance of the pure quadrupolar magnetic excitations in the spin dynamics of S = 1 systems.
Results
Excitations in Haldane spin chains
In a valence bond singlet scheme, the Heisenberg model’s ground state in the Haldane phase can be represented as a macroscopic Stot = 0 state comprised of pairs of fictitious spin-\(\frac{1}{2}\) particles on neighbouring sites that form antisymmetric singlets on each bond8 (Fig. 1c). A single local spin-flip breaks a bond singlet to form a triplet excitation, raising the chain’s total spin quantum number to Stot = 1. In contrast, a local double spin-flip would disrupt singlets on either side of the excited site, creating a pair of triplet excitations and raising the spin quantum number to Stot = 2. In the RIXS process, it is also possible to have a total spin-conserved two-site excitation with ΔStot = 0 (see Fig. 1c), which appears as a two-magnon continuum. To simplify our notation, we will refer to the single-site single-spin-flip induced dipolar ΔStot = 1 excitation as ΔS1, the single-site double-spin-flip induced quadrupolar ΔStot = 2 excitation as ΔS2, and the two-site ΔStot = 0 two-magnon excitation as ΔS0.
Figure 2a shows a RIXS intensity map collected on Y2BaNiO5 (see Methods). The feature with the largest spectral weight follows a dispersion relation consistent with inelastic neutron scattering (INS) results for the dipolar ΔS1 excitation4,5,24. This feature is also reproduced in our density matrix renormalisation group (DMRG) calculations of the dynamical structure factor S1(q∥, ω) for an isotropic Heisenberg model (see Fig. 2b and Methods). Ni L3-edge RIXS is unable to reach the exact antiferromagnetic zone center (q∥ = 0.5, in units of 2π/c throughout), where the Haldane gap of ~ 8.5 meV exists. But it does probe an equally interesting region close to q∥ = 0. Prior work4,7,25 has focused on observing the breakdown of the well-defined ΔS1 quasiparticle into a two-magnon continuum for q∥ ≾ 0.12 and the spectral weight vanishing as \({q}_{\parallel }^{2}\). Although we notice a reduction in the intensity of the ΔS1 excitation in our experiment, we also observe significant inelastic spectral weight near zero energy close to q∥ = 0 (also see Fig. 2e for the line spectrum at q∥ = 0.01). Interestingly, a new dispersing excitation is clearly visible with an energy maximum of ~ 136 meV at q∥ = 0. Of the calculated S0(q∥, ω), S1(q∥, ω), S2(q∥, ω) dynamical structure factors, shown in Fig. 2d, b, c, respectively, only S2(q∥, ω) has spectral weight in this region. Moreover, the S2(q∥ ~ 0, ω) line profile has two components: a broad low-energy continuum and a sharp high-energy peak, as shown in Fig. 2f. It therefore appears that both the low- and high-energy spectral components seen in the experiment can be described by the quadrupolar ΔS2 excitation in this region of momentum space.
a Experimental RIXS intensity map at Ni L3-edge at 11 K. Dashed line is a semiquantitative dispersion \({\omega }^{2}({q}_{\parallel })={{{\Delta }}}_{{{{{{{{\rm{H}}}}}}}}}^{2}+{v}^{2}{\sin }^{2}{q}_{\parallel }+{\alpha }^{2}{\cos }^{2}\frac{{q}_{\parallel }}{2}\) with J = 24 meV, ΔH = 0.41J, v = 2.55J and α = 1.1J4–6,49. The vertical bar shows the experimental energy resolution. DMRG calculated dynamic spin susceptibility intensity maps for the b, ΔS1, c, ΔS2 and d, ΔS0 excitations (see Methods for details). In panel c we show the continuum boundaries expected for two independent triplet excitations (equivalent to two-magnon continuum boundaries). e RIXS line profile at q∥ = 0.01 and a shaded elastic peak profile. f Calculated profile for ΔS2 at q∥ = 0.01 from DMRG. The ΔS2 spectral weight can be decomposed into a broad continuum and a sharp peak (see Methods).
To evaluate the relative contributions of each excitation, we decomposed the RIXS spectra across the momentum space into the dynamical structure factors calculated by DMRG. Figure 3a–c show representative RIXS spectra. The data are fitted with an elastic peak and experimental energy-resolution convoluted line profiles of Sα(q∥, ω) (α = 0, 1, 2, see Methods). While the spectra are dominated by the dipolar ΔS1 excitations at high q∥ values, the spectral weight close to q∥ = 0 can be fitted with only the quadrupolar ΔS2 excitation. Figure 3d and e show the RIXS spectra after subtracting other fitted components to keep only the ΔS1 and ΔS2 contributions, respectively, along with their fitted profiles from DMRG. This analysis shows that the low-energy RIXS spectral weight is carried by the low-energy continuum component of the ΔS2 excitations below the quasiparticle decay threshold momentum. This component is gapped and has a peak energy of ~19 meV at q∥ ~ 0, reminiscent of the lower boundary of the two-magnon continuum at 2ΔH predicted for Haldane spin chains7. We note that the energy gap at this momentum has not yet been confirmed for any Haldane spin chain by INS due to the small scattering cross-sections. Figure 3f shows the RIXS intensity map after subtracting only the elastic peaks and Fig. 3g shows the combined DMRG dynamical structure factors S0(q∥, ω), S1(q∥, ω), and S2(q∥, ω) obtained by fitting the RIXS spectra. The ΔS0 type of two-magnon continuum excitations provide a negligible contribution to the RIXS spectra (see Methods for the contributions from each type of excitation). Undoubtedly, the two-component excitation (the broad low-energy continuum and the sharp high-energy component), and its dispersion in the momentum space (Fig. 3e) is well described only by the quadrupolar ΔS2 excitation.
Representative RIXS spectra at q∥ = a, 0.47, b, 0.25, and c, 0.01 with fits using spin susceptibilities obtained from DMRG (see Methods). Note that an additional peak is included in the fits in panel c to account for a multimagnon spectral tail around 200 meV, which may originate from higher-order contributions not considered in the expansion of the RIXS response. d RIXS line spectra after subtraction of elastic, ΔS2 and the high energy tail structure visible in panel c. Shaded areas are fitted profiles from DMRG for ΔS1. e RIXS line spectra after subtraction of elastic, ΔS1 and the high energy tail structure visible in panel c. Shaded areas are fitted profiles from DMRG for ΔS2. The vertical shaded bar represents twice the ΔH value from ref. 5. f Experimental RIXS intensity map with elastic contribution subtracted. g DMRG intensity map with summed contributions from ΔS0, ΔS1 and ΔS2 excitations determined by fitting experimental RIXS spectra using Eq. (5).
Quadrupolar excitations at finite T
To further understand the character of the two-component ΔS2 quadrupolar excitations, we also studied their thermal evolution. Figure 4a shows the RIXS spectra at q∥ = 0.01, with contributions from the ΔS2 excitations, for increasing temperatures. For comparison, Fig. 4b shows finite temperature DMRG simulations for the S2(q∥ = 0.01, ω) excitations, convoluted with the experimental energy resolution. Since the raw DMRG data for the ΔS2 channel (Fig. 2f) contains a two-peak structure with an asymmetric peak appearing at low energy and a symmetric peak at high energy, we fit the experimental S2(q∥ = 0.01, ω) finite temperature data using two components (see methods). Our results show that only the ΔS2 excitations obtained from DMRG are needed to reproduce the experimental RIXS spectra, even at finite temperatures. As shown in Fig. 4c, the peak energy of the lower component increases with temperatures following twice of the system’s Haldane gap from ref. 5. Conversely, the high-energy peak begins to soften above the Haldane gap temperature of ~ 100 K. The highest energy value of the ΔS1 peak at q∥ = 0.25 also follows this trend. The bandwidth reduction of the ΔS1 triplet dispersion with temperature occurs due to the thermal blocking of propagation lengths and decoherence26. In a simple picture, if one considers a continuum from pairs of non-interacting triplets due to single spin-flips at multiple sites, then bandwidth reduction of each would manifest as the overall raising and lowering of the lower and upper boundaries of the continuum, respectively (see Supplementary Note 3). A similar thermal effect on the propagation of the quadrupolar ΔS2 excitation should occur. The spectral weight of the two components in the ΔS2 excitation, however, behave differently with temperature. The low-energy continuum intensity varies little, while the high-energy peak diminishes rapidly with increasing temperature and the rate of decay is comparable to the ΔS1 peak at q∥ = 0.47 (see Fig. 4d). The DMRG calculated correlation lengths (in lattice units) of the ΔS1 and ΔS2 excitations, as shown in Fig. 4e, also decrease in a similar way with temperature.
a RIXS spectra (open circles) at q∥ = 0.01 with fitted elastic contributions subtracted, at different temperatures. The ΔS2 contributions have been fitted to extract the positions and amplitudes of the two branches shown by dashed lines (see Methods). The shaded regions show the complete fit profiles. b ΔS2 profiles obtained from DMRG for corresponding temperatures. c Energy variations with temperature of the two branches of the ΔS2 excitations extracted from RIXS shown in panel a. Blackline with circles shows the thermal variation of twice the Haldane gap energy obtained from ref. 5. Redline with circles shows the thermal variation of twice the ΔS1 peak energy at q∥ = 0.25. d Thermal variation in amplitudes of ΔS1 peak and the high energy peak of the ΔS2 extracted from fitted RIXS spectra at q∥ = 0.47 and 0.01, respectively, normalised to corresponding amplitudes at 11 K. e Dipolar and quadrupolar correlation lengths for ΔStot = 1 and 2 excitations obtained from DMRG static dipolar and quadrupolar correlation functions (see Methods). Error bars are least-square-fit errors.
Dual nature of the quadrupolar excitations
The energy-momentum and temperature dependence of the quadrupolar ΔS2 excitations implies that their low- and high-energy components are different in nature. At low-energy, a conceivable picture is that immediately after a pair of triplets are created by a single-site excitation, they decay into two noninteracting triplets (see Fig. 1d) propagating incoherently along the chain and giving rise to the broad low-energy continuum (see Fig. 2c for the expected continuum boundaries). This behaviour is remarkably similar to the fractionalisation of a ΔStot = 1 excitation into a two-spinon continuum in isotropic spin-1/2 chains27, but having a distinct origin.
The sharpness of the high-energy component and its rapid decay with temperature, on the other hand, hints that it behaves as a distinct quasiparticle formed from pairs of triplets propagating coherently (see Fig. 1d)28,29. In low-dimensional systems, sharp peaks in the magnetic spectrum may either originate from a van Hove singularity in the density of states of quasiparticles (in our case, non-interacting triplet pairs) or from the formation of a bound state (in our case, bound triplet pairs). In Fig. 2c, the lower and upper boundaries of the continuum from pairs of non-interacting triplets (equivalent to the two-magnon continuum) are shown. The high-energy component of ΔS2 appears above the upper boundary of the continuum, ruling out the van Hove singularity scenario and suggesting the formation of a bound state. The peak energy of the high-energy component is slightly larger than twice the highest energy value of the ΔS1 peak (by ~ 7 meV at T = 11 K) and, surprisingly, remains so up to the highest measured temperature. The small positive energy difference suggests a weak repulsive interaction between the bound triplets formed after a quadrupolar ΔS2 excitation9,30. Supplementary Note 6 provides a semi-quantitative energy scale based argument to support the notion of the bound state of weakly repulsing triplets excitations.
The correlation length of the ΔS1 excitations in Haldane spin chains decay exponentially in the presence of a non-local order, which can be viewed to originate from alternating Sz = ±1 sites intervened by Sz = 0 sites. The ΔS2 excitations also have an exponentially decaying correlation length, albeit smaller than ΔS1 excitations. The difference in correlation length is likely due to the fact that the creation of quadrupolar wave excitations costs energetically at least twice as much the single spin-flip magnon-like excitations at any wave-vector. As such, they may provide a means to detect the hidden non-local order that, at present, is only estimated theoretically by considering the Sz = ±1 states in Haldane spin chains2,31,32. Overall, we show that the ΔS2 excitations sustain the isotropic properties, the exchange interactions, and the coherence inherent to the system.
Discussion and outlook
Magnetic excitations provide vital information about a system’s thermodynamic, magneto-transport, ultrafast magnetic, spintronic, or superconducting properties. Moreover, higher-order multipolar spin and orbital degrees of freedom give rise to exotic non-classical phenomena like the Kitaev spin liquid33, multispinons34, spin-nematicity15, on-site multiferroicity12, and bound-magnon states 14,16, in a wide variety of magnetic systems. However, as noted earlier, multipolar excitations are challenging to detect using conventional probes35. It was shown recently that quadrupolar excitations in S = 1 FeI2 appear in INS only due to their hybridisation with dipolar excitations through anisotropic spin-exchanges14. In the presence of a strong anisotropy, bound magnetic excitations from ΔStot = 2 spin-flips at energies higher than the two-magnon continuum have also been observed in S = 1 spin chains using high-field electron spin resonance36,37. However, our demonstration of pure quadrupolar spin dynamics in an isotropic Haldane system, without invoking anistropic interactions, suggests that simultaneous confinement and propagation of excitations can occur entirely via higher-order quantum correlations38. This work thus illustrates RIXS’s capability of detecting higher-order dispersing excitations, irrespective of the presence of dipolar excitations14, and thus may be the preferable way to study quadrupolar excitations in, for instance, spin-nematic systems, where the dipolar excitations are suppressed39,40. Also recently, it has been seen that Cu L3-edge RIXS can probe spin-conserved and non-spin-conserved higher-order four-spinons in spin-1/2 Heisenberg antiferromagnetic spin chains41. Our present work further consolidates L-edge RIXS (in comparison to O K-edge)34, as a powerful probe for characterising nonlocal long-range magnetic correlations via the study of higher-order spin-flip excitations, thereby, extending both the energy-momentum phase space and the diversity of the magnetic quantum systems that can be explored. On the other hand, exploring the physics of high-energy excitations and/or eigenstates of a simple nonintegrable spin chain model is in itself of great theoretical interest. We provide a simple physical intuition about the nature of one of the high-energy eigenstates of the one-dimensional Heisenberg model and our findings may have important consequences for many-body correlated states of matter and thermalisation in quantum systems42. Looking forward, it would be interesting to learn how the quadrupolar excitations can be manipulated with intrinsic perturbations like anisotropy or extrinsic ones like a magnetic field. The indications of a propagating quadrupolar bound excitation in a real material can also have important ramifications for realising quantum information transfer in form of qubit pairs43,44.
Methods
Experiments
A single crystal of Y2BaNiO5 grown by the floating-zone method was used for the RIXS measurements. The momentum transfer along the chain direction q∥ was varied by changing the x-ray incident angle θ while keeping the scattering angle fixed at 154∘. The lattice constant along the chain or the c-axis used for the calculation of momemtum transfer is 3.77 Å. The crystal was cleaved in vacuum and the pressure in the experimental chamber was maintained below ~5 × 10−10 mbar throughout the experiment. High energy-resolution RIXS data (ΔE ≃ 37 meV) at the Ni L3-edge were collected at I21 RIXS beamline, Diamond Light Source, United Kingdom45. The zero-energy position and resolution of the RIXS spectra were determined from subsequent measurements of elastic peaks from an adjacent carbon tape. The polarization vector of the incident x-ray was parallel to the scattering plane (i.e. π polarization). See Supplementary Note 1 for more details of the experimental configuration.
Theory
In the main text, we pointed out that the S = 1 Haldane chain system Y2BaNiO5 might present negligibly small single-ion anisotropy ~0.035J, exchange-anisotropy ~0.011J terms in a Heisenberg model description at low energies. We have verified numerically that these small corrections do not change our magnetic spectra qualitatively, and therefore a pure isotropic Heisenberg model has been adopted throughout our study.
Zero and finite temperature DMRG Calculations
T = 0 DMRG calculations on 100 site chains with open boundary conditions (OBC) were carried out with the correction-vector method46 using the Krylov decomposition47, as implemented in the DMRG++ code48. This approach requires real-space representation for the dynamical structure factors in the frequency domain, which can be found in the Supplementary Note 4. For T > 0 calculations we used the ancilla (or purification) method with a system of 32 physical and 32 ancilla sites, also with OBC. For more details see Supplementary Note 7.
For both the zero temperature and finite temperature calculations we kept up to m = 2000 DMRG states to maintain a truncation error below 10−7 and 10−6, respectively and introduced a spectral broadening in the correction-vector approach fixed at η = 0.25J = 6 meV.
Dynamical spin correlation functions
We consider three correlation functions S0(q∥, ω), S1(q∥, ω), and S2(q∥, ω) giving information about ΔStot = 0, ΔStot = 1, and ΔStot = 2 excitations, respectively. To make the expressions more transparent, we use the Lehmann representation and construct the corresponding excitation operators in momentum space. The relevant correlation functions are
where \(\left|f\right\rangle\) are the final states of the RIXS process and
The three dynamical correlation functions given by Eq. (1) appear at the lowest order of a ultrashort core-hole lifetime expansion of the full RIXS cross-section. As the single-site ΔStot = 0 RIXS scattering operator is trivial (identity operator) in a low-energy description in terms of spin S = 1 sites, the lowest order operator would involve two-sites and, by rotational symmetry, involves a scalar product of neighbouring spin operators [see Eq. (2)]. Single and double spin-flip RIXS scattering operators, on the other hand, lead to ΔStot = 1 and ΔStot = 2 excitations and can be naturally described in terms of onsite \({S}_{j}^{+}\) and \({({S}_{j}^{+})}^{2}\) operators, respectively [Eqs. (3) & (4)]. In the Supplementary Note 5 we provide analysis of the three dynamical correlation functions in terms of single triplet excitations or magnon states in the Haldane chain.
Correlation lengths
Figure 4e of the main text shows dipolar and quadrupolar correlation lengths as a function of temperature. These have been obtained by computing \(\left\langle \psi (\beta )\right|{S}_{j}^{+}{S}_{j+r}^{-}\left|\psi (\beta )\right\rangle\) and \(\left\langle \psi (\beta )\right|{({S}_{j}^{+})}^{2}{({S}_{j+r}^{-})}^{2}\left|\psi (\beta )\right\rangle\) correlation functions from the center of the chain j = c, respectively, and fitting with a exponential decay relationship f(r) = Ae−r/ξ.
RIXS data fitting
RIXS data were normalised to the incident photon flux and corrected for x-ray self-absorption effects prior to fitting. The elastic peak was fit with a Gaussian function with a width set by the energy resolution. The RIXS spin excitations in Fig. 3 were modeled with the Bose factor weighted dynamical spin susceptibilities obtained from our T = 0 DMRG calculations for ΔStot = 0, 1, and 2 (S0, S1 and S2, respectively) after they were convoluted with a Gaussian function capturing the experimental energy resolution. The total model intensity is given by
where the coefficients C0, C1 and C2 account for the varying RIXS scattering cross section for each spin excitation with varying θ (q∥). The reader is referred to the Supplementary Note 2 for the extracted values of coefficients and the fit profiles. As seen in Fig. 3c, S2 from DMRG for ΔStot = 2 transitions do not capture the additional spectral weight on the high energy side in the RIXS signal. A ‘half’-Lorentzian truncated damped harmonic oscillator (HLDHO) function centered at 0.175 eV was therefore included in the fits to account for this tail. In Fig. 4, the ΔStot = 2 excitations at q∥ = 0.01(2π/c) are decomposed using a DHO function for the sharp high energy peak and a skewed Gaussian function for the broad lower continuum. Both functions are energy-resolution convoluted and weighted by a Bose factor. DHO functions were used similarly for fitting ΔStot = 1 triplet excitations at q∥ = 0.47 (see Supplementary Note 2).
Data availability
The instruction to build the input scripts for the DMRG++ package to reproduce our results can be found in the Supplementary Material. The data to reproduce our figures is available as a public data set at https://doi.org/10.5281/zenodo.6394852. Raw data files will be made available upon request.
Code availability
The numerical results reported in this work were obtained with DMRG++ versions 6.01 and PsimagLite versions 3.01. The DMRG++ computer program48 is available at https://github.com/g1257/dmrgpp.git (see Supplementary Note 7 for more details.)
References
Haldane, F. Continuum dynamics of the 1-D Heisenberg antiferromagnet: Identification with the O(3) nonlinear sigma model. Phys. Lett. A 93, 464–468 (1983).
Kennedy, T. & Tasaki, H. Hidden symmetry breaking and the Haldane phase in S = 1 quantum spin chains. Commun. Math. Phys. 147, 431–484 (1992).
Kenzelmann, M. et al. Properties of Haldane excitations and multiparticle states in the antiferromagnetic spin-1 chain compounds CsNiCl3. Phys. Rev. B 66, 024407 (2002).
Zaliznyak, I. A., Lee, S.-H. & Petrov, S. V. Continuum in the spin-excitation spectrum of a Haldane chain observed by neutron scattering in CsNiCl3. Phys. Rev. Lett. 87, 017202 (2001).
Xu, G. et al. Mesoscopic phase coherence in a quantum spin fluid. Science 317, 1049–1052 (2007).
Xu, G. et al. Y2BaNiO5: A nearly ideal realization of the S = 1 Heisenberg chain with antiferromagnetic interactions. Phys. Rev. B 54, R6827–R6830 (1996).
White, S. R. & Affleck, I. Spectral function for the S = 1 Heisenberg antiferromagetic chain. Phys. Rev. B 77, 134437 (2008).
Affleck, I., Kennedy, T., Lieb, E. H. & Tasaki, H. Valence bond ground states in isotropic quantum antiferromagnets. Commun. Math. Phys. 115, 477–528 (1988).
Chiu-Tsao, S. T., Levy, P. M. & Paulson, C. Elementary excitations of high-degree pair interactions: The two-spin-deviation spectra for a spin-1 ferromagnet. Phys. Rev. B 12, 1819–1838 (1975).
Sivardiere, J. Elementary excitations in S = 1 quadrupolar systems. J. Magn. Magn. Mater. 1, 23–38 (1975).
Liu, C., Lu, X., Dai, P., Yu, R. & Si, Q. Anisotropic magnetic excitations of a frustrated bilinear-biquadratic spin model: Implications for spin waves of detwinned iron pnictides. Phys. Rev. B 101, 024510 (2020).
Akaki, M. et al. Direct observation of spin-quadrupolar excitations in Sr2CoGe2O7 by high-field electron spin resonance. Phys. Rev. B 96, 214406 (2017).
Ward, S. et al. Bound states and field-polarized Haldane modes in a quantum spin ladder. Phys. Rev. Lett. 118, 177202 (2017).
Bai, X. et al. Hybridized quadrupolar excitations in the spin-anisotropic frustrated magnet FeI2. Nat. Phys. 17, 467–472 (2021).
Kohama, Y. et al. Possible observation of quantum spin-nematic phase in a frustrated magnet. Proc. Natl Acad. Sci. USA 116, 10686–10690 (2019).
Dally, R. L. et al. Three-magnon bound state in the quasi-one-dimensional antiferromagnet α-NaMnO2. Phys. Rev. Lett. 124, 197203 (2020).
Patri, A. S. et al. Unveiling hidden multipolar orders with magnetostriction. Nat. Commun. 10, 4092 (2019).
Binder, M. & Barthel, T. Low-energy physics of isotropic spin-1 chains in the critical and Haldane phases. Phys. Rev. B 102, 014447 (2020).
Fabbris, G. et al. Doping dependence of collective spin and orbital excitations in the spin-1 quantum antiferromagnet La2−xSrxNiO4 observed by X rays. Phys. Rev. Lett. 118, 156402 (2017).
Lin, J. Q. et al. Strong superexchange in a d9−δ nickelate revealed by resonant inelastic x-ray scattering. Phys. Rev. Lett. 126, 087001 (2021).
Nag, A. et al. Many-body physics of single and double spin-flip excitations in NiO. Phys. Rev. Lett. 124, 067202 (2020).
de Groot, F. M. F., Kuiper, P. & Sawatzky, G. A. Local spin-flip spectral distribution obtained by resonant x-ray Raman scattering. Phys. Rev. B 57, 14584–14587 (1998).
Haverkort, M. W. Theory of resonant inelastic X-ray scattering by collective magnetic excitations. Phys. Rev. Lett. 105, 167404 (2010).
Sakaguchi, T., Kakurai, K., Yokoo, T. & Akimitsu, J. Neutron scattering study of magnetic excitations in the spin S= 1 one-dimensional Heisenberg antiferromagnet Y2BaNiO5. J. Phys. Soc. Jpn. 65, 3025–3031 (1996).
Stone, M. B., Zaliznyak, I. A., Hong, T., Broholm, C. L. & Reich, D. H. Quasiparticle breakdown in a quantum spin liquid. Nature 440, 187–190 (2006).
Kenzelmann, M. et al. Evolution of spin excitations in a gapped antiferromagnet from the quantum to the high-temperature limit. Phys. Rev. B 66, 174412 (2002).
Mourigal, M. et al. Fractional spinon excitations in the quantum Heisenberg antiferromagnetic chain. Nat. Phys. 9, 435–441 (2013).
Knetter, C., Schmidt, K. P., Grüninger, M. & Uhrig, G. S. Fractional and integer excitations in quantum antiferromagnetic spin 1/2 ladders. Phys. Rev. Lett. 87, 167204 (2001).
Kohno, M., Starykh, O. A. & Balents, L. Spinons and triplons in spatially anisotropic frustrated antiferromagnets. Nat. Phys. 3, 790–795 (2007).
White, S. R. & Huse, D. A. Numerical renormalization-group study of low-lying eigenstates of the antiferromagnetic S=1 Heisenberg chain. Phys. Rev. B 48, 3844–3852 (1993).
García-Ripoll, J. J., Martin-Delgado, M. A. & Cirac, J. I. Implementation of spin Hamiltonians in optical lattices. Phys. Rev. Lett. 93, 250405 (2004).
Hilker, T. A. et al. Revealing hidden antiferromagnetic correlations in doped Hubbard chains via string correlators. Science 357, 484–487 (2017).
Takagi, H., Takayama, T., Jackeli, G., Khaliullin, G. & Nagler, S. E. Concept and realization of Kitaev quantum spin liquids. Nat. Rev. Phys. 1, 264–280 (2019).
Schlappa, J. et al. Probing multi-spinon excitations outside of the two-spinon continuum in the antiferromagnetic spin chain cuprate Sr2CuO3. Nat. Commun. 9, 5394 (2018).
Savary, L. & Senthil, T. Probing hidden orders with resonant inelastic x-ray scattering. Preprint at https://arxiv.org/abs/1506.04752 (2015).
Zvyagin, S. A. et al. Magnetic excitations in the spin-1 anisotropic Heisenberg antiferromagnetic chain system NiCl2-4SC(NH2)2. Phys. Rev. Lett. 98, 047205 (2007).
Papanicolaou, N., Orendáčová, A. & Orendáč, M. Electron-spin resonance in spin-1 planar magnetic chains. Phys. Rev. B 56, 8786–8798 (1997).
Lake, B. et al. Confinement of fractional quantum number particles in a condensed-matter system. Nat. Phys. 6, 50–55 (2010).
Smerald, A. & Shannon, N. Theory of spin excitations in a quantum spin-nematic state. Phys. Rev. B 88, 184430 (2013).
Fernandes, R., Chubukov, A. & Schmalian, J. What drives nematic order in iron-based superconductors? Nat. Phys. 10, 97–104 (2014).
Kumar, U. et al. Unraveling higher-order corrections in the spin dynamics of rixs spectra. Preprint at https://arxiv.org/abs/2110.03186 (2021).
Nandkishore, R. & Huse, D. A. Many-body localization and thermalization in quantum statistical mechanics. Annu. Rev. Condens. Matter Phys. 6, 15–38 (2015).
Subrahmanyam, V. Entanglement dynamics and quantum-state transport in spin chains. Phys. Rev. A 69, 034304 (2004).
Bose, S. Quantum togetherness. Nature 502, 40–41 (2013).
Zhou, K.-J. et al. I21: an advanced high-resolution resonant inelastic X-ray scattering beamline at Diamond Light Source. J. Synchrotron Radiat. 29, 563–580 (2022).
Kühner, T. D. & White, S. R. Dynamical correlation functions using the density matrix renormalization group. Phys. Rev. B 60, 335–343 (1999).
Nocera, A. & Alvarez, G. Spectral functions with the density matrix renormalization group: Krylov-space approach for correction vectors. Phys. Rev. E 94, 053308 (2016).
Alvarez, G. The density matrix renormalization group for strongly correlated electron systems: A generic implementation. Comput. Phys. Commun. 180, 1572–1578 (2009).
Gómez-Santos, G. Variational approach to the xxz spin-1 linear chain: Elementary excitations and haldane conjecture. Phys. Rev. Lett. 63, 790–793 (1989).
Acknowledgements
We thank I. Affleck, J.-G. Park, S. Hayden, A. Aligia, and K. Wohlfeld for insightful discussions. We are grateful to C. Bastista for suggesting the possibility of a van Hove singularity in our results. All data were taken at the I21 RIXS beam line of Diamond Light Source (United Kingdom) using the RIXS spectrometer designed, built, and owned by Diamond Light Source. We acknowledge Diamond Light Source for providing the beam time on beam line I21 under Proposal MM24593. S. J. acknowledges support from the National Science Foundation under Grant No. DMR-1842056. A. Nocera acknowledges support from the Max Planck-UBC-UTokyo Center for Quantum Materials and Canada First Research Excellence Fund (CFREF) Quantum Materials and Future Technologies Program of the Stewart Blusson Quantum Matter Institute (SBQMI), and the Natural Sciences and Engineering Research Council of Canada (NSERC). S.-W.C. was supported by the DOE under Grant No. DOE: DE-FG02-07ER46382. This work used computational resources and services provided by Compute Canada and Advanced Research Computing at the University of British Columbia. We acknowledge T. Rice for the technical support throughout the beam times. We also thank G. B. G. Stenning and D. W. Nye for help on the Laue instrument in the Materials Characterisation Laboratory at the ISIS Neutron and Muon Source.
Author information
Authors and Affiliations
Contributions
K.-J.Z. conceived the project; K.-J.Z., A. Nag, A. Nocera, and S.J. supervised the project. A. Nag, K.-J.Z., S.A., M.G.-F., and A.C.W. performed RIXS measurements. A. Nag, S.A., and K.-J.Z. analysed RIXS data. S.-W.C. synthesized and characterised the sample. A. Nocera and S.J. performed DMRG calculations. A. Nag, K.-J.Z., A. Nocera, and S.J. wrote the manuscript with comments from all the authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Nag, A., Nocera, A., Agrestini, S. et al. Quadrupolar magnetic excitations in an isotropic spin-1 antiferromagnet. Nat Commun 13, 2327 (2022). https://doi.org/10.1038/s41467-022-30065-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-30065-5
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.