Abstract
Pressure-induced thermal changes in solids—barocaloric effects—can be used to drive cooling cycles that offer a promising alternative to traditional vapor-compression technologies. Efficient barocaloric cooling requires materials that undergo reversible phase transitions with large entropy changes, high sensitivity to hydrostatic pressure, and minimal hysteresis, the combination of which has been challenging to achieve in existing barocaloric materials. Here, we report a new mechanism for achieving colossal barocaloric effects that leverages the large volume and conformational entropy changes of hydrocarbon order–disorder transitions within the organic bilayers of select two-dimensional metal–halide perovskites. Significantly, we show how the confined nature of these order–disorder phase transitions and the synthetic tunability of layered perovskites can be leveraged to reduce phase transition hysteresis through careful control over the inorganic–organic interface. The combination of ultralow hysteresis and high pressure sensitivity leads to colossal reversible isothermal entropy changes (>200 J kg−1 K−1) at record-low pressures (<300 bar).
Similar content being viewed by others
Introduction
Nearly 4400 TWh of electricity—20% of the total consumed in the world—is used each year by refrigerators, air conditioners, and heat pumps for cooling1. In addition to the 2.3 Gt of carbon dioxide emitted during the generation of this electricity, the vapor-compression-based devices that provided the bulk of this cooling emitted fluorocarbon refrigerants with a global warming potential equivalent to 1.5 Gt of carbon dioxide into the atmosphere2. With population and economic growth expected to dramatically increase over the next several decades, the development of alternative cooling technologies with improved efficiency and reduced emissions will be critical to meeting global cooling needs in a more sustainable fashion3.
Caloric materials, which undergo thermal changes in response to an applied magnetic, electric, or stress field, offer the potential for solid-state cooling with high energy efficiency and zero direct emissions, as well as faster start-up times, quieter operation, greater amenability to miniaturization, and better recyclability than conventional vapor-compression systems4,5,6. Caloric effects are particularly strong in ferroic materials near first-order phase transitions, where small changes to the magnitude of an applied field can induce the large isothermal entropy and adiabatic temperature changes required for commercially viable cooling cycles.
Although magnetocaloric and electrocaloric effects have received the most attention for solid-state cooling, transitions between states with different magnetic ordering or electric polarization typically involve much smaller entropy changes than those that occur during the liquid–vapor transition of a hydrofluorocarbon refrigerant and can be complicated by the need to generate large magnetic fields or to avoid dielectric breakdown7,8. Alternatively, the sensitivity of structural phase transitions to hydrostatic pressure and uniaxial strain can be leveraged to realize even larger entropy changes in barocaloric and elastocaloric materials, respectively9,10. In particular, reversible structural transitions that are accompanied by a substantial change in volume can produce barocaloric effects with large entropy changes and high sensitivity to pressure.
An ideal material for barocaloric cooling would feature a phase transition with (i) a large isothermal entropy change (ΔSit) and adiabatic temperature change (ΔTad), (ii) a large barocaloric coefficient (dTtr/dP) that reflects a high sensitivity of the transition temperature, Ttr, to pressure, P, and (iii) a low reversible pressure, Prev, which represents the minimum pressure required to induce a reversible entropy change and is proportional, in part, to the thermal hysteresis of the phase transition11. Among the limited range of compounds that have been investigated as candidate barocaloric materials, certain organic plastic crystals, such as neopentylglycol, have recently been shown to exhibit order–disorder phase transitions in the solid state that yield colossal barocaloric effects with entropy changes approaching those of commercial hydrofluorocarbon refrigerants11,12,13. These transitions, however, often have large thermal hysteresis, occur away from ambient temperature, or have only moderate sensitivity to applied pressure. This highlights a longstanding challenge across all classes of caloric materials: field-induced phase transitions that lead to large isothermal entropy and adiabatic temperature changes are often accompanied by substantial hysteresis, which increases the magnitude of the applied field required to capture the full entropy of the transition and reduces the efficiency of each cooling cycle14,15,16,17.
In pursuit of a new strategy to target barocaloric effects with low hysteresis, high sensitivity to pressure, and large entropy changes near ambient temperature, we sought a phase transition mechanism that would offer access to large volume changes and disordered states with high entropy but could take place within a microenvironment tailored to promote reversibility. To this end, we recognized that long-chain hydrocarbons undergo order–disorder transitions with far higher entropy changes than have ever been realized in a caloric effect. For instance, the entropy of n-decane (C10H22) increases by 829 J kg–1 K–1 (118 J mol–1 K–1) upon melting18, which is even larger than the 520 J kg–1 K–1 (53 J mol–1 K–1) increase in entropy of the commercial refrigerant HFC-134a (CH2FCF3) upon vaporization19. These high entropy changes arise from increases in orientational, conformational, and positional entropy as molecules restricted in the crystalline state gain access to more rotational, vibrational, and translational degrees of freedom in the disordered—and expanded—molten state20.
The entropy and latent heat changes associated with hydrocarbon melting transitions are already exploited for thermal energy storage in paraffin-based solid–liquid phase-change materials21. Similar types of phase transitions are also known to occur in the solid state in several classes of layered materials, including two-dimensional (2-D) metal–halide perovskites of the form (R-NH3)2MX4 (R = CnH2n+1; M = Mn, Fe, Cu, Cd, Pb; X = Cl, Br, or I)22,23. In these compounds, sheets of corner-sharing MX6 octahedra create anionic pockets—defined by the axial halides of four adjacent metal centers—that template the arrangement of bilayers of alkylammonium cations through charge-assisted hydrogen bonds. When long-chain hydrocarbon molecules (n > 3) are incorporated, many layered perovskites undergo thermally induced, first-order phase transitions between low- and high-entropy states driven by a partial disordering transition of the hydrocarbon bilayers (Supplementary Tables 1–3). These transitions are often referred to as “chain-melting” transitions because of the liquid-like conformational degrees of freedom associated with the hydrocarbon chains in the disordered phase, even though the transition occurs entirely in the solid state23,24. As such, we anticipated that 2-D perovskites would serve as a highly tunable solid-state platform to leverage the large changes in entropy and enthalpy that accompany hydrocarbon order–disorder transitions for barocaloric cooling (Fig. 1a). Moreover, since the inorganic layers and organic bilayers of 2-D perovskites can be independently manipulated, we further expected that phase transition hysteresis could be minimized through confinement effects and careful control of the organic–inorganic interfaces. We note that 2-D perovskites were also independently identified as promising barocaloric materials by Lloveras and coworkers while our work was under peer review25.
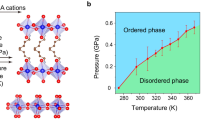
a Illustration of how the pressure dependence of hydrocarbon order–disorder transitions in the organic bilayers of hybrid 2-D perovskites can be leveraged to drive a barocaloric cooling cycle. Each cooling cycle begins with an adiabatic (Brayton-like cycle) or isothermal (Stirling-like cycle) increase in pressure that induces a first-order phase transition from an expanded, high-entropy phase of the 2-D perovskite to a contracted, low-entropy phase. Heat released during this exothermic transition is dissipated to a heat sink, returning the material to its original temperature but now at a lower entropy. The pressure is then adiabatically or isothermally decreased to reverse the phase transition and cool a heat source. b Comparison of phase transition entropies, ΔStr, and transition temperatures, Ttr, for order–disorder transitions in select 2-D perovskites of the form (CnH2n+1NH3)2MX4 (n = 7–16; M = Mn, Cd, Cu, or Pb; X = Cl, Br, or I). Thermally induced phase transitions in 2-D perovskites are often accompanied by large changes in entropy that are sensitive to the length of the hydrocarbon chain and the identity of the metal and halide in the inorganic layer. Many of these order–disorder transitions involve one or more minor transitions that occur at lower or higher temperatures than the major transition, but (DA)2MnCl4 (DA = decylammonium) features a single order–disorder transition with a large entropy change near ambient temperature.
Here, we report a comprehensive study of barocaloric effects in two representative 2-D perovskites (DA)2MnCl4 (DA = decylammonium) and (NA)2CuBr4 (NA = nonylammonium). Through a combination of high-pressure calorimetry and X-ray diffraction experiments, we show that these materials feature phase transitions with large entropy changes, high sensitivity to pressure, and minimal hysteresis, which collectively leads to outstanding barocaloric performance. Moreover, we demonstrate how the chemical tunability of 2-D perovskites and the decoupling of extrinsic and intrinsic factors that influence phase-change kinetics can be leveraged to drive reversible barocaloric effects with pressures approaching those used in vapor-compression cooling systems. These results are further supported by detailed crystallographic and spectroscopic characterization, which provide molecular-level insights into barocaloric effects in 2-D perovskites, including compensation effects between entropy changes, hysteresis, and pressure sensitivity. Our work establishes hydrocarbon phase transitions in 2-D perovskites as a generalizable mechanism for achieving large and reversible barocaloric effects at low driving pressures.
Results
Pressure dependence of phase transitions in (DA)2MnCl4
The 2-D perovskite (DA)2MnCl4 was selected as a potential barocaloric material because of its large phase transition entropy (ΔStr = 230 J kg−1 K−1) and enthalpy (ΔHtr = 71 kJ kg−1), near-ambient phase transition temperature (Ttr = 310 K), and lightweight, nontoxic elemental composition (Fig. 1b). At ambient temperature and pressure, (DA)2MnCl4 adopts an ordered monoclinic structure (low-temperature, LT, phase) with bilayers of hydrocarbon chains—each of which contains a single gauche C–C bond (C2–C3) and seven trans C–C bonds—aligned parallel to one another and tilted 48.3(1)° with respect to the Mn–Cleq (equatorial chloride) plane (Fig. 2e)26. Upon heating above 310 K, the compound undergoes a first-order phase transition to an expanded orthorhombic lattice (high-temperature, HT, phase) with disordered hydrocarbon chains that have increased conformational and rotational degrees of freedom27. The large increase in entropy during the transition can be attributed to flipping of the alkylammonium cations between two favorable orientations within the Mn–Cl pockets, internal rotations of C–C bonds that create dynamically disordered conformational defects within the hydrocarbon chains, and a substantial increase in volume (Supplementary Notes 1–3)24.
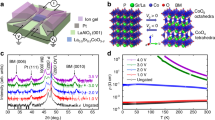
Differential scanning calorimetry (DSC) traces for powder samples of (a) (DA)2MnCl4 and (b) (NA)2CuBr4 at 1 bar with heating (red) and cooling (blue) rates of 2 K min−1. Thermal hysteresis (ΔThys) is indicated by the vertical gray bars. Note that ΔThys is calculated as the difference between heating and cooling transition onset temperatures, with ΔThys = Ttr,heating – Ttr,cooling. Specific volumes obtained from variable-temperature powder X-ray diffraction and He pycnometry measurements are used to determine the volume changes, ΔV, that accompany the order–disorder transition for (c) (DA)2MnCl4 and (d) (NA)2CuBr4. Variable-temperature crystal structures of the low-temperature (LT) and high-temperature (HT) phases of (e) (DA)2MnCl4 and (f) (NA)2CuBr4. Note that the LT crystal structures were both obtained at 270 K, while the HT crystal structures were obtained at 330 K and 335 K for (DA)2MnCl4 and (NA)2CuBr4, respectively. Purple, orange, green, brown, gray, and blue spheres represent Mn, Cu, Cl, Br, C, and N atoms, respectively. H atoms are omitted for clarity. Note that DA chains are disordered over a special position in both the LT and HT phases, while NA chains are modeled with two-part disorder in the LT phase and disordered over a special position in the HT phase. Geometric parameters obtained from single-crystal X-ray diffraction experiments are summarized in Supplementary Tables 14–22.
Differential scanning calorimetry (DSC) measurements at ambient pressure showed that the hydrocarbon order–disorder transition is sharp and fully reversible with a thermal hysteresis, ΔThys, of just 1.4 K for a microcrystalline powder sample at a scan rate of 2 K min−1 (Fig. 2a). Variable-temperature powder X-ray diffraction (PXRD) experiments at ambient pressure revealed that the phase transition is accompanied by an increase in interlayer distance of 1.88 Å (7.0%) as the alkylammonium cations tilt further away from the Mn–Cleq plane to create additional space between disordered hydrocarbon chains in the HT phase (Supplementary Fig. 1). This expansion leads to an 8.0% overall increase in the volume of the compound (ΔVtr = 65.9 cm3 kg−1; Fig. 2c). Based on the measured volume and entropy changes, the Clausius–Clapeyron relation, dT/dP = ΔVtr/ΔStr, can be used to predict a barocaloric coefficient for (DA)2MnCl4 of 28.7 K kbar−1, which would represent one of the highest values reported for a barocaloric material (Supplementary Table 5). We note that select 3-D hybrid perovskites also exhibit similarly high barocaloric coefficients28,29.
To directly evaluate the pressure dependence of the phase transition temperature, isobaric DSC experiments were performed under applied hydrostatic pressures of up to 150 bar using He as the pressure-transmitting medium (Fig. 3a). As expected, the phase transition shifts to higher temperatures as the pressure is increased, with a measured dT/dP of 22.5 ± 0.3 K kbar–1 during heating and 20.2 ± 1.1 K kbar–1 during cooling (Fig. 3h, Supplementary Fig. 6). Importantly, the application of pressure does not lead to any significant changes to the phase transition width, and ΔStr remains within 96% of its ambient pressure value at 150 bar (Supplementary Fig. 10). Variable temperature and pressure PXRD experiments (performed at beamline 17-BM of the Advanced Photon Source at Argonne National Laboratory) confirm that similar order–disorder transitions still occur at pressures up to at least 360 bar (Fig. 3g, Supplementary Figs. 23–25), with small decreases in overall volume changes at higher pressures that are consistent with a higher compressibility for the HT phase relative to the LT phase (Supplementary Table 9).
DSC measurements under applied hydrostatic pressure for single-crystal samples of (a) (DA)2MnCl4 and (d) (NA)2CuBr4 with heating and cooling rates of 2 K min−1. Isothermal entropy changes, ΔSit, are calculated by the quasi-direct method for (b) (DA)2MnCl4 and (e) (NA)2CuBr4 for compression from ambient pressure and for decompression to ambient pressure. The shaded area indicates the reversible ΔSit within this pressure range. Isobaric entropy curves are shown in Supplementary Figs. 10 and 11. Direct evaluation of pressure hysteresis, ΔPhys, through quasi-isothermal DSC experiments for (c) (DA)2MnCl4 and (f) (NA)2CuBr4 at 311 K and 306 K, with pressure cycling from 1 to 150 bar and to 105 bar, respectively. ΔPhys is calculated as the difference between the onset pressure for the compression-induced exotherm and the decompression-induced endotherm and is indicated by the horizontal green bar. Variable-temperature powder X-ray diffraction (PXRD) patterns for (g) (DA)2MnCl4 and (i) (NA)2CuBr4 at 360 bar and 300 bar of He, respectively, while cooling from 325 K to 280 K, with an X-ray wavelength of 0.45237 Å. The pressure dependence of the order–disorder transition temperature as determined by HP-DSC (diamonds) and PXRD (squares) is used to calculate the barocaloric coefficient, dT/dP, for (h) (DA)2MnCl4 and (j) (NA)2CuBr4. Red and blue symbols indicate the phase transition temperatures during heating and cooling, respectively. Barocaloric coefficients are summarized in Supplementary Table 8.
Interestingly, the dT/dP values for (DA)2MnCl4 determined by PXRD and HP-DSC are lower than those predicted using the Clausius–Clapeyron equation. One possible explanation for this is that the effective volume change in the presence of a pressure-transmitting medium is less than the crystallographic volume change30. This could occur if He was excluded from the dense, crystalline organic bilayer of the LT phase but could permeate into the disordered organic bilayer of the HT phase—owing to its increased free volume—which would reduce the amount of additional volume that was occupied by the expanded phase. Indeed, the volume change that is directly measured by He pycnometry is 17 cm3 kg–1 smaller than that determined by crystallography (Fig. 2c), and using this lower effective volume change in the Clausius–Clapeyron equation yields a predicted dT/dP of 21.4 ± 1.5 K kbar–1 that matches the HP-DSC and PXRD values (Supplementary Table 10). Although effects of the pressure-transmitting medium are not typically considered when evaluating barocaloric materials, this result provides a pathway to realizing a higher dT/dP by preventing the pressure-transmitting medium from entering the disordered phase through encapsulation or the use of a more sterically bulky fluid. Regardless, the dT/dP that can be achieved using He to transmit hydrostatic pressure is higher than for many barocaloric materials, which, along with the large ΔStr and small hysteresis, presents considerable advantages for barocaloric cooling.
Reversible barocaloric effects in (DA)2MnCl4
Under the cyclic operating conditions of a barocaloric cooling system, the lowest possible operating pressure will be set by the pressure, Prev, that must be applied to induce a reversible isothermal entropy change, which can be used to drive a Stirling-like cooling cycle31, when cycling to and from ambient pressure. For a normal barocaloric effect, Prev corresponds to the pressure at which the onset temperature of the exothermic phase transition at applied pressure is equal to the onset temperature of the endothermic phase transition at 1 bar (ref. 11). As such, Prev is proportional to the thermal hysteresis at 1 bar and inversely proportional to the barocaloric coefficient for the exothermic transition, with Prev = ΔThys/(dT/dP)cooling. In addition, the minimum pressure required to induce a reversible adiabatic temperature change, Prev,ad, corresponds to the pressure at which the completion temperature of the exothermic phase transition at applied pressure is equal to the completion temperature of the endothermic phase transition at 1 bar (Supplementary Note 4). As such, Prev,ad is also affected by the transition peak width in addition to the thermal hysteresis and barocaloric coefficient, with smaller peak widths leading to lower Prev,ad. During our isobaric DSC experiments, we found that the transition peak widths of powder samples of (DA)2MnCl4 were much broader than those of single-crystal samples (Fig. 4a, c). We attribute the narrower peak widths of the single-crystal samples to improved thermal contact between single crystals and the DSC sample pan, as poor thermal contact is known to lead to thermal gradients that cause increased peak widths32. Accordingly, single-crystal samples of (DA)2MnCl4 with high-quality thermal contact have a lower Prev,ad than powder samples (178 bar and 265 bar, respectively), even though powder samples have a slightly lower Prev because of their smaller thermal hysteresis (Supplementary Table 7, Supplementary Note 5). This demonstrates the importance of considering the influence of extrinsic factors, such as the quality of thermal contact between the sample and sample holder, when evaluating the intrinsic potential of new barocaloric materials.
The phase boundary determined from HP-DSC experiments for (a–d) (DA)2MnCl4 and (e–h) (NA)2CuBr4, using (a, b, e, f) single-crystal samples with improved thermal contact and (c, d, g, h) powder samples. Scan rates of 2 K min–1 were used for all experiments, and He was used as the pressure-transmitting medium. DSC traces at ambient pressure are show in the left panel, with transition peak width highlighted in red and blue shades for heating and cooling, respectively. Onset temperatures are highlighted in dashed gray lines, with thermal hysteresis marked using black arrows. The pressure dependence of the onset and completion transition temperatures is shown in the right panels, and these phase boundaries illustrate the impact of the transition width on the minimum pressure required to drive a reversible isothermal entropy change (Prev) and a reversible adiabatic temperature change (Prev,ad). Note that the isobaric HP-DSC data for the powder samples is shown in Supplementary Fig. 16. Reversible barocaloric effects for powder and single-crystal samples are summarized in Supplementary Table 7.
Owing to its low ΔThys and high dT/dP, a single-crystal sample of (DA)2MnCl4 has a Prev of just 92 bar, which ranks among the lowest values reported for barocaloric materials (Supplementary Table 5). This low Prev was further confirmed by calculating reversible isothermal entropy changes (ΔSit) as a function of pressure from the difference between isobaric entropy changes, ΔSib, at ambient pressure and elevated pressures. Here, ΔSib values obtained from heating data correspond to the disordering transition induced by a decrease in pressure (ΔSit > 0), while ΔSib values from cooling data correspond to the ordering transition induced by an increase in pressure (ΔSit < 0) (Supplementary Fig. 10). Excitingly, these ΔSit curves confirm that a non-zero reversible entropy change of 13 J kg−1 K−1 can be induced at 100 bar (Fig. 3b). Moreover, a reversible entropy change of 190 J kg−1 K−1 can be accessed at a driving pressure of 150 bar (Fig. 3b, Supplementary Fig. 17b, e). To the best of our knowledge, inducing a reversible entropy change of this magnitude through a pressure shift of only 150 bar is unprecedented in barocaloric materials (Supplementary Table 5). As a result, (DA)2MnCl4 displays a record-high barocaloric strength—defined as the reversible isothermal entropy change normalized by the driving pressure33—of 1267 J kg −1 K−1 kbar−1 at 150 bar (Supplementary Table 6). Based on variable-temperature heat capacity, cp, measurements at ambient pressure (Supplementary Fig. 31), a maximum adiabatic temperature change, ΔTad,max, of 45 K can be estimated from the indirect calculation ΔTad(T) = –TΔSit/cp, which also ranks among the highest values yet reported for barocaloric materials (Supplementary Table 6).
In order to evaluate reversible adiabatic temperature changes, we performed additional HP-DSC experiments at a higher pressure range of 300–500 bar for a powder sample of (DA)2MnCl4 (Fig. 5a–c). This data shows that the order–disorder phase transition persists to at least 500 bar of hydrostatic pressure while maintaining 94% of the ambient pressure entropy change (Supplementary Fig. 20). At a 500-bar operating pressure, (DA)2MnCl4 has a maximum reversible isothermal entropy change, ΔSit,rev,max, of 248 kg–1 K–1 and a maximum reversible adiabatic temperature change, ΔTad,rev,max, of 7 K (Fig. 6a, Supplementary Fig. 22). We note that the single order–disorder phase transition splits into a major transition (93% of the total entropy change) and a minor phase transition (7% of the total entropy change) at pressures above 400 bar, with the minor transition occurring at a slightly higher temperature than the major transition (Fig. 5a, Supplementary Fig. 8a). This is consistent with similar splitting—albeit at much higher pressures—and entropy changes that were recently reported in an independent study of the barocaloric properties of (DA)2MnCl4 at pressures above 300 bar while this manuscript was under peer review25.
DSC measurements under applied hydrostatic pressure for powder samples of (a) (DA)2MnCl4 and (d) (NA)2CuBr4 up to 500 bar, with heating and cooling rates of 0.5 K min–1. Note that He was used as the pressure-transmitting medium. Isothermal entropy changes (ΔSit) calculated by the quasi-direct method for (b) (DA)2MnCl4 and (e) (NA)2CuBr4. The shaded area indicates the reversible ΔSit within this pressure range. Maximum reversible isothermal entropy change (ΔSit,rev,max) and reversible refrigeration capacity (RCrev) for (c) (DA)2MnCl4 and (f) (NA)2CuBr4 as a function of operating pressure, with the minimum pressures required to induce a reversible isothermal entropy change (Prev) and a reversible adiabatic temperature change (Prev,ad) marked using vertical lines. Note that ΔSit,rev,max is equivalent to the peak value of each reversible isothermal entropy curve, and RCrev is calculated as ΔSit,rev,max × ΔTFWHM. The dependence of RCrev on operating pressure above Prev,ad is highlighted using blue dashed lines. The pressure dependence of RCrev is 4524 J kbar–1 kg–1 and 1830 J kbar–1 kg–1 for (DA)2MnCl4 and (NA)2CuBr4, respectively.
Isobaric entropy changes (ΔSib) during heating and cooling at ambient pressure and 500 bar are shown for (a) (DA)2MnCl4 and (b) (NA)2CuBr4. Note that the ΔSib curves include contributions from the heat capacity. The area between ΔSib(T, 1 bar)heating and ΔSib(T, 500 bar)cooling curves denotes the temperature range over which both reversible isothermal entropy changes (ΔSit,rev) and reversible adiabatic temperature changes (ΔTad,rev) are accessible.
Although quasi-direct methods of calculating isothermal changes—and adiabatic changes—from isobaric experiments are commonly used to evaluate barocaloric materials due to the challenge of maintaining isothermality—or adiabaticity—during direct variable-pressure measurements33, we also performed quasi-isothermal HP-DSC experiments to more directly evaluate Prev by measuring pressure hysteresis. Specifically, we measured heat flow signals over three cycles of increasing and decreasing hydrostatic pressure between 1 bar and 150 bar at 311 K. By comparing the onset pressures for compression-induced exotherms and decompression-induced endotherms, we were able to directly measure a pressure hysteresis of 62 ± 4 bar for (DA)2MnCl4, which is in excellent agreement with the predicted value of 70 bar at 311 K (Fig. 3c, Supplementary Fig. 18, Supplementary Table 11).
Reversible barocaloric effects in (NA)2CuBr4
In an effort to target barocaloric materials with large reversible entropy and adiabatic temperature changes at even lower pressures, we searched for a 2-D perovskite that undergoes a hydrocarbon order–disorder transition near ambient temperature with a thermal hysteresis of less than 1 K. Unlike (DA)2MnCl4, however, the total entropy of the order–disorder transition in most 2-D perovskites is partitioned across one or more minor—lower entropy—phase transitions in addition to the principal transition (Fig. 1b, Supplementary Tables 1–3). Although not necessarily detrimental to barocaloric cooling performance34, the presence of multiple successive transitions at different temperatures complicates the evaluation of barocaloric properties because each minor and major transition has an independent hysteresis loop—often greater than 1 K—with different pressure dependences (Supplementary Table 4). With a lack of suitable existing compounds, we endeavored to synthesize a new 2-D perovskite that features a sharp order–disorder transition near ambient temperature with ultralow hysteresis and a high sensitivity to pressure.
After screening different combinations of metal cations, halide anions, and alkylammonium chain lengths, we discovered a 2-D perovskite (NA)2CuBr4 (NA = nonylammonium) that undergoes an order–disorder transition at 305 K with a high ΔStr (76 J kg–1 K–1) and hysteresis of only 0.4 K for a powder sample (Fig. 2b) and 1.0 K for a single-crystal sample (Fig. 4e). Variable-temperature PXRD experiments, combined with single-crystal structures at 270 K and 335 K, revealed that the phase transition involves a 4.0% increase in volume (ΔVtr = 25.3 cm3 kg−1) and a 2.9% (0.67 Å) increase in interlayer distance (Fig. 2d, f; Supplementary Figs. 1 and 4). The crystallographic volume change yields a predicted barocaloric coefficient of 33.3 K kbar−1, while the volume change determined by He pycnometry (ΔVtr = 20.0 cm3 kg–1)—which accounts for He permeation—yields a predicted barocaloric coefficient of 26.3 ± 2.5 K kbar–1 (Supplementary Table 10).
Isobaric HP-DSC experiments confirmed that (NA)2CuBr4 features high barocaloric coefficients of 26.7 ± 0.4 K kbar–1 during both heating and cooling (Fig. 3d, j; Supplementary Fig. 11, Supplementary Table 8). In fact, these values represent one of the highest sets of barocaloric coefficients ever measured (Supplementary Table 5). As a result of its high barocaloric coefficient, ultralow hysteresis, and extremely sharp transition, the powder sample of (NA)2CuBr4 has, to the best of our knowledge, the lowest reported Prev for a barocaloric material of 16 bar (Fig. 7b), which is within the pressure range already accessed during commercial vapor-compression refrigeration cycles19. The low value of Prev was further confirmed through quasi-isothermal pressure cycling experiments at 306 K, where we directly measured a pressure hysteresis of 18 bar (Fig. 3f, Supplementary Fig. 19). Moreover, a large reversible entropy change, with a maximum value of 68 J kg−1 K−1 (90% of ΔStr at 1 bar), is accessible over the temperature range of 2 K at an operation pressure of 150 bar for the powder sample (Supplementary Fig. 16c, d). Through additional HP-DSC experiments conducted at higher pressure ranges up to 500 bar, we demonstrated that a large reversible entropy change of 78 J kg−1 K−1—equivalent to the full transition entropy—is accessible over a wider temperature range of 5 K and 10 K at 300 bar and 500 bar, respectively (Figs. 5d–f, 6b; Supplementary Figs. 21 and 22). Note that the order–disorder transition over this extended pressure range is associated with a similar volume change (21–25 cm3 kg–1) as revealed by PXRD experiments (Supplementary Figs. 4, 26–29; Supplementary Table 12), and thus maintains a high sensitivity to pressure of 24 K kbar−1 (Fig. 3i, j; Supplementary Fig. 7; Supplementary Table 8).
a Comparison of the phase-change entropy, ΔStr, and temperature, Ttr, for different classes of barocaloric materials. Note that ΔStr and Ttr are shown for endothermic transitions, and ΔStr represents the maximum isothermal entropy change that could be driven by the pressure-induced phase transition. b Comparison of thermal hysteresis, ΔThys, and barocaloric coefficient, dT/dP, for leading barocaloric materials, with dT/dP values corresponding to exothermic transitions for materials that exhibit conventional barocaloric effects and endothermic transitions for materials that exhibit inverse barocaloric effects. The minimum pressure required to achieve a reversible entropy change, Prev, is calculated as Prev = ΔThys/|dT/dP| and indicated by shading from blue (high Prev) to white (low Prev). A comprehensive tabulation of barocaloric properties, including reversible and irreversible ΔSit values, is provided in Supplementary Tables 5 and 6.
Impact of thermal contact on low-pressure reversibility
Our results for single-crystal samples of (DA)2MnCl4 and (NA)2CuBr4 show how improved thermal contact can lead to even larger reversible barocaloric effects at lower pressures (Fig. 4, Supplementary Fig. 17). For instance, at a 150-bar driving pressure, the maximum value of ΔSit,rev increases from 75 J kg−1 K−1 (powder with poor thermal contact) to 190 J kg−1 K−1 (single crystal with improved thermal contact) for (DA)2MnCl4 and from 68 J kg−1 K−1 (powder) to 78 J kg−1 K−1 (single crystal) for (NA)2CuBr4 (Supplementary Table 7). At even lower pressures, (NA)2CuBr4 features a reversible isothermal entropy change of 4 J kg−1 K−1 and 11 J kg−1 K−1 at 20 bar and 40 bar, respectively, for a powder sample (Fig. 5f, Supplementary Fig. 16d) and of 5 J kg−1 K−1 and 49 J kg−1 K−1 at 40 and 60 bar, respectively, for a single-crystal sample (Fig. 3e, Supplementary Fig. 17f). Notably, the single-crystal sample of (NA)2CuBr4 exhibits a reversible adiabatic temperature change (ΔTad,rev) of 2.3 K at a 150-bar driving pressure (Supplementary Fig. 17g), which represents, to the best of our knowledge, the first demonstration of ΔTad,rev of a sizable magnitude—sufficient to create much wider temperature spans through regeneration35—near room temperature at a more practically accessible pressure for a barocaloric material.
Relationships between entropy changes and reversibility
To provide additional insight into the structural and chemical factors that influence barocaloric effects in 2-D perovskites, we used X-ray crystallography and infrared (IR) spectroscopy to compare the nature of the hydrocarbon order–disorder transition in (NA)2CuBr4 and (DA)2MnCl4. In particular, we hypothesized that the increased size of the halide pocket in (NA)2CuBr4 (30.5 Å2) relative to (DA)2MnCl4 (26.3 Å2)—coupled with weaker N−H⋅⋅⋅Br hydrogen bonds at the organic–inorganic interface—would lead to increased free volume in the organic bilayer of the Cu compound (Supplementary Figs. 34 and 35) and, as a result, greater disorder in the LT phase. As anticipated, the atoms in the NA chains of (NA)2CuBr4 have much larger atomic displacement parameters in the LT phase than those in the DA chains of the LT phase of (DA)2MnCl4 (Fig. 8). This is consistent with the LT phase of (NA)2CuBr4 having increased vibrational and conformational degrees of freedom, which would reduce the entropy difference between the LT and HT phases (Supplementary Notes 1 and 2).
Conformations of the alkylammonium chains in the LT and HT phases of (a) (DA)2MnCl4 and (b) (NA)2CuBr4, with atomic displacement parameters shown at 50% probability for the C and N atoms of the alkylammonium chains. In the LT phase, decylammonium (DA) chains in (DA)2MnCl4 display one conformation, with a single gauche C–C bond (C2–C3), while nonylammonium (NA) chains in (NA)2CuBr4 adopt two conformations, alternating between chains with a gauche C1–C2 bond (chain A) and those with a gauche C2–C3 bond (chain B). Purple, orange, green, brown, gray, and blue spheres represent Mn, Cu, Cl, Br, C, and N atoms, respectively. H atoms are omitted for clarity. Note that DA chains are disordered over a special position in both the LT and HT phases, while NA chains are modeled with two-part disorder in the LT phase and disordered over a special position in the HT phase. Temperature dependence of Uequiv (equivalent isotropic displacement parameters) is shown for alkylammonium cations in (c) (DA)2MnCl4 and (d) (NA)2CuBr4, at 100 K, 270 K (LT phase), and 330/335 K (HT phase). Error bars represent standard uncertainties.
The increased entropy of the alkylammonium chains of (NA)2CuBr4 prior to the phase transition is further corroborated by a broad feature in the heat capacity from 220–250 K that is consistent with a gradual activation of conformational degrees of freedom from the fully ordered organic bilayer that is present at 100 K (Supplementary Figs. 32 and 36). Variable-temperature IR spectra are also consistent with increased conformational entropy for the hydrocarbon chains in the LT phase of (NA)2CuBr4. Specifically, IR spectra show a band near 1360 cm–1, which can be assigned to CH2 wagging from gt2n+1g′-type kinks, that is present below the phase transition temperature for (NA)2CuBr4 but only above the phase transition temperature for (DA)2MnCl4 (Supplementary Fig. 37). As discussed in greater detail in Supplementary Note 6, the IR spectra also suggest that the local environment around the chain ends (CH3) and headgroups (NH3+) is more similar in the LT and HT phases of (NA)2CuBr4 than in those of (DA)2MnCl4 (Supplementary Table 13).
Although increasing the halide pocket size through Br substitution leads to a decreased entropy change (Fig. 7a), it also likely contributes to the enhanced reversibility of the (NA)2CuBr4 phase transition through two primary effects. First, the softer nature of Br anions—along with the higher degree of disorder in the alkylammonium chains in the LT phase—makes the (NA)2CuBr4 lattice more compressible than the (DA)2MnCl4 lattice (Supplementary Table 9). Since the barocaloric coefficient dT/dP of a solid tends to increase with increasing compressibility12,36, this causes the phase transition in (NA)2CuBr4 to be more sensitive to pressure, which reduces the minimum pressure required to overcome hysteresis and induce a reversible phase transition. Indeed, dT/dP for the ordering transition in (NA)2CuBr4 is 29% higher than for (DA)2MnCl4 (Supplementary Table 7). Second, the increased free volume and presence of additional vibrational and conformational degrees of freedom in both the LT and HT phases should render the two phases more compatible, reducing the activation energy barrier for nucleation of a more ordered bilayer phase during cooling—or compression—and lowering both the isobaric and isothermal hysteresis37.
Impact of hysteresis on thermodynamic efficiency
In addition to its influence on operating pressure, hysteresis adversely impacts the second-law efficiency and coefficient of performance (COP) of any caloric cooling cycle because of dissipative heat losses16,17. The impact of hysteresis on efficiency can be quantified by calculating an idealized thermodynamic efficiency, η—relative to the Carnot efficiency—with a simple material model that accounts for dissipative losses due to hysteresis in a Carnot-like cycle16:
Based on this model, caloric materials with ΔThys/ΔTad,max of less than 10% will have idealized second-law efficiencies competitive with those of conventional vapor compression-based systems (~85%)38. Notably, (DA)2MnCl4 and (NA)2CuBr4 have the potential to reach the second-law efficiencies of 82 and 79%, respectively, based on their intrinsic barocaloric properties (Supplementary Table 6). Further, both compounds display very large reversible refrigeration capacities (RCrev) under easily accessible pressures (Fig. 5c, f).
Discussion
Overall, these results highlight exciting opportunities to exploit the tunability of 2-D perovskites to independently manipulate the hysteresis, sharpness, entropy, and sensitivity to pressure of hydrocarbon order–disorder phase transitions for improved barocaloric performance. For instance, it should be possible to realize phase transitions with even higher entropy changes through functionalization of the organic bilayers—such as by introducing hydrogen bond donor–acceptor pairs39,40—and even lower hysteresis through modification of the organic–inorganic interface—such as by incorporating mixtures of different halide anions or introducing defects. Further, the modular nature and high tunability of 2-D perovskites can be leveraged to optimize, in addition to intrinsic barocaloric properties, a host of factors that are critical to realizing scalable and efficient solid-state cooling technologies, including safety, flammability, and thermal conductivity (Supplementary Figs. 39–42). In addition, the anisotropic nature of the order–disorder transition in (DA)2MnCl4 and (NA)2CuBr4—as highlighted by variable-temperature atomic force microscopy (AFM) experiments on single crystals directly grown on a Si wafer (Fig. 9, Supplementary Fig. 43)—suggests that uniaxial stress, which can be readily applied through mechanical actuation, may be able to drive large elastocaloric effects in 2-D perovskites and that barocaloric effects should be accessible in 2-D perovskites with sub-micron thickness. More broadly, solid-state hydrocarbon order–disorder transitions are not unique to 2-D perovskites, and many other classes of layered materials—including di-n-alkylammonium salts41, alkylammonium-modified layered silicates42, and metal-alkylphosphonate salts43—undergo reversible phase transitions near ambient temperature that should produce colossal barocaloric effects and have yet to be explored.
a Optical images of (DA)2MnCl4 single crystals directly grown on Si substrates through an anti-solvent vapor-assisted capping crystallization method. b Bright field (top) and dark field (bottom) images of a sub-micron thick single crystal. c Variable-temperature atomic force microscope (AFM) imaging experiments for a sub-micron thick (DA)2MnCl4 single crystal. d Height profiles of a sub-micron thick (DA)2MnCl4 single crystal in the low-temperature (LT, left) and high-temperature (HT, right) phases. e Thickness of a single crystal of (DA)2MnCl4 as a function of temperature. The heating-induced transition from the LT phase to HT phase gives rise to an 7.9% change in height, which agrees well with the 7.4% predicted from crystallographic data obtained from variable-temperature PXRD experiments at 30 °C and 45 °C. Error bars were obtained from the mean square difference between all data points in the scan region and the fitted step height. Thermal cycling AFM experiments are described in Supplementary Fig. 43.
Methods
Materials
All compounds were synthesized and handled in air unless otherwise noted. Anhydrous diethyl ether was obtained from a Pure Process Technology anhydrous solvent system. Anhydrous methanol and ethanol were purchased from a commercial vendor and used as received. All other reagents were purchased from commercial vendors and used as received.
Synthesis of (DA)2MnCl4 (DA = decylammonium, C10H21NH3)
Decylamine (≥99.0% purity) and hydrochloric acid (HCl, 37 wt %) were purchased from Sigma Aldrich and used without further purification. Decylammonium chloride (C10H21NH3Cl, (DA)Cl) was first synthesized by adding HCl (550 μL, 6.6 mmol) into a solution of decylamine (1.1 mL, 5.5 mmol) in ca. 5 mL ethanol in an ice water bath with stirring. After evaporating the solvent under reduced pressure, the resulting white powder of (DA)Cl was washed with diethyl ether and dried under vacuum at room temperature for 1 day. Crystalline powders of (DA)2MnCl4 were prepared in a similar manner to previously reported syntheses26,44. Specifically, (DA)Cl (96.9 mg, 0.5 mmol) was first dissolved in 4.0 mL of ethanol. After several minutes of stirring, MnCl2·4H2O (49.5 mg, 0.25 mmol) was added to the solution, and the solution was heated to 65 °C. Pale-pink crystals were obtained upon cooling the resulting solution to room temperature at a rate of 4 K h−1. The crystals were filtered, washed with diethyl ether (5 × 10 mL), and dried under vacuum for 6 h to afford 45.2 mg (35.2% yield) of product. Single crystals suitable for X-ray structure determination were obtained by cooling at a rate of 2 K h−1.
Synthesis of (NA)2CuBr4 (NA = decylammonium, C9H19NH3)
Nonylamine (≥99.5% purity) and hydrobromic acid (HBr, 48 wt %) were purchased from Sigma Aldrich and used without further purification. Nonylammonium bromide (C9H19NH3Br, (NA)Br) was first synthesized by adding HBr (545 μL, 4.8 mmol) into a solution of nonylamine (733 μL, 4.0 mmol) in ca. 5 mL ethanol in an ice water bath with stirring. After evaporating the solvent under reduced pressure, the resulting white powder of (NA)Br was washed with diethyl ether and dried under vacuum at room temperature for 1 day. Crystalline powders of (NA)2CuBr4 were prepared by dissolving of CuBr2 (402 mg, 1.8 mmol) and (NA)Br (807 mg, 3.6 mol) in 2 mL of ethanol at 65 °C. The solution was slowly cooled to room temperature at a rate of 4 K h−1 and then further cooled to 5 °C for 1 h. The resulting dark purple precipitate was filtered, washed with diethyl ether (5 × 10 mL), and dried under vacuum for 12 h to afford 705 mg (58.3% yield) of product. Single crystals suitable for X-ray structure determination were obtained by slow evaporation of a 1-mL solution of (NA)2CuBr4 (202 mg, 0.3 mmol) in methanol. Anal. Calcd. for (C9H19NH3)2CuBr4: C: 32.19%, H: 6.60%, N: 4.17%, Br: 47.58%. Found: C: 31.84%, H: 6.69%, N: 4.43%, Br: 47.76%.
Growth and characterization of isolated single crystals on substrates
Single crystals of (DA)2MnCl4 were grown onto p-type <100> Si substrates based on an anti-solvent vapor-assisted capping crystallization (AVCC) method45. Specifically, crystals of (DA)2MnCl4 were dissolved at a concentration of 100 mM in a 1:1 solution of ethanol and methanol, which was then pipetted onto plasma-cleaned Si substrates and immediately capped with polished c-plane sapphire discs. The capped substrates were placed alongside vials of diethyl ether in a closed jar and allowed to dry over several days. Optical images of crystals were taken using a Motic Panthera TEC microscope. Thickness and roughness of crystals grown by the AVCC method were measured using an atomic force microscope (Jupiter XR, Asylum Research, Santa Barbara, CA, USA) in tapping mode. The step height was calculated in the Gwyddion software by fitting the scanned region with a piecewise function over the crystal surface and the substrate. Variable temperature measurements were performed using the PolyHeater accessory.
Thermogravimetric analysis
Samples were loaded into a TGA 550 from TA Instruments in open aluminum pans with a stainless-steel bail under air and heated at a rate of 4 K min–1 from ambient to 500 °C under a 10 mL min–1 N2 flow with an empty aluminum pan/stainless-steel bail used as a reference counterweight. The TGA mass was calibrated using a series of 3 reference masses, while the TGA temperature was calibrated to the Curie temperature of nickel. The thermogravimetric analyses of (DA)2MnCl4 and (NA)2CuBr4 are shown in Supplementary Figs. 39 and 40.
High-pressure differential scanning calorimetry (HP-DSC)
DSC measurements over the pressure range from 1 to 150 bar were carried out in a Netzsch high-pressure DSC (DSC 204 HP Phoenix) equipped with a liquid nitrogen cooling system. The DSC sample cell is surrounded by an autoclave, where the internal pressure and gas flow are regulated by an electronic pressure control device. The autoclave is connected to a circulating water bath that provides an additional source of external temperature control during experiments. Temperature and heat flow signals were calibrated at each measured pressure using an indium standard46. Helium gas (ultra-high purity, 99.999%) was used as a pressure-transmitting medium. All DSC samples were prepared in air. For powder samples, 5–10 mg of loosely packed ground single crystals were sealed in an aluminum pan with a pierced lid. For single-crystal samples, a large single-crystal flake was lightly pressed onto the bottom of an aluminum pan, which was then sealed with a pierced lid. An empty, aluminum pan with a pierced lid was used as a reference. All measurements were carried out under flowing gas with a He flow rate of 50 mL min–1. Unless otherwise noted, heating and cooling rates of 2 K min−1 were used for isobaric measurements.
DSC measurements over the pressure range from 300 to 500 bar were conducted in a Setaram high-pressure DSC (Microcalvet) using microcrystalline powder samples. The calorimeter was calibrated based on the Joule effect, which does not require reference materials. For each set of measurements, 7 mg of sample was encapsulated in the high-pressure vessel of the calorimeter, and the pressure was generated by a compressing piston using Helium gas as a pressure-transmitting medium.
Determination of T tr, ΔH tr, and ΔS tr
Phase transition temperatures, Ttr, and enthalpies, ΔHtr, were determined using the TRIOS software from TA Instruments. Peaks were selected for analysis by defining a temperature range containing the peak of interest. The lower and upper bounds of the temperature range were chosen to encompass the phase transition, which starts with a deviation from the baseline and ends with a return to baseline. Prior to determination of Ttr or ΔHtr, a baseline, which models the heat flow in the absence of a phase transition, must be generated to approximate the baseline in the transition region. Baselines were generated within the defined temperature range to determine the slope of the lower and higher temperature limits and shape of the baseline. Baselines were generated using mutual tangent slopes before and after the transition peak with a sigmoidal baseline, which we found to produce the most physically reasonable baselines. The extrapolated onset temperature was reported as the transition temperature, as is standard in DSC data analysis, because the onset temperature—unlike the peak temperature—is relatively independent of experimental parameters like heating rate or sample mass. The onset temperature was determined by identifying the region of the onset transition peak that has the steepest slope, defining a tangent to that region, and then extending the tangent to the generated baseline. The intersection between the baseline and the tangent is reported as Ttr. Transition peaks were integrated between the upper and lower temperature limits with the baseline subtracted to provide ∆Htr, and phase transition entropies, ∆Str, were calculated as ∆Str = ∆Htr/Ttr. If physically reasonable limits were chosen, Ttr and ∆Htr did not depend strongly on the choice of the temperature limits, and such variations were within the error of the measurements, which is estimated to be ± 0.04 °C for Ttr and <3% for ∆Htr based on repeated measurements of the melting transition of an indium standard.
Construction of isobaric entropy curves
Isobaric entropy changes, ΔSib, were calculated as a function of temperature and pressure by integrating the HP-DSC heat flow signal Q, obtained at a scan rate of \(\dot{T}\) near the transition peak over the temperature range from Ti to Tf after baseline subtraction33,47:
In a typical isobaric measurement with a scan rate of 2 K min−1 at pressures up to 150 bar, the temperature range for peak integration, ΔTint = Tf – Ti, was set to 16 K for microcrystalline powder samples, for consistency, with Ti = Ttr − 8 K and Tf = Ttr + 8 K. For single-crystal samples, due to their sharper transition peak width, a narrower temperature range was chosen, with ΔTint of 5 K and 2 K for (DA)2MnCl4 and (NA)2CuBr4, respectively. For isobaric measurements with a scan rate of 0.5 K min−1 over the pressure range of 300 to 500 bar, ΔTint of 12 K and 10 K were chosen for (DA)2MnCl4 and (NA)2CuBr4, respectively. Baselines for peak integration were generated using mutual tangent slopes, and the tangents before and after the transition peak were created from Ti – 4 K to Ti and from Tf to Tf + 4 K, respectively. Tangent slopes were created over this extended temperature range to minimize any uncertainty in integration, particularly at higher gas pressures which lead to more noisy baselines. Since the integration was carried out near the transition without taking into account the heat capacity of each phase to emphasize the contributions from the order–disorder transition, the isobaric entropy curves are flat before and after the phase transition region (Supplementary Figs. 10, 11, 14, 15, 20, 21).
A positive slope in the isobaric entropy curves was introduced by adding the entropy contribution from heat capacity [Sc(T)], calculated through Eq. (3), to the isobaric entropy changes associated with the phase transition.
For both compounds, the reference temperature T0 was set to 290 K, with Sc(T0) = 0. The heat capacity values during the phase transition (between Ti and Tf) were estimated through \({c}_{p}\,=\,(1-x){c}_{P}^{{{{{{\rm{LT}}}}}}}\,+\,x{c}_{P}^{{{{{{\rm{HT}}}}}}}\) where x is the phase fraction of the material in the HT phase at the temperature T.
The dependence of the heat capacity contribution Sc(T) on applied pressure can be estimated by calculating the pressure-induced changes in isothermal entropy that arises outside of the phase transition region. This entropy contribution, ΔS+, is often referred to as the elastic heating contribution4,48 and can be calculated using the following formula derived from the Maxwell relation (∂V/∂T)P = −(∂S/∂P)T:
For normal barocaloric materials with (∂V/∂T)P > 0, this entropy contribution originates from the applied pressure counteracting entropy increases due to thermal fluctuations. By assuming that the thermal expansion coefficient is independent of pressure, ΔS+ can be estimated as
where V, ΔP, and α denote the specific volume, driving pressure ΔP = Pf − Pi, and thermal expansion coefficient at ambient pressure, respectively, with α = V−1(∂V/∂T)P=0. Equation (5) is commonly used to estimate ΔS+ since high-pressure heat capacity measurements are difficult to perform accurately. At a given driving pressure ΔP, isobaric entropy curves that include the contributions from heat capacity were obtained by adding Sc(T) to ΔSib and shifting the curves downward by ΔS+ of the LT phase.
Although both (DA)2MnCl4 and (NA)2CuBr4 display large thermal expansion coefficients on the order of 10−4 K−1, their estimated ΔS+ values are small relative to their transition entropies at pressures up to 150 bar. For example, for a driving pressure of 150 bar, ΔS+ in the LT phases of (DA)2MnCl4 and (NA)2CuBr4 is predicted to be just −3 J kg−1 K−1 and −4 J kg−1 K−1, respectively. We note, however, that ΔS+ can become significant at higher driving pressures and can further enhance the barocaloric effect. The calculated ΔS+ values are summarized in Supplementary Table 9.
Evaluation of isothermal entropy changes
Pressure-induced isothermal entropy changes, ΔSit, were calculated by the quasi-direct method33 as the difference between ΔSib at ambient pressure P0 of 1 bar, ΔSib(T, P0), and ΔSib at elevated pressure, ΔSib(T, P). For ΔSit corresponding to the endothermic, disordering transition induced by decompression (P → P0), ΔSib values were obtained from heating data:
For ΔSit corresponding to the exothermic, ordering transition induced by compression (P0 → P), ΔSib values were obtained from cooling data:
For operating pressures above Prev, the reversible values of ΔSit were estimated from the overlap between compression-induced and decompression-induced ΔSit curves reflected across the temperature axis. From the reversible isothermal entropy curves, the reversible refrigeration capacity values, RCrev, were calculated as ΔSit,rev,max × ΔTFWHM, where ΔSit,rev,max is the maximum reversible isothermal entropy change for a given pressure and ΔTFWHM is the full width at half maximum of the reversible isothermal entropy peak at a given pressure (Fig. 5c, f).
Evaluation of adiabatic temperature changes
For evaluations of adiabatic temperature changes, two different methods were used: (i) the indirect method and (ii) the quasi-direct method. The indirect method is based on the simple relationship ΔTad,indirect = –TΔSit/cp (for specific values used for the calculation, see Supplementary Table 6). Although the indirect method is a useful way of evaluating an upper bound for the magnitude of an adiabatic temperature that could be achieved with a given material, this approach is not appropriate for calculating the dependence of ΔTad on operating pressure or the magnitude of ΔTad that can be accessed under reversible conditions. Moreover, the indirect method is accurate only when cp is relatively independent of pressure and ΔTad,indirect is sufficiently smaller than T (ref. 33.).
The magnitude of the adiabatic temperature change that can be accessed for a given pressure shift, however, can be evaluated through the so-called quasi-direct method by constructing two isobaric curves on a temperature (T) vs. entropy (S) plot at two different pressures (typically ambient pressure, P0, and applied pressure, P) (refs. 11,33). In such a plot, the width of horizontal—and adiabatic—lines between two isobaric entropy curves corresponds to the magnitude of the adiabatic temperature change that will be accessible for a given change in pressure. For the adiabatic temperature change that is induced by the first pressure change (decompression-induced cooling, for instance), the irreversible ΔTad,q-d is calculated as ΔTad,q-d = T(S, P0)heating − T(S, P)heating (Supplementary Fig. 33). For compression-induced heating, the irreversible ΔTad,q-d is similarly calculated as ΔTad,q-d = T(S, P)cooling − T(S, P0)cooling. For reversible adiabatic temperature changes upon cyclic pressure changes to above Prev,ad (the pressure that must be exceeded in order to fully overcome the hysteresis loop), the reversible temperature change is evaluated by calculating the difference between the temperature curves for cooling at applied pressure and heating at ambient pressure, with ΔTad,rev = |T(S, P)cooling − T(S, P0)heating| (see Supplementary Note 4 for details). We note that direct measurements under adiabatic conditions—although still challenging for barocaloric materials—will be important for the more accurate and reliable evaluation of adiabatic temperature changes.
Quasi-isothermal HP-DSC
During quasi-isothermal pressure cycling experiments, heat flow signals were measured as a function of time while applying or removing a hydrostatic pressure of 150 bar and 105 bar for (DA)2MnCl4 and (NA)2CuBr4, respectively. The temperature was held at 311.1 K for (DA)2MnCl4 and 305.5 K for (NA)2CuBr4, respectively. The pressure was increased linearly at a rate of 6 bar min–1 and decreased asymptotically at an average rate of 13 bar min–1. To distinguish heat flow signals associated with the pressure-induced phase transitions of each compound from those associated with compression and decompression of He gas, 5 mg of (C12H25NH3)2MnCl4, which was prepared according to a previously reported procedure49, was used as a control sample because it does not undergo any phase transitions until above 330 K, well above the transition temperatures for (DA)2MnCl4 and (NA)2CuBr4. The heat flow signals measured during pressure cycling (C12H25NH3)2MnCl4 at 311 K and 306 K were modeled as a baseline and subtracted from the raw sample data for (DA)2MnCl4 and (NA)2CuBr4, respectively, to yield pressure-induced heat flow signals as a function of time (Supplementary Figs. 18d, 19d). Similar to the determination of the transition temperature, Ttr, the extrapolated onset pressures were defined as the transition pressure for pressure-induced endotherms and exotherms. Specifically, the onset pressure was determined by first generating baselines using mutual tangent slopes before and after the pressure-induced transition peak, with the intersection between the baseline and the tangent of the peak representing the onset point. The corresponding pressure at the onset time is reported as the phase transition pressure, and the pressure hysteresis is calculated as the difference between the phase transition pressures during compression and decompression.
During pressure cycling, quasi-isothermal conditions were maintained by adjusting the set temperature of the circulating water bath surrounding the autoclave to compensate for small temperature fluctuations induced by gas compression and decompression. Note that the external thermal control measures were identical for all three samples (control, (DA)2MnCl4, and (NA)2CuBr4). Since the rate at which the pressure was decreased was faster than the rate it was increased, decompression resulted in a larger change in temperature (1 K) than compression (<0.3 K) (Supplementary Figs. 18c, 19c). However, these small temperature changes were quickly recovered, such that the measured sample temperatures near the phase transition onsets were in close proximity during both compression and decompression (<0.2 K) (Supplementary Figs. 18e, 19e).
Heat capacity measurements
A Discovery 2500 DSC with a RCS 90 cooling system (TA Instruments) was used to measure the heat capacity of (DA)2MnCl4 and (NA)2CuBr4 using the ASTM Standard E1269. All runs used to calculate heat capacity were performed under the standard manufacturer calibrations. This includes the Tzero calibration, which achieves flat (<5 µW variation) baselines by calibrating the cell to a heat flow model containing thermal resistance and capacitance terms for the sample and reference sides of the cell. In addition, an indium standard was used to calibrate the temperature and cell constant.
The ASTM E1269 method calculates heat capacity from three separate DSC runs, which are performed sequentially. All three runs were comprised of a temperature ramp (10 K min–1) over the temperature range of interest with 10 min isothermal holds at the minimum and maximum temperatures to stabilize heat flows before and after the temperature ramps. The first run was conducted with empty pans in the sample and reference position of the DSC to establish a baseline in the absence of sample. Though the DSC baseline is calibrated using the Tzero method, that calibration returns a flat baseline of zero heat flow to an empty cell, while the ASTM baseline accounts for asymmetries that may be introduced due to the introduction of pans to the sample and reference position. The second run was conducted with an empty reference pan and a sample pan containing a sapphire disc to calibrate the heat capacity, and the third run was conducted by replacing the sample pan containing the sapphire with a sample pan containing either (DA)2MnCl4 or (NA)2CuBr4.
All samples of (DA)2MnCl4 and (NA)2CuBr4 for heat capacity measurements were prepared under an N2 atmosphere in Tzero aluminum pans and sealed using a Tzero aluminum press. To ensure adequate heat flows and heat capacity signal, 10 mg or more of sample were used for each heat capacity measurement. In addition, the samples were packed into the pan using the Tzero powder preparation kit to improve thermal contact. The ASTM method specifies that the masses of the empty sample and reference pans should be matched, with ASTM recommending ±0.01 mg variation and TA instruments recommending ±0.05 mg variation. The DSC 2500, however, accounts for pan mass differences and the resulting heat flows due to the heat capacity of aluminum using the T4P heat flow. Therefore, when using the T4P heat flow, the pan mass matching criterion is not as stringent. Nevertheless, pan masses were selected here to be within ±0.1 mg, with the total empty pan mass being near 50 mg.
Non-hermetic Tzero pans were used to allow for He gas to be present over the sample to be consistent with high-pressure DSC measurements and because the non-hermetic lids press directly on the sample, improving thermal contact. The DSC 2500 also features a robotic autosampler, which precisely and repeatably loads the sample and reference pans into the DSC cell. For all three runs, the reference pan remained in the cell and was not moved, with only the sample pan being exchanged by the autosampler. The cell purge gas was He at a flow rate of 50 mL min–1. Samples were held under He for at least 30 min prior to the temperature ramp.
To examine the variability in our measurement and obtain a representative average heat capacity curve, the measurements of (DA)2MnCl4 and (NA)2CuBr4 were each conducted 8 times. The same reference pan and sapphire pan were used for all measurements, while a new sample pan with new sample was used for each measurement. All (DA)2MnCl4 and (NA)2CuBr4 heat capacity measurements were conducted between at least 230 and 360 K, and the averaged data is shown in Supplementary Fig. 31. After noticing a low-temperature feature in the heat capacity of (NA)2CuBr4, several additional runs were conducted down to 190 K, and an additional run of (DA)2MnCl4 was also conducted down to 190 K (Supplementary Fig. 32). The ASTM heat capacity was calculated using a feature in the TRIOS software (TA Instruments), which calculates the heat capacity from a set of three ASTM runs (the baseline, sapphire, and sample runs) with each heat capacity calculation representing a unique set of three runs. The heat capacity data was interpolated onto a common temperature axis and averaged at each temperature point to arrive at an average heat capacity curve for (DA)2MnCl4 and (NA)2CuBr4. The error was also calculated at each temperature point and is based on the ASTM recommendation, which specifies reporting an error of 2.8 times the standard deviation.
Powder X-ray diffraction (PXRD)
PXRD data for (DA)2MnCl4 and (NA)2CuBr4 were collected on beamline 17-BM-B at the Advanced Photon Source (APS) at Argonne National Laboratory, with an X-ray wavelength of 0.45237 Å. For variable temperature and pressure experiments, approximately 10 mg of sample was loaded into a sapphire capillary (1.52 mm × 1.07 mm × 50.8 mm, Saint-Gobain Crystals). Each capillary was attached to a custom-designed flow cell equipped with a gas valve, which was mounted onto the goniometer head. A syringe pump (Teledyne ISCO D65) was then connected via a 1/16″ gas line to the flow cell and used to control the hydrostatic pressure of He gas (ultra-high purity, 99.999%) from 80 to 360 bar. The internal sample temperature was monitored during PXRD experiments via a K-type thermocouple (0.1 K accuracy) that was in contact with the powder sample within the capillary. The sample temperature was controlled by an Oxford Cryostream (Oxford Cryostream 800+).
In a typical isobaric, variable-temperature PXRD experiment, the sapphire capillary was first equilibrated at 370 K for 10–20 min and then the Cryostream temperature was decreased from 370 to 250 K at a rate of 6 K min−1, which led to a change in sample temperature from 335 to 275 K at an average rate of ~3 K min−1. During cooling, powder patterns were collected every 10–20 seconds at a temperature interval of ~1 K. Isothermal, variable-pressure experiments were carried out to determine the compressibility of the LT and HT phases of each sample. Prior to each measurement, samples were equilibrated at the set temperature for 20 minutes. Powder patterns were then collected every 5 bar from 80 to 300 bar, equilibrating for 2 min at each pressure.
Diffraction patterns were analyzed using the software TOPAS-Academic50. Unit cell parameters of diffraction patterns were determined by using a standard peak search followed by indexing with a single value decomposition approach51. A structureless Le Bail refinement was then performed to refine the unit cell parameters. Variable-temperature PXRD data obtained under isobaric conditions are shown in Supplementary Figs. 23–25 for (DA)2MnCl4 and Supplementary Figs. 26–29 for (NA)2CuBr4. Comparisons with simulated powder patterns are provided in Supplementary Fig. 30. For both compounds, the temperature and pressure dependence of interlayer distances, unit cell parameters, and specific volumes are provided in Supplementary Figs. 1–5. The thermal expansion coefficients, isothermal compressibility, and volume change during transition each compound are tabulated in Supplementary Tables 9 and 12, and unit cell parameters are tabulated in Supplementary Tables 14 and 15.
Determination of T tr from PXRD
Isobaric, variable-temperature experiments were carried out from 80 to 360 bar to determine the phase transition temperature, Ttr, for (DA)2MnCl4 and (NA)2CuBr4 (Supplementary Figs. 23–29). In particular, we evaluated the pressure dependence of the exothermic transition from the high-temperature (HT) to low-temperature (LT) phases during cooling, Ttr,cooling, because temperature control during cooling was more reliable than during heating. To identify Ttr, changes in the high-intensity (00l) peaks in the low-angle region (<4°) of the powder patterns were monitored, with a particular focus on the emergence of a higher-angle shoulder on the right side of each peak that indicates the emergence of the smaller unit cell of the LT. Note that the shoulder intensity as small as 2% of the parental peak intensity was discernible. Since the sample temperature was varied continuously—similar to DSC experiments—the onset temperature for the emergence of the LT phase is reported as Ttr. More specifically, the transition onset temperature was estimated to be just above the temperature at which the first powder pattern with the shoulder peaks was. This approach enabled the identification of transition temperatures with an estimated accuracy of 1–2 K.
To further improve the accuracy of Ttr determination, we used data from the thermocouple embedded in the sample capillary that recorded the sample temperature every 2 s. During cooling, the thermocouple temperature trace features a peak, which is attributed to the latent heat of the exothermic transition. Despite the seemingly small signal, this feature can be clearly detected by monitoring the change in sample cooling rate over time. Specifically, the phase transition leads to a sudden spike in the first derivative of sample temperature with respect to time. The onset of the phase transition was assigned to the temperature at which the first local maximum of the cooling rate curve appears, as this feature—which corresponds to the tangent of the onset transition peak—can be reliably identified across all datasets. Additionally, the uncertainty associated with the determination of the transition onset temperature was defined as the full width at half maximum of the cooling rate peak, which ranges from 1 to 2 K. Note that the Ttr values were determined using the sample thermocouple temperature data. At ambient pressure, the onset transition temperatures, Ttr,cooling, determined by these PXRD experiments were in excellent agreement with those determined by DSC, with a difference of less than 0.4 K. Since the goal of these experiments was to determine the pressure dependence of Ttr, rather than the absolute values of Ttr, the transition temperatures determined via PXRD were calibrated using the Ttr,cooling value determined by DSC at ambient pressure for consistency.
Determination of ΔV tr from PXRD
From the temperature dependence of unit cell volumes at ambient pressure, the specific volume change during the order–disorder transition, ΔVtr, was calculated as the difference between the LT and HT phase volume at the transition temperature (Ttr), with ΔVtr = VHT,tr – VLT,tr (Supplementary Fig. 4). The volume at Ttr for the LT and HT phases was extrapolated from unit cells determined below and above Ttr, respectively, using thermal expansion coefficients for each phase determined at ambient pressure. Specific volume changes from 200 to 300 bar were determined using unit cell volumes measured as a function of pressure at constant temperature (273 K for both LT phases, 323 K for the HT phase of (DA)2MnCl4, and 314 K for the HT phase of (NA)2CuBr4). Thermal expansion coefficients were assumed to be independent of pressure over this pressure range, and the thermal expansion coefficients determined for each phase at 1 bar were used to extrapolate the isothermal specific volumes to Ttr at each pressure.
Helium pycnometry
Skeletal densities of the samples were determined using an InstruQuest μ-ThermoPyc He pycnometer. In a typical measurement, ~150 mg of sample was transferred to the sample holder, and the sample mass was obtained. The holder was then placed in the instrument test chamber, and the headspace was evacuated and refilled five times with He. The sample was then cycled multiple times through the phase transition, with the chamber volume determined every 2–5 °C away from the transition and every 0.5–1.0 °C close to the transition. For a measurement of unknown volume in a sample holder, Vtest, in the sample chamber with a known volume of Vsc, at a temperature Tsc, the sample chamber was first pressurized to ~200 kPa and the initial pressure (Pi) was measured. A reference chamber of known volume (Vrc) was initially equilibrated with ambient pressure (Pa) and temperature (Trc). The sample chamber was then connected to a reference chamber. After equilibration, the final pressure in the combined chamber, Pf, was measured. Since the system is closed when the two chambers are connected, the ideal gas law and conservation of moles can be used to provide the following relationship:
where the left- and right-hand sides denote the moles of gas before and after connecting the sample and reference chamber, respectively.
Solving for Vtest gives:
Since Vtest includes the volume of the empty sample holder (Vh) that had been measured previously, sample volume (Vsample) was determined by subtracting Vh from Vtest, with Vsample = Vtest − Vh. For each volume measurement, the temperature was fully equilibrated until the temperature variation was less than 0.2 °C. At each temperature, the chamber volumes were measured five times to obtain good statistics. Prior to measurement of the sample, a calibration run of the empty sample holder was performed over the same temperature range. The sample mass was redetermined after the measurement and found to have decreased by no more than 0.5 mg. Uncertainties of the reported densities were determined by propagation of the standard deviations of the empty and filled chamber volumes and the sample mass. ΔVtr values for both compounds are summarized in Supplementary Table 10.
X-ray crystallography
X-ray diffraction analyses were performed on single crystals coated with Paratone-N oil and mounted on MiTeGen microloops using Dow Corning high vacuum grease. The temperature during data collection was controlled from 100 to 335 K using an Oxford Cryostreams nitrogen flow apparatus. Crystals were first mounted at 270 K, and 270 K datasets were collected. Crystals were then cooled to 100 K for 100 K data collection. After 100 K datasets, high-temperature datasets were collected: 330 K for (DA)2MnCl4 and 335 K for (NA)2CuBr4. The temperature was manipulated at a rate of 60 K h–1. The intensities of the reflections were collected by a Bruker D8 diffractometer with CMOS area detector (MoKα radiation, λ = 0.71073 Å). The collection method involved 0.5° scans in ω at 23° in 2θ with a detector distance of 9 cm for (DA)2MnCl4 and 8 cm for (NA)2CuBr4. Data integration down to 0.84 Å resolution was carried out using SAINT V8.37A with reflection spot size optimization52. Absorption corrections were made with the program SADABS52. All single-crystal structures were solved by the Intrinsic Phasing methods and refined by least-squares methods against F2 using SHELXT-201453 and SHELXL-201854 with the OLEX2 interface55. All non-H atoms, including all the disorder atoms, were located in difference-Fourier maps and then refined anisotropically. Hydrogen atoms were placed at idealized positions and refined using a riding model. The isotropic displacement parameters of all hydrogen atoms were constrained to be 1.2 times the parameters of the atoms they were linked to (1.5 times for methyl groups). Space groups were determined based on the systematic absences and the statistical indicators, such as the E-value and the CFOM values. The absence of higher symmetry was further confirmed by Platon/Addsym56. Unit cell information from ambient-pressure PXRD experiments was used to help select an appropriate data collection strategy. Atomic displacement parameter plots of alkylammonium cations are provided in and Fig. 8 and Supplementary Fig. 36, and hydrogen bonding geometry of (DA)2MnCl4 and (NA)2CuBr4 are shown in Supplementary Figs. 34 and 35, respectively. Selected geometric parameters are tabulated in Supplementary Tables 16–20, and details of data collection and refinement are summarized in Supplementary Tables 21 and 22. We acknowledge that there are limitations with using X-ray single crystal diffraction to determine the geometry of small organic cations in a heavy element inorganic framework, especially at high temperatures and when substantial disorder is expected to be present.
Thermal conductivity measurements
The thermal conductivity of each sample was measured by the flash diffusivity method (ASTM E1461-13) using a Netzsch LFA 467 HyperFlash instrument (Supplementary Fig. 42). The samples were prepared in pellets of approximately 12.9 mm in diameter and 1 mm thickness. The measurements were carried out under a Helium atmosphere at 10 °C below and 15 °C above the transition temperature for the LT and HT phases, respectively, of (DA)2MnCl4, and at 10 °C below and above the transition temperature for the LT and HT phases, respectively, of (NA)2CuBr4. The measurement results were not corrected for thermal expansion due to phase changes.
Data availability
The main data supporting the findings of this study are available within the paper and its Supplementary Information. Other data are available from the corresponding author upon request. Crystallographic data have been made available free of charge from the Cambridge Crystallographic Data Centre under reference numbers CCDC 2075108–2075113.
References
Dupont, J. L., Domanski, P., Lebrun, P. & Ziegler, F. The Role of Refrigeration in the Global Economy. 38th Note on Refrigeration Technologies (International Institute of Refrigeration, 2019).
Coulomb, D., Dupont, J.-L. & Morlet, V. The Impact of the Refrigeration Sector on Climate Change. 35th Note on Refrigeration Technologies (International Institute of Refrigeration, 2017).
International Enegy Agency. The Future of Cooling: Opportunities for Energy-Efficient Air Conditioning (IEA, 2018).
Moya, X. & Mathur, N. D. Caloric materials for cooling and heating. Science 370, 797–803 (2020).
Office of Energy Efficiency and Renewable Energy. Energy Savings Potential and RD&D Opportunities for Commercial Building HVAC Systems (U.S. Department of Energy, 2017).
Takeuchi, I. & Sandeman, K. Solid-state cooling with caloric materials. Phys. Today 68, 48–54 (2015).
Gottschall, T. et al. Making a cool choice: The materials library of magnetic refrigeration. Adv. Energy Mater. 9, 1901322 (2019).
Nair, B. et al. Large electrocaloric effects in oxide multilayer capacitors over a wide temperature range. Nature 575, 468–472 (2019).
Mañosa, L. & Planes, A. Solid-state cooling by stress: A perspective. Appl. Phys. Lett. 116, 050501 (2020).
Cazorla, C. Novel mechanocaloric materials for solid-state cooling applications. Appl. Phys. Rev. 6, 041316 (2019).
Aznar, A. et al. Reversible and irreversible colossal barocaloric effects in plastic crystals. J. Mater. Chem. A 8, 639–647 (2019).
Li, B. et al. Colossal barocaloric effects in plastic crystals. Nature 567, 506–510 (2019).
Lloveras, P. et al. Colossal barocaloric effects near room temperature in plastic crystals of neopentylglycol. Nat. Commun. 10, 1803 (2019).
Gutfleisch, O. et al. Mastering hysteresis in magnetocaloric materials. Philos. Trans. R. Soc. A 374, 20150308 (2016).
Brown, T. D., Buffington, T. & Shamberger, P. J. Effects of hysteresis and Brayton cycle constraints on magnetocaloric refrigerant performance. J. Appl. Phys. 123, 185101 (2018).
Hess, T. et al. Thermal hysteresis and its impact on the efficiency of first-order caloric materials. J. Appl. Phys. 127, 075103 (2020).
Masche, M., Ianniciello, L., Tušek, J. & Engelbrecht, K. Impact of hysteresis on caloric cooling performance. Int. J. Refrig 121, 302–312 (2021).
Domalski, E. S. & Hearing, E. D. Heat capacities and entropies of organic compounds in the condensed phase. Volume III. J. Phys. Chem. Ref. Data 25, 1–525 (1996).
McLinden, M. O. Thermophysical Properties of Refrigerants. ASHRAE Handbook: Fundamentals (ASHRAE, 2009).
Turturro, A. & Bianchi, U. Conformational contribution to the entropy of melting. I. Linear chain hydrocarbons. J. Chem. Phys. 62, 1668–1673 (1975).
Sharma, A., Tyagi, V. V., Chen, C. R. & Buddhi, D. Review on thermal energy storage with phase change materials and applications. Renew. Sustain. Energy Rev. 13, 318–345 (2009).
Busico, V., Carfagna, C., Salerno, V., Vacatello, M. & Fittipaldi, F. The layer perovskites as thermal energy storage systems. Sol. Energy 24, 575–579 (1980).
Mitzi, D. B. Synthesis, Structure, and Properties of Organic–Inorganic Perovskites and Related Materials. in Progress in Inorganic Chemistry 48, 1–121 (Wiley, 1999).
Kind, R. et al. Dynamics of the n‐decylammonium chains in the perovskite‐type layer structure compound (C10H21NH3)2CdCl4. J. Chem. Phys. 71, 2118–2130 (1979).
Li, J. et al. Colossal reversible barocaloric effects in layered hybrid perovskite (C10H21NH3)2MnCl4 under low pressure near room temperature. Adv. Funct. Mater. 31, 2105154 (2021).
Ciajolo, M. R., Corradini, P. & Pavone, V. Comparative studies of layer structures: the crystal structure of bis(monodecylammonium)tetrachloromanganate(II). Gazz. Chim. Ital. 106, 807 (1976).
Guillaume, F. et al. Molecular motions of decylammonium chains in the perovskite type layered compound (C10H21NH3)2MnCl4. Mol. Phys. 67, 665–679 (1989).
Bermúdez-García, J. M. et al. Giant barocaloric effect in the ferroic organic–inorganic hybrid [TPrA][Mn(dca)3] perovskite under easily accessible pressures. Nat. Commun. 8, 15715 (2017).
Bermúdez-García, J. M. et al. Giant barocaloric tunability in [(CH3CH2CH2)4N]Cd[N(CN)2]3 hybrid perovskite. J. Mater. Chem. C. 6, 9867–9874 (2018).
Samara, G. A. et al. Effects of pressure and ambient species on the orientational ordering in solid C60. Phys. Rev. B 47, 4756–4764 (1993).
Qian, S. et al. A review of elastocaloric cooling: Materials, cycles and system integrations. Int. J. Refrig. 64, 1–19 (2016).
Gabbott, P. A Practical introduction to differential scanning calorimetry. in Principles and Applications of Thermal Analysis 1–50 (Wiley, 2008).
Moya, X., Kar-Narayan, S. & Mathur, N. D. Caloric materials near ferroic phase transitions. Nat. Mater. 13, 439–450 (2014).
Gorev, M. V., Bogdanov, E. V. & Flerov, I. N. T–p phase diagrams and the barocaloric effect in materials with successive phase transitions. J. Phys. D: Appl. Phys. 50, 384002 (2017).
Brown, G. V. Magnetic heat pumping near room temperature. J. Appl. Phys. 47, 3673–3680 (1976).
Fultz, B. Phase Transitions in Materials (Cambridge University Press, 2014).
James, R. D. & Zhang, Z. A way to search for multiferroic materials with “unlikely” combinations of physical properties. in Magnetism and Structure in Functional Materials 159–175 (Springer, 2005).
Domanski, P. A., Steven Brown, J., Heo, J., Wojtusiak, J. & McLinden, M. O. A thermodynamic analysis of refrigerants: Performance limits of the vapor compression cycle. Int. J. Refrig. 38, 71–79 (2014).
Li, X., Hoffman, J. M. & Kanatzidis, M. G. The 2D halide perovskite rulebook: How the spacer influences everything from the structure to optoelectronic device efficiency. Chem. Rev. 121, 2230–2291 (2021).
Smith, I. C., Smith, M. D., Jaffe, A., Lin, Y. & Karunadasa, H. I. Between the sheets: Postsynthetic transformations in hybrid perovskites. Chem. Mater. 29, 1868–1884 (2017).
Steinert, S., Voigt, W., Glausch, R. & Neuschütz, M. Thermal characteristics of solid–solid phase transitions in long-chain dialkyl ammonium salts. Thermochim. Acta 435, 28–33 (2005).
Osman, M. A., Ploetze, M. & Skrabal, P. Structure and properties of alkylammonium monolayers self-assembled on montmorillonite platelets. J. Phys. Chem. B 108, 2580–2588 (2004).
Almeida, O. J. & Dixon, B. G. Lamellar metallo-alkylphosphonates as solid-state phase-change materials. Chem. Mater. 7, 2039–2044 (1995).
Arend, H., Huber, W., Mischgofsky, F. H. & Richter-Van Leeuwen, G. K. Layer perovskites of the (CnH2n+1NH3)2MX4 and NH3(CH2)mNH3MX4 families with M = Cd, Cu, Fe, Mn or Pd and X = Cl or Br: Importance, solubilities and simple growth techniques. J. Cryst. Growth 43, 213–223 (1978).
Lédée, F. et al. Fast growth of monocrystalline thin films of 2D layered hybrid perovskite. CrystEngComm 19, 2598–2602 (2017).
Ledru, J., Imrie, C. T., Hutchinson, J. M. & Höhne, G. W. H. High pressure differential scanning calorimetry: Aspects of calibration. Thermochim. Acta 446, 66–72 (2006).
Mañosa, L. et al. Giant solid-state barocaloric effect in the Ni–Mn–In magnetic shape-memory alloy. Nat. Mater. 9, 478–481 (2010).
Lloveras, P. et al. Giant barocaloric effects at low pressure in ferrielectric ammonium sulphate. Nat. Commun. 6, 1–6 (2015).
Needham, G. F., Willett, R. D. & Franzen, H. F. Phase transitions in crystalline models of bilayers. 1. Differential scanning calorimetric and X-ray studies of (C12H25NH3)2MCl4 and (NH3C14H29NH3)2MCl4 salts (M = Mn2+, Cd2+, Cu2+). J. Phys. Chem. 88, 674–680 (1984).
Coelho, A. A. TOPAS-Academic v.4.1 (Coelho Software, 2007).
Coelho, A. A. Indexing of powder diffraction patterns by iterative use of singular value decomposition. J. Appl. Cryst. 36, 86–95 (2003).
Bruker Analytical X-ray Systems. APEX3, SAINT and SADABS (Bruker Analytical X-ray Systems, 2016).
Sheldrick, G. M. SHELXT – Integrated space-group and crystal-structure determination. Acta Cryst. A 71, 3–8 (2015).
Sheldrick, G. M. Crystal structure refinement with SHELXL. Acta Cryst. C 71, 3–8 (2015).
Dolomanov, O. V., Bourhis, L. J., Gildea, R. J., Howard, J. A. K. & Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Cryst. 42, 339–341 (2009).
Spek, A. L. Single-crystal structure validation with the program PLATON. J. Appl. Cryst. 36, 7–13 (2003).
Acknowledgements
This research was partially supported by the Climate Change Solutions Funds at Harvard University and by the Arnold and Mabel Beckman Foundation through a Beckman Young Investigator grant awarded to J.A.M. and a Beckman Postdoctoral Fellowship to A.H.S. We also thank the Korea Foundation for Advanced Studies for a graduate fellowship awarded to J.S. X-ray diffraction data were collected on beamline 17-BM at the Advanced Photon Source at Argonne National Laboratory, which is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-06CH11357. We thank Dr. Marc-Antoine Thermitus, Dr. Stefan Schmölzer, and Dr. Steve Sauerbrunn for helpful discussions on high-pressure calorimetry, Gaëlle Lebourleux and Jorge Martinez for assisting with high-pressure calorimetry experiments, and Dr. Harish Banda and Katherine Stone for assisting with thermal diffusivity measurements. The authors also thank Malia Wenny for helpful discussions.
Author information
Authors and Affiliations
Contributions
J.S. and J.A.M. formulated the project. J.S. synthesized the compounds. J.S., R.D.M., A.H.S., S.Z., and A.A.Y. collected and analyzed the powder X-ray diffraction data. J.S., R.D.M., A.H.S., and S.-L.Z. collected and analyzed single-crystal X-ray diffraction data. R.U. carried out AFM experiments. J.S. collected and analyzed the high-pressure calorimetry data. J.S. and J.A.M. wrote the paper, and all authors contributed to revising the paper.
Corresponding author
Ethics declarations
Competing interests
J.S. and J.A.M. are inventors on a patent application related to this work held and submitted by Harvard University that covers barocaloric properties of two-dimensional perovskites and related compounds. The remaining authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Seo, J., McGillicuddy, R.D., Slavney, A.H. et al. Colossal barocaloric effects with ultralow hysteresis in two-dimensional metal–halide perovskites. Nat Commun 13, 2536 (2022). https://doi.org/10.1038/s41467-022-29800-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-29800-9
This article is cited by
-
Prediction and understanding of barocaloric effects in orientationally disordered materials from molecular dynamics simulations
npj Computational Materials (2024)
-
Research progress of metal halide perovskites in the preparation of nanosemiconductor lasers
Journal of Materials Science (2024)
-
Low pressure reversibly driving colossal barocaloric effect in two-dimensional vdW alkylammonium halides
Nature Communications (2024)
-
Giant adiabatic temperature change and its direct measurement of a barocaloric effect in a charge-transfer solid
Nature Communications (2023)
-
Phase transition regulation and caloric effect
Frontiers in Energy (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.