Abstract
Glass-to-glass transitions are useful for us to understand the glass nature, but it remains difficult to tune the metallic glass into significantly different glass states. Here, we have demonstrated that the high-entropy can enhance the degree of disorder in an equiatomic high-entropy metallic glass NbNiZrTiCo and elevate it to a high-energy glass state. An unusual glass-to-glass phase transition is discovered during heating with an enormous heat release even larger than that of the following crystallization at higher temperatures. Dramatic atomic rearrangement with a short- and medium-range ordering is revealed by in-situ synchrotron X-ray diffraction analyses. This glass-to-glass transition leads to a significant improvement in the modulus, hardness, and thermal stability, all of which could promote their applications. Based on the proposed high-entropy effect, two high-entropy metallic glasses are developed and they show similar glass-to-glass transitions. These findings uncover a high-entropy effect in metallic glasses and create a pathway for tuning the glass states and properties.
Similar content being viewed by others
Introduction
Among the material world, metallic glasses (MGs) constitute an attractive and unusual class of advanced materials for fundamental studies and structural applications. Their amorphous structure without a long-range periodicity renders MGs with very unique and excellent properties1,2,3,4 and tunable glass states5,6,7 with different atomic structures and energies. The exothermic signal detected by calorimetry provides the most straightforward method to characterize the energy states of glasses8, which is closely related to their structures and properties9,10. However, typical structural relaxation in MGs only involves limited local atom position adjustment with small heat release before the crystallization11,12.
Compared with the local structural relaxation mediated transitions of different glass states, glass-to-glass phase transitions of MGs could tune the glass states and energies more significantly, but they are rarely observed. An extremely high pressure has been reported as a possible method to introduce the phase transition in some MGs, but the high-pressure-state MGs cannot be maintained at an ambient pressure for further characterization13,14, and they are also limited to particular compositions with elements prone to pressure-induced electronic transitions. Recent literature reported that the reentrant glass transition and the hidden amorphous phase existed in ternary Pd-Ni-P alloys15,16. The presence of anomalous exothermic peaks (AEPs) in their supercooled liquid regions was attributed to the change of atomic structure, while the detailed thermodynamic mechanism and structural change remain to be discovered. To gain an in-depth understanding and harness the glass-to-glass transition, it is highly desirable to discover a pathway to access distinct MGs through glass-to-glass transitions with a significant structural change and property improvement.
Besides enthalpy, entropy, a fundamental thermodynamic parameter and the measurement of disorder, is also proposed to play an important role in the glass formation by affecting the atomic packing17. However, the entropy is seldom introduced as an effective tool to control the glass states in practice18. The main reasons are the relatively small contribution of entropy to the energy and the difficulty in harnessing it in conventional MGs. This might be overcome by the emergence of high-entropy alloys (HEAs) with equal or near-equal mole fractions of five or more constituent elements in alloy compositions19. With a continuously increasing research interest in HEAs20,21, the concept of the high-entropy has quickly spread into diverse material systems22,23. The high-entropy metallic glasses (HEMGs), with amorphous structures and HEA-like compositions, not only expand the composition space for searching MGs, but also have already shown unique properties, such as high crystallization resistance and excellent mechanical properties24,25,26,27,28,29,30. However, the effect of high-entropy on the glass structures and glass-to-glass transition remains to be resolved.
In this work, we have demonstrated that the high-entropy can effectively enhance the degree of the disorder in an equiatomic NbNiZrTiCo HEMG and enables the formation of a very high-energy glass state. This high-energy glass can transform into a stable low-energy glass via a glass-to-glass transition with an enormous exotherm even larger than that of its crystallization.
Results
The glass-to-glass transition and the glass structures of the HEMG
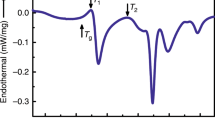
Figure 1a displays the obtained differential scanning calorimetry (DSC) scan curve of the as-prepared NbNiZrTiCo alloy, which has an amorphous structure as evidenced by the X-ray diffraction (XRD) (the As-prep. curve in Fig. 1c). Three exothermic peaks are observed at 781, 911, and 1016 K in the DSC curve with released heats of 1.65, 1.27, and 1.59 kJ mol−1, respectively. No obvious glass transition temperature (Tg) is observed in the conventional DSC curve of the as-prepared sample. The Tg of the as-prepared sample can be observed before the first exothermic peak with heating rates higher than 1000 K s−1 by Flash DSC (Supplementary Note 1 and Supplementary Fig. 7). DSC analyses with multiple heating rates are also performed (10, 20, 30, 40, and 50 K min−1, including the heating rate for the in-situ diffraction experiments shown later), and the activation energies corresponding to the three exothermic peaks are obtained to be 281, 384, and 249 kJ mol−1, respectively (Supplementary Note 2 and Supplementary Fig. 8). To investigate the structural evolution of the HEMG underlying each exothermic peak, the as-prepared HEMG is heated to the temperatures just above each exothermic peak (TA: 855 K, TB: 963 K, and TC: 1076 K, respectively, as shown in Fig. 1a), and then cooled down to room temperature for further characterization. Surprisingly, the sample heated to TA (denoted as heat-treated sample hereinafter) remains amorphous (see the corresponding XRD pattern denoted as TA in Fig. 1c). A hexagonal close-packed (HCP) structure is formed after heated to TB (TB curve in Fig. 1c), while a dual-phase structure of compositional disordered body-centered cubic (BCC) and ordered BCC (B2) is obtained after heated to TC (TC curve in Fig. 1c). It should be noted that some weak diffraction peaks (marked with x) on the spectra of the samples heated to TB and TC cannot be well identified due to their low intensities and the limited number of peaks. They are considered not significant enough because the current work is mainly focused on the glass-to-glass transition below TA.
a DSC curve of the as-prepared sample. The structures of the alloy are denoted and the anomalous exothermic peak (filled in green) shows heat release comparable to that of crystallization. During heating, the HEMG undergoes phase transitions from a high-energy glass state to a low-energy glass state and further to a crystallized state (red arrow). b DSC curve of the heat-treated sample. The first exothermic peak in the as-prepared sample disappears. To highlight the phase transitions, the curve of the crystallized HEMG (samples heated to 1173 K) was subtracted in a and b. c XRD results of the as-prepared and heat-treated samples. The TA, TB, and TC denote the heat treatment temperatures. As-prep.: As-prepared sample. d Synchrotron X-ray diffraction results of the as-prepared and heat-treated samples in real space measured at room temperature. e Synchrotron X-ray diffraction results of the as-prepared and heat-treated samples in Q-space measured at room temperature. Inset: enlarged first diffraction peak in the dotted box. f HRTEM (scale bar: 5 nm) and SAED (inset, scale bar: 5 nm−1) result of the as-prepared sample. g HAADF (scale bar: 20 nm) result of the as-prepared sample. h–i Same as f–g but for the heat-treated sample. The results show the heat-treated sample remains amorphous with different glass structure and no crystallization or detectable compositional inhomogeneity. Additional HRTEM results are in Supplementary Note 3.
Based on the above experimental results, it can be concluded that the exothermic reaction corresponding to the first exothermic peak on the DSC curve does not lead to the crystallization, although its heat release is even larger than that of the following crystallization. Since both the as-prepared sample and heated-treated sample are glasses (Tg in Supplementary Note 1 and Fig. 1b), it is indicated that the as-prepared sample experiences a glass-to-glass transition from a high-energy state to a low-energy state with a large energy reduction. The second exothermic peak corresponds to crystallization, and the third exothermic peak corresponds to a crystalline-to-crystalline transition.
To further investigate the structural differences associated with the transition, the synchrotron X-ray diffraction is applied on the as-prepared and heat-treated samples at room temperature. The as-prepared sample shows a typical reduced pair-distribution function G(r) (As-prepared curve in Fig. 1d), and a total structure function S(Q) (as-prepared curve in Fig. 1e) of MGs with no sharp Bragg diffraction pattern. The amorphous structure is also confirmed by the high-resolution transmission electron microscopy (HRTEM) and selected area electron diffraction (SAED) results (Fig. 1f, more images in Supplementary Note 3 and Supplementary Figs. 9, 10, 11, 12), which show a uniform amorphous structure and a typical diffraction pattern of MGs without nanocrystals. Figure 1g shows the high-angle annular dark-field (HAADF) image acquired in the scanning transmission electron microscopy (STEM) mode for the as-prepared sample. The HAADF image is sensitive to the atomic number of the constituent elements of the sample, and the acquired image shows no clear contrast, indicating that the element distribution is homogeneous at the nanometer scale.
As for the heat-treated sample, Fig. 1b shows its DSC curve where only the latter two exothermic peaks can be observed. The first exothermic peak noticed in the as-prepared sample disappears while a clear glass transition signal can be observed with a glass transition temperature (Tg) at ~764 K, which indicates that the glass-to-glass transition corresponding to the first exothermic peak is completed and irreversible. Synchrotron X-ray diffraction results show that the heat-treated sample possesses an amorphous structure, but its G(r) (heat-treated curve in Fig. 1d) at room temperature is quite different from that of the as-prepared sample. Specifically, the intensity maximum moves from the left side (as-prepared curve in Fig. 1d) to the right side (heat-treated curve in Fig. 1d) of the first peak in G(r). Moreover, a clearer peak splitting is noticed in the second G(r) peak of the HEMG after heat treatment. These changes observed in G(r) suggest a significant short- and medium-range structural change, which is quite different from that of the typical structural relaxation31,32,33,34,35,36,37. As for the S(Q) (Fig. 1e), slight peak position shifting and sharpening of the first peak can be observed with a clearer splitting in the second peak, which reflects a structural ordering of the short- and medium-range structures as well38,39,40,41. Synchrotron small-angle X-ray scattering (SAXS) experiments are further performed and confirm the amorphous structure (Supplementary Note 4 and Supplementary Fig. 13). The HRTEM and SAED results (Fig. 1h) further confirm the heat-treated sample remains amorphous with no crystalline phase, which is confirmed by additional HRTEM analyses (Supplementary Note 3), while the HAADF image (Fig. 1i) shows slight contrast. During isothermal annealing experiments, the amorphous structure of the heat-treated sample remains stable after annealed at Tg – 5 K (759 K) for 2 h and even at Tg + 30 K (794 K) for 2 or 10 h (Supplementary Note 5 and Supplementary Fig. 14), respectively, which demonstrates the excellent thermal stability of the low-energy MG. Based on these results, an irreversible glass-to-glass transition from a high-energy HEMG (the as-prepared sample) to a low-energy HEMG (the heat-treated sample) is discovered, which is accompanied by an enormous heat release and a significant short- and medium-range structural change.
Atom probe tomography (APT) analyses
Figure 2a, b display the APT results of the as-prepared and heat-treated samples, respectively. Both samples show uniform element distribution within a sub-nanometer scale. Besides, the APT results show a low oxygen content (<0.4 at.%) in the samples, which could be introduced during the sample preparation process or from the chamber of the APT tests. Together with the HAADF results, it is suggested that no compositional inhomogeneity is detected in either nanometer or sub-nanometer scales before or after the glass-to-glass transition, excluding the possibility of spinodal decomposition. These results are further confirmed by additional APT measurements and quantitative analyses (Supplementary Note 6, Supplementary Figs. 15, 16, Supplementary Table 2). However, the detailed structural change cannot be detected due to the limited spatial resolution of the APT.
a The APT results of the as-prepared sample. b The APT results of the heat-treated sample. The results show no compositional heterogeneity. Scale bar: 20 nm. Additional APT results and quantitative analyses in Supplementary Note 6.
In-situ high-temperature synchrotron X-ray diffraction
In-situ synchrotron X-ray diffraction is applied to reveal the structure evolution of the HEMG through the glass-to-glass transition during heating. Figure 3a shows the evolution of the S(Q) of the sample during continuous heating with a heating rate of 30 K min−1 from room temperature (305 K) to 803 K, which is close to the upper-temperature limit of the heating furnace and above the onset temperature of the first exothermic peak (denoted as Tstart at 717 K, obtained from the 30 K min−1 DSC curve in Supplementary Fig. 8). To highlight the structural change, the difference curves ΔS(Q) are plotted in Fig. 3b, where the S(Q) at 305 K is subtracted as a reference. As the temperature increases, the first peak in S(Q) shows a continuously linear shift to the low-Q direction. When the temperature is close to Tstart, the shift of the peak position deviates from the linear variation steeply (Supplementary Fig. 4), and even turns backward to high-Q direction. During the later cooling process, the position of the first peak of S(Q) shifts to the high-Q part linearly but with a slightly different slope (Fig. 3c, S(Q) curve during cooling in Supplementary Fig. 1). Integration of the | ΔS(Q) | (Supplementary Fig. 3) provides the overall peak changes as a function of temperature, which shows a linear increase at low temperatures with an accelerated change from ~Tstart. Moreover, a significant decrease of the full width at half maximum (FWHM) is observed (Fig. 3d). The narrowing of the first peak indicates that the sample enters a more ordered glass state42. Overall, a significant non-linear and irreversible peak position and shape change of the first peak in S(Q) is observed during the glass-to-glass transition, which is consistent with the changes observed on the heat-treated sample measured at room temperature (Fig. 1e).
a Evolution of structure function S(Q) of the as-prepared sample during heating. b The respective differences in structure functions obtained by subtracting the reference pattern at T = 305 K. c The evolution of the first peak position of S(Q) as a function of temperature. d The evolution of the full width at half maximum (FWHM) of the first peak as a function of temperature. The start temperature of the first exothermic peak in the 30 K min−1 DSC curve is denoted as Tstart in c and d. The first peak shows irreversible shifting towards high angle and narrowing.
To obtain more detailed information of the structure evolution in real space, the reduced pair-distribution function curve, G(r), is derived from S(Q) with Fourier transform (Fig. 4a). The differential curves ΔG(r) where the G(r) at 305 K is subtracted as the reference (Fig. 4b, G(r) curves during cooling are shown in Supplementary Fig. 2). To highlight the local structural change, the enlarged image of the first peak is shown in Fig. 4c. The most obvious change is the asymmetric shape change in the first peak of G(r), which shows an intensity maximum on the left side at low temperatures and gradually shifts to the right side at high temperatures. More quantitative information of the local structural change can be obtained by fitting the peak positions of G(r). For this five-component alloy, there are fifteen atomic pairs with overlapped peaks in the G(r) curve, which hinder the separation of these atomic pairs. To obtain a realistic analysis, a practical method is to employ minimized numbers of Gaussian functions to obtain a good fitting of the G(r) peak regardless of the multiple atomic pairs43,44,45. For this sample, two Gaussian sub-peaks, r11 and r12, can fit the first peak of G(r) very well with a coefficient of determination (R2) better than 0.999 (Supplementary Note 7 and Supplementary Fig. 17). As the temperature increases, the relative changes of the peak positions and peak heights of r11 and r12 are shown in Fig. 4d, e, respectively, by normalized to the corresponding values at 305 K. In Fig. 4d, it is found that r11 and r12 consistently shift to the low-r part as the temperature increases over the entire temperature range. This peak position contraction contradicts the normal thermal expansion and indicates a significant short- and medium-range structural change. In Fig. 4e, the peak height of r11 decreases significantly, while the peak height of r12 slightly decreases and then increases after Tstart. The inconsistent variation of the peak heights of the two sub-peaks causes the dramatic shape change of the first peak in G(r) (Fig. 4c). A similar method is also applied to the second peak of G(r) to quantify its peak splitting (Fig. 4d, f). Before Tstart, the peak positions and peak heights of the r21 and r22 peaks change consistently during heating. After Tstart, the bifurcations of both the peak positions and peak heights of r21 and r22 can be clearly noticed, which suggest that the splitting of the second peak of G(r) becomes prominent. These results indicate that the glass-to-glass transition is associated with significant short- and medium-range structural changes, and the changes in the short-range structures is much stronger than typical structural relaxation31,32,33,34,35,36,37 and glass-to-glass or liquid-to-liquid transitions15,16,46. Based on these results, a schematic structural change of the phase transition is prepared (Supplementary Note 7 and Supplementary Fig. 18).
a Evolution of the reduced pair-distribution functions G(r) of the as-prepared sample during heating. b The respective differences in the reduced pair-distribution functions obtained by subtracting the reference pattern at T = 305 K. c The enlarged image of the evolution of the first peak as a function of temperature. d Evolution of the peak positions of the first and second peaks as a function of temperature. e Evolution of the peak intensities of the sub-peaks of the first peak as a function of temperature. f Evolution of the peak intensities of the sub-peaks of the second peak as a function of temperature. The start temperature of the first exothermic peak in the 30 K min−1 DSC curve is denoted as Tstart. Both peaks are fitted with two Gaussian functions.
Accompanying the structural change, significant changes in the mechanical properties are also observed by the dynamic mechanical analysis (DMA) (Supplementary Note 8 and Supplementary Fig. 19) and nanoindentation (Supplementary Note 9 and Supplementary Fig. 20 and Supplementary Table 3) measurements. Both measurements show a significantly increased modulus and the nanoindentation result shows a drastic increase of ~40% in the hardness from 6.78 to 9.46 GPa after the glass-to-glass transition, suggesting the formation of stronger atomic bonds in the low-energy MG after structural changes involved in the glass-to-glass transition.
Discussions
Compared to other MGs with AEPs, the heat release of the AEP in NbNiZrTiCo HEMG is very large as shown in Fig. 5a. It can be noticed that the typical anomalous exotherm of other reported MGs is usually less than 16% of the crystallization exotherm, while the exotherm of NbNiZrTiCo HEMG is ~130% of the following crystallization exotherm, resulting in a unique glass-to-glass transition. The value of this exotherm is also much larger than the energy increase by thermal cycling47. To show the dynamic and thermodynamic pictures of this glass-to-glass transition, Fig. 5b illustrates the temperature dependence of the enthalpy of the NbNiZrTiCo HEMG at a constant pressure. It has been observed that the crystallization can be avoided upon cooling below the freezing point Tm, if the liquid is cooled sufficiently fast (104–106 K s−1 in melt-spinning). The “confusion principle” and the Inoue criteria point out that the more elements involved, the lower the chance that the alloy can select viable crystal structures and the easier for the formation of glasses18,48. As a result, the formation of most MGs requires two or more elements and the monoatomic MG is rare to make49. The reason behind this is that the increased number of elements increases the entropy by enlarging the configuration space, and may cause a sluggish diffusion effect50,51,52,53 by hindering the configurational sampling. Hence, the glass may not reach a low-energy state dynamically because the atomic reconstruction is limited during the fast vitrification process. This mechanism is expected to be applicable to the selection of glass states as the more elements involved, the lower is the chance for the alloy to access low-energy glass states within a limited time window during quenching. In other words, for a given high-entropy alloy, the high cooling rate and the high-entropy effect can dynamically stabilize the high-energy melt54,55. As the measurement of disorder, entropy thus bridges the atomic structure in terms of the atomic packing and its energy state of a given alloy system. How the high-entropy induces the unusual glass-to-glass transition is the key to a deeper understanding of the high-entropy effect in glass formation.
a The ratios of the anomalous exotherm to the crystallization exotherm of NbNiZrTiCo and other typical MGs with AEPs15,71,72,73,74,75. Anomalous Exo./Crys. Exo.: Anomalous exotherm/crystallization exotherm. b Upon fast cooling, the liquid could form a high-energy glass and transform into a low-energy glass by glass-to-glass transition and releasing energy \((\Delta {H}_{{{H}}-{{L}}})\). The heat-treated glass could crystallize by further releasing energy \((\Delta {H}_{{{L}}-{{C}}})\).
The major configurational entropy term of the MGs and HEAs is considered as the configurational entropy of mixing for an ideal solution (denoted as SC)21. First, a comparison of the SC for the conventional low SC Nb–Ni–Ti-based MGs (denoted by green circles) and the NbNiZrTiCo HEMG (denoted by a red star) has been performed in Fig. 6. Compared to the NbNiZrTiCo HEMG, none of the conventional low SC Nb–Ni–Zr-based BMGs shows any exceptional exothermic peak or glass-to-glass transition56. Therefore, it is reasonable to assume that the high SC in the NbNiZrTiCo HEMG plays an important role in inducing the glass-to-glass transition, provided that these MGs contain the same constituent elements. However, to our best knowledge, such glass-to-glass transition has never been reported in other HEMGs so far. This indicates that the high SC alone may not be sufficient for inducing the glass-to-glass transition. In fact, the total configurational entropy of mixing ST of an alloy can be written as ST = SC + SE, where SE denotes the excess configurational entropy of mixing, which excludes the contribution from an ideal solution and can be related to the atomic size misfit in the atomic packing57,58,59. Although all HEMGs have more or less high SC, the SE of some HEMGs can be rather low, and thus these HEMGs do not have high ST. For example, the Sr20Ca20Yb20Mg20Zn20 HEMG60 shows a SE of −6.73 J mol−1 K−1, while the NbNiZrTiCo HEMG in this work shows a SE of −2.75 J mol−1 K−1. Although the two HEMGs have the same SC of 13.38 J mol−1 K−1, they have significantly different ST of 6.65 and 10.63 J mol−1 K−1, respectively, where the ST of the NbNiZrTiCo HEMG is ~60 % higher. A comparison of the SE of the previously reported HEMGs (denoted by blue circles) and the present NbNiZrTiCo HEMG is also performed in Fig. 6. It is found that the previously reported HEMGs form a low SE region, whereas the NbNiZrTiCo HEMG deviates from this region by showing a higher SE than those without glass-to-glass transition. This indicates that the excess configurational entropy also plays an important role in inducing the glass-to-glass transition and further confirms the high-entropy effect. Combining the above results, it can be concluded that the high-entropy indeed induces the glass-to-glass transition. The importance of SE can also be seen from the perspective of atomic packing and glass formation. SE is related to the atomic size misfit and the atomic packing fraction57,58,59, which are the key factors in the phase formation of solid solutions, amorphous phases or intermetallic compounds and their phase stabilities, especially the glass formation of the MGs18. The lower the value of SE, the larger the atomic size difference and usually the higher the atomic packing density61. As a result, the MGs with lower SE usually show higher glass-forming ability and are expected to form conventional low-energy glasses with high atomic packing fractions62,63. The conventional glasses are usually stable, and thus similar phase transition is rare. To experimentally confirm the high-entropy effect, we substitute the Co with Cu in the NbNiZrTiCo HEMG because the Co and Cu have similar atomic radiuses (125 and 128 pm64, respectively), and thus the NbNiZrTiCo and NbNiZrTiCu HEMGs have similar high SE (−2.75 and −2.50 J mol−1 K−1, respectively), and the NbNiZrTiCu HEMG still keeps the high SC (13.38 J mol−1 K−1) as shown in Fig. 6 (denoted by a red star). As expected, the NbNiZrTiCu HEMG indeed shows a glass-to-glass transition (Fig. 7), similar to that of the NbNiZrTiCo HEMG. To further confirm the high-entropy effect, a six-element NbNiZrTiCoCu HEMG is developed (SC: 14.90 J mol−1 K−1, SE: −2.73 J mol−1 K−1) by adding Cu to the NbNiZrTiCo HEMG. As expected, this alloy also shows the glass-to-glass transition as expected (Fig. 8). The SC, SE, and ST of these MGs are listed in Supplementary Table 1. These experimental results further support the proposed high-entropy effect in inducing the glass-to-glass transition. The resulted low-energy glasses also show increased modulus and hardness by nanoindentation (Supplementary Note 10, Supplementary Table 4), as well as excellent thermal stabilities (Supplementary Note 11, Supplementary Fig. 21). These additional results further suggest that a high-entropy effect is discovered, which enables a wide tunability of the glass states, and indicate that such glass-to-glass transitions would not be limited in the present HEMGs. Compared to the previous works on MGs with metalloid elements (e.g., P15,16) or rare earth elements (e.g., La, Ce46), the proposed high-entropy effect moves the phenomenon from the special cases to general cases with a series of HEMGs discovered, instead of only one special MG. In such consideration, the HEMGs may serve as model materials in exploring the glass-to-glass transitions and glass nature in the fields of materials science and condensed-matter physics.
a DSC curve of the as-prepared and heat-treated sample. The as-prepared sample shows a Tg of 633 K. After heated to TA-NbNiZrTiCu = 833 K, the previous first exothermic peak disappears and the heat-treated sample shows a Tg of 708 K. To highlight the phase transitions, the curve of the crystallized HEMG (samples heated to 1173 K) was subtracted. b XRD results of the as-prepared and heat-treated samples. c Synchrotron X-ray diffraction results of the as-prepared and heat-treated samples in real space measured at room temperature. d Synchrotron X-ray diffraction results of the as-prepared and heat-treated samples in Q-space measured at room temperature. e HRTEM (scale bar: 5 nm) and SAED (inset, scale bar: 5 nm−1) result of the as-prepared sample. f HAADF (scale bar: 20 nm) result of the as-prepared sample. g, h Same as e, f but for the heat-treated sample. The results show the heat-treated sample remains amorphous with different glass structures and no crystallization or detectable compositional inhomogeneity. Additional HRTEM results are in Supplementary Note 3.
a DSC curve of the as-prepared and heat-treated sample. After heated to TA-NbNiZrTiCoCu = 803 K, the previous first exothermic peak disappears and the heat-treated sample shows a Tg of 708 K and Tx of 813 K. To highlight the phase transitions, the curve of the crystallized HEMG (samples heated to 1173 K) was subtracted. It should be noted that the first two exothermal peaks (corresponding to the glass-to-glass transition and crystallization in the NbNiZrTiCoCu HEMG, respectively) are not completely separated but slightly overlap in the DSC curve. Such peak overlapping results in a partial crystallization when the sample was heated above the first exothermic peak (816 K) (Supplementary Fig. 5), while the sample still remains amorphous when heated to 803 K, which is below the crystallization temperature (813 K, denoted as Tx). b XRD results of the as-prepared and heat-treated samples. c Synchrotron X-ray diffraction results of the as-prepared and heat-treated samples in real space measured at room temperature. d Synchrotron X-ray diffraction results of the as-prepared and heat-treated samples in Q-space measured at room temperature. e HRTEM (scale bar: 5 nm) and SAED (inset, scale bar: 5 nm−1) result of the as-prepared sample. f HAADF (scale bar: 20 nm) result of the as-prepared sample. g, h Same as e, f but for the heat-treated sample. The results show that the heat-treated sample remains amorphous with different glass structures and no crystallization or detectable compositional inhomogeneity. Additional HRTEM results are in Supplementary Note 3.
In conclusion, we discovered an unusual glass-to-glass transition in a NbNiZrTiCo HEMG with a large exotherm. It was found that the high-entropy effect could dynamically elevate the MG to a high-energy glass state and thermodynamically enable the glass-to-glass transition from the high-energy glass state to a low-energy glass state during heating. Through this simple and non-destructive heat-treating process, this glass-to-glass transition can alter the modulus and hardness more remarkably than rejuvenation by thermal cycling47 or mechanical deformation65. Besides, the HEMGs might also be applied as promising energetic materials, where the large anomalous exotherm may contribute to their combustion heats and lower the ignition temperatures66. In addition, the obtained low-energy state HEMGs exhibit excellent thermal stability. The present results provide an opportunity for further tuning the glass structure and property and addressing the fundamental issues of MGs.
Methods
Sample preparation
The NbNiZrTiCo, NbNiZrTiCu, and NbNiZrTiCoCu ingots were prepared by arc melting the mixtures of pure Nb, Ni, Zr, Ti, Co, and Cu (purity ≥ 99.9 wt.%) under a high-purity argon atmosphere. The ingots were flipped and remelted five times to ensure their homogeneity. Ribbons with a thickness of ~45 μm were produced by melt-spinning method with a single-copper roller at a wheel surface velocity of 32 m s−1 under a high-purity argon atmosphere.
Differential scanning calorimetry (DSC)
DSC curves were measured using Al2O3 crucibles with a synchronous thermal analyzer (STA-449 F3, NETZSCH, Germany) under a high-purity argon atmosphere. The weight of each tested sample was ~20 mg and the heating rate was 20 K min−1. For the heat-treated samples, the heat treatment was conducted by a tube furnace and the heating rate and cooling rate were both 20 K min−1. The sample was sealed in a glass tube under a high-purity argon atmosphere to avoid oxidation. The temperature of the sample in the furnace was calibrated by a K-type thermocouple thermometer (DT-3891G, CEM, China) heated together with the sample. The thermocouple was inside another tube with the opening blocked by an aluminum foil ball, and the tube itself was identical to the tube containing the sample. The sample and the thermocouple were set in the furnace as close as possible. The temperature of the sample in the furnace was calibrated by the thermocouple, which could compensate the temperature lags. To confirm that the temperature lag of sample heat-treated in the furnace has been excluded, we compared the DSC curves of the sample heat-treated in the furnace and the sample heat-treated in the DSC (Supplementary Fig. 24). The two DSC curves show consistent results and confirm that the temperature lag has been excluded. To highlight the phase transitions, the DSC curve of the crystallized HEMG (samples heated to 1173 K) was subtracted.
X-ray diffraction (XRD)
The XRD experiments were performed using an X-ray diffractometer (D/max-RB, Rigaku Inc., Japan) with Cu Kα radiation (wavelength 1.5406 Å) at room temperature. The XRD experiments were performed using a θ–2θ mode with a scanning rate of 3 degrees min−1.
Transmission electron microscopy (TEM) related analyses
TEM samples were ground by 2000 mesh sandpaper to ~30 μm in thickness and then thinned by an ion mill (Gatan 695, U.S.). The samples were first ion milled at 5 keV, 5°/6° for ~4 h, followed by 3 keV, 2°/3° for ~20 min. The high-resolution transmission electron microscopy (HRTEM) measurements and high-angle annular dark-field (HAADF) measurements under scanning transmission electron microscopy (STEM) mode were performed by a high-resolution transmission electron microscopy (JEM-2100F, JEOL, Japan) at 200 kV. The probe size in STEM mode was ~1.5 nm.
Atom probe tomography (APT) analyses
APT analyses were applied to the as-prepared and heat-treated samples to investigate the element distribution in three dimensions up to a sub-nanometer spatial resolution. Needle-shaped specimens required for APT were fabricated by lift-outs and annular milled in a FEI Scios focused ion beam/scanning electron microscope (FIB/SEM). The APT characterizations were performed in a local electrode atom probe (CAMECA LEAP 5000 XR). The specimens were analyzed at 65 K in voltage mode with a pulse repetition rate of 200 kHz, a pulse fraction of 20%, and an evaporation detection rate of 0.3% atom per pulse. The spatial resolution of the APT could reach ~0.2 nm. Imago Visualization and Analysis Software (IVAS) version 3.8 was used for creating the 3D reconstructions and data analyses.
Synchrotron X-ray diffraction and pair-distribution functions analyses
In-situ heating high-energy synchrotron X-ray diffraction experiments were conducted at the beamline 11-IDC of the Advanced Photon Source (APS), Argonne National Laboratory (ANL). The wavelength of the X-ray beam was 0.1173 Å (105.711 keV). The beam size was 0.2 × 0.2 mm. Diffraction was performed in a transmission mode by using a two-dimensional (2D) Perkin Elmer amorphous silicon detector with 2048 × 2048 pixels and pixel size of 200 × 200 μm2. Ten layers of ribbon samples were folded up to increase the sample thickness and enhance the scattering signal. The samples were tightly sandwiched with two Cu sheets with a tiny hole at the center, and then fixed on the silver heater by a ring clam in the Linkam furnace. For continuous heating and cooling experiments, the Linkam THMS600 heating oven was used to heat the samples from 305 K (room temperature) to 803 K (530 °C) with a heating rate of 30 K min−1 and a cooling rate of 50 K min−1 to room temperature after annealed at 803 K for 1 min. All patterns were collected with a total exposure time of 10 s, which consists of 10 sub-frames with an exposure time of 1 s for each frame to avoid detector saturation. Representative 2D diffraction images are shown in Supplementary Fig. 6.
The synchrotron X-ray diffraction results of the as-prepared and heat-treated samples were obtained at room temperature. The synchrotron X-ray diffraction of the heat-treated NbNiZrTiCo sample was performed at the beamline 13-IDD of APS, ANL. The wavelength of the X-ray beam was 0.3344 Å (37.0 keV). The beam size was 3.5 × 2 μm. Diffraction was performed in a transmission mode by using a 2D Pilatus 300 K detector with 1043 × 981 pixels and a pixel size of 172 × 172 μm2. The synchrotron X-ray diffraction of other samples were performed at the beamline 11-IDD of APS, ANL. The wavelength of the X-ray beam was 0.1173 Å (105.711 keV). The beam size was 0.2 × 0.2 mm. Diffraction was performed in a transmission mode by using a 2D Perkin Elmer amorphous silicon detector with 2048*2048 pixels and pixel size of 200 × 200 μm2.
The one-dimensional diffraction patterns were obtained by integrating the 2D diffraction images using Fit2D software67. The total scattering factor S(Q) (\(Q=4\pi \,\sin \theta /\lambda\), where λ is the X-ray wavelength and 2θ is the angle between diffraction beam and incident beam)68, and the reduced pair-distribution functions G(r) were obtained using PDFgetX3 software package69. To show the reliability of the PDFgetX3 software in this work, we have compared the diffraction results of the as-prepared NbNiZrTiCo sample processed by the PDFgetX3, PDFgetX2 and GSASII softwares, and find that the use of PDFgetX3 software does not have a significant influence on the shapes and the peak positions of the result (Supplementary Note 12 and Supplementary Figs. 22 and 23). The peak positions and the FWHMs of the first S(Q) peak were obtained by fitting the Voigt function. The total structure function S(Q) was obtained from the integrated intensities \({I}^{{{{{{\rm{coh}}}}}}}(Q)\) after the correction of Laue diffuse scattering and normalization to the atomic X-ray form factor \({{\langle\, f^{2}\rangle }}\) by
The G(r) function was obtained from the sine-Fourier transform of the total scattering factor S(Q) by
where ρ(r) is the pair density functions and ρ0 is the average number density.
Calculations of the entropy, enthalpy, and energy
The quantitative difference in enthalpy between the two glasses can be obtained from the DSC curve as \(\Delta {H}_{H-L}=-1.65\;{{{{{\mathrm{kJ mo}}}}}}{{{{{{\mathrm{l}}}}}}}^{-1}\). The lower limit of the difference in entropy can be obtained from the DSC curve by
where dS is the infinitesimal entropy change, đQ is the infinitesimal heat release during the phase transition, T is the absolute temperature, and the integration range is from the start temperature to the end temperature of the phase transition. This integration results in \(\Delta {S}_{{{H}}-{{L}}}=-1.96\;{{{{{\mathrm{J mo}}}}}}{{{{{{\mathrm{l}}}}}}}^{-1}{{{{{{\mathrm{ K}}}}}}}^{-1}\), which is the lower limit of the entropy change because the observed phase transition is an irreversible process. The upper limit difference in Gibbs free energy can be obtained by \(\Delta {G}_{H-L}=\Delta {H}_{H-L}-T\Delta {S}_{H-L}\), which is a function of temperature and gives −1.06, −0.24, −0.12, and 0.03 kJ mol−1 at 300 K, the start temperature of the first exothermic peak (Tstart, 717 K), the peak temperature of the first exothermic peak (781 K) and the end temperature of the first exothermic peak (TA, 855 K), respectively. It should be emphasized that the negative \(\Delta {H}_{H-L}\) and negative \(\Delta {S}_{{{H}}-{{L}}}\) are not contradictory to the proposed high-entropy effect. The high-entropy effect elevates the HEMG to a high-energy glass state, which allows the following transition.
The SC can be given by the regular solution model widely applied to high-entropy alloys21 by
where xi is the mole fraction of element i, m is the number of elements and R is the ideal gas constant. For the studied equiatomic NbNiZrTiCo HEMG with five elements, this model gives \({S}_{{{{{{\mathrm{C}}}}}}}=13.38\;{{{{{\mathrm{J mo}}}}}}{{{{{{\mathrm{l}}}}}}}^{-1}{{{{{{\mathrm{ K}}}}}}}^{-1}\).
The SE can be given by the Carnahan and Starling theory58,59 by
in which:
where di is the atomic diameter of the ith element, ci is the mole fraction of the ith element, ξ is the atomic packing fraction and kB is the Boltzmann constant. The atomic diameter of metallic elements were taken from the metallic diameters64, and the atomic diameter of non-metallic elements were taken from the empirical diameters70. The SE was computed by averaging the values obtained, respectively, at the atomic packing fraction of 0.68 (BCC-like packing) and 0.74 (FCC-like packing)58.
Data availability
The data that support the findings of this study are available within the paper and the Supplementary Information, and all data are available from the authors on reasonable request.
References
Tian, L. et al. Approaching the ideal elastic limit of metallic glasses. Nat. Commun. 3, 609 (2012).
Jang, D. & Greer, J. R. Transition from a strong-yet-brittle to a stronger-and-ductile state by size reduction of metallic glasses. Nat. Mater. 9, 215–219 (2010).
Hofmann, D. C. et al. Designing metallic glass matrix composites with high toughness and tensile ductility. Nature 451, 1085–1089 (2008).
Li, M. X. et al. High-temperature bulk metallic glasses developed by combinatorial methods. Nature 569, 99–103 (2019).
Luo, P. et al. Ultrastable metallic glasses formed on cold substrates. Nat. Commun. 9, 1389 (2018).
Chen, H. S. The influence of structural relaxation on the density and Young’s modulus of metallic glasses. J. Appl. Phys. 49, 3289–3291 (1978).
Ma, E. Tuning order in disorder. Nat. Mater. 14, 547–552 (2015).
Slipenyuk, A. & Eckert, J. Correlation between enthalpy change and free volume reduction during structural relaxation of Zr55Cu30Al10Ni5 metallic glass. Scr. Mater. 50, 39–44 (2004).
Luo, P., Li, Y. Z., Bai, H. Y., Wen, P. & Wang, W. H. Memory effect manifested by a Boson peak in metallic glass. Phys. Rev. Lett. 116, 175901 (2016).
Pan, J., Ivanov, Y. P., Zhou, W. H., Li, Y. & Greer, A. L. Strain-hardening and suppression of shear-banding in rejuvenated bulk metallic glass. Nature 578, 559–562 (2020).
Zheng, Q. et al. Understanding glass through differential scanning calorimetry. Chem. Rev. 119, 7848–7939 (2019).
Ye, J. C., Lu, J., Liu, C. T., Wang, Q. & Yang, Y. Atomistic free-volume zones and inelastic deformation of metallic glasses. Nat. Mater. 9, 619–623 (2010).
Zeng, Q. et al. Long-range topological order in metallic glass. Science 332, 1404–1406 (2011).
Sheng, H. W. et al. Polyamorphism in a metallic glass. Nat. Mater. 6, 192–197 (2007).
Lan, S. et al. Hidden amorphous phase and reentrant supercooled liquid in Pd-Ni-P metallic glasses. Nat. Commun. 8, 14679 (2017).
Du, Q. et al. Reentrant glass transition leading to ultrastable metallic glass. Mater. Today 34, 66–77 (2020).
Debenedetti, P. G. & Stillinger, F. H. Supercooled liquids and the glass transition. Nature 410, 259–267 (2001).
Inoue, A. Stabilization of metallic supercooled liquid and bulk amorphous alloys. Acta Mater. 48, 279–306 (2000).
Yeh, J. W. et al. Nanostructured high-entropy alloys with multiple principal elements: Novel alloy design concepts and outcomes. Adv. Eng. Mater. 6, 299–303 (2004).
George, E. P., Raabe, D. & Ritchie, R. O. High-entropy alloys. Nat. Rev. Mater. 4, 515–534 (2019).
Miracle, D. B. & Senkov, O. N. A critical review of high entropy alloys and related concepts. Acta Mater. 122, 448–511 (2017).
Rost, C. M. et al. Entropy-stabilized oxides. Nat. Commun. 6, 8485 (2015).
Oses, C., Toher, C. & Curtarolo, S. High-entropy ceramics. Nat. Rev. Mater. 5, 295–309 (2020).
Tong, Y., Qiao, J. C., Zhang, C., Pelletier, J. M. & Yao, Y. Mechanical properties of Ti16.7Zr16.7Hf16.7Cu16.7Ni16.7Be16.7 high-entropy bulk metallic glass. J. Non-Cryst. Solids 452, 57–61 (2016).
Zhao, S. F. et al. High strain rate sensitivity of hardness in quinary Ti-Zr-Hf-Cu-Ni high entropy metallic glass thin films. Phys. E Low. Dimens. Syst. Nanostruct. 94, 100–105 (2017).
Wei, R. et al. Soft magnetic Fe26.7Co26.7Ni26.6Si9B11 high entropy metallic glass with good bending ductility. Mater. Lett. 197, 87–89 (2017).
Ding, H. Y. & Yao, K. F. High entropy Ti20Zr20Cu20Ni20Be20 bulk metallic glass. J. Non-Cryst. Solids 364, 9–12 (2013).
Gong, P., Zhao, S. F., Ding, H. Y., Yao, K. F. & Wang, X. Nonisothermal crystallization kinetics, fragility and thermodynamics of Ti20Zr20Cu20Ni20Be20 high entropy bulk metallic glass. J. Mater. Res. 30, 2772–2782 (2015).
Gong, P., Yao, K. F. & Ding, H. Y. Crystallization kinetics of TiZrHfCuNiBe high entropy bulk metallic glass. Mater. Lett. 156, 146–149 (2015).
Zhao, S. F., Yang, G. N., Ding, H. Y. & Yao, K. F. A quinary Ti–Zr–Hf–Be–Cu high entropy bulk metallic glass with a critical size of 12 mm. Intermetallics 61, 47–50 (2015).
Mattern, N., Stoica, M., Vaughan, G. & Eckert, J. Thermal behaviour of Pd40Cu30Ni10P20 bulk metallic glass. Acta Mater. 60, 517–524 (2012).
Yavari, A. R. et al. Excess free volume in metallic glasses measured by X-ray diffraction. Acta Mater. 53, 1611–1619 (2005).
Chen, H. S. Glassy metals. Rep. Prog. Phys. 43, 353–432 (1980).
Castellero, A., Moser, B., Uhlenhaut, D. I., Torre, F. H. D. & Löffler, J. F. Room-temperature creep and structural relaxation of Mg–Cu–Y metallic glasses. Acta Mater. 56, 3777–3785 (2008).
Georgarakis, K. et al. Variations in atomic structural features of a supercooled Pd–Ni–Cu–P glass forming liquid during in situ vitrification. Acta Mater. 59, 708–716 (2011).
Schuh, C. A., Hufnagel, T. C. & Ramamurty, U. Mechanical behavior of amorphous alloys. Acta Mater. 55, 4067–4109 (2007).
Xu, J., Ramamurty, U. & Ma, E. The fracture toughness of bulk metallic glasses. JOM 62, 10–18 (2010).
Ma, D. et al. Elastic moduli inheritance and the weakest link in bulk metallic glasses. Phys. Rev. Lett. 108, 085501 (2012).
Suzuki, Y., Haimovich, J. & Egami, T. Bond-orientational anisotropy in metallic glasses observed by x-ray diffraction. Phys. Rev. B 35, 2162–2168 (1987).
Cargill, G. III Structure of metallic alloy glasses. Solid State Phys. 30, 227–320 (1975).
Ma, D., Stoica, A. D. & Wang, X. L. Power-law scaling and fractal nature of medium-range order in metallic glasses. Nat. Mater. 8, 30–34 (2009).
Wei, S. et al. Liquid-liquid transition in a strong bulk metallic glass-forming liquid. Nat. Commun. 4, 2083 (2013).
Bednarcik, J. et al. Thermal expansion of a La-based bulk metallic glass: insight from in situ high-energy x-ray diffraction. J. Phys. Condens. Matter 23, 254204 (2011).
Qu, D. D. et al. On the atomic anisotropy of thermal expansion in bulk metallic glass. Adv. Eng. Mater. 13, 861–864 (2011).
Georgarakis, K. et al. Probing the structure of a liquid metal during vitrification. Acta Mater. 87, 174–186 (2015).
Shen, J. et al. Metallic glacial glass formation by a first-order liquid–liquid transition. J. Phys. Chem. Lett. 11, 6718–6723 (2020).
Ketov, S. V. et al. Rejuvenation of metallic glasses by non-affine thermal strain. Nature 524, 200–203 (2015).
Greer, A. L. Materials science—confusion by design. Nature 366, 303–304 (1993).
Zhong, L., Wang, J., Sheng, H., Zhang, Z. & Mao, S. X. Formation of monatomic metallic glasses through ultrafast liquid quenching. Nature 512, 177–180 (2014).
Tsai, K. Y., Tsai, M. H. & Yeh, J. W. Sluggish diffusion in Co–Cr–Fe–Mn–Ni high-entropy alloys. Acta Mater. 61, 4887–4897 (2013).
Divinski, S. V., Pokoev, A. V., Esakkiraja, N. & Paul, A. A mystery of “sluggish diffusion” in high-entropy alloys: the truth or a myth? Diffus. Found. 17, 69–104 (2018).
Ng, C., Guo, S., Luan, J. H., Shi, S. Q. & Liu, C. T. Entropy-driven phase stability and slow diffusion kinetics in an Al0.5CoCrCuFeNi high entropy alloy. Intermetallics 31, 165–172 (2012).
Sastry, S. The relationship between fragility, configurational entropy and the potential energy landscape of glass-forming liquids. Nature 409, 164–167 (2001).
Chen, C., Wong, K., Krishnan, R. P., Embs, J. P. & Chathoth, S. M. A slow atomic diffusion process in high-entropy glass-forming metallic melts. J. Phys. D: Appl. Phys. 51, 145301 (2018).
Chen, C. et al. Highly collective atomic transport mechanism in high-entropy glass-forming metallic liquids. J. Mater. Sci. Technol. 35, 44–47 (2019).
Hu, H., Chen, L., Wang, X., Cao, Q. & Jiang, J. Formation of Ni–Nb–Zr–X (X = Ti, Ta, Fe, Cu, Co) bulk metallic glasses. J. Alloy. Compd. 460, 714–718 (2008).
Ye, Y., Wang, Q., Lu, J., Liu, C. & Yang, Y. Design of high entropy alloys: A single-parameter thermodynamic rule. Scr. Mater. 104, 53–55 (2015).
Ye, Y., Wang, Q., Lu, J., Liu, C. & Yang, Y. The generalized thermodynamic rule for phase selection in multicomponent alloys. Intermetallics 59, 75–80 (2015).
Mansoori, G., Carnahan, N. F., Starling, K. & Leland, T. Jr. Equilibrium thermodynamic properties of the mixture of hard spheres. J. Chem. Phys. 54, 1523–1525 (1971).
Gao, X. Q. et al. High mixing entropy bulk metallic glasses. J. Non-Cryst. Solids 357, 3557–3560 (2011).
Senkov, O. N. & Miracle, D. B. Effect of the atomic size distribution on glass forming ability of amorphous metallic alloys. Mater. Res. Bull. 36, 2183–2198 (2001).
Ye, Y. F., Liu, X. D., Wang, S., Liu, C. T. & Yang, Y. The general effect of atomic size misfit on glass formation in conventional and high-entropy alloys. Intermetallics 78, 30–41 (2016).
Yun, Y. S., Nam, H. S., Cha, P. R., Kim, W. T. & Kim, D. H. Effects of atomic size difference and heat of mixing parameters on the local structure of a model metallic glass system. Met. Mater. Int. 20, 105–111 (2014).
Greenwood, N. N. & Earnshaw, A. Chemistry of the Elements. (Elsevier, Amsterdam, 2012).
Ding, G. et al. Ultrafast extreme rejuvenation of metallic glasses by shock compression. Sci. Adv. 5, eaaw6249 (2019).
Yu, B. S., Sun, Y. H., Bai, H. Y. & Wang, W. H. Highly energetic and flammable metallic glasses. Sci. China Phys. Mech. 63, 276112 (2020).
Hammersley, A. P., Svensson, S. O., Hanfland, M., Fitch, A. N. & Hausermann, D. Two-dimensional detector software: From real detector to idealised image or two-theta scan. High. Press Res. 14, 235–248 (1996).
Egami, T. & Billinge, S. J. L. Underneath the Bragg peaks: Structural Analysis of Complex Materials. (Elsevier, 2003).
Juhas, P., Davis, T., Farrow, C. L. & Billinge, S. J. L. PDFgetX3: a rapid and highly automatable program for processing powder diffraction data into total scattering pair distribution functions. J. Appl. Crystallogr. 46, 560–566 (2013).
Slater, J. C. Atomic radii in crystals. J. Chem. Phys. 41, 3199–3204 (1964).
Kumar, G., Nagahama, D., Ohnuma, M., Ohkubo, T. & Hono, K. Structural evolution in the supercooled liquid of Zr36Ti24Be40 metallic glass. Scr. Mater. 54, 801–805 (2006).
Huang, X. M., Wang, X. D., He, Y., Cao, Q. P. & Jiang, J. Z. Are there two glass transitions in Fe–M–Y–B (M = Mo, W, Nb) bulk metallic glasses? Scr. Mater. 60, 152–155 (2009).
Na, J. H., Sohn, S. W., Kim, W. T. & Kim, D. H. Two-step-like anomalous glass transition behavior in Ni–Zr–Nb–Al–Ta metallic glass alloys. Scr. Mater. 57, 225–228 (2007).
Park, E. S., Lee, J. Y. & Kim, D. H. Effect of Ag addition on the improvement of glass-forming ability and plasticity of Mg–Cu–Gd bulk metallic glass. J. Mater. Res. 20, 2379–2385 (2005).
Yavari, A. R., Hamar-Thibault, S. & Sinning, H. R. On the microstructure of amorphous Pd46Ni36P18 with two glass transitions. Scr. Metal. 22, 1231–1234 (1988).
Acknowledgements
We would like to thank Dr. Yang Ren, Dr. Hongbo Lou, Dr. Jianrong Zeng, Tao Liang, Xiehang Chen for their assistance with the synchrotron X-ray diffraction experiment. This work is sponsored by the National Natural Science Foundation of China (Grant Nos.: 51871129, 51771096, and 51871054), National Key Basic Research and Development Program (Grant No.: 2016YFB00300500) and National Natural Science Fund for Excellent Young Scholars (Grant No.: 51922053). Atom probe tomography research was conducted at the Inter-University 3D Atom Probe Tomography Unit of City University of Hong Kong supported by the CityU grant 9360161. H.D. would like to thank the Youth Fund of Jiangsu Natural Science Foundation, Grant No. BK20190979. This research used beamlines 11-ID-C of the Advanced Photon Source (APS), a U.S. Department of Energy (DOE) Office of Science User Facility operated for the DOE Office of Science by Argonne National Laboratory (ANL) under Contract No. DE-AC02-06CH11357. Portions of the synchrotron XRD measurements were done at the beamline 15U1 at Shanghai Synchrotron Radiation Facility (SSRF), China. SAXS experiments were performed at the beamline BL16B1 of the Shanghai Synchrotron Radiation Facility (SSRF), China.
Author information
Authors and Affiliations
Contributions
H.D., H.L., and H.B. designed the composition of the HEMG and prepared the samples. X.Z., F.Z., Q.Y., and Q.Z. conducted the in-situ synchrotron X-ray diffraction experiments and data analyses. H.L., Y.-C.Y., Y.S., and J.G. conducted the HRTEM, SAED, and HAADF measurements and data analyses. H.L., H.B., and R.W. contributed to the measurement and analyses of the DSC, DMA, and nanoindentation experiments. J.H.L., Z.B.J., and C.T.L. contributed to the measurement and analyses of the APT measurements. Q.Z. and X.Z. contributed to the SAXS and the Flash DSC experiments. N.C. and H.L. proposed the concept of high-entropy effect. H.L. and C.S. contributed to the thermodynamic calculations of the glass-to-glass transition. H.L., N.C., Y.S., Q.Z., and X.Z. wrote the manuscript draft. Y.S., Q.Z., N.C., and K.-F.Y. supervised the research project and coordinated the research collaborations. All participated in the revisions of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Dong Ma, Jerzy Antonowicz and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Luan, H., Zhang, X., Ding, H. et al. High-entropy induced a glass-to-glass transition in a metallic glass. Nat Commun 13, 2183 (2022). https://doi.org/10.1038/s41467-022-29789-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-29789-1
This article is cited by
-
Continuous polyamorphic transition in high-entropy metallic glass
Nature Communications (2024)
-
Revealing the hidden structure of disordered materials by parameterizing their local structural manifold
Nature Communications (2024)
-
Lightweight single-phase Al-based complex concentrated alloy with high specific strength
Nature Communications (2024)
-
Absence of ultrasonic-vibration-induced plasticity in metallic glacial glasses
Rare Metals (2024)
-
Frontiers in high entropy alloys and high entropy functional materials
Rare Metals (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.