Abstract
Recent attempts to synthesize hybrid perovskites with large chirality have been hampered by large size mismatch and weak interaction between their structure and the wavelength of light. Here we adopt a planar nanostructure design to overcome these limitations and realize all-dielectric perovskite metasurfaces with giant superstructural chirality. We identify a direct spectral correspondence between the near- and the far- field chirality, and tune the electric and magnetic multipole moments of the resonant chiral metamolecules to obtain large anisotropy factor of 0.49 and circular dichroism of 6350 mdeg. Simulations show that larger area metasurfaces could yield even higher optical activity, approaching the theoretical limits. Our results clearly demonstrate the advantages of nanostructrure engineering for the implementation of perovskite chiral photonic, optoelectronic, and spintronic devices.
Similar content being viewed by others
Introduction
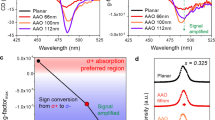
Combining chirality with the remarkable optical1,2,3, electrical4,5,6,7, and spintronic properties8,9,10 of perovskites, chiral hybrid organic-inorganic perovskites are receiving considerable attention for applications in chiral optoelectronics11,12,13,14 and spintronics15,16, such as spin transport and control15,16,17,18, circularly polarized light (CPL) detection and emission18,19,20,21,22,23,24,25, second-harmonic generation26,27,28, and other linear and nonlinear chiroptical effects29. Nonetheless, due to the weak chirality transfer (limited degree of structural twisting) from chiral molecules to the perovskite framework, optical activity, and distinguishability of circularly polarization imparted on light passing through the sample is rather poor. Together with circular dichroism (CD), the degree of chirality of a medium can be quantified by the anisotropy factor (gCD). While CD measures the difference in absorption of circularly polarized light of opposite handedness30, which is proportional to the rotational strength of the medium, gCD provides the degree of ellipticity a linearly polarized light acquires after traversing the chiral medium. The CD can therefore be defined as \({CD}={T}_{{{{{{\rm{RCP}}}}}}}-{T}_{{{{{{\rm{LCP}}}}}}}={A}_{{{{{{\rm{LCP}}}}}}}-{A}_{{{{{{\rm{RCP}}}}}}}\), if \({R}_{{{{{{\rm{RCP}}}}}}}={R}_{{{{{{\rm{LCP}}}}}}}\)(Supplementary Note 1). Expressed in millidegrees, the CD, θ (mdeg), can alternatively be defined as: \(\theta \left({{{{{\rm{mdeg}}}}}}\right)=\frac{180000}{\pi }{\arctan }(\frac{\sqrt{{T}_{{{{{{\rm{RCP}}}}}}}}-\sqrt{{T}_{{{{{{\rm{LCP}}}}}}}}}{\sqrt{{T}_{{{{{{\rm{RCP}}}}}}}}+\sqrt{{T}_{{{{{{\rm{LCP}}}}}}}}})\), while the anisotropy factor31 is given by \({g}_{{{{{{\rm{CD}}}}}}}=\frac{2({{lg}T}_{{{{{{\rm{RCP}}}}}}}-{{lg}T}_{{{{{{\rm{LCP}}}}}}})}{{{lg}T}_{{{{{{\rm{RCP}}}}}}}+{{lg}T}_{{{{{{\rm{LCP}}}}}}}}\) (Supplementary Note 2). As shown in Fig. 1, the highest anisotropy factor (gCD) of circularly polarized absorption reported to date in perovskites with structural chirality obtained by “bottom-up” synthesis is only 0.0425, far from the actual requirements of practical chiral optoelectronic and spintronic devices11,32,33. Further increase of chirality through molecular design is very challenging due to the negligible and hardly tunable magnetic transition dipole moment of chiral perovskites23. Thus, alternative strategies to produce chiral perovskite structures with strong optical activity34 are in high demand.
In 2017, Moon et al. first investigated the chiroptical properties of 2D chiral perovskite film, reporting CD of 155 mdeg and gCD of 0.00514. In 2018, Sargent et al. achieved CD of 200 mdeg and gCD of 0.006 in a 2D bromide chiral perovskite film. In 2019, Tang et al. reported circularly polarized photodetectors based on a 1D chiral perovskite film with CD of 200 mdeg and gCD of 0.0219. In 2020, Miyasaka et al. reported an encouraging CD of 3200 mdeg and gCD of 0.04 after morphology optimization of the 1D chiral perovskite film25. Switching from structural to superstructural chirality, this work reports high CD of 6350 mdeg and large gCD of 0.49 in a perovskite chiral metasurface obtained by nanostructure engineering. Numerical simulations predict CD of 18900 mdeg and gCD of 1.1 in large area samples, coming closer to the theoretical limits of both parameters. The diamonds and 4-point stars indicate representative studies where metasurface with strong chirality were obtained using conventional optical materials like Au40 and TiO237. The theoretical limits for CD ( ± 45000 mdeg) and gCD (±2) are obtained using the formulas defined in the introduction and correspond to the case of one circular polarization (e.g. LCP) being fully absorbed and the other (e.g. RCP) fully transmitted.
Nanostrucure engineering, through “top-down” fabrication of metasurfaces with chiral shapes or arrangements, has proven to be an effective strategy to impart strong superstructural chirality to achiral media35,36,37,38,39,40,41,42,43,44. This approach can deliver chiral metasurfaces with large optical activity using high-throughput screening of metamolecule designs by electromagnetic wave numerical simulations, thus saving significant time and reagent consumption needed in bottom-up synthetic approach. At the same time, the high and compositionally tunable refractive index (n > 1.9)2,3 of hybrid perovskites has enabled the realization of dielectric metasurfaces45,46,47,48 and photonic crystals with high-resolution structural colors45,49,50, enhanced photoluminescence48,51,52,53,54,55, anomalous reflection38, optical phase control56, third harmonic generation and three-photon luminecence57, and a variety of applications ranging from optical encryption49 and encoding57 to THz emission58, microlasers49,51,59,60,61, holography50,56, and ultrafast all-optical switching62. Here we show that a combination of metasurface design and perovskite nanostructuring45,55 can yield perovskite metasurfaces with giant superstructural chirality.
Specifically, we identify a previously unrecognized spectral correspondence between near- and far-field chirality, and use it to fine tune the electric and magnetic multipole moments of the resonant chiral metamolecules via high-throughput screening of the nanostructure design. We experimentally demonstrate a 20 µm × 20 µm planar-chiral perovskite metasurface with large anisotropy factor of gCD = 0.49 and circular dichroism of CD = 6350 mdeg, and predict by simulations that gCD = 1.11 and CD~18900 mdeg would be achievable in larger area metasurfaces. The methodological transition from chemical structure engineering to optical design of the metamolecules ensures continuity of the exponential improvement of perovskite circular dichroism and anisotropy factor, taking them closer to their theoretical limits (Fig. 1). We argue that superstrucural chirality opens new opportunities to couple optical chirality with compositional engineering, light-emission and detection, structural phase change, and spin-dependent transport properties of hybrid perovskites.
Results
Perovskite metasurfaces with high optical activity
For a proof-of-principle demonstration, we selected the methylammonium lead iodide perovskite, CH3NH3PbI3 (MAPbI3), a reliable high refractive index achiral platform for all-dielectric perovskite metasurfaces45,56. Thin perovskite films (~315 nm) were spin-cast on quartz substrates and used for fabricating the chiral metasurface. The dielectric functions of MAPbI345 and quartz were used to design metasurfaces comprising of planar chiral metamolecules of mirror twist (Supplementary Fig. 1), with both unit cell size and period of 730 nm, targeting optical resonances in the low-loss, sub-band edge region of the perovskite.
The representative unit of the perovskite chiral superstructure is shown in Fig. 2a. The gammadion metamolecule design was chosen based on the better performance compared to other possible designs (Supplementary Fig. 2). Optimal design parameters, bound by state-of-the-art nanofabrication tolerances and limits, were obtained by high-throughput superstructure screening via full wave electromagnetic Finite-Difference Time-Domain (FDTD) simulations (Supplementary Fig. 3), yielding s = 120 nm, r = 305 nm, w = 120 nm, l = 500 nm, h = 315 nm, and p = 730 nm. The FDTD simulations predict this resonant perovskite chiral metasurface design could generate a giant CD of 45% (Supplementary Fig. 4) at 767 nm under normal incidence, around the band edge of the MAPbI3, on-par with the best performing conventional planar dielectric nanostructures to date37. Two planar-chiral nanostructured perovskite metasurfaces of opposite handedness were carved on the MAPbI3 perovskite film by focused ion beam (FIB) milling, in arrays of about 20 µm × 20 µm area (Supplementary Fig. 5). The CD of perovskite chiral metasurface of both handedness and unpatterned MAPbI3 films was measured in transmission at quasi-normal incidence, using a microscope objective with NA = 0.1 (solid angle ϕ ~ 5.74°). The spectra were collected across the entire visible region, under both right- and left-handed circularly polarized light illumination, and detected using a grating spectrometer, as shown in Fig. 2b. Consistent with the simulation results (Supplementary Fig. 6), distinct peaks were observed in the experimental transmission spectra around 747 nm (Supplementary Fig. 7), leading to a remarkable circular dichroism experimental value of 16% (as shown in Fig. 2c). As expected, mirror symmetric left-handed (LPCM) and right-handed perovskite chiral metasurfaces (RPCM) exhibit opposite CD, whereas the unpatterned area of MAPbI3, or metasurfaces with achiral metamolecules (Supplementary Fig. 8), exhibit negligible CD through the entire visible region. When expressed in millidegrees, θ (mdeg), the CD of perovskite metasurface with superstructural chirality reaches a peak value of 6350 mdeg at 747 nm (Supplementary Fig. 9), an almost two-fold increase over the highest reported CD for “bottom-up” perovskite with structural chirality (3200 mdeg)25. At the same time. the gCD = 0.49 of the perovskite metasurface with superstructural chirality (Supplementary Fig. 10) is almost 12 times higher than the best value for “bottom-up” perovskite with structural chirality reported so far (gCD = 0.0425). Note that, while losses induced by the FIB milling process may affect the circular dichroism of the perovskite metasurfaces, it should be safe to neglect them in structures where the exposed regions are completely removed (see discussion in Supplementary Note 3 and Supplementary Fig. 18).
a Schematic of a left-handed perovskite chiral metamolecule on quartz substrate (s = 120 nm, r = 305 nm, w = 120 nm, l = 500 nm, g = 70 nm, h = 315 nm, p = 730 nm). b Micro-spectrometer setup for the measurement of circular dichroism on small area metasurfaces. c Experimental circular dichroism of unpatterned MAPbI3 film, right- and left-handed perovskite chiral metasurfaces (RPCM and LPCM), illuminated over a solid angle with NA of 0.1. The insets show scanning electron microscope images of 3×3 unit cells of LPCM and RPCM. d Color map of simulated circular dichroism of the LPCM as a function of wavelength and incidence angle ϕ. e Spectra of the simulated circular dichroism of the RPCM and LPCM for an incidence angle ϕ = 5.74o.
Angle-dependent numerical simulations allow examining the difference between predicted and experimentally measured CD spectra at incidence angles off the normal. The color map in Fig. 2d illustrates the dependence of CD spectra on incidence angle: the CD intensity decreases and broadens rapidly away from normal incidence, becoming almost featureless for ϕ > 7°. Within a ϕ ~ 5.74o (corresponding to a numerical aperture of NA = 0.1) solid angle of incidence, the numerically simulated CD is in excellent agreement with the experimental results. This confirms that the role of optical losses induced by the FIB fabrication is negligible. Circular dichroism values well exceeding 40% (θ (mdeg)~18,900 mdeg) and anisotropy factor values higher than 1 (gCD = 1.11), as shown in Supplementary Fig 11), are expected in large area devices illuminated at quasi-normal incidence, which could be realized by high-throughput nanofabrication techniques like nanoimprint lithography.
Spectral correspondence of optical chirality and circular dichroism
The origin of the giant CD generated by the perovskite chiral metasurfaces can be understood by investigating the near-field interaction of the metamolecules with the incident light and how this relates to the chiral response observed in the far-field. The chirality of the optical near-field can be gauged by the optical chirality, OC63, while the combination of electromagnetic multipoles can be employed to predict how the near-field mode distribution radiates into the far-field. OC is a time-even pseudoscalar, introduced as a measurement of field chirality, that describes the rate to which, at each point in space, electric and magnetic field vectors coil around a helical axis64. This is particularly interesting in the near-field of nanostructures where so-called superchiral fields65 are generated by the complex interaction with circularly polarized light. The analytical expression for the OC, proposed mathematically in 196466, and recently correlated to the chiral asymmetry of the rate of excitation of a small chiral molecule67, can be approximated by
where ε0 is the permittivity of free space, w is angular frequency, E and B are the complex amplitudes of the electric field and magnetic field, respectively. Simulated OCs induced by light waves of opposite helicity were integrated on the output surface of the perovskite chiral metasurface, and their difference was derived as a function of excitation wavelength. The differential OC and the numerically calculated CD reveal a remarkable spectral correspondence (Fig. 3a), thus providing a direct link between far- and near-field chirality. The near-field chiral interaction opens the possibility to tune the perovskite intrinsic optical properties such as Purcell enhancement leading to luminescence increase45 and lasing68 and modification of optical selection rules through the creation of virtual optical states69. Figure 3b–e show the optical chirality maps for a metamolecule of the left-handed chiral metasurface at the differential OC peak wavelengths, 767 nm and 821 nm, under both left- and right-handed circularly polarized incident light. As expected for gammadion metamolecules63, the optical chirality maps exhibit strong hotspots and distinct anti-clockwise twists at both wavelengths, yet with some notable differences. While the color maps for 767 nm-LCP (Fig. 3b) and RCP (Fig. 3c) incident light exhibit both positive OC, with different spatial distribution, the color maps for 821nm-LCP (Fig. 3d) and RCP (Fig. 3e) incident light have opposite OC values. These differences suggest that the strong CD of the perovskite metasurface at 767 nm and 821 nm shall be attributed to different combinations of electromagnetic modes of the metamolecule.
a Simulated differential optical chirality (integrated over the bottom surface) as a function of wavelength for a left-handed perovskite chiral metasurface, closely following the behavior of circular dichroism. b–e Color maps showing dissimilar spatial distributions of optical chirality for a left-handed chiral gammadion metamolecule at b 767 nm under LCP illumination, c 767 nm under RCP illumination, d 821 nm under LCP illumination, and e 821 nm under RCP illumination. All maps refer to the escaping surface upon which the light is incident.
Contribution of scattering multiples to circular dichroism
Decomposition into multipoles of the metamolecule scattering cross sections, under both left- and right-handed circularly polarized illumination, allows identifying the electromagnetic modes responsible for the giant CD. The modes are expected to have components of electric and magnetic moments parallel to each other (i.e., resulting electric fields aligned perpendicularly), which induce polarization rotation and optical activity. This is a generalization of the so-called Rosenfeld criterion30,70, which requires a non-null cross-product of the net electric and magnetic dipole moments, \({{{{{\boldsymbol{p}}}}}}{{{{{\boldsymbol{\cdot }}}}}}{{{{{\boldsymbol{m}}}}}}\ne 0\), as condition to observe chiro-optical activity (see Supplementary Figs. 12–15). The total scattering dichroism can be defined as \({{CD}}_{{C}_{S}}=({C}_{{S}_{L}}-{C}_{{S}_{R}})\), where \({C}_{{S}_{L}}\)and \({C}_{{S}_{R}}\) are the total scattering cross sections of a metamolecule of chosen handedness under left-handed and right-handed circularly polarized light, respectively. The spectral response of \({{CD}}_{{C}_{S}}\) follows closely that of CD, with a distinct peak around 767 nm and dip around 821 nm (Fig. 4a). The small discrepancy between the curves can be attributed to the different definitions of total scattering cross section and transmission (see Methods). Since the total scattering cross-section is proportional to the sum of scattering intensities of the multipoles, \({C}_{S}\propto {\sum }_{i}{C}_{{S}_{i}}\) (see Methods for exact formulation), the total scattering dichroism can be expressed as the sum of individual multipoles scattering dichroisms, \({{CD}}_{{C}_{S}}={\sum }_{i}{{CD}}_{{C}_{E}}\left(i\right)+{{CD}}_{{C}_{M}}\left(i\right)\), where \({{CD}}_{{C}_{E/M}}\left(i\right)\) is the dichroism of the scattering cross section of the electric/magnetic multipole of order i. This makes it possible to quantify the contribution of each multipole to the dichroism.
a Closely matching response of total scattering dichroism, \({{CD}}_{{C}_{S}}\) (black curve), and circular dichroism, CD (yellow curve), as functions of the wavelength. b–d Contribution of individual multipoles to the strong dichroism of the perovskite chiral metasurface: b electric (red curve) and magnetic (blue curve) dipole scattering dichroisms, \({{CD}}_{{C}_{{ED}}}\) and, \({{CD}}_{{C}_{{MD}}}\), as function of the wavelength; c electric (red curve) and magnetic (blue curve) quadrupole scattering dichroisms, \({{CD}}_{{C}_{{EQ}}}\) and, \({{CD}}_{{C}_{{MQ}}}\), as function of the wavelength; d electric (red curve) and magnetic (blue curve) octupole scattering dichroisms, \({{CD}}_{{C}_{{EO}}}\)and, \({{CD}}_{{C}_{{MO}}}\), as function of the wavelength. The vertical black dotted lines indicate the peaks of the CD spectrum, while the pink dotted lines correspond to the peaks of the \({{CD}}_{{C}_{S}}\) spectrum.
The multipoles mainly responsible for the chiral response of the perovskite gammadion metamolecules are the electric and magnetic dipoles (ED, MD), quadrupoles (EQ, MQ), and octupoles (EO, MO); their scattering dichroisms are shown in Fig. 4b–d. Other modes such as electric and magnetic hexadecapoles (EH, MH) are negligible (Supplementary Fig. 16). It is worth noting that the spectral distribution of the CD does not correlate with high-intensity multipoles, rather with their individual scattering dichroism. For example, while the magnetic dipole is the strongest scattering multipole at wavelengths longer than 800 nm (Supplementary Fig. 17), the high circular dichroism at 821 nm is mainly caused by the difference in scattering strengths of the electric and magnetic quadrupoles for LCP and RCP excitation (Fig. 4c), not of the magnetic dipoles. On the other hand, the chiral response of the strong circular dichroism at shorter wavelengths (767 nm) stems from the cooperative effect of all electric and magnetic multipoles up to the third order (Fig. 4b–d).
Discussion
We demonstrated a dielectric perovskite metasurface with giant chirality. Circular dichroism of 6350 mdeg and anisotropy factor of 0.49 were achieved experimentally, with simulations showing that larger area metasurfaces could yield anisotropy factor of 1.11 and circular dichroism of ~18900 mdeg, close to their theoretical limits. The remarkably strong chiroptical behavior results from the fine tuning of geometrical parameters and electromagnetic multipole moments competition, following the newly recognized spectral correspondence between near- and far-field chirality. These results show that the change in methodology, from chemical to superstructural engineering can perpetuate the exponential improvement of perovskite circular dichroism and anisotropy factor. The nanostructure engineering approach, aided by high-throughput screening of metamolecule shapes and parameters via electromagnetic wave numerical simulations, can extend this paradigm to the entire visible and near infrared spectrum, while saving considerable time and use of reagents needed in bottom-up synthesis. Furthermore, as circular dichroism may also be imprinted onto the light emitted by perovskite metasurfaces, this approach may open the way to new types of polarization-encoding light emitting devices. Overall, the concurrence of high refractive index, strong optical activity, excellent radiative properties, and large area manufacturability, makes hybrid perovskite metasurfaces a truly unique platform for chiral photonic, optoelectronic and spintronic devices.
Methods
Thin-film fabrication
MAPbI3 solution was prepared by predesigned amount of PbI2 (165.96 mg, TCI, 99.99%) and methylammonium iodide (57.2 mg, Dyesol) in stoichiometric ratio dissolved in 0.3 mL DMF (anhydrous, Sigma Aldrich). The 1.2 M solution was stirred overnight at room temperature in a N2 filled glovebox, then filtered by a polyvinylidene fluoride (PVDF) syringe filter (0.45 μm) and left stirring at 100 °C for one hour before spin coating. The resulting solution was then spin coated with a one-step process at 3500 rpm for 30 s onto pre-cleaned 1 × 1 cm2 quartz substrates in N2 atmosphere. After 6 s from the beginning of the spin coating process, 500 μL of toluene (anhydrous, Sigma Aldrich) was poured onto the spinning sample. The resulting films were then annealed at 100 °C for 15 min to improve crystallization. The thickness of the perovskite film is ca. 315 nm.
Metasurface fabrication
The 20 × 20 µm arrays of gammadion metasurfaces, of opposite handedness, were patterned on the perovskite film, spin-coated on a quartz substrate, with a Helios 650 NanoLab Focused Ion Beam system, using a nominal beam current <5 pA.
FDTD simulations
The circular dichroism of the perovskite chiral metasurface was simulated by finite difference time-domain method (Lumerical FDTD Solutions). The representative unit of the perovskite chiral superstructure is shown in Fig. 2a, with design parameters s = 120 nm, r = 305 nm, w = 120 nm, l = 500 nm, h = 315 nm and p = 730 nm, respectively. Right (Left) circularly polarized light is incident along z-axis. Perfect Matched Layers (PML) are used in the propagation direction of the incident light and periodic boundary conditions are used in the directions normal to the propagation direction. The optical chirality is calculated according to Eq. 1 based on the electromagnetic field at the bottom surface of the superstructure. For the angle-dependent CD, the Bloch boundary conditions are applied to the directions normal to the light propagation direction.
Circular dichroism spectra
The circular dichroism spectra were obtained by measuring the optical transmission of right- and left-handed chiral metasurfaces, under right- and left-handed circularly polarized illumination, in a Nikon inverted optical microscope, equipped with a halogen lamp (as shown in Fig. 2b). The polarizations of the incident light were prepared by sending the light through a polarizer and a broadband λ/4 waveplate (Thorlabs AQWP05M-580) with nearly achromatic transmission, 0.95 < T < 0.98, and retardance, 0.24 < ρ < 0.26, in the spectral region investigated. The light was focused on the sample using a Nikon LWD Achromat Condenser, with 10 mm working distance and adjustable NA. To ensure light collection from a spot smaller than the metasurface array, we used a Nikon ×100 objective with 0.7 NA and a multimode optical fiber, acting as pinhole. The spectra were recorded using an Acton SpectraPro 2300i monochromator and spectrograph.
Multipole decomposition
To identify the electromagnetic modes responsible for the giant CD, a multipole decomposition of the scattering cross sections of a single gammadion metamolecule in the arrays under both left-handed and right-handed circularly polarized illumination is first conducted using FDTD71. The origin of the coordinate of multipole decomposition is chosen to be at the center of the metamolecule to minimize unnecessary high-order multipolar contributions.
The electric field E(r) inside the metamolecule is extracted from the simulation to define the polarization current \(J\left({{{{{\boldsymbol{r}}}}}}\right)=-{{{{{\rm{i}}}}}}{{{{{\rm{\omega }}}}}}{\varepsilon }_{0}[{\varepsilon }_{r}\left({{{{{\boldsymbol{r}}}}}}\right)-1]E({{{{{\boldsymbol{r}}}}}})\). The electric \({a}_{E}\left(l,m\right)\) and magnetic \({a}_{m}\left(l,m\right)\) spherical multipole coefficients can then be calculated as follows71,
where η is the impedance of free space; \({\varPsi }_{l}\left({kr}\right)={kr}{j}_{l}\left({kr}\right)\) are the Riccati-Bessel functions and \({\varPsi }_{l}^{{\prime} }\left({kr}\right)\) and \({\varPsi }_{l}^{{\prime} {\prime} }\left({kr}\right)\) are their first and second derivatives with respect to the argument kr; \({P}_{l}^{m}\) are the associated Legendre polynomials; \({O}_{{lm}}=\frac{1}{{[l(l+1)]}^{1/2}}{[\frac{2l+1}{4\pi }\frac{\left(l-m\right)!}{\left(l+m\right)!}]}^{1/2}\); \({\tau }_{{lm}}\left(\theta \right)=\frac{d}{d\theta }{P}_{l}^{m}({\cos }\theta )\); \({\pi }_{{lm}}\left(\theta \right)=\frac{m}{{\sin }\theta }{P}_{l}^{m}({\cos }\theta )\).
The total scattering cross section Cs of the metamolecule can be written as the sum of contributions from these multipoles,
These equations allow to calculate the scattering cross sections from spherical multipoles of arbitrarily order l.
Data availability
The authors declare that all data supporting the findings of this study are available within this article and its supplementary information and are openly available in NTU research data repository DR-NTU (Data) at https://doi.org/10.21979/N9/N43DZX. Additional data related to this paper may be requested from the authors.
References
Zhang, Y. et al. Photonics and optoelectronics using nano-structured hybrid perovskite media and their optical cavities. Phys. Rep. 795, 1–51 (2019).
Berestennikov, A. S., Voroshilov, P. M., Makarov, S. V. & Kivshar, Y. S. Active meta-optics and nanophotonics with halide perovskites. Appl. Phys. Rev. 6, 031307 (2019).
Makarov, S. et al. Halide-perovskite resonant nanophotonics. Adv. Opt. Mater. 7, 1800784 (2019).
Stranks, S. D. et al. Electron-hole diffusion lengths exceeding 1 micrometer in an organometal trihalide perovskite absorber. Science 342, 341–344 (2013).
Dong, Q. et al. Electron-hole diffusion lengths >175 μm in solution-grown CH3NH3PbI3 single crystals. Science 347, 967 (2015).
Shi, D. et al. Low trap-state density and long carrier diffusion in organolead trihalide perovskite single crystals. Science 347, 519–522 (2015).
Liu, Y. et al. Chemical nature of ferroelastic twin domains in CH3NH3PbI3 perovskite. Nat. Mater. 17, 1013–1019 (2018).
Zhang, C. et al. Magnetic field effects in hybrid perovskite devices. Nat. Phys. 11, 427 (2015).
Wang, J. et al. Spin-optoelectronic devices based on hybrid organic-inorganic trihalide perovskites. Nat. Commun. 10, 129 (2019).
Qin, W., Xu, H. & Hu, B. Effects of spin states on photovoltaic actions in organo-metal halide perovskite solar cells based on circularly polarized photoexcitation. ACS Photon. 4, 2821–2827 (2017).
Long, G. et al. Chiral-perovskite optoelectronics. Nat. Rev. Mater. 5, 423–439 (2020).
He, T. et al. Spectroscopic studies of chiral perovskite nanocrystals. Appl. Phys. Lett. 111, 151102 (2017).
Georgieva, Z. N., Bloom, B. P., Ghosh, S. & Waldeck, D. H. Imprinting chirality onto the electronic states of colloidal perovskite nanoplatelets. Adv. Mater. 30, 1800097 (2018).
Ahn, J. et al. A new class of chiral semiconductors: chiral-organic-molecule-incorporating organic–inorganic hybrid perovskites. Mater. Horiz. 4, 851–856 (2017).
Lu, H. et al. Spin-dependent charge transport through 2D chiral hybrid lead-iodide perovskites. Sci. Adv. 5, eaay0571 (2019).
Long, G. et al. Spin control in reduced-dimensional chiral perovskites. Nat. Photon. 12, 528–533 (2018).
Sun, B. et al. Two-dimensional perovskite chiral ferromagnets. Chem. Mater. 32, 8914–8920 (2020).
Kim, Y.-H. et al. Chiral-induced spin selectivity enables a room-temperature spin light-emitting diode. Science 371, 1129–1133 (2021).
Chen, C. et al. Circularly polarized light detection using chiral hybrid perovskite. Nat. Commun. 10, 1927 (2019).
Wang, L. et al. A chiral reduced-dimension perovskite for an efficient flexible circularly polarized light photodetector. Angew. Chem. Int. Ed. 132, 6504–6512 (2020).
Dang, Y. et al. Bulk chiral halide perovskite single crystals for active circular dichroism and circularly polarized luminescence. J. Phys. Chem. Lett. 11, 1689–1696 (2020).
Ma, J. et al. Chiral 2D perovskites with a high degree of circularly polarized photoluminescence. ACS Nano 13, 3659–3665 (2019).
Di Nuzzo, D. et al. Circularly polarized photoluminescence from chiral perovskite thin films at room temperature. ACS Nano 14, 7610–7616 (2020).
Gao, J.-X., Zhang, W.-Y., Wu, Z.-G., Zheng, Y.-X. & Fu, D.-W. Enantiomorphic perovskite ferroelectrics with circularly polarized luminescence. J. Am. Chem. Soc. 142, 4756–4761 (2020).
Ishii, A. & Miyasaka, T. Direct detection of circular polarized light in helical 1D perovskite-based photodiode. Sci. Adv. 6, eabd3274 (2020).
Dehnhardt, N. et al. Band gap-tunable, chiral hybrid metal halides displaying second-harmonic generation. Chem. Mater. 32, 4801–4807 (2020).
Yuan, C. et al. Chiral lead halide perovskite nanowires for second-order nonlinear optics. Nano Lett. 18, 5411–5417 (2018).
Schmitt, T. et al. Control of crystal symmetry breaking with halogen-substituted benzylammonium in layered hybrid metal-halide perovskites. J. Am. Chem. Soc. 142, 5060–5067 (2020).
Chen, W. et al. Two-photon absorption-based upconverted circularly polarized luminescence generated in chiral perovskite nanocrystals. J. Phys. Chem. Lett. 10, 3290–3295 (2019).
Berova, N., N. Koji; Woody, R. W. Circular Dichorism: Principels and Applications. 2nd edn. (Wiley-VCH, 2000).
Schäferling, M. Chiral Nanophotonics. page 141 (Springer, 2017).
Yang, S.-H., Naaman, R., Paltiel, Y. & Parkin, S. S. P. Chiral spintronics. Nat. Rev. Phys. 3, 328–343 (2021).
Huang, Y. et al. Room-temperature electron spin polarization exceeding 90% in an opto-spintronic semiconductor nanostructure via remote spin filtering. Nat. Photon. 15, 475–482 (2021).
Ayuso, D. et al. Synthetic chiral light for efficient control of chiral light–matter interaction. Nat. Photon. 13, 866–871 (2019).
Rajaei, M. et al. Giant circular dichroism at visible frequencies enabled by plasmonic ramp-shaped nanostructures. ACS Photon. 6, 924–931 (2019).
Wang, W. et al. Generation of hot electrons with chiral metamaterial perfect absorbers: giant optical chirality for polarization-sensitive. Photochem. ACS Photon. 6, 3241–3252 (2019).
Zhu, A. Y. et al. Giant intrinsic chiro-optical activity in planar dielectric nanostructures. Light Sci. Appl. 7, 17158–17158 (2018).
Chen, Y., Gao, J. & Yang, X. Chiral metamaterials of plasmonic slanted nanoapertures with symmetry breaking. Nano Lett. 18, 520–527 (2018).
Tanaka, K. et al. Chiral bilayer all-dielectric metasurfaces. ACS Nano 14, 15926–15935 (2020).
Zhao, Y. et al. Chirality detection of enantiomers using twisted optical metamaterials. Nat. Commun. 8, 14180 (2017).
Rogacheva, A. V., Fedotov, V. A., Schwanecke, A. S. & Zheludev, N. I. Giant gyrotropy due to electromagnetic-field coupling in a bilayered chiral structure. Phys. Rev. Lett. 97, 177401 (2006).
Gansel, J. K. et al. Gold helix photonic metamaterial as broadband circular polarizer. Science 325, 1513–1515 (2009).
Zhang, S. et al. Photoinduced handedness switching in terahertz chiral metamolecules. Nat. Commun. 3, 942 (2012).
Hentschel, M., Schäferling, M., Weiss, T., Liu, N. & Giessen, H. Three-dimensional chiral plasmonic oligomers. Nano Lett. 12, 2542–2547 (2012).
Gholipour, B. et al. Organometallic perovskite metasurfaces. Adv. Mater. 29, 1604268 (2017).
Alias, M. S. et al. Focused-ion beam patterning of organolead trihalide perovskite for subwavelength grating nanophotonic applications. J. Vac. Sci. Technol. B 33, 051207 (2015).
Lin, C.-H. et al. Orthogonal lithography for halide perovskite optoelectronic nanodevices. ACS Nano 13, 1168–1176 (2019).
Makarov, S. V. et al. Multifold emission enhancement in nanoimprinted hybrid perovskite metasurfaces. ACS Photon. 4, 728–735 (2017).
Zhizhchenko, A. Y. et al. Light-emitting nanophotonic designs enabled by ultrafast laser processing of halide perovskites. Small 16, 2000410 (2020).
Gao, Y. et al. Lead halide perovskite nanostructures for dynamic color display. ACS Nano 12, 8847–8854 (2018).
Pourdavoud, N. et al. Photonic nanostructures patterned by thermal nanoimprint directly into organo-metal halide perovskites. Adv. Mater. 29, 1605003 (2017).
Tiguntseva, E. et al. Resonant silicon nanoparticles for enhancement of light absorption and photoluminescence from hybrid perovskite films and metasurfaces. Nanoscale 9, 12486–12493 (2017).
Hou, S. et al. Concurrent inhibition and redistribution of spontaneous emission from all inorganic perovskite photonic crystals. ACS Photon. 6, 1331–1337 (2019).
Li, Z. et al. Active perovskite hyperbolic metasurface. ACS Photon. 7, 1754 (2020).
Adamo, G. et al. Metamaterial enhancement of metal-halide perovskite luminescence. Nano Lett. 20, 7906–7911 (2020).
Zhang, C. et al. Lead halide perovskite-based dynamic metasurfaces. Laser Photon. Rev. 13, 1900079 (2019).
Fan, Y. et al. Resonance-enhanced three-photon luminesce via lead halide perovskite metasurfaces for optical encoding. Nat. Commun. 10, 2085 (2019).
Korolev, V. I. et al. Enhanced terahertz emission from imprinted halide perovskite nanostructures. Nanophotonics 9, 187 (2019).
Li, Z. et al. Room-temperature continuous-wave operation of organometal halide perovskite lasers. ACS Nano 12, 10968–10976 (2018).
Bar-On, O., Brenner, P., Lemmer, U. & Scheuer, J. Micro lasers by scalable lithography of metal-halide perovskites. Adv. Mater. Technol. 3, 1800212 (2018).
Brittman, S. et al. Controlling crystallization to imprint nanophotonic structures into halide perovskites using soft lithography. J. Mater. Chem. C 5, 8301–8307 (2017).
Huang, C. et al. Ultrafast control of vortex microlasers. Science 367, 1018–1021 (2020).
Schäferling, M., Dregely, D., Hentschel, M. & Giessen, H. Tailoring enhanced optical chirality: design principles for chiral plasmonic nanostructures. Phys. Rev. X 2, 031010 (2012).
Tang, Y. & Cohen, A. E. Enhanced enantioselectivity in excitation of chiral molecules by superchiral light. Science 332, 333–336 (2011).
Mun, J. et al. Electromagnetic chirality: from fundamentals to nontraditional chiroptical phenomena. Light Sci. Appl. 9, 139 (2020).
Lipkin, D. M. Existence of a new conservation law in electromagnetic theory. J. Math. Phys. 5, 696–700 (1964).
Tang, Y. & Cohen, A. E. Optical chirality and its interaction with matter. Phys. Rev. Lett. 104, 163901 (2010).
Tian, J. et al. Phase-change perovskite tunable microlaser. arXiv https://doi.org/10.48550/arXiv.2107.05239 (2021).
Tian, J. et al. Optical Rashba effect in a light-emitting perovskite metasurface. Adv. Mater. 34, 2109157 (2022).
Rosenfeld, L. Quantenmechanische theorie der natürlichen optischen aktivität von flüssigkeiten und gasen. Z. Phys. Chem. (N. F.) 52, 161–174 (1929).
Grahn, P., Shevchenko, A. & Kaivola, M. Electromagnetic multipole theory for optical nanomaterials. New J. Phys. 14, 093033 (2012).
Acknowledgements
We acknowledge support from the Singapore National Research Foundation (CRP Award No. NRF-CRP14–2014-03, C.S.), the A*STAR-AME programmatic fund on Nanoantenna Spatial Light Modulators for Next-Gen Display Technologies (Grant A18A7b0058, C.S.), the Singapore Ministry of Education (MOE2016-T3-1-006, C.S.), and from the Fundamental Research Funds for Central Universities, Nankai University (Grant Number: 023-63213067, G.L.) and the NSFC (52103218, G.L.) of China.
Author information
Authors and Affiliations
Contributions
C.S., G.L., and G.A. conceived the idea and designed the experiments. G.L. performed the chiral structure screening with help from J.T. and G.A.; G.A. and G.L. performed the circular dichroism measurements. E.F. and M.K. prepared the MAPbI3 film. G.A. fabricated the metasurfaces. J.T. performed the multipole decomposition. H.K. fitted the refractive index and extinction coefficients of MAPbI3 and quartz. G.L., G.A., J.T., H.W., and C.S. analyzed the data. G.L., G.A., and C.S. drafted the manuscript. All authors read and commented on the manuscript. C.S. supervised the work.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Long, G., Adamo, G., Tian, J. et al. Perovskite metasurfaces with large superstructural chirality. Nat Commun 13, 1551 (2022). https://doi.org/10.1038/s41467-022-29253-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-29253-0
This article is cited by
-
Advances on broadband and resonant chiral metasurfaces
npj Nanophotonics (2024)
-
Switchable unidirectional emissions from hydrogel gratings with integrated carbon quantum dots
Nature Communications (2024)
-
Controlling the broadband enhanced light chirality with L-shaped dielectric metamaterials
Nature Communications (2024)
-
The first chiral cerium halide towards circularly-polarized luminescence in the UV region
Science China Chemistry (2024)
-
Development and challenges in perovskite scintillators for high-resolution imaging and timing applications
Communications Materials (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.