Abstract
We report an experimental realization of a three-terminal photonic heat transport device based on a superconducting quantum circuit. The central element of the device is a flux qubit made of a superconducting loop containing three Josephson junctions, which can be tuned by magnetic flux. It is connected to three resonators terminated by resistors. By heating one of the resistors and monitoring the temperatures of the other two, we determine photonic heat currents in the system and demonstrate their tunability by magnetic field at the level of 1 aW. We determine system parameters by performing microwave transmission measurements on a separate nominally identical sample and, in this way, demonstrate clear correlation between the level splitting of the qubit and the heat currents flowing through it. Our experiment is an important step towards realization of heat transistors, heat amplifiers, masers pumped by heat and other quantum heat transport devices.
Similar content being viewed by others
Introduction
Recent achievements in superconducting circuit QED techniques in combination with ultrasensitive nanoscale thermometry1,2,3,4 stimulated theoretical discussion and experimental realization of on-chip refrigerators5,6,7,8, quantum heat engines9, heat rectifiers10, interferometers11, and other thermal devices. Superconducting loops containing Josephson junctions and coupled to superconducting resonators are essential parts of such systems because they allow one to control photonic heat currents by magnetic field. Recent examples based on this architecture include quantum heat valve based on the resonator-qubit-resonator assembly12 and heat rectifier with unequal frequency resonators13.
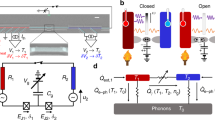
So far most experiments in this field have been carried out in two terminal devices. However, according to the theory, moving to three terminal setup14 should open up new opportunities. Indeed, there exist theory proposals for thermal transistors15,16,17,18, heat amplifiers19,20, quantum absorption refrigerators21,22 and thermally pumped masers23,24, which are heat engines from thermodynamical point of view, in this configuration. Motivated by these ideas, we have fabricated a three terminal heat transport device containing an Xmon qubit, which acts as a tunable element and controls photonic heat currents between the terminals. Basic schematics of our device is shown in Fig. 1. Its main element is the flux qubit made of a superconducting loop containing three identical Josephson junctions. Qubit frequency can be tuned by application of magnetic field, which induces the magnetic flux inside the loop. The qubit is coupled to three resonators—the left, the right and the hot one, which filter thermal noises emitted by three ohmic resistors. The temperature of the hot resistor can be varied by application of the heating current to it and the temperatures of the two other resistors are monitored by electronic thermometers. Heating the hot resistor we bring the whole system into the non-equilibrium steady state and vary the heat currents by magnetic flux. In this way, we demonstrate the control of the photonic heat power at the level of 10−18 W. In order to get more information about the system parameters, we have performed microwave transmission measurements on the nominally identical twin sample. We have also developed a theory model, which reasonably well explains the experimental findings. We are confident that further technological developments will soon permit practical implementation of the interesting theoretical proposals mentioned above and investigation of the effects of quantum coherence on the performance of heat transport devices22.
Results
Experimental
In order to fully characterize the system, we have fabricated two samples with nominally identical parameters on the same wafer, but designed for different measurement setups. The parameters of these samples may differ due to fabrication uncertainties, which we roughly estimate as 10%. The first of these devices, sample I shown in Fig. 2a, contains three resistors and was used for DC measurements of the photonic heat currents between the resistors. In the second device, sample II presented in Fig. 2c, we have replaced one of the resistors by a transmission line, which allowed us to carry out detailed spectroscopic measurements of the qubit in the microwave frequency range.
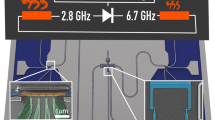
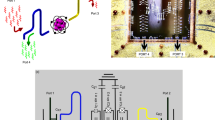
Images of the sample I used in the heat transport experiment (a) and of the sample II used for the microwave spectroscopy (c). Both samples contain a cross-shaped Xmon-type superconducting qubit, which is capacitively coupled to three superconducting coplanar waveguide resonators. Samples size 7 × 7 mm. b Equivalent lumped-element circuit of the sample I and (d) of the sample II. e Scanning electron micrograph of the Xmon qubit island (scale bar: 100 μm) and (f) of the flux qubit loop with three Josephson junctions (scale bar: 2 μm).
Sample I contains centrally located cross-shaped superconducting island, which is capacitively coupled to three superconducting λ/2 coplanar waveguide (CPW) resonators with the characteristic impedance Z0 = 50 Ω as schematically shown in Fig. 2b. The bottom leg of the cross is connected to the qubit, see Fig. 2e, which is realized as a superconducting loop with three asymmetrically arranged Josephson junctions, similar to the conventional persistent-current flux qubit25. The SEM image of the three junction loop is presented in Fig. 2f. The top resistor, Rh, is heated by DC bias current and serves as the heater for the whole system. Two other resistors, RL and RR, are passively heated by the power emitted by the hot resistor and their temperatures are monitored. The resistors are realized as copper islands with the resistances RL = RR = 4 Ω and Rh = 5 Ω and the volumes \({{{{{{{{\mathcal{V}}}}}}}}}_{L}={{{{{{{{\mathcal{V}}}}}}}}}_{R}=0.036\,\mu\)m3 and \({{{{{{{{\mathcal{V}}}}}}}}}_{h}=0.048\,\mu\)m3. Their images are shown in Fig. 3d, e. The coupling between the qubit and the resonators is mediated by the capacitors with the designed values CL = 3.81 fF, Ch = 4.51 fF, and CR = 4.66 fF. Additional capacitors having designed values \({C}_{L}^{\prime}=70\) fF, \({C}_{h}^{\prime}=30\) fF and \({C}_{R}^{\prime}=48\) fF are inserted between the resonators and the resistors in order to keep the quality factors of the resonators sufficiently high. Their images are shown in Fig. 3a–c. The quality factors of the resonators are given as \({Q}_{i}=\pi /(2{\omega }_{i}^{2}{Z}_{0}{R}_{i}{C^{\prime} }^{2})\) for i = L, R or h26, where ωi = 2πfi are the resonator frequencies. With the parameters listed above and with measured resonator frequencies we estimate QL = 2450, QR = 4690 and Qh = 2720. Finally, the capacitances to the ground, schematically shown in Fig. 2b, are found to be CgL = 48.8 fF, CgR = 54 fF, Cgh = 60.4 fF and Cg = 42 fF. All capacitance values listed above, as well as the self-capacitance of the Xmon island27 and the design of the SQUID are optimized by device simulation using finite element modeling COMSOL Multiphysics software packet. The designed value for the charging energy is EC/h = 0.3 GHz, and for the Josephson energy - EJ/h = 4.6 GHz. The latter value corresponds to the critical current of a single junction IC = 9.3 nA. The resonators are designed in such a way that the frequencies of the left and the right resonators are close to each other and to the qubit frequency, while the frequency of the hot resonator is approximately two times higher, see the Spectroscopy section for details.
Scanning electron micrograph of the capacitors between resonators and right resistor \({C}_{R}^{\prime}=48fF\) (a) (scale bar: 10 μm), hot resistor \({C}_{h}^{\prime}=30fF\) (b) (scale bar: 10 μm), and left resistor \({C}_{L}^{\prime}=70fF\) (c) (scale bar: 20 μm). The indicated capacitance values are obtained from COMSOL simulations. d Hot resistor Rh = 5 Ω (d) (scale bar: 200 μm). e Left and right resistors have the same design and nominal values RL = RR = 4 Ω (e) (scale bar: 200 μm).
As shown in Fig. 3d, e, each normal metal (N) resistor has aluminum superconducting (S) probes, separated by a thin insulating (I) layer, which we use for thermal control and readout. Four superconducting probes allow us to control and simultaneously measure the resistor temperature. We change the temperature by applying voltage bias between the two superconducting probes. For bias voltages above the superconducting energy gap the resistor is heated up, while for voltages below the gap it is cooled. The electronic temperature readout is performed by applying current bias between another pair of NIS tunnel junctions in a SINIS configuration3. The details of electronic thermometry are presented in the Methods section. The Andreev mirrors at the aluminum-copper boundaries on both sides of each resistor help to localize the heat, and, at the same time, they ensure good electric contact between the resistors, the ground electrode and the resonators. The dominating heat relaxation channel in the resistors is the electron-phonon coupling. Power leakage to the phonons is estimated in the usual way:
where Σ = 2 × 109 Wm−3 K−5 is the electron-phonon coupling constant, \({{{{{{{\mathcal{V}}}}}}}}\) is volume of the copper resistor, Tel and Tph are the temperatures of electrons and phonons respectively. In the steady state the power dissipated in the resistor equals to the power leaking to the phonons. Thus, measuring the electronic temperature Tel with the thermometer and knowing the substrate temperature Tph one can easily estimate the dissipated power from Eq. (1). Alternatively, knowing Joule heating power dissipated in the hot resistor, from Eq. (1) one can estimate its electronic temperature Tel.
Sample II, shown in Fig. 2c, d, and designed for the microwave spectroscopy, has nominally the same design and parameters. However, this sample does not have a hot resistor and the top resonator serves for diagnostic purposes. The latter has the same length as the top resonator of the sample I, but it is realized as λ/4-resonator with its upper end grounded. As a result, its frequency becomes two times lower than that in the sample I. This modification in the design brings the diagnostic resonator frequency closer to the frequencies of the two other resonators and to the transition frequency between the two lowest levels of the qubit, and makes the spectroscopy more accurate.
Theory model
We describe the flux qubit loop containing three identical Josephson junctions with the theory model of ref. 25. The loop contains two superconducting islands. The first island, denoted as I1, is large and includes the cross-like aluminum electrode. It is restricted by coupling capacitors CL, Ch and CR and the Josephson junctions numbered 1 and 3, as shown in Fig. 1b by red dashed line. The second island I2 is much smaller, in Fig. 1b it is indicated by the blue dashed line and sandwiched between the junctions 1 and 2. We introduce the operators nI1 and nI2 representing the number of Cooper pairs in the islands I1 and I2, and the operators φi with i = 1, 2 or 3, corresponding to the Josephson phase differences across the ith junction. The Hamiltonian of the flux qubit is25
where φext = 2πΦ/Φ0, Φ is the normalized magnetic flux threading the loop, Φ0 = h/2e is the magnetic flux quantum, EJ = ℏIC/2e is the Josephson energy of a single junction having the critical current IC, \({({E}_{C})}_{kl}={e}^{2}{({C}^{-1})}_{kl}/2\), and \({({C}^{-1})}_{kl}\) are the elements of the inverse of the 2 × 2 capacitance matrix
Here CI1 = CL + Ch + CR + Cg + 2C and CI2 = 2C are the total capacitances of the islands 1 and 2, respectively. We diagonalize the Hamiltonian (Eq. 2) numerically in the basis of two dimensional plane waves having the form \(\exp (-i{n}_{I1}{\varphi }_{3}-i{n}_{I2}{\varphi }_{2})/2\pi\). Since EJ ≫ EC = e2/2CI1 for all values of Φ except the narrow region close to Φ0/2, we neglect weak dependence of the eigen-energies En of the Hamiltonian (Eq. 2) on the gate charges induced by, for example, charged impurities.
In order to fit the experimental data on the heat power transmitted between the resistors we use the Landauer formula for the total power Pi carried by photons and dissipated in the resistor with the number i,
Here the indexes i and j enumerate the resistors, i.e. they can take the values L, R or h, and Ti are the resistor temperatures. Here we have also introduced the heat currents \({P}_{ij}^{{{{{{{{\rm{ph}}}}}}}}}\) flowing from the resistor j to the resistor i. In order to derive the expression for the photon transmission probabilities τij(ω), we linearize Josephson dynamics and replace all three junctions in the loop by the identical inductors with the inductance L = ℏ/2eIC. Solving the corresponding Kirchhoff equations with thermal Nyquist noise sources connected in parallel with the resistors, as outlined in ref. 28 for example, we find
Here we have introduced the impedances of the three segments of the electric circuit depicted in Fig. 1b, which contain individual resonators, resistors and coupling capacitors. They are defined as
where Zrj(ω) have the form
Here tj is the flight time of a photon between the two ends of a given resonator which is proportional to its length. The impedance of the three junction loop for the flux values ∣Φ∣ ≤ Φ0/2 takes the form
and it should be periodically extended with the period Φ0 for ∣Φ∣ > Φ0/2. Transmission probabilities (Eq. 6) exhibit multiple peaks centered at frequencies corresponding to the modes of the resonators and one additional narrow peak at the resonance frequency of the three junction loop
Here CΣ = Cg + 3C/2 + CL + CR + Ch is effective capacitance of the qubit, which is similar, but slightly different from CI1. The frequency ω0 is close to the exact transition frequency between the two lowest levels of the non-linear qubit 2πf01 = (E1 − E0)/ℏ, but deviates from it in the vicinity of the flux point Φ = Φ0/2, where qubit anharmonicity becomes significant.
As shown in ref. 28, the Landauer formula ((Eq. 4), (Eq. 5)) can be derived from the Kirchhoff’s equations relating the Fourier components Ii,ω of the four fluctuating in time currents Ii(t), which flow from the central cross shaped island of the device in the left (i = L), the hot (i = h), the right (i = R) resonators and in the qubit (i = q), with the island potential Visl,
Here ξi,ω are the Fourier components of the noise currents with the spectral densities determined by the fluctuation-dissipation theorem,
These noises are generated by the resistors Ri and acquire the spectrum (Eq. 12) close to the island due to the filtering effect of the resonators. The qubit does not generate any noise, which means ξq,ω = 0. Equation (11) should be supplemented by the current conservation condition
The power dissipated in the resistor Ri is expressed as
Solving Eqs. (11), (13) we express the currents Ij,ω and the potential Visl,ω via the three noises ξL, ξh and ξR. Substituting the result in Eq. (14) and taking the averages with the aid of Eq. (12), we arrive at Eqs. (4), (5).
As we mentioned, Eqs. (5), (6) rely on replacing the non-linear Josephson junctions by linear inductors. This approximation is formally valid in the two limits: at low temperatures kBTi ≪ Ub and at high temperatures kBTi ≫ Ub, where Ub is the height of the potential barrier in the potential (Eq. 2) varying from Ub = 4EJ at Φ = 0 to Ub = EJ/2 at Φ = 0.5Φ0. In the former case, Josephson phases fluctuate close to the bottom of the potential well where one can use harmonic approximation; in the latter case one can put EJ = 0, which again makes the system linear and the Landauer formula (Eq. 5), (Eq. 6) valid. In the intermediate regime kBTi ~ Ub the non-linearity of the junctions is important, but even in this case Eqs. (5), (6) reasonably well describe the heat transport29.
Microwave spectroscopy
In order to obtain accurate information about the device parameters, we performed microwave spectroscopy on the Sample II. In Fig. 4 we show the results of the two-tone spectroscopy and plot the absolute value of the transmission coefficient ∣S21∣ between the ports 2 and 1, shown in Fig. 2d, as a function of the magnetic flux Φ and the frequency of the probe signal. The spectroscopy reveals a series of lines. In particular, we observe single photon transitions at frequencies f01, f12, f02 and f25, where fij = (Ej − Ei)/h is the transition frequency between the energy levels of the qubit Ei and Ej, and several two-photon transitions corresponding to the frequencies f02/2, f24/2.
Next, we compare the experimental results with the theory model based on the Hamiltonian (Eq. 2). Adjusting the model parameters, we have managed to fit the positions of the experimental spectral lines with high accuracy. In this way, we have obtained the total capacitance of the Xmon island CI1 = 70.26 fF and the junction capacitances C = CI2/2 = 4.13 fF. From the same fit we have also obtained the values of the Josephson energy of a single junction, EJ/h = 4.86 GHz and the charging energy of the island I1, EC/h = 276 MHz. The errors in the fit is estimated as 3% for EJ and 4% for capacitance CI1 − 2CJ. All these values are close to the designed ones. In addition, microwave spectroscopy provides accurate values of the resonator frequencies, fL = 4.074 GHz, fR = 4.292 GHz, and the frequency of the diagnostic λ/4-resonator fd = 4.464 GHz with its quality factor Qd = 935. The resonator lines shown in Fig. 4 have small dispersive shifts induced by the coupling to the qubit, however, they are not visible on the scale of the figure. For example, for the right resonator we obtained the dispersive shift χR = 1.8 MHz. Importantly, the qubit frequency f01(Φ) does not cross the frequencies of the resonators and stays below them for all values of the magnetic flux. In this regime the coupling constants between the resonators and the qubit can be estimated from the dispersive shifts as \({g}_{j}=\sqrt{({f}_{j}-{f}_{01}^{\max }){\chi }_{j}}\), where j = L, R, d and \({f}_{01}^{\max }=3.6\) GHz is the maximum 0 ↔ 1 transition frequency. In this way we obtain gR = 35 MHz. In the next section we use these parameters to describe the heat transport in the Sample I, which has been fabricated in the same way. However, sample to sample scattering of the capacitances and the junction resistances during the fabrication can reach 10%, therefore we slightly adjust the capacitance CgR to achieve better fit.
Having determined the system parameters from the fits, in Fig. 5 we plot the two-dimensional potential of the three junction loop, defined in Eq. (2), for three values of the magnetic flux, Φ/Φ0 = 0, 0.25 and 0.5. In the same figure we also plot the squared absolute values of the wavefunctions of the three lowest energy levels. We observe that at flux values Φ = 0 and Φ = 0.25Φ0 the wavefunction of the nth level shows n nodes in the φ2 direction, as expected for a one-dimensional potential. Thus, in this case the two-dimensional wave function can be approximately factorized into the product Ψn(φ2, φ3) ≈ ψn(φ2)ψ0(φ3), where ψ0(φ3) is the ground state wave function in φ3 direction. Since such factorization is exact for a harmonic potential well, we conclude that at these flux values the linearized model of the qubit, on which Eqs. (5), (6) are based, should work reasonably well. However, at Φ = 0.5Φ0 this approximation is no longer accurate because the potential well becomes shallow and hence anharmonic.
Two dimensional potential of the flux qubit for three different values of the magnetic flux: Φ = 0 (a), Φ = 0.25Φ0 (e) and Φ = 0.5Φ0 (i). The squared wave functions of the ground state with n = 0 are shown in b, f, j; of the first excited level with n = 1—in c, g, k; and the second excited level with n = 2—in d, h, l.
Photonic heat transport
We performed heat transport measurements in Sample I, which has nominally identical parameters with Sample II. The hot resistor was heated up by the DC voltage Vh, and the temperatures of the left and the right resistors were monitored with SINIS thermometers, as it was explained above. We will focus on the data taken at the heating voltage Vh = 0.9 mV and plotted in Fig. 6a as functions of the magnetic flux Φ. First, we have estimated the power dissipated in the hot resistor as Ph = IhVh/2 (see the calibration curve in Fig. 7l measured on a different device, which has parameters identical to Sample I), and further using Eq. (1) we have found the temperature of the hot resistor, Th = 393 mK. This temperature is rather high and, therefore, cannot be accurately measured by the thermometer. The temperatures of the left and of the right resistors, which were lower, have been directly measured by SINIS thermometers and have been found to be TL = 168 mK and TR = 164 mK. Varying the magnetic flux applied to the SQUID loop, we have observed small oscillations of these temperatures with the amplitudes δTL,R ~ 0.01 mK. The measured temperatures have been converted to powers dissipated in the left (PL) and in the right (PR) resistors using Eq. (1). PL(Φ) and PR(Φ) oscillate with the period Φ0 following the qubit frequency f01(Φ) shown in Fig. 4. These oscillations have opposite signs for the two resistors, i.e when PL increases PR goes down and vice versa. The oscillation amplitudes are similar for both resistors, that is why the average value (PL + PR)/2, shown by black dots, is almost constant. This interesting observation suggests that the flux dependent contributions to PL and PR originate from the heat current between these two resistors PLR. Similar behavior of the dissipated powers PL, PR has been observed for other values of the heating voltage Vh.
a Experimentally observed flux dependent heat powers dissipated in the left resistor (PL, red dots), in the right resistor (PR, blue dots) and the average value (PL + PR)/2 (black dots). Heating voltage Vh = 0.9 mV has been applied to the hot resistor, which resulted in the resistor temperatures Th = 393 mK, TL = 168 mK and TR = 164 mK. The temperature of the mixing chamber was TMXC = 127 mK. b Theory prediction, based on Eqs. (4), (5), for the photonic heat powers dissipated in the left (\({P}_{L}^{{{{{{{{\rm{ph}}}}}}}}}\) red line) and the right (\({P}_{R}^{{{{{{{{\rm{ph}}}}}}}}}\) blue line) resistors. Black line in the bottom panel is the average value \(({P}_{L}^{{{{{{{{\rm{ph}}}}}}}}}+{P}_{R}^{{{{{{{{\rm{ph}}}}}}}}})/2\). We assumed the following resistor temperatures: Th = 393 mK, TL = 176 mK and TR = 156 mK. c The sum of the photon transmission probabilities τLh(ω, Φ) + τRh(ω, Φ), given by Eq. (6), assuming the same fit parameters as in the (b). Black circles indicate the double frequency of the three junction loop, 2ω0(Φ)/(2π), where ω0(Φ) is defined in Eq. (10).
Calibration of the SINIS thermometer connected to the left resistor RL indicated by blue (a), to the right resistor RR—green (b) and to the hot resistor Rh—red (c). The dashed lines indicate the polynomial data fitting. In all these plots the horizontal axis shows the voltage drop across the SINIS structure at fixed bias current and the vertical axis—the temperature of the mixing chamber. Figures d, h, l show the dependence of the power dissipated in, respectively, left, right and hot resistors versus heating voltage applied to the same resistor. Figures g, j show the non-local response in the system, where the power dissipated in the left resistor is plotted versus the heating voltages applied to the right (g) and to the hot (j) resistors. We also plot the non-local response of the right resistor on the bias voltages applied to left (e) and to the hot ((k) resistors, and of the hot resistor on the bias applied to left (f) and right (i) resistors.
In order to understand the flux dependence of the powers PL and PR better, we have numerically evaluated the photonic heat currents ((Eq. 4), (Eq. 5)) for a circuit depicted in Fig. 2b. Theoretical results are very sensitive to the parameter values. For example, the variation of the capacitances CL and CR within 10%, which is the estimated fabrication error, may change the heat fluxes by the factor 103–104. The origin of such sensitivity is simple—any mismatch between the narrow spectral lines of the resonators and of the qubit strongly reduces the heat flow. For this reason, we do not aim at the perfect fit, our goal is to show that with the nominal parameters of the experiment the theoretical model produces qualitatively similar results. Thus, for this simulation we have used the values of the resistances and capacitances given in sections Experiment and Spectroscopy. We have made only few adjustments of the parameters in order to increase the oscillation amplitudes of the heat powers PL, PR. Namely, we have chosen slightly larger value for the ground capacitance CgR = 70.5 fF and thus brought the right resonator in resonance with the left one, so that fL = fR = 4.292 GHz. The frequency of the hot resonator was taken to be fh = 8.237 GHz, i.e. it is two times higher than the frequency of the diagnostic resonator of the Sample II. We have also increased the temperature difference between the left and the right resistors by choosing TL = 176 mK and TR = 156 mK. Such increase in TL − TR is within the experimental uncertainty. Finally, we have reduced the Josephson energy to EJ/h = 3.63 GHz to achieve better agreement between spectroscopy plots of Figs. 4 (experiment) and 6c (theory). Photonic heat powers \({P}_{L}^{{{{{{{{\rm{ph}}}}}}}}}({{\Phi }})\) and \({P}_{R}^{{{{{{{{\rm{ph}}}}}}}}}({{\Phi }})\), obtained in this way, are plotted in Fig. 6b. They indeed behave similarly to the experimental ones, namely, they oscillate in opposite directions and the average power \(({P}_{L}^{{{{{{{{\rm{ph}}}}}}}}}+{P}_{R}^{{{{{{{{\rm{ph}}}}}}}}})/2\) is almost independent of the flux. Theory modeling clarifies the origin of this effect. Indeed, according to Eq. (4) the photonic heat powers dissipated in the resistors are expressed as \({P}_{L}^{{{{{{{{\rm{ph}}}}}}}}}={P}_{Lh}^{{{{{{{{\rm{ph}}}}}}}}}+{P}_{LR}^{{{{{{{{\rm{ph}}}}}}}}}\), \({P}_{R}^{{{{{{{{\rm{ph}}}}}}}}}={P}_{Rh}^{{{{{{{{\rm{ph}}}}}}}}}-{P}_{LR}^{{{{{{{{\rm{ph}}}}}}}}}\). Numerically we find that the currents flowing from the hot resistor to the left and the right ones, \({P}_{Lh}^{{{{{{{{\rm{ph}}}}}}}}}\) and \({P}_{Rh}^{{{{{{{{\rm{ph}}}}}}}}}\), weakly depend on magnetic flux because of the strong detuning between the qubit and the hot resonator. Thus, the flux dependence of the powers \({P}_{L}^{{{{{{{{\rm{ph}}}}}}}}}\) and \({P}_{R}^{{{{{{{{\rm{ph}}}}}}}}}\) predominantly comes from the photonic heat current flowing from the right to the left resistor \({P}_{LR}^{{{{{{{{\rm{ph}}}}}}}}}({{\Phi }})\), which contributes to them with opposite signs due to energy conservation. Comparing Fig. 6a and b, we notice the similarity in the shape of the experimental and the theoretical power-flux dependences for the right resistor. However, the theoretical curve for the left resistor is inverted and shifted by one half of the flux quantum relative to the experimental one. By tuning the system parameters further one can, in principle, reproduce the right shape of the \({P}_{L}^{{{{{{{{\rm{ph}}}}}}}}}({{\Phi }})\) dependence.
In Fig. 6c we plot the sum of the two transmission probabilities τLh(ω, ϕ) + τRh(ω, Φ) (Eq. 6) evaluated with the same fit parameters as in the theory plots of Fig. 6b. We note close resemblance of this plot with Fig. 4, in which the measured value of the transmission coefficient ∣S21(ω, Φ)∣ is presented. This similarity is expected because the two values are approximately related as ∣S21∣2 ≈ 1 − α(τLh + τRh), where the constant α depends on the system parameters. It also demonstrates that our model rather accurately describes the system even though it neglects the anharmonicity of the qubit. In addition, Fig. 6c helps to clarify the origin of the unusual non-sinusoidal shape of the power oscillations in Fig. 6a, b. Indeed, since the qubit and the resonator frequencies do not cross each other and the contribution of the qubit spectral lines to the heat transport is quite weak, one can rather accurately expand the heat current \({P}_{LR}^{{{{{{{{\rm{ph}}}}}}}}}\) in powers of the resonance frequency ω0(Φ), \({P}_{LR}({{\Phi }})\approx {P}_{LR}^{(0)}+A{\omega }_{0}^{2}({{\Phi }})\), where A is a pre-factor. The last term in this expression \(\propto {\omega }_{0}^{2}({{\Phi }})\) produces the cusps visible in PL,R(Φ) dependencies both in Fig. 6a, b. They occur at Φ = Φ0/2 where the dependence ω0(Φ) also has a cusp, see the lowest yellow line in Fig. 6c. The cusps become a bit rounded if one proceeds more accurately and replaces the frequency ω0(Φ)/2π by the qubit transition frequency f01(Φ) in the expansion. At the flux point Φ = 0.5Φ0 the harmonic approximation becomes inaccurate. Indeed, at this point the qubit frequency ωJ/2π is a bit higher than the frequency f01 computed with full quantum approach, cf. (Figs. 4 and 6c).
The absolute values of experimentally measured (Fig. 6a) powers exceed the numerically estimated ones (Fig. 6b) by a factor ~103. Thus, most of the heat power between the resistors is transmitted by the substrate phonons or by other mechanisms not included in our model. It is typical for this type of experiments, see e.g. refs. 12,13. Indeed, one has to heat the system strongly to make the small photonic heat flux measurable, but other contributions to the heat flux grow even stronger with rising temperature. The theoretical power modulation amplitudes also differ the experimental ones: we find δPL ≈ 13 aW and δPR ≈ 10 aW in the experiment, and \(\delta {P}_{L}^{{{{{{{{\rm{ph}}}}}}}}}=\delta {P}_{R}^{{{{{{{{\rm{ph}}}}}}}}}\approx 0.54\) aW in the simulation. In theory one can increase the power modulation by, for example, increasing the qubit frequency so that it crosses the frequencies of the resonators. In general, we have noticed that the model systematically underestimates the modulation amplitude of the powers PL and PR. Further research is required in order to resolve this problem.
Discussion
We have studied the heat transport by photons in a three terminal system containing a flux qubit realized as superconducting loop with three identical Josephson junctions. We have combined the DC heat transport measurements with the microwave spectroscopy performed on a separate sample with nominally identical parameters. In this way, we have verified that the flux qubit operates as a quantum system with its level spacing modulated by magnetic flux, and related this effect to the modulation of the heat power in DC measurements. Employing the standard theory models, we have described both the changes in the qubit spectrum and the modulation of the heat flux by magnetic field with the same set of parameters. Our experiment is an important step towards practical realization of on-chip quantum heat transistors, thermal amplifiers and heat pumped masers.
Methods
Fabrication. The devices are fabricated using three steps of electron-beam lithography (EBL) to create a mask on a silicon substrate. First EBL mask to prepare the niobium pattern and the groundplane of the device: feedline, resonators, cross-shape island and superconducting probes for thermometry are formed by reactive ion etching a 200 nm niobium metal film deposited by DC magnetron sputtering onto the high-resistivity silicon wafer. A 20-nm-thick aluminum film has been grown by atomic layer deposition on the wafer prior to Nb sputtering. The characteristic impedance of the coplanar waveguides used for the feedline and resonators is 50 Ω. Second, the SQUID with three Josephson junctions is realized with shadow-mask EBL, formed using two layers of poly(methylmetalcrylate-methacrylic) acid P(MMA-MAA) resist spun for 60 s at 4000 rpm followed by one layer of polymethyl-metacrylate (PMMA) spun for 60 s at 4000 rpm, all resist layers are immediately baked at 160 C, and followed by thin film physical vapor deposition in an electron-beam evaporator with an intermediate oxidation, using the Dolan bridge technique. The evaporation was preceded by argon ion plasma milling to facilitate the clean contact between aluminum and niobium. Third, the normal metal resistors and the normal-insulator-superconductor (NIS) tunnel junction elements for thermometry are also patterned by EBL, using the same resist, and then similarly deposited onto the wafer in three steps: Al with an in situ oxidation to make NIS junctions, Cu for reservoirs and Al. The fabrication is completed by spin-coating a protective layer of photoresist (AZ5214E) and dicing by diamond-embedded resin blade to 7 × 7 mm size samples. The resist was then removed using acetone. The resistance of the SIS \({{{{{{{\mathcal{R}}}}}}}}=28\pm 1\,{{{{{{{\rm{k}}}}}}}}{{\Omega }}\) and NIS tunnel junctions \({{{{{{{\mathcal{R}}}}}}}}=12\pm 1\,{{{{{{{\rm{k}}}}}}}}{{\Omega }}\) was measured on the test structures of the same dimensions on the same chip as shown in Fig. 2a. Both devices for heat transport measurements (Fig. 2a) and RF characterization (Fig. 2b) were fabricated simultaneously on the same wafer.
RF spectroscopy. The sample for RF spectroscopy was cooled in a BlueFors dilution refrigerator with a base temperature of 10 mK. In this design, a 7.4 GHz spectroscopy resonator connects the top terminal of the cross-shaped island to a feedline for spectroscopy characterization via transmission microwave readout. The spectroscopy measurements were performed using a vector network analyzer (VNA) at room temperature with the signal reaching the sample via an RF line and attenuated at different temperatures inside the cryostat. This scheme is presented in Fig. 2e. The output signal is then passed through two circulators at base temperature to a low noise HEMT amplifier mounted at 4 K, providing 46 dB gain, followed by an additional 28 dB amplifier outside of the cryostat. Characterization started by measuring the transmission S21 through the feedline to identify the λ/4 diagnostic resonator. To characterize the qubit and qubit-resonator couplings we perform two-tone spectroscopy by first applying a microwave low-power probe tone, followed by a second tone, whose frequency is swept. The Josephson energy is tuned by applying the magnetic flux with an external coil.
Thermal conductance measurements were performed in a custom-made plastic dilution refrigerator with a mixing chamber (MXC) temperature varied in the range 90–400 mK. The device is wire-bonded in a custom-made brass stage enclosed by two brass Faraday shields and fixed to the MXC with a proper thermalization. The readout scheme consists of thermocoax-filtered cryogenic lines with effective signal bandwidth of 0–10 kHz, for low-impedance loads. At room temperature, the voltage signal is amplified by a low noise amplifier Femto DLVPA-100-F-D. Heating of the thermal reservoir is realized by DC/AC signals, which were applied by programmable function generators and read on the control thermal reservoirs by multimeter/lock-in amplifier, synchronised to the square-wave modulation f ~ 77 Hz of the heated voltage bias. Thermometry was performed in SINIS configuration3, calibration of thermometers, presented in Fig. 7a–c for left RL, right RR and hot Rh resistors, was done by monitoring the voltage while applying a current bias between the superconducting probes and varying the MXC temperature up to 400 mK. The device is well thermalized to the MXC, therefore we can assume that the phonon temperature is in equilibrium with the MXC temperature, which is monitored by a ruthenium oxide thermometer that has been calibrated against a Coulomb blockade thermometer. The energy conservation among three thermal reservoirs is verified by performing three measurements: (1) heating the left resistor RL and performing local thermometry on RL and remote on the right resistor RR and hot resistor Rh (Fig. 7d–f); (2) heating and local thermometry on the right resistor RR and remote thermometry on the left resistor RL and hot resistor Rh (Fig. 7g–i); (3) heating and local thermometry on the hot resistor Rh and remote thermometry on the left resistor RL and right resistor RR (Fig. 7j–l). In Fig. 6 the magnetic flux is tuned by a superconducting solenoid encompassing the entire sample stage assembly, inside of a high-permeability magnetic shield, which is mounted inside the refrigerator at 4 K.
Data availability
The data that support the plots within this article are available from the corresponding author upon reasonable request.
Code availability
The codes that support the findings of this study are available from the corresponding author upon reasonable request.
References
Blais, A., Grimsmo, A. L., Girvin, S. M. & Wallraff, A. Circuit quantum electrodynamics. Rev. Mod. Phys. 93, 025005 (2021).
Meschke, M., Guichard, W. & Pekola, J. P. Single-mode heat conduction by photons. Nature 444, 187–190 (2006).
Giazotto, F., Heikkilä, T. T., Luukanen, A., Savin, A. M. & Pekola, J. P. Opportunities for mesoscopics in thermometry and refrigeration: Physics and applications. Rev. Mod. Phys. 78, 217–274 (2006).
Pekola, J. P. & Karimi, B. Colloquium: Quantum heat transport in condensed matter systems. Rev. Mod. Phys. 93, 041001 (2021).
Timofeev, A. V., Helle, M., Meschke, M., Möttönen, M. & Pekola, J. P. Electronic refrigeration at the quantum limit. Phys. Rev. Lett. 102, 200801 (2009).
Tan, K. Y. et al. Quantum-circuit refrigerator. Nat. Commun. 8, 15189 (2017).
Partanen, M. et al. Quantum-limited heat conduction over macroscopic distances. Nat. Phys. 12, 460–464 (2016).
Karimi, B. & Pekola, J. P. Otto refrigerator based on a superconducting qubit: Classical and quantum performance. Phys. Rev. B 94, 184503 (2016).
Kosloff, R. & Levy, A. Quantum heat engines and refrigerators: Continuous devices. Annu. Rev. Phys. Chem. 65, 365–393 (2014). PMID: 24689798.
Fornieri, A., Martínez-Pérez, M. J. & Giazotto, F. Electronic heat current rectification in hybrid superconducting devices. AIP Adv. 5, 53301 (2015).
Giazotto, F. & Martínez-Pérez, M. J. The josephson heat interferometer. Nature 492, 401–405 (2012).
Ronzani, A. et al. Tunable photonic heat transport in a quantum heat valve. Nat. Phys. 14, 991–995 (2018).
Senior, J. et al. Heat rectification via a superconducting artificial atom. Commun. Phys. 3, 40 (2020).
Díaz, I. & Sánchez, R. The qutrit as a heat diode and circulator. N. J. Phys. 23, 125006 (2021).
Joulain, K., Drevillon, J., Ezzahri, Y. & Ordonez-Miranda, J. Quantum thermal transistor. Phys. Rev. Lett. 116, 200601 (2016).
Zhang, Y. et al. Coulomb-coupled quantum-dot thermal transistors. EPL (Europhys. Lett.) 122, 17002 (2018).
Majland, M., Christensen, K. S. & Zinner, N. T. Quantum thermal transistor in superconducting circuits. Phys. Rev. B 101, 184510 (2020).
Naseem, M. T., Misra, A., Müstecaplioğlu, O. E. & Kurizki, G. Minimal quantum heat manager boosted by bath spectral filtering. Phys. Rev. Res. 2, 033285 (2020).
Liu, H., Wang, C., Wang, L.-Q. & Ren, J. Strong system-bath coupling induces negative differential thermal conductance and heat amplification in nonequilibrium two-qubit systems. Phys. Rev. E 99, 032114 (2019).
Wang, C., Xu, D., Liu, H. & Gao, X. Thermal rectification and heat amplification in a nonequilibrium v-type three-level system. Phys. Rev. E 99, 042102 (2019).
Levy, A. & Kosloff, R. Quantum absorption refrigerator. Phys. Rev. Lett. 108, 070604 (2012).
Kilgour, M. & Segal, D. Coherence and decoherence in quantum absorption refrigerators. Phys. Rev. E 98, 012117 (2018).
Scovil, H. E. D. & Schulz-DuBois, E. O. Three-level masers as heat engines. Phys. Rev. Lett. 2, 262–263 (1959).
Thomas, G., Gubaydullin, A., Golubev, D. S. & Pekola, J. P. Thermally pumped on-chip maser. Phys. Rev. B 102, 104503 (2020).
Orlando, T. P. et al. Superconducting persistent-current qubit. Phys. Rev. B 60, 15398–15413 (1999).
Palacios-Laloy, A. et al. Tunable resonators for quantum circuits. J. Low. Temp. Phys. 151, 1034–1042 (2008).
Barends, R. et al. Coherent josephson qubit suitable for scalable quantum integrated circuits. Phys. Rev. Lett. 111, 080502 (2013).
Pascal, L. M. A., Courtois, H. & Hekking, F. W. J. Circuit approach to photonic heat transport. Phys. Rev. B 83, 125113 (2011).
Thomas, G., Pekola, J. P. & Golubev, D. S. Photonic heat transport across a josephson junction. Phys. Rev. B 100, 094508 (2019).
Acknowledgements
We acknowledge valuable discussions with J. Ankerhold and G. Kurizki. This work was supported by the Academy of Finland Centre of Excellence program (project 312057), by the European Union’s Horizon 2020 research and innovation programme under the European Research Council (ERC) programme (grant agreement 742559), and Marie Sklodowska-Curie grant agreement No 843706. We acknowledge the provision of facilities and technical support of the Low Temperature Laboratory at Aalto University and the Otaniemi research infrastructure for Micro and Nanotechnologies (OtaNano). We also thank VTT Technical Research Center for depositing the Nb used in this work.
Author information
Authors and Affiliations
Contributions
A.G., G.T., D.S.G., and J.P.P. conceived the experiment and model and interpreted the results. A.G. designed, fabricated, and measured the samples with contributions from J.T.P. and D.L. Theoretical contributions were conceived and solved by D.S.G. with inputs from G.T. All authors have been involved in the analysis, and discussion of results, and manuscript preparation.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Jose Ordonez-Miranda, Özgür Müstecaplíoğlu and the other anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Gubaydullin, A., Thomas, G., Golubev, D.S. et al. Photonic heat transport in three terminal superconducting circuit. Nat Commun 13, 1552 (2022). https://doi.org/10.1038/s41467-022-29078-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-29078-x
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.