Abstract
Nuclear magnetic resonance imaging (MRI) at the atomic scale offers exciting prospects for determining the structure and function of individual molecules and proteins. Quantum defects in diamond have recently emerged as a promising platform towards reaching this goal, and allowed for the detection and localization of single nuclear spins under ambient conditions. Here, we present an efficient strategy for extending imaging to large nuclear spin clusters, fulfilling an important requirement towards a single-molecule MRI technique. Our method combines the concepts of weak quantum measurements, phase encoding and simulated annealing to detect three-dimensional positions from many nuclei in parallel. Detection is spatially selective, allowing us to probe nuclei at a chosen target radius while avoiding interference from strongly-coupled proximal nuclei. We demonstrate our strategy by imaging clusters containing more than 20 carbon-13 nuclear spins within a radius of 2.4 nm from single, near-surface nitrogen–vacancy centers at room temperature. The radius extrapolates to 5–6 nm for 1H. Beside taking an important step in nanoscale MRI, our experiment also provides an efficient tool for the characterization of large nuclear spin registers in the context of quantum simulators and quantum network nodes.
Similar content being viewed by others
Introduction
Nuclear magnetic resonance (NMR) spectroscopy and magnetic resonance imaging (MRI) are powerful tools for molecular analysis and medical diagnostics. While conventional NMR operates on millimeter-sized samples containing large ensembles of molecules, much effort has been directed toward improving the resolution to the nanometer scale1,2 where the atomic structure could be analyzed at the level of individual molecules3. Such a “single-molecule MRI” technique would enable direct imaging of molecular structures with three-dimensional resolution and elemental specificity1 and the monitoring of chemical reactions and binding4,5. This capability could lead to many applications in biology, chemistry, and nanosciences, especially because MRI avoids important limitations of other structural techniques (like X-ray diffraction or electron microscopy) such as radiation damage and the need for ensemble averaging6,7.
Quantum sensors based on nitrogen-vacancy (NV) centers in diamond have recently generated exciting progress in micron-scale8,9 and nanoscale10,11,12 NMR spectroscopy. Early experiments have demonstrated the detection of single nuclear spins within the diamond crystal13,14,15 as well as of nanoscale films deposited on diamond surfaces10,11,12,16. A recent refinement of protocols has led to tremendous advances in sensitivity and spectral resolution8,17,18, allowing for the three-dimensional localization of individual nuclear spins19,20,21,22, spin pairs23,24,25, and the chemical fingerprinting of molecular ensembles with high spectral resolution8,26. Most recently, Abobeih et al.27 reported the milestone achievement of a complete mapping of a 27-nuclear-spin cluster at cryogenic temperatures.
To extend experiments to the imaging of single molecules, approaches are needed that are compatible with near-surface NV centers (≲5 nm) and preferably an ambient environment. Moreover, methods are required that can efficiently detect and precisely localize a large number of distant nuclear spins in parallel. While advanced strategies have been developed to solve the latter challenge of nuclear spin detection and localization27,28,29,30,31,32, many of these strategies require very long coherence times or a single-shot readout of the quantum sensor to reach adequate sensitivity and spectral resolution27,33. These conditions are difficult to realize with shallow defect centers at room temperature34,35.
In this work, we demonstrate a powerful method for the sensitive detection and spatial mapping of individual nuclei in large nuclear spins clusters. Our approach combines the concepts of weak quantum measurements36,37, phase encoding21,22, and simulated annealing38,39 to detect signals and extract precise three-dimensional distances from many nuclei in parallel. We further show that our detection is spatially selective, allowing us to probe nuclei at a chosen target radius while avoiding interference from strongly-coupled proximal nuclei. We demonstrate our strategy by mapping the 13C environment of two NV centers containing 20 and 29 nuclei, respectively. Because our experiments are performed on near-surface spin defects and at room temperature, they are compatible with the demanding environment of prospective single-molecule MRI investigations. Besides taking an important step in developing a single-molecule MRI platform, our experiment also provides an efficient tool for the characterization of large qubit registers in the context of quantum simulators40, quantum network nodes33,41,42, and multi-qubit quantum processors43,44.
Results
Imaging concept
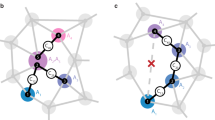
Our concept and the experimental situation is sketched in Fig. 1a. We consider a central electronic spin surrounded by a group of nuclear spins whose three-dimensional locations we aim to determine. Here, both the electronic and nuclear spins are embedded in the solid matrix of a diamond crystal, but our concept is applicable to a general situation of a localized electronic spin45,46,47 and a nearby nuclear ensemble, including surface molecules10,11,48 or crystalline layers49. The electronic spin plays a dual role in our arrangement30: first, it acts as a local sensor for the weak magnetic fields produced by the nearby nuclei. Second, it generates a strong magnetic dipole field that we exploit for spatial imaging. In a reference frame where z is the common quantization axis (Fig. 1b), the dipole field is given by:
where a is the hyperfine vector (see Fig. 1b), r = (r, ϑ, ϕ) are the polar coordinates of the nuclear spin relative to the electron spin situated at the origin, ez is a unit vector along z, mS is the magnetic quantum number of the electronic spin (\({m}_{S}\in \left\{-1,0,1\right\}\) for the NV center). Because we will be detecting distant 13C spins, the Fermi contact interaction can be safely neglected20,50. Further, μ0 is the vacuum permeability, ℏ the reduced Planck constant, and γe and γn are the electronic and nuclear gyromagnetic ratios, respectively. Thus, by measuring the three components of the hyperfine vector a, the distance vector r can be directly inferred (up to an inversion symmetry at the origin), revealing a spin’s three-dimensional spatial location.
a We detect and image nuclear spins (black) surrounding a central electronic spin (purple). In our experiments, spins are embedded in a nanostructured diamond chip, manipulated by microwave and radio-frequency (RF) pulses, and detected by optical means. b Spatial imaging is enabled through the hyperfine field \({{{{{{{\bf{a}}}}}}}}=({a}_{\perp }\cos \phi ,{a}_{\perp }\sin \phi ,{a}_{| | })\), whose magnitude and direction strongly depend on the three-dimensional position r = (r, ϑ, ϕ). We determine the radius r and polar angle ϑ by measuring the parallel and transverse hyperfine components, a∣∣ = a ⋅ ez and a⊥ = ∣a × ez∣19,54. The azimuth ϕ is equal to the phase of the nuclear precession21,22. ez is a unit vector pointing along the electronic quantization axis and B0∣∣ez is an external bias field. Bcoil∣∣ex is the direction of the RF field.
Parallel signal acquisition
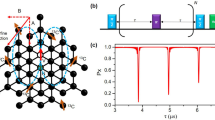
While this scheme of three-dimensional localization has been demonstrated on individual nuclear spins19,20,21,22, the principal challenge lies in extending these experiments to large numbers of nuclei. We address this challenge by exploiting the principle of weak quantum measurements36,51, which closely resembles the detection of a free induction decay (FID) signal in canonical Fourier NMR spectroscopy. Figure 2 introduces our experimental protocol, consisting of a polarization, excitation, and read-out step. We begin by hyperpolarizing nuclear spins through a polarization transfer from the optically-aligned electronic spin (Fig. 2a). This initial step, when applied repetitively and for a sufficiently long time, leads to a volume of near-fully polarized nuclei around the central electronic spin52. We then excite all nuclei simultaneously using a broad-band π/2 pulse and detect the free nuclear precession signal by sampling the transverse nuclear magnetization using weak measurements36. The procedure yields an FID signal of the form:
where n is the number of nuclear spins. Further, A(βi) is the probability amplitude17, Γ(βi) the dephasing rate, ωi the precession frequency, and ϕi the initial phase of the signal belonging to the i’th nucleus. The parameter:
is a “measurement gain” parameter that is proportional to the hyperfine coupling constant a⊥,i multiplied by the interaction time tβ of the ac detection (Fig. 2b). The parameter βi, discussed in Section V, plays an important role in single-spin FID detection as it governs the balance between signal gain and quantum back-action36,37,53. We sample the FID at instances t = kts, where ts is the sampling time, k = 1 \(\ldots\) K, and where K is the number of points in the FID trace (Fig. 2).
We polarize the nuclear spins by a repeated NOVEL sequence (gray, inset a)87,88, initiate simultaneous precession of all nuclei by applying a π/2 pulse with an external RF coil (blue)62, and detect the precession by repeated sampling of the transverse nuclear magnetization (purple)17,18,89. tpol is the polarization time, ts is the sampling time and K is the number of samples. Each weak-measurement read-out block (inset b) consists of a Carr–Purcell–Meiboom–Gill (CPMG) pulse train90,91,92 of 4−24 equidistant π pulses (orange) separated by a delay time τ = 1/(2γnB0), followed by an optical read-out pulse (green). Red blocks are π/2 pulses. The duration of the CPMG sequence defines the interaction time tβ. An additional π pulse (*) is used to average over the electronic mS = 0, −1 states. See the Supplementary Information for the full-timing diagram and experimental parameters.
Hyperfine parameters
We next show that an FID trace described by Eq. (2) contains all the information needed to reconstruct the hyperfine vectors ai, and hence, the three-dimensional locations ri of the nuclear spins. First, the parallel components a∣∣,i (see Fig. 1b) can be determined from the spectral positions of the nuclear resonances, given by the free precession frequencies:
where the approximation is for small a∣∣,i, a⊥,i ≪ ω0 (fulfilled in our experiments but not required for the analysis) and where ω0 = −γnB0, with B0∣∣ez being the external magnetic bias field54.
The amplitudes A(βi) and decay rates Γ(βi) encode information about the perpendicular components a⊥,i (See Supplementary Materials accompanying this manuscript):
where p0,i is the initial polarization of the i’th nuclear spin. Note that the p0,i also contain any pulse errors and other imperfections of the pulse sequence, and therefore rather reflect pre-scaling factors and a lower bound for the nuclear polarization. The dephasing rate Γ(βi) is influenced by three effects: a measurement-induced dephasing proportional to \({a}_{\perp ,i}^{2}{t}_{\beta }^{2}\) due to quantum back-action36. (ii) An additional decay rate proportional to \({a}_{| | ,i}^{2}{t}_{\ell }^{2}\) that is specific to the stochastic optical read-out process of the NV center with effective duration tℓ36. (iii) An intrinsic \({T}_{2,i}^{* }\) decay that accounts for all dephasing mechanisms not associated with the read-out process, such as spin-lattice effects or unresolved nuclear-nuclear couplings.
Finally, the azimuth ϕi is encoded in the complex phase of the nuclear FID signal. Because we initiate the FID by applying a π/2 pulse with an external RF coil, all nuclei are rotated around a common laboratory-frame axis and start precession with the same phase. By contrast, the ac detection of the FID is phase-sensitive with respect to each nucleus’ individual hyperfine field. As a consequence, the phase ϕi is equal to the spatial angle between the coil and hyperfine axes in the laboratory frame (Fig. 1b)21,22. Analysis of the complex FID signal therefore directly reveals the desired azimuth ϕi.
In the following, we will make three important assumptions that are necessary for keeping the maximum likelihood fitting of spectra tractable. First, we assume that all nuclei carry approximately the same polarization, p0,i ≈ p0. Because we repeat the polarization transfer process for typically >103 cycles (i.e., longer than the FID duration), we expect that all nuclei within the sensitive radius become close to fully polarized. The polarization level may be slightly reduced for spin pairs55 or due to residual spin diffusion, however, these effects are small for our dilute 13C concentration. Our assumption of nearly full polarization is consistent with the observation that spectra show little change in peak intensities once the number of cycles is increased beyond ≳103 36. Similar saturation behavior is suggested by ref. 52. Second, we treat \({T}_{2,i}^{* }\approx {T}_{2}^{* }\) as a global parameter. Although this assumption is likely wrong in general, the role of \({T}_{2}^{* }\) here is that of an upper bound in the FID decay. Because the FID is for most spins dominated by the measurement-induced dephasing (i) and (ii), our method is not very sensitive to variations in \({T}_{2}^{* }\). We find that our fit results for \({T}_{2}^{* }\) are similar to those expected from the drift in the bias field, suggesting that our linewidths are limited by external field stability. Third, we will neglect nuclear-nuclear couplings, discussed further below.
Sensitive slice
The magnitude of the FID signal strongly depends on a spin’s three-dimensional position r, because of the position dependence of the hyperfine interaction. We can capture the spatial dependence by calculating a sensitivity function \({{{{{{{\mathcal{S}}}}}}}}({{{{{{{\bf{r}}}}}}}})\) that quantifies the signal contribution as a function of spin location r. The sensitivity function is expressed as a signal-to-noise ratio and given by:
where β = a⊥tβ/π (Eq. (3)) encodes the spatial position (via the hyperfine parameter a⊥), and where K, ts, tβ, and tpol are experimental parameters defined in Fig. 2.
Figure 3 plots \({{{{{{{\mathcal{S}}}}}}}}({{{{{{{\bf{r}}}}}}}})\) as a function of vertical and radial distance to the central electronic spin. Interestingly, the sensitivity does not monotonically decay with distance, as might be expected from the a⊥ ∝ r−3 scaling of the hyperfine interaction. Rather, \({{{{{{{\mathcal{S}}}}}}}}\) is initially low, and increases with r until it reaches a maximum at a characteristic radius rslice before showing the expected r−3 decay. The suppression of signal from close spins is a consequence of quantum back-action36: Because these spins are strongly coupled, their measurement strength parameter β is large, leading to a rapid signal decay 1/Γ(β) ∝ β−2 → 0 (Eq. (5b)). Conversely, distant spins with small β generate weak signals because A(β) → 0 (Eq. (5a)). Maximum sensitivity results at an intermediate value where the two effects are balanced,
The optimum point of sensitivity is approximately reached when intrinsic and induced decay rates are commensurate, \({({T}_{2,{{{{{{{\rm{n}}}}}}}}}^{* })}^{-1}={\beta }^{2}/(4{t}_{{{{{{{{\rm{s}}}}}}}}})\) and when the FID record length is matched to the decay rate, Kts = 1/Γ.
ρz-plot of the sensitive slice for different interaction times tβ, where \(z=r\cos \vartheta\) and \(\rho =r\sin \vartheta\) are vertical and radial distance, respectively. Bright shading color codes the signal-to-noise ratio. By varying tβ the sensitive slice can be tuned to spins in close (1), intermediate (2), or far (3) distance from the central electronic spin (panels from left to right). The dashed contour is the a⊥ isoline where β = β(opt). rslice is the characteristic radius of a slice. Plots assume tℓ = 0 and \({({T}_{2,{{{{{{{\rm{n}}}}}}}}}^{* })}^{-1}=0\).
As shown in Fig. 3, the points of maximum sensitivity are located along a contour of constant a⊥ = πβ(opt)/tβ. We denote this contour as the “sensitive slice” associated with the interaction time tβ. By varying tβ, we can vary the radius of the sensitive slice rslice and tune detection from close to distant nuclear spins (Fig. 3, left to right). Because a⊥ ∝ r−3, the radius of the sensitive slice scales as \({r}_{{{{{{{{\rm{slice}}}}}}}}}\propto {t}_{\beta }^{1/6}\). The spatial selectivity is an important feature of our method, since it allows us to selectively probe nuclear spins at a defined (far) distance from the central electronic spin while avoiding interference from strongly-coupled nuclei in close proximity. Further, by sweeping tβ, we can collect FID traces from several sensitive slices and cover an extended spatial volume in the sample.
Maximum likelihood estimation by simulated annealing
Armed with a protocol for measuring the signals and coupling constants from many nuclei in parallel, we develop a maximum likelihood protocol to extract the hyperfine parameters and position vectors from an FID trace (Eq. 2).
We begin by setting up a likelihood model. Assuming n spins are contributing to the signal, our model contains M = 3n + 3 unknown parameters, including the three hyperfine parameters a∣∣,i, a⊥,i, and ϕi for each spin i plus three additional, global parameters accounting for an initial polarization p0 and dephasing times \({T}_{2,{{{{{{{\rm{n}}}}}}}}}^{* }\) and tℓ [see Eq. (5)]. Note that because the number of spins n is a priori unknown, M is itself a free parameter. To proceed, we collect the unknown parameters in the parameter vector \({{{{{{{\boldsymbol{\theta }}}}}}}}=\left\{{\theta }_{m}\right\}\), where m = 1…M. Our goal is to balance goodness of the fit and model complexity by minimizing a cost function of the form:
where G(θ, x) is a measure of the goodness of the fit, \({{{{{{{\bf{x}}}}}}}}=\left\{{x}_{k}\right\}\), where k = 1…K, is the set of measured data points, and P(K, M) is a penalty term to prevent over-fitting56. Eq. (8) is the generic form of a so-called information criterion (IC). In our likelihood framework, G(θ, x) can be expressed in terms of a negative likelihood function57:
where the argument of the logarithm is the residual sum of squares. The function \({\tilde{x}}_{k}({{{{{{{\boldsymbol{\theta }}}}}}}})\) represents the estimated data points calculated from Eq. (2) using the parameter vector θ. For the penalty term P(K, M), we choose the so-called weighted-average information criterion (WIC)58 that is a weighted average of the Akaike and Bayesian information criteria (AIC59 and BIC60, respectively, see (See Supplementary Materials accompanying this manuscript for definition). The advantage of the WIC is that it performs well regardless of sample size K.
Minimization of Eq. (8) is highly nontrivial, as the number of fit parameters is large and M is itself an unknown. In this work, we implement generalized simulated annealing (GSA)38,39,61 algorithm to address this challenge. GSA is well-posed in our case because it works well for the global optimization of complicated, multi-dimensional systems with large numbers of local minima. To further improve the GSA, we run the minimization over a large number of random starting configurations for θ. Finally, once a best-estimate (lowest IC) set of parameters has been found, we compute the three-dimensional locations ri of nuclei from the hyperfine vector ai by inverting Eq. (1) (see Eqs. (10, 11) in the Methods).
Experimental demonstration
We experimentally demonstrate our three-dimensional nuclear localization strategy by imaging the 13C environment of shallow NV centers in diamond. We focus on two NV centers in this work, labeled NV1 and NV2, out of five recorded datasets. The two NV centers are selected for favorable optical contrast and electron spin coherence times, but not for their 13C environment. Their shallow depth (~10 nm) is not important for this study except for demonstrating that our method is compatible with near-surface NV centers. We probe the NV centers at room temperature using non-resonant optical excitation and a single-photon counting module. Electronic and nuclear spins are manipulated via two arbitrary waveform generators connected to a separate microwave transmission line and RF micro-coil circuits, respectively21,62. Experiments use a bias field B0 ~ 200 mT aligned to within 1∘ of the NV symmetry axis (Fig. 1b). A description of diamond samples and the experimental setup is provided in the Methods section.
Figure 4a shows an example of an FID time trace from NV2 for tβ = 4.944 μs, and Fig. 4b, c shows the complete dataset of 13C Fourier spectra obtained for both NV centers. For each NV center, we record four spectra with different values of the interaction time tβ to sample different radii of the sensitive slice and to add redundancy. For each dataset, we plot the power spectrum, the real and imaginary parts of the complex Fourier spectrum, as well as the fit residues. Clearly, the spectra show a rich peak structure, indicating that we are detecting a large number of 13C resonances.
a Example FID trace from NV2. Each data point reflects the probability amplitude x(t) from one read-out block, integrated over ~106 repetitions of the full sequence (see Fig. 2). Measurement parameters are tpol = 40 ms, ts = 11.48 μs, tβ = 4.944 μs and K = 800, and total measurement time is 11 h. b Complex Fourier spectra of the 13C environment of NV1 for a series of interaction times tβ. Shown are from top to bottom (vertically offset for clarity): power spectrum (PSD), real part of the complex spectrum (\({{{{{{{\rm{Re}}}}}}}}[{{{{{{{\rm{FFT}}}}}}}}]\)), fit residues for \({{{{{{{\rm{Re}}}}}}}}[{{{{{{{\rm{FFT}}}}}}}}]\), the imaginary part of the complex spectrum (\({{{{{{{\rm{Im}}}}}}}}[{{{{{{{\rm{FFT}}}}}}}}]\)), and fit residues for \({{{{{{{\rm{Im}}}}}}}}[{{{{{{{\rm{FFT}}}}}}}}]\). Blue traces are best fits (see text). The horizontal axis shows the spectral shift relative to the 13C Larmor frequency at 2.156 MHz calibrated using correlation spectroscopy54. The bias field is B0 = 201.29 mT. The PSD data of NV1 are the same as in ref. 36, Extended Data Fig. 5a. c Fourier spectra of the 13C environment of NV2. Bias field is B0 = 188.89 mT. d Cost function (IC, Eq. (8)) plotted as a function of the number of spins n. Best fits are obtained for n = 20 (NV1) and n = 29 (NV2). Since only differences in the cost function are meaningful, the minimum of the IC has been set to zero.
To fit the spectra, we add the likelihood functions [Eq. 9] from all four spectra and minimize the total cost function [Eq. 8] using a single set of hyperfine parameters. We begin by randomly initializing each parameter, and then minimize the residues between the experimental and computed spectra using a GSA algorithm on a high-performance computer cluster63. To improve robustness, we fit the spectra, rather than the FID traces. We compute separate residues for real and imaginary parts of the complex spectrum as well as for their magnitude squared and minimize the sum of all residues. Additionally, we penalize configurations where the distance between any two 13C is less than one bond length. To accelerate the search for a global minimum, we repeat the procedure for a large number (~102) of starting values randomly chosen from predefined parameter intervals. Finally, to determine the number of spins we run the minimization routine for different n and select the configuration with the smallest global IC value (Fig. 4d). Once the minimization has terminated and n has been determined, we perform bootstrapping on the final fit residues64 to obtain an estimate for the fit uncertainties for all parameters.
The calculated spectra for the most likely nuclear configurations are displayed as blue solid lines in Fig. 4b, c. For the two datasets, we find n = 20 for NV1 and n = 29 for NV2 (Fig. 4d). The large IC >10 of the next-best configurations n ± 1 indicates that our n are well-defined. (An IC >10 is equivalent to an evidence ratio of e0.5IC > 102, meaning that our estimated n is >102 more likely than neighboring n ± 1.) This statistical finding is supported by the good agreement between fit and experimental data (gray dots) and the small residues (green), which are of the same order as the measurement noise. We have verified the calculated spectra by performing a full density matrix simulation using the final parameter set (Fig. S2). All fit results are collected in Tables S3 and S4.
Figure 5 shows visualizations of the three-dimensional locations of nuclei. We find that nuclear positions are clustered between ca. r = 0.7–2.4 nm and ca. ϑ = 30–75∘. This clustering is a consequence of the spatial selectivity of our method: although the 13C nuclei are distributed randomly over the diamond lattice, only spins falling within the sensitive slice are picked up by the weak-measurement detection sequence. Proximal spins (r < 0.7 nm) could be detected by further reducing tβ or by employing techniques developed for strongly-coupled nuclei19,20. More distant spins (r > 2.4 nm) can be addressed by increasing tβ, up to a limit set by the electronic coherence time T2,e.
a Fitted spatial locations of the 13C spins of NV1 (dots) shown in a ρz-plot. The central NV spin is located at the origin. Note that our method is ambiguous with respect to an inversion at the origin. Therefore, all nuclei are plotted in the upper hemisphere. Color coding reflects the combined sensitive slice [Eq. (6)] taking all tβ values as well as finite tℓ and \({T}_{2,{{{{{{{\rm{n}}}}}}}}}^{* }\) into account. b Polar plot showing the azimuth ϕ on the xy-plane. c Three-dimensional view of the nuclear positions. d–f Corresponding plots for the carbon spins of NV2. Uncertainties (±1 standard error) are shown as shaded areas or volumes, respectively, and are omitted if smaller than the data points. Index labels refer to Tables S3 and S4 in the Supplementary Information.
We find that the combined sensitive slice for all measurements (color-coded in Fig. 5a, d), taking the tβ values of the four spectra, tℓ and \({T}_{2,{{{{{{{\rm{n}}}}}}}}}^{* }\) dephasing into account, agrees well with the extracted 13C positions. (The tℓ dephasing suppresses signal from nuclei with large a∣∣, leading to low sensitivity for spins near ϑ = 0∘ and 90∘). Figure 5 also clearly shows that the spatial precision of our method is highest and well below 1 Å for 13C’s that are located near the maximum of the sensitive slice, while the precision can be poor for spins located at the fringe of the slice.
The solution presented in Fig. 5 is a maximum likelihood estimate based on the assumptions of global values for the polarization and intrinsic dephasing as well as an absence of nuclear-nuclear couplings (see Section “Hyperfine parameters”). Our solution represents the three-dimensional nuclear spin configuration that has the highest likelihood, but there is no guarantee that it represents the “true” configuration of 13C nuclei on the diamond carbon lattice. This probabilistic aspect is a standard feature of large-scale structure determination65. For example, because our method does not account for nuclear couplings, it is possible that spin pairs or clusters of 13C are erroneously assigned a single-spin position. In addition, because of the inversion symmetry of the dipolar interaction [Eq. (1)], our method does not discriminate between spins lying in the upper and lower hemisphere. Looking forward, this ambiguity will be naturally lifted for outside molecules. Further, both issues can be alleviated by introducing additional spatial constraints, especially by measuring nuclear spin-spin distances using two-dimensional NMR spectroscopy27 (see Discussion).
To verify the three-dimensional nuclear configuration, we perform a set of basic statistical tests on the density, spatial distribution, and fit uncertainty of 13C positions. Comparing the volume uncertainties δV of the 13C (indicated by orange shading in Fig. 5c, e and tabulated in Supplementary Materials accompanying this manuscript.) with the volume per carbon atom in the diamond lattice (V = 5.67 Å3 66), we find that 13 out of 20 spins (NV1) and 21 out of 29 spins (NV2) have δV < V and therefore likely represent single nuclei. Next, defining the volume of the sensitive region by the volume in space contributing 50% to the total signal10, we find sensitive volumes of V = 9.3 nm3 and 14.8 nm3 for NV1 and NV2, respectively. Considering an average density ρ(13C) = 1.94 nm−3 for 13C nuclei in diamond at natural isotope abundance (1.1%), the average number of 13C in the sensitive slices are 18.0 and 28.6, respectively, in good agreement with our experimental result. Further, a χ2 test for the angular distributions of the azimuth angles yields p-values well above the 5% level (54 and 70%, respectively), as expected for a random 13C distribution. Within these statistics, our experimental results are fully consistent with a stochastic distribution of 13C atoms around the NV centers. Finally, the r > 0.7 nm in retrospect justifies neglecting the Fermi contact interaction in our model20,50.
Discussion
We conclude with a roadmap for extending the present experiment to samples outside of diamond, including individual molecules and complex spin structures (Fig. 6). Reaching this ambitious goal requires overcoming four central challenges:
-
(i)
To image outside nuclear spins, near-surface NV centers are needed. Although our scheme is compatible with near-surface NV centers, their properties are known to degrade. The degradation manifests itself both in a reduced coherence time and reduced stability of the negative NV charge state. Recently, there has been remarkable progress in stabilizing very shallow NV centers. In particular, ref. 67 reports coherence times of T2,e ~ 40 μs for 5-nm-deep NV centers. In our experiments, we find similar values (T2,e ~ 50 μs for a 3.5-nm-deep NV center). Extrapolating the r ~ 2.4 nm for 13C (#12) in Fig. 5 using the \(r\propto {\gamma }_{{{{{{{{\rm{n}}}}}}}}}^{1/3}{t}_{\beta }^{1/6}\) scaling of the sensitive radius, the above T2,e implies a maximum radius of ca. 5–6 nm for single őr 19F nuclei (see Suppl. Fig. S5). This radius is compatible with the above shallow NV centers.
-
(ii)
Single molecules must be immobilized and isolated on the diamond surface. This step can be achieved using surface functionalization5,48,68. To further protect the molecules and inhibit diffusion, molecules may be embedded in a spin-free matrix layer (Fig. 6)69.
-
(iii)
Nuclear spins in molecules will behave differently from internal 13C nuclei. In particular, nuclear spin interactions will likely dominate over the hyperfine interaction. Nuclear spin interactions can be mitigated by homo- and heteronuclear decoupling techniques70 and by isotope dilution71; however, they also are an important resource for structural information and a central element in our molecular imaging strategy, see next point.
-
(iv)
Advanced spectroscopy and imaging techniques are needed that can efficiently retrieve the desired structure. A promising strategy is to combine the global distance information available by our scheme with local distance constraints obtained by solid-state NMR methods27 (dashed and dotted lines in Fig. 6). For example, two-dimensional spectroscopy9,25,72 and double-echo techniques27,73 can be conveniently integrated with our protocol, because of its similarity to conventional FID detection. Additionally, efficient computational methods will be required to speed up data analysis and optimally extract the desired spatial information, including, for example, sparse sampling29,74, gradient Monte Carlo75, and machine learning techniques76,77,78.
A few molecules of interest are immobilized on a diamond surface containing <5-nm-deep NV centers. Molecules are protected by a spin-free “matrix” layer (blue shading). The global position and conformation of molecules are imaged by our weak-measurement localization scheme (dashed lines), while precise local distances between nuclei are measured using two-dimensional NMR (dotted lines). Computational analysis is used to extract three-dimensional atomic coordinates.
By demonstrating three-dimensional mapping of nuclear spins in ambient conditions, our work takes an important step forward towards the ambitious goal of single-molecule MRI. Looking beyond the milestone of structural imaging, the technique could be extended to study chemical binding and chemical surface reactions at the single-molecule level. For example, in a biological context, surface NMR may allow investigation of a priori unknown substrate binding sites in enzymes79, as well as conformational changes in biomolecules associated with allosteric regulation80, protein aggregation81, or aptamer-target recognition82. These applications are particularly appealing because NMR can provide complementary information to other surface-sensitive techniques, such as surface-enhanced Raman spectroscopy (SERS), photoelectron spectroscopies, and fluorescence microscopy.
Besides magnetic imaging of single spins, our work also provides interesting perspectives for the characterization of large qubit registers in quantum applications. For example, our method can be applied to efficiently map out the coupling network of quantum nodes built from a central electronic spin backed by a nuclear spin register83,84. Such quantum nodes are central elements in emerging optical85 or electronic86 quantum interconnects. Another application is a nuclear quantum simulation using an electronic qubit for initialization and readout40. Finally, our parallel measurement protocol could provide a rapid means for calibrating cross-talk in superconducting qubit architectures43,44.
Methods
Diamond samples
Two single-crystal diamond plates were used for experiments. Both sample A (NV1) and sample B (NV2) were electronic-grade, natural abundance (1.1% 13C) diamond membranes. NV centers were created by 15N+ ion implantation at an energy of 5 keV and doses of 5 × 1011 cm−2 and 4 × 1010 cm−2 for samples A and B, respectively. Samples were subsequently annealed at 850 °C to form NV centers. We chose the 15N species to discriminate implanted NV centers from native (14N) NV centers. Both samples were cleaned in a 1:1:1 mixture of H2SO4:HNO3:HClO4 and baked at 465 °C in the air before mounting them in the setup. Whenever organic contamination was spotted, samples were cleaned in a 2:1 mixture of H2SO4:H2O2 (Piranha). We etched nano-pillars into the membrane surfaces to increase the photon collection efficiency. The continuous wave (CW) photon count rate was 250–500 kC/s.
Experimental setup
Experiments were performed using a custom-built confocal microscope equipped with a green λ = 532 nm frequency-doubled Nd:YAG excitation laser (CNI Laser MSL-FN-532nm) and a 630−800 nm detection path using a single-photon avalanche photodiode (APD, Pelkin Elmer SPCM-AQR Series). Optical pulses were generated by an acousto-optic modulator (AOM, Crystal Technology 3200-144) in a double-pass configuration, and gating of arriving photons was realized by time-tagging (NI-PCIe-6363) and software binning of photon counts. Typical laser excitation powers were on the order of 100 μW.
We synthesized microwave pulses for manipulating the electronic spin using an arbitrary waveform generator (AWG, Tektronix AWG5012C) and up-converted them to ~2.5 GHz using a local oscillator (Hittite HMC-T2100) and a quadrature mixer (Marki microwave IQ1545). Pulses were subsequently amplified (Gigatronics GT-1000A) prior to delivery to the NV center using a coplanar waveguide (CPW) photo-lithographically defined on a quartz cover slip. The transmission line was terminated on an external 50 Ω load (Meca 490-2). We synthesized radio-frequency (RF) pulses for nuclear spin manipulation using an AWG (National Instruments PCI-5421) and subsequently amplified them (Mini-Circuits LZY-22+). The pulses were transmitted using a planar micro-coil connected in series with a 50 Ω termination (Meca 697-30-1). The measured micro-coil inductance was L = 0.77 μH. The 50 Ω termination increased the rf-circuit bandwidth (Q = L/R) at the expense of efficiency (most power was dissipated in the load). The micro-coil circuit had a 3-dB-bandwidth of ~19 MHz. 13C Rabi frequencies were typically around 25 kHz. A layout of the micro-coil arrangement is given in ref. 62.
We used a cylindrical samarium-cobalt permanent magnet (TC-SmCo, reversible temperature coefficient 0.001%/°C) to create a bias field B0 ~ 190 mT at the NV center location. To align B0 with the NV symmetry axis, we adjusted the relative location of the permanent magnet by fitting it to a set of electron paramagnetic resonance (EPR) lines recorded at different magnet locations and subsequently by maximizing the CW photon count rate.
Tracking of magnetic field drifts
The net magnetic bias field drifted by typically a few μT, leading to variations in the EPR frequency of order ±100 kHz and variations in the 13C Larmor frequency of order ±50 Hz. This limited the observed 13C linewidths to ~100 Hz. Field drifts were the dominating source of line broadening for the 13C NMR. We continuously tracked and logged magnetic field drifts by measuring the EPR resonance of the NV center and periodically readjusted the microwave excitation frequency during the course of the experiment.
Hyperfine vector a and position r
The radius r and polar angle ϑ are computed from the parallel and transverse hyperfine parameters a∣∣ and a⊥ as follows (see ref. 54, Eq. S28 and S29):
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
Code availability
The code that was used to perform the GSA minimization is available from the corresponding author upon request.
References
Degen, C. L., Poggio, M., Mamin, H. J., Rettner, C. T. & Rugar, D. Nanoscale magnetic resonance imaging. Proc. Natl Acad. Sci. USA 106, 1313 (2009).
Rose, W. et al. High-resolution nanoscale solid-state nuclear magnetic resonance spectroscopy. Phys. Rev. X 8, 011030 (2018).
Sidles, J. A. Noninductive detection of single-proton magnetic resonance. Appl. Phys. Lett. 58, 2854 (1991).
Ziarek, J. J., Peterson, F. C., Lytle, B. L. & Volkman, B. F. Binding site identification and structure determination of protein-ligand complexes by nmr a semiautomated approach. Methods Enzymol. 493, 241–275 (2011).
Liu, K. S. et al. Surface NMR using quantum sensors in diamond. Proc. Natl. Acad. Sci. USA 115, e2111607119 (2022).
Glaeser, R. M. Cryo-electron microscopy of biological nanostructures. Phys. Today 61, 48 (2008).
Garman, E. F. Radiation damage in macromolecular crystallography: what is it and why should we care. Acta Cryst. D 66, 339–351 (2010).
Glenn, D. R. et al. High-resolution magnetic resonance spectroscopy using a solid-state spin sensor. Nature 555, 351 (2018).
Smits, J. et al. Two-dimensional nuclear magnetic resonance spectroscopy with a microfluidic diamond quantum sensor. Sci. Adv. 5, eaaw7895 (2019).
Mamin, H. J. et al. Nanoscale nuclear magnetic resonance with a nitrogen-vacancy spin sensor. Science 339, 557–560 (2013).
Staudacher, T. et al. Nuclear magnetic resonance spectroscopy on a (5-nanometer)3 sample volume. Science 339, 561–563 (2013).
Loretz, M., Pezzagna, S., Meijer, J. & Degen, C. L. Nanoscale nuclear magnetic resonance with a 1.9-nm-deep nitrogen-vacancy sensor. Appl. Phys. Lett. 104, 033102 (2014).
Jelezko, F. et al. Observation of coherent oscillation of a single nuclear spin and realization of a two-qubit conditional quantum gate. Phys. Rev. Lett. 93, 130501 (2004).
Dutt, M. V. G. et al. Quantum register based on individual electronic and nuclear spin qubits in diamond. Science 316, 1312 (2007).
Dreau, A., Spinicelli, P., Maze, J. R., Roch, J. & Jacques, V. Single-shot readout of multiple nuclear spin qubits in diamond under ambient conditions. Phys. Rev. Lett. 110, 060502 (2013).
Muller, C. et al. Nuclear magnetic resonance spectroscopy with single spin sensitivity. Nat. Commun. 5, 4703–4703 (2014).
Boss, J. M., Cujia, K. S., Zopes, J. & Degen, C. L. Quantum sensing with arbitrary frequency resolution. Science 356, 837–840 (2017).
Schmitt, S. et al. Submillihertz magnetic spectroscopy performed with a nanoscale quantum sensor. Science 356, 832 (2017).
Zhao, N. et al. Sensing single remote nuclear spins. Nat. Nano. 7, 657 (2012).
Zopes, J. et al. Three-dimensional localization spectroscopy of individual nuclear spins with sub-angstrom resolution. Nat. Commun. 9, 4678 (2018).
Zopes, J., Herb, K., Cujia, K. S. & Degen, C. L. Three-dimensional nuclear spin positioning using coherent radio-frequency control. Phys. Rev. Lett. 121, 170801 (2018).
Sasaki, K., Itoh, K. M. & Abe, E. Determination of the position of a single nuclear spin from free nuclear precessions detected by a solid-state quantum sensor. Phys. Rev. B 98, 121405 (2018).
Shi, F. et al. Sensing and atomic-scale structure analysis of single nuclear-spin clusters in diamond. Nat. Phys. 10, 21–25 (2014).
Abobeih, M. H. et al. One-second coherence for a single electron spin coupled to a multi-qubit nuclear-spin environment. Nat. Commun. 9, 2552 (2018).
Yang, Z. et al. Structural analysis of nuclear spin clusters via 2d nanoscale nuclear magnetic resonance spectroscopy. Adv. Quant. Technol. 3, 1900136 (2020).
Aslam, N. et al. Nanoscale nuclear magnetic resonance with chemical resolution. Science 357, 67–71 (2017).
Abobeih, M. H. et al. Atomic-scale imaging of a 27-nuclear-spin cluster using a quantum sensor. Nature 576, 411–415 (2019).
Ajoy, A., Bissbort, U., Lukin, M. D., Walsworth, R. L. & Cappellaro, P. Atomic-scale nuclear spin imaging using quantum-assisted sensors in diamond. Phys. Rev. X 5, 011001 (2015).
Kost, M., Cai, J. & Plenio, M. B. Resolving single molecule structures with nitrogen-vacancy centers in diamond. Sci. Rep. 5, 11007 (2015).
Perunicic, V. S., Hill, C. D., Hall, L. T. & Hollenberg, L. A quantum spin-probe molecular microscope. Nat. Commun. 7, 12667 (2016).
Wang, Z.-Y., Haase, J. F., Casanova, J. & Plenio, M. B. Positioning nuclear spins in interacting clusters for quantum technologies and bioimaging. Phys. Rev. B 93, 174104 (2016).
Schwartz, I. et al. Blueprint for nanoscale NMR. Sci. Rep. 9, 6938 (2019).
Bradley, C. et al. A ten-qubit solid-state spin register with quantum memory up to one minute. Phys. Rev. X 9, 031045 (2019).
Neumann, P. et al. Single-shot readout of a single nuclear spin. Science 329, 542–544 (2010).
Shields, B., Unterreithmeier, Q. P., de Leon, N. P., Park, H. & Lukin, M. D. Efficient readout of a single spin state in diamond via spin-to-charge conversion. Phys. Rev. Lett. 114, 136402 (2015).
Cujia, K. S., Boss, J. M., Herb, K., Zopes, J. & Degen, C. L. Tracking the precession of single nuclear spins by weak measurements. Nature 571, 230 (2019).
Pfender, M. et al. High-resolution spectroscopy of single nuclear spins via sequential weak measurements. Nat. Commun. 10, 594 (2019).
Kirkpatrick, S., Gelatt, C. D. & Vecchi, M. P. Optimization by simulated annealing. Science 220, 671–680 (1983).
Tsallis, C. & Stariolo, D. A. Generalized simulated annealing. Phys. A Stat. Mech. Appl. 233, 395 – 406 (1996).
Cai, J. M., Retzker, A., Jelezko, F. & Plenio, M. B. A large-scale quantum simulator on a diamond surface at room temperature. Nat. Phys. 9, 168–173 (2013).
Waldherr, G. et al. Quantum error correction in a solid-state hybrid spin register. Nature 506, 204–207 (2014).
Wolfowicz, G. et al. 29si nuclear spins as a resource for donor spin qubits in silicon. New J. Phys. 18, 023021 (2016).
Krinner, S. et al. Benchmarking coherent errors in controlled-phase gates due to spectator qubits. Phys. Rev. Appl. 14, 024042 (2020).
Tsunoda, T., Bhole, G., Jones, S. A., Jones, J. A. & Leek, P. J. Efficient hamiltonian programming in qubit arrays with nearest-neighbor couplings. Phys. Rev. A 102, 032405 (2020).
Christle, D. J. et al. Isolated electron spins in silicon carbide with millisecond coherence times. Nat. Mater. 14, 160–163 (2015).
Iwasaki, T. et al. Germanium-vacancy single color centers in diamond. Sci. Rep. 5, 12882 (2015).
Sukachev, D. et al. Silicon-vacancy spin qubit in diamond: a quantum memory exceeding 10 ms with single-shot state readout. Phys. Rev. Lett. 119, 223602 (2017).
Lovchinsky, I. et al. Nuclear magnetic resonance detection and spectroscopy of single proteins using quantum logic. Science 351, 836 (2016).
Lovchinsky, I. et al. Magnetic resonance spectroscopy of an atomically thin material using a single-spin qubit. Science 355, 503 (2017).
Nizovtsev, A. P. et al. Non-flipping 13 c spins near an nv center in diamond: hyperfine and spatial characteristics by density functional theory simulation of the c 510 [nv]h 252 cluster. New J. Phys. 20, 023022 (2018).
Colangelo, G., Ciurana, F. M., Bianchet, L. C., Sewell, R. J. & Mitchell, M. W. Simultaneous tracking of spin angle and amplitude beyond classical limits. Nature 543, 525–528 (2017).
Broadway, D. A. et al. Quantum probe hyperpolarisation of molecular nuclear spins. Nat. Commun. 9, 1246 (2018).
Gefen, T., Khodas, M., McGuinness, L. P., Jelezko, F. & Retzker, A. Quantum spectroscopy of single spins assisted by a classical clock. Phys. Rev. A 98, 013844 (2018).
Boss, J. M. et al. One- and two-dimensional nuclear magnetic resonance spectroscopy with a diamond quantum sensor. Phys. Rev. Lett. 116, 197601 (2016).
Villazon, T., Chandran, A. & Claeys, P. W. Integrability and dark states in an anisotropic central spin model. Phys. Rev. Res. 2, 032052 (2020).
Knowles, H. S., Kara, D. M. & Atature, M. Demonstration of a coherent electronic spin cluster in diamond. Phys. Rev. Lett. 117, 100802 (2016).
Burnham, K. P. & Anderson, D. R. Model Selection and Multimodel Inference (Springer, 2002).
Wu, T.-J. & Sepulveda, A. The weighted average information criterion for order selection in time series and regression models. Stat. Probab. Lett. 39, 1–10 (1998).
Akaike, H. A new look at the statistical model identification. IEEE Trans. Automat. Contr. 19, 716–723 (1974).
Schwarz, G. Estimating the dimension of a model. Ann. Statist. 6, 461–464 (1978).
Szu, H. & Hartley, R. Fast simulated annealing. Physics Lett. A 122, 157 – 162 (1987).
Herb, K., Zopes, J., Cujia, K. S. & Degen, C. L. Broadband radio-frequency transmitter for fast nuclear spin control. Rev. Sci. Instrum. 91, 113106 (2020).
ETH Zurich. Euler cluster. https://scicomp.ethz.ch (2020).
Efron, B. Bootstrap methods: another look at the jackknife. Ann. Statist. 7, 1–26 (1979).
Shen, Y., Delaglio, F., Cornilescu, G. & Bax, A. Talos+: a hybrid method for predicting protein backbone torsion angles from nmr chemical shifts. J. Biomol. NMR 44, 213–223 (2009).
Shikata, S. et al. Precise measurements of diamond lattice constant using bond method. Jpn. J. Appl. Phys. 57, 111301 (2018).
Sangtawesin, S. et al. Origins of diamond surface noise probed by correlating single-spin measurements with surface spectroscopy. Phys. Rev. X 9, 031052 (2019).
Sushkov, A. et al. Magnetic resonance detection of individual proton spins using quantum reporters. Phys. Rev. Lett. 113, 197601 (2014).
Mamin, H. J., Sherwood, M. H. & Rugar, D. Detecting external electron spins using nitrogen-vacancy centers. Phys. Rev. B 86, 195422 (2012).
Slichter, C. P. Principles of Magnetic Resonance 3rd edn (Springer, 1990).
Loquet, A., Lv, G., Giller, K., Becker, S. & Lange, A. 13c spin dilution for simplified and complete solid-state nmr resonance assignment of insoluble biological assemblies. J. Am. Chem. Soc. 133, 4722–4725 (2011).
Aue, W. P., Bartholdi, E. & Ernst, R. R. Two-dimensional spectroscopy. application to nuclear magnetic resonance. J. Chem. Phys. 64, 2229 (1976).
Ludwig, C. & Viant, M. R. Two-dimensional j-resolved nmr spectroscopy: review of a key methodology in the metabolomics toolbox. Phytochem Anal. 21, 22–32 (2010).
Mobli, M., Maciejewski, M. W., Schuyler, A. D., Stern, A. S. & Hoch, J. C. Sparse sampling methods in multidimensional NMR. Phys. Chem. Chem. Phys. 14, 10835–10843 (2012).
Hu, X., Beratan, D. N. & Yang, W. A gradient-directed monte carlo method for global optimization in a discrete space: application to protein sequence design and folding. J. Chem. Phys. 131, 154117–154117 (2009).
Aharon, N. et al. NV-center-based nano-NMR enhanced by deep learning. Sci. Rep. 9, 17802 (2019).
Kong, X. et al. Artificial intelligence enhanced two-dimensional nanoscale nuclear magnetic resonance spectroscopy. npj Quantum Inf. 6, 79 (2020).
Jung, K. et al. Deep learning enhanced individual nuclear-spin detection. npj Quantum Inf. 7, 41 (2021).
Mistry, J., Bateman, A. & Finn, R. D. Predicting active site residue annotations in the pfam database. BMC Bioinformatics 8, 298 (2007).
Gunasekaran, K., Ma, B. & Nussinov, R. Is allostery an intrinsic property of all dynamic proteins. Proteins 57, 433–443 (2004).
Ross, C. A. & Poirier, M. A. What is the role of protein aggregation in neurodegeneration. Nat. Rev. Mol. Cell Biol. 6, 891–898 (2005).
Nakatsuka, N. et al. Aptamer-field-effect transistors overcome debye length limitations for small-molecule sensing. Science 362, 319 (2018).
Awschalom, D. D., Hanson, R., Wrachtrup, J. & Zhou, B. B. Quantum technologies with optically interfaced solid-state spins. Nat. Photonics 12, 516–527 (2018).
Zwanenburg, F. A. et al. Silicon quantum electronics. Rev. Mod. Phys. 85, 961–1019 (2013).
Bernien, H. et al. Heralded entanglement between solid-state qubits separated by three metres. Nature 497, 86–90 (2013).
Tosi, G. et al. Silicon quantum processor with robust long-distance qubit couplings. Nat. Commun. 8, 450 (2017).
Henstra, A., Dirksen, P., Schmidt, J. & Wenckebach, W. Nuclear spin orientation via electron spin locking (NOVEL). J. Magn. Reson. 77, 389–393 (1988).
London, P. et al. Detecting and polarizing nuclear spins with double resonance on a single electron spin. Phys. Rev. Lett. 111, 067601 (2013).
Degen, C., Reinhard, F. & Cappellaro, P. Quantum sensing. Rev. Mod. Phys. 89, 035002 (2017).
Lange, G. D., Riste, D., Dobrovitski, V. V. & Hanson, R. Single-spin magnetometry with multipulse sensing sequences. Phys. Rev. Lett. 106, 080802 (2011).
Alvarez, G. A. & Suter, D. Measuring the spectrum of colored noise by dynamical decoupling. Phys. Rev. Lett. 107, 230501 (2011).
Kotler, S., Akerman, N., Glickman, Y., Keselman, A. & Ozeri, R. Single-ion quantum lock-in amplifier. Nature 473, 61–65 (2011).
Acknowledgements
We thank M. L. Palm for helpful discussions and acknowledge technical support from the machine shop of the Department of Physics at ETH Zurich. This work has been supported by Swiss National Science Foundation (SNSF) Project Grant No. 200020_175600, the National Center of Competence in Research in Quantum Science and Technology (NCCR QSIT), and the Advancing Science and TEchnology thRough dIamond Quantum Sensing (ASTERQIS) program, Grant No. 820394, of the European Commission.
Author information
Authors and Affiliations
Contributions
C.L.D. initiated the project. K.S.C. performed the experiments on a setup built by K.S.C. and K.H. K.S.C. developed the GSA minimization and analyzed the data. K.S.C. and C.L.D. co-wrote the paper with input from K.H., J.Z., and J.M.A. All authors discussed the results.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cujia, K.S., Herb, K., Zopes, J. et al. Parallel detection and spatial mapping of large nuclear spin clusters. Nat Commun 13, 1260 (2022). https://doi.org/10.1038/s41467-022-28935-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-28935-z
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.