Abstract
Lithium-ion-encapsulated fullerenes (Li+@C60) are 3D superatoms with rich oxidative states. Here we show a conductive and magnetically frustrated metal–fullerene-bonded framework {[Cu4(Li@C60)(L)(py)4](NTf2)(hexane)}n (1) (L = 1,2,4,5-tetrakis(methanesulfonamido)benzene, py = pyridine, NTf2− = bis(trifluoromethane)sulfonamide anion) prepared from redox-active dinuclear metal complex Cu2(L)(py)4 and lithium-ion-encapsulated fullerene salt (Li+@C60)(NTf2−). Electron donor Cu2(L)(py)2 bonds to acceptor Li+@C60 via eight Cu‒C bonds. Cu–C bond formation stems from spontaneous charge transfer (CT) between Cu2(L)(py)4 and (Li+@C60)(NTf2−) by removing the two-terminal py molecules, yielding triplet ground state [Cu2(L)(py)2]+(Li+@C60•−), evidenced by absorption and electron paramagnetic resonance (EPR) spectra, magnetic properties and quantum chemical calculations. Moreover, Li+@C60•− radicals (S = ½) and Cu2+ ions (S = ½) interact antiferromagnetically in triangular spin lattices in the absence of long-range magnetic ordering to 1.8 K. The low-temperature heat capacity indicated that compound 1 is a potential candidate for an S = ½ quantum spin liquid (QSL).
Similar content being viewed by others
Introduction
Since the pure form of the lithium-ion-encapsulated fullerene salt [Li@C60](SbCl6) was isolated and structurally determined by X-ray diffraction analysis in 20101, studies on this smallest endohedral metallofullerene (EMF) have taken precedence over photoinduced electron transfer (ET) in noncovalent donor–acceptor (D–A) complexes2,3,4,5,6, covalent metal complexes7, organic photovoltaics8, and molecular electronics9 over the past decade because of the salt’s unique structure and electronic properties relative to pristine C6010,11,12,13,14. Although the optical bandgap (Eg) is very close to that of pristine C60, the lowest unoccupied molecular orbital (LUMO) of Li+@C60 has been observed to decline significantly to −3.90 eV with an initial reduction potential at −0.39 V versus Fc/Fc+ in o-dichlorobenzene (o-DCB)1. Furthermore, the oxidisation state of Li+@C60 can be easily tuned from 1+ to 3− by external chemical stimuli to realise various electronic states1. Therefore, this compound has been widely used as a π-electron acceptor owing to the small reorganisation energy required, which leads to highly delocalised π-electrons over a 3D sphere2,3. It is possible that Li+@C60 can be doped by alkali metals to produce A3(Li@C60) species (A = K+, Rb+, and Cs+) in imitation of A3C60 superconductors with three electrons accommodated in the triply degenerated LUMO15,16,17,18. In particular, the emergence of Li+@C60•− requires a milder chemical oxidant than for C60•−. Such a low reduction potential provides many opportunities for coordination chemistry. According to the Mulliken theory19,20,21,22, the formation of the CT complex requires efficient orbital overlap between the highest occupied molecular orbital (HOMO) of D and the LUMO of A. The CT interactions in the ground state increase with a decrease in the energy difference between the HOMO of D and LUMO of A. In this regard, Martin and co-workers reported several CT complexes between comparatively strong electron donors such as π-extended tetrathiafulvalene derivatives and fullerenes23,24. Additionally, Yamada et al. observed a triplet charge-separated state by laser-exciting a curved π-surface donor and Li+@C60 in solution3.
Although C60 is an ideal ligand to realise topological architectures owing to its isotropic coordination environment25, to date, reports on the preparation of electrically conductive and magnetically frustrated solids based on Li+@C60 remain elusive. On the other hand, the S = ½ electronic system holds promise for exploring interesting quantum phenomena such as unconventional superconductivity26,27,28,29 and QSLs, which are commonly observed in triangular or kagomé lattices30,31,32,33,34,35,36. Herein, we selected an electronically active donor, Cu2(L)(py)4, and a 3D charge-tuneable metallofullerene, Li+@C60, as both the ligand and electron acceptor to construct a conductive and spin-frustrated framework based on the Mulliken theory.
In this work, an S = ½ electronic framework {[Cu4(Li+@C60)(L)(py)4](NTf2)(hexane)}n (1) is isolated by constructing the donor and acceptor. The donor is bonded to the acceptor via Cu–C bonds. It is noteworthy that the HOMO of Cu2(L)(py)4 has the equivalent energy level of the LUMO of Li+@C60, thereby facilitating CT interactions in the ground state. From our calculations, we find that the dxz orbitals of the Cu ions in Cu2(L)(py)4 are delocalised and strongly coupled with the N(pz) orbitals (π-electrons) of the ligand, thereby yielding delocalised electrons in the HOMO. In 1, the four-terminal dxz orbitals of Cu ions coordinate with one Li+@C60 cage and the remaining four Cu ions coordinate with the next Li+@C60 cage to form an infinitely scaled 1D chain structure. The four Cu(L)(py) sites transfer a single electron into the Li+@C60 cage, and the resulting four Cu2+ (S = ½) ions and Li+@C60•− (S = ½) interact with each other and exhibit magnetic frustration in a triangular-like lattice. Our study demonstrates long-range electrical conductivity (σ) and spin frustration using Li+@C60 superatoms in such a bonded D–A-type framework.
Results and discussion
Metal-fullerene bonded donor‒acceptor-type framework
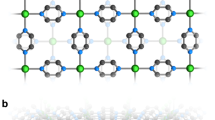
Compound 1 was synthesised by reaction of Cu2(L)(py)4 and (Li+@C60)(NTf2−) with a molar ratio of 2:1 in o-DCB solution. It crystallises in the triclinic \({P}_{1}^{-}\) space group with the unit-cell dimensionality of a = 9.9963(3) Å, b = 13.3087(3) Å, c = 19.7031(5) Å, α = 77.323(2)°, β = 76.572(2)°, and γ = 69.500(2)° at 120 K. One Li+@C60 cage coordinates with four Cu ions from four Cu2(L)(py)2 molecules (Fig. 1a), and the remaining four Cu ions coordinate with the next Li+@C60 cage to afford infinite 1D ladder-like structures along the b-axis (Fig. 2a). Each Cu ion exhibits an equivalent of five coordination numbers (two Cu‒C and three Cu‒N bonds) in a distorted trigonal bipyramid geometry (Supporting Information Fig. 1). The rectangular plane formed by the four Cu ions perfectly divides the C60 cage into two (Fig. 1b), and the shell-like Li+ ion is off-centred and localised above or below the Cu plane with thermal ellipsoids at 50% probability. Similar Li+-ion arrangements are also observed in the other forms of Li+@C60 salts37,38. The inner Li+ ion coordinates with the six-carbon ring with Li–C bond lengths in the range of 2.337–2.527 Å, which are consistent with the reported results7,39. The encapsulated Li+ ions should strengthen the π back-bonding from the transition-metal centre to the fullerene cage7; however, the Cu ions do not coordinate with the rings of the six-carbon (pink atoms in Fig. 2) owing to the highly symmetrical array of the four Cu ions.
a The coordination geometry of [Cu(N)3]4(Li+@C60) and the arrangement of Li-ion. One Li+@C60 coordinates with four Cu ions. The four Cu ions form a rectangular-like plane with a length and width of 9.5 and 5.5 Å, respectively. b The Li-ion coordinates with six carbon-ring and locates above or below the Cu-plane with thermal ellipsoids at the 50% probability. The Cu-plane perfectly splits the Li+@C60 cage in half. c The structure of the donor, Cu2(L) and its bond length. Colour code: C (black), Cu (blue), N (cyan), S (yellow), O (red) and Li (pastel blue).
a 1D ladder-like structure along the b-axis in the bc plane (anion NTf2− and hexane molecules are omitted). One Li+@C60 cage coordinates with four Cu ions and the remaining four-terminal Cu ions coordinate with the adjacent Li+@C60 cage to form a 1D ladder-like structure. Distance rπ between adjacent Li+@C60 cages is 6.5 Å. The Li atoms are off-centred and polarised above/below the Cu plane. b Top view of the 1D ladder-like structure in the ac plane. Each structure stacks along the a-axis to form a 2D interacting sheet with intermolecular distance = 3.2 Å between two Li+@C60 cages. Colour code: Cu (blue), sulphur (yellow), oxygen (red), nitrogen (pastel cyan), carbon (black/pink). Hydrogen atoms are omitted for clarity.
The benzene ring of the ligand is slightly distorted (Supporting Information Fig. 2), and the bond patterns indicate the loss of aromaticity (Fig. 1c). On the other hand, the hexane molecules are trapped inside the squared structure of [Cu2(L)(py)3(Li+@C60)]2 and strongly disordered along two lines (Supporting Information Fig. 3). Close to the square structure, the NTf2− molecules interact electrostatically with ligands through hydrogen bonds. Inside the ladder chain, the π···π distance (rπ) between the two Li+@C60 cages is 6.5 Å (Fig. 2a), indicating well-separated π electrons along the b-axis. The 1D ladder structures self-stack along the a-axis to form 2D interacting nanosheets with rπ of 3.2 Å (Fig. 2b). To determine the structure phase purity, the temperature dependence of crystal structures were determined at various temperature points (25, 50, 100, 200, and 300 K) by using synchrotron radiation. The structure analysis indicated that there are no structural changes or distortions in 25–300 K (PXRD patterns in Supporting Information Fig. 4). Above 100 K, we did not detect the Li+ position because of the fast motion of the Li+ ion inside the cage. Below 100 K, the Li+ ion was disordered and localised at two equivalent positions due to the symmetry. As the localised Li+ ions strongly attract the negative radicals (via Li–C bonds), the C60•− radicals localised on the six-carbon ring (pink atoms in Fig. 2).
Spontaneous charge transfer between Cu2(L)(py)4 and (Li+@C60)(NTf2 −) by precise control of the redox activities
Figure 3a shows the CV plot to Fc/Fc+. Four reversible redox processes with the first and second oxidisation potentials are observed at −0.36 and −0.04 V, respectively. Meanwhile, the first and second reduction potentials are observed at −0.92 and −1.08 V, respectively. The potential at −0.36 V corresponds to the first oxidisation process of Cu2(L)(py)4 to [Cu2(L)(py)4]+. In this regard, Aoyagi et al. reported that the first reduction process from Li+@C60 to Li+@C60•− occurs at −0.39 eV in o-DCB versus Fc/Fc+1. Consequently, the HOMO energy level of Cu2(L)(py)4 can be simply treated as equivalent to the LUMO energy level of Li+@C60 if the dissolution-free energy effect is ignored (Fig. 3b). According to the Mulliken theory, ET from Cu2(L)(py)4 (donor) to Li+@C60 (acceptor) can spontaneously occur without external energy to generate a triplet ground state [Cu2(L)(py)4]+[Li+@C60•−]. The solution-state absorption spectra in Fig. 3c evidence this mechanism. (Li+@C60)(NTf2−) does not show any absorption band from 750 to 1500 nm whereas Cu2(L)(py)4 shows a strong and broadband at 920 nm. Once the two pristine molecules are mixed in o-DCB, two new bands at 886 and 1032 nm are observed, strongly indicating that Li+@C60•− is generated40. Moreover, the strong band at 920 nm in Cu2(L)(py)4 vanishes from the mixed solution, strongly indicating ET occurrence. The solid-state absorption spectrum of 1 shows several broad absorption bands at 1.30, 1.91, 2.42, and 3.48 eV (Supporting Information Fig. 5), where the band at 1.30 eV extends to the IR region (inset of Supporting Information Fig. 5), which indicates that 1 has a small optical bandgap (Eg). Figure 3d shows the Tauc plot of the Kubelka–Munk-transformed spectrum, with Eg = 0.57 eV, as obtained from a linear fit to the low-energy onset of absorption. However, it is difficult to assign the Li+@C60•− band owing to absorption-band superpositions. Nevertheless, the generated Li+@C60•− can be detected by the EPR spectra. Figure 3e shows the temperature dependence of the EPR spectra of 1 for 3.5–300 K with all spectra showing two EPR active bands. At the lower magnetic field, parallel gII values of 2.45(3), 2.32(1), and perpendicular g⊥ value of 2.09(1) are observed at 300 K. The g values and peak-to-peak linewidth, ∆Hpp = 217.5(4) G, are entirely consistent with the Cu2+ ion (S = ½)41,42. Another weak signal observed near the Cu2+ signal with g = 2.0008(3) and ∆Hpp = 8.1(2) G, signifies the presence of electronically active Li+@C60•− radical3,40,43. However, it is difficult to assign significant interactions between Cu2+ ions and Li+@C60•− radical from the EPR spectra, probably owing to the superposition of the two characterised bands, but the spectra demonstrate that spontaneous ET occurs from Cu2L(py)4 to Li+@C60 and 1 remains in a triplet ground state up to 3.5 K.
a Cyclic voltammogram (−2.0 to 0.8 V versus Fc/Fc+) of Cu2(L)(py)4 in o-DCB with 0.1 M TBAPF6 as the supporting electrolyte. The pale blue dot at E = −0.39 eV represents the first reduction potential from Li+@C60 to Li+@C60•−. b Schematic of charge-transfer interactions of HOMO and LUMO orbital energies between Cu2(L)(py)4 and Li+@C60 calculated from the cyclic voltammogram. The HOMO energy level of Cu2(L)(py)4 is identical to the LUMO energy level of Li+@C60, indicating strong CT interactions. c In situ solution-state UV–Vis-NIR absorption spectra at room temperature. d Tauc plot of room-temperature diffuse reflectance UV−vis−NIR spectra of 1 from 0.05 to 3.3 eV, obtained via Kubelka–Munk transforms (F(R)) for indirect allowed transition. The optical bandgap is determined as 0.57 eV by the linear fit (orange dots) of absorption onset in the NIR energy region. e First-derivative solid-state X-band absorption EPR spectra of 1 for 3.5‒300 K.
S = ½ heterospin frustration between Cu2+ and Li+@C60 •− in the ladder-like chains
The intensity of main peaks in the EPR spectra mimics the thermal dependence of the magnetic susceptibility (χ). The χ−T plot of 1 does not show any magnetic phase transition from 1.8 to 300 K under 1 T (Fig. 4a) and 4 T fields (Supporting Information Fig. 6), thereby indicating no long-range magnetic ordering. In addition, no sign of a spin-glass state is observed in the rectangular Cu lattices, as there is no deviation between the zero-field-cooled (ZFC) and field-cooled (FC) measurements. This suggests that Li+@C60•− radicals are involved in the magnetic reactions. Fitting the (χ − χ0)−1 to the Curie–Weiss law at high temperatures (T > 175 K) yields a large negative Curie–Weiss temperature, θcw = −190 K, suggesting strong antiferromagnetic (AF) interactions between the spins (χ0 is defined as core diamagnetic or Van–Vleck paramagnetic susceptibility44 and determined to be 8.8 × 10−4 cm3 mol−1 in Supporting Information Fig. 7). Even the fitted low-temperature χ−1 (T = 1.8–10 K) results in a θcw = −1.6 K, indicating significant AF interactions. The (χ − χ0)T value at 300 K is 1.71 cm3 K mol−1 (Supporting Information Fig. 8), which follows the theoretical prediction of four Cu2+ ions and one Li+@C60•− radical per unit (χTcalc = 0.375 × 5 = 1.875 cm3 K mol−1). The rapid decrease in (χ − χ0)T with temperature reduction indicates that AF exchange interactions are dominant. In addition, the magnetic-field dependence of magnetisation from 1.8 to 300 K does not show any visible hysteresis loops (Fig. 4b).
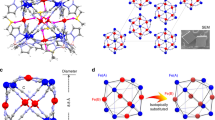
a The temperature dependence of magnetic susceptibility product (χ − χ0) of 1 in FC, ZFC modes and the corresponding (χ − χ0)−1‒T plots under a 1 T field from 1.8 to 300 K. The black curve represents the best fit for (χ − χ0) by considering the possible exchange interaction between spins. The black line represents the best fit by the Curie‒Weiss law. A large negative θcw = −190 K is observed, suggesting strong AF exchange interactions. b Magnetic-field dependence of magnetisation of 1 at 1.8, 20, 50, and 300 K. There is no hysteresis loop at these temperatures. c Spin orientations of the Cu2+ ions and Li+@C60•− superatoms emerging in the 1D ladder-like magnetic chain; the four Cu ions and Li+@C60•− superatoms are aligned in a triangular-like lattice and antiferromagnetically interact with each other.
To elucidate such strong exchange coupling in 1, we consider Fig. 4c, which shows the spin arrangements in a ladder-like structure with four Cu2+ ions positioned at the corner of the rectangular plane and one Li+@C60•− at the centre. In this magnetic pattern, owing to symmetry, one Cu2+ ion magnetically interacts with three adjacent Cu2+ ions (J12 and J13), which are magnetically linked by the Li+@C60•− radicals. Moreover, the Cu2+ ions interact with \({{{{{{{\rm{Li}}}}}}}^+@{{{{{{\rm{C}}}}}}}_{60}^{\cdot -}}({J}_{{{{{{\rm{Cu}}}}}}-{{{{{{\rm{C}}}}}}}_{60}^{\cdot -}})\) via Cu‒C bonds. Such complicated and competitive interactions lead to a magnetically frustrated ground state. To obtain the J values, we used the following spin Hamiltonian \(\hat{H}\) using Eq. 1 by considering two kinds of exchange coupling JCu‒Cu and \({J}_{{{{{{\rm{Cu}}}}}}\;-\;{{{{{{\rm{C}}}}}}}_{60}^{\cdot -}}\).
To avoid overparameterization, we assumed the interactions of J14 and J23 are ignored compared to J12, J34 and \({J}_{{{{{{\rm{Cu}}}}}}-{{{{{{\rm{C}}}}}}}_{60}^{\cdot -}}\) due to their long metal-metal distances and the interactions between C60•− and Cu1, Cu2 are equivalent. The effective exchange coupling parameters of JCu–Cu = −170(5) K and \({J}_{{{{{{\rm{1}}}}}}-{{{{{{\rm{C}}}}}}}_{60}^{\cdot -}}={J}_{{{{{{\rm{2}}}}}}-{{{{{{\rm{C}}}}}}}_{60}^{\cdot -}}=-185(3)\;{{{{{\rm{K}}}}}}\) with gCu = 2.09(0) were obtained after the best fit (gC60•− was fixed to 2.0). The negative JCu–Cu and \({J}_{{{{{{\rm{Cu}}}}}}-{{{{{{\rm{C}}}}}}}_{60}^{\cdot -}}\) values confirm that any two neighbouring spins are AF coupled. Therefore, in this rectangular spin-lattice, composed of several triangular lattices (such as ∆Cu1Cu2C60•−), we can observe the three spins exhibiting competing interactions. Frustration parameter45 f = |θcw | /TN is >105 (TN < 1.8 K), indicating that 1 has a highly frustrated ground state. In addition, the real-part alternating current magnetic susceptibility (χʼ) measurements indicated the absence of magnetic ordering to 1.8 K (Supporting Information Fig. 9). Such a frustrated lattice leads to inner Li+ ions locating far away from the four coordinated Cu2+ ions. Moreover, because of the pull forces from the eight external Cu–C bonds and six internal Li–C bonds, the Li+@C60 cage is geometrically distorted with the diagonal lengths of 6.4 and 7.1 Å, respectively (Supporting Information Fig. 10).
Heat capacity and electrical conductivity
To further demonstrate the absence of magnetic phase transitions, the temperature dependence of heat capacity (C) was measured. The C versus T and C/T versus T plots (Fig. 5a, b) clearly showed that there is no sharp thermal anomaly in 2–20 K, indicative of no magnetic ordering in this temperature range. Usually, heat capacity is mathematically expressed as C = γT + βT3, where the γT and βT3 terms are relevant to the density of state and crystal lattice, respectively. The data at low temperatures below 7 K, shown in Fig. 5c, clearly manifests the existence of a linearly temperature-dependent term (the γ term) despite the semiconducting ground state. The magnitude of γ in 2–7 K is estimated at 12 ± 2 mJ K−2 mol−1 from the linear extrapolation of the C/T versus T2 plot down to zero K. This finite γ value was reported in organic 2D triangular κ-(BEDT-TTF)2Cu2(CN)3 and inorganic honeycomb H3LiIr2O6 QSLs32,46, suggesting possible QSL state of 1. In addition, the black colour of the single-crystals with metallic surfaces indicates that 1 could be electrically conductive. Figure 5d shows the temperature dependence of σ in the range of 250–300 K, obtained with a two-probe dc method. The σ value at 300 K is (4.4–8.2) × 10−5 S cm−1 based on measuring several single-crystals. Parameter σ decreases with temperature reduction, indicating that 1 behaves as a semiconductor. The activation energy (Ea) is determined to be 0.44 eV by using the Arrhenius function.
Using generalised charge decomposition analysis (GCDA) method to understand donor–acceptor bonded interactions
To further elucidate the electronic ground states, we first calculated the orbital energy for Cu2(L)(py)4 using the TD-DFT method. The calculated absorption spectrum coincides with the experimental data in the range of 300–1500 nm (Supporting Information Fig. 11 and Supporting Information Table 1). The strong absorption band at 920 nm (1.35 eV) is 100% attributed to ET from the HOMO (Fig. 6a) to LUMO (Fig. 6b). The electrons are predominantly located at both terminal Cu ions and the central ligand in the HOMO. Our calculations showed strong hybridisation with 58% dxz(Cu) electron density and 25% pz(N) electron densities, thus indicating that the electrons are delocalised in HOMO. Thus, the electron-intensive dxz(Cu) orbitals are highly capable of donating electrons to the Li+@C60 cage through Cu–C bonds. The higher energy absorption band at 443 nm (2.80 eV) calculated at 402 nm (3.08 eV) is 78% assigned to ET from HOMO −1 to LUMO +1 (Supporting Information Fig. 12).
a HOMO of Cu2(L)(py)4. b LUMO of Cu2(L)(py)4. c Orbital interaction diagram and molecular orbitals in α electron form. d Orbital interaction diagram and molecular orbitals in β electron form. The black solid lines and dotted lines represent the occupied and virtual orbitals, respectively. The orange and violet lines represent the contribution to the HOMO and LUMO and other orbitals, respectively. The isovalue for the electrons is set at 0.02.
To better understand the D–A bonding interactions, we used GCDA to investigate the electron-transfer amounts from Cu2L(py)3 (by adding a pyridine molecule to the Cu2L(py)2 molecule) to the Li+@C60 cage and the generation of complex orbitals by the fragments molecular orbitals in such an open-shell system. Figure 6c, d shows the calculated α and β forms of the orbital interaction diagrams for the triplet Cu2L(py)3Li+@C60 complex, respectively. The [Cu2L(py)3]+ fragment was assumed to be a doublet with a positive charge, and the other fragment (Li+@C60•−) contained an anionic radical in the C60 cage (doublet). We calculated the net CT value as 0.275e‒ (Supporting Information Table 2) by estimating the difference between electron donation and back-donation between the fragments. The partial CT interactions can be understood as follows: each Cu2(L)(py)3 can only transfer 0.25e− to the Li+@C60 cage as the Li+@C60 cage is coordinated with four Cu2(L)(py)2. Thus, the GCDA calculation shows good agreement with the CV and magnetic results. From Fig. 6c, we note that the HOMO and LUMO of the complex are quite similar with an energy gap of 0.40 eV in the α form. The small bandgap is due to the significant contributions from HOMO of Li+@C60 and LUMO of Cu2(L)(py)3. The electron densities are mainly observed on the central ligand and the Li+@C60 cage. The HOMO of the complex originates from the mixture of 45% LUMO of Cu2L(py)3 and 32% HOMO and 21% LUMO of Li+@C60; similarly, the LUMO is mixed with 52% Cu2L(py)3 LUMO, 33% Li+@C60 HOMO, and 12% Li+@C60 LUMO. This result indicates that the electrons in the complex’s HOMO are solely derived from the HOMO of Li+@C60; there is no electron contribution from the occupied Cu2L(py)3 orbitals. Therefore, the complex’s orbitals are not strongly mixed by fragments in the α form. In contrast, β electrons exhibit a deeper frontier orbital toward α electrons, indicating that β electrons are more electronically stable. Figure 6d shows that the frontier occupied orbitals of the complex in β form are doubly degenerated, indicating the significant contributions of fullerene orbitals. The electrons in the complex’s HOMO are mainly delocalised on the Li+@C60 cage and a small fraction in the dXZ orbital of Cu ions, and these electrons originate from 11% HOMO, 4% HOMO−1 (Supporting Information Fig. 13), 2% HOMO−2 (Supporting Information Fig. 14) of Cu2L(py)3, 29% HOMO, 5% HOMO−1 (Supporting Information Fig. 15), and 42% HOMO−3 of Li+@C60. It is worth noting that a large number of delocalised dXZ electrons of Cu ions were observed in the HOMO of Cu2L(py)3; however, the number diminished in the complex’s HOMO. This result strongly suggests that electrons transferred from Cu2L(py)3 to the Li+@C60 cage once Cu–C bonds were established. Thus, the bandgap is expected to be small because the orbital interactions between the fragments are strong. However, the calculated bandgap (∆E = 1.17 eV) is only slightly smaller than that of undoped Li+@C60 (∆E ~ 1.5 eV), which is probably caused by the strong onsite Coulomb interactions.
In summary, we succeeded in observing a conductive metal-fullerene-bonded framework with strong spin frustration, constructed by using redox-active Cu2(L)(py)4 and Li+@C60 molecules. Via the precise control of the redox activities in each species, the chemical bonds between the dinuclear electronic donor and the 3D spherical Li+@C60 acceptor allow for an interesting S = ½ spin-lattice in a 1D ladder-like magnetic chain. The metal–fullerene bond accompanied by CT leads to a strong spin frustration ground state. Such a heterospin system is promising for the development of high-performance molecule-based spintronic devices and can aid in exploring new QSL candidates. Further studies in this direction aim to control the spin dynamics in a triangular or kagomé network using Li+@C60 superatoms.
Methods
Experimental synthesis
A pure form of (Li+@C60)(NTf2−) was obtained from Idea International Co., Ltd. Sendai, Japan. (Li+@C60)(NTf2−) was synthesised by anion exchange from (Li+@C60)(PF6−). Typically, Li+@C60)(PF6−) (10 mg, 0.0115 mmol) and LiNTf2 (5.0 mg, 0.0174 mmol) dissolved in 2.5 mL dichloromethane (DCM) and then sonicated 10 minutes to give a purple suspension. The suspension was filtered and the resulting clean solution was diffused by diethyl ether at 3 °C for 3 days to produce black solids. The solids were washed with a small amount of DCM and dried at room temperature (Yield: quantitative).
Synthesis of ligand (H4L = 1,2,4,5-tetrakis(methanesulfonamido)benzene). H4L was synthesised from the reaction of 1,2,4,5-tetraaminobenzene (138.2 mg, 1.0 mmol) and methylsulfonyl chloride (458.3 mg, 4.0 mmol) in 40 mL pyridine, and the resulting dark brown solution was stirred continuously for 3 h and then quenched in 15% aq. HCl. The resulting pale brown solid was collected by filtration, washed with distilled water (2 × 10 mL), and dried at 80 °C overnight (yield: 321 mg, 72%). IR in attenuated total reflection (ATR) mode: ν(N–H) = 3250 cm−1; ν(CH3) = 2933 cm−1; ν(S=O) = 1142 cm−1.
Synthesis of Cu2(L)(py)4. Cu(acetate)2 solid (363.3 mg, 2.0 mmol) was slowly added to 10 mL H4L (446.5 mg, 1.0 mmol) pyridine solution under dry N2 gas. The resulting pale brown suspension immediately turned into a clear deep-blue solution, which was subsequently stirred for 12 h. Black block-like crystals were obtained by diethyl ether slowly diffused into the above solution (yield: 717.6 mg, 81%). The crystal structure was determined via single-crystal X-ray diffraction analysis. The purity was confirmed by CHN analysis (Supporting Information Table 3) and PXRD pattern (Supporting Information Fig. 16).
Synthesis of {[Cu4(Li+@C60)(L)(py)4](NTf2)(hexane)}n (1). This experiment was conducted in an argon-filled glovebox. First, (Li+@C60)(NTf2−) (1.0 mg, 0.001 mmol) was dissolved in 1 mL dry o-DCB, and the resulting pink solution was slowly added to Cu2(L)(py)4 (1.8 mg, 0.002 mmol) in 10.0 mL o-DCB solution. The molar ratio between (Li+@C60)(NTf2−) and Cu2(L)(py)4 was 1:2. The mixture solution immediately turned dark brown. It was stirred for 3 h, after which the solution was filtered. Small shiny black crystals with a typical size of 0.04 × 0.01 × 0.001 cm were obtained by slow diffusion with hexane in one week (yield: 1.0 mg, 33%). The purity was confirmed by CHN analysis (Supporting Information Table 2) and PXRD pattern (Supporting Information Fig. 17).
Physical characterisation
Single-crystal crystallographic data (exp_860) were collected at 120 K using a Rigaku Saturn 70 CCD diffractometer (Rigaku, Tokyo, Japan) with graphite monochromated Mo Kα radiation (λ = 0.71073 Å) generated by a VariMax microfocus X-ray rotating anode source. The single-crystal X-ray diffractions were measured at additional temperature points at 25, 50, 100, 200, and 300 K by using synchrotron radiation at Spring-8, Japan. The structures were solved by using Olex2 software47. Cyclic voltammetry (CV) was performed using an ALS/HCH Model 620D electrochemical analyser. A glassy carbon (3 mm diameter) electrode was used as the working electrode, a Pt wire was used as the counter electrode, and an Ag/Ag+ was used as the reference electrode. The supporting electrolyte was 0.1 M tetrabutylammonium hexafluorophosphate (TBA·PF6) in dry o-DCB. The solid-state absorption spectra were acquired by compound 1 was embedded in KBr pellets with the use of a Shimadzu UV-3100PC instrument, and subsequently, the pellets were inserted into a transparent sealed cell and protected by argon gas. The solution-state absorption spectra were measured in a sealed plate tube filled with argon gas. The temperature dependence of the solid-state EPR spectra was examined by using the JEOL JES-FA100 device. Magnetic susceptibility measurements were conducted on a polycrystalline sample using a Quantum Design SQUID magnetometer (MPMS-7L). The magnetic susceptibility data were fitted by PHI software48. The temperature dependence of heat capacity was measured by using the Quantum Design PPMS. The temperature dependence of σ was measured on single-crystals via a two-probe method by using the Quantum Design PPMS 6000 instrument.
Quantum chemical calculation
Geometry optimisation was performed by using density-functional theory (DFT) at the B3LYP/6-31G(d, p) level for pristine Cu2(L)(py)4. The absorption spectrum was calculated for the optimised geometry by using the TD-DFT method at the CAM-B3LYP/def2TZVP level. The Cu2(L)(py)3(Li+@C60) complex was cut from the X-ray structure by adding one pyridine molecule as the terminal ligand, and the resulting structure was optimised by applying DFT at the UB3LYP/6-31G(d, p) level. The optimised structure was decomposed into two fragments, [Cu2(L)(py)3]+ and Li+@C60•−, for single-point calculation. The GCDA49 was used for the open-shell form of this complex and the two fragments by applying DFT at the UB3LYP/def2tzvp level. All calculations were performed using Gaussian 16 software50, and the output results were analysed using the Multiwfn programme49,51.
Data availability
The crystallographic data generated in this study have been deposited in the CCDC database under accession codes 2039740 (compound 1 at 120 K), 2039286 (Cu2(L)(py)4 at 120 K), and 2121505–2121509 (compound 1 at 25, 50, 100, 200, and 300 K). The data generated in this manuscript are available within the manuscript, its supplementary information, or from the authors upon request.
References
Aoyagi, S. et al. A layered ionic crystal of polar Li@C60 superatoms. Nat. Chem. 2, 678–683 (2010).
Stasyuk, A. J., Stasyuk, O. A., Solà, M. & Voityuk, A. A. Hypsochromic solvent shift of the charge separation band in ionic donor-acceptor Li+@C60⊂ [10]CPP. Chem. Commun. 55, 11195–11198 (2019).
Yamada, M., Ohkubo, K., Shionoya, M. & Fukuzumi, S. Photoinduced electron transfer in a charge-transfer complex formed between corannulene and Li+@C60 by concave–convex π–π interactions. J. Am. Chem. Soc. 136, 13240–13248 (2014).
Rehman, H. U., McKee, N. A. & McKee, M. L. Saturn systems. J. Comput. Chem. 37, 194–209 (2016).
Stasyuk, A. J., Stasyuk, O. A., Sola, M. & Voityuk, A. A. Hypsochromic solvent shift of the charge separation band in ionic donor–acceptor Li+@C60 subset of[10]CPP. Chem. Commun. 55, 11195–11198 (2019).
Gonzalez-Veloso, I., Rodriguez-Otero, J. & Cabaleiro-Lago, E. M. Endohedral alkali cations promote charge transfer transitions in complexes of C60 with [10]cycloparaphenylenes. Phys. Chem. Chem. Phys. 21, 16665–16675 (2019).
Watanabe, T. et al. Iridium and platinum complexes of Li+@C60. Organometallics 33, 608–611 (2013).
Jeon, I. et al. Lithium-ion endohedral fullerene (Li+@C60) dopants in stable perovskite solar cells induce instant doping and anti-oxidation. Angew. Chem. Int. Ed 57, 4607–4611 (2018).
Chandler, H. J., Stefanou, M., Campbell, E. E. B. & Schaub, R. Li@C60 as a multi-state molecular switch. Nat. Commun. 10, 2283 (2019).
Krawez, N., Gromov, A., Buttke, K. & Campbell, E. E. B. Thermal stability of Li@C60. Eur. Phys. J. D. 9, 345–349 (1999).
Bernshtein, V. & Oref, I. Surface migrations of endohedral Li+ on the inner wall of C60. Phys. Rev. A. 62, 033201 (2000).
Lu, X., Feng, L., Akasaka, T. & Nagase, S. Current status and future developments of endohedral metallofullerenes. Chem. Soc. Rev. 41, 7723–7760 (2012).
Aoyagi, S. et al. Rock-salt-type crystal of thermally contracted C60 with encapsulated lithium cation. Angew. Chem. Int. Ed. 51, 3377–3381 (2012).
Lee, C. H. et al. Ferromagnetic ordering in superatomic solids. J. Am. Chem. Soc. 136, 16926–16931 (2014).
Hebard, A. F. et al. Superconductivity at 18 K in potassium-doped C60. Nature 350, 600–601 (1991).
Tanigaki, K. et al. Superconductivity at 33 K in CsxRbyC60. Nature 352, 222–223 (1991).
Hebard, A. F. Superconductivity in doped fullerenes. Phys. Today. 45, 26–32 (1992).
Ganin, A. Y. et al. Bulk superconductivity at 38 K in a molecular system. Nat. Mater. 7, 367–371 (2008).
Mulliken, R. S. Molecular compounds and their spectra. II. J. Am. Chem. Soc. 74, 811–824 (1952).
Foster, R. Organic Charge-Transfer Complexes (Academic Press, New York, 1969).
Mulliken, R. S. P & Person, W. B. Molecular Complexes, A Lecture And Reprint Volume (Wiley-Interscience, New York, 1969).
Fukuzumi, S., Wong, C. L. & Kochi, J. K. Unified view of Marcus electron transfer and Mulliken charge transfer theories in organometallic chemistry—steric effects in alkylmetals as quantitative probes for outer-sphere and inner-sphere mechanisms. J. Am. Chem. Soc. 102, 2928–2939 (1980).
Canevet, D. et al. Macrocyclic hosts for fullerenes: Extreme changes in binding abilities with small structural variations. J. Am. Chem. Soc. 133, 3184–3190 (2011).
Canevet, D., Perez, E. M. & Martin, N. Wraparound hosts for fullerenes: Tailored macrocycles and cages. Angew. Chem. Int. Ed. 50, 9248–9259 (2011).
Otsuka, A. et al. Design of spin-frustrated monomer-type C60•− Mott insulator. Crystals 8, 115 (2018).
Li, W. M. et al. Superconductivity in a unique type of copper oxide. Proc. Natl. Acad. Sci. USA 116, 12156–12160 (2019).
Jerome, D., Mazaud, A., Ribault, M. & Bechgaard, K. Superconductivity in a synthetic organic conductor (TMTSF)2PF6. Cr. Acad. Sci. B. Phys. 290, 27–30 (1980).
Oshima, K., Urayama, H., Yamochi, H. & Saito, G. A new ambient pressure organic superconductor (BEDT-TTF)2Cu(NCS)2 with Tc above 10 K. Physica C 153, 1148–1152 (1988).
Kobayashi, H., Cui, H. B. & Kobayashi, A. Organic metals and superconductors based on BETS (BETS = Bis(ethylenedithio)tetraselenafulvalene). Chem. Rev. 104, 5265–5288 (2004).
Shimizu, Y., Miyagawa, K., Kanoda, K., Maesato, M. & Saito, G. Spin liquid state in an organic Mott insulator with a triangular lattice. Phys. Rev. Lett. 91, 107001 (2003).
Itou, T., Oyamada, A., Maegawa, S., Tamura, M. & Kato, R. Spin-liquid state in an organic spin-1/2 system on a triangular lattice, EtMe3Sb[Pd(dmit)2]2. J. Phys.: Condens. Mater. 19, 145247 (2007).
Yamashita, S. et al. Thermodynamic properties of a spin-1/2 spin-liquid state in a κ-type organic salt. Nat. Phys. 4, 459–462 (2008).
Okamoto, Y., Yoshida, H. & Hiroi, Z. Vesignieite BaCu3V2O8(OH)2 as a candidate Spin-1/2 Kagome antiferromagnet. J. Phys. Soc. Jpn. 78, 033701 (2009).
Isono, T. et al. Gapless quantum spin liquid in an organic spin-1/2 triangular-lattice κ–H3(Cat-EDT-TTF)2. Phys. Rev. Lett. 112, 177201 (2014).
Watanabe, K., Kawamura, H., Nakano, H. & Sakai, T. Quantum spin-liquid behavior in the spin-1/2 random Heisenberg antiferromagnet on the triangular lattice. J. Phys. Soc. Jpn. 83, 034714 (2014).
Fu, M. X., Imai, T., Han, T. H. & Lee, Y. S. Evidence for a gapped spin-liquid ground state in a Kagome Heisenberg antiferromagnet. Science 350, 655–658 (2015).
Aoyagi, S. et al. Structure of [60]fullerene with a mobile lithium cation inside. R. Soc. Open. Sci 5, 180337 (2018).
Aoyagi, S. et al. Tunneling motion and antiferroelectric ordering of lithium cations trapped inside carbon cages. J. Phys. Soc. Jpn. 85, 094605 (2016).
Ueno, H. et al. Electrochemical reduction of cationic Li+@C60 to neutral Li+@C60˙−: isolation and characterisation of endohedral [60]fulleride. Chem. Sci. 7, 5770–5774 (2016).
Ueno, H. et al. Ionic conductivity of [Li+@C60](PF6−) in organic solvents and its electrochemical reduction to Li+@C60˙−. Chem. Commun. 49, 7376–7378 (2013).
Henke, W., Kremer, S. & Reinen, D. Copper(2+) in five-coordination: A case of a pseudo-Jahn-Teller effect. 1. Structure and spectroscopy of the compounds Cu(terpy)X2.nH2O. Inorg. Chem. 22, 2858–2863 (1983).
Godiksen, A. et al. Coordination environment of copper sites in Cu-CHA zeolite investigated by electron paramagnetic resonance. J. Phys. Chem. C. 118, 23126–23138 (2014).
Reed, C. A. & Bolskar, R. D. Discrete fulleride anions and fullerenium cations. Chem. Rev. 100, 1075–1119 (2000).
Nag, A. & Ray, S. Misjudging frustrations in spin liquids from oversimplified use of Curie–Weiss law. J. Magn. Magn. Mater. 424, 93–98 (2017).
Ramirez, A. P. Strongly geometrically frustrated magnets. Annu. Rev. Mater. Sci. 24, 453–480 (1994).
Kitagawa, K., Takayama, T., Matsumoto, Y., Kato, A., Takano, R. & Kishimoto, Y. et al. A spin-orbital-entangled quantum liquid on a honeycomb lattice. Nature. 554, 341 (2018).
Dolomanov, O. V., Bourhis, L. J., Gildea, R. J., Howard, J. A. K. & Puschmann, H. OLEX2: A complete structure solution, refinement and analysis program. J. Appl. Crystallogr. 42, 339–341 (2009).
Chilton, N. F., Anderson, R. P., Turner, L. D., Soncini, A. & Murray, K. S. PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes. J. Comput. Chem. 34, 1164–1175 (2013).
Xiao, M. & Lu, T. Generalized charge decomposition analysis (GCDA) method. J. Adv. Phys. Chem. 04, 111–124 (2015).
Frisch, M. J. et al. Gaussian 16. Rev. C.01. Wallingford, CT https://gaussian.com/citation/ (2016).
Lu, T. & Chen, F. W. Multiwfn: A multifunctional wavefunction analyzer. J. Comput. Chem. 33, 580–592 (2012).
Acknowledgements
This work was supported by JSPS KAKENHI Grant Numbers JP19H05631 (S.T. and M.Y.). M.Y. acknowledges the support of the 111 Project (B18030) from China. Computations were carried out using the computer resources offered under the category of the Trial Use Project by the Research Institute for Information Technology, Kyushu University.
Author information
Authors and Affiliations
Contributions
Y.S. conceived and designed the project. Y.S. synthesised, characterised, and analysed all compounds. M.C. measured the optical spectra. K.S. measured low-temperature single-crystal X-ray diffraction. E.K., K.K. and Y.K. provided (Li+@C60)(NTf2) salt. Y.S., T.Y., N.H., and T.A. measured the EPR spectra. H.K and T.F. measured heat capacity. Y.S. performed and analysed the GCDA and DT-DFT calculations. Y.S. wrote the paper with input from M.Y., S.T., T.T.H.K. and A.O.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Lipiao Bao and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Shen, Y., Cui, M., Takaishi, S. et al. Heterospin frustration in a metal-fullerene-bonded semiconductive antiferromagnet. Nat Commun 13, 495 (2022). https://doi.org/10.1038/s41467-022-28134-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-022-28134-w
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.