Abstract
Riboswitches are structured non-coding RNAs often located upstream of essential genes in bacterial messenger RNAs. Such RNAs regulate expression of downstream genes by recognizing a specific cellular effector. Although nearly 50 riboswitch classes are known, only a handful recognize multiple effectors. Here, we report the 2.60-Å resolution co-crystal structure of a class I type I preQ1-sensing riboswitch that reveals two effectors stacked atop one another in a single binding pocket. These effectors bind with positive cooperativity in vitro and both molecules are necessary for gene regulation in bacterial cells. Stacked effector recognition appears to be a hallmark of the largest subgroup of preQ1 riboswitches, including those from pathogens such as Neisseria gonorrhoeae. We postulate that binding to stacked effectors arose in the RNA World to closely position two substrates for RNA-mediated catalysis. These findings expand known effector recognition capabilities of riboswitches and have implications for antimicrobial development.
Similar content being viewed by others
Introduction
Riboswitches are found primarily in the 5′ leader sequences of bacterial mRNAs where they regulate the expression of genes by recognizing a cognate effector1,2,3. These RNA-control elements usually comprise two domains: an aptamer that recognizes a metabolite with high specificity and an expression platform that contains gene-regulatory sequences1. Upon ligand binding, the expression platform undergoes conformational changes that alter the accessibility of key regulatory regions, such as the Shine-Dalgarno sequence (SDS), which must be unobstructed to initiate translation3. Direct observation of ligand-mediated transitions in riboswitches has enriched our understanding of RNA allostery and folding4,5,6,7. Riboswitches are also promising antimicrobial targets due to their presence in numerous human pathogens2 and the finding that riboswitch dysregulation can compromise bacterial virulence8.
PreQ1-I (class I) riboswitches are the founding group of bacterial gene regulators that control the cellular concentration of queuosine (Q)9 (Fig. 1a)—a hypermodified 7-deazapurine nucleobase required for translational fidelity in mammals and bacteria10,11,12. Although Q is not essential in bacteria, Q deficiency is associated with slow mid-log growth13, compromised stationary-phase viability11, and loss of virulence14. Previous preQ1-I riboswitch structures revealed an H-type pseudoknot fold, which recognizes a single preQ1 ligand that completes coaxial stacking between flanking helices, thus stabilizing the expression platform15,16,17,18. The small size and well-defined fold of this class have spurred investigations of its folding and dynamics4,15,19,20,21, effector specificity9,22, the ligand-free to bound-state transition4,18,19,22,23 and targeting with drug-like molecules24,25. Multiple bacterial species exhibit 1:1 riboswitch-to-preQ1 stoichiometry15,16,17,18,22,24,26, which is the prevailing ligand-binding mode of most riboswitches2.
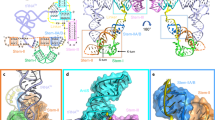
a The queuosine (Q) biosynthetic pathway proceeds through the 7-deazapurine metabolite preQ169. b PreQ1-I riboswitch subtypes shown as secondary structures based on covariation27. Red, black and gray positions indicate 97, 90, and 75% sequence conservation. Asterisk indicates a specificity base predicted to recognize preQ1. c Secondary structure of the Can riboswitch. Colors correspond to specific pseudoknot base pairing (P) and loop (L) sequences. PreQ1 is depicted as “Q”. Noncanonical pairing is indicated by Leontis–Westhof symbols70. The Shine-Dalgarno sequence (SDS) and anti-(a)SDS are highlighted in yellow and cyan. d Ribbon diagram of the global Can riboswitch fold. e Binding pocket floor overview wherein floor bases comprise the A28•G5-C18 base triple. Dashed lines depict hydrogen bonds here and elsewhere. f Overview of the pocket ceiling, which comprises the U32•A12•C8 base triple. The view highlights P2 bases in the aSDS and SDS.
Importantly, the latter preQ1-I riboswitch analyses have considered relatively few sequences. Recent work further classified preQ1-I riboswitches into three subgroups called types I-III27. Inspection of the associated consensus models reveals that types I and II adopt similar secondary structures (Fig. 1b & Supplementary Fig. 1a, b). Although preQ1-III (type II) sequences prefer adenosine before the cytidine specificity base, preQ1-II sequences prefer uracil followed by CUA in the 3′-expression platform9,27. This observation and the results we describe in this study suggest that all previously studied sequences are preQ1-III riboswitches. Importantly, preQ1-II riboswitches, found in gram-positive and -negative bacteria, are more represented than all other preQ1 riboswitch subgroups and classes combined27.
To elucidate the gene-regulatory properties of preQ1-II riboswitches, we determined the co-crystal structure of a preQ1-II riboswitch from Carnobacterium antarcticus28 (Can). The H-type pseudoknot structure unexpectedly reveals two bound preQ1 effectors in a single aptamer (Fig. 1c, d). Although several riboswitches can recognize two effectors, these binding pockets are spatially separated29,30,31,32,33,34. In this respect, the Can preQ1-II riboswitch is exceptional because the metabolites stack tandemly, forming an unprecedented ligand-ligand interface within a single pocket. Using isothermal titration calorimetry (ITC) with in-house software that models two interdependent binding sites, we demonstrated that two preQ1 effectors bind with positive cooperativity. Mutants at each effector site reduce binding affinity and raise the concentration of preQ1 required for gene repression in a bacterial reporter assay. We also found that additional preQ1-II sequences from Haemophilus influenzae (Hin) and Neisseria gonorrhoeae (Ngo) sense two preQ1 effectors with positive cooperativity, suggesting that tandem, stacked effector binding is a hallmark of all preQ1-II riboswitches. Use of a single binding pocket to recognize two effectors has implications for the development of new antimicrobials that utilize a chemical scaffold that avoids cross-reactivity with naturally occurring metabolites.
Results
Features of the Can riboswitch fold
To identify a suitable preQ1-II riboswitch for structural and functional analysis, we searched previously curated type I sequences27 (Fig. 1b and Supplementary Fig. 1a) for a strong SDS (5′-AGGAG-3′) to use in a bacterial reporter assay13. We found several candidates, such as that from Paenibacillus terrae, but NCBI BLAST searches led to the discovery of an unreported sequence from Can28. This riboswitch crystallized readily from low salt solutions and the preQ1-bound co-crystal structure was determined by molecular replacement. The structure was refined to 2.60 Å-resolution yielding Rwork/Rfree values of 0.23/0.27 with acceptable quality-control metrics (Supplementary Table 1). Three crystallographically independent molecules were built, which showed varied quality in electron-density maps. Chains A and B are well defined, but the chain C P1-L3 junction shows a break (Supplementary Fig. 2a). Importantly, both effectors and the core aptamer are well-resolved in each chain (Supplementary Fig. 2b), providing a firm foundation to guide functional experiments.
The overall fold of the Can preQ1-II riboswitch is an H-type pseudoknot (Fig. 1c, d). P1 is a canonical A-form helix whose minor groove is recognized by six A-amino-kissing interactions donated by the A-rich patch in L3 (Supplementary Fig. 3). This stabilizing segment culminates with a A28•G5-C18•A29 base-triple variation that forms the binding pocket floor and is reminiscent of preQ1-III riboswitch structures from Thermoanaerobacter tengcongensis (Tte)16,18,22 and Bacillus subtilis (Bsu)15,17 (Fig. 1e). The pocket ceiling comprises an C8•A12•U32 base triple derived entirely from P2 (Fig. 1f). This configuration contrasts with preQ1-III riboswitches, in which the ceiling is formed by bases from both P2 and the L2 loop9,16,17. The preference for C8 and U32 in preQ1-II riboswitches appears to be incompatible with the base quadruple ceiling observed in preQ1-III riboswitches that require an adenine immediately before the cytosine specificity base (Fig. 1b & Supplementary Figs. 1a, b).
P2 also contains the expression platform, wherein the Watson-Crick (WC) face of A33 of the SDS pairs non-canonically with G9 and its 2´-hydroxyl interacts with the WC face of A11 (Fig. 1f). These SDS-anti(a)SDS interactions presumably attenuate translation. Although we hypothesize that SDS nucleobase G34 makes a WC pair with C10, the former is involved in a crystal contact (Supplementary Fig. 2c). Notably, the Tte preQ1-III riboswitch forms the expected aSDS-SDS C-G intramolecular WC pair, while also exhibiting non-canonical pairing in its expression platform16,18,22, as observed here for the Can preQ1-II riboswitch.
Stacked metabolites in a small aptamer
A distinguishing feature of our structure is two preQ1 molecules, which we term α and β, stacked in a single aptamer pocket (Fig. 2a). Recognition at the α site is conserved among preQ1-II and preQ1-III riboswitches, wherein specificity is conferred by a cytidine that recognizes preQ1 by a cis WC interaction. Other conserved α-site contributions include the WC face of A30, the major-groove edge of U6 and the major-groove edge of G5, which interacts with the preQ1 methylamine (Fig. 2b & Supplementary Figs. 4a–c). In contrast, the β site has not been observed previously. Bases C31 and U7, which are highly conserved among type I sequences, confer specificity for preQ1 by contributing three hydrogen bonds that recognize the metabolite edge (Fig. 2c & Supplementary Fig. 1a). The β-site preQ1 interacts with the α-site effector through aromatic stacking and donation of a hydrogen bond from the methylamine to both the keto oxygen of the α-site effector and O4 of U16 (Fig. 2a, c). The mode of β-site effector recognition differs from all known preQ1 riboswitches, including preQ1-II35 and preQ1-III36, which utilize trans WC-pairing to read the preQ1 face (Supplementary Figs. 4d, e). Although other riboswitches bind two effectors, these examples involve distinct binding pockets that spatially separate the ligands32,33,34,37. To our knowledge, recognition of two interacting ligands in a single aptamer pocket is unprecedented in RNA biology.
Stacked recognition is cooperative
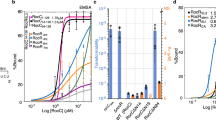
Interacting ligands should cooperatively influence each other’s binding. Analysis of the Can riboswitch by ITC at 25 °C showed that the wildtype (WT) sequence binds preQ1 with an average macroscopic KD of 32.0 ± 2.0 nM and a ligand-to-receptor ratio (N) of 1.8 (Fig. 2d). Fitting to a single-phase isotherm supports binding with positive cooperativity, in accord with our structure. Enthalpy drives binding and offsets the predicted entropic cost of ordering two ligands, producing a favorable ΔG° (Supplementary Table 2). Analysis at 37 °C to accentuate cooperative binding produced a parabolic thermogram best described by a binding model wherein two interdependent ligands occupy non-equivalent sites (Supplementary Figs. 5a, b). We implemented this model to assess the macroscopic binding constant of each interaction, which yielded KD1 of 891 nM and KD2 of 461 nM for the first and second binding events. The improved affinity observed for the second preQ1 relative to the first indicates positive cooperativity, exemplified by the macroscopic cooperativity constant, γ, of 7.7 (Supplementary Table 3).
We next generated Can riboswitch mutants to probe recognition at the α and β sites. Position 17 is a major determinant of α-site specificity (Fig. 2a, b) and the C17U mutation severely weakened binding as indicated by macroscopic KD1 and KD2 values of 3.13 µM and 1.30 µM (Supplementary Fig. 5c & Supplementary Table 3). This result is consistent with the position of C17 in our structure and an equivalent nucleobase in the Bsu preQ1-II aptamer9. C17U showed a parabolic isotherm suggesting retention of two binding events. Likewise, position 31 shows a prominent role in β-site specificity (Fig. 2a, c). The C31U mutation produced a comparable parabolic isotherm, corresponding to KD1 and KD2 values of 6.64 µM and 10.26 µM (Supplementary Fig. 5d & Supplementary Table 3). As expected from the structure, C31U severely affects β-site recognition. Both C17U and C31U retain positive cooperativity with γ values of 9.6 and 2.6 (Supplementary Table 3).
Dual-binding signatures in other preQ1-II riboswitches
C17 and C31 are highly conserved in the type I consensus model (Fig. 1b & Supplementary Fig. 1a) and the importance of each is confirmed by our structure and ITC experiments. We next asked if dual binding is evident in other type I riboswitches. We used ITC at 25 °C to evaluate sequences from Hin and Ngo, which belong to the Proteobacteria phyla rather than the Firmicutes (Supplementary Fig. 1a). The Hin riboswitch binds preQ1 with a KD of 52.9 ± 0.2 nM whereas the Ngo riboswitch binds with a KD of 50.5 ± 1.3 nM; like WT Can, each binds with an N of ~2 (Supplementary Table 2 & Supplementary Figs. 5e, f). Analysis at 37 °C accentuates the cooperative character of isotherms (Supplementary Figs. 5g, h), resulting in γ values of 26.7 and 32.9 that indicate substantial positive cooperativity for each (Supplementary Table 3). We note a high degree of sequence identity exists in the binding pocket of the Can, Hin and Ngo riboswitches (Supplementary Fig. 1a). Significantly, each possesses key nucleobases required for α and β site preQ1 recognition including U6, U7, U16, C17, A30, and C31 (Supplementary Fig. 6). Given ITC evidence of cooperativity for all three riboswitches, it appears that each riboswitch uses a similar mode of dual, stacked preQ1 recognition.
Gene regulation requires two effectors
Using a GFPuv reporter gene13,38 controlled by the Can riboswitch in live cells, we asked whether both preQ1 molecules were required for effective gene regulation (Fig. 3a). We hypothesized that when both sites are occupied the SDS would be less accessible, leading to greater repression of GFPuv translation (Fig. 3b); likewise, intermediate levels of translation would occur if one site is occupied. Dose-response analysis of the WT riboswitch produced a biphasic curve with EC50 values of 96 ± 14 nM (EC50, 1) and 7100 ± 360 nM (EC50, 2) (Fig. 3c & Supplementary Table 4). Collectively, both binding events confer 15.4-fold repression, comparable to the 14.9-fold repression observed for the Lactobacillus rhamnosus (Lrh) preQ1-II riboswitch35, which binds a single ligand with an EC50 of 15 nM13 (Fig. 3c, inset, 3d & Supplementary Table 4). Notably, the Can riboswitch sensing range is broader than the Lrh riboswitch in this assay, suggesting that it detects preQ1 over a wider range of effector concentrations. At present, the basis for this apparent sensing difference is uncertain (see below). To ensure that the changes in GFPuv expression were riboswitch driven, we evaluated a positive control containing an SDS without an upstream riboswitch and a negative control lacking the SDS13. As expected, neither control responded to changes in preQ1 concentration (Fig. 3c, d). In accord with ITC data, C17U and C31U mutants each showed poorer EC50 values that were ~60-fold higher and ~210-fold higher than WT (Fig. 3c-e & Supplementary Table 4). While each mutant retains dual binding in vitro, the elevated EC50 values imply that preQ1 levels must be significantly higher inside cells to elicit an efficient gene-regulatory response, underscoring the importance of each effector binding site for gene regulation.
a Schematic of the plasmid reporter. b Two-site binding model wherein preQ1 can bind either site first. c Average GFPuv emission dependence on preQ1; (inset) one-site binding by the Lrh preQ1 riboswitch38. d Bar graph showing fold repression of GFPuv emission for the Can, Lrh and mutant riboswitches with individual points shown. e Bar graph showing fold change in average EC50 relative to Can riboswitch EC50,2. Significance was determined by a two-tailed Student’s t test with Welch’s Correction (n = 3 biological replicates. *p ≤ 0.05). S.E.M. is shown in c and d; propagated errors are shown in e.
Although our data cannot differentiate a preferred order of preQ1 binding, impairment of the β site had a more pronounced effect on gene regulation (Fig. 3d, e). While C17U elicited a sixfold repression, the C31U variant repressed GFPuv expression by only twofold (Fig. 3d, e). This functional disparity—also reflected by poorer C31U KD1 and KD2 values (Supplementary Table 3)—could be due to the requirement of the β effector to serve as a scaffold that supports the binding pocket ceiling via stacking (Fig. 1f). In this manner, the β site orders P2 in the gene off state while binding at the α site either orders the β site pocket or stabilizes effector binding at the β site.
Discussion
We described the structure and cooperative binding of a small riboswitch that senses two stacked effectors in a single binding pocket. Examination of all known preQ1-I sequences encompassing multiple phyla revealed that nucleobases that compose the α and β binding sites are conserved only within preQ1-II sequences (Supplementary Fig. 1a). In contrast, only nucleobases associated with α site recognition are conserved within preQ1-III sequences, consistent with known Tte and Bsu riboswitches structures (Supplementary Figs. 1b, 4b, c, & 6) and previous bioinformatic analysis27. Although experimental analysis of the preQ1-IIII riboswitch is sparse, it appears that nucleobases associated with α site recognition are conserved in preQ1-III representatives, but not those associated with β site recognition (Supplementary Fig. 1c). This is consistent with previous ITC experiments, which demonstrated that this riboswitch binds with a 1:1 stiochiometry39—like preQ1-III representatives. Accordingly, the unprecedented mode of dual effector recognition appears to be a hallmark of the most common and taxonomically diverse preQ1 riboswitch group2,27, the preQ1-II riboswitch, which has been overlooked until now.
Cooperative riboswitches are posited to show a steep “digital” dose-response40, yet the Can riboswitch exhibits a broad, biphasic dose-response in our in-cell GFPuv assay despite the positive cooperativity we observe in our ITC analysis (Supplementary Table 3). Although it is tempting to associate each transition in our GFPuv assay with an individual preQ1 binding event, the intracellular concentration of preQ1 is not known in such assays and depends on multiple factors, such as the efficacy of 7-deazapurine transporters41,42. Additionally, we cannot rule out possible competition between preQ1 and other metabolites in the cellular milieu43, as observed for the glmS riboswitch44. These, or other factors, likely influence the shape of the Can riboswitch dose-response curve (Fig. 3c); nevertheless, the preQ1-II riboswitch is expected to maintain positive cooperativity inside the cell43.
Our data allow us to conclude that dual-effector recognition is critical for efficient gene regulation by preQ1-II riboswitches—as indicated by the deleterious effects caused specific α and β site mutants. However, we can only speculate on the reason why cooperativity evolved in preQ1-II riboswitches but not in other types or classes of the preQ1 riboswitch family. Our data suggest that the level of regulation attained is similar between the preQ1-II Can riboswitch and the preQ1-II Lrh riboswitch, despite differences in preQ1 binding stoichiometry35 (Fig. 3d). This result suggests that these two disparate riboswitch folds evolved equally effective chemical networks to sense a common effector for gene regulation. Yet, cooperativity is expected to provide notable benefits in regulation efficiency. One such advantage is that gene expression is permitted when metabolite levels are low (Fig. 3b, middle panel), while assuring the ability to quickly attenuate expression before excess effector accrues in the cell43. This is reasonable considering that many preQ1-II riboswitches control the translation of transporters that salvage Q-precursor metabolites from the extracellular environment9,27,45.
Although the Can and Lrh riboswitches differ in terms of binding stoichiometry and overall fold, each positions its expression platform near the binding pocket. This organization raises the question of whether dual, stacked metabolite binding could be effective to regulate folds wherein the aptamer is located distally from the expression platform. PreQ1-III riboswitches exemplify this organization, wherein the expression platform can be as far as 40 Å away from the aptamer36. Communication between the single-effector binding pocket and an orthogonal SDS-antiSDS helix is mediated by an A-minor base that makes a T-shaped contact with the edge of preQ136 (Supplementary Fig. 4e). The preQ1-II riboswitch uses a similar pocket35 and the A-minor base was shown to be essential for gene-regulatory function38. It is conceivable that dual, stacked effector recognition could be used by the preQ1-III riboswitch fold, if the effectors promoted coaxial helical stacking, and one or both ligands were detected by the A-minor motif. Accordingly, we predict that additional riboswitches that bind dual, stacked effectors exist in nature.
Extant riboswitches can also provide clues about the organization of extinct ribozymes46. Riboswitches that utilize distal binding domains to accommodate a single ligand suggest how the folds of early ribozymes were organized to position substrates46. Our findings extend this concept to single-domain ribozymes. In particular, the Can aptamer shows how a ribozyme could position two substrates in one pocket to promote covalent bond formation. Intriguingly, the α-site primary amine is solvent accessible (Supplementary Fig. 7), providing a key functional group absent from the RNA chemical repertoire47; in contrast, the β-preQ1 WC face is solvent accessible. Notably, O6-methyl preQ1 shows site-specific preQ1-III riboswitch methylation48, providing a precedent for ligand-mediated chemical transformation of RNA. These observations collectively suggest how a ribozyme could position two substrates within a single compact fold to facilitate chemistries required for prebiotic metabolism.
PreQ1-II riboswitches are prominent in human pathogens9,27 including Ngo, an urgent public-health threat49. The mode of effector recognition by the preQ1-II riboswitch provides new opportunities to target such regulatory RNAs. For example, a single small molecule that simultaneously occupies both α and β binding sites could reduce cross-reactivity with targets that recognize preQ1-like molecules (e.g., guanine), yielding greater potency and reduced toxicity. Our results suggest that such riboswitches merit further exploration for their potential as antimicrobial targets.
Methods
Data reporting
No statistical methods were used to predetermine sample size. The experiments were not randomized and the investigators were not blinded to allocation during experiments and outcome assessment.
RNA purification
RNA strands were synthesized by Dharmacon (Lafayette, CO) as described by the manufacturer except that deprotection heating was 30 min at 65 °C. RNA was purified by 15% denaturing PAGE and DEAE chromatography50. DEAE buffer was replaced with 0.02 M Na-HEPES pH 6.8, 0.10 M ammonium acetate, and 0.002 M EDTA; care was taken to minimize UV exposure51. After ethanol precipitation of pooled DEAE fractions, RNA was dissolved in Nanopure™ UV/UF (ThermoFisher) water and desalted on a PD-10 column (GE Healthcare). Quality was assessed by analytical PAGE stained with SYBR Gold (Thermo-Fisher) and visualized on a GelDoc (BioRad XR + ). The yield was measured spectrophotometrically. Lyophilized RNA was stored at −20 °C.
Structure determination
Lyophilized RNA was dissolved in 20 μL of 0.01 M sodium cacodylate pH 7.0 and concentrated to 800 µM by centrifugation. Separate volumes of the concentrated riboswitch and an equal volume of folding buffer (0.004 M MgCl2, 0.01 M sodium cacodylate pH 7.0 and 0.0016 M preQ1) were heated at 65 °C for 3 min. The folding mix was added dropwise to the RNA and heated 3 min at 65 °C, followed by slow cooling to 24 °C.
Crystals were grown from VDX plates (Hampton Research) by hanging-drop vapor-diffusion. A 1 μL volume of RNA was combined with 1 μL of precipitant drawn from 1 mL in the well. Crystals grew from solutions of 30% (v/v) 2-methyl-2,4-pentanediol, 0.08 M KCl, 0.012 M NaCl, 0.04 M sodium cacodylate pH 5.5, and 0.002 M hexammine cobalt (III) chloride. Crystals grew in 3 weeks at 20 °C as hexagonal rods of size 0.125 mm × 0.040 mm × 0.040 mm. Crystals were cryo-protected by 2 min transfers into well solution supplemented with 40% to 60% (v/v) 2-methyl-2,4-pentanediol. Single rods were captured in nylon loops using 16 mm copper pins (Hampton Research) with the c*-axis oriented parallel to the φ axis. Crystals were plunged into N2(l) for shipping to the Stanford Synchrotron Radiation Lightsource (SSRL).
X-ray data were collected remotely on beamline 12-2 using Blu-Ice software and the Stanford Auto-Mounter52,54,,53 at a λ of 0.9800 Å with a Δφ of 0.15°, an exposure time of 0.7 s per image with 450 total images, and a sample-to-detector distance of 425 mm at 100 K. All data were recorded on a PILATUS 6 M detector (Dectris Inc). Data-collection strategies were generated using Web-Ice54. Diffraction data were reduced with autoxds55 using XDS, as well as CCP4 programs POINTLESS, AIMLESS and TRUNCATE56,57. The structure was determined by molecular replacement in PHENIX58 starting from the B. subtilis preQ1-I riboswitch (Protein Data Bank entry 3FU2). The top solution for three molecules in the asymmetric unit produced a TFZ of 9.2 and a log-likelihood gain of 289. The structure was built in COOT with additional refinement in PHENIX58. Intensity and refinement statistics are in Supplementary Table 1. Cartoons, schematic diagrams and surface renderings of coordinates were generated in PyMOL (Schrödinger LLC). In Supplementary Fig. 7, preQ1 atoms were colored by solvent accessible surface area using the color area (solvent) function in PyMOL (Schrödinger LLC). The reported solvent accessible surface area were calculated in PISA59 (PDBe PISA v1.52) for chain A, as implemented in CCP457.
Isothermal titration calorimetry
Each sample was folded by dissolving lyophilized RNA in 250 μL 0.01 M sodium cacodylate pH 7.0. RNA was heated to 65 °C for 3 min and mixed with an equal volume of preheated folding buffer at 65 °C comprising 0.01 M sodium cacodylate pH 7.0 and 0.004 M MgCl2. The combined solution was heated for an additional 3 min, then slow cooled to 24 °C followed by overnight dialysis against 2 L of ITC buffer (0.050 M Na-HEPES pH 7.0, 0.10 M NaCl and 0.004 M MgCl2) using a 3500 MWCO Slide-A-Lyzer Dialysis Cassette G2 (Thermo-Scientific). PreQ1 from a 0.020 M stock in water was diluted to 0.0010 M in ITC buffer.
ITC was conducted using two different instruments. Experiments with WT Can, Ngo and Hin riboswitches at 25 °C were conducted on a PEAQ-ITC (Malvern) with RNA in the cell and preQ1 in the syringe over 19 injections. Experiments were carried out with an injection volume of 4 µL (0.5 µL technical injection) and a spacing of 150 s. These thermograms were analyzed with MicroCal PEAQ-ITC Analysis software (Malvern Panalytical, Inc) using a ‘single-sites’ binding model, which corresponds to the independent sites model below.
To obtain additional data points for cooperativity analysis, WT experiments were also conducted at 37 °C on a VP-ITC (MicroCal). Experiments were carried out with an injection volume of 10 µL (6 µL technical injection) and a spacing of 240 s with RNA in the cell and preQ1 in the syringe over 29 injections. Mutant riboswitches were analyzed similarly but at 25 °C due to poor binding. These thermograms were analyzed using a ‘two-interdependent non-equivalent sites’ model (Supplementary Fig. 5b) as described below.
In each case, at least two measurements were performed for each RNA sample on the appropriate instrument. Representative thermograms and curve fits are provided in Supplementary Fig. 5. Thermodynamic parameters for experiments performed on the PEAQ ITC are in Supplementary Table 2 and experiments on the VP-ITC are in Supplementary Table 3. Macroscopic ΔG° values for mutant riboswitches represent the sum of microscopic ΔG° values, which were obtained by calculating Krel at each binding event versus the WT riboswitch at 25 °C. The concentrations of RNA and preQ1 used in ITC experiments are reported in the source data file.
Least-squares regression analysis of ITC experiments (two interdependent non-equivalent sites model)
ITC experiments performed on the VP instrument produced parabolic thermograms indicative of cooperativity but these could not be satisfactorily fit with conventional ITC software as noted37. Structural evidence indicates that the preQ1 ligands interact in their respective binding pockets, suggesting that a cooperative binding model in which the two effector-binding sites are nonequivalent and interdependent was appropriate. We implemented this model (Supplementary Fig. 5b) in a custom Python program based on the binding polynomial theory60.
Rather than fitting an apparent stoichiometry, we fixed the number of binding sites to exactly two and fit a nuisance parameter that represents the effective concentration of active riboswitch RNA in the ITC cell relative to the recorded concentration60,61. Although the binding model describes a binding enthalpy and a microscopic dissociation constant for each of four distinct binding equilibria (Supplementary Fig. 5b), there are only three independent microscopic dissociation constants:
Likewise, there are only three independent binding enthalpies because enthalpy is a state function; completing a thermodynamic cycle must result in no enthalpy change.
The binding polynomial results in a cubic equation in the concentration of free ligand \(\left[L\right]\)
where \({R}_{T}=\left[R\right]+\left[R{L}_{A}\right]+\left[R{L}_{B}\right]+\left[R{L}_{{AB}}\right]\) is the total concentration of RNA in the ITC cell and \({L}_{T}=\left[L\right]+\left[R{L}_{A}\right]+\left[R{L}_{B}\right]+2\left[R{L}_{{AB}}\right]\) is the total concentration of preQ1 in the ITC cell. We solved this cubic equation analytically by choosing the root that satisfies \([L]=0\) when \({L}_{T}=0\).
Inspired by several approaches62,63,64, we explicitly accounted for the dilution of all chemical species present due to displacement of the liquid in the ITC cell by the injection volume. The differential changes in the concentrations of bound species due to a differential injected volume \({dV}\) are
where \({V}_{0}\) is the volume of the ITC cell and \({\Phi }_{i}\) is the flux through the binding equilibrium \(i\). The enthalpy can be expressed as a function of the total injected volume \(V\)
The enthalpy change associated with a particular injection that brings the stoichiometric ratio of ligand to receptor \(S\) from \({S}_{i-1}\) to \({S}_{i}\) is given by the average value of the enthalpy over this interval.
Inserting Eqs. 1–3 and Eqs. 5–6 into Eq. 7 and using integration by parts gives the injection enthalpy change in terms of the fit parameters, the ITC cell volume, the initial concentrations of RNA in the ITC cell \({R}_{0}\) and of ligand in the syringe \({L}_{0}\), and the concentration of free ligand obtained as the solution to Eq. 4.
We used a trust-region reflective algorithm65 implemented in the optimize.least_squares() method of SciPy66 to minimize the following cost function:
where \(N\) is the number of observed injections and \(M\) is the number of fit parameters. The first term is a least-squares term describing the goodness-of-fit between the estimated and observed injection enthalpy changes. The second term is an L2 regularization term—whose relative strength is controlled by the hyperparameter \(\lambda\)—that prevents overfitting by penalizing deviations of the fit parameters \(\theta\) from a target value \({\theta }_{0}\). In a Bayesian framework, this penalty is interpreted as a Gaussian prior on the fit parameters with mean \({\theta }_{0}\) and standard deviation \(w\)67. For the three independent microscopic dissociation constants, regularization was applied to the natural logarithm of the dissociation constant. The regularization targets were set to the values of the fit parameters from a binding model assuming two independent and equivalent binding sites, i.e. the model used by most commercial ITC software. We derived analytical derivatives of the cost function given by Eq. 9 with respect to the fit parameters to take advantage of computationally efficient gradient-based optimization methods.
For each RNA sequence, we performed a global fit to obtain a single set of fit parameters informed by multiple experiments in which the initial concentrations of riboswitch receptor and ligand vary in order to interrogate different regions of the resulting thermogram. One offset parameter, a constant added to the estimated injection enthalpy changes, was fit for each experiment. The hyperparameter \(\lambda\) controlling the relative strength of the regularization term was optimized for each RNA sequence individually by cross validation across experiments. Each experiment was fit individually for a sequence of \(\lambda\) with logarithmic spacing—\({{{\log}}}_{10}\lambda\) was varied from −6 to +6 in steps of 0.125. The resulting fit parameters were used to estimate the value of the cost function for the other experiments involving the same RNA sequence. The value of \(\lambda\) with the smallest average value of the cost function for experiments not used to train the parameters was chosen for the global fit.
Two sets of values were used for the regularization weights \(w\). For Can WT, Can C31U and Hin WT, the regularization weights were \(16{k}_{B}T\) for the binding enthalpies and \({{\log}}10\) for the logarithms of the dissociation constants, where \({k}_{B}\) is the Boltzmann constant and \(T\) is the absolute temperature. However, these weights produced poor quality fits for Can C17U and Ngo WT, as revealed by fit parameters with large bootstrapped uncertainties. As such, the regularization weights for these sequences were \(16{k}_{B}T\) for both the binding enthalpies and the logarithms of the dissociation constants. For all RNA sequences, the regularization weights were 1 kcal mol−1 for the offsets and 0.05 for the nuisance parameter describing the effective RNA concentration.
To derive estimates and 95% confidence intervals for the fit parameters, we used a bootstrapping method to resample the fitting target in the nonlinear regression68. In each bootstrap iteration, we added the residual from the initial fit multiplied by a random number sampled from a standard normal distribution to the observed injection enthalpy changes. The resulting distributions of fit parameters are non-normal, and so we report the estimate of each fit parameter as the median of the bootstrap parameter distribution. We also report a 95% confidence interval as the (2.5, 97.5) percentiles of this bootstrap distribution.
In addition to the fit parameters, we also calculate the following derived parameters: cooperativity \(C\), macroscopic dissociation constants \({K}_{D,1}\) and \({K}_{D2}\), and a macroscopic cooperativity \(\gamma\).
We obtained estimates and 95% confidence intervals for derived parameters by calculating the derived parameters for each bootstrap iteration and then reporting the median and (2.5, 97.5) percentile of the bootstrap parameter distribution.
In-cell GFPuv reporter assay
The WT Can riboswitch was placed into the pBR327-Lrh(WT)-GFPuv plasmid upstream of the GFPuv reporter gene (Fig. 3a). Riboswitch mutants were prepared by site-directed mutagenesis (GenScript Inc.) on the WT sequence, which were verified by DNA sequencing. For experiments involving the Lrh riboswitch, the parent pBR327-Lrh(WT)-GFPuv plasmid was used13.
The assay was performed as described13,38 with some exceptions. E. coli strain JW2765 ΔqueF cells (Coli Genetic Stock Center, Yale University)—incapable of preQ1 biosynthesis—were transformed with the desired plasmid and grown on CSB agar plates containing both ampicillin (100 μg mL−1) and kanamycin (50 μg mL−1). Single colonies were isolated to inoculate overnight liquid cultures of 3 mL CSB-amp-kan media. These were used to inoculate 2 mL of fresh CSB-amp-kan media with varying concentrations of preQ1: 0, 1 nM, 10 nM, 50 nM, 75 nM, 100 nM, 250 nM, 500 nM, 750 nM, 1 μM, 2.5 μM, 5 μM, 7.5 μM 10 μM, 50 μM, 100 μM, 500 μM, 1 mM, and 3 mM; the highest concentration corresponds to the solubility limit of preQ1 in CSB13. Three or more biological replicates were measured for each concentration. All measurements and analysis were performed as described13 using Prism (GraphPad Software, Inc). The replicates in each construct were compared using the “compare datasets” function before analysis. The WT Can curve showed a biphasic model whereas others were best described by a log(inhibitor) dose versus response (three parameters).
An unpaired student’s t-test with a Welch’s correction was used to analyze fold repression data (Fig. 3d). The p value for WT Can vs. WT Lrh was 0.6429 (t = 0.503, degrees of freedom (df) = 3.76, 95% confidence interval = -4.515–6.453). The p value for WT Can vs. C17U Can was 0.0125 (t = 5.94, df = 2.72, 95% confidence interval = -15.47 to -4.266). The p value for WT Can vs C31U Can was 0.0112 (t = 9.23, df = 2.02, 95% confidence interval = -20.61 to -7.583). The p value for WT Can vs. the negative control was 0.0106 (t = 9.59, df = 2.01, 95% confidence interval = -21.16 to -8.076). The p value for WT Can vs the positive control was 0.0103 (t = 9.71, df = 2.01, 95% confidence interval = -21.3400 to -8.2800).
Notably, fluorescence emission in the absence of preQ1 is comparable between all riboswitch constructs and the positive control; moreover, the WT Can and Lrh sequences repress GFPuv fluorescence emission to a level comparable to the negative control —demonstrating the rigor of the assay (Supplementary Fig. 8). An unpaired student’s t-test with a Welch’s correction was also used to analyze fluorescence emission data. The p value for WT Can was 0.0037 (t = 14.96, df = 2.09, 95% confidence interval = -173452 to -98511). The p value for C17U Can was 0.0175 (t = 6.64, df = 2.18, 95% confidence interval = -212164 to -53149). The p value for C31U Can was 0.1263 (t = 2.05, df = 3.22, 95% confidence interval = -107817 to -21313). The p value for WT Lrh was 0.0006 (t = 33.92, degrees of freedom (df) = 2.15, 95% confidence interval = ‐437151 to ‐344271). The p value for the positive control was 0.7441 (t = 0.35, df = 3.45, 95% confidence interval = ‐61691 to 48527). The p value for the negative control was 0.0631 (t = 2.60, df = 3.80, 95% confidence interval = -11377 to 488.8).
Reporting Summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
The data supporting the findings of this study are available from the corresponding authors upon reasonable request. Structure factor amplitudes and coordinates for the Can preQ1-II riboswitch were deposited in the Protein Data Bank under accession code 7REX. Publicly available PDB entries used in this study are: 6VUI, 3FU2, 4RZD, and 4JF2. Source data includes injection data for ITC, and fluorescence emission and cell growth readings for in-cell assays. Source data are provided with this paper.
Code availability
The ITC fitting software and parameter fits are available on GitHub at https://github.com/chapincavender/itc_two_site_fit, distributed under the MIT license.
References
Nahvi, A. et al. Genetic control by a metabolite binding mRNA. Chem. Biol. 9, 1043–1049 (2002).
McCown, P. J. et al. Riboswitch diversity and distribution. RNA 7, 995–1011 (2017).
Breaker, R. R. Riboswitches and Translation Control. Cold Spring Harb. Perspect. Biol. 10, 1–14 (2018).
Suddala, K. C. et al. Single transcriptional and translational preQ1 riboswitches adopt similar pre-folded ensembles that follow distinct folding pathways into the same ligand-bound structure. Nucleic Acids Res. 41, 10462–10475 (2013).
Hua, B. et al. Real-time monitoring of single ZTP riboswitches reveals a complex and kinetically controlled decision landscape. Nat. Commun. 11, 4531–4531 (2020).
Stagno, J. R. et al. Structures of riboswitch RNA reaction states by mix-and-inject XFEL serial crystallography. Nature 541, 242–246 (2017).
Frieda, K. L. & Block, S. M. Direct Observation of cotranscriptional folding in an adenine riboswitch. Science 338, 397–400 (2012).
Babina, A. M., Lea, N. E. & Meyer, M. M. In vivo behavior of the tandem glycine riboswitch in Bacillus subtilis. mBio 8, 5 (2017).
Roth, A. et al. A riboswitch selective for the queuosine precursor preQ1 contains an unusually small aptamer domain. Nat. Struct. Mol. Biol. 14, 308–317 (2007).
Harada, F. & Nishimura, S. Possible anticodon sequences of tRNAHis, tRNAAsn, and tRNAAsp from Escherichia coli. Universal presence of nucleoside O in the first position of the anticodons of these transfer ribonucleic acid. Biochemistry 11, 301–308 (1972).
Noguchi, S., Nishimura, Y., Hirota, Y. & Nishimura, S. Isolation and characterization of an Escherichia coli mutant lacking tRNA-guanine transglycosylase. Function and biosynthesis of queuosine in tRNA. J. Biol. Chem. 257, 6544–6550 (1982).
Tuorto, F. et al. Queuosine-modified tRNAs confer nutritional control of protein translation. EMBO J. 37, e99777 (2018).
Dutta, D., Belashov, I. A. & Wedekind, J. E. Coupling green fluorescent protein expression with chemical modification to probe functionally relevant riboswitch conformations in live bacteria. Biochemistry 57, 4620–4628 (2018).
Hurt, J. K., Olgen, S. & Garcia, G. A. Site-specific modification of Shigella flexneri virF mRNA by tRNA-guanine transglycosylase in vitro. Nucleic Acids Res. 35, 4905–4913 (2007).
Kang, M., Peterson, R. & Feigon, J. Structural Insights into riboswitch control of the biosynthesis of queuosine, a modified nucleotide found in the anticodon of tRNA. Mol. Cell 33, 784–790 (2009).
Spitale, R. C., Torelli, A. T., Krucinska, J., Bandarian, V. & Wedekind, J. E. The structural basis for recognition of the preQ0 metabolite by an unusually small riboswitch aptamer domain. J. Biol. Chem. 284, 11012–11016 (2009).
Klein, D. J., Edwards, T. E. & Ferre-D’Amare, A. R. Cocrystal structure of a class I preQ1 riboswitch reveals a pseudoknot recognizing an essential hypermodified nucleobase. Nat. Struc. Mol. Biol. 16, 343–344 (2009).
Schroeder, G. M. et al. Analysis of a preQ1-I riboswitch in effector-free and bound states reveals a metabolite-programmed nucleobase-stacking spine that controls gene regulation. Nucleic Acids Res. 48, 8146–8164 (2020).
Rinaldi, A. J., Lund, P. E., Blanco, M. R. & Walter, N. G. The Shine-Dalgarno sequence of riboswitch-regulated single mRNAs shows ligand-dependent accessibility bursts. Nat. Commun. 7, 8976 (2016).
Banas, P., Sklenovsky, P., Wedekind, J. E., Sponer, J. & Otyepka, M. Molecular mechanism of preQ1 riboswitch action: a molecular dynamics study. J. Phys. Chem. B 116, 12721–12734 (2012).
Rieder, U., Lang, K., Kreutz, C., Polacek, N. & Micura, R. Evidence for pseudoknot formation of class I preQ1 riboswitch aptamers. Chembiochem 10, 1141–1144 (2009).
Jenkins, J. L., Krucinska, J., McCarty, R. M., Bandarian, V. & Wedekind, J. E. Comparison of a preQ1 riboswitch aptamer in metabolite-bound and free states with implications for gene regulation. J. Biol. Chem. 286, 24626–24637 (2011).
Suddala, K. C., Wang, J., Hou, Q. & Walter, N. G. Mg2+ shifts ligand-mediated folding of a riboswitch from induced-fit to conformational selection. J. Am. Chem. Soc. 137, 14075–14083 (2015).
Connelly, C. M. et al. Synthetic ligands for PreQ1 riboswitches provide structural and mechanistic insights into targeting RNA tertiary structure. Nat. Commun. 10, 1501 (2019).
Neuner, E., Frener, M., Lusser, A. & Micura, R. Superior cellular activities of azido- over amino-functionalized ligands for engineered preQ1 riboswitches in E. coli. RNA Biol. 15, 1376–1383 (2018).
Eichhorn, C. D., Kang, M. & Feigon, J. Structure and function of preQ1 riboswitches. Biochim. Biophys. Acta 1839, 939–950 (2014).
McCown, P. J., Liang, J. J., Weinberg, Z. & Breaker, R. R. Structural, functional, and taxonomic diversity of three preQ1 riboswitch classes. Chem. Biol. 21, 880–889 (2014).
Zhu, S. et al. Complete genome sequence of hemolysin-containing Carnobacterium sp. strain CP1 isolated from the antarctic. Genome Announc. 4, e00690–16 (2016).
Ren, A. & Patel, D. J. c-di-AMP binds the ydaO riboswitch in two pseudo-symmetry-related pockets. Nat. Chem. Biol. 10, 780–786 (2014).
Jones, C. P. & Ferre-D’Amare, A. R. Crystal structure of a c-di-AMP riboswitch reveals an internally pseudo-dimeric RNA. EMBO J. 33, 2692–2703 (2014).
Reiss, C. W. & Strobel, S. A. Structural basis for ligand binding to the guanidine-II riboswitch. RNA 23, 1338–1343 (2017).
Trausch, J. J., Ceres, P., Reyes, F. E. & Batey, R. T. The structure of a tetrahydrofolate-sensing riboswitch reveals two ligand binding sites in a single aptamer. Structure 19, 1413–1423 (2011).
Huang, L., Wang, J. & Lilley, D. M. J. The structure of the guanidine-II riboswitch. Cell Chem. Biol. 24, 695–702.e2 (2017).
Gao, A. & Serganov, A. Structural insights into recognition of c-di-AMP by the ydaO riboswitch. Nat. Chem. Biol. 10, 787–792 (2014).
Liberman, J. A., Salim, M., Krucinska, J. & Wedekind, J. E. Structure of a class II preQ1 riboswitch reveals ligand recognition by a new fold. Nat. Chem. Biol. 9, 353–355 (2013).
Liberman, J. A. et al. Structural analysis of a class III preQ1 riboswitch reveals an aptamer distant from a ribosome-binding site regulated by fast dynamics. Proc. Natl Acad. Sci. USA 112, E3485–E3494 (2015).
Huang, L., Serganov, A. & Patel, D. J. Structural insights into ligand recognition by a sensing domain of the cooperative glycine riboswitch. Mol. Cell. 40, 774–786 (2010).
Dutta, D. & Wedekind, J. E. Nucleobase mutants of a bacterial preQ1-II riboswitch that uncouple metabolite sensing from gene regulation. J. Biol. Chem. 295, 2555–2567 (2020).
Liberman, J. A., Bogue, J. T., Jenkins, J. L., Salim, M. & Wedekind, J. E. ITC analysis of ligand binding to preQ1 riboswitches. Meth. Enzymol. 549, 435–450 (2014).
Sudarsan, N. et al. Tandem riboswitch architectures exhibit complex gene control functions. Science 314, 300–304 (2006).
Zallot, R., Yuan, Y. & de Crecy-Lagard, V. The Escherichia coli COG1738 member YhhQ is involved in 7-Cyanodeazaguanine preQ0 transport. Biomolecules 7, 1–13 (2017).
Yuan, Y. et al. Discovery of novel bacterial queuine salvage enzymes and pathways in human pathogens. Proc. Natl Acad. Sci. USA 116, 19126–19135 (2019).
Breaker, R. R. Riboswitches and the RNA world. Cold Spring Harb. Perspect. Biol. 4, a003566 (2012).
Watson, P. Y. & Fedor, M. J. The glmS riboswitch integrates signals from activating and inhibitory metabolites in vivo. Nat. Struct. Mol. Biol. 18, 359–363 (2011).
Rodionov, D. A. et al. A novel class of modular transporters for vitamins in prokaryotes. J. Bacteriol. 191, 42–51 (2009).
Breaker, R. R. Imaginary Ribozymes. ACS Chem. Biol. 15, 2020–2030 (2020).
Wilson, T. J. & Lilley, D. M. J. The potential versatility of RNA catalysis. Wiley Interdiscip. Rev. RNA. 12, e1651 (2021).
Flemmich, L., Heel, S., Moreno, S., Breuker, K. & Micura, R. A natural riboswitch scaffold with self-methylation activity. Nat. Commun. 12, 3877 (2021).
CDC Biggest Threats and Data: 2019 Antibiotic Resistance Threats Report. https://www.cdc.gov/drugresistance/biggest-threats.html.
Lippa, G. M. et al. Crystallographic analysis of small ribozymes and riboswitches. Methods Mol. Biol. 848, 159–184 (2012).
Kladwang, W., Hum, J. & Das, R. Ultraviolet shadowing of RNA can cause significant chemical damage in seconds. Sci. Rep. 2, 517 (2012).
Soltis, S. M. et al. New paradigm for macromolecular crystallography experiments at SSRL: automated crystal screening and remote data collection. Acta Crystallogr D. Biol. Crystallogr 64, 1210–1221 (2008).
McPhillips, T. M. et al. Blu-Ice and the distributed control system: software for data acquisition and instrument control at macromolecular crystallography beamlines. J. Synchrotron Radiat. 9, 401–406 (2002).
Gonzalez, A. et al. Web-Ice: integrated data collection and analysis for macromolecular crystallography. J. Appl. Cryst. 41, 176–184 (2008).
Gonzalez, A. &. Tsai, Y. Autoxds. http://smb.slac.stanford.edu/facilities/software/xds/#autoxds_script.
Kabsch, W. XDS. Acta Crystallogr D. Biol. Crystallogr 66, 125–132 (2010).
Winn, M. D. et al. Overview of the CCP4 suite and current developments. Acta Crystallogr D. Biol. Crystallogr 67, 235–242 (2011).
Adams, P. D. et al. PHENIX: a comprehensive Python-based system for macromolecular structure solution. Acta Crystallogr. D. Biol. Crystallogr 66, 213–221 (2010).
Krissinel, E. & Henrick, K. Inference of macromolecular assemblies from crystalline state. J. Mol. Biol. 372, 774–797 (2007).
Freire, E., Schön, A. & Velazquez‐Campoy, A. Chapter 5 Isothermal Titration Calorimetry: general formalism using binding polynomials. Methods Enzymol. 455, 127–155 (2009).
Duvvuri, H., Wheeler, L. C. & Harms, M. J. PYTC: open-source Python software for global analyses of isothermal titration calorimetry data. Biochemistry 57, 2578–2583 (2018).
Dumas, P. Rigorous equations for isothermal titration calorimetry: theoretical and practical consequences. Preprint at https://www.biorxiv.org/content/10.1101/512780v3 (2019).
Herrera, I. & Winnik, M. A. Differential Binding Models for Direct and Reverse Isothermal Titration Calorimetry. J. Phys. Chem. B 120, 2077–2086 (2016).
Sigurskjold, B. W. Exact Analysis of Competition Ligand Binding by Displacement Isothermal Titration Calorimetry. Analyt. Biochem. 277, 260–266 (2000).
Branch, M. A., Coleman, T. F. & Li, Y. A subspace, interior, and conjugate gradient method for large-scale bound-constrained minimization problems. SIAM J. Sci. Comput. 21, 1–23 (1999).
Virtanen, P. et al. SciPy 1.0: Fundamental algorithms for scientific computing in Python. Nat. Methods 17, 261–272 (2020).
Williams, P. M. Bayesian regularization and pruning using a Laplace prior. Neural Comput. 7, 117–143 (1995).
Wu, C. F. J. Jackknife, Bootstrap and other resampling methods in regression analysis. Ann. Stat. 14, 1261–1295 (1986).
McCarty, R. M. & Bandarian, V. Biosynthesis of pyrrolopyrimidines. Bioorg. Chem. 43, 15–25 (2012).
Leontis, N. B. & Westhof, E. Geometric nomenclature and classification of RNA base pairs. RNA 7, 499–512 (2001).
Acknowledgements
We thank members of the Wedekind and Mathews labs for technical assistance and helpful discussions. We thank Dr. P. Dumas for binding model inspiration based on his unpublished work cited herein. Support for this research was provided by the National Institutes of Health National Institute of General Medical Sciences (NIH NIGMS) grants R01 GM132185 to D.H.M and R01 GM063162 to J.E.W. G.M.S. was supported by training grant T32 GM118283, and C.E.C was supported by training grant T32 AI049815 to J.E.W. and an Elon Huntington Hooker graduate fellowship. Use of the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515. The SSRL Structural Molecular Biology Program is supported by the DOE Office of Biological and Environmental Research, and by NIH NIGMS (P30 GM133894). The contents of this publication are solely the responsibility of the authors and do not necessarily represent the official views of NIH or NIGMS.
Author information
Authors and Affiliations
Contributions
GMS, CEC, DHM, and JEW designed experiments. GMS, MEB performed experiments. GMS, CEC, JLJ, DHM, and JEW analyzed the data. GMS, CEC, and JEW wrote the paper. All authors reviewed the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review information
Nature Communications thanks Robert Batey and the other, anonymous, reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schroeder, G.M., Cavender, C.E., Blau, M.E. et al. A small RNA that cooperatively senses two stacked metabolites in one pocket for gene control. Nat Commun 13, 199 (2022). https://doi.org/10.1038/s41467-021-27790-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-021-27790-8
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.