Abstract
Two-dimensional (2D) Sn-based perovskites are a kind of non-toxic environment-friendly luminescent material. However, the research on the luminescence mechanism of this type of perovskite is still very controversial, which greatly limits the further improvement and application of the luminescence performance. At present, the focus of controversy is defects and phonon scattering rates. In this work, we combine the organic cation control engineering with temperature-dependent transient absorption spectroscopy to systematically study the interband exciton relaxation pathways in layered A2SnI4 (A = PEA+, BA+, HA+, and OA+) structures. It is revealed that exciton-phonon scattering and exciton-defect scattering have different effects on exciton relaxation. Our study further confirms that the deformation potential scattering by charged defects, not by the non-polar optical phonons, dominates the excitons interband relaxation, which is largely different from the Pb-based perovskites. These results enhance the understanding of the origin of the non-radiative pathway in Sn-based perovskite materials.
Similar content being viewed by others
Introduction
Since 2012, organic‐inorganic lead halide perovskite materials with different dimensions have been attracting significant attention from researchers in energy, physics, and other disciplines mainly because of their applications in solar cells1,2, photodetectors3,4, light communications5,6,7, light-emitting diodes (LEDs)8,9,10, lasers11, and so on. However, the issue associated with long‐term stability against moisture and the toxicity of lead is still a challenge, hindering the use of Pb-based perovskites for practical applications12. Two‐dimensional (2D) perovskites with organic cations sandwiching the perovskite slabs which are similar to those of semiconductor quantum wells have recently received more attention not only for improving the stability due to the hydrophobic organic cationic layer which protects the chemical properties of the inorganic layer but also adjusting exciton binding energy by changing the type of organic cations13. Considering the negative environmental impacts of Pb2+, Sn2+ is nontoxic and has the most similar ionic radius compared to Pb2+. Accordingly, the lattice parameters obtained by Sn2+ substitution will not be seriously changed in principle; thus, Sn-based perovskites are expected to replace Pb-based perovskites in the future. Interestingly, the emission wavelength of single-octahedral-layer Sn-based perovskite is about 630 nm, which is suitable for use in pure red displays14. At the same time, the limitation of Sn-based perovskites is that the oxidation potential of Sn2+/Sn4+ (−0.15 eV) is considerably lower than that of Pb2+/Pb4+ (−1.8 eV)15. Sargent et al. used valeric acid to protect Sn2+ from undesired oxidation and reduced Sn4+ content14, which enables perovskite LEDs with full width at half maximum (FWHM) of 20 nm and the external quantum efficiency (EQE) of 5%, but that is much lower than the EQE of 9.5% of organic‐inorganic hybrid Pb-based perovskites10. Tan et al. have shown that strong exciton-phonon coupling can cause the low photoluminescence quantum yield (PLQY) of 2D Sn-based halide perovskites, besides the high Sn4+ defect state density16. But the effects of key parameters, such as defects and phonon scattering rates, on the luminescence properties, remain ambiguous. Therefore, it is necessary to study the temperature-dependent carrier dynamics to further reveal how these two factors affect the luminescence properties of 2D Sn-based perovskites, to achieve better luminescence performance of 2D Sn-based perovskite than that of 2D Pb-based perovskite.
For the luminescence properties of 2D Pb-based perovskites, through time-resolved and temperature-dependent PL studies, Huang et al. revealed that the scattering of excitons with acoustic phonons and nonpolar optical phonons is the main factor affecting the luminous efficiency of mechanically stripped 2D Pb-based perovskite sheets17. Through theoretical calculations, Ghosh et al. revealed that the higher the rigidity of the organic cation, the smaller the fluctuation of the inorganic framework structure, the weaker the exciton–phonon interaction, and the higher the PLQY18. Additionally, the electron–phonon scattering phenomenon in polar semiconductors such as perovskites induces self-trapping states, which can also significantly influence their optical properties and energy transport mechanism19. We note that the structural composition of the organic cationic layer can influence the defect state density and the exciton–phonon interaction20, so we can vary the types of organic cationic layers and compare the effects of different cations on the luminescence properties and carrier dynamics of 2D Sn-based perovskites to distinguish how defects and phonon scattering affect the optical properties of materials, and furtherly reveal the difference in the factors affecting the luminescence properties between Sn-based and Pb-based perovskites.
In this work, we select two representative kinds of organic cations, one is phenyl-ethylammonium (C6H5CH2CH2NH3+ (PEA+)) cation and the other are the derivatives of alkyl–ammonium chain with different numbers of carbon atoms which are n-butylammonium ((CH3(CH2)3NH3+ (BA+)), hexylammonium (CH3(CH2)5NH3+ (HA+)), and octylammonium (CH3(CH2)7NH3+ (OA+)). The PEA+ cations have the CH–π stacking characteristics that alkyl chain cations lack, which limit their thermal movement between the inorganic octahedron layers, and different lengths of alkyl chains distort the inorganic octahedron frame in different degrees. So these organic cations not only regulate the exciton–phonon scattering process but also affect the structural characteristics and the density of defect states in the materials. The effects of defect scattering and optical phonon scattering on the relaxation dynamics of excitons were investigated by temperature-dependent PL spectroscopy and transient absorption (TA) spectroscopy. We find it is the deformation potential scattering by charged defects, not by the optical phonons, that dominates the interband exciton relaxation, leading to an increase in the proportion of non-radiative relaxation of photogenerated carriers, for the 2D Sn-based perovskite materials. So it is different from the Pb-based perovskites which the main scattering mechanisms for excitons are deformation potential by acoustic and homopolar optical phonons. Besides, compared with alkyl–ammonium chain cations, PEA+ cation has a stronger ability to prevent Sn2+ oxidation, reduce the Sn4+/Sn2+ ratio, increase the exciton radiative recombination ratio, and weaken the exciton–phonon scattering intensity. These results enhance the understanding of the origin of the non-radiative pathway and provide physical support for the future synthesis of high-performance luminescent 2D Sn-based perovskite materials.
Results and discussion
Sample structure characteristics
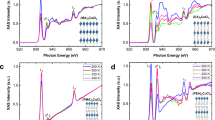
To study the correlation between the structures and optical properties, we used single-crystal X-ray diffraction (SCXRD) to reveal the influence of four organic spacer cations with different chain lengths and geometry on the structures of the materials are shown in Fig. 1. We used the spin-coating method to prepare four kinds of perovskite thin films to explain the physical mechanism that affects the optical properties of 2D Sn-based perovskites. The influence of different cations on the film formation quality was studied through observing the surface morphology of the samples by scanning electron microscopy (SEM), and we found that the PEA+ cation helps to form large size grains with obvious grain boundaries without pinholes. For BA+, large and discontinuous perovskite islands were formed. For HA+, small size grains with pinholes were observed. For OA+, the top surface became blurry (Supplementary Fig. 1). Furtherly, we systematically investigated the effect of different organic cationic layers on the density of defect states in the material using X-ray photoelectron spectroscopy (XPS) and ultraviolet photoelectron spectroscopy (UPS) experiments. The oxidation potential of Sn2+/Sn4+ (−0.15 eV) is considerably lower than that of Pb2+/Pb4+ (−1.8 eV)15. Consequently, Sn-based perovskites have higher Sn4+ defect states than the Pb-based perovskites. To prove this point, we applied XPS to study the influence of the organic cations on the chemical and elemental states of Sn. Supplementary Fig. 2 shows the high-resolution XPS spectra of the Sn 3d3/2 and Sn 3d5/2 regions of the 2D Sn-based perovskite films with different organic cations (PEA+, BA+, HA+, and OA+), which are fitted by two Gaussian distributions representing the distributions of Sn2+ (486.6 and 495.1 eV) and Sn4+ (487.4 and 488.9 eV), respectively16,21. In this way, we calculate the Sn4+/Sn2+ ratio of (PEA)2SnI4 to be 0.12, which is considerably smaller than those of (BA)2SnI4 (0.6), (HA)2SnI4 (0.58), and (OA)2SnI4 (0.77). These results show that PEA+ cations have a stronger ability to protect Sn2+ from oxidation than the organic alkyl chain spacers (BA+, HA+, and OA+), and this protection ability weakens as the alkyl chain length increases. So this illustrates that the Sn4+ defect state density in the (PEA)2SnI4 sample is much lower than that in the alkyl chain samples, which is consistent with the density functional theory (DFT) calculation result18. The main reason is that the large molecules of ammonium organic ions are beneficial for the formation of the compact pinhole-free films and block moisture ingress at the boundaries of perovskite nanolayers20. BA+ ions increased the defect formation energy of Sn4+ by 0.33 eV, while PEA+ could increase the defect formation energy of Sn4+ by 0.6 eV22. Therefore, compared to BA+, PEA+ effectively hinders the formation of tin vacancies and tin oxidation. The increase in the Sn4+ defect concentration can make the Fermi level (EF) of the material approach the valence band maximum (VBM), and this phenomenon was further verified by the UPS experiment (Supplementary Note 2)21. Supplementary Fig. 3 presents the derived energy band diagrams of (PEA)2SnI4, (BA)2SnI4, (HA)2SnI4, and (OA)2SnI4. The energy differences between the VBM and EF are 1.0, 0.66, 0.77, and 0.53 eV for (PEA)2SnI4, (BA)2SnI4, (HA)2SnI4, and (OA)2SnI4 samples, respectively, which confirms that the EF values of the perovskite samples containing organic alkyl chain cations are closer to the VBM compared with that of the PEA+ case and the EF decreases as the alkyl chain length increases.
Two-dimensional Sn−I octahedron layers can be seen stacked on top of each other separated by two layers of organic cations (PEA+, BA+, HA+, and OA+). Magenta represents I atoms, dark green represents Sn atoms, dark blue represents N atoms, milky white represents C atoms, and gray represents H atoms. The detailed crystal structure data are shown in Supplementary Table 1 and Supplementary Note 1.
Fundamental optical properties
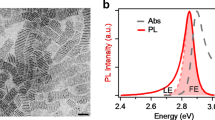
The fundamental optical properties of the four perovskite thin films were investigated via UV − Vis absorption and steady-state PL spectroscopy analyses, and the results (Fig. 2a) revealed that the four perovskite polycrystalline thin films have similar optical characteristics. For (PEA)2SnI4, three main absorption peaks were observed. The first peak at 420 nm (2.95 eV) was assigned to the high-energy exciton transition energy levels, and the second peak at 520 nm (2.38 eV) was assigned to the intraband transition process in the perovskite layer rather than the charge transfer transition between the organic spacer cations and the inorganic layers23,24,25. The relevant discussions are discussed in Supplementary Note 3. And the sharp peak at 613 nm (2.02 eV) was attributed to the intrinsic band-edge exciton absorption26. The PL peak of (PEA)2SnI4 is located at 624 nm (1.987 eV), with a narrow FWHM of 28 nm (91 meV), which are slightly lower than the values reported in the literature27 (PL peak position: 628.2 nm, FWHM: 104 meV). The small Stokes shift and narrow bandwidth suggest that the emission almost results from the recombination of the intrinsic excitons (Supplementary Table 2)28. On further observation, both the optical bandgap and PL emission peak exhibit a blueshift, indicating the increase in the optical bandgap (Supplementary Table 2 and Supplementary Fig. 6). From a physical viewpoint, 2D perovskite materials possess the characteristics of quantum wells in which the thickness of the inorganic layers and the structure and dielectric coefficient ε of organic cations can change the electronic band structure and affect the exciton binding energy (Eb) of the materials. In 2D layered perovskites, different cations can influence the octahedral tilting angle and the length of the Sn-I bond to modulate the bandgap of the material18,29. The influence of cations on the bandgap can be explained more comprehensively using theoretical calculations based on density functional theory calculations (DFT). Through DFT calculations, we found that the bandgap of (PEA)2SnI4 is the smallest and that of (BA)2SnI4, (HA)2SnI4, and (OA)2SnI4 are increasing in order (Supplementary Fig. 7); this is consistent with our results obtained using steady-state spectroscopy and other previously reported results29,30. The experimental results of the excitation intensity-dependent integral PL intensity indicate that the power-law dependence 1 < K < 2 holds in the four materials (Supplementary Fig. 8); this implies that excitons are the nature of optical transitions in the materials28. For (A)2SnI4 (A: PEA+, BA+, HA+, and OA+), εA is smaller than εw (w: SnI4), leading to enhanced the Coulomb interaction between the electron and hole to compose the exciton because of the reduced dielectric screening of the exciton electric field13,31. There are many methods to determine Eb, such as the absorption spectrum, temperature-dependent PL, and magneto-optical investigation31,32,33,34. However, the polar nature of perovskites and the associated polaron effects are neglected; this makes the Eb values obtained by different methods under different experimental conditions highly discrepant33. The accuracy of Eb obtained by fitting the temperature-dependent PL based on the Arrhenius formula is severely affected by other recombination processes, such as shallow defect trapping excitons and Auger recombination33. Therefore, Eb was obtained by fitting the steady-state absorption spectrum using a more rigorous Elliott theory (Supplementary Fig. 9 and Supplementary Note 4.)34, in which the Eb of (PEA)2SnI4 is 213 ± 2 meV smaller than that of (BA)2SnI4 (245 ± 1.6 meV) because εBA is smaller than εPEA. Eb is greater than the thermal energy (KBT ≈25 meV at 300 K), which further reveals excitons dominate the optical transitions of the 2D layer Sn-based perovskites at room temperature31. Although the broadening factor affects the true value of Eb obtained through Elliott’s theory at room temperature, it still provides a qualitative comparison of the effect of the dielectric constants of organic cations on the Eb.
It can be found that with the PEA+ spacer cations substituted by the alkyl–ammonium chain (such as BA+, HA+, and OA+), PLQY more significantly decreases (Fig. 2b), indicating that (PEA)2SnI4 has the lowest defect states density among these four materials. The non-radiative recombination process in the materials is related not only to the defect density but also to the interaction between excitons and phonons. To further investigate the influence of different organic cations on the interactions between excitons and phonons in the materials, a temperature-dependent PL experiment was conducted.
Exciton−phonon coupling
The results of the temperature-dependent PL experiment are shown in Fig. 3a–d. And the information regarding traps, phase transitions, and bandgap evolution with temperature provided by temperature-dependent PL spectroscopy are analyzed and given in detail in Supplementary Note 5.
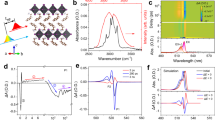
Contour map of the temperature-dependent normalized PL spectra: a (PEA)2SnI4, b (BA)2SnI4, c (HA)2SnI4, and d (OA)2SnI4 films obtained under continuous wave (CW) laser excitation at a wavelength of 473 nm, a power density of 2 µJ cm−2, and from 300 to 77 K with 25 K intervals. The color scales represent the intensity of normalized PL. Temperature-dependent FWHM for e (PEA)2SnI4, f (BA)2SnI4, g (HA)2SnI4, and h (OA)2SnI4. The blue dot represents the experimental data, the short lines above and below the blue dots represent the error bars, and the red solid lines represent the fitting results of the exciton–phonon coupling model (3) in Supplementary Note 6. Average atomic displacement Ueq of chemical elements (H, C, N, Sn, and I) in (PEA)2SnI4, (BA)2SnI4, (HA)2SnI4, and (OA)2SnI4 at i 275 K and j 125 K extracted from single-crystal X-ray diffraction (SCXRD) data (Supplementary Information). k Characteristics of the ratio (PTE/PFE) of trapping -state exciton PL intensity to free exciton PL intensity as a function of temperature. l the PLQY of (BA)2PbI4 and (BA)2SnI4 obtained under the same experimental conditions.
The analysis of the temperature-dependent FWHM of PL is the main means to evaluate the mechanisms of electron–phonon coupling in various semiconductors35. The variation of the FWHM with temperature involves various scattering physical processes including the scattering process between electrons, optical phonons, and acoustic phonons in the material, which causes the electrons to shift to the thermal equilibrium position, thus affecting the electronic band structure of the material and changing the characteristics of the PL spectra. For most semiconductors, using the first-order perturbation theory, the temperature-dependent characteristics of the PL peak can be simplified to four scattering mechanisms as follows in Supplementary Note 635. Based on the exciton–phonon coupling model, the best-fitting parameters listed in Table 1 are obtained using a simulated annealing algorithm, and Fig. 3e–h plot the fitting results (red lines) of the FWHM data. To improve the credibility of the fitting results, we used the optical phonon energies obtained from the steady-state Raman experiments (Supplementary Fig. 13). A Raman peak is located at 454.3 cm−1 (56.3 meV) for (PEA)2SnI4 and 472.1 cm−1 (58.5 meV) for the alkyl chain group samples. The interpretation of these Raman peaks requires strict theoretical calculations, which are beyond the scope of this study. Compared with the alkyl chain samples, the (PEA)2SnI4 sample not only has a smaller Γ0 but also has a relatively smaller Fröhlich coupling intensity (ΓLO). The results indicate that the (PEA)2SnI4 sample is more ordered, and the non-radiative energy loss is smaller than that of the alkyl chain samples. The main reason is that the PEA+ cation has the CH–π stacking characteristics that alkyl chain cations lack, which limits their thermal movement between the inorganic layers, and weak dynamic changes are induced in the SnI4 structure18. For the samples with an alkyl chain, (HA)2SnI4 (254.9 ± 5 meV) has the lowest ΓLO, followed by (BA)2SnI4 (272.8 ± 4 meV), and finally (OA)2SnI4 (320.2 ± 7 meV). This implies that the longer alkyl–ammonium chain tends to enhance the intensity of exciton–phonon scattering. Notably, the exciton–phonon Fröhlich interaction of the 2D Sn-based perovskites that was studied is over one order of magnitude larger than that reported for lead perovskites (Supplementary Table 3), which can lead to an increase in the FWHM of PL and the possibility of forming self-trapped exciton (STE) states. The STE further may further couple with defect states to result in the interband PL36,37,38,39. To furtherly investigate the relationship between the material structure and electron−phonon interactions, we also studied the atomic displacement parameters Ueq extracted from SCXRD data of the four materials9. The results revealed that the atomic displacements of the different atoms Ueq of A2SnI4 (A: BA+, HA+, and OA+) were distinctly larger than those of (PEA)2SnI4, as shown in Fig. 3i, j. Thus, (PEA)2SnI4 has a more rigid structure than that of (BA)2SnI4, (HA)2SnI4, and (OA)2SnI4; this is consistent with the results of the exciton–phonon coupling model and theoretical calculations18. Although organic cations cannot directly participate in the band-edge electronic states of the materials in this research, their structural packing and dynamic coupling with the inorganic framework of Sn–I–Sn affect the luminescent properties of the materials18,30,40. Thus, in the 2D perovskite system, the more rigid the structure, the more beneficial it is to improve the color purity of the emitted light and reduce the energy loss of non-radiative recombination.
Exciton relaxation dynamics
TA experiments are often used to understand the photoexcited carrier dynamics and transport mechanisms in perovskites. Fig. 4 shows the false-color 2D TA mappings of the (PEA)2SnI4, (BA)2SnI4, (HA)2SnI4, and (OA)2SnI4 thin films. Since the characteristics of the steady-state absorption spectrum and the TA spectrum of the four materials are essentially similar, the (PEA)2SnI4 sample is applied as the representative. There are two main photobleaching (PB) peaks whose centers are at 615 and 525 nm, corresponding to the absorption peaks in the linear absorption spectra attributed to the band filling effect. A weak and broad (650–730 nm) PB signal below the bandgap is caused by the defect states with low absorption cross-sections below the optical bandgap filled by the photogenerated carriers19,41. Besides the PB signals, positive photoinduced absorption (PIA) signals exist on both sides of the bleaching peak.
The relaxation kinetics of photogenerated carriers have been fitted globally with three relaxation components (Supplementary Fig. 14), in which the lifetime of the first component (I) is of the order of sub picoseconds, that of the second component (II) is approximately 100 ps, while that of the third component (III) is of the order of nanoseconds, exceeding the system test range (1.6 ns); this component is not discussed in detail here for accuracy. The effect of each process on the PL properties is further studied by combining temperature-dependent and pump fluence-dependent TA experiments. For (BA)2SnI4 and (OA)2SnI4 samples, the bleaching peak below 200 K is blue-shifted mainly due to the increase in bandgap caused by the phase transition mentioned earlier. (Supplementary Fig. 15), However, for the (PEA)2SnI4 and (HA)2SnI4 samples, the TA spectra were characterized by a redshift and a gradual increase in the intensity of the bleaching peak at the band edge with decreasing temperature between 340 and 77 K. Here (PEA)2SnI4 is still applied as the representative material. The redshift of the bleaching peak of component I with a subpicosecond lifetime (277 fs) usually involves different physical processes, such as bandgap renormalization42,43, optical Stark effect44, exciton formation42,45, and trap states trapping19,46,47. In the recent study of TA kinetics, the component I was attributed to the surface defect trapping exciton process (<1 ps) in 2D (CH3(CH2)8NH3)2PbBr4 perovskite47, the surface trap states trapping exciton process (600 fs) for monolayer MoS2 materials46, and the exciton formation (<1 ps) in monolayer WS2 materials42,48. Several reports have shown that the temperature affects the dielectric shielding effect in the material49,50, i.e., in the low-temperature phase, the exciton binding energy increases, inducing an increase in the proportion and the formation rate of excitons50. The fact is that the relaxation rate of component I does not depend on the temperature (Fig. 5a). Therefore, component I is not attributed to the formation of excitons. The photoexcited free carriers may form excitons in the generation process of band-edge bleaching peak, which is difficult to distinguish for fast process systems with time scales of femtosecond magnitude. For the trap states in the 2D perovskites, we need to distinguish the nature of the trap states, that is, whether they are intrinsic STE states, defect trapping states, or extrinsic STE states. In the temperature-dependent PL experiment, using the multi-peak fitting methods (Supplementary Note 5), the PTE/PFE decreases with decreasing temperature (Fig. 3k). This is evidently opposite to the feature of the intrinsic STE states emissions, in which the stronger luminescence from the intrinsic STE states and the band-edge exciton luminescence intensity decreases as the temperature decreases, mainly because the thermal activation of the detrapping process cannot meet the requirements of the detrapping barrier and the STEs cannot return to the band edge at low temperatures36,39,51,52. More precisely, this luminescence of trap states below the bandgap may be the emission of the extrinsic STE states; that is, intrinsic STE is influenced by the local heterogeneity of the permanent lattice defects to obtain a different trapping depth37,39,53. In the TA spectrum of the four materials (Fig. 4), there are a broad (640–750 nm) and weak PB feature below the optical gap; this is also consistent with the permanent defect states being filled, not the intrinsic STE states featured by a broad PIA at energies below the optical gap because of the formation of transient light-induced trap states19,36,37. The relaxation kinetics of different wavelengths show that the process of filling and bleaching of these defect states (663.4 nm), the relaxation process of the PIA signal (624.1 nm of PL center) changing from positive PIA to negative PB, and reaching the maximum are synchronous with the component I of the band-edge exciton (614.8 nm) relaxation (Fig. 5b), indicating that the band-edge excitons are trapped in the in-gap defect states. To further demonstrate that excitons are trapped by chemical defects, we applied stoichiometry engineering of the cations where the PEAI: SnI2 ratio was 2.6:1 in (PEA)2SnI4 (PEAI-rich)39,54. We reduced the defect density in PEAI-rich to improve the PLQY of the PEAI-rich to 2.2% (Fig. 5c), and we also found that the occupancy ratio and relaxation rate of component I of the band-edge exciton relaxation processes in the PEAI-rich sample were significantly lower than those of the (PEA)2SnI4 sample (Fig. 5d). In addition, at high excitation intensities (10 μJ cm−2.), the bleaching signal intensity and the relaxation rate of 676 nm were smaller for PEAI-rich than for (PEA)2SnI4 (Fig. 5e). In summary, component I contains the process of defect states trapping excitons. The increasingly serious broad-spectrum PL trailing phenomena can be explained by the extrinsic STE effect in (HA)2SnI4, (BA)2SnI4, and (OA)2SnI4, notably (OA)2SnI4 (Supplementary Fig. 12). Deschler et al. indicated that the broad emission below the optical gap observed at low temperatures in <001> oriented 2D perovskite materials was because of the light-induced formation of localized trap states, associated with interstitial iodide and iodide Frenkel defects that act as color centers in the crystal53. In addition, Loi et al. highlighted the extrinsic in-gap states in the crystal bulk are responsible for the broadband emission39. Since (OA)2SnI4 has the strongest exciton–phonon coupling intensity with the highest density of defects among the four materials, there is a relatively wide PL trailing below the bandgap and this PL trailing is more pronounced at 77 K (Supplementary Fig. 12). Despite the relaxation rate and the proportion of the component I decrease at high pump fluences, as shown in Fig. 5f, this property does not imply that the defect states are filled; rather, it must be determined if the excited exciton density approaches the Mott density, resulting in exciton fission, or whether the material is degenerate as a result of strong light excitation. Assuming an exciton Bohr radius of 1 nm55, the exciton saturation density is estimated to be ~1014 cm−2. The saturation of component I only somewhat occurs at a high excitation fluence of more than 40 µJ cm−2 (1.1 × 1014 cm−2), thus, the excitation intensity exceeds the saturation density causing the saturation of the component I cannot be characterized as a defect states trapping process. In the TA spectrum within 1 ps (Fig. 4), a redshift of the PB peak of the band-edge exciton leading to the PIA center at 625 nm appears; this is attributed to the bandgap renormalization caused by the hot excitons19. Besides, the maximum amplitude −∆T/T of the pump fluence-dependent PIA satisfies a linear relationship with the excitation intensity n1/2 (Fig. 5g)56,57,58. Therefore, this result further confirms the presence of the bandgap renormalization process in component I. To clearly distinguish which of these two processes plays a role in component I, we further investigated the pump fluence-dependent TA spectra of the PEAI-rich and (PEA)2SnI4. We found that component I was more significantly affected by the defect states at a weak excitation fluence, approximately no more than 10 µJ cm−2 (Fig. 5d). When pump fluency is more than 10 µJ cm−2, component I appears as the defect state density-independent and the excitation fluence-independent relaxation characteristics (Fig. 5h) so that the bandgap renormalization process dominates the component I19,41. After the process of bandgap renormalization, the band filling effect gradually increases the blueshift of the PB59, as shown in Supplementary Fig. 16. The change in the position of band-edge PB peak at a delay time of 1.25 ps with the pump fluence is shown in Fig. 5i when the redshift process ends. When the pump fluence was lower than 15 µJ cm−2, the position of the PB peak did not change, and the blueshift occurred and was proportional to n2/3 as the pump fluence increased due to the band filling effect (Supplementary Note 7)59. Additionally, the optical Stark effect can be excluded because the redshift is well beyond the duration of the pump laser pulse19,44. So the component I is attributed to the combination of the defect trapping exciton process and the bandgap renormalization process induced by hot excitons, that is, the defect trapping excitons process plays a leading role at low pump fluence, and the bandgap renormalization process dominates in component I at high pump fluence. The density of defect states is the lowest in (PEA)2SnI4, so the trapping rate and the proportion of component I in relaxation dynamics are the lowest, which is consistent with our experimental data (Fig. 6a and Supplementary Fig. 14).
a Temperature-dependent normalized band-edge exciton relaxation kinetics of the (PEA)2SnI4 sample within 5 ps under the pump fluence of 2 µJ cm−2. b Relaxation kinetics of the different wavelength labeled by the black dotted line in Fig. 4a within 3 ps. c PLQY of (PEA)2SnI4 and PEAI-rich. d Normalized band-edge exciton relaxation kinetics of the (PEA)2SnI4 and PEAI-rich samples under the pump fluence of 2 µJ cm−2. e Relaxation process of the trapped state excitons of (PEA)2SnI4 and PEAI-rich under the pump fluence of 10 µJ cm−2. f Pump fluence-dependent normalized band-edge exciton relaxation kinetics of the (PEA)2SnI4 sample within 5 ps. g Pump fluence-dependent maximum value of the PIA signal at 625 nm of the (PEA)2SnI4 sample. The pink dotted line represents a linear relationship and the blue solid line represents a one-half power relationship. h Pump fluence-dependent normalized band-edge exciton relaxation kinetics of the (PEA)2SnI4 and PEAI-rich. i The PB peak as a function of the pump fluence at 1.25 ps of the (PEA)2SnI4 sample. The blue data are extracted from the inset, and the red curve is fitting with the band filling theory. The internal illustration is the normalized pump fluence-dependent band-edge bleaching peak with a delay time of 1.25 ps. n is the density of the photoinduced exciton that is proportional to the pump fluence F (µJ cm−2). The first component (I) is prominently marked with a light blue background.
a Normalized band-edge GSB relaxation process under the pump fluence of 2 µJ cm−2 for the (PEA)2SnI4, (BA)2SnI4, (HA)2SnI4, and (OA)2SnI4 thin films. The internal illustration shows the relaxation process of the four materials within 2 ps. b Change in the lifetime of component II in the TA spectra of the (PEA)2SnI4 sample with temperature. c Band-edge exciton relaxation process of (PEA)2SnI4 (red represents) and PEAI-rich (blue represents) under the pump fluence of 2 µJ cm−2. d Schematic diagram of the TA relaxation process with excitation at 520 nm. e Relationship between the lifetime (blue represents) of the Auger process and the pump fluence; the red curve is the fitting result of the two-body interaction theory of excitons.
The second component (II) is characterized as follows: (a) its lifetime, τ2, is in the order of hundreds of picoseconds, and (b) its relaxation rate is affected by the temperature, pump fluence, and defect state density (Fig. 6b, c and Supplementary Fig. 18c). The low temperature and high pump fluence can increase the relaxation rate and proportion of component II during the entire relaxation process. In particular, the relaxation rate is noticeably affected by the temperature between 200 and 300 K; however, the relaxation process is independent of temperature in the ranges of 300–340 K and 77–200 K (Fig. 6b). In contrast, the relaxation rate of component III, with a nanosecond lifetime, did not exhibit temperature-dependent characteristics, except that its proportion decreased with the decreasing temperature (Supplementary Fig. 18e). Combined the results of reduced PTE/PFE with those of increased PL intensity of the (PEA)2SnI4 sample as the temperature decreases (Fig. 3k and Supplementary Fig. 17a), we concluded that the proportion of free excitons that undergo band-side radiative recombination increases with decreasing temperature in the exciton relaxation process. Furthermore, compared to (PEA)2SnI4, the occupancy of component I and the relaxation rate of component II of PEAI-rich decreased, which improves PLQY (Fig. 5c, d and Fig. 6c). From the above, it can infer that reduced charged defect scattering can improve the radiative recombination efficiency of free excitons. Despite the interband recombination rate of free carriers increase with decreasing temperature in the 3D perovskites60, the factors that have a major impact are usually different, and the reason for this may lie in the fact that three-dimensional perovskites have higher ion mobility, high defect tolerance, and very weak interaction between free electrons and holes. Huang et al. revealed that the temperature-dependent time-resolved PL relaxation rate in ultrathin flakes of the mechanically stripped 2D Pb-based perovskite single crystals decreases with temperature. The main reason is that the efficient screening of the Coulomb potential suppresses the scattering of polar optical phonons and charged defects, and the deformation potential scattering by acoustic phonons and nonpolar optical phonons is the dominant factor in exciton relaxation17. This result contradicts our time-resolved PL and temperature-dependent TA experimental results obtained under the pump fluence of 2 µJ cm−2 to avoid high-order recombination processes (exciton–exciton annihilation) (Supplementary Figs. 17b, 18a), primarily because the 2D Sn-based perovskites have higher defect states than the 2D Pb-based perovskites, Which confirmed by the PLQY measured under the same experimental conditions (Fig. 3i). Moreover, we studied the polycrystalline thin films, which are more likely to have grain boundaries and defects other than flakes stripped from single crystals. Therefore, component II derived from the band-edge free exciton recombination process is mainly affected by charge defects and this effect can annihilate the radiative recombination of excitons and accelerate the non-radiative relaxation rate61. So, the relaxation rate of component II in PEAI-rich with smaller defect state density was slower than that of (PEA)2SnI4, which further confirmed that the effect of deformation potential scattering by charged defects on exciton interband recombination in 2D Sn-based perovskites is weakened by reducing the density of defect states. Besides, component III, with a nanosecond lifetime, is attributed to defect-assisted exciton recombination32,39,53,62, which involves the radiative recombination induced by relatively shallow extrinsic STE states. Here, the PTE/PFE is approximately 30% at room temperature (Fig. 3k); moreover, the non-radiative recombination processes are induced by deep defects, which make the PLQY extremely low. A schematic diagram of the TA relaxation process is shown in Fig. 6d. By comparing the lifetime and percentage ratio of the components I and II, we can conclude that it is the deformation potential scattering by charged defects, not by the nonpolar optical phonons, that dominates the interband relaxation of excitons and diminishes the PLQY, for the 2D Sn-based perovskite materials. This is in contrast to the observation regarding 2D Pb-based perovskites. Due to the fact that the τ2 of (PEA)2SnI4 is the longest among those of the four samples at a low pump fluence at 300 K, (Supplementary Fig. 14 and Fig. 6a), we may conclude that among the four samples, (PEA)2SnI4 has the lowest defect concentration, which is consistent with the experimental results of SCXRD, UPS, and PLQY.
With the increase in the pump fluence, a proportion of excitons could induce the Auger recombination48, which is the non-radiative recombination process of the two-body exciton interaction (Supplementary Fig. 18f). By adding the Auger recombination component to exploit the four exponents for global fitting to obtain τ4, the lifetime of the Auger recombination process decreases with the increase in the pump fluence (Fig. 6e), which corresponds well to the bimolecular recombination model (Supplementary Note 8)32. Different organic cations regulate not only the exciton−phonon coupling effect but also the density of defect states in the materials in 2D Sn-based perovskites, more in-depth research work is needed to elucidate the effect of the defect states and exciton−phonon coupling on the AR process. This investigation will help reveal the factor that plays a dominant role in the AR process to improve the PLQY in Sn-based LEDs.
In summary, different cations indicate that the materials have different potential barriers, which affect the optical properties of the materials in the 2D perovskite system. By effectively regulating the kinds of cations (PEA+ vs BA+, HA+, and OA+) and combining the results of temperature-dependent PL spectra and TA spectra, we drew the following conclusions. First, compared with the alkyl chain group samples, reduced structural fluctuations in relatively rigid (PEA)2SnI4 can improve the surface uniformity, increase crystallization quality, weaken the oxidation of Sn2+ to decrease the defect density, prolong the exciton radiative recombination ratio, and increase the PLQY. Moreover, they can reduce the fluctuation of the inorganic layer structure to weaken the scattering effect between excitons and optical phonons, thus reducing the FWHM of the PL and stably maintaining its luminous color in the temperature range of 77–300 K with no structural phase transition lower than 200 K. Second, through the TA experiment, we discovered that it is the deformation potential scattering by charged defects, not by the optical phonons, that dominates the interband excitons relaxation, diminishing the PLQY for the 2D Sn-based perovskite materials. Therefore, it is different from the Pb-based perovskite characterized by fewer defect states, in which the main scattering mechanisms for excitons are the scatterings via deformation potential by acoustic and homopolar optical phonons. The relaxation process of excitons is divided into three components. For the first component (I), with a subpicosecond lifetime, it is attributed to the combination of the defect trapping exciton process and the bandgap renormalization process induced by hot excitons, that is, the defect-trapping exciton process plays a leading role at low pump fluences and a new process appears due to the bandgap renormalization process induced by hot excitons dominates in the process I at the high pump fluences via the pump fluence-dependent, temperature-dependent TA experiments and the stoichiometry engineering of the cations. Meanwhile, we excluded the exciton formation process and optical Stark effect in the first component (I). For the second component (II), with a lifetime of 100 ps, the interband radiation recombination process is mainly affected by the deformation potential scattering by charged defects, not the exciton splitting into free carriers; thus, the relaxation rate increases with the decrease in temperature and defect state density. The third long relaxation component (III), with a nanosecond lifetime, was derived from the defect-assisted exciton recombination process. Because the defect density is the lowest in the (PEA)2SnI4 samples, the relaxation rate of the second process was the slowest among these samples. Our results reveal the complex contributions of significant materials that improve the luminous efficiency of Sn-based perovskites and provide directional guidance for further improving their luminous properties, that is, a more precise structural design is needed for 2D Sn-based perovskite to reduce the electron–phonon scattering intensity and reduce Sn2+ oxidation.
Methods
Synthesis of the four perovskites polycrystalline thin films ((PEA)2SnI4, (BA)2SnI4, (HA)2SnI4, and (OA)2SnI4)
The glass substrate was cleaned sequentially with detergent, deionized water, ethanol, and isopropanol. Then the substrate was treated with oxygen plasma for 10 min and dried in an argon flow. For the synthesis of (BA)2SnI4 perovskite film, 0.1 mmol SnI2 and 0.2 mmol BAI were dissolved in 1 ml dimethyl formamidine (DMF): dimethyl sulfoxide (DMSO) (v:v = 4:1) to form the perovskite precursor solution, which was heated and stirred at 70 °C for a few hours before use. Subsequently, the above-mentioned precursor solution was deposited on top of the glass substrate via a spin-coating process at 2500 rpm for 60 s in the argon-filled atmosphere. Then the perovskite film was obtained after thermal annealing at 70 °C for 5 min. The fabrication procedure of (HA)2SnI4, (OA)2SnI4, and (PEA)2SnI4 perovskite thin films is identical to that of (BA)2SnI4.
Synthesis of the four tin-based perovskite single crystals
The single crystals were obtained by the solvent evaporation method. Briefly, for the synthesis of (BA)2SnI4 single crystals, 0.2 mmol SnI2, and 0.4 mmol BAI were dissolved in 1.2 ml acetonitrile (ACN) to form the precursor solution in a sealed glass bottle. The precursor solution was heated to 75 °C and stirred continuously for about 30 min to achieve complete dissolution. Then, the lid of the glass bottle was removed and the solvent was slowly evaporated at 75 °C for 2.3 h. Finally, the glass bottle was sealed again and the precursor solution was slowly cooled down to room temperature at 0.1 °C min−1 to obtain the dark-brown flaky crystals. The fabrication procedure of (HA)2SnI4, (OA)2SnI4, and (PEA)2SnI4 perovskite single crystals is similar to that of (BA)2SnI4, except that for (HA)2SnI4, (OA)2SnI4, and (PEA)2SnI4, the corresponding precursors were dissolved in 1.1, 1, and 1.6 ml ACN, respectively, and the solvent was evaporated for 2.2, 2, and 2.5 h, respectively.
Scanning electron microscope (SEM)
The morphologies of the samples were identified by scanning electron microscope (FEI Nova Nano SEM 450).
Single-crystal X-ray diffraction (SCXRD)
SCXRD was performed using a Bruker D8 Venture diffractometer operating with Mo Kα radiation and equipped with a Triumph monochromator and a Photon100 area detector at 125 and 275 K, respectively. The sample was mounted in a nylon loop using cryo-oil and cooled using a nitrogen flow from an Oxford Cryosystems Cryostream Plus.
Crystallographic data for each of the new/redetermined structures have been deposited with the Cambridge Crystallographic Data Centre. The CCDC Nos. for (PEA)2SnI4 at 275 K, (PEA)2SnI4 at 125 K, (BA)2SnI4 at 275 K, (BA)2SnI4 at 125 K, (HA)2SnI4 at 275 K, (HA)2SnI4 at 125 K, (OA)2SnI4 at 275 K, and (OA)2SnI4 at 125 K are 2109461, 2109462, 2109463, 2109464, 2109465, 2109466, 2109467, and 2109468, respectively. These data can be obtained free of charge at www.ccdc.cam.ac.uk/data_request/cif.
X-ray photoelectron spectroscopy (XPS)
XPS was performed on the polycrystalline thin films prepared on Si substrates using a Thermo Scientific K-Alpha photoelectron spectrometer with Al Kα radiation (hv = 1486.6 eV). The peak area and atomic ratio were determined using the XPS data.
Ultraviolet photoelectron spectroscopy (UPS)
UPS was performed on the polycrystalline thin films prepared on Si substrates by Thermo Scientific Escalab 250Xi system with an hv = 21.22 eV under an applied negative bias of 5.0 V and pass energy of 2.0 eV.
Temperature-dependent photoluminescence (PL) measurement
For temperature-dependent PL measurement, polycrystalline thin films prepared on quartz substrates were mounted in a cryostat (Janis ST-100) and cooled by liquid nitrogen. The samples were excited by the continuous wave (CW) laser excitation at a wavelength of 473 nm, power density of 2 µJ cm−2, and 25 K intervals. Fluorescence is separated by the 150 g/mm grating in the Monochromator SP2500 of the Princeton Instruments. Then, the spectral information was collected by the PIXIS-100BX CCD at −75 °C.
Photoluminescence quantum yield (PLQY)
PLQY of polycrystalline thin films prepared on quartz substrates was measured using the Edinburgh FLS1000 instrument with an excitation wavelength of 520 nm at 300 K.
Raman spectra
Raman spectra of polycrystalline thin films prepared on quartz substrates were obtained with a Raman spectrometer (LHA19120048) using a CW laser (325 nm) as the emission source at room temperature.
UV-visible (UV-Vis) absorption
UV-Vis absorption spectra of polycrystalline thin films prepared on quartz substrates were collected by Lambda 950 UV-Vis spectrometer.
Transient absorption spectrum (TAS)
Femtosecond transient absorption spectroscopy (fs-TAS) measurements of polycrystalline thin films prepared on quartz substrates were performed using our home-built TAS setup. The frequency-doubled 520 nm output from a Spectra-Physics Spirit laser (350 fs, 1 kHz, 40 μJ/pulse) was used for the pump beam, while a fraction was used for WLC generation using a sapphire crystal. The pump beam was chopped at 500 Hz, and the WLC probe signals were collected using an ultrafast fiber optic spectrometer. The time window of the TAS measurement was 1.6 ns. The samples on quartz substrates were mounted in a cryostat (Janis ST-100) and cooled by liquid nitrogen, 25 K intervals from 340 to 77 K. Schematic diagram of the TA system is shown in Supplementary Fig. 20.
Time-resolved PL (TRPL)
TRPL kinetics was detected by HORIBA DeltaFlex ultrafast time-resolved fluorescence spectrometer, where the excitation wavelength was 405 nm at 1 µJ cm−2 and the detection time scale was 40 ns.
Density functional theory (DFT) calculation
All calculations in this study were performed with the Vienna ab initio Simulation Package within the frame of DFT63. The exchange–correlation interactions of the electron were described via the generalized gradient approximation (GGA) with PBE functional29, and the projector augmented wave (PAW) method was used to describe the interactions of electron and ion64. The Monkhorst–Pack scheme with a 3 × 3 × 1 k-point mesh was used for the integration in the irreducible Brillouin zone. The kinetic energy cut-off of 500 eV was chosen for the plane wave expansion. The lattice parameters and ionic position were fully relaxed, and the total energy was converged within 10−5 eV per formula unit. The final forces on all ions were less than 0.02/Å.
Statistics and reproducibility
For the temperature-dependent PL experiments, temperature-dependent TA experiments, temperature-dependent TRPL experiments, PLQY, and Raman spectra experiments of the four 2D A2SnI4 (A = PEA+, BA+, HA+, and OA+), we have repeated the experiments more than four times under the same experimental conditions, and each time the results have the same rule with similar experimental results.
Data availability
The authors declare that the main data supporting the findings of this study are available within the article and its Supplementary Information files. Extra data are available from the corresponding author upon reasonable request.
Code availability
All custom codes used to generate results in the current study are available from the corresponding author upon reasonable request.
References
Green, M. A., Ho-Baillie, A. & Snaith, H. J. The emergence of perovskite solar cells. Nat. Photonics 8, 506–514 (2014).
Lin, L. Y. et al. Inorganic electron transport materials in perovskite solar cells. Adv. Funct. Mater. 31, 2008300 (2020).
Li, G. H. et al. High detectivity photodetectors based on perovskite nanowires with suppressed surface defects. Photon. Res. 8, 1862–1874 (2020).
Dou, L. et al. Solution-processed hybrid perovskite photodetectors with high detectivity. Nat. Commun. 5, 5044 (2014).
Shan, Q. et al. Perovskite light-emitting/detecting bifunctional fibres for wearable LiFi communication. Light Sci. Appl. 9, 163 (2020).
Mica, N. A. et al. Triple-cation perovskite solar cells for visible light communications. Photon Res. 8, A16–A24 (2020).
Cao, Z. L. et al. Optical studies of semiconductor perovskite nanocrystals for classical optoelectronic applications and quantum information technologies: a review. Adv. Photon. 2, 054001 (2020).
Mo, Q. et al. Room temperature synthesis of stable silica-coated CsPbBr3 quantum dots for amplified spontaneous emission. Photon. Res. 8, 1605–1612 (2020).
Gong, X. et al. Electron-phonon interaction in efficient perovskite blue emitters. Nat. Mater. 17, 550–556 (2018).
Liu, Y. et al. Efficient blue light-emitting diodes based on quantum-confined bromide perovskite nanostructures. Nat. Photonics 13, 760–764 (2019).
Liu, Z. et al. Mode selection and high-quality upconversion lasing from perovskite CsPb2Br5 microplates. Photon Res. 8, A31–A38 (2020).
Zheng, H. Y. et al. The effect of hydrophobicity of ammonium salts on stability of quasi-2D perovskite materials in moist condition. Adv. Energy Mater. 8, 1800051 (2018).
Lin, J. T. et al. Harnessing dielectric confinement on tin perovskites to achieve emission quantum yield up to 21%. J. Am. Chem. Soc. 141, 10324–10330 (2019).
Yuan, F. et al. Color-pure red light-emitting diodes based on two-dimensional lead-free perovskites. Sci. Adv. 6, eabb0253 (2020).
Swarnkar, A., Ravi, V. K. & Nag, A. Beyond colloidal cesium lead halide perovskite nanocrystals: analogous metal halides and doping. ACS Energy Lett. 2, 1089–1098 (2017).
Wang, Z. et al. Efficient two-dimensional tin halide perovskite light-emitting diodes via a spacer cation substitution strategy. J. Phys. Chem. Lett. 11, 1120–1127 (2020).
Guo, Z., Wu, X., Zhu, T., Zhu, X. & Huang, L. Electron–phonon scattering in atomically thin 2D perovskites. ACS Nano 10, 9992–9998 (2016).
Ghosh, D., Neukirch, A. J. & Tretiak, S. Optoelectronic properties of two-dimensional bromide perovskites: influences of spacer cations. J. Phys. Chem. Lett. 11, 2955–2964 (2020).
Wu, X. et al. Trap states in lead iodide perovskites. J. Am. Chem. Soc. 137, 2089–2096 (2015).
Liao, Y. et al. Highly oriented low-dimensional tin halide perovskites with enhanced stability and photovoltaic performance. J. Am. Chem. Soc. 139, 6693–6699 (2017).
Li, F. et al. Effects of alkyl chain length on crystal growth and oxidation process of two-dimensional tin halide perovskites. ACS Energy Lett. 5, 1422–1429 (2020).
Mahata, A., Meggiolaro, D., Gregori, L. & De Angelis, F. Suppression of tin oxidation by 3D/2D perovskite interfacing. J. Mater. Chem. C. 125, 10901–10908 (2021).
Leveillee, J. et al. Tuning electronic structure in layered hybrid perovskites with organic spacer substitution. Nano Lett. 19, 8732–8740 (2019).
Xing, G. et al. Long-range balanced electron- and hole-transport lengths in organic-inorganic CH3NH3PbI3. Science 342, 344–347 (2013).
Ishihara, T., Takahashi, J. & Goto, T. Exciton-state in two-dimensional perovskite semiconductor (C10H21NH3)2PbI4. Solid State Commun. 69, 933–936 (1989).
Ishihara, T., Takahashi, J. & Goto, T. Optical properties due to electronic transitions in two-dimensional semiconductors (CnH2n+1NH3)2PbI4. Phys. Rev. B: Condens. Matter Mater. Phys. 42, 11099–11107 (1990).
Weidman, M. C., Seitz, M., Stranks, S. D. & Tisdale, W. A. Highly tunable colloidal perovskite nanoplatelets through variable cation, metal, and halide composition. ACS Nano 10, 7830–7839 (2016).
He, H. et al. Exciton localization in solution-processed organolead trihalide perovskites. Nat. Commun. 7, 10896 (2016).
Traore, B. et al. Composite nature of layered hybrid perovskites: assessment on quantum and dielectric confinements and band alignment. ACS Nano 12, 3321–3332 (2018).
Quarti, C., Marchal, N. & Beljonne, D. Tuning the optoelectronic properties of two-dimensional hybrid perovskite semiconductors with alkyl chain spacers. J. Phys. Chem. Lett. 9, 3416–3424 (2018).
Blancon, J. C. et al. Scaling law for excitons in 2D perovskite quantum wells. Nat. Commun. 9, 2254 (2018).
Yang, B. et al. Colloidal synthesis and charge-carrier dynamics of Cs2AgSb1-yBiyX6 (X: Br, Cl; 0 ≤y ≤1) double perovskite nanocrystals. Angew. Chem. Int. Ed. 58, 2278–2283 (2019).
Baranowski, M. & Plochocka, P. Excitons in metal‐halide perovskites. Adv. Energy Mater. 10, 1903659 (2020).
Neutzner, S. et al. Exciton-polaron spectral structures in two-dimensional hybrid lead-halide perovskites. Phys. Rev. Mater. 2, 064605 (2018).
Rudin, S., Reinecke, T. L. & Segall, B. Temperature-dependent exciton linewidths in semiconductors. Phys. Rev. B: Condens. Matter Mater. Phys. 42, 11218–11231 (1990).
Smith, M. D. & Karunadasa, H. I. White-light emission from layered halide perovskites. Acc. Chem. Res. 51, 619–627 (2018).
Hu, T. et al. Mechanism for broadband white-light emission from two-dimensional (110) hybrid perovskites. J. Phys. Chem. Lett. 7, 2258–2263 (2016).
Dohner, E. R., Jaffe, A., Bradshaw, L. R. & Karunadasa, H. I. Intrinsic white-light emission from layered hybrid perovskites. J. Am. Chem. Soc. 136, 13154–13157 (2014).
Kahmann, S., Tekelenburg, E. K., Duim, H., Kamminga, M. E. & Loi, M. A. Extrinsic nature of the broad photoluminescence in lead iodide-based Ruddlesden-Popper perovskites. Nat. Commun. 11, 2344 (2020).
Sheikh, T. et al. Molecular intercalation and electronic two dimensionality in layered hybrid perovskites. Angew. Chem. Int. Ed. 59, 11653–11659 (2020).
Wu, X., Trinh, M. T. & Zhu, X. Y. Excitonic many-body interactions in two-dimensional lead iodide perovskite quantum wells. J. Phys. Chem. C. 119, 14714–14721 (2015).
Cunningham, P. D., Hanbicki, A. T., McCreary, K. M. & Jonker, B. T. Photoinduced bandgap renormalization and exciton binding energy reduction in WS2. ACS Nano 11, 12601–12608 (2017).
Chernikov, A., Ruppert, C., Hill, H. M., Rigosi, A. F. & Heinz, T. F. Population inversion and giant bandgap renormalization in atomically thin WS2 layers. Nat. Photonics 9, 466–470 (2015).
Borzda, T. et al. Charge photogeneration in few-layer MoS2. Adv. Funct. Mater. 25, 3351–3358 (2015).
Steinleitner, P. et al. Direct observation of ultrafast exciton formation in a monolayer of WSe2. Nano Lett. 17, 1455–1460 (2017).
Cunningham, P. D. et al. Charge trapping and exciton dynamics in large-area CVD grown MoS2. J. Phys. Chem. C. 120, 5819–5826 (2016).
Li, X. L. et al. Defect-related broadband emission in two-dimensional lead bromide perovskite microsheets. J. Phys. Chem. Lett. 11, 8157–8163 (2020).
Cunningham, P. D., McCreary, K. M. & Jonker, B. T. Auger recombination in chemical vapor deposition-grown monolayer WS2. J. Phys. Chem. Lett. 7, 5242–5246 (2016).
Milot, R. L., Eperon, G. E., Snaith, H. J., Johnston, M. B. & Herz, L. M. Temperature-dependent charge-carrier dynamics in CH3NH3PbI3 perovskite thin films. Adv. Funct. Mater. 25, 6218–6227 (2015).
Mondal, N. et al. Dynamical interconversion between excitons and geminate charge pairs in two-dimensional perovskite layers described by the Onsager-Braun model. J. Phys. Chem. Lett. 11, 1112–1119 (2020).
Smith, M. D., Connor, B. A. & Karunadasa, H. I. Tuning the luminescence of layered halide perovskites. Chem. Rev. 119, 3104–3139 (2019).
Gautier, R., Paris, M. & Massuyeau, F. Exciton self-trapping in hybrid lead halides: role of halogen. J. Am. Chem. Soc. 141, 12619–12623 (2019).
Booker, E. P. et al. Formation of long-lived color centers for broadband visible light emission in low-dimensional layered perovskites. J. Am. Chem. Soc. 139, 18632–18639 (2017).
Duim, H., Adjokatse, S., Kahmann, S., ten Brink, G. H. & Loi, M. A. The impact of stoichiometry on the photophysical properties of Ruddlesden–Popper perovskites. Adv. Funct. Mater. 30, 1907505 (2019).
Deng, S. et al. Long-range exciton transport and slow annihilation in two-dimensional hybrid perovskites. Nat. Commun. 11, 664 (2020).
Guo, Z. et al. Long-range hot-carrier transport in hybrid perovskites visualized by ultrafast microscopy. Science 356, 59–62 (2017).
Yang, Y. et al. Observation of a hot-phonon bottleneck in lead-iodide perovskites. Nat. Photonics 10, 53–59 (2015).
Lu, J. G. et al. Carrier concentration dependence of band gap shift in n-type ZnO:Al films. J. Appl. Phys. 101, 083705 (2007).
Manser, J. S. & Kamat, P. V. Band filling with free charge carriers in organometal halide perovskites. Nat. Photonics 8, 737–743 (2014).
Trimpl, M. J. et al. Charge‐carrier trapping and radiative recombination in metal halide perovskite semiconductors. Adv. Funct. Mater. 30, 2004312 (2020).
Kim, S. et al. High-mobility and low-power thin-film transistors based on multilayer MoS2 crystals. Nat. Commun. 3, 1011 (2012).
Chen, J. et al. Review on the study of carrier dynamic process in all-inorganic halide perovskites by photoluminescence measurement. Photon. Res. 9, 151–170 (2021).
Kresse, G. & Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B: Condens. Matter Mater. Phys. 54, 11169–11186 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B Condens. Matter Mater. Phys. 59, 1758–1775 (1999).
Acknowledgements
The work was supported by the NSFC (Nos. 61975221, 11904375, 12174246, and 61875119), the Strategic Priority Research Program of CAS (Nos. XDB16030700 and XDB43010303), Shanghai Science and Technology International Cooperation Fund (No. 19520710200), the Program for Professor of Special Appointment (Eastern Scholar) at Shanghai Institutions of Higher Learning, Shanghai Rising-Star Program (Grant No. 19QA1404000), Youth Innovation Promotion Association CAS (2016237), the “Chen Guang” project supported by Shanghai Municipal Education Commission and Shanghai Education Development Foundation (Grant No. 18CG63). The author thanks Dr. Chen from Instrumentation and Service Center for Molecular Sciences at Westlake University for supporting the Temperature-dependent steady-state PL spectra measurement and PLQY measurement.
Author information
Authors and Affiliations
Contributions
J.W. and J.L. supervised the execution of the project. T.Z. and J.L. conceived the idea and designed the experiments. T.Z. independently designed and built a TA spectrum testing device. C.Z. prepared perovskite samples. T.Z. carried out the UPS, XPS, SEM, PLQY, SCXRD, Raman spectra, UV/Visible absorption, TRPL, PL spectra, and TA spectra measurement and analysis. X.F. and H.C. contributed to the single crystal testing and structural analysis, J.L. analyzed the SCXRD data. T.Z. wrote and checked the paper. J.L., J.W., N.D., X.C., and L.Z. checked the manuscript. All authors commented on the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review information
Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Zhang, T., Zhou, C., Feng, X. et al. Regulation of the luminescence mechanism of two-dimensional tin halide perovskites. Nat Commun 13, 60 (2022). https://doi.org/10.1038/s41467-021-27663-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-021-27663-0
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.