Abstract
Single photon emitters in atomically-thin semiconductors can be deterministically positioned using strain induced by underlying nano-structures. Here, we couple monolayer WSe2 to high-refractive-index gallium phosphide dielectric nano-antennas providing both optical enhancement and monolayer deformation. For single photon emitters formed on such nano-antennas, we find very low (femto-Joule) saturation pulse energies and up to 104 times brighter photoluminescence than in WSe2 placed on low-refractive-index SiO2 pillars. We show that the key to these observations is the increase on average by a factor of 5 of the quantum efficiency of the emitters coupled to the nano-antennas. This further allows us to gain new insights into their photoluminescence dynamics, revealing the roles of the dark exciton reservoir and Auger processes. We also find that the coherence time of such emitters is limited by intrinsic dephasing processes. Our work establishes dielectric nano-antennas as a platform for high-efficiency quantum light generation in monolayer semiconductors.
Similar content being viewed by others
Introduction
Single-photon emitters (SPEs) in two-dimensional (2D) semiconducting WSe21,2,3,4,5 open attractive perspectives for few-atom-thick devices for quantum technologies owing to favorable excitonic properties6 and the integration with arbitrary substrates, including nanostructured surfaces7,8. Several theoretical models have been proposed to provide insight into the origin of SPEs observed in the cryogenic photoluminescence (PL) spectra of 2D WSe29,10,11,12. Their occurrence was explained by the presence of strain-induced potential traps for excitons9, momentum-dark states10, or various types of defects11,12. While the exact origin is still under debate, the first significant steps have been made to integrate WSe2 SPEs in devices, including electroluminescent structures13,14,15, waveguides16,17, and tunable high-Q microcavities18.
An appealing approach for the scalable and controllable fabrication of SPEs in WSe2 is the use of strain engineering for their deterministic positioning. Based on this idea, SiO219 or polymer nanopillars20 have been employed to induce arrays of SPEs in atomically thin WSe2. In a similar approach, nanostructures made of noble metals were also employed where, due to the enhancement of the near-field intensity by plasmonic resonances, increased spontaneous emission rates were demonstrated21. However, plasmonic nanoantennas are known for large nonradiative losses, particularly detrimental for quantum-technology applications. Thus, special care needs to be taken to separate SPEs from metallic surfaces with a dielectric spacer, which on the other hand will reduce the desired near-field coupling21.
In contrast, the high-refractive-index dielectric materials used in our work offer a lossless alternative to metals22. Sub-wavelength dielectric nano-antennas exhibit optical Mie resonances carrying both electric and magnetic responses23. High-index dielectric nano-antennas have also been recently shown to provide an efficient approach for the enhancement of light–matter interaction as well as improved emitted light directionality in molecules24, colloidal quantum dots25, and excitons in 2D semiconductors7,26.
Here, we realize SPEs by placing monolayer WSe2 on top of dielectric nano-antennas made from high-refractive index GaP. Such SPEs show considerably enhanced PL counts per unit excitation power compared with previously reported emitters in WSe2 as well as the SPEs realized on low-index SiO2 nanopillars in our work. The nano-antennas act as broadband optical cavities and also create strain pockets where the SPEs form. For such SPEs, our numerical simulations predict PL enhancement factors 〈EF〉7,27 up to 800, compared with a more standard realization of WSe2 SPEs on SiO2 pillars19. However, owing to the substantially enhanced quantum efficiency (QE) in the SPEs on GaP nanoantennas, we can employ low-excitation powers below fJ per laser pulse for their efficient operation. Thus, when we compare SPEs on GaP nanoantennas and SiO2 pillars experimentally, we find up to 104 brighter PL per unit laser power in the former system. We show that this substantial improvement in the operation of the SPEs is related to the low QE of the SPEs on SiO2, 4 ± 2% on average, compared with 21 ± 3% average and up to 86% maximum in SPEs on GaP nanoantennas. For the latter, we find that for the pumping laser repetition rate of 80 MHz, the SPE generates an effective single photons rate as high as 69 MHz under laser pulse energies around a fJ, corresponding to the single-photon rate of 5.5 MHz at the first lens.
Our approach allows further insight into the exciton dynamics in the hybrid 2D/0D system (2D monolayer/SPE) at very low-excitation densities. We observe that as the pumping power is increased, exciton–exciton annihilation28,29, in our case of dark excitons, prevents the efficient population of SPEs. This insight allows to develop a fuller understanding of the limitations of the low QE systems, in our case the SPEs on SiO2. There, the requirement for increased pumping power leads to a fast nonradiative depletion of excitons in 2D WSe2 and eventually results in a low single-photon generation rate, that cannot be overcome by further increasing the pumping power. Our results thus highlight that the high-refractive-index nanoantennas, exhibiting near-field optical enhancement, provide strong advantages for producing bright SPEs in WSe2 monolayers.
Results
Optical properties of WSe2 SPEs positioned on GaP nanoantennas
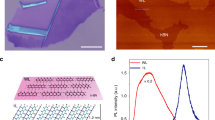
We use GaP nanoantennas composed of two closely spaced nanopillars (Fig. 1a), referred to as “dimer” below (see also Supplementary Fig. 1a). They exhibit an enhancement of the electromagnetic near-field intensity, as a result of the high refractive index (nGaP ≈ 3.2) and the hybridization of the optical resonances of each individual pillars (see Supplementary Notes I and II). This is demonstrated in Fig. 1a, where we show the calculated electric field intensity of the scattered radiation, ∣E∣2, normalized by the intensity ∣E0∣2 of the normally incident plane wave with linear polarization along the axis connecting the centers of the nanopillars. The profile in Fig. 1a corresponds to the top surface of the GaP dimer (z = 200 nm) having individual pillar radii of 150 nm. The enhancement of ∣E∣2 compared with ∣E0∣2 exceeds ten times and is particularly pronounced in the gap between the pillars7,24,30. The field is also strongly enhanced at the outer edges of the dimer where we expect SPEs to be located, as discussed further below and in Supplementary Note I. As shown in Fig. 1b, under the same excitation conditions, a SiO2 nanopillar (r = 150 nm, h = 100 nm) does not show strong electromagnetic resonances, as a consequence of its low refractive index (\({n}_{{{{{{{{{\rm{SiO}}}}}}}}}_{2}}\approx 1.5\)).
a, b Top panel: schematics of monolayer WSe2 on top of GaP nanoantennas (a) and SiO2 nanopillar (b). Lower panel: calculated relative intensity of the electric field in the scattered wave (E) over that in the incident wave (E0). Results are shown for (a) a GaP dimer nano-antenna (r = 150 nm, h = 200 nm, gap = 50 nm) and (b) SiO2 nanopillar (r = 150 nm, h = 100 nm). The calculated intensity is shown for the plane at the top of each structure. Scale bar: 150 nm. c–e The calculated Purcell enhancement factor (c), excitation rate (d), and light collection efficiency (e) for a dipole emitter placed at the position of the highest field enhancement shown in (a) and (b) of the GaP dimer nanoantennas (red) and SiO2 nanopillars (dark blue) relative to the same parameters for this dipole in a vacuum. See further details in “Methods “and Supplementary Note I. f A T = 4 K PL spectrum of a WSe2 SPE on a GaP nano-antenna (r = 250 nm, h = 200 nm, gap = 50 nm), excited` with a 638 nm pulsed laser with 20 MHz repetition rate and an average power of 15 nW. Inset: map of the integrated PL intensity of this monolayer (T = 4 K). g Second-order photon correlation curve for the PL signal in (f).
A dipole emitter, such as an exciton in an SPE, spectrally and spatially overlapping with the near-field of the antenna, is expected to exhibit an enhanced light emission intensity27. This is a result of the product of the three main factors giving rise to the PL enhancement factor 〈EF〉7,27. Depending on the relative position and orientation of its dipole moment, the emitter experiences an increased local density of states and thus an enhanced spontaneous emission rate31 via the Purcell effect, introducing a factor Fp, directly improving the overall quantum efficiency, QE = Fpγrad/(Fpγrad + γnr), where γrad and γnr are the rates of the radiative and nonradiative decay, respectively. In the absence of the Purcell effect, Fp = 1 and we assumed γrad ≪ γnr. The antenna also modifies the dipole far-field emission pattern, leading to an increased light collection efficiency above the antenna (ηobj) within the given numerical aperture (NA) of the objective lens used in the detection system. Finally, the enhanced absorption of light in the material coupled to the antenna (in our case, a monolayer WSe2), quantified by the excitation rate proportional to the intensity of the local near-field, \({\gamma }_{{{{{{{{\rm{exc}}}}}}}}}\propto {(| E| /| {E}_{0}| )}^{2}\) (Fig. 1a, b), should in principle lead to a more efficient excitation of an SPE.
As shown in Fig. 1c–e, we carried out numerical simulations (see “Methods” and Supplementary Note I) to extract the values of these three parameters for a dipole emitting at λem = 750 nm coupled to either GaP dimer nanoantennas (data in red) or to SiO2 nanopillars (dark blue). The dipole is placed at the edge of the dimers, where the interaction is maximized7, and is aligned perpendicularly to the edge of the nanopillar (Supplementary Fig. 1). For the dimers with radii above 200 nm, the field enhancement at the outer edges is comparable to that in the gap (Supplementary Fig. 1a). As shown in Fig. 1c–e, a GaP nano-antenna may induce an enhancement of the PL intensity by at least two orders of magnitude7,24,30, compared to SiO2 nanopillars, as a consequence of the increase in both the spontaneous emission rate Fp (Fig. 1c), the excitation rate γexc (Fig. 1d), and a relatively modest effect in the collection efficiency ηobj (Fig. 1e), as expected from the similar geometries of dimers and single pillars.
We note, that due to the high refractive index, for GaP most of the emitted light is directed downwards into the substrate, allowing only about 10% or less to be collected in the first lens (see further details in Supplementary Note 1). The highest single-photon rate of 69 MHz, which we quote in this work, corresponds to the total number of photons emitted by the SPE, whereas in the experiments reported below we measure only up to 5.5 MHz generation rate at the first lens.
In order to experimentally examine these effects, we transferred WSe2 monolayers on top of an array of GaP nanoantennas (see “Methods” and Supplementary Note III) and on SiO2 nanopillars as a reference (see Supplementary Note IV). With this approach, we achieve localized strain in the monolayer, introduced by the underlying nano-structure8, which promotes the occurrence of localized SPEs at cryogenic temperatures. We find that the SPEs are formed on nearly all nanoantennas with a yield above 90%, in agreement with previous reports19,20. For some nanoantennas, we find multiple emitters (see Supplementary Note III).
The samples are placed in a gas exchange cryostat, at a temperature of T = 4 K, and excited (unless stated otherwise) with a non-resonant pulsed laser at 638 nm with 90 ps pulse width and a variable repetition rate. The laser excites below the GaP bandgap and is absorbed only by the WSe2 monolayer. The inset in Fig. 1f shows a map of the integrated PL intensity from a WSe2 monolayer deposited on top of a GaP dimer nano-antenna (r = 250 nm). The PL signal exhibits a strong localization at the nano-antenna position, with negligible emission from the surrounding area where the unstrained WSe2 monolayer is positioned. As shown in Fig. 1f, we observe bright and narrow PL lines, with suppressed background PL from the band of localized states in WSe2 as is usually observed when WSe2 is deposited on SiO2 pillars (Supplementary Fig. 7a). We demonstrate the single-photon operation of the localized emitters in photon correlation measurements (see “Methods”). Figure 1g shows the second-order correlation function, g(2)(τ), for the emitter shown in Fig. 1f, excited at λexc = 725 nm, ~35 meV below the WSe2 A-exciton resonance. The pronounced anti-bunching behavior at zero time delay exhibits g(2)(0) = 0.26 ± 0.03, confirming the nonclassical photon emission statistics. In Supplementary Note V, we further correlate the SPEs emission energy to the strain induced in the 2D layer by the nanoantennas. Stretching of the WSe2 monolayer results in a progressively larger red-shift of the SPE emission when deposited on nanoantennas with smaller radii8. This behavior, analogous to the red-shift of WSe2 excitons under tensile deformation8, confirms the impact of strain on the confinement potential and emission energy of WSe2 SPEs.
The position of the SPE and the orientation of the emitter dipole relative to the nano-antenna are important factors for the PL enhancement7. We expect that the SPEs will tend to form naturally around the edges of the nanopillars (Fig. 1a), where both the tensile strain and photonic enhancement are maximized as follows from our previously reported theoretical and experimental results (see ref. 8 and Supplementary Note V). In these outer edge positions, the SPEs still experience a strong enhancement of the electric field, which for the nanopillars with the radii above 200 nm is comparable with the enhancement in the gap between the pillars (see Supplementary Fig. 1a).
In our experiments (not reported here), we find that WSe2 SPEs on planar SiO2 have comparable PL intensities and lifetimes to those formed on SiO2 pillars, with the latter having the advantage of controlled positioning. Furthermore, we did not observe SPEs of reliably measurable PL intensity on planar GaP, where we find that overall PL of WSe2 is quenched as seen for example in Fig. 1f. In what follows, we focus on GaP dimer nanoantennas, as these provide pronounced and interesting photonic effects, as was shown in our preliminary work7,8. On the other hand, less studied GaP monomers (single nanopillars) may also be useful for achieving SPE positioning and improved PL in WSe2 monolayers. This may be a subject of another investigation beyond our current work.
Quantum efficiency enhancement of SPEs on GaP nanoantennas
We analyzed more than 50 SPEs on GaP dimer nanoantennas, with radii ranging from 150 nm up to 300 nm, selecting localized WSe2 emitters with sub-meV linewidths. For these emitters, we observed common features such as linearly polarized emission, saturation of the PL intensity under increased excitation power, as well as PL lifetimes in the ns range (see Supplementary Note III). We observed no preferential orientation in the SPEs polarization, with different orientations of polarization even for emitters created on the same nano-antenna. Figure 2a shows the values of the PL intensity for SPEs on GaP nanoantennas (red dots) and on SiO2 nanopillars (dark blue dots), acquired in the PL saturation regime and normalized to the average excitation pump power. The plot also shows the PL peak position for each studied SPE, where no correlation between the intensity and spectral position is observed. For SPEs coupled to GaP nanoantennas, we observe from two to four orders of magnitude higher power-normalized PL intensity, compared to SPEs found on SiO2 nanopillars. Further insight into this behavior is provided by the SPE PL saturation powers, presented in Fig. 2b. Since we used different repetition rates from 5 to 80 MHz in these measurements due to a large variation in the PL lifetimes, in Fig. 2b we plot the energy per pulse value Psat, defined as the time-integrated average power divided by the laser repetition rate. We readily observe more than three orders of magnitude lower saturation pulse energies for the emitters on GaP nanoantennas. In our case, 1 fJ pulse energy corresponds to the energy density per pulse of 30 nJ/cm2. Nonetheless, for such low powers, the SPEs coupled to GaP nanoantennas provide some of the highest counts per second (> 30,000) so far observed in TMD monolayers. In what follows, we will consider the factors that could contribute to this observation.
Data for SPEs on GaP dimer nanoantennas are shown in red and for SPEs on SiO2 nanopillars is shown in dark blue. a PL intensity normalized by the average laser excitation power measured in the SPE saturation regime. The histogram on the right shows the occurrence of the observed PL intensity values. b Energy per laser pulse required for SPE saturation, Psat. See Supplementary Fig. 4 for more details on how Psat is extracted from the PL data. c PL decay times (main plot) and its occurrence (right). d SPE PL peak intensity divided by the laser repetition rate plotted versus SPE PL decay time. The red and blue areas of the plot correspond to SPEs with QE > 10% and QE < 10%, respectively. See main text and Supplementary Note VI for more details of how QE was estimated.
One of the obvious factors, expected to contribute to the reduced values of Psat is the enhanced absorption rate (γexc) in WSe2 monolayers coupled to GaP nanoantennas. However, this can only account for a reduction of the saturation power of up to 40 times as predicted by our simulations (Fig. 1d). A similar maximum enhancement for the power-normalized PL intensity may be expected due to the enhanced γexc. Thus, additional factors need to be considered, mostly linked to the exciton dynamics and QE of the combined 2D-WSe2/SPE system.
In Fig. 2c, we compare PL lifetimes of SPEs on GaP and on SiO2. For the SPEs on the SiO2 nanopillars, we observe lifetimes of the order of 10 ns, consistent with previous reports19,20. On the contrary, the SPEs on the GaP nanoantennas exhibit a broad distribution of lifetime values, ranging from 2 ns up to more than 200 ns. The radiative and nonradiative population decay rates in WSe2 SPEs (Γnr and Γr in Fig. 3d) are dependent on the shape and confinement energy of the strain potential, and the PL decay dynamics is defined by the relationship between them: if one of the rates is much higher than the other, it will define the PL decay time.
a Schematic showing the conduction (CB) and valence band (VB) behavior as a function of strain (shown in the top panel with a red line), and a single exciton trapping from the reservoir in 2D WSe2 into a strain-induced potential minimum, giving rise to the nonclassical light red-shifted from the emission in the unstrained monolayer. b Time-integrated PL spectrum of the strain-induced WSe2 SPE with a QE of 86% and saturation power of 57 nW for 80 MHz repetition rate, for which the data in (c), (e), and (f) are presented. c PL decay curves for the SPE in (b) measured at different laser powers. The instrument response function (IRF) is shown in gray. Inset: zoom-in of the PL traces also showing fitting with the analytical model discussed in Supplementary Note VII. The PL traces in the inset are plotted on a linear scale and shifted vertically for display purposes. d Schematic of the three-level system representing the dark exciton reservoir (nX), the exciton in the SPE (n1) and the ground level (n0), and the processes describing radiative and nonradiative decay of nX and n1 populations. See text for more details. e, f PL decay (e) and PL rise (f) times, as a function of the excitation power, obtained from the data fitting in Fig. 3c. For 3000 nW, τrise approaches the instrument resolution (gray dashed line). The error bars are calculated from the standard deviation of the fit values.
In order to shed light on the relationship between these rates, in Fig. 2d we plot the SPEs fluorescence lifetime intensity distribution32. The SPEs on SiO2 exhibit low PL emission with relatively short lifetimes (blue area). In SPEs coupled to GaP nanoantennas, we observe either a much higher PL intensity and similar lifetimes, or longer lifetimes with comparable brightness (red area in Fig. 2d). The QE of an SPE under pulsed excitation can be estimated from the number of detected photons at saturation, divided by the laser repetition rate21. After taking into account the losses of the experimental setup and the collection efficiency of the nano-antenna from numerical simulations (see additional details in Supplementary Note VI), we estimate an average QE for SPEs coupled to GaP nanoantennas of 21 ± 3%, with a maximum value reaching 86%. For SPEs on SiO2 nanopillars, we estimate an average QE of 4 ± 2% consistent with the previous reports21.
We thus conclude that the PL decay times of SPEs on SiO2 nanopillars are mainly defined by nonradiative processes (i.e., Γnr ≫ Γr), and that the true radiative lifetimes should by far exceed the measured decay times of ≈ 10 ns. On the other hand, for the SPEs on GaP nanoantennas exhibiting high QE, the lifetimes are mostly defined by the radiative decay (i.e., Γnr < Γr or Γnr ≪ Γr), which, as we can conclude from Fig. 2d, vary between 2 and 200 ns. Comparing this with the SPEs on SiO2, we can conclude that the high QE SPEs on GaP exhibiting lifetimes of the order of 10 ns or shorter are most likely affected by the Purcell enhancement increasing their radiative rates, and thus are possibly positioned in the near-field hotspots.
The high QE SPEs with PL decay times > 10 ns clearly must experience much slower nonradiative processes than SPEs on SiO2, as the nonradiative lifetimes must be slower than the measured PL decay times. This is also in contrast to previously reported SPEs coupled to plasmonic structures21, where despite the very large Purcell enhancement and sub-ns PL lifetimes, the maximum QE of 12.6% was reported for WSe2 monolayers extracted similarly to our work from bulk crystals grown by chemical vapor transport. This implies high nonradiative rates in this system (Γnr > Γr). On the other hand, SPEs with PL lifetimes in the range of 100 ns were previously observed only in monolayer WSe2 encapsulated in hexagonal boron nitride12, known for suppressing the nonradiative processes. In our case, possible causes for suppression of nonradiative decay could be the high surface quality of crystalline GaP structures, or that some SPEs are formed in the suspended parts of the monolayer in proximity to the near-field hotspots and between the pillars8. We cannot exclude that some of the high QE SPEs with PL decay times > 10 ns still experience Purcell enhancement, implying that the true radiative times in some WSe2 SPEs may reach hundreds of ns. Further detailed insight in the PL dynamics is given below in the discussion of Fig. 3.
Dynamics of exciton formation in strain-induced SPEs
SPEs in WSe2 are attributed to the occurrence of strain-induced local potential minima20,33, essentially zero-dimensional (0D), that can host a small number of confined excitons, similar for example to semiconductor quantum dots34. Contrary to other group-VI TMDs, tensile strain in WSe2 results in the lowering of the conduction band (CB) minimum and the rise of the valence band (VB) maximum, as shown in Fig. 3a, both located at the K points in the momentum space8,35. This creates an energy landscape where a very small fraction of the 2D exciton population may be captured into such 0D centers, giving rise to nonclassical light emission from confined states, at photon energies lower than that of both bright and dark excitons in unstrained WSe2.
As shown in Fig. 2, in the case of WSe2 placed on GaP nanoantennas, both the quantum yield and brightness of the SPEs are greatly enhanced, allowing new insight into the exciton dynamics in this hybrid 2D–0D system. Figure 3b shows a PL spectrum for an SPE exhibiting QE of 86 ± 3%. Figure 3c shows the time-resolved PL decay for the same SPE measured with 20 MHz repetition rate. The PL decay curves are obtained at different powers of 1, 100, and 1000 nW considerably below, close, and considerably above the saturation power, respectively. For clarity, the inset zooms in on the short times after the laser pulse excitation. At low power, we clearly observe a ns-scale rise time, which shortens as the power is increased also accompanied by a relatively weak shortening of the PL decay time.
We fit the data with a simple empirical model assuming an exciton reservoir, which feeds excitons into the SPE. The model can be solved analytically (see Supplementary Note VII for more details) and is used to fit the data, as shown in the inset of Fig. 3c, providing rise and decay times plotted in Fig. 3e and f. Here, we see that as the power is increased, the rise time, τrise, changes strongly from 1.7 ns to times approaching the experimental resolution, whereas the PL decay time τdecay decreases from 8.5 to 7.4 ns.
In order to understand this behavior, we consider several processes, which influence both the populations of the high energy 2D exciton reservoir and the SPE itself. We argue that the exciton reservoir with the population nX in Fig. 3d corresponds to the population of dark excitons, which we infer from the very slow PL rise time of 1.7 ns at low power, in contrast to the expected lifetime of the bright excitons of a few ps36,37. The dark excitons decay mostly via sample-specific nonradiative recombination with a rate \({{{\Gamma }}}_{{{{{{{{\rm{nr}}}}}}}}}^{{{{{{{{\rm{X}}}}}}}}}\) and, importantly, via the exciton–exciton (Auger) annihilation28,29, which grows with the increasing power as \({{{\Gamma }}}_{{{{{{{{\rm{A}}}}}}}}}{n}_{{{{{{{{\rm{X}}}}}}}}}^{2}\). Trapping of dark excitons with a rate Γtrap into the strain-induced SPE is responsible for a negligible reduction of nX, as the anti-bunching photon emission implies that only one exciton per laser excitation cycle can be created in the SPE. We thus also introduce a probability n1 for the SPE to be filled with an exciton with 0 ≤ n1 ≤1. The trapping of the dark excitons is the only source of the SPE population, and is included as a term Γtrap(1 − n1)nX in the equations below. Here, we take into account the effect of the SPE occupancy on the reduced efficiency of the exciton trapping with the factor (1 − n1), providing one of the mechanisms for the PL saturation with increasing power observed in the experiment. The population of the SPE decays radiatively and non-radiatively with rates Γr and Γnr, respectively. Here, for simplicity, we neglect the SPE’s internal confined-state structure, which we uncover in PL excitation experiments (see Fig. 4 for details). The rate equations capturing the behavior of the three-level system depicted in Fig. 3d are shown below:
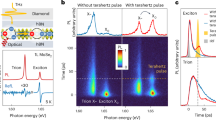
a PL emission (yellow) and the PL excitation (PLE) spectra (purple) from a WSe2 SPE. The PLE signal exhibits a series of confined exciton peaks below the neutral exciton PL peak position (X). b Interference fringe contrast, ν(τ) for two different excitation laser wavelengths. The dependence for the above-band excitation (dark blue dots) is obtained at 1.96 eV (638 nm) and yields a coherence time of T2 = 2.83 ± 0.20 (fitting shown with a dashed line). The dependence for the quasi-resonant excitation (orange dots) is obtained with a laser tuned to 1.71 eV (725 nm), lower than the A-exciton in unstrained monolayer WSe2, yielding a coherence time of T2 = 3.12 ± 0.40. The error bars are calculated form the standard deviation of the fit values. Inset: SPE PL spectrum under the quasi-resonant excitation (black dots) fitted with a single Lorentzian peak (yellow solid line) with a linewidth of 450 μeV, corresponding to a coherence time of T2 = 2.9 ps, in close agreement with the values obtained from the interferometric measurements.
We estimate that for 1 nW laser power at 20 MHz repetition rate and 5% light absorption in WSe2, the dark exciton density nx ≈ 3 × 108 cm−2 will be created. This is probably the lower bound, as the near-field electric field enhancement can locally lead to the increase of this value by a factor exceeding 10. At this low-power limit, the Auger annihilation can be neglected28 and the unsaturated SPE emission leads to an average (per pulse) n1 ≪ 1. The PL rise dynamics is then defined by the predominately nonradiative decay of the dark exciton reservoir with the rate \({{{\Gamma }}}_{{{{{{{{\rm{nr}}}}}}}}}^{{{{{{{{\rm{X}}}}}}}}}\). As the power is increased, and both nX and n1 grow, two additional processes become important: the Auger annihilation described by the term \({{{\Gamma }}}_{{{{{{{{\rm{A}}}}}}}}}{n}_{{{{{{{{\rm{X}}}}}}}}}^{2}\) and the saturation of the SPE with the corresponding term Γtrap(1 − n1)nX. For the powers presented in Fig. 3, nX(t = 0) is estimated to be of the order of 1010 cm−2 for the power of 100 nW and 1011 cm−2 for 1000 nW, in the range where the Auger annihilation was found to be very efficient28,29.
While a more detailed study at low powers could help to separate the contributions from the Auger annihilation and SPE saturation, it is possible that in the high power regime the SPE PL saturation is influenced not only by the state-filling effect but also by the nonradiative depletion of the dark exciton reservoir. In the case of the bright and high QE SPEs in WSe2/GaP nano-antenna system, high photon counts can be achieved at low-excitation powers, thus circumventing the requirement for increased pumping. On the other hand, in the SPEs in WSe2 on SiO2 nanopillars, where both the QE and brightness are low, increased pumping is required to observe the SPE PL. This has a negative effect on the population of the reservoir via the Auger annihilation and thus, through such negative feedback, leads to the requirement to further increase the power. Eventually, both the low QE and its further reduction due to the Auger annihilation lead to a very large three order of magnitude increase in the saturation powers in the SPEs in WSe2 on SiO2 nanopillars compared with those on GaP nanoantennas, as seen in Fig. 2. In support of these conclusions, we also note that high saturation powers, similar to those observed by us in WSe2 SPEs on SiO2 were also reported in SPEs coupled to plasmonic structures21, where very fast nonradiative processes in the 2D WSe2 should be expected.
Coherence of a strain-induced SPE
The coherence of WSe2 SPEs has been previously investigated only under high power densities and non-resonant excitation21. Here, we evaluated the first-order correlation function, g(1)(τ), for the SPE shown in Fig. 4a, in a Mach–Zender interferometer setup38 and compared different excitation schemes (see “Methods”). We employed an above-band excitation using a 1.96 eV (638 nm) cw laser, corresponding to energy higher than the A-exciton resonance in monolayer WSe2 (dashed line in Fig. 4a). Under these conditions, high energy excitons are created in the continuum of states above the excitonic resonance, introducing dephasing for instance via scattering with phonons and impurities or via exciton–exciton interactions. To reduce the impact of such processes, we also used a quasi-resonant excitation with a cw laser at 1.71 eV (725 nm). As shown in Fig. 4a, this excitation is resonant with higher energy states within the SPE1. Figure 4b shows the measured fringe contrast, ν(τ), of the WSe2 SPE under the two excitation schemes (see “Methods”). By fitting the observed decay of the fringe contrast with a single exponential decay function, \({g}^{(1)}(\tau )\approx \exp (-| \tau | /{T}_{2})\), we extract a coherence time of T2 = 3.12 ± 0.40 ps under quasi-resonant excitation, and of T2 = 2.83 ± 0.20 ps for above-band excitation. The differences between the excitation schemes have a negligible effect on the SPE dephasing time, implying a complex relaxation process within the confined states of the SPE. We find that the PL full-width at half maximum (FWHM) of ≈ 450 μeV corresponds to T2 = 2.9 ps (FWHM = 2Γ = 2ℏ/T2) close to the observed T2 values, indicating that the coherence of the studied SPE is limited by pure dephasing, which we attribute to interactions with phonons during the exciton relaxation39, as for the excitation power < 20 nW used in the experiment the contribution of the Auger annihilation can be excluded. The observed SPE T2 values are one order of magnitude higher than those reported for monolayer WSe2 of 0.3 ps39. Excitation in resonance with the lowest energy optical transition in the SPE could be employed to gain access to the intrinsic coherence times of the confined excitons.
Discussion
In summary, we have demonstrated that high-refractive-index GaP nanoantennas offer an efficient approach for nano-scale positioning and QE enhancement in strain-induced SPEs in monolayer WSe2. We found 102 to 104 enhancement of the PL intensity for WSe2 SPEs coupled to GaP nanoantennas compared with those formed on low-refractive-index SiO2 nanopillars. We demonstrate that this is primarily caused by the greatly increased QE in the 2D/0D WSe2 system coupled to GaP nanoantennas arising from the enhancement of the radiative rates in such SPEs through the Purcell effect, as well as the reduction of the nonradiative decay rates. Importantly, this allows bright emission from the SPEs to be excited with energy densities per laser pulse below 30 nJ/cm2 corresponding to the energy per pulse below 1 fJ, enabling the SPE operation at low exciton densities in the 2D WSe2, thus avoiding the exciton–exciton annihilation. The powers at which SPEs on GaP nanoantennas provide bright emission are approximately three orders of magnitude below those required for the operation of the SPEs on SiO2 pillars studied in this work, as well as those previously reported for SPEs formed on plasmonic nanostructures21, despite the large Purcell enhancement factors found in the latter system21. Further improvement and consistency of the operation of SPEs can possibly be achieved by employing deterministic defect placement40,41, while the required excitation powers can be further reduced by employing much cleaner WSe2 grown by the so-called flux technique21. The photon collection efficiency in our approach can be potentially improved by engineering the nanocavity geometry and materials, for instance by using nanoantennas made from high-index TMDs42,43. These materials can be deposited on any type of substrate. By placing them on a metallic mirror similarly to the strategy pursued by Luo et al. in ref. 21, most of the light can be redirected upward, and the collection efficiency in the first lens can be considerably increased. Overall, our work suggests that hybrid systems composed of 2D semiconductors coupled to dielectric nanoantennas are a powerful means for controlling quantum light generation.
Methods
Sample fabrication
The GaP dimer nanoantennas were fabricated using electron-beam lithography, followed by several wet and dry etching steps as described in ref. 24. Arrays of nanoantennas separated by 4 μm were made. The dimers had a gap of ≈ 50 nm, a height of 200 nm, and nanopillar radii (r) of 150, 200, 250, and 300 nm. Atomically thin monolayers of WSe2 were mechanically exfoliated from commercially available bulk single crystals (HQ Graphene) onto polydimethylsiloxane (PDMS) polymer substrates. The monolayer thickness was identified by examining room temperature PL with an imaging method described in ref. 44. The monolayers were then transferred on top of the GaP nano-antenna array, by using the same PDMS substrates, with an all-dry transfer technique in a home-built transfer setup45.
Optical spectroscopy
Low-temperature PL spectroscopy was carried out with a sample placed in low-pressure He exchange gas within a confocal microscope platform allowing free space optical access and high precision sample positioning (Attocube). The whole microscope stick was inserted in a liquid helium transport dewar (Cryo Anlagenbau Gmbh) and a nominal sample temperature of 4 K was used in all reported experiments. The excitation from the lasers used in this work was delivered through single-mode fibers to the optical breadboard placed at the top of the microscope stick, where it was collimated and directed onto the sample through a window at the top of the stick. For pulsed excitation, we used a diode laser (PicoQuant) at 638 nm, with a variable repetition rate from 5 to 80 MHz and a pulse width of 90 ps. For continuous-wave excitation, we used a tunable Ti-Sapphire laser (M Squared SOLSTIS). PL emitted by the sample was collected with an aspheric lens (NA = 0.64) and coupled at the breadboard into a single-mode optical fiber, which delivered it to a spectrometer (Princeton Instruments SP2750), where it was detected with high-sensitivity liquid nitrogen cooled charge-coupled device (Princeton Instruments PyLoN). For the time-resolved spectroscopy, the PL was also sent through the spectrometer to another exit port, where it was measured with an avalanche photodiode (ID100-MMF50) connected to a photon-counting card (Becker and Hickl SP-130). A Hanbury Brown-Twiss setup used for the evaluation of the second-order correlation function (g(2)(τ)) was equipped with two superconducting nanowire single-photon detectors (Single Quantum) and a similar photon-counting card. The SPE was excited with a continuous-wave diode laser (Thorlabs HL7302MG) at 730 nm with a power of 2 nW. Light from the SPE was directed to the nanowire detectors with a multimode fiber. The emitted light from the SPE was filtered with a pair of filters (Thorlabs FESH800 and Thorlabs FELH750) providing a transparency window between 750 and 800 nm.
Coherence measurements
For evaluation of the first-order correlation function (g(1)(τ)), we used a Mach–Zender interferometer setup38 with a phase shifter in one arm and a variable optical delay in the other. By sweeping the voltage of the phase shifter, the interference of light emitted by the SPE was measured using an avalanche photodiode at one output port of the interferometer. By measuring the intensity at the local maxima (\({I}_{\max }\)) and minima (\({I}_{\min }\)) of the interference fringes, we evaluate the fringe contrast (ν) as:
This procedure was repeated for increasing delay times until the fringes were no longer resolved. The relationship between the fringe contrast and the first-order correlation function is given by the following equation:
where 1 − ϵ is the maximum resolvable fringe contrast in the setup and ∣g(1)(τ)∣ is the first-order correlation function, excluding the fast oscillations at the emitter frequency.38. In the absence of any spectral diffusion, the fringe contrast as a function of time follows a single exponential decay, with an exponential fit allowing the evaluation of the coherence time (T2) of the emitter.
Simulations
The distributions of the electric field in Fig. 1 were calculated with a commercial finite-difference time-domain software (Lumerical Inc.). In the simulations, we illuminated the structure with a linearly polarized plane wave at λ = 750 nm with a normal incidence from the vacuum side of the substrate. See Supplementary Note I for further details on the simulations.
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
References
Tonndorf, P. et al. Single-photon emission from localized excitons in an atomically thin semiconductor. Optica 2, 347 (2015).
Srivastava, A. et al. Optically active quantum dots in monolayer WSe2. Nat. Nanotechnol. 10, 491 (2015).
Koperski, M. et al. Single photon emitters in exfoliated WSe2 structures. Nat. Nanotechnol. 10, 503 (2015).
He, Y.-M. et al. Single quantum emitters in monolayer semiconductors. Nat. Nanotechnol. 10, 497 (2015).
Chakraborty, C., Kinnischtzke, L., Goodfellow, K. M., Beams, R. & Vamivakas, A. N. Voltage-controlled quantum light from an atomically thin semiconductor. Nat. Nanotechnol. 10, 507 (2015).
Wang, G. et al. Colloquium: excitons in atomically thin transition metal dichalcogenides. Rev. Mod. Phys. 90, 021001 (2018).
Sortino, L. et al. Enhanced light-matter interaction in an atomically thin semiconductor coupled with dielectric nano-antennas. Nat. Commun. 10, 5119 (2019).
Sortino, L. et al. Dielectric nanoantennas for strain engineering in atomically thin two-dimensional semiconductors. ACS Photonics 7, 2413 (2020).
Feierabend, M., Brem, S. & Malic, E. Optical fingerprint of bright and dark localized excitonic states in atomically thin 2D materials. Phys. Chem. Chem. Phys. 21, 26077 (2019).
Lindlau, J. et al. The role of momentum-dark excitons in the elementary optical response of bilayer WSe2. Nat. Commun. 9, 2586 (2018).
Linhart, L. et al. Localized intervalley defect excitons as single-photon emitters in WSe2. Phys. Rev. Lett. 123, 146401 (2019).
Dass, C. K. et al. Ultra-long lifetimes of single quantum emitters in monolayer WSe2/hBN heterostructures. Adv. Quantum Technol. 2, 1900022 (2019).
Palacios-Berraquero, C. et al. Atomically thin quantum light-emitting diodes. Nat. Commun. 7, 12978 (2016).
Schwarz, S. et al. Electrically pumped single-defect light emitters in WSe2. 2D Mater. 3, 025038 (2016).
Clark, G. et al. Single defect light-emitting diode in a van der Waals heterostructure. Nano Lett. 16, 3944 (2016).
Blauth, M. et al. Coupling single photons from discrete quantum emitters in WSe2 to lithographically defined plasmonic slot waveguides. Nano Lett. 18, 6812 (2018).
Peyskens, F., Chakraborty, C., Muneeb, M., Van Thourhout, D. & Englund, D. Integration of single photon emitters in 2D layered materials with a silicon nitride photonic chip. Nat. Commun. 10, 4435 (2019).
Flatten, L. C. et al. Microcavity enhanced single photon emission from two-dimensional WSe2. Appl. Phys. Lett. 112, 191105 (2018).
Palacios-Berraquero, C. et al. Large-scale quantum-emitter arrays in atomically thin semiconductors. Nat. Commun. 8, 15093 (2017).
Branny, A., Kumar, S., Proux, R. & Gerardot, B. D. Deterministic strain-induced arrays of quantum emitters in a two-dimensional semiconductor. Nat. Commun. 8, 15053 (2017).
Luo, Y. et al. Deterministic coupling of site-controlled quantum emitters in monolayer WSe2 to plasmonic nanocavities. Nat. Nanotechnol. 13, 1137 (2018).
Caldarola, M. et al. Non-plasmonic nanoantennas for surface enhanced spectroscopies with ultra-low heat conversion. Nat. Commun. 6, 7915 (2015).
Koshelev, K. & Kivshar, Y. Dielectric resonant metaphotonics. ACS Photonics 8, 102 (2021).
Cambiasso, J. et al. Bridging the gap between dielectric nanophotonics and the visible regime with effectively lossless gallium phosphide antennas. Nano Lett. 17, 1219 (2017).
Kolchin, P. et al. High purcell factor due to coupling of a single emitter to a dielectric slot waveguide. Nano Lett. 15, 464 (2015).
Cihan, A. F., Curto, A. G., Raza, S., Kik, P. G. & Brongersma, M. L. Silicon Mie resonators for highly directional light emission from monolayer MoS2. Nat. Photonics 12, 284 (2018).
Koenderink, A. F. Single-photon nanoantennas. ACS Photonics 4, 710 (2017).
Mouri, S. et al. Nonlinear photoluminescence in atomically thin layered WSe2 arising from diffusion-assisted exciton-exciton annihilation. Phys. Rev. B 90, 155449 (2014).
Danovich, M., Zólyomi, V., Fal’ko, V. I. & Aleiner, I. L. Auger recombination of dark excitons in WS2 and WSe2 monolayers. 2D Mater. 3, 035011 (2016).
Albella, P. et al. Low-loss electric and magnetic field-enhanced spectroscopy with subwavelength silicon dimers. J. Phys. Chem. C. 117, 13573 (2013).
Mignuzzi, S. et al. Nanoscale design of the local density of optical states. Nano Lett. 19, 1613 (2019).
Morozov, S. et al. Electrical control of single-photon emission in highly charged individual colloidal quantum dots. Sci. Adv. 6, eabb1821 (2020).
Liu, X. & Hersam, M. C. 2D materials for quantum information science. Nat. Rev. Mater. 4, 669 (2019).
Warburton, R. J. et al. Optical emission from a charge-tunable quantum ring. Nature 405, 926 (2000).
Chang, C.-H., Fan, X., Lin, S.-H. & Kuo, J.-L. Orbital analysis of electronic structure and phonon dispersion in MoS2, MoSe2, WS2 and WSe2 monolayers under strain. Phys. Rev. B 88, 195420 (2013).
Godde, T. et al. Exciton and trion dynamics in atomically thin MoSe2 and WSe2: effect of localization. Phys. Rev. B 94, 165301 (2016).
Fang, H. H. et al. Control of the exciton radiative lifetime in van der Waals heterostructures. Phys. Rev. Lett. 123, 067401 (2019).
Brash, A. J. et al. Light scattering from solid-state quantum emitters: beyond the atomic picture. Phys. Rev. Lett. 123, 167403 (2019).
Dey, P. et al. Optical coherence in atomic-monolayer transition-metal dichalcogenides limited by electron-phonon interactions. Phys. Rev. Lett. 116, 127402 (2016).
Klein, J. et al. Engineering the luminescence and generation of individual defect emitters in atomically thin MoS2. ACS Photonics 8, 669 (2021).
Parto, K., Azzam, S. I., Banerjee, K. & Moody, G. Defect and strain engineering of monolayer WSe2 enables site-controlled single-photon emission up to 150 K. Nat. Commun. 12, 3585 (2021).
Zotev, P. G. et al. Transition metal dichalcogenide dimer nano-antennas with ultra-small gaps. Preprint at https://arxiv.org/abs/2105.09201 (2021).
Verre, R. et al. Transition metal dichalcogenide nanodisks as high-index dielectric Mie nanoresonators. Nat. Nanotechnol. 14, 679 (2019).
Alexeev, E. M. et al. Imaging of interlayer coupling in van der Waals heterostructures using a bright-field optical microscope. Nano Lett. 17, 5342 (2017).
Castellanos-Gomez, A. et al. Deterministic transfer of two-dimensional materials by all-dry viscoelastic stamping. 2D Mater. 1, 011002 (2014).
Acknowledgements
L.S., P.G.Z., and A.I.T. thank the financial support of the European Graphene Flagship Project under grant agreements 881603 and EPSRC grant EP/S030751/1. L.S. and A.I.T. thank the European Union’s Horizon 2020 research and innovation programme under ITN Spin-NANO Marie Sklodowska-Curie grant agreement no. 676108. P.G.Z. and A.I.T. thank the European Union’s Horizon 2020 research and innovation programme under ITN 4PHOTON Marie Sklodowska-Curie grant agreement no. 721394. J.C., S.A.M., and R.S. acknowledge funding by EPSRC (EP/P033369 and EP/M013812). C.L.P., A.J.B., A.I.T., and A.M.F. acknowledge funding by EPSRC Programme Grant EP/N031776/1. S.A.M. acknowledges the Lee-Lucas Chair in Physics, the Solar Energies go Hybrid (SolTech) programme, and the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy - EXC 2089/1 - 390776260.
Author information
Authors and Affiliations
Contributions
L.S., P.G.Z., A.I.T., S.A.M., and R.S. conceived the idea of the experiment. L.S. and P.G.Z. fabricated WSe2 layers, transferred them on GaP nanoantennas, and carried out numerical modeling. L.S., P.G.Z., C.L.P., and A.J.B. carried out optical spectroscopy measurements on WSe2. J.C. fabricated GaP nanoantennas. J.C. and R.S. designed GaP nanoantennas. L.S. and E.M. designed and analyzed the rate equation model. L.S., P.G.Z., C.L.P., A.J.B., and A.I.T. analyzed optical spectroscopy data. S.A.M., R.S., A.M.F., and A.I.T. managed various aspects of the project. L.S., P.G.Z., and A.I.T. wrote the manuscript with contributions from all co-authors. A.I.T. oversaw the whole project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sortino, L., Zotev, P.G., Phillips, C.L. et al. Bright single photon emitters with enhanced quantum efficiency in a two-dimensional semiconductor coupled with dielectric nano-antennas. Nat Commun 12, 6063 (2021). https://doi.org/10.1038/s41467-021-26262-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-021-26262-3
This article is cited by
-
Programmable nanowrinkle-induced room-temperature exciton localization in monolayer WSe2
Nature Communications (2024)
-
Photoluminescence imaging of single photon emitters within nanoscale strain profiles in monolayer WSe2
Nature Communications (2023)
-
Chemomechanical modification of quantum emission in monolayer WSe2
Nature Communications (2023)
-
Tunable phononic coupling in excitonic quantum emitters
Nature Nanotechnology (2023)
-
Radiative suppression of exciton–exciton annihilation in a two-dimensional semiconductor
Light: Science & Applications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.