Abstract
The excellent optoelectronic performance of lead halide perovskites has generated great interest in their fundamental properties. The polar nature of the perovskite lattice means that electron-lattice coupling is governed by the Fröhlich interaction. Still, considerable ambiguity exists regarding the phonon modes that participate in this crucial mechanism. Here, we use multiphonon Raman scattering and THz time-domain spectroscopy to investigate Fröhlich coupling in CsPbBr3. We identify a longitudinal optical phonon mode that dominates the interaction, and surmise that this mode effectively defines exciton-phonon scattering in CsPbBr3, and possibly similar materials. It is additionally revealed that the observed strength of the Fröhlich interaction is significantly higher than the expected intrinsic value for CsPbBr3, and is likely enhanced by carrier localization in the colloidal perovskite nanocrystals. Our experiments also unearthed a dipole-related dielectric relaxation mechanism which may impact transport properties.
Similar content being viewed by others
Introduction
Lead halide perovskites are prime materials for optoelectronic applications, with promising results in solar cells and light-emitting devices. Despite the enthusiasm for these materials, relatively little is understood regarding the fundamental properties and mechanisms responsible for strong device performance. It has become widely accepted that the Fröhlich interaction is crucial in describing carrier behavior in the polar lattice of lead halide perovskites1,2,3,4,5,6,7. Most discussions on polaron physics in perovskites concern hybrid organic–inorganic lead iodides, from which highly efficient solar cells have been developed. These materials have a low exciton binding energy, enabling conduction with free electrons and holes that strongly polarize the lattice. However, some halide perovskite species, such as the fully inorganic CsPbBr38, or layered two-dimensional hybrid perovskites9 exhibit room-temperature stable excitons, which are highly desirable for light emission applications. Due to the high exciton binding energy, the Fröhlich interaction in these materials will produce excitonic polarons. Consequently, the interaction is expected to be very weak, as the phonon clouds of electron and hole polarons mutually compensate when overlapping. However, a relatively strong Fröhlich interaction occurs in CsPbBr3 nanostructures2,10, implying a reduced compensation of the electron and hole charges. It is also well-known that spectral broadening in lead halide perovskites at room temperature is dominated by the contribution of longitudinal optical (LO) phonons2,11,12, meaning that the Fröhlich mechanism defines the color purity of light-emitting devices under ambient conditions.
We remark that the underlying reason for the excellent efficiency of perovskite-based optoelectronic devices is still under debate13. A number of theories exist, including the scarcity of mid-gap defect states (which would otherwise impact the emission and carrier diffusion lengths through Shockley–Read–Hall recombination), the low rate of nonradiative recombination (determined by the low energies of involved phonons), or the contribution of polaronic carrier screening. Here we address the large polaron model, which appropriately describes carrier–LO phonon interactions in CsPbBr3 and related materials, as evidenced by the direct observation of the transient elastic strain fields associated with polaron formation14. We note, however, that anharmonic lattice vibrations may account for discrepancies between first-principles calculations within the Fröhlich model and experimentally measured carrier mobilities15,16,17,18. Additionally, strong anharmonicity has been shown to significantly modify the vibrational dynamics of lead halide perovskites19. Finally, phonon-defect scattering can lead to phonon dephasing, which may further disrupt the fully-harmonic picture of the perovskite lattice that the Fröhlich model assumes20. Regardless of such complications, we maintain that the Fröhlich interaction remains a driving mechanism in perovskite physics, which requires proper consideration. Indeed, it has been shown experimentally that the Fröhlich interaction shapes the room-temperature electronic band structure of CsPbBr3 (ref. 21), and is therefore essential in the description of carrier behavior in potential devices. A good starting point for probing the Fröhlich interaction is to conduct measurements at cryogenic temperatures, noting that the impact of the Fröhlich interaction on carrier behavior should only increase towards higher temperatures, as LO phonons become thermally available.
We note that the relative coupling strengths for different LO phonon modes are linked to the magnitude of the macroscopic electric field that each mode generates. Furthermore, if the relative contribution of one mode (LO or otherwise) dominates over those of all other phonons, the mode in question may be referred to as a killer mode22. This term was introduced for molecular semiconductors, where the phonon mode that contributes most strongly to electron–phonon coupling also drives thermal disorder. However, we do not consider thermal disorder here, instead defining a killer mode as a mode that dominates carrier–phonon scattering in a certain material. To illustrate the significance of killer mode identification, it is worth noting that, in the context of orthorhombic perovskites like CsPbBr3, the presence of such a mode would lead to great simplifications in the description of carrier–phonon coupling, reducing the number of significant contributions to a single one, from a total 60 normal modes23. Note that for an accurate experimental overview of carrier–phonon scattering, all modes must be detectable via the chosen technique. As such, conventional Raman scattering and other related methods with similar selection rules are typically insufficient in perovskites, due to the Raman inactivity of LO phonons in centro-symmetric crystals, which excludes the Fröhlich interaction from the scattering analysis.
Consequently, while carrier–LO phonon coupling via the Fröhlich interaction has been reported in many types of lead halide perovskites2,3,11,12,24,25,26,27,28, an experimental investigation of the full phonon spectrum has not been carried out thus far. It has been suggested in two separate studies that polaron formation in hybrid perovskites involves mainly low-frequency phonons related to the inorganic sublattice29,30. However, the investigated materials had a tetragonal crystal structure, as opposed to the orthorhombic structure of CsPbBr3, such that the relevance of these results in the inorganic species is not immediately apparent. Moreover, both studies employed the technique of femtosecond impulsive stimulated Raman spectroscopy which, once again, cannot directly probe the LO phonons that contribute to the Fröhlich interaction in centro-symmetric materials31. The contributions of various low-energy LO phonons to the Fröhlich interaction have been reported in lead halide perovskites32,33, but no real consensus exists regarding the modes which dominate the interaction. A somewhat definitive answer was reached for MAPbI3, where a single effective LO mode around 15 meV was identified as coupling to electronic motion34. Conversely, in CsPbBr3, two lower-energy modes of the lead halide sublattice at 3.7 and 6.3 meV were seen dominating the resonant Raman scattering spectrum at cryogenic temperatures35. However, the symmetry of these modes was not well established, and not all of the known normal modes of the perovskite lattice were observed. Moreover, an abnormal decrease of the scattering intensity with increasing temperature introduced additional uncertainty regarding the scattering mechanism responsible for the observed peaks. Further confusion on this topic is generated by the fact that the energies of LO phonons involved in temperature-dependent PL line broadening in CsPbBr3 do not always coincide with the LO phonon energies found in low-temperature PL spectra36. Additionally, the former are much larger than the energies of the two modes mentioned above. Consequently, the topic of Fröhlich-active modes in inorganic lead halide perovskites remains open, and requires further analysis via a suitable experimental technique. Note that, under certain conditions, resonant Raman scattering spectroscopy can be used to probe both Raman-active and Raman-inactive modes37, and is thus suitable for identifying the most significant Fröhlich-active modes in a given material.
We further note that the strength of the Fröhlich interaction in a material is directly linked to the polar nature of its crystal lattice. In a highly polar material the Coulomb field of a carrier (or exciton) couples more easily to the polar vibrations (i.e. LO phonons) of the lattice, resulting in strong Fröhlich coupling. The static and high-frequency values of the dielectric function provide a means of quantifying the polar nature of a material, such that further insight into the Fröhlich interaction can be gained via dielectric characterization.
In this work, we employ a combination of resonant multiphonon Raman scattering (MPRS) and THz time-domain spectroscopy (THz-TDS—Supplementary Note 8) to describe the carrier–LO phonon interaction in CsPbBr3 NCs. We record the full phonon spectrum of the material, including both Raman-active and inactive modes. We observe an LO phonon mode that dominates over all carrier–phonon interactions identifying it as a killer mode. Furthermore, the strength of the Fröhlich interaction for the mode in question is quantified and compared to theoretical expectations, given the dielectric response of the material. It becomes clear that the observed low-temperature exciton–phonon interactions cannot simply be due to the polar nature of the lattice. By means of a well-established model, we reveal that these observations can be fully explained by localization which enhances the net charge density of the exciton. Finally, we discuss the unexpected presence of a low-frequency dielectric response of CsPbBr3 at room temperature. We tentatively explain the observation as a universal dielectric relaxation linked to the reorientation of dynamic dipoles which may stem from surface defects. We remark that the Fröhlich interaction in CsPbBr3 nanocrystals (NCs) is representative also for bulk systems and, moreover, that there should be no significant structural differences between the CsPbBr3 lattices at cryogenic and room temperature (Supplementary Note 5). Consequently, our analysis provides a general view of the Fröhlich interaction in CsPbBr3 and related materials.
Results
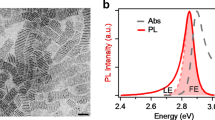
CsPbBr3 NCs were synthesized via a hot injection method. Initial characterization was conducted via TEM, as well as PL, and PLE spectroscopy, and the results are shown in Supplementary Fig. 1. The 4 K PL data suggests that the NCs exhibit only weak quantum confinement. We note that, at room temperature and below, the crystal structure of CsPbBr3 is orthorhombic, both in bulk and NC form, whereas all crystal phase transitions occur exclusively above room temperature2,15,38.
Multiphonon Raman scattering
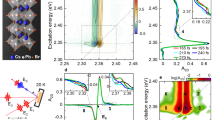
The results of MPRS on CsPbBr3 NCs at 3.8 K are shown in Fig. 1a. The MPRS spectrum shows several intense peaks shifted by near multiples of 155 cm−1 (19.2 meV). These represent the multiphonon progression of an LO phonon mode, labeled M0, also observed in previous studies2,12,39,40,41. In the “Discussion” section it will be shown that the observation of mode M0 in this study is strictly linked to the resonant experimental conditions in conjunction with symmetry-breaking factors. As is typical of multiphonon Raman scattering via the Fröhlich interaction37, the overtone energies were slightly lower than exact multiples of the phonon energy, each peak exhibiting a red-shift smaller than their respective FWHM. This is a consequence of the forbidden nature of Fröhlich scattering at the center of the Brillouin zone (see “Discussion”), such that the observed peaks are the result of scattering by lower-energy LO phonons of non-zero momentum. The broadening of the overtones with increasing order (Fig. 1a, inset) suggests that the multiphonon spectrum is produced by resonant Raman scattering, as opposed to hot luminescence (Supplementary Note 4). The M0 overtones have an asymmetric lineshape, presenting increased scattering on the lower-energy side. Such asymmetry of Raman scattering peaks in NCs has previously been linked to Fano interference42, quantum confinement43, or scattering by lower-energy phonons, related to the NC surface44,45.
a MPRS spectrum of CsPbBr3 NCs at 3.8 K. The labels represent the different phonon modes observed and their combinations. The inset shows an increase of the FWHM for consecutive overtones. The FWHM values and their respective errorbars were obtained via Gaussian fitting of each peak. The red line is a guide to the eye. b Experimental and calculated intensities of the M0 replicas in a. Calculations assume S = 0.39, σ = 32.5 meV, Γ0 = 1 meV, and \({E}_{g}^{0}=2.375\) eV. The maximum relative measurement error corresponds to the third-order replica, and is around 10%, due to the subtraction of the PL background. The sum of squared residuals for the fit is 0.005.
At lower energies in the spectrum, three low-intensity peaks are present, also observed in Raman spectroscopy of single crystal CsPbBr315. The low-energy modes at 28 cm−1 (3.5 meV), 53 cm−1 (6.6 meV), and 75 cm−1 (9.3 meV) are labeled M1, M2, and M3, respectively. For a tentative symmetry assignment of the low-energy modes, we compare the Raman spectrum of CsPbBr3 with the known vibrational spectrum of the orthorhombic perovskite CsPbCl346. When the two materials have the same crystal phase, the phonon modes of CsPbCl3 all have equivalent modes in CsPbBr3. The mode energies and splittings are renormalized according to the differences in ionic mass and octahedral rotation angles, respectively. The renormalized mode energies can be obtained by modeling the phonons as harmonic vibrations of chains of alternating lead and halogen atoms. While the proposed model is quite simple, we find very good agreement between the CsPbCl3 phonon energies adjusted with respect to a change in anion from Cl to Br and the energies of the CsPbBr3 peaks observed in the spectrum of Fig. 1a. We thus tentatively identify M1, M2, and M3 as TO modes for CsPbBr3. Finally, second-order Raman scattering peaks are also observed in the MPRS spectrum. The second-order peaks involve combinations of mode M0 and each of the three other modes (correspondingly marked M0 + M1, M0 + M2, and M0 + M3 in Fig. 1a).
Before proceeding we must note that the CsPbX3 lattice also supports LO modes at energies below M032,46,47. These additional modes should be energetically close to the non-polar TO modes M1, M2, and M3, and may therefore be hidden in the measured spectrum. However, strong Fröhlich scattering comparable to that involving mode M0 should still produce visible overtones of these hidden modes. In the MPRS spectrum, no multiphonon progressions are observed in the low-energy range, meaning that M0 must be the dominant contributor to the Fröhlich interaction in CsPbBr3. Furthermore, since scattering by M0 clearly dominates the MPRS spectrum, which contains contributions from both Raman-allowed and forbidden modes, M0 in fact represents the strongest overall contributor to carrier–phonon scattering (Fröhlich or otherwise) in CsPbBr3, and thus behaves as a killer phonon mode in the material.
Terahertz time-domain spectroscopy
In order to quantify the polar nature of CsPbBr3, THz-TDS analysis was used to determine the frequency-dependent real and imaginary dielectric function of CsPbBr3 NCs at room temperature. The results are shown in Fig. 2a. A trusted frequency range, with a strong signal-to-noise ratio, is defined between 0.2 and 1.7 THz (Supplementary Fig. 7). The experimental data are modeled with a modified Debye–Lorentz dependence, where the first term corresponds to a low-frequency dipolar relaxation48,49 and the second term represents a lattice resonance:
Here εS and ε∞ are the static and high-frequency dielectric constants, while \({\varepsilon }_{\infty }^{\mathrm {CD}}\) is an intermediate value of the dielectric function, which would constitute the high-frequency value in the absence of the Lorentz term. The Debye-like term is known as a Cole–Davidson dependence, and contains a skewing factor β which accounts for a distribution of relaxation times τ. Finally, ω0 and γ represent the Lorentzian resonance frequency and damping factor, respectively. As shown in Fig. 2b, the standard Debye model fails to accurately reproduce the low-frequency dielectric function. The Cole–Davidson skewing factor 0 < β < 1 stretches out the relaxation towards higher frequencies, producing a better fit of the experimental data than the Debye model.
a Measured real (red) and imaginary (blue) dielectric function of CsPbBr3 NCs from THz-TDS. The data are fitted with Eq. (1). b Comparison of the Debye and Cole Davidson model for the real dielectric function. In this subfigure, both models are restricted to the low-frequency region, thereby excluding the Lorentz resonance. The Cole–Davidson fit corresponds to τ = 21 ps and β = 0.71, giving a sum of squared residuals of 11.5, compared to 77.8 for the Debye model. Errors in the THz-TDS analysis are discussed in Supplementary Note 7.
Note that the measurement data do not cover the entire frequency range of the dielectric relaxation, such that the time constant τ is not well-defined. To more accurately determine the relaxation time, data points corresponding to lower frequencies must be added. To this end, the experimentally obtained dielectric function of CsPbBr3 in the MHz range is used here. The value of the real dielectric function at 1.08 MHz, of \({\varepsilon }_{1.08{\mathrm {MHz}}}^{\prime}=20.5\) (ref. 50), is added to the measurement data, thereby obtaining τ = 32 ± 1 ps, and a skewing factor β = 0.61 ± 0.01 (Fig. 2a).
The low-frequency relaxation is not observed in the reference measurement of the solvent (Supplementary Fig. 9) and is thus definitively attributed to the presence of CsPbBr3 NCs in the measured sample. The Lorentz resonance is situated at 2.02 ± 0.01 THz. While this lies outside the trusted frequency range, the feature is also convincingly attributed to the presence of CsPbBr3 NCs in the sample solution (Supplementary Fig. 9). Moreover, the corresponding energy is close to an optical phonon energy of CsPbBr3, at 70–80 cm−1 (2.1–2.4 THz)15.
From our model we obtain the static and high-frequency dielectric constants εS = 20.5 ± 0.2 and ε∞ = 4.8 ± 0.1. The value of ε∞ is consistent with previous calculations3,8,51 and experimental results52, while εS is fixed by the experimental value at 1.08 MHz50.
Discussion
In interpreting the MPRS results, we note once again that non-resonant Raman scattering involving Fröhlich-active (i.e. polar) LO modes (like M0) is symmetry-forbidden in crystals with a center of inversion, such as orthorhombic lead halide perovskites. Specifically, while modes M1, M2, and M3 are non-polar TO phonons which are Raman-active, M0 scattering remains negligible under non-resonant conditions15. However, under resonant conditions, the energy of incoming photons corresponds to that of excited electronic states, which couple to LO phonons through the Fröhlich interaction. Strong forbidden multiphonon scattering involving LO phonons thus becomes possible in resonant Raman experiments, thereby explaining the high scattering intensity of the peaks involving mode M0 in our MPRS spectrum37. Note that, even at resonance, Raman scattering by a single LO phonon must obey the condition k ≃ 0, and remains nominally forbidden. However, this restriction is lifted by symmetry-breaking factors53. One commonly considered factor are defects, which relax crystal momentum conservation, allowing scattering to occur away from the center of the Brillouin zone. As shallow trapping of carriers has indeed been reported in CsPbBr3 NCs2,54,55, defects may well be the reason for the occurrence of first-order forbidden scattering by M0 phonons in our experiment.
A quantitative analysis of Fröhlich scattering in CsPbBr3 can be obtained by considering the relative cross-sections of the M0 overtones. The relative cross-sections are estimated through a configuration-coordinate model44,53,56 (Supplementary Note 6). The n-phonon Raman cross-section at low temperature is then44:
where μ is the dipole moment of the electronic transition, Eg is the excitonic transition energy, ℏωL is the energy of incident photons, ℏω0 is the LO phonon energy, and Γ0 is the single-NC PL linewidth. The brackets 〈e, u∣g, v〉 are overlap integrals between vibrational levels of the ground and excited electronic states, and are defined for u ≥ v as
while for u < v, the identity 〈e, v∣g, u〉 = (−1)u+v〈e, u∣g, v〉 holds. In the above equation, S is the so-called Huang–Rhys factor, which is used to quantify the strength of carrier–phonon coupling for a given mode (Supplementary Information, Section 5).
The relative intensities of the M0, 2M0, and 3M0 lines are estimated using Eq. (2), which is integrated over a Gaussian distribution of Eg (Supplementary Note 6), with a variance σ comparable to that of the 4 K PL lineshape. The parameters used in the calculation are given in Table 1.
The low-temperature PL linewidth of single CsPbBr3 NCs is typically Γ0 < 2 meV57,58, and thus the assumption of Γ0 ≃ 1 meV is reasonable. The Huang–Rhys factor, S = 0.39, is obtained via nonlinear least-squares regression for the relative intensities of the M0, 2M0, and 3M0 peaks, and excellently reproduces the experimental progression, as shown in Fig. 1b. This value of S is in good agreement with previous reports2,10. Note that any choice of the estimated parameters within the experimental uncertainty produces the same order of magnitude of S (Supplementary Fig. 4). Finally, we note that one previous study has shown that phonon replicas may appear in the low-temperature PL spectrum of CsPbBr3 NCs with a similar Huang–Rhys factor2. We remark however that the linewidth of our PL emission (Supplementary Fig. 1) is twice as large as that in the respective reference. Since phonon replicas are only visible if the linewidth is sufficiently low in comparison to the phonon energy, a doubling of the linewidth can thus completely erase any trace of multiple PL bands, even for much higher S values than the one found here59.
By definition, the Fröhlich interaction couples the Coulomb field of a carrier with the macroscopic electric field of LO phonons, forming a lower-energy, heavier quasiparticle called a polaron. The intrinsic carrier–LO phonon coupling strength is given by the Fröhlich constant60:
which determines the self-trapping energy and enhanced mass of a carrier of effective mass m interacting with the lattice61,62. The quantity \(\frac{1}{\bar{\varepsilon }}=(\frac{1}{{\varepsilon }_{\infty }}-\frac{1}{{\varepsilon }_{\mathrm S}})\) is known as the dielectric contrast, and effectively quantifies the ionic nature of a material, thereby determining the strength of the carrier–lattice interaction. Using experimental values for εS, ε∞, and ℏω0, along with the carrier effective masses given by Yettapu et al.51, of me = 0.22 and mh = 0.24, the Fröhlich constant in CsPbBr3 is α ≃ 2 for both electrons and holes. While in the case of excitons the reduced mass is sometimes used to calculate the Fröhlich constant, this approach does not provide an accurate picture of the behavior and physics of excitonic polarons. Still, any argument regarding the strength of electron–phonon coupling remains qualitatively valid for exciton–phonon coupling as well, keeping in mind that the latter is likely weaker than the former, due to the compensation of the electron and hole charges upon exciton formation, which diminishes their respective phonon clouds. We further note that the Huang–Rhys factor is directly proportional to the Fröhlich constant (Supplementary Note 6). Additionally, the magnitude of the Huang–Rhys factor is determined by a summation over all available phonon wave vectors63. In the case of free electron or hole polarons, the phonon occupation is determined by the thermal energy and polaron mass (Supplementary Eqs. (4) and (5)). At the 3.8 K corresponding to our MPRS experiment, to reach the value S = 0.39, the low thermal energy must be compensated by an absurdly large polaron mass, more than 20 times the bare electron mass. This would require α ≫ 160,62,64. For an excitonic polaron, an even greater mass enhancement is likely necessary, as suggested above. For CsPbBr3, the value of α ≃ 2 corresponds to an intermediate carrier–lattice coupling regime, where the effective mass correction remains relatively small. Cyclotron resonance measurements and estimations of the bare carrier mass via density functional theory suggest that the polaron is only ~50% heavier21,51,65,66, which is insufficient to account for the measured Huang–Rhys factor, instead resulting in S ≃ 0.07.
Note that the requirement of an unrealistic carrier mass is unlikely to result from a faulty estimation of εS and ε∞, since the values used here are reasonably close to previous reports. Furthermore, the polaron mass enhancement is linearly dependent on \(\alpha \propto {\bar{\varepsilon }}^{-1}\), which is a relatively slowly-varying function of the two dielectric constants. Finally, we recall from the introduction that anharmonicity effects may influence carrier–phonon scattering in lead halide perovskites15,16,17,18. In fact, the anharmonic nature of the CsPbBr3 lattice at room temperature may even be linked to strong self-trapping of excitonic polarons67. However, strong anharmonic contributions at room temperature are known to give rise to a strong central peak in the Raman spectrum of a material—an effect that has not been observed at cryogenic temperatures in lead halide perovskites, neither in previous experiments below 77 K15,68,69, nor in our own experiment, presented here. We can therefore surmise that the lattice anharmonicity is significantly reduced at the low temperature of our experiment (3.8 K), and thus the S factor cannot be intrinsically accounted for.
We therefore look for extrinsic factors that may enhance the Fröhlich interaction. The occurrence of first-order forbidden LO phonon scattering in our MPRS experiment is thus very telling, as it suggests that the exciton–phonon interaction involves a breaking of the lattice symmetry, likely in the presence of defects. Models involving defect-localized charges have been used extensively to explain strong Fröhlich interactions in nanostructures44,56,70,71,72,73,74, as well as in the bulk53,63. Localization is also known to enhance Fröhlich coupling in bulk CsPbBr375, thus supporting the implementation of such a model in describing our observations. The broken lattice periodicity at a defect enables the relaxation of wave vector conservation rules, thereby enabling carrier–phonon coupling with k > 063. In this case, the Huang–Rhys factor is determined by the extent of the exciton charge distribution in Fourier space, which is enhanced by the trapping potential (Supplementary Note 6). To estimate the Huang–Rhys factor in the case of a defect-bound exciton, a model charge distribution may be used, where one carrier is pinned, while its counterpart is delocalized over the NC44,56,71,72. The accessible volume in Fourier space is then defined by the average NC size (~11 ± 3 nm), and the Huang–Rhys factor is S = 0.42 ± 0.11, in excellent agreement with our experimental result. We therefore argue that exciton localization can fully explain the strong low-temperature Fröhlich interaction in CsPbBr3.
It must however be emphasized that M0 is in fact a normal mode of the orthorhombic perovskite lattice, meaning it does not arise due to any distortion generated by defects, but occurs naturally in the pristine material as well. Furthermore, exciton localization modifies only the carrier contribution to the Fröhlich carrier–lattice interaction (Supplementary Note 6), meaning that the macroscopic electric field of each LO phonon remains unaffected. That means that a free carrier (or, indeed, any other type of carrier) will also interact most strongly with mode M0, out of all available LO modes. The dominance of M0 over the Fröhlich interaction is thus not exclusively defect-related instead reflecting the intrinsic properties of the CsPbBr3 system.
Finally, the low-frequency dielectric response of CsPbBr3 has significant influence on carrier transport, even beyond the Fröhlich interaction. This is because dielectric relaxations below the lattice resonance frequency are attributed to dipolar reorientation and ionic motion, leading to carrier screening, which affects mobility.6,7,76 In Fig. 2a, we observed a relaxation in the sub-THz range, which results in a doubling of the dielectric loss over less than one decade of frequency. A similar relaxation has been measured in the hybrid perovskite MAPbBr3, and it has been attributed to the rotation of MA+ cations, which possess an intrinsic dipole moment6,7,76. It has been suggested that a similar response should be observable in the fully inorganic CsPbBr3, even in the absence of rotating dipoles, the response arising instead from the rattling motion of the Cs+ cations in their atomic lattice positions6. Indeed, collective displacements of lattice ions in many ionic materials lead to so-called configurational tunneling, which produces what has been referred to as a universal dielectric response below the lattice frequency48,49. However, recent results on the dielectric response of single crystals77 suggest that such a relaxation is completely absent in fully inorganic halide perovskites, while our measurements clearly show that a low-frequency response is in fact present in CsPbBr3 NCs. The absence of the relaxation in bulk single crystals indicates that this response cannot be related to the Cs+ ion motion. We therefore propose that the low-frequency relaxation we observed is produced by configurational tunneling involving a different entity. The response may, for example, be associated with defects, related to the NC surface. Note that most defects in the perovskite lattice have a favorable energetic position close to the edges of the valence and conduction bands78, and do not increase the rate of nonradiative recombination. Therefore the proposition that defects may contribute to the observed dielectric response does not contradict the excellent PL efficiency of CsPbBr3 NCs. The link between the dipolar relaxation and lattice defects in CsPbBr3 is supported by molecular dynamics simulations, which have shown that the positions of lattice ions at halide vacancies fluctuate on a similar time scale (5 ps)79 as our measured relaxation (τ = 32 ps) (by comparison, relaxation due to Cs+ motion occurs on a time scale of around 100 fs15). The charge density around a defect depends strongly on the positions of neighboring ions, such that these fluctuations may induce a dipole which can respond to an electromagnetic field, as required for configurational tunneling. We further note that in the current scenario, the analysis was conducted in such a way as to extract only the response of the perovskite lattice to the applied field (Supplementary Note 8). That is, the organic ligands were excluded from the volume fraction of the NC inclusions. Consequently, the dipolar relaxation is not attributable to the ligands. Finally, we note that the possible involvement of defects in the enhancement of the Fröhlich interaction as well as the generation of a dielectric response does not imply that the two effects are inter-related. This is immediately apparent when considering that the first mechanism describes the effects of localization on the carrier–phonon interaction, while the defect itself may be substituted by other symmetry-breaking factors. Conversely, the second mechanism is strictly related to the dynamics of defect-neighboring ions, and not the carriers themselves.
In conclusion, we have shown that the LO phonon mode around 20 meV acts as a killer mode, being chiefly responsible for carrier–phonon scattering in CsPbBr3. The low-temperature Huang–Rhys factor S ≃ 0.39 was determined from the relative resonant Raman cross-section of consecutive overtones. The dielectric response of CsPbBr3, investigated by means of THz-TDS, indicates that the intrinsic strength of the Fröhlich interaction is incompatible with the low-temperature Huang–Rhys factor. We have shown that localization may enhance carrier–phonon coupling sufficiently to explain this experimental observation. As the Huang–Rhys factor obtained here falls within the typical range of reported values for lead halide perovskites, it thus becomes necessary to consider that such enhancements may in fact play a role in many reported cases of carrier–LO phonon coupling in this class of materials.
Concerning the significance of mode M0 in the context of polaron formation, we recall the recent report that the self-trapping of excitons in CsPbBr3 NCs involves two lower-energy phonon modes35, which seems to contradict our results. We note however that the spectrum recorded in the reference was likely incomplete, due to the absence of the resonance with mode M0. We hereby underscored the importance of recording the full phonon spectrum in order to properly describe carrier–phonon interactions in any material, as an incomplete analysis can produce misleading conclusions. In the current study we managed to alleviate the existing confusion in the field by recording the full phonon spectrum of CsPbBr3, including both Raman-allowed and Raman-forbidden modes over a broad energy range. While scattering via M0 has also been observed, to a certain degree, in other experiments15,40, the forbidden nature of LO phonon scattering resulted in a weak Raman signal and could not provide any indication of the strength of the Fröhlich interaction. By contrast, our experiment was done under resonant conditions, and the symmetry-related selection rules were broken. This fully enabled the observation of forbidden Fröhlich scattering, even in the first order, thereby allowing the quantification of the strength of carrier–lattice interaction. As such, we were able to unambiguously identify M0 as the main contributor to the Fröhlich interaction, and thereby polaron formation and scattering in CsPbBr3. This fact should henceforth be considered in the interpretation of scattering-related experiments and polaronic phenomena in this material and likely other perovskite species with an orthorhombic structure.
Additionally, the low-frequency dielectric response of CsPbBr3 merits consideration. Here we tentatively linked the observed Debye-like dielectric relaxation to surface defects, due to the low probability of finding internal imperfections under a NC geometry. Presumably, a similar response can arise from a wide range of defects occurring in the CsPbBr3 lattice. Consequently, defect-prone materials such as polycrystalline thin films may present a similar dielectric relaxation, which would have an impact on carrier transport, by modifying the amount of carrier screening from defects. A more focused analysis should be conducted to determine whether such a relaxation does in fact occur in other systems, whether its effect on carrier transport is considerable, and whether this effect is positive or negative.
Ultimately, different applications require different material characteristics, and improving the performance of any device is fully reliant on a good understanding of the basic properties of the materials used. For the intended optoelectronic applications of CsPbBr3, this involves knowledge of carrier relaxation, recombination, and transport, all of which are inextricably linked to the Fröhlich interaction. As such, the defining features of this interaction identified here constitute a step towards the full understanding of CsPbBr3, and possibly other perovskite species, in the interest of developing novel optoelectronic devices.
Methods
Materials used for CsPbBr3 NC synthesis
Cesium carbonate (Cs2CO3, Sigma-Aldrich, 99.9%), 1-octadecene (ODE, Sigma-Aldrich, 90%), oleic acid (OA, Sigma-Aldrich, 90%), lead bromide (PbBr2, Sigma-Aldrich, 99.999%), oleylamine (OLAM, Sigma-Aldrich, 70%), anhydrous toluene (Sigma-Aldrich, 99.8%), and anhydrous hexane (Sigma-Aldrich, 95%) were used. OLAM and OA were degassed under reduced pressure at 120 ∘C for 1 h prior to use. All other chemicals were used as received.
Sample fabrication and measurements
NCs were synthesized via the reaction of Cs-oleate with PbBr2 in octadecene at 140–200 ∘C. The NCs were stabilized in suspension by adding a 1:1 mixture of oleylamine and oleic acid. The obtained solution was centrifuged for 3 min at 10,000 r.p.m. and the colored supernatant was discarded. Then, 300 μL of hexane was added and the NCs were dispersed using a vortex mixer. Subsequently, the suspension was again centrifuged for 3 min at 10,000 r.p.m., after which the precipitate, containing larger NCs and agglomerates, was discarded. Another 300 μL of hexane was added to the supernatant, resulting in a colloidal dispersion of CsPbBr3 NCs. Raman scattering measurements were performed at the High Field Magnet Laboratory (Radboud University). To achieve low temperatures, samples were placed in a liquid 4He optical cryostat (Microstat Oxford). Samples were probed in backscattering geometry with an incident laser line at 2.54 eV (488 nm) from a solid-state laser, well above the low-temperature NC emission energy at 2.38 eV (521 nm). The scattered light was filtered by a RazorEdge ultra steep long-pass edge filter and analyzed by a 1 m long single grating (1200 gr/mm) FHR-1000 Horiba spectrometer equipped with a nitrogen-cooled PyLoN CCD camera (Princeton Instruments). Dielectric spectroscopy was carried out via THz-TDS at room temperature, on a colloidal CsPbBr3 NC sample dispersed in hexane, with an average NC size of 9.5 ± 1.3 nm. A focused THz wave packet was used to probe a high-density colloidal suspension of CsPbBr3 NCs, and the frequency-dependent transfer function of the sample was analyzed in order to extract the complex refractive index \(\tilde{n}=n+i\kappa\), where n is the real refractive index and κ is the extinction coefficient. The technique is described in detail in Supplementary Note 8.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request. Source data are provided with this paper.
References
Zheng, F. & Wang, L. Large polaron formation and its effect on electron transport in hybrid perovskites. Energy Environ. Sci. 12, 1219–1230 (2018).
Iaru, C. M., Geuchies, J. J., Koenraad, P. M., Vanmaekelbergh, D. & Silov, A. Y. Strong carrier-phonon coupling in lead halide perovskite nanocrystals. ACS Nano 11, 11024–11030 (2017).
Miyata, K. et al. Large polarons in lead halide perovskites. Sci. Adv. 3, e1701217 (2017).
Zhu, X. Y. & Podzorov, V. Charge carriers in hybrid organic-inorganic lead halide perovskites might be protected as large polarons. J. Phys. Chem. Lett. 6, 4758–4761 (2015).
Herz, L. M. Charge-carrier mobilities in metal halide perovskites: fundamental mechanisms and limits. ACS Energy Lett. 2, 1539–1548 (2017).
Bonn, M., Miyata, K., Hendry, E. & Zhu, X.-Y. Role of dielectric drag in polaron mobility in lead halide perovskites. ACS Energy Lett. 2, 2555–2562 (2017).
Anusca, I. et al. Dielectric response: answer to many questions in the methylammonium lead halide solar cell absorbers. Adv. Energy Mater. 7, 1700600 (2017).
Protesescu, L. et al. Nanocrystals of cesium lead halide perovskites (CsPbX3, X = Cl, Br, and I): novel optoelectronic materials showing bright emission with wide color gamut. Nano Lett. 15, 3692–3696 (2015).
Pedesseau, L. et al. Advances and promises of layered halide hybrid perovskite semiconductors. ACS Nano 10, 9776–9786 (2016).
Lao, X. et al. Anomalous temperature-dependent exciton-phonon coupling in cesium lead bromide perovskite nanosheets. J. Phys. Chem. C 123, 5128–5135 (2019).
Wright, A. D. et al. Electron-phonon coupling in hybrid lead halide perovskites. Nat. Commun. 7, 11755 (2016).
Shinde, A., Gahlaut, R. & Mahamuni, S. Low-temperature photoluminescence studies of CsPbBr3 quantum dots. J. Phys. Chem. C 121, 14872–14878 (2017).
Kirchartz, T., Markvart, T., Rau, U. & Egger, D. A. Impact of small phonon energies on the charge-carrier lifetimes in metal-halide perovskites. J. Phys. Chem. Lett. 9, 939–946 (2018).
Guzelturk, B. et al. Visualization of dynamic polaronic strain fields in hybrid lead halide perovskites. Nat. Mater. 20, 618–623 (2021).
Yaffe, O. et al. Local polar fluctuations in lead halide perovskite crystals. Phys. Rev. Lett. 118, 136001 (2017).
Gold-Parker, A. et al. Acoustic phonon lifetimes limit thermal transport in methylammonium lead iodide. Proc. Natl Acad. Sci. USA 115, 11905–11910 (2018).
Gehrmann, C. & Egger, D. A. Dynamic shortening of disorder potentials in anharmonic halide perovskites. Nat. Commun. 10, 3141 (2019).
Lahnsteiner, J. & Bokdam, M. Anharmonic lattice dynamics in large thermodynamic ensembles with machine-learning force fields: the breakdown of the phonon quasiparticle picture in CsPbBr3. Preprint at https://arxiv.org/abs/2101.06099 (2021).
Debnath, T. et al. Coherent vibrational dynamics reveals lattice anharmonicity in organic-inorganic halide perovskite nanocrystals. Nat. Commun. 12, 2629 (2021).
Hase, M., Ishioka, K., Kitajima, M., Ushida, K. & Hishita, S. Dephasing of coherent phonons by lattice defects in bismuth films. Appl. Phys. Lett. 76, 1258–1260 (2000).
Puppin, M. et al. Evidence of large polarons in photoemission band mapping of the perovskite semiconductor CsPbBr3. Phys. Rev. Lett. 124, 206402 (2000).
Schweicher, G. et al. Chasing the "killer” phonon mode for rational design of low-disorder, high-mobility molecular semiconductors. Adv. Mater. 31, 1902407 (2019).
Islam, M. A., Rondinelli, J. M. & Spanier, J. E. Normal mode determination of perovskite crystal structures with octahedral rotations: theory and applications. J. Phys. Condens. Matter 25, 175902 (2013).
Ghosh, S. et al. Phonon coupling with excitons and free carriers in formamidinium lead bromide perovskite nanocrystals. J. Phys. Chem. Lett. 9, 4245–4250 (2019).
Saran, R., Heuer-Jungemann, A., Kanaras, A. G. & Curry, R. J. Giant bandgap renormalization and exciton-phonon scattering in perovskite nanocrystals. Adv. Opt. Mater. 5, 1700231 (2017).
Chen, Z. et al. Remote phononic effects in epitaxial ruddlesden-popper halide perovskites. J. Phys. Chem. Lett. 9, 6676–6682 (2018).
Straus, D. B. et al. Direct observation of electron-phonon coupling and slow vibrational relaxation in organic-inorganic hybrid perovskites. J. Am. Chem. Soc. 138, 13798–13801 (2016).
Gong, X. et al. Electron-phonon interaction in efficient perovskite blue emitters. Nat. Mater. 17, 550–556 (2018).
Park, M. et al. Excited-state vibrational dynamics toward the polaron in methylammonium lead iodide perovskite. Nat. Commun. 9, 2525 (2018).
Batignani, G. et al. Probing femtosecond lattice displacement upon photo-carrier generation in lead halide perovskite. Nat. Commun. 9, 1971 (2018).
Ishioka, K., Basak, A. K. & Petek, H. Allowed and forbidden Raman scattering mechanisms for detection of coherent LO phonon and plasmon-coupled modes in GaAs. Phys. Rev. B 84, 235202 (2011).
Fu, M. et al. Unraveling exciton-phonon coupling in individual FAPbI3 nanocrystals emitting near-infrared single photons. Nat. Commun. 9, 3318 (2018).
Thouin, F. et al. Phonon coherences reveal the polaronic character of excitons in two-dimensional lead-halide perovskites. Nat. Mater. 18, 349–356 (2019).
Lan, Y. et al. Ultrafast correlated charge and lattice motion in a hybrid metal halide perovskite. Sci. Adv. 5, eaaw5558 (2019).
Ma, X. et al. Local phonon modes concerned with the self-trapped exciton state in CsPbBr3 nanocrystals. J. Phys. Chem. C 124, 27130–27135 (2020).
Manoli, A. et al. Surface functionalization of CsPbBr3 nanocrystals for photonic applications. ACS Appl. Nano Mater. 4, 5084–5097 (2021).
Cardona, M. & Güntherodt, G. Light Scattering in Solids II. Basic Concepts and Instrumentation (Springer, 1982).
Cottingham, P. & Brutchey, R. L. On the crystal structure of colloidally prepared CsPbBr3 quantum dots. Chem. Commun. 52, 5246–5249 (2016).
Sebastian, M. et al. Excitonic emissions and above-band-gap luminescence in the single-crystal perovskite semiconductors CsPbBr3 and CsPbCl3. Phys. Rev. B 92, 235210 (2015).
Stoumpos, C. C. et al. Crystal growth of the perovskite semiconductor CsPbBr3: a new material for high-energy radiation detection. Cryst. Growth Des. 13, 2722–2727 (2013).
Ramade, J. et al. Exciton-phonon coupling in a CsPbBr3 single nanocrystal. Proc. Natl Acad. Sci. USA 115, 11905–11910 (2018).
Sagar, D. M. et al. Quantum confined electron-phonon interaction in silicon nanocrystals. Nano Lett. 15, 1511–1516 (2015).
Campbell, I. H. & Fauchet, P. M. The effects of microcrystal size and shape on the pne phonon raman spectra of crystalline semiconductors. Solid State Commun. 58, 739–741 (1986).
Klein, M. C., Hache, F., Ricard, D. & Flytzanis, C. Size dependence of electron-phonon coupling in semiconductor nanospheres: the case of CdSe. Phys. Rev. B 42, 11123 (1990).
Lin, C., Kelley, D. F., Rico, M. & MyersKelley, A. The “surface optical” phonon in CdSe nanocrystals. ACS Nano 8, 3928–3938 (2014).
Calistru, D. M., Mihut, L., Lefrant, S. & Baltog, I. Identification of the symmetry of phonon modes in CsPbCl3 in phase IV by Raman and resonance-Raman scattering. J. Appl. Phys. 82, 5391–5395 (1997).
Pérez-Osorio, M. A. et al. Vibrational properties of the organic-inorganic halide perovskite CH3NH3PbI3 from theory and experiment: factor group analysis, first-principles calculations, and low-temperature infrared spectra. J. Phys. Chem. C 119, 25703–25718 (2015).
Jonscher, A. K. A new understanding of the dielectric relaxation of solids. J. Mater. Sci. 16, 2037–2060 (1981).
Jonscher, A. K. The ‘universal’ dielectric response. Nature 267, 673–679 (1977).
Govinda, S. et al. Behavior of methylammonium dipoles in MAPbX3 (X = Br and I). J. Phys. Chem. Lett. 8, 4113–412 (2017).
Yettapu, G. R. et al. Terahertz conductivity within colloidal CsPbBr3 perovskite nanocrystals: remarkably high carrier mobilities and large diffusion lengths. Nano Lett. 16, 4838–4848 (2016).
Dirin, D. N., Cherniukh, I., Yakunin, S., Shynkarenko, Y. & Kovalenko, M. V. Solution-grown CsPbBr3 perovskite single crystals for photon detection. Chem. Mater. 28, 8470–8474 (2016).
Merlin, R. et al. Multiphonon processes in YbS. Phys. Rev. B 17, 4951–4958 (1978).
Dey, A., Rathod, P. & Kabra, D. Role of localized states in the photoluminescence dynamics of high optical gain CsPbBr3 nanocrystals. Adv. Opt. Mater. 6, 1800109 (2018).
Seth, S., Ahmed, T. & Samanta, A. Photoluminescence flickering and blinking of single CsPbBr3 perovskite nanocrystals: revealing explicit carrier recombination dynamics. J. Phys. Chem. Lett. 9, 7007–7014 (2018).
Alivisatos, A. P., Harris, T., Carroll, P., Steigerwald, M. L. & Brus, L. E. Electron-vibration coupling in Semiconductor clusters studied by resonance Raman spectroscopy. J. Chem. Phys. 90, 3463–3468 (1989).
Rainò, G. et al. Single cesium lead halide perovskite nanocrystals at low temperature: fast single-photon emission, reduced blinking, and exciton fine structure. ACS Nano 12, 2485–2490 (2016).
Becker, M. A. et al. Bright triplet excitons in caesium lead halide perovskites. Nature 553, 189–193 (2018).
de Jong, M., Seijo, L., Meijerink, A. & Rabouw, F. T. Resolving the ambiguity in the relation between Stokes shift and Huang-Rhys parameter. Phys. Chem. Chem. Phys. 217, 16959–16969 (2015).
Devreese, J. T. in Encyclopedia of Applied Physics Vol. 14, 383–409, Ed. by G. L. Trigg (Wiley-VCH Publishers, Inc., 1996).
Alexandrov, A. S. & Devreese, J. T. Advances in Polaron Physics (Springer, 2010).
Emin, D. Polarons (Cambridge University Press, 2013).
Hopfield, J. J. A theory of edge-emission phenomena in CdS, ZnS and ZnO. J. Phys. Chem. Solids 10, 110–119 (1959).
Mitra, T. K., Chatterjee, A. & Mukhopadhyay, S. Polarons. Phys. Rep. 153, 91–207 (1987).
Yang, Z. et al. Impact of halide cage on the electronic properties of fully inorganic cesium lead halide perovskites. ACS Energy Lett. 2, 1621–1627 (2017).
Buizza, L. R. V. & Herz, L. M. Polarons and charge localization in metal-halide semiconductors for photovoltaic and light-emitting devices. Adv. Mater. 33, 2007057 (2021).
Sonnichsen, C. D., Strandell, D. P., Brosseau, P. J. & Kambhampati, P. Polaronic quantum confinement in bulk CsPbBr3 perovskite crystals revealed by state-resolved pump/probe spectroscopy. Phys. Rev. Res. 3, 023147 (2021).
Guo, Y. et al. Dynamic emission Stokes shift and liquid-like dielectric solvation of band edge carriers in lead-halide perovskites. Nat. Commun. 10, 1175 (2019).
Green, M. A., Jiang, Y., Soufiani, A. M. & Ho-Baillie, A. Optical properties of photovoltaic organic-inorganic lead halide perovskites. J. Phys. Chem. Lett. 6, 4774–4785 (2015).
Nash, K. J. & Mowbray, D. J. Exciton-phonon interactions in quantum wells and superlattices. J. Lumin. 44, 315–346 (1989).
Nirmal, M., Murray, C. B. & Bawendi, M. G. Fluorescence-line narrowing in CdSe quantum dots: surface localization of the photogenerated exciton. Phys. Rev. B 50, 2293–2300 (1994).
Krauss, T. D. & Wise, F. W. Raman scattering study of exciton-phonon coupling in PbS nanocrystals. Phys. Rev. B 55, 9860–9865 (1997).
Sashchiuk, A. et al. Optical and conductivity properties of PbS nanocrystals in amorphous zirconia sol-gel films. J. Sol-Gel Sci. Technol. 24, 31–38 (2002).
Nomura, S. & Kobayashi, T. Exciton-LO-phonon couplings in spherical semiconductor microcrystallites. Phys. Rev. B 45, 1305–1316 (1992).
Shibata, K., Yan, J., Hazama, Y., Chen, S. & Akiyama, H. Exciton localization and enhancement of the exciton-LO phonon interaction in a CsPbBr3 single crystal. J. Phys. Chem. C. 124, 18257–18263 (2020).
Herz, L. M. How lattice dynamics moderate the electronic properties of metal-halide perovskites. J. Phys. Chem. Lett. 9, 6853–6863 (2018).
Miyata, K. et al. Liquid-like dielectric response is an origin of long polaron lifetime exceeding 10 μs in lead bromide perovskites. J. Chem. Phys. 152, 084704 (2020).
Kang, J. & Wang, L. High defect tolerance in lead halide perovskite CsPbBr3. J. Phys. Chem. Lett. 8, 489–493 (2017).
Cohen, A. V., Egger, D. A., Rappe, A. M. & Kronik, L. Breakdown of the static picture of defect energetics in halide perovskites: the case of the Br vacancy in CsPbBr3. J. Phys. Chem. Lett. 10, 4490–4498 (2019).
Acknowledgements
This work is part of the research program entitled “Designing Dirac Carriers in Semiconductor Superlattices” (DDC13), which is supported by the Foundation for Fundamental Research on Matter (FOM) which is part of the Netherlands Organization for Scientific Research (NWO).
Author information
Authors and Affiliations
Contributions
The idea for the manuscript is the result of continuous interaction between C.M.I. and A.Y.S.; NC samples were fabricated and characterized by F.M. and S.B., while A.B. and J.B. conducted the MPRS experiment; C.M.I. conducted the THz-TDS measurements with the help and supervision of N.J.J.v.H. and S.E.T.t.H.; C.M.I. analyzed the experimental data and wrote the manuscript with input from A.B., N.J.J.v.H, S.E.T.t.H., J.B., F.M., S.B., P.C.M.C., D.V., C.d.M.D, J.G.R., P.M.K., and A.Y.S.; A.Y.S. and P.M.K. directly supervised the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Ajay Ram Srimath Kandada, Adam Wrigh and the other, anonymous, reviewer for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Iaru, C.M., Brodu, A., van Hoof, N.J.J. et al. Fröhlich interaction dominated by a single phonon mode in CsPbBr3. Nat Commun 12, 5844 (2021). https://doi.org/10.1038/s41467-021-26192-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-021-26192-0
This article is cited by
-
Exploring the lead-free halide Cs2MGaBr6 (M = Li, Na) double perovskites for sustainable energy applications
Scientific Reports (2024)
-
Disentangling the effects of structure and lone-pair electrons in the lattice dynamics of halide perovskites
Nature Communications (2024)
-
How spin relaxes and dephases in bulk halide perovskites
Nature Communications (2024)
-
Simultaneous improving luminescence intensity and stability of CsPbBr3:SCN−@Eu/Zr-Uio-66-NH2 with tunable emissions from blue to green and applications in indoor photovoltaics
Nano Research (2024)
-
Coupling to octahedral tilts in halide perovskite nanocrystals induces phonon-mediated attractive interactions between excitons
Nature Physics (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.