Abstract
The Zintl thermoelectric phase Eu2ZnSb2 has a remarkable combination of high mobility and low thermal conductivity that leads to good thermoelectric performance. The key feature of this compound is a crystal structure that has a Zn-site with a 50% occupancy. Here we use comparison of experimental thermal conductivity measurements and first principles thermal conductivity calculations to characterize the thermal conductivity reduction. We find that partial ordering, characterized by local order, but Zn-site disorder on longer scales, leads to an intrinsic nanostructuring induced reduction in thermal conductivity, while retaining electron mobility. This provides a direction for identifying Zintl compounds with ultralow lattice thermal conductivity and good electrical conductivity.
Similar content being viewed by others
Introduction
Understanding heat conduction in solids is an ongoing challenge in condensed matter physics with important practical implications1,2,3,4,5,6,7. This is particularly so in low thermal conductivity materials of importance for thermoelectrics and in thermal barrier materials, where for example perturbative pictures based on phonons and phonon scattering may breakdown due to strong scattering from disorder and/or strong anharmonicity. Moreover, identifying mechanisms that allow reduction of thermal conductivity without commensurate reductions in electrical conductivity remains a central problem in thermoelectrics research5,8,9,10,11,12. It has been addressed by the introduction of rattling modes associated with weakly bound atoms12,13,14, alloy scattering15, disorder, nanostructuring16, anharmonic bonds associated with lone pairs17,18,19,20, and the selection of materials with complex Zintl structures21,22,23 or soft anharmonic phonons24,25, for example near structural phase transitions26. High thermoelectric performance has been achieved in materials with intrinsic low thermal conductivity including Cu2Se27, SnSe28, MgAgSb29, Yb14MnSb1130, and Ag9GaSe631. These results illustrate the importance of searching for materials with low thermal conductivity to find thermoelectric compositions.
However, all approaches for achieving low thermal conductivity have limitations. In particular, phonon-based approaches generally yield very low thermal conductivities only at high temperatures, where the effects of anharmonic phonon scattering are strongest, while disorder-based approaches typically lower the thermal conductivity, but also in general strongly affect electronic conductivity so that only certain amounts and types of disorder can be used. Thus, understanding mechanisms for obtaining low thermal conductivity without degraded electrical properties remains an important challenge.
Here we demonstrate a direction, where a partially filled site behaves as if it is ordered for electrons but disordered for heat conduction. This can be understood in terms of the different length scales for phonon and electron scattering and represents an intrinsic nanostructure induced thermal conductivity reduction analogous to observed enhancements in thermoelectric performance in certain artificially nanostructured bulk thermoelectrics16,32.
Zintl-phase Eu2ZnSb2 exhibits an intrinsically ultralow thermal conductivity combined with high electrical mobility, leading to a high thermoelectric figure of merit, ZT~1.0 at high temperature33,34. Crystal structure refinement yields a hexagonal structure with partial occupancy of the Zn site35,36. This partial occupancy implies disorder. However, locally a reasonably high degree of order is expected. This is based on electron microscopy and also on electronic structure calculations that show the band gap formation is highly sensitive to Zn ordering35. The compound has a carrier mobility of 50 cm2 V−1 s−1 or above at ambient temperature, which is a value that is not generally consistent with the high degree of carrier scattering that would be expected with extensive disorder on a site that contains a mixture of cations and vacancies and which is intimately involved in the band structure formation. The combination of high mobility and very low thermal conductivity is very unusual, as is the fact that the low thermal conductivity exists not only at very high temperature, but at ambient temperature as well. Here we combine experiment and analysis based on model behavior and first principles calculations, including anharmonic phonon scattering to understand the low thermal conductivity of this material.
Results and discussion
Crystallographic structure properties
As shown in Fig. 1, Zintl-phase Eu2ZnSb2 and EuAgSb are based on the same hexagonal crystal structure (space group: P63/mmc). In the case of Eu2ZnSb2 there are 50% vacancies on the Zn site. This is understood in terms of the Zintl concept as providing electronic charge balance as monovalent Ag+ is replaced by divalent Zn2+. Thus the vacancies are needed for obtaining a semiconducting gap. Such a semiconducting gap is observed and is essential for thermoelectric performance. In addition, the stoichiometry is supported by X-ray diffraction Rietveld refinement35. In contrast, the site is fully occupied by Ag atoms in EuAgSb36,37. However, as noted, electronic structure calculations show that the details of the electronic structure near the band edges are dependent on the specific ordering of the Zn vacancies. In other words, there is an important interplay between Zn vacancy order and the electronic structure near the band edge35. This implies strong electron scattering, and resulting low mobility, if the Zn atoms are strongly disordered on length scales comparable to electron mean free paths. Thus, although the exact structure is as yet unknown, two things are known, specifically that the Zn site in the average structure is at 50% occupancy and that there must be a high degree of Zn order at least locally. This is supported by imaging data shown in Supplementary materials, Fig. S1.
a Crystal structure of Eu2ZnSb2. The golden, green, and red spheres represent the europium, antimony, and zinc, respectively. b Zig-zag-type crystal structure of Eu2ZnSb2. c Crystal structure of EuAgSb. d Anionic AgSb layer in EuAgSb. See also Supplementary Material, Fig. S2.
Thermoelectric properties
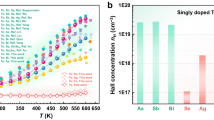
Thermoelectric samples of EuAgSb have both higher carrier concentration and carrier mobility38, as compared with Eu2ZnSb2 (see Fig. 2). The high carrier mobility of EuAgSb is understood as mainly a consequence of the Ag–Sb framework, which is fully occupied and beneficial to the carrier transport. Temperature-dependent thermoelectric properties are shown in Fig. 3. Compared with Eu2ZnSb2, the higher carrier concentration of EuAgSb leads to higher electrical conductivity and smaller Seebeck coefficient, as usual. The maximum power factor of Eu2ZnSb2 is only ~3.5 μW cm−1 K−2. This compares with the higher maximum power factor of EuAgSb, which can be greater than ~10 μW cm−1 K−2.
a Carrier concentration and b Hall mobility of Eu2ZnSb2 and EuAgSb33.
a Electrical conductivity and Seebeck coefficient. b Power factor. c Thermal conductivity and lattice thermal conductivity. d ZT values of Eu2ZnSb2 and EuAgSb33.
However, the thermal conductivity of EuAgSb is much higher than that of Eu2ZnSb2. This total thermal conductivity includes both the lattice and electronic contributions. In order to obtain the lattice thermal conductivity, κL, the electronic contribution, κc was subtracted from the measured total thermal conductivity, κ. The value of κc was estimated based on the Wiedemann–Franz relationship (κc = LσT). Here L is the single parabolic band (SPB) model Lorenz number39. This SPB model captures the reduction in L near band edges of thermoelectric materials, and is based on the Seebeck coefficient that can be obtained experimentally. The agreement of this model with full Boltzmann transport calculations is generally reasonable, and going beyond it requires the detailed band structure and scattering models, which would depend on the details of the presently unknown Zn vacancy ordering40. The electronic contribution is particularly important at higher temperature, where the limitations of this model should be kept in mind.
Importantly, the lattice thermal conductivity of Eu2ZnSb2 is close to that of EuAgSb at high temperature, but the value at room temperature is much lower. This leads to a higher ZT for Eu2ZnSb2, especially at lower temperature. Thermoelectric device efficiency is governed by a temperature average, the so-called engineering ZT41. The lower temperature range, while not enhancing the peak ZT is important for the engineering ZT and the efficiency of devices that might be made from this material. Understanding this difference in thermal conductivity is therefore key to understanding the high ZT of Eu2ZnSb2. The phonon dispersion relations of Eu2ZnSb2 and EuAgSb as obtained from density functional theory calculations are shown in Fig. 4. For Eu2ZnSb2 these were obtained using ordered structures, with zig-zag ordering of Zn vacancies within the ZnSb2 plane. As mentioned, the electronic structure of Eu2ZnSb2 at the band edges depends on the details of the Zn ordering, and in fact there are interesting topological aspects to this dependence35. However, the bonding and chemistry is expected to be less sensitive to the particular ordering. Importantly, we find that this ordering yields dynamical stability as characterized both by stable phonons and stable ab initio molecular dynamics. This structure has a space group symmetry, Pmm2, which is lower than the global space group symmetry of Eu2ZnSb2. It should be noted that the dispersions show flat optic phonon branches in Eu2ZnSb2 at low energy starting below 1 THz. This leads to a strong peak in the phonon density of states, which has primary Zn character.
Physical properties of Eu2ZnSb2 and EuAgSb are listed in Table 1. Measured and calculated sound velocities, Debye temperatures, and bulk moduli are given. The measured values are in accord with the calculated properties. This supports the reasonableness of the structural model. There are not clear differences between the two compounds, and specifically none that would imply strong general softness of the lattice of Eu2ZnSb2 relative to that of EuAgSb, although Eu2ZnSb2 does have relatively soft acoustic phonons, as characterized by the low longitudinal sound velocity and the corresponding Debye temperature. These properties are comparable to those in EuAgSb, which as noted has a much higher thermal conductivity. Thus, while some of the differences in thermal conductivity could be ascribed to the softer lattice, the effect is not nearly large enough to explain the difference in thermal conductivity.
It is important to note that as temperature increases the experimental thermal conductivity approaches but is not lower than the minimum thermal conductivities allowed within a phonon model42,43. The calculated minimum lattice thermal conductivities are 0.42 W/mK and 0.52 W/mK for Eu2ZnSb2 and EuAgSb, respectively. Thus, the temperature dependence where the thermal conductivity decreases toward a constant value as temperature is increased can be viewed as related to increased phonon scattering as temperature is increased, but the considerably weaker than 1/T temperature dependence for Eu2ZnSb2 suggests additional scattering beyond anharmonic phonon scattering. It is also noteworthy that in addition to the weak temperature dependence of the thermal conductivity in Eu2ZnSb2 there is a small but noticeable upturn at high temperature. Such upturns can be a consequence of increased thermal conductivity due to transport in localized vibrational modes, as in glassy materials, or bipolar electronic conduction. Such bipolar effects are possible in Eu2ZnSb2 due to the small ~0.17 eV band gap33, and relatively low carrier concentration of ~4.5 × 1018 cm−3 at ambient temperature. This is also consistent with the fact that, as shown in Fig. 3a, the Seebeck coefficient of Eu2ZnSb2 decreases with temperature at high temperature, while the conductivity is increasing.
Figure 4 shows the theoretical phonon dispersion curves and the (projected) phonon density of states (PDOS) of Eu2ZnSb2 and EuAgSb. Both compounds are dynamically stable, as expected. These dispersions show low frequency modes leading to peaks in the PDOS that come from the Zn and Ag. Specifically, there are a set of relatively flat phonon branches leading to a large peak in the PDOS near 1 THz in Eu2ZnSb2. This is reminiscent of a rattling ion peak, as in clathrates14 and filled skutterudites8,13,44, where rattling has been associated with very low thermal conductivity. Importantly, this peak has Zn character. This shows that the Zn vibrations can be of particular importance in reducing the thermal conductivity. However, while rattling is expected to lower the thermal conductivity, it does not explain the temperature dependence of the thermal conductivity by itself as discussed below.
The calculated lattice thermal conductivities of Eu2ZnSb2 and EuAgSb are shown in Fig. 5, based on anharmonic phonon scattering. As seen, the calculated thermal conductivity of Eu2ZnSb2 is indeed lower than that of EuAgSb at all temperatures. However, it is higher than the experimental lattice thermal conductivity, in the lower temperature region. The calculated lattice thermal conductivities of Eu2ZnSb2 are 0.55 W/mK and 0.21 W/mK at 300 K and 800 K, respectively. This may signal a breakdown of the phonon picture at high temperature, though not at ambient temperature. Specifically, at high temperatures or in highly disordered materials, strong scattering leads to localization and a breakdown of the phonon Boltzmann theory in certain materials. This type of breakdown is typically signified by (1) a flat temperature dependence of the thermal conductivity and (2) a thermal conductivity that is higher than the phonon Boltzmann theory due to the contribution to heat conduction of localized incoherent vibrations2,5,45. The present calculated result in comparison with experiment indicates that Eu2ZnSb2 is not in this strong scattering regime at least near ambient temperature though it apparently is at high temperature.
The very low lattice thermal conductivity of Eu2ZnSb2 compared to EuAgSb is due to a larger scattering phase space, as shown on a log scale in Fig. 6. This is the case over a wide frequency range starting below 1 THz. The enhancement in scattering phase space is particularly significant in the frequency range between approximately 0.8 THz and 3.5 THz. This reflects in part the Zn-related peak in the PDOS. There is also a significant difference in the anharmonic scattering rates. These are enhanced in Eu2ZnSb2 relative to EuAgSb, particularly below 2 THz, which is the range that is generally most important for thermal conductivity.
It is noteworthy that the Zn contribution to the PDOS has a two-peak structure in this frequency range, with a sharp peak and then a much broader peak at higher frequency, extending to approximately 3.5 THz. This can be understood as reflecting hybridization between soft Zn vibrations and the “host” lattice Eu–Sb modes. This is in analogy with filled skutterudites where a two-peak feature is also seen in neutron scattering experiments and is associated with thermal conductivity reduction46. This provides a general explanation of why Eu2ZnSb2 has a lower thermal conductivity than EuAgSb, specifically anharmonic scattering involving relatively low-frequency Zn vibrations in analogy with rattling in filled skutterudites. It is interesting that in Eu2ZnSb2 the rattling atom is the lightest atom in the chemical formula, reflecting weak bonding of the Zn. This underlies the low thermal conductivity near 800 K. However, due to the expected 1/T behavior at lower temperature, different from the experimental temperature dependence, the anharmonic phonon scattering picture does not fully explain the lower temperature data.
The experimental data show behavior consistent with anharmonic phonon scattering for EuAgSb with a strong decrease in κl as a function of temperature. In contrast, the nearly temperature-independent thermal conductivity in the lower temperature regime for Eu2ZnSb2 is instead consistent with a constant mean free path for the heat carrying phonons. At high temperature this mean free path is constrained by anharmonic phonon scattering, associated with the rattling behavior of the weakly bonded Zn atoms, constrained by the minimum thermal conductivity. This behavior and the difference from the behavior of EuAgSb point to disorder on the Zn site leading to a constrained mean free path as the key mechanism for thermal conductivity reduction at lower temperature. However, since Zn and its ordering play important roles in the band formation, random disorder would be expected to strongly depress the electronic mobility. This would be highly detrimental to the thermoelectric performance, in disagreement with the observed good performance of Eu2ZnSb2. Thus, there must be disorder on length scales that are of importance for the thermal conductivity and at the same time effective order on the shorter length scales needed for the favorable electronic behavior. This is similar to observations for artificially nanostructured thermoelectrics, where thermal conductivity has been found to be more sensitive to scattering at longer length scales compared to electronic transport. Due to shorter electron mean free paths electronic transport is affected by shorter length scales but can be relatively unaffected by scattering due to structure on longer length scales16,47,48.
The Callaway model is useful for analyzing this. Considering the anharmonic phonon scattering due to the rattling like Zn vibrations, we focus on the low-frequency acoustic branches. We then apply the Callaway model to the longitudinal and two transverse acoustic modes, with velocities as in Table 1 and a fixed mean free path, l. Above room temperature, the model is κl = (CLvLl + CTvTl)/3, where vL and vT are the longitudinal and transverse sound velocities, respectively, and the specific heats are taken as the classical harmonic values of R per branch (one longitudinal, two transverse), per mole and the factor of 1/3 is due to the direction averaging. This leads to an estimation of l ≈ 150 Å needed for obtaining κl = 0.4 W/mK. This is much larger than the lattice parameter and the Zn–Zn spacing in the lattice. This Zn–Zn spacing is the scale that would be provided by random occupancy of the Zn sublattice, so the present result implies that the relevant length scale, l is much longer than that which would be provided by fully random Zn occupancy. The effect of the Zn disorder is then to provide phonon scattering similar to a very fine-grained nanostructure, with length scale of approximately 150 Å.
Thus, apparently the Zn atoms in Eu2ZnSb2 are not fully long-range ordered. When considered at short length scales that are important for the electronic properties the material behaves as if it is ordered, but at length scales of l ~ 150 Å disorder is important and scatters phonons. This then allows a separation of length scales, where disorder is important at the longer length scales characteristic of mean free paths of heat-carrying phonons, but is less important at the shorter length scales important for electronic conduction. This is analogous to the effect of artificial nanostructuring where small grain sizes and associated interfaces on length scales important for heat-carrying phonons lower the thermal conductivity, without affecting the electronic transport as strongly16,32,47. While the present results do not exclude other mechanisms for thermal conductivity reduction, they do illustrate a way of obtaining phonon–glass, electron–crystal behavior8,12, specifically ultralow thermal conductivities over a wide temperature range accompanied by favorable electrical transport.
The intrinsic phonon–phonon interactions with rattling behavior, low bulk modulus, and scattering from disorder on the Zn sublattice lead to low lattice thermal conductivity of Eu2ZnSb2. This leads to a semiconducting Zintl material with a lattice thermal conductivity close to the minimum thermal conductivity over a very broad temperature range starting at 300 K and extending to high temperature. At the same time, in contrast to the normal situation with a high degree of random disorder, Eu2ZnSb2 maintains a good mobility leading to high thermoelectric performance. Weakly bonding Zn plays a key role in this. This points the way to a mechanism that can be applied to Zintl-phase materials, particularly the design of systems with disorder on one sublattice, but a local ordering tendency that produces different behavior on different length scales, effectively an intrinsic bulk nanostructured material.
Methods
Density functional calculations
Calculations are done using the generalized gradient approximation of Perdew, Burke, and Ernzerhof (PBE-GGA)49. Orthorhombic cells corresponding to the zig-zag structure of Eu2ZnSb2 are used for this compound as well as EuAgSb although EuAgSb has a higher hexagonal symmetry. This is to facilitate comparison of the two compounds. The calculations are done using the projector augmented wave (PAW) method as implemented in the Vienna Ab-initio Simulation Package (VASP) code50,51. Geometry optimization is done. A planewave energy cutoff of 500 eV is used along with a 10 × 10 × 10 uniform mesh for Brillouin zone sampling and an energy convergence criterion for self-consistency of 10−7 eV. The lattice constants are changed relative to the ideal (disordered) hexagonal structure following \({a}_{0}={a}_{h}\times 2\), \({b}_{0}={b}_{h}\times \sqrt{3}\), \({c}_{0}={c}_{h}\), where \({a}_{0}\), \({b}_{0}\), and \({c}_{0}\) are the unit cell parameters in the orthorhombic crystal system, and \({a}_{h}\), \({b}_{h}\), \({c}_{h}\) are the unit cell parameters in the hexagonal structure. The optimized orthorhombic lattice parameters are 9.18, 15.94, and 8.20 Å for the zig-zag supercell Eu2ZnSb2. The bulk modulus and related data in Table 1 are from zero K fitting of stress–strain curves. The temperature-dependent effective potential (TDEP) method is used to extract anharmonic force constants52,53. This is done to provide a stable well constrained interatomic force constants (IFCs) for the complex crystal structure of these compounds. The TDEP calculation is based on Born–Oppenheimer molecular dynamics with the PAW method at 300 K with Nose thermostat temperature control54. A simulation time of 140 ps, with a time step of 1 fs and planewave cutoff of 440 eV are used. An 80 atom zig-zag model supercell of Eu2ZnSb2 is used for the TDEP calculation for that compound, and a 96 atom supercell is used for EuAgSb. The phonon dispersions are obtained from the effective second-order IFCs using the Phonopy package55. The structure is dynamically stable. The thermal conductivities are obtained using the third-order anharmonic IFCs and the ShengBTE package56. The convergence with respect to the reciprocal space grid was tested, as shown in Supplemental Material Fig. S3. The temperature dependence of the thermal conductivity is obtained using the temperature-dependent phonon occupations based on the 300 K IFCs.
Sample preparation and characterization
The samples were prepared by weighing out stoichiometric amounts of silver (Ag, 99.9%, shots), europium (Eu, 99.9%, chunks), zinc (Zn, 99.999%, chunks), and antimony (Sb, 99.999%, shots). These were for the EuAgSb and Eu2ZnSb2 stoichiometries. These were then loaded into stainless-steel jars. This was done in an argon-filled glove box. The mixtures were ball-milled for 10 h using a high energy ball mill (SPEX 8000M) and subsequently sintered for 2 min using spark plasma sintering under an axial pressure of 60 MPa at 853 K, resulting in dense disks. The density of the resulting Eu2ZnSb2 sample was 6.46 g/cm3, which is approximately 97% of the theoretical density of 6.66 g/cm3.
The experimental Young’s modulus, shear modulus, Poisson ratio, Debye temperature, and bulk modulus are approximated from the standard expressions in terms of sound velocities57. The longitudinal (vL) and transverse (vT) components of the sound velocity were measured using an ultrasonic pulse receiver (Olympus) equipped with an oscilloscope (Tektronix). The Seebeck coefficient (S) and electrical conductivity (σ) were measured with a ZEM-3 apparatus. The Hall coefficient (RH) as a function of temperature was measured using the van-der-Pauw technique with a reversible magnetic field of 1.5 T. The Hall mobility, μH, and Hall carrier concentration, nH, were calculated as μH = σRH and nH = 1/(eRH), respectively. The thermal conductivity (к) was obtained from the thermal diffusivity, specifically к = DαCp. Here, D is the volumetric density, which was determined by the Archimedes method, α is the thermal diffusivity, which was measured using a laser flash apparatus (Netzsch LFA 457), and Cp is the specific heat, which was obtained using a differential scanning calorimetry thermal analyzer (Netzsch DSC 404 F3). We then calculated the lattice thermal conductivity by κL = κ – LσT, where the Lorenz number (L) is from the SPB formula and the measured Seebeck coefficients39.
Data availability
Data supporting the conclusions is included in the article. Additional data are available from the corresponding authors upon reasonable request.
References
Niedziela, J. L. et al. Selective breakdown of phonon quasiparticles across superionic transition in CuCrSe2. Nat. Phys. 15, 73–78 (2019).
Simoncelli, M., Marzari, N. & Mauri, F. Unified theory of thermal transport in crystals and glasses. Nat. Phys. 15, 809–813 (2019).
Lv, W. & Henry, A. Direct calculation of modal contributions to thermal conductivity via Green–Kubo modal analysis. New J. Phys. 18, 013028 (2016).
Wingert, M. C., Zheng, J., Kwon, S. & Chen, R. Thermal transport in amorphous materials: a review. Semiconductor Sci. Technol. 31, 113003 (2016).
Mukhopadhyay, S. et al. Two-channel model for ultralow thermal conductivity of crystalline Tl3VSe4. Science 360, 1455 (2018).
Marcolongo, A., Umari, P. & Baroni, S. Microscopic theory and quantum simulation of atomic heat transport. Nat. Phys. 12, 80–84 (2016).
Lindsay, L., Hua, C., Ruan, X. L. & Lee, S. Survey of ab initio phonon thermal transport. Mater. Today Phys. 7, 106–120 (2018).
Nolas, G. S., Morelli, D. T. & Tritt, T. M. Skutterudites: a phonon-glass-electron crystal approach to advanced thermoelectric energy conversion applications. Annu. Rev. Mater. Sci. 29, 89–116 (1999).
He, J. & Tritt, T. M. Advances in thermoelectric materials research: looking back and moving forward. Science 357, eaak9997 (2017).
Rowe, D. M., Shukla, V. S. & Savvides, N. Phonon scattering at grain boundaries in heavily doped fine-grained silicon–germanium alloys. Nature 290, 765–766 (1981).
Xi, Q. et al. A ubiquitous thermal conductivity formula for liquids, polymer glass, and amorphous solids. Chin. Phys. Lett. 37, 104401 (2020).
Beekman, M., Morelli, D. T. & Nolas, G. S. Better thermoelectrics through glass-like crystals. Nat. Mater. 14, 1182–1185 (2015).
Sales, B. C., Mandrus, D., Chakoumakos, B. C., Keppens, V. & Thompson, J. R. Filled skutterudite antimonides: electron crystals and phonon glasses. Phys. Rev. B 56, 15081–15089 (1997).
Takabatake, T., Suekuni, K., Nakayama, T. & Kaneshita, E. Phonon-glass electron-crystal thermoelectric clathrates: experiments and theory. Rev. Mod. Phys. 86, 669–716 (2014).
Xie, H. et al. Beneficial contribution of alloy disorder to electron and phonon transport in half-heusler thermoelectric materials. Adv. Funct. Mater. 23, 5123–5130 (2013).
Poudel, B. et al. High-thermoelectric performance of nanostructured bismuth antimony telluride bulk alloys. Science 320, 634 (2008).
Nielsen, M. D., Ozolins, V. & Heremans, J. P. Lone pair electrons minimize lattice thermal conductivity. Energy Environ. Sci. 6, 570–578 (2013).
Isaacs, E. B., Lu, G. M. & Wolverton, C. Inverse design of ultralow lattice thermal conductivity materials via materials database screening of lone pair cation coordination environment. J. Phys. Chem. Lett. 11, 5577–5583 (2020).
Skoug, E. J. & Morelli, D. T. Role of lone-pair electrons in producing minimum thermal conductivity in nitrogen-group chalcogenide compounds. Phys. Rev. Lett. 107, 235901 (2011).
Mukhopadhyay, S., Singh, D. J. & Reinecke, T. L. Ultralow thermal conductivity in Cs–Sb–Se compounds: lattice instability versus lone-pair electrons. Chem. Mater. 32, 8906–8913 (2020).
Toberer, E. S., Zevalkink, A. & Snyder, G. J. Phonon engineering through crystal chemistry. J. Mater. Chem. 21, 15843–15852 (2011).
Shuai, J. et al. Recent progress and future challenges on thermoelectric Zintl materials. Mater. Today Phys. 1, 74–95 (2017).
Sun, J. F., Shuai, J., Ren, Z. F. & Singh, D. J. Computational modelling of the thermoelectric properties of p-type Zintl compound CaMg2Bi2. Mater. Today Phys. 2, 40–45 (2017).
Feng, Z., Fu, Y., Zhang, Y. & Singh, D. J. Characterization of rattling in relation to thermal conductivity: Ordered half-Heusler semiconductors. Phys. Rev. B 101, 064301 (2020).
Pandey, T., Nissimagoudar, A. S., Mishra, A. & Singh, A. K. Ultralow thermal conductivity and high thermoelectric figure of merit in mixed valence In5X5Br (X = S, and Se) compounds. J. Mater. Chem. A 8, 13812–13819 (2020).
Lanigan-Atkins, T. et al. Extended anharmonic collapse of phonon dispersions in SnS and SnSe. Nat. Commun. 11, 4430 (2020).
Qiu, P., Shi, X. & Chen, L. Cu-based thermoelectric materials. Energy Storage Mater. 3, 85–97 (2016).
Zhao, L.-D. et al. Ultralow thermal conductivity and high thermoelectric figure of merit in SnSe crystals. Nature 508, 373–377 (2014).
Li, X. et al. Ultralow thermal conductivity from transverse acoustic phonon suppression in distorted crystalline α-MgAgSb. Nat. Commun. 11, 942 (2020).
Toberer, E. S., Brown, S. R., Ikeda, T., Kauzlarich, S. M. & Jeffrey Snyder, G. High thermoelectric efficiency in lanthanum doped Yb14MnSb11. Appl. Phys. Lett. 93, 062110 (2008).
Lin, S. et al. High thermoelectric performance of Ag9GaSe6 enabled by low cutoff frequency of acoustic phonons. Joule 1, 816–830 (2017).
Minnich, A. J., Dresselhaus, M. S., Ren, Z. F. & Chen, G. Bulk nanostructured thermoelectric materials: current research and future prospects. Energy Environ. Sci. 2, 466–479 (2009).
Chen, C. et al. Zintl-phase Eu2ZnSb2: a promising thermoelectric material with ultralow thermal conductivity. Proc. Natl Acad. Sci. 116, 2831 (2019).
Chanakian, S. et al. Exceptionally high electronic mobility in defect-rich Eu2ZnSb2−xBix alloys. J. Mater. Chem. A 8, 6004–6012 (2020).
Yao, H. et al. Vacancy ordering induced topological electronic transition in bulk Eu2ZnSb2. Sci. Adv. 7, eabd6162 (2021).
Wilson, D. K., Saparov, B. & Bobev, S. Synthesis, crystal structures and properties of the Zintl phases Sr2ZnP2, Sr2ZnAs2, A2ZnSb2 and A2ZnBi2 (A = Sr and Eu). Z. Anorganische Allg. Chem. 637, 2018–2025 (2011).
Mishra, T., Schellenberg, I., Eul, M. & Pöttgen, R. Structure and properties of EuTSb (T= Cu, Pd, Ag, Pt, Au) and YbIrSb. Z. Kristallogr 226, 590–601 (2011).
Zhang, W. et al. Promising Zintl-phase thermoelectric compound SrAgSb. Chem. Mater. 32, 6983–6989 (2020).
Kim, H.-S., Gibbs, Z. M., Tang, Y., Wang, H. & Snyder, G. J. Characterization of Lorenz number with Seebeck coefficient measurement. APL Mater. 3, 041506 (2015).
Putatunda, A. & Singh, D. J. Lorenz number in relation to estimates based on the Seebeck coefficient. Mater. Today Phys. 8, 49–55 (2019).
Kim, H. S., Liu, W., Chen, G., Chu, C.-W. & Ren, Z. Relationship between thermoelectric figure of merit and energy conversion efficiency. Proc. Natl Acad. Sci. USA 112, 8205 (2015).
Cahill, D. G. & Pohl, R. O. Lattice vibrations and heat transport in crystals and glasses. Annu. Rev. Phys. Chem. 39, 93–121 (1988).
Cahill, D. G., Watson, S. K. & Pohl, R. O. Lower limit to the thermal conductivity of disordered crystals. Phys. Rev. B 46, 6131–6140 (1992).
Shi, X. et al. Multiple-filled skutterudites: high thermoelectric figure of merit through separately optimizing electrical and thermal transports. J. Am. Chem. Soc. 133, 7837–7846 (2011).
Seyf, H. R. et al. Rethinking phonons: the issue of disorder. npj Comput Mater. 3, 49 (2017).
Feldman, J. L., Singh, D. J., Mazin, I. I., Mandrus, D. & Sales, B. C. Lattice dynamics and reduced thermal conductivity of filled skutterudites. Phys. Rev. B 61, R9209–R9212 (2000).
Hori, T., Shiomi, J. & Dames, C. Effective phonon mean free path in polycrystalline nanostructures. Appl. Phys. Lett. 106, 171901 (2015).
Qiu, B. et al. First-principles simulation of electron mean-free-path spectra and thermoelectric properties in silicon. EPL 109, 57006 (2015).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Kresse, G. & Furthmuller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Hellman, O., Abrikosov, I. A. & Simak, S. I. Lattice dynamics of anharmonic solids from first principles. Phys. Rev. B 84, 180301 (2011).
Hellman, O. & Abrikosov, I. A. Temperature-dependent effective third-order interatomic force constants from first principles. Phys. Rev. B 88, 144301 (2013).
Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 52, 255–268 (1984).
Togo, A. & Tanaka, I. First principles phonon calculations in materials science. Scr. Mater 108, 1–5 (2015).
Li, W., Carrete, J., A. Katcho, N. & Mingo, N. ShengBTE: a solver of the Boltzmann transport equation for phonons. Comput Phys. Commun. 185, 1747–1758 (2014).
Xiao, Y. et al. Origin of low thermal conductivity in SnSe. Phys. Rev. B 94, 125203 (2016).
Acknowledgements
This work was funded by the National Natural Science Foundation of China (51871081, 11674078, 51971081, 52101248, 52001339, and 12047518), the Cheung Kong Scholar Reward Program Young Scholar Program of China (Q2018239), the Natural Science Foundation for Distinguished Young Scholars of Guangdong Province of China (2020B1515020023), the Shenzhen Science and Technology Program (Grant No. KQTD20200820113045081), the Shenzhen Science and Technology Innovation Plan (KQJSCX20180328165435202 and JCYJ20180307154619840), the National Key Research and Development Program of China (2017YFA0303600), the China Postdoctoral Science Foundation (2020TQ0088, 2021M690906). Work at the University of Missouri was supported by the U.S. Department of Energy, Award Number DE-SC0019114.
Author information
Authors and Affiliations
Contributions
Z.F., H.Y., B.H.L. and D.J.S. did theoretical work, first principles calculations and modeling. C.C., F.C., Y.W., Y.C., and Q.Z. did experimental measurements. C.C., F.C., and Q.Z. contributed samples. D.J.S. analyzed results. D.J.S. and Q.Z. wrote the manuscript, with assistance from all the authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chen, C., Feng, Z., Yao, H. et al. Intrinsic nanostructure induced ultralow thermal conductivity yields enhanced thermoelectric performance in Zintl phase Eu2ZnSb2. Nat Commun 12, 5718 (2021). https://doi.org/10.1038/s41467-021-25483-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-021-25483-w
This article is cited by
-
Vacancies tailoring lattice anharmonicity of Zintl-type thermoelectrics
Nature Communications (2024)
-
Planar Zintl-phase high-temperature thermoelectric materials XCuSb (X = Ca, Sr, Ba) with low lattice thermal conductivity
Journal of Advanced Ceramics (2022)
-
Realizing high thermoelectric performance in p-type RbZn4P3 Zintl compound: a first-principles investigation
Journal of Materials Science (2022)
-
Local order in a disordered Zintl phase boosts its thermoelectric performance
Communications Chemistry (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.