Abstract
Femtosecond light-induced phase transitions between different macroscopic orders provide the possibility to tune the functional properties of condensed matter on ultrafast timescales. In first-order phase transitions, transient non-equilibrium phases and inherent phase coexistence often preclude non-ambiguous detection of transition precursors and their temporal onset. Here, we present a study combining time-resolved photoelectron spectroscopy and ab-initio electron dynamics calculations elucidating the transient subpicosecond processes governing the photoinduced generation of ferromagnetic order in antiferromagnetic FeRh. The transient photoemission spectra are accounted for by assuming that not only the occupation of electronic states is modified during the photoexcitation process. Instead, the photo-generated non-thermal distribution of electrons modifies the electronic band structure. The ferromagnetic phase of FeRh, characterized by a minority band near the Fermi energy, is established 350 ± 30 fs after the laser excitation. Ab-initio calculations indicate that the phase transition is initiated by a photoinduced Rh-to-Fe charge transfer.
Similar content being viewed by others
Introduction
Emergence of long-range ordered states in condensed matter is typically a consequence of a fine interplay between the coupled spin, charge, orbital, and lattice degrees of freedom1,2,3,4. The mechanisms vary between different correlated oxides and metallic systems leading to specific dynamical behavior. Excitation with ultrashort electromagnetic pulses offers the most efficient means to control the physical properties of condensed matter systems on a femtosecond time scale5,6,7. Materials featuring first-order phase transitions (FOPTs) with abrupt changes in their order parameters are especially appealing for ultrafast devices based on a functionality switch. In this regard, prominent examples are the insulator-metal transition in VO28,9 or 1T–TaS210,11.
In order to obtain a good understanding of the relevant mechanisms triggering the transition, it is necessary to explore the fundamental timescale of FOPTs. However, this is often challenging with multiple coupled degrees of freedom displaying complex dynamics upon laser-induced excitation. Moreover, macroscopic phase coexistence at the FOPT, specifically, the processes of nucleation and domain growth, complicate the disentanglement of dynamic changes in order parameters. The fundamental question, whether the modification of electronic structure drives the transition, is extensively debated in the literature, giving key arguments on the role of photoexcited states in double-exchange interactions12, electronic precursors closing the insulating gap13, or the existence of intermediate transient phases2,9,14,15.
In the case of ferromagnetic materials, magnetization dynamics triggered by a laser pulse leads to ultrafast demagnetization16, associated with changes in the spin polarization17,18,19,20, which is impacted by the spin-dependent mobility of electrons21,22,23. In contrast, disentangling the ultrafast response of coupled order parameters of magnetic FOPTs has been far less investigated. Ultrafast generation of ferromagnetic (FM) order has been observed so far in a relatively small group of materials such as manganites1,24 or CuB2O425. Understanding the phenomenon of laser-induced subpicosecond generation of FM order across a FOPT is still a major challenge in femtomagnetism26.
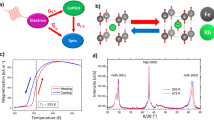
In this work, we focus on FeRh, a metallic material that undergoes a metamagnetic FOPT from antiferromagnetic (AFM) to FM order at TM ~ 360 K and exhibits coupled structural, magnetic and electronic order parameters27,28 (see Fig. 1a). The thermally induced, quasi-static phase transition in FeRh (depicted in Fig. 1b by the green arrow) has been extensively studied by following the sample magnetization, lattice parameter or resistivity29,30,31,32. Moreover, numerous works have studied the AFM-FM phase transition by means of time-resolved techniques, where photoexcitation above a threshold intensity results in a nonzero net magnetization. Seminal pump-probe magneto-optical studies of FeRh films suggested subpicosecond generation of FM order33,34. Bergman et al. later suggested a scenario in which FM domain nucleation occurs at ultrafast time scales, but the subsequent establishment of long range magnetic order is naturally slower, a process consisting of FM domain growth, coalescence, and magnetic moment alignment35. Subsequent research efforts tracking the net magnetic moment correspondingly found a much slower transition on the order of several picoseconds35,36,37. Thus, detection techniques susceptible to the magnetization direction result in a perceived delay in the emergence of FM order. Besides, time-resolved x-ray diffraction experiments indicated that the speed of the transition might be set by the time scale of the structural changes and therefore limited by the speed of sound (~5 nm/ps), so that magnetic and structural order emerge concurrently37,38.
a Sketch of the isostructural metamagnetic phase transition in FeRh. At room temperature (top) the system is AFM showing atomic magnetic moments only at the Fe atom sites (mFe = ±3.3μB). Above 360 K (bottom) the system has ferromagnetically coupled magnetic moments at the Fe (mFe = 3.1 μB) and Rh (mRh = 0.9 μB) sites. The whole unit cell expands isotropically by about 1% in volume69. b Schematic representation of the two possible paths in the AFM to FM phase transition: direct thermally-driven transition to the FM phase (green arrow), and two-step transition going through a transient electronic state reached during photoexcitation (red arrow) followed by relaxation to the equilibrium FM state (blue and black arrows). c Calculated spin-resolved electronic density of states in the AFM and FM phases. The filled areas represent the electronic occupation at thermal equilibrium, with the green area highlighting the position of the Fe minority band (see manuscript text). d Measured x-ray photoelectron spectra of FeRh in the AFM (black dots) and FM (red dots) phase. The solid curve at the bottom of the graph is the difference between the two spectra, which allows to appreciate the relative electron density change across the transition. The data correspond to quasi-static thermal cycling experiments prior to the time-resolved measurements.
However, FM order can also be traced by directly exploiting the specifics of the electronic structure, naturally manifested in terms of spin unbalance and the appearance of majority and minority spin bands39,40,41. This is independent of spin alignment along a particular direction, and thus allows inspecting FM order via x-ray photoelectron spectroscopy (XPS)42,43,44. Similar to the electronic signature of the insulator-metal transition8,10, it was demonstrated that the modification of electronic bands might prove equally useful to investigate the laser-induced generation of FM order across the magnetic FOPT in FeRh45.
Here, utilizing time-resolved photoelectron momentum microscopy and supported by first principle calculations, we demonstrate that it is the light-induced modification of the electronic band structure that triggers the phase transition in FeRh. In particular, we show that ultrafast laser excitation induces a charge transfer between the Rh and Fe atoms, serving as a non-equilibrium precursor for the formation of the FM band structure on the subpicosecond timescale.
Results
The sample under study consists of an epitaxial 80-nm-thick FeRh(001) film grown on a single-crystal MgO(001) substrate, undergoing the AFM-to-FM phase transition at 377 K (see Supplementary Fig. 1). The establishment of the FM phase in FeRh is accompanied by the appearance of a narrow peak in the electronic density of states, located about 150 meV below the Fermi energy EF, as a result of the occupation of a spin-polarized Fe band (see green highlighted area in Fig. 1c). The photoelectron spectroscopy data shown in Fig. 1d are the momentum integrated energy distribution curves measured at room temperature for the AFM phase (black dots) and at 420 K for the FM phase (red dots). We use this spectral feature to follow the emergence of the FM phase after laser excitation. Pump-probe experiments were performed at the FLASH Free Electron Laser (FEL) in Hamburg using near-infrared (800 nm, 1.55 eV) pulses of 90 fs coupled with 130 fs soft x-ray pulses with a photon energy of ℏω = 123.5 eV (see “Methods” for details).
Figure 2a presents the time-resolved, k-integrated photoelectron spectra measured as a function of the delay between the optical pump and x-ray probe pulses, focusing on a 4 ps window around time zero t0. The laser fluence in this pump-probe experiment was 5.6 mJ/cm2, which is above the threshold value to induce the FOPT (see Supplementary Fig. 2 for additional experiments at different laser fluences). One can clearly identify distinct regions in the time-dependent spectra: the temporal overlap between the optical and x-ray pulses (about 100 fs around t0), the relaxation of electrons toward the Fermi energy on the 100 fs timescale, and the subsequent changes in the density of states near the Fermi level, associated with the formation of the Fe minority band. Differential energy-dependent profiles, reported in Fig. 2b, provide a clearer picture. These are retrieved by averaging the measured photoelectron spectra within a ±50 fs temporal region for each of the indicated time delays, and subtracting the average photoelectron spectra at negative time delays.
a Energy- and delay-dependent matrix of the measured spectra. The vertical dashed line marks the position of the Fermi level EF, while the horizontal solid line designates the time zero, t0. The appearance of electronic density in the unoccupied states is a fingerprint of the laser excitation. We used this spectral feature to identify the temporal overlap between the optical pump and the x-ray probe pulses. b Differential photoelectron spectra at selected delays. To enhance the signal to noise ratio, we average the unpumped spectra (between −1 ps and −0.5 ps) and subtract the average spectrum from each row of the matrix. This allows evaluating the statistical noise at negative time delays (−500 fs) as well as accentuating the temporal evolution of the photoelectron spectra. Red and blue shaded areas indicate an increase and a reduction of the electron density with respect to the spectra at negative delays, respectively.
The photoexcited electrons relax via electron-electron and electron-phonon scattering, leading to the onset of a Fermi-like distribution (see the red shaded areas for E − EF > 0 in Fig. 2b). A reduction of the electron density below the Fermi level is also observed around t0 (blue shaded areas for E − EF < 0 in Fig. 2b). At the same delay, the spectrum shows excitation of electrons up to 3.1 eV above EF (see also the inset in Fig. 3). Note that the electron density above 1.5 eV is almost two orders of magnitude lower. The changes in the population above the Fermi level can be explained by one- and two-photon absorption processes, such that laser excitation (ℏωp = 1.55 eV) promotes electrons into states within the energy range [EF, EF + 2ℏωp]. Then, electrons start to relax toward the Fermi level and accumulate in an energy region of a few hundred meV above EF. On the other hand, the transient depletion of electronic density below the Fermi level is concentrated between −3.1 eV and −1.55 eV [EF − 2ℏωp, EF − ℏωp]. Assuming the photo-induced depletion, one would expect to observe measurable changes in the photoelectron yield only for energies 1.55 eV below the EF (as the two-photon contribution should be negligible). This suggests that the laser induced changes in the electronic distribution close to the Fermi level cause severe modifications of the deeper lying bands, meaning that the in-fieri FOPT involves changes in the overall electronic structure of the system.
Experimental spectra (dots) at equilibrium (t = −0.5 ps, red) and at the maximum of the pump pulse (t = 0 ps, blue) are compared in linear (top panel) and logarithmic scales (inset) to the TD-DFT calculations (solid lines) of the electronic structure of FeRh in the AFM phase (red) and at laser excitation (blue). The bottom panel displays the difference between the corresponding experimental and theoretical spectra in the top panel. The green (red) region represents the energy range to (from) which electrons are excited with one-photon (1.55 eV) processes. The light green region in the top panel inset identifies the energy range that can be reached by two-photon (3.1 eV) processes.
To elucidate the electronic dynamics near the zero time delay, we compare the experimental results with time-dependent density functional theory (TD-DFT) calculations of the electronic structure performed on FeRh (see Fig. 3). Here, we select a laser fluence which gives a good quantitative agreement with the measured photoelectron spectra (see “Methods”). The calculated one- and two-photon absorption intensity above the Fermi level presented in the inset of Fig. 3 corresponds to an excitation of 0.25 electrons per FM unit cell of FeRh (see Fig. 1a), i.e., ~1022 cm−3. This is close to the experimental estimate of 0.15 electrons per unit cell for a 5.6 mJ/cm2 fluence. In Fig. 3, the calculated XPS spectrum and its time evolution are obtained considering (i) the time evolution of the electronic distribution function fnk(t), and (ii) the time evolution of the electronic band structure ϵnk(t) (see “Methods”). The changes in fnk(t) can give a significant signal only in the red and green shaded regions between −1.55 eV and +1.55 eV, since the electron redistribution caused by two-photon absorption process is negligible. Thus, the signal below −1.55 eV is fully due to changes in ϵnk(t). The fact that it is negative implies a reduction in the density of states (see the relative height difference of the red and blue solid curves in Fig. 3). On the other hand, the changes in the region between −1.55 eV and 0 eV result from two effects that sum up to a negligible signal. fnk(t) gives a negative contribution due to the promotion of electrons to states above the Fermi level. For the overall signal to be negligible, the change in ϵnk(t) must result in an increase of the density of states which compensates the reduction in the occupations. Such compensation is almost exact in the experimental data, leading to an overall signal that appears as a reduction of the broad peak at ≈−2 eV. The same compensation is only partial in the simulation leading to an overall signal that appears as a shift of the same peak. The region above the Fermi level seems to be mainly governed by fnk(t). The overall agreement between theory and experiment is very good. The observed slight differences may be due to relaxation processes in the experiment already active during the pumping phase, making the electron distribution more peaked toward the Fermi level.
The relaxation of excited electrons proceeds with the formation of a peak above the Fermi level between 100 fs and 300 fs (see Fig. 2b). At a time delay of around 400 fs, the peak crosses the Fermi level and after 500 fs, its position stabilizes at the energy value which is characteristic for the Fe minority band of the FM phase in FeRh45. We also observe a modest but perceptible decrease (increase) of the spectral weight around −0.5 eV (−1.4 eV) binding energy for t > 0.3 ps, a characteristic that matches the difference of the static AFM and FM photoelectron spectra in Fig. 1b. Additional pump-probe experiments at a slightly lower laser fluence of 4.5 mJ/cm2 show entirely equivalent electron dynamics in terms of the pump-induced increase in the density of states above EF, the subsequent relaxation of electrons and the subpicosecond formation of the minority band (see Supplementary Fig. 2). The fingerprint of the FOPT for laser fluences above ~3 mJ/cm2 remains 20 ps after the laser pulse (see Supplementary Fig. 2) and beyond (see ref. 45). Photoexcitation at fluences below this threshold gives rise to transient changes in the electronic occupation landscape, but does not cause a persistent modification of the band structure (see Supplementary Fig. 2).
Further insights into the FOPT dynamics are obtained from the complete differential matrix, presented in Fig. 4a, monitoring the modification of the electronic density at different time delays. We selected three energy ranges marked by the red, blue, and black bars placed on the right hand side of Fig. 4a. The first (red) accounts for the electronic density above 200 meV and identifies the total number of electrons injected into the unoccupied states upon photoexcitation. The second (blue) goes from −240 meV to 0 meV and is used to monitor the formation of the Fe minority peak across the phase transition. The third (black) includes the region from −2.8 eV to −1.8 eV and is used to follow the modification of deeper bands.
a Energy- and delay-dependent differential matrix of the measured photoelectron spectra. We subtracted the average of unpumped spectra (between −1 ps and −0.5 ps) from each measured spectrum. The effect of laser excitation is evident around time zero, indicating depletion of the occupied states and the corresponding population of the empty states. In addition, an increase in the electronic density close to the Fermi level is observed at positive time delays. The red, blue, and black bars on the right hand side mark the representative integration regions for tracking the electronic dynamics in the unoccupied states, the formation of the Fe minority peak, and the modification of the deeper bands, respectively. b Temporal evolution of the electronic density in the three characteristic energy regions marked in (a). The population of states above the Fermi level shows a fast rise and a consecutive decay around t0 (empty red circles). The deeper bands (empty black diamonds) show a corresponding depletion and recovery which reflects the dynamics of the unoccupied states. However, their occupation level stabilizes 300 fs after t0 and remains constant thereafter. The electronic density slightly below EF (filled blue circles) shows a moderate increase during the laser excitation up to 300 fs delay, followed by a pronounced increase due to the shift of Fe minority band below EF at a delay tD of 350 fs. This value was extracted by fitting the error function to the experimental results (black solid line). Subsequently, the minority Fe band peak intensity remains constant throughout the investigated delay range.
Figure 4b shows the time evolution of the integrated signal in each range. The injection of electrons into the unoccupied states takes place near zero delay (we recall that our system’s response function is 150 fs) and then rapidly decays (red empty circles), the process being finished by about 500 fs. The intensity at the position of the Fe minority peak starts to grow already during the laser excitation (filled blue circles), due to both the modification of the electronic structure and the Fermi level smearing. More specifically, this modest intensity growth starting at t = 0 is linked to the presence of an instantaneous increase in the density of states peaking right above the Fermi level (see Fig. 2b, t = 0 ps) and can be considered as a precursor of the metamagnetic phase transition. However, it is only about 300 fs after the excitation that the electronic density corresponding to the minority band peak displays a sharp increase, associated with a persistent band structure modification. The characteristic time delay tD and subsequent rise time τ of the transition are obtained by fitting the integrated electron density at the Fe minority peak region with an error function (see “Methods”) and yields values of tD = 350 ± 30 fs and τ = 220 ± 110 fs. In addition, the data represented by black diamonds in Fig. 4b, which indicate the time-dependent population of bands in a region below EF, nearly mirror the population of the unoccupied levels up to 300 fs, with a fast depletion and recovery. The curve stabilizes thereafter at a finite value, implying permanent modifications of the deeper bands already after 300 fs, during which the Fe minority peak is still shifting toward its final position at 150 meV below EF. Similar differences in the behavior of the electronic density at and below the Fermi level have been observed during ultrafast demagnetization process in Fe17 and Co18. In the present case, this behavior shows that the FOPT in FeRh is mediated by a transient electronic phase in which the electronic structure is different from both the AFM and FM phases. This precursory phase exists in a delay range from time zero up to 500 fs after laser excitation.
Discussion
The unexpected reduction of the photoelectron yield below the one-photon absorption range (~1.55 eV), an energy region where the electronic populations fnk(t) cannot be strongly affected by the laser excitation, is explained by theoretical calculations. The effect can only be accounted for by considering the photoinduced change in the electronic band structure (i.e., density of states). Time-resolved XPS spectra are usually described and interpreted in terms of changes in the population fnk(t) only. This is clearly insufficient for the ultrafast dynamics in FeRh, since changes in ϵnk(t) must be considered on the same level even before the phase transition is complete.
The changes in ϵnk(t) during and after photoexcitation provide insights into why FeRh would relax toward the FM phase. The photoexcitation process in the AFM state depletes the valence states, which are characterised by hybridized Fe-Rh bonding states, and fills the unoccupied states, where empty Fe “local minority-spin” anti-bonding states are mainly available. As a result two processes occur: a charge (and spin) transfer from Rh to Fe (Rh → Fe), and a symmetric spin transfer from Fe “local majority” → Fe “local minority” (Fe(↑) ↔ Fe(↓)). Simulated charge and spin density changes upon photoexcitation clearly show this, Fig. 5. Here, the blue regions around the Rh atoms indicate a charge depletion, which can only partially be explained by a local redistribution. Most of the charge is transferred to the Fe atoms (see Fig. 5a), while there is a strong charge depletion around Rh atoms (see Fig. 5b). The Rh → Fe process also increases the local spin density, along the Rh − Fe bonds, around the Rh atoms (see Fig. 5c). On the other hand, the Fe(↑) ↔ Fe(↓) is a pure spin transfer process, with a strong reduction (~10%) of the local momentum of the Fe atoms, which is transferred into the vicinity of the Rh atoms (see Fig. 5c).
a, b Changes in the charge density n(r, tf) − neq(r) and (c) spin density \({S}_{z}({{{{{{{\bf{r}}}}}}}},{t}_{f})-{S}_{z}^{eq}({{{{{{{\bf{r}}}}}}}})\) at the end of the laser pulse (t = tf) with respect to the equilibrium configuration. Densities are in atomic units ([\(e/{a}_{0}^{3}\)] and [\({\mu }_{{{\mbox{B}}}}/{a}_{0}^{3}\)], where a0 = 5.29 × 10−11 m is the Bohr radius. 0.25 electron per unit cell corresponds to a density of \(7\times 1{0}^{-4}\ e/{a}_{0}^{3}\).) on two different FeRh{111}-planes: the plane just below the Fe(↑) atoms (a) and the plane containing the Rh atoms (b, c). Fe and Rh atom positions are indicated by red and gray segments of the lattice, respectively. Charge is transferred from the occupied (bonding) orbitals of Rh atoms (panel b), to the unoccupied (anti-bonding) orbitals of Rh and Fe (a). Since the Fe anti-bonding levels are filled in this process, the local Fe spin density is reduced. As a result, there is a redistribution of spin density around the Rh atoms and a reduction of the local spin moment at the Fe atoms (c). The movies in the Supplementary Information show the simulated time evolution of the charge density variations at the Fe and Rh sites as represented in (a) and (b) at the beginning and the end of the laser pulse.
In the AFM phase, the zero magnetic moment around the Rh atoms is a result of a non-vanishing spin density that integrates to zero because of the hybridization with surrounding Fe atoms with opposite moments3,41,46. The photoexcitation alters this delicate balance. As shown for the magnetic disorder associated with the temperature increase, the decrease of the Fe-Fe first-neighbor AFM couplings favors the FM order of the Fe subsystem, while inducing magnetic fluctuations on the Rh sites3. In turn, the induced Rh magnetic moments stabilize the FM over the AFM state3,33,47,48. Our simulations therefore suggest that the change of Fe-Rh hybridization (Rh → Fe process) and the optically induced intersite spin transfer (OISTR, Fe(↑) ↔ Fe(↓) process) play a crucial role in the photo-induced transition. The OISTR process has been recently proposed, on the basis of TD-DFT simulations, as a key mechanism also in other multicomponent magnetic materials49,50,51. Here, it causes to weaken the AFM ordering but is not sufficient to trigger the magnetic transition alone (just after the photoexcitation, the system is still in the AFM phase).
The theoretical simulation, not including dissipating effects, cannot describe the dynamics after the photoexcitation when electron-electron, electron-phonon and electron-magnon interactions are at play, and the actual phase transition takes place. Taking into account dissipating effects, one would expect further dynamics of both fnk(t) and ϵnk(t): the formation of a Fermi distribution and its subsequent cooling (for fnk(t)), and the formation of the FM band structure (for ϵnk(t)). Instead, our experimental time resolution is fast enough to allow the identification of a bottleneck time in this process, i.e., the metamagnetic transformation exhibiting a 350 fs delay. It is associated with a change in the band structure, with the spin-minority Fe band slightly pushed below the Fermi level and getting filled by the electrons that progressively cool down. This transformation occurs on a subpicosecond timescale that is faster than what was determined by previous experiments on FeRh with a lower time resolution45. Most importantly, our results set a new timescale that is faster than the lattice expansion and the establishment of the macroscopic, long-range magnetic order35,36,37.
The process is schematically depicted in Fig. 1b. Immediately after the action of the pulse, a significant number of electrons is excited to unoccupied states, with a non-thermal distribution of electrons fnk(t) (red arrow in Fig. 1b) decaying toward the Fermi level on a time scale of about 200 fs. This initial stage can be considered as a precursor of the FM phase and is accompanied by the slower dynamics of the band structure ϵnk with the formation of the peak of the Fe minority band. The peak crosses the Fermi level at about 350 fs delay, and stabilizes at −150 meV binding energy after 400 fs. During this step, the system undergoes a purely electronic transition through a transient phase, where the electronic band configuration evolves from ϵnk(t) to an intermediate electronic FM phase \({\epsilon }_{n{{{{{{{\bf{k}}}}}}}}}^{e-FM}\) (blue arrow in Fig. 1b). Once the electronic distribution reaches the configuration of the FM phase (after 400 fs), the relaxation of the lattice parameter toward the equilibrium value of the FM phase then follows on a longer time scale (black arrow in Fig. 1b).
In conclusion, we determine the existence of a transient electronic phase needed to induce the AFM to FM phase transition of FeRh using pump-probe photoelectron spectroscopy at the FLASH FEL facility. The results are supported by electronic structure calculations, which explain the details of the dynamics following the laser excitation. The time-resolved photoemission experiment at a laser fluence of 5.6 mJ/cm2 is well reproduced assuming the excitation of 0.25 electrons per unit cell of FeRh. At these fluences, the photon absorption cannot be described simply as promotion of electrons from filled to empty states of the calculated band structure, but the modified electron population induces a modification of the band structure as well, which is confirmed by the good agreement between theory and experiments. The laser excitation results in the transfer of electrons from the occupied d orbitals below the Fermi level to the unoccupied d orbitals above the Fermi level, with a partial transfer of electrons from the Rh to the Fe sites. The transient electronic phase exists up to 500 fs after the laser excitation. The emergence of the FM phase can be followed by the appearance and position of the Fe minority band near the Fermi level with characteristic time of τ = 220 ± 110 fs. Photoexcited electrons relax across the Fermi level and establish the FM electronic band structure 400 fs after the laser excitation. We thus conclude that metamagnetism in FeRh is triggered on a subpicosecond time scale. Further exploration of the laser-induced dynamics in ultrathin and nanoscale confined FeRh31 could lead to ultrafast devices based on magnetic order-order phase transitions at room temperature.
Methods
Sample and surface preparation
The sample consists of an epitaxial 80-nm-thick FeRh(001) film grown onto a MgO(001) substrate by dc magnetron sputtering using an equiatomic target. The films were grown at 725 K and post-annealed in situ at 1070 K for 45 min in order to achieve CsCl-type chemical ordering52. Upon cooling down the samples in the ultra high vacuum chamber, single-layer graphene is formed on top of the FeRh surface by segregating the carbon from the film53. This provides oxidation protection in air and avoids the need for further capping layers of the FeRh layer to be transported to the FEL facility without degradation. The sample surface was prepared via annealing only, in order to preserve the graphene layer, and tested with XPS prior to the time-resolved experiments as described in earlier works41,45. Examination with low-energy electron diffraction revealed the expected reconstruction pattern of the FeRh(001) surface.
Structural and magnetic characterization of FeRh films
X-ray reflectivity and x-ray diffraction measurements confirm the smooth character and high-quality FeRh(001) texture of the film. The existence of the magnetic phase transition was confirmed via temperature-dependent magnetization measurements using vibrating sample magnetometry (see Supplementary Fig. 1 for sample characterization and ref. 52 for additional information on FeRh films grown under equivalent conditions).
Experiment
The experiments are performed at the plane grating monochromator beamline54,55 at FLASH56,57, using the HEXTOF end-station58. The pump-probe scheme is established by a near-infrared pulse of 90 fs coupled with a FEL pulse of about 130 fs (both values are the full width half maximum, FWHM), which provide an estimated system response function58, i.e., the effective pump-probe correlation, of ~150 fs FWHM. The optical pump and x-ray probe energies were set to 1.55 eV and 123.5 eV, respectively. The energy resolution of ~150 meV is extracted from the Fermi level fit.
The sample temperature was kept at 348 K in the experimental chamber during all pump-probe photoelectron spectroscopy experiments reported here. At this temperature, the FeRh film is in the AFM phase during both the heating and cooling cycles (see Supplementary Fig. 1), which ensures the relaxation of the FeRh film back to the AFM phase between consecutive laser pulses.
Photoexcited electrons near normal emission were detected using a momentum microscope, which has an acceptance angle of 2π above the sample surface and can image the full Brillouin zone (BZ) with up to 7 Å−1 diameter58,59. We used a negative extractor voltage (~40 V with respect to the sample potential). This retarding field between the sample and extractor effectively removes the slow secondary electrons originating from the x-ray photons and pump-laser-induced slow electrons. All background electrons with energies less than ~4 eV are thus repelled within the first 400 μm above the sample surface. This removal of space charge comes at the expenses of k-resolution and causes a reduction of the k-field-of-view to 1.3 Å−1. Integrating over this k-field represents the integral of 60% of the BZ of FeRh, which was sufficient to well identify the peak associated with the FM phase. We characterize the sample surface by measuring the spectra of the system in the AFM and FM phases at fixed temperatures, and obtained line-shapes equivalent to those reported in ref. 45 (see Fig. 1d). The presence of the peak at about ~150 meV below the Fermi level is the signature of the Fe minority band characteristic of the FM phase. To fit the experimental data in Fig. 4b, we used an error function of the following form:
where y0 is a vertical offset, A is the amplitude, tD is the temporal onset of the transition (with respect to t0), and τ is the characteristic rise time.
Theory
We calculate from first principles the equilibrium and non–equilibrium properties of FeRh using the pw.x and yambo codes60,61,62,63 within Density Functional Theory (DFT) and its Time Dependent (TD–DFT) extension. At equilibrium both the FM and AFM phases are computed within the local density approximation (LDA) fully including spin–orbit coupling (SOC). An energy cut-off of 65 Ry is used for the wave–functions with a 5 × 5 × 5 sampling of the BZ for the self–consistent calculation. The experimental lattice parameter, 5.966 Å, is chosen for the AFM structure: an FCC unit cell containing 4 atoms (there is a factor 2 compared to the parameter of the BCC unit cell with 2 atoms used in ref. 64). The FM ground state is then computed for the same unit cell and for a unit cell with a 1% lattice expansion. LDA gives a low negative stress using the experimental value of the lattice parameters in both the FM and the AFM phase. We use the experimental values and we verified that changes in the lattice parameters very weakly affect the electronic density of states.
We also verified that the Generalized Gradient Approximation (GGA) gives small improvements in comparison with experimental values, which however are not relevant to the present work. For this reason we used LDA which is more easily handled in the non equilibrium TD–DFT simulations with SOC. Finally we verified that the AFM structure displays a phonon instability as reported in the literature64,65,66.
Subsequently, a non self–consistent calculation (NSCF) on a 8 × 8 × 8 sampling of the BZ is performed. The electronic density of states (DOS) of the two structures reported in Fig. 1c is computed starting from such NSCF calculation. We then construct the XPS spectrum from the projection of the DOS on the atomic orbitals of Fe and Rh. The projected DOS are weighted using tabulated photoionization cross sections67 for a probe of 125 eV (in practice the signal is dictated by Fe(3d) orbitals). Moreover, we use energy dependent lifetimes of the form \({\gamma }_{n{{{{{{{\bf{k}}}}}}}}}=A+B\ d({\epsilon }_{n{{{{{{{\bf{k}}}}}}}}})+C{({\epsilon }_{F}-{\epsilon }_{n{{{{{{{\bf{k}}}}}}}}})}^{2}\), where the first constant contribution A = 60 meV mimics the experimental resolution, the second term B, proportional to the electronic DOS d(ϵ), mimics the electron–phonon lifetimes, and the term which grows quadratically away from the Fermi level mimics the electron–electron lifetimes. Finally, the effect of temperature is included in the Fermi distribution used for the electronic occupations. The resulting spectrum is shown in Fig. 1c.
The TD–DFT simulations, as implemented in the yambo code68, are then performed propagating the Kohn–Sham density matrix in the basis–set of the equilibrium wave–functions under the action of the same pump pulse used in the experiment. The NSCF DFT calculation is used as a starting point for TD–DFT. The laser pulse parameters are equivalent to the experimental conditions. In particular, the fluence is chosen considering: (i) the experimental fluence, (ii) the fact that part of the pulse is reflected by the sample, and (iii) the fact that the external field is renormalized by the induced field. The effect of both (ii) and (iii) is estimated taking into account the dielectric function of bulk FeRh. In particular, point (iii) needs to be considered since we adopt the so called transverse gauge, where the macroscopic (or G = 0) component of the Hartree field is subtracted from the microscopic TD-DFT equations. In the input file we set the pulse intensity of 5 × 107 kW/cm2 and the FWHM of the intensity profile is 100 fs. We use a Gaussian envelope times a \(\sin (\omega t)\) function with ℏω = 1.55 eV. The code computes the fluence during the simulation corresponding to an absorbed fluence of 1.881 mJ/cm2. This compares fairly well with the experimental estimate. Using 1 − R ≈ 0.3138 and a laser fluence of 5.6 mJ/cm2, about 0.3138 × 5.6 mJ/cm2 ≈ 1.757 mJ/cm2 is absorbed by the sample. The density matrix is calculated on a 8 × 8 × 8 grid of k points in the BZ including all states from −3.5 up to 5.5 eV. The Kohn–Sham field felt by the electrons is updated at each time step during the simulation. The non-equilibrium DOS is then computed by diagonalizing the Hamiltonian evaluated from the photoexcited electron density after the action of the pump pulse. The adiabatic non-equilibrium XPS spectrum is finally computed using the same smearing used for the equilibrium spectra. The electronic occupation is obtained from the diagonal elements of the density matrix in the basis updated during the course of the simulation.
Code availability
The data that support the findings of this study are available from the corresponding author upon reasonable request. The codes used for the ab-initio electron dynamics calculations are freely distributed under GPL license under the link https://github.com/yambo-code/yambo.
Change history
03 May 2023
A Correction to this paper has been published: https://doi.org/10.1038/s41467-023-38263-5
References
Li, T. et al. Femtosecond switching of magnetism via strongly correlated spin–charge quantum excitations. Nature 496, 69–73 (2013).
De Jong, S. et al. Speed limit of the insulator–metal transition in magnetite. Nat. Mater. 12, 882–886 (2013).
Polesya, S., Mankovsky, S., Ködderitzsch, D., Minár, J. & Ebert, H. Finite-temperature magnetism of ferh compounds. Phys. Rev. B 93, 024423 (2016).
Wollmann, L., Nayak, A. K., Parkin, S. S. & Felser, C. Heusler 4.0: tunable materials. Annu. Rev. Mater. Res. 47, 247–270 (2017).
Rohwer, T. et al. Collapse of long-range charge order tracked by time-resolved photoemission at high momenta. Nature 471, 490–493 (2011).
Fausti, D. et al. Light-induced superconductivity in a stripe-ordered cuprate. Science 331, 189–191 (2011).
Singer, A. et al. Photoinduced enhancement of the charge density wave amplitude. Phys. Rev. Lett. 117, 056401 (2016).
Wegkamp, D. et al. Instantaneous band gap collapse in photoexcited monoclinic vo2 due to photocarrier doping. Phys. Rev. Lett. 113, 216401 (2014).
Shao, Z., Cao, X., Luo, H. & Jin, P. Recent progress in the phase-transition mechanism and modulation of vanadium dioxide materials. NPG Asia Mater. 10, 581–605 (2018).
Perfetti, L. et al. Time evolution of the electronic structure of 1t − tas2 through the insulator-metal transition. Phys. Rev. Lett. 97, 067402 (2006).
Stojchevska, L. et al. Ultrafast switching to a stable hidden quantum state in an electronic crystal. Science 344, 177–180 (2014).
Ono, A. & Ishihara, S. Double-exchange interaction in optically induced nonequilibrium state: A conversion from ferromagnetic to antiferromagnetic structure. Phys. Rev. Lett. 119, 207202 (2017).
Gray, A. X. et al. Correlation-driven insulator-metal transition in near-ideal vanadium dioxide films. Phys. Rev. Lett. 116, 116403 (2016).
Wall, S. et al. Tracking the evolution of electronic and structural properties of vo2 during the ultrafast photoinduced insulator-metal transition. Phys. Rev. B 87, 115126 (2013).
Morrison, V. R. et al. A photoinduced metal-like phase of monoclinic vo2 revealed by ultrafast electron diffraction. Science 346, 445–448 (2014).
Beaurepaire, E., Merle, J.-C., Daunois, A. & Bigot, J.-Y. Ultrafast spin dynamics in ferromagnetic nickel. Phys. Rev. Lett. 76, 4250–4253 (1996).
Gort, R. et al. Early stages of ultrafast spin dynamics in a 3d ferromagnet. Phys. Rev. Lett. 121, 087206 (2018).
Eich, S. et al. Band structure evolution during the ultrafast ferromagnetic-paramagnetic phase transition in cobalt. Sci. Adv. 3, e1602094 (2017).
Tengdin, P. et al. Critical behavior within 20 fs drives the out-of-equilibrium laser-induced magnetic phase transition in nickel. Sci. Adv. 4, eaap9744 (2018).
Andres, B. & Weinelt, M. Spin-resolved electronic structure of 3d transition metals during ultrafast demagnetization. J. Magn. Magn. Mater. 501, 166475 (2020).
Eschenlohr, A. et al. Ultrafast spin transport as key to femtosecond demagnetization. Nat. Mater. 12, 332–336 (2013).
Bergeard, N. et al. Hot-electron-induced ultrafast demagnetization in Co/Pt multilayers. Phys. Rev. Lett. 117, 147203 (2016).
Carva, K., Battiato, M., Legut, D. & Oppeneer, P. M. Ab initio theory of electron-phonon mediated ultrafast spin relaxation of laser-excited hot electrons in transition-metal ferromagnets. Phys. Rev. B 87, 184425 (2013).
Matsubara, M. et al. Ultrafast photoinduced insulator-ferromagnet transition in the perovskite manganite gd0.55sr0.45mno3. Phys. Rev. Lett. 99, 207401 (2007).
Bossini, D. et al. Femtosecond activation of magnetoelectricity. Nat. Phys. 14, 370–374 (2018).
Kirilyuk, A., Kimel, A. V. & Rasing, T. Ultrafast optical manipulation of magnetic order. Rev. Mod. Phys. 82, 2731–2784 (2010).
Fallot, M. & Hocart, R. Sur l’apparition du ferromagnétisme par élévation du température dans des alliages de fer et de rhodium. Rev. Sci. 77, 498–501 (1939).
Kouvel, J. S. & Hartelius, C. C. Anomalous magnetic moments and transformations in the ordered alloy FeRh. J. Appl. Phys. 33, 1343–1344 (1962).
Maat, S., Thiele, J.-U. U. & Fullerton, E. E. Temperature and field hysteresis of the antiferromagnetic-to-ferromagnetic phase transition in epitaxial FeRh films. Phys. Rev. B 72, 214432 (2005).
Baldasseroni, C. et al. Temperature-driven nucleation of ferromagnetic domains in FeRh thin films. Appl. Phys. Lett. 100, 262401 (2012).
Uhlíř, V., Arregi, J. A. & Fullerton, E. E. Colossal magnetic phase transition asymmetry in mesoscale ferh stripes. Nat. Commun. 7, 13113 (2016).
Keavney, D. J. et al. Phase coexistence and kinetic arrest in the magnetostructural transition of the ordered alloy ferh. Sci. Rep. 8, 1778 (2018).
Ju, G. et al. Ultrafast generation of ferromagnetic order via a laser-induced phase transformation in FeRh thin films. Phys. Rev. Lett. 93, 197403 (2004).
Thiele, J.-U., Buess, M. & Back, C. H. Spin dynamics of the antiferromagnetic-to-ferromagnetic phase transition in ferh on a sub-picosecond time scale. Appl. Phys. Lett. 85, 2857–2859 (2004).
Bergman, B. et al. Identifying growth mechanisms for laser-induced magnetization in ferh. Phys. Rev. B 73, 060407(R) (2006).
Radu, I. et al. Laser-induced generation and quenching of magnetization on FeRh studied with time-resolved x-ray magnetic circular dichroism. Phys. Rev. B 81, 104415 (2010).
Mariager, S. O. et al. Structural and magnetic dynamics of a laser induced phase transition in ferh. Phys. Rev. Lett. 108, 087201 (2012).
Quirin, F. et al. Structural dynamics in FeRh during a laser-induced metamagnetic phase transition. Phys. Rev. B 85, 020103(R) (2012).
Lee, J. S., Vescovo, E., Plucinski, L., Schneider, C. M. & Kao, C. C. Electronic structure and magnetic properties of epitaxial FeRh(001) ultra-thin films on W(100). Phys. Rev. B 82, 224410 (2010).
Gray, A. X. et al. Electronic structure changes across the metamagnetic transition in FeRh via hard X-ray photoemission. Phys. Rev. Lett. 108, 257208 (2012).
Pressacco, F. et al. Stable room-temperature ferromagnetic phase at the FeRh(100) surface. Sci. Rep. 6, 22383 (2016).
Maiti, K., Malagoli, M. C., Magnano, E., Dallmeyer, A. & Carbone, C. Electronic band structure of gd: A consistent description. Phys. Rev. Lett. 86, 2846–2849 (2001).
Beaulieu, N. et al. Probing ultrafast dynamics in electronic structure of epitaxial gd(0001) on w(110). J. Electron Spectrosc. 189, 40–45 (2013).
Sirotti, F. et al. Multiphoton k-resolved photoemission from gold surface states with 800-nm femtosecond laser pulses. Phys. Rev. B 90, 035401 (2014).
Pressacco, F. et al. Laser induced phase transition in epitaxial FeRh layers studied by pump-probe valence band photoemission. Struct. Dyn. 5, 034501 (2018).
Sandratskii, L. M. & Mavropoulos, P. Magnetic excitations and femtomagnetism of ferh: A first-principles study. Phys. Rev. B 83, 174408 (2011).
Gruner, M. E., Hoffmann, E. & Entel, P. Instability of the rhodium magnetic moment as the origin of the metamagnetic phase transition in α − FeRh. Phys. Rev. B 67, 064415 (2003).
Gu, R. Y. & Antropov, V. P. Dominance of the spin-wave contribution to the magnetic phase transition in ferh. Phys. Rev. B 72, 012403 (2005).
lliott, P., Müller, T., Dewhurst, J. K., Sharma, S. & Gross, E. K. U. Ultrafast laser induced local magnetization dynamics in heusler compounds. Sci. Rep. 6, 38911 (2016).
Dewhurst, J. K., Elliott, P., Shallcross, S., Gross, E. K. U. & Sharma, S. Laser-induced intersite spin transfer. Nano Lett. 18, 1842–1848 (2018).
Hofherr, M. et al. Ultrafast optically induced spin transfer in ferromagnetic alloys. Sci. Adv. 6, eaay8717 (2020).
Arregi, J. A., Caha, O. & Uhlíř, V. Evolution of strain across the magnetostructural phase transition in epitaxial FeRh films on different substrates. Phys. Rev. B 101, 174413 (2020).
Uhlíř, V. et al. Single-layer graphene on epitaxial FeRh thin films. Appl. Surf. Sci. 514, 145923 (2020).
Martins, M. et al. Monochromator beamline for FLASH. Rev. Sci. Instr. 77, 115108 (2006).
Gerasimova, N., Dziarzhytski, S. & Feldhaus, J. The monochromator beamline at flash: performance, capabilities and upgrade plans. J. Mod. Opt. 58, 1480–1485 (2011).
Ackermann, W. et al. Operation of a free-electron laser from the extreme ultraviolet to the water window. Nat. Photonics 1, 336–342 (2007).
Rossbach, J., Schneider, J. R. & Wurth, W. 10 years of pioneering x-ray science at the free-electron laser flash at desy. Phys. Rep. 808, 1–74 (2019).
Kutnyakhov, D. et al. Time-and momentum-resolved photoemission studies using time-of-flight momentum microscopy at a free-electron laser. Rev. Sci. Instrum. 91, 013109 (2020).
Schönhense, G., Medjanik, K. & Elmers, H. J. Space-, time- and spin-resolved photoemission. J. Electron Spectros. Relat. Phenomena 200, 94–118 (2015).
Giannozzi, P. et al. Quantum espresso: a modular and open-source software project for quantum simulations of materials. J. Phys.: Condens. Matter 21, 395502 (2009).
Giannozzi, P. et al. Advanced capabilities for materials modelling with quantum espresso. J. Phys.: Condens. Matter 29, 465901 (2017).
Marini, A., Hogan, C., Grüning, M. & Varsano, D. yambo: An ab initio tool for excited state calculations. Comput. Phys. Commun. 180, 1392–1403 (2009).
Sangalli, D. & Marini, A. Ultra-fast carriers relaxation in bulk silicon following photo-excitation with a short and polarized laser pulse. Europhys. Lett. 110, 47004 (2015).
Aschauer, U., Braddell, R., Brechbühl, S. A., Derlet, P. M. & Spaldin, N. A. Strain-induced structural instability in ferh. Phys. Rev. B 94, 014109 (2016).
Wolloch, M. et al. Impact of lattice dynamics on the phase stability of metamagnetic ferh: Bulk and thin films. Phys. Rev. B 94, 174435 (2016).
Zarkevich, N. A. & Johnson, D. D. Ferh ground state and martensitic transformation. Phys. Rev. B 97, 014202 (2018).
Yeh, J. & Lindau, I. Atomic subshell photoionization cross sections and asymmetry parameters: 1≤ z ≤103. At. Data Nucl. Data Tables 32, 1–155 (1985).
Sangalli, D. et al. Many-body perturbation theory calculations using the yambo code. J. Phys.: Condens. Matter 31, 325902 (2019).
Shirane, G., Chen, C., Flinn, P. & Nathans, R. Hyperfine fields and magnetic moments in the fe–rh system. J. Appl. Phys. 34, 1044–1045 (1963).
Acknowledgements
This work is dedicated to Wilfried Wurth, who passed away on May 8, 2019. We acknowledge support by the scientific and technical staff of FLASH, as well as Holger Meyer and Sven Gieschen form University of Hamburg. This work was supported by the excellence cluster “The Hamburg Centre for Ultrafast Imaging—Structure, Dynamics and Control of Matter at the Atomic Scale” of the Deutsche Forschungsgemeinschaft (DFG EXC 1074) and through the SFB 925 “Lichtinduzierte Dynamik und Kontrolle korrelierter Quantensysteme” (project B2). It received funding from the EU-H2020 research and innovation program under European Union projects “MaX” Materials design at the eXascale H2020-EINFRA-2015-1 (Grant Agreement No. 824143) and “NFFA” Nanoscience Foundries and Fine Analysis-Europe H2020-INFRAIA-2014-2015 (Grant Agreement No. 654360) having benefited from the access provided by the ISM node (CNR, Italy), user-project IDs 247 and 669. We acknowlege the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—TRR 173—268565370 (projects A02 and A05). Access to the CEITEC Nano Research Infrastructure was supported by the Ministry of Education, Youth and Sports (MEYS) of the Czech Republic under the projects CEITEC 2020 (LQ1601) and CzechNanoLab (LM2018110). We acknowledge funding from the Italian project MIUR PRIN Grant No. 20173B72NB. This work has received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie and it is co-financed by the South Moravian Region under grant agreement No. 665860.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
F.P., V.U., J.A.A., M.G., D.S., and F.S. designed the project. F.P., D.K., M.H., S.Y.A., G.B., H.R., D.V., V.U., J.A.A., and F.S. performed the time-resolved XPS experiments and analyzed the data. M.G., D.S., and A.M. designed the theoretical approach to the problem. J.A.A. and V.U. prepared and characterized the samples. All authors discussed the results. F.P., V.U., J.A.A., D.S., M.G., and F.S. wrote the paper with contributions from all authors and critical revision from J.D., G.S., and W.W.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks J. Kay Dewhurst and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pressacco, F., Sangalli, D., Uhlíř, V. et al. Subpicosecond metamagnetic phase transition in FeRh driven by non-equilibrium electron dynamics. Nat Commun 12, 5088 (2021). https://doi.org/10.1038/s41467-021-25347-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-021-25347-3
This article is cited by
-
Ultra-high spin emission from antiferromagnetic FeRh
Nature Communications (2024)
-
Spin current driven by ultrafast magnetization of FeRh
Nature Communications (2023)
-
High-speed metamagnetic switching of FeRh through Joule heating
Scientific Reports (2022)
-
Ultrafast kinetics of the antiferromagnetic-ferromagnetic phase transition in FeRh
Nature Communications (2022)
-
Determination of sub-ps lattice dynamics in FeRh thin films
Scientific Reports (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.