Abstract
Knowledge of electrolyte transport and thermodynamic properties in Li-ion and beyond Li-ion technologies is vital for their continued development and success. Here, we present a method for fully characterising electrolyte systems. By measuring the electrolyte concentration gradient over time via operando Raman microspectroscopy, in tandem with potentiostatic electrochemical impedance spectroscopy, the Fickian “apparent” diffusion coefficient, transference number, thermodynamic factor, ionic conductivity and resistance of charge-transfer were quantified within a single experimental setup. Using lithium bis(fluorosulfonyl)imide (LiFSI) in tetraglyme (G4) as a model system, our study provides a visualisation of the electrolyte concentration gradient; a method for determining key electrolyte properties, and a necessary technique for correlating bulk intermolecular electrolyte structure with the described transport and thermodynamic properties.
Similar content being viewed by others
Introduction
Since the commercial development of lithium-ion batteries (LIBs) in the early 1990s, they have been employed in many applications that society now depends on.1 Research into “beyond lithium-ion” technologies, such as lithium metal batteries (LMBs), has also surged in popularity in recent years, with demand for secondary battery technologies increasing considerably as governments aim to become carbon neutral.2 Battery performance is highly dependent on the transport and thermodynamic properties of their electrolyte.3 In LMBs specifically, the uniformity of lithium plating is severely affected by the transport properties of the electrolyte, thus playing a crucial role in the formation and propagation of lithium dendrites.4,5 It is therefore of paramount importance to be able to accurately measure and ultimately improve these properties for the continued development of innovative battery technologies.
For a full understanding of an electrolyte system, the ionic conductivity (κ), Fickian “apparent” diffusion coefficient (Dapp), cationic transference number (\({t}_{+}^{0}\)), molar thermodynamic factor (χM) and interfacial charge-transfer resistance (Rct) are key parameters.6,7,8 Each of these concentration-dependent properties provides information toward a comprehensive picture of the electrolyte’s transport, thermodynamic state, and interfacial kinetics.
Dapp and \({t}_{+}^{0}\) dictate whether, and to what extent, concentration gradients across cells form. The formation of such gradients leads to concentration overpotential (ηc), which can be harmful to all battery types’ performance, especially their rate capability.9,10Dapp is characterised through Fick’s laws of diffusion, and \({t}_{+}^{0}\) is defined as the proportion of current carried by the cation. Each is conventionally measured through different electrochemical techniques, with Dapp occasionally assessed using restricted-diffusion cells,7,11,12 and \({t}_{+}^{0}\) from either the Hittorf method7,11,13,14,15, pulsed-field gradient NMR16 or a “steady-state current” method, like the Bruce–Vincent.17,18,19 Each have their limitations, with Hittorf often requiring large volumes of electrolyte and not being able to measure in situ concentration changes, and steady-state methods making assumptions such as the electrolyte being infinitely dilute (perfectly ideal).20
χM provides a link between observed concentration and thermodynamic activity.21,22 It is influenced by ion association, with the formation of solvent-separated ion pairs (SSIPs), contact ion pairs (CIPs) and aggregates (AGGs), and the extent and orientation of solvation. It is classically explored by measuring the liquid-junction potential in a concentration cell, between a “test” concentration and a “reference” concentration7,13,14,15,23. The measurement is quite rarely performed when characterising new electrolytes but is of critical importance for understanding how its thermodynamic state is influenced by electrolyte structure.
In addition, with electrolyte intermolecular structure influencing interfacial resistances, through charge-transfer, and compositional influence on the solid electrolyte interphase (SEI),24 measurings Rct is critical.8,25
While others have reported individual setups for measuring electrolyte properties, here we disclose a unified method for determining κ, Dapp, \({t}_{+}^{0}\), χM and Rct. This was achieved by visualising and fitting electrolyte concentration gradients using operando scanning Raman microspectroscopy, in tandem with potentiostatic electrochemical impedance spectroscopy (PEIS). The fitting of concentration gradients over time allowed for the direct measurement of the evolving diffusion length (Ld) and interfacial gradient (dcs/dz∣z = 0,L), which led to the determination of Dapp and \({t}_{+}^{0}\) respectively. Also, by monitoring the progressing concentration at each cell extreme as the gradient was forming, and using chronopotentiometry (CP) data and PEIS to calculate ηc, χM was calculated. This is the first time χM has been measured in such a dynamic setup. Moreover, by measuring Dapp, \({t}_{+}^{0}\), κ and the χM, a detailed picture of the multi-component electrolyte system was obtained through Stefan–Maxwell coefficients,21 which describes the frictional interaction between species. Our described setup is advantageous for numerous reasons: namely, the amount of information one can obtain in a single experiment; the small instrumental error involved by having one method to measure all properties; the small volume of electrolyte required (<1 mL), reducing waste and allowing for analysis even at small scale, and its compatibility with concentrated-solution theory.21
Importantly, by determining these electrolyte properties using a spectroscopic technique such as Raman microspectroscopy, microscopic electrolyte structural information can be correlated to macroscopically determined phenomena such as those listed above. Although there have been some Raman spectroscopy studies measuring [Li+],26,27,28,29, this is the first that measures the entire concentration gradient formation as current is passed, with the extraction of critical electrolyte properties. X-ray30 and NMR31,32,33 techniques have also been recently used to measure concentration gradients, with an aim of understanding \({t}_{+}^{0}\) specifically. These methods are often unavailable to many researchers, so our technique provides a more readily available alternative. Furthermore, our focus here is to fully characterise the electrolyte by clearly measuring five key parameters, when other studies only calculate one or two.
We applied our method to lithium bis(fluorosulfonyl)imide (LiFSI) in tetraethylene glycol dimethyl ether (tetraglyme—G4) over a concentration range of 0.25–2 m. LiFSI is an increasingly popular salt used in lithium metal anode studies due to its low viscosity in typical solvents and desirable decomposition products (e.g., LiF) that form the SEI.8 Fluoride-rich SEI layers have shown to be effective at suppressing dendrite growth due to the electronic insulation and high surface energy of LiF.34,35 Glymes are also popular for use against lithium metal (in LMBs) because of their cathodic stability and low viscosity. G4 has been shown to exhibit low flammability, low volatility and cathodic stabilities below 0 V vs. Li+/Li.36 They have been studied for their use in Li–O2 and Li–S batteries in particular.
In summary, this study demonstrates a novel experimental setup that uses operando Raman microspectroscopy to measure concentration gradients, enabling the determination of fundamental concentration-dependent electrolyte properties: κ, Rct, Dapp, \({t}_{+}^{0}\) and χM. Using LiFSI in G4, each described electrolyte property is measured and reported, gaining valuable insight into the electrolyte system. We hope our study provides a foundation for the full characterisation of electrolytes using operando Raman microspectroscopy.
Results
The developing Li+ concentration gradient between the electrodes of a symmetric lithium cell was determined using a scanning confocal Raman microspectrometer (Renishaw inVia Reflex); specifically acquiring a time-series of one-dimensional (1D) Raman lines scans across the interelectrode space of a custom-built optical cell, with 8 mm diameter electrodes, while the current was passed. Line scans, consisting of 50 scanning points covering a distance of 1.5 cm, were performed every 4 h for 24–48 h depending on the LiFSI concentration being investigated. Concentrated electrolytes required a longer investigation period for a substantial gradient to form. Each line scan took 20 min to complete. Measurements were performed at 20 °C.
Through isolation of a concentration sensitive FSI− Raman band, we were able to equate each Raman spectrum in a line scan to the local Li+ concentration. This was following an instrument calibration of LiFSI solutions of known concentration, equating [FSI−] with [Li+]. Specifically, we normalised each spectral peak against the 1471 cm−1 –CH2 bending/scissoring mode solvent peak height, and correlated the 717 cm−1 FSI− S–N–S bend peak area with concentration. The increasing area of the 717 cm−1 peaks is illustrated in Fig. 2b, along with the emergence of CIPs and AGGs with increasing concentration, as the shoulder peaks begin to dominate. The calibration curve is illustrated in Fig. 2c. Also labelled in Fig. 2a is the peak at 868 cm−1; as noted in Supplementary Fig. 8a, its increasing intensity with concentration signifies the complexation of Li+ ions with G4, [Li(G4)]+. The 868 cm−1 peak represents the breathing mode of this crown ether-like structure.36 The description of the intermolecular structure that these peaks provide will be used in subsequent sections to understand each macroscopic trend.
By fitting the acquired spectra and the resulting concentration gradients we were able to extract Dapp, t\({}_{+}^{0}\) and χM of the studied electrolyte system. Complementary PEIS measurements at open circuit potential, first after an initial rest period of 4 h, and then interspaced between Raman line scans, enabled us to measure κ and the evolution of Rct. The latter allowing an accurate measurement of the concentration overpotential (ηc) over time.
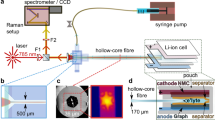
Figure 1 illustrates both the setup used and the extracted properties that were measured. Important to note, the operando cell was placed vertically on the scanning stage, with plating Li+ occurring at the top and stripping from the bottom of the cell. This avoided detrimental natural convection, as illustrated in Supplementary Fig. 3a. To ensure the validity of the diffusion equation boundary conditions (Eqs. (1)–(3)) used to extract the stated parameters, an interelectrode distance of 1.5 cm was chosen. The optimal measurement current density was determined to be 100 μA cm−2, ensuring the development of a concentration gradient detectable by the instrumentation, while equally avoiding dendrite formation. Instrumentation and acquisition details are provided in Supplementary Figs. 1–3 and the “Methods”.
Li+ concentration (cs) gradient formation in an optical Li/Li symmetric cell, while current is passed. Using a scanning confocal Raman microspectrometer, a time-series of one-dimensional line scans was performed to obtain a progression of concentration gradients; measured with the stage moving in the z-direction. The cell was placed vertically on the stage to avoid natural convection. Potentiostatic electrochemical impedance spectroscopy (PEIS) was also performed prior to passing current to quantify ionic conductivity (κ) and resistance of charge-transfer (Rct), and between line scans to obtain an accurate concentration overpotential (ηc). Using the diffusion length (Ld), interfacial gradient (dcs/dz∣z = 0,L) and ηc from each concentration profile, the Fickian “apparent” diffusion coefficient (Dapp), cation transference number (\({t}_{+}^{0}\)), and molar thermodynamic factor (χM), were calculated.
To validate and test the described methodology, a 1 m LiFSI in the G4 system was chosen as a model system. Molalities were used for increased reliability and accuracy of electrolyte preparation; for density measurements, and molarity equivalents see Supplementary Method 1.
Figure 3a shows the concentration gradient of the 1 m electrolyte after 12 h, illustrating a clear drop in concentration on the plating side and an equally noteworthy concentration increase on the stripping side. Profiles were fitted using non-linear least-squares minimisation with equation (1). Equation (1) is a solution to the diffusion equation,21,37 in a symmetric cell setup, using the cation flux law as a spatial boundary condition. A full derivation of this equation is presented in Supplementary Note 1, Eqs. (6)–(19).
Where:
\({c}_{s}^{* }\) is the initial concentration, cs is the concentration of the salt, t is time, L is the distance between the electrodes, J is the applied current density, n is the number of moles, and the final factor in parentheses represents how solvent concentration is changing with respect to salt concentration at the interface, which we termed the “solvent velocity factor”. By including this factor, the cationic transference number is labelled \({t}_{+}^{0}\). If not referenced against the solvent velocity, t+ is used. Supplementary Fig. 6b illustrates how this factor changes with concentration, showing that its inclusion becomes increasingly important at high concentrations. b is equal to the diffusion length (Ld), and a as the interfacial salt concentration gradient (dcs/dz∣z = 0,L). c0 is equal to (1 − Vscs)/V0, where Vs and V0 are the partial molar volumes of the salt and solvent respectively.21 Supplementary Method 2 describes how Vs and V0 were calculated, and how the resulting solvent concentration is distributed across the cell (Supplementary Fig. 6c).
Figure 3b shows concentration profiles with an 8 h gap between each line scan. As predicted, the interfacial gradient dcs/dz∣z = 0,L remained constant. Also one can note Ld extending into the centre of the cell with increasing time.
To measure Dapp, Ld was plotted vs. t1/2 in Fig. 3c, and the points were fitted to Ld = (Dt)1/2, with the error bars representing standard error from Eq. (1) fitting. From the weighted gradient fitting, Dapp was calculated as 7.22 ± 0.55 × 10−11 m2 s−1. This compared well to the often-used method in the literature that follows the semilog open-circuit voltage (OCV) vs. time,7,14 which we calculated as 6.98 × 10−11 m2 s−1. See Supplementary Note 5 for further details.
\({t}_{+}^{0}\) was calculated from dcs/dz∣z = 0,L (Eq. (2)), using Dapp from the previous calculation. Because dcs/dz∣z = 0,L remained constant over the measured time frame, \({t}_{+}^{0}\) was quantified from each measured gradient and averaged along with its standard error. Due to the concentration differences on each side of the cell, the solvent velocity factor from equation (2) was slightly different at each interface, leading to somewhat different \({t}_{+}^{0}\) values throughout the cell. Nevertheless, due to the error from the fitting, this difference was deemed negligible for the calculation. The solvent velocity factor at the central point of the cell was therefore used, which was equal to 1.08 for 1 m. \({t}_{0}^{+}\) was subsequently calculated as 0.352 ± 0.056. The values compared well to a Hittorf-style analysis using the same setup, where \({t}_{+}^{0}\) was calculated as 0.392 ± 0.006. See Supplementary Note 6 for more details. To check the reliability of the method the measurement was repeated twice more.
From the fitted profiles, the concentration at each interface was measured and using Eq. (4) below21χM was calculated from the gradient of a weighted linear fit, see Fig. 3d. The error bars represent uncertainty in interfacial concentration from the fitted profiles in the x-axis and error in the \({t}_{+}^{0}\) calculation in the y-axis.
Where f± is the molar activity coefficient. Using the PEIS data prior to each line scan, ηc was calculated by ηc = ηtotal − I(Rbulk + Rct), where ηtotal is measured from the chronopotentiometry data. Supplementary Fig. 8b illustrates how Rct was changing, showing that little change was occurring at the interface over time while applying 100 μA cm−2. χM for the 1 m electrolyte was calculated as 1.41 ± 0.33, which implied a higher “effective concentration” than the molarity that is used.38 This is a result of depleting free solvent, and increasing bound solvent, as is illustrated by the increasing 868 cm−1 peak intensity from Fig. 2b.
a Raman spectrum of 2 m LiFSI in G4 normalised to peak intensity at 1471 cm−1; identifying the 717 cm−1 FSI− S–N–S bending mode peak, 868 cm−1 [Li(G4)]+ crown ether-like breathing mode peak, 1471 cm−1 –CH2 bending/scissoring mode peak. b Normalised 717 cm−1 peak, showing broadening of the peak with concentration, indicating the evolution of CIPs and AGGs, as illustrated. c Calibration curve equating normalised 717 cm−1 peak area to concentration, which was used to determine the concentration gradient via operando Raman microspectroscopy 1D line scans. Error bars represent the propagated standard error from the balance and density measurements (x-axis) and area calculation from three separate Raman acquisitions (y-axis).
The Nyquist plot from PEIS, which was run after 4 h rest, is plotted in Fig. 3e. The ionic conductivity (κ) was determined with Eq. (5).
a The Li+ concentration profile in 1 m LiFSI in G4 electrolyte after applying 100 μA cm−2 of current for 12 h, with fitting (Eq. (1)). b Progression of a concentration gradient in 1 m electrolyte, after 4 h, 12 h, 20 h, 28 h. c Movement of Li+ diffusion length (Ld) with time1/2, showing linear behaviour for the Dapp calculation. Dapp = 7.22 ± 0.55 × 10−11 m2 s−1. d Plotting Eq. (4), illustrating how the ηc function changes linearly with respect to the natural log of concentration ratio of each cell extreme, to measure χM. χM = 1.41 ± 0.31. e PEIS Nyquist plot, with the equivalent circuit, of 1 m electrolyte, prior to current being passed, after 4 h rest, equating to κ = 2.70 ± 0.03 mS cm−1 and Rct = 92 ± 12 Ω cm2.
Where A is the electrode area. Using an optical cell makes it especially straightforward and accurate to measure L, which can be a problem when conventionally measuring Dapp and κ, where L can be difficult to control. For 1 m, κ = 2.70 ± 0.03 mS cm−1 and Rct = 92 ± 12 Ω cm2. Rct was assumed to be a combination of both resistances of classical charge transfer, and SEI resistance.39. For further information on error estimation calculations, refer to Supplementary Note 2.
Effect of concentration
The above method was applied to 0.25 m, 0.5 m, 1 m, 1.5 m and 2 m electrolyte solutions to compare κ, Rct, Dapp, \({t}_{+}^{0}\) and χM, for a broader understanding of the electrolyte system. Repeat runs were taken at each concentration, both with and without PEIS between each line scan to check the PEIS measurement was not affecting the gradient measurement.
Ionic conductivity and resistance of charge transfer
Supplementary Fig. 4 indicates clear differences in impedance with concentration. κ vs. concentration was plotted (Fig. 4a) and fitted with the function proposed by Casteel and Amis,40 see Supplementary Eq. (S22). κmax was calculated as 2.67 mS cm−1 at 0.99 M. κmax is lower than more conventional electrolytes, such as LP30 (~11 mS cm−1), due to its increased viscosity. cmax is very similar to most binary non-aqueous electrolytes based on carbonates or ethers, i.e., 1 M.6
a κ, fitted with the Casteel–Amis equation, κmax was calculated as 2.67 mS cm−1 and cmax as 0.99 M. b Rct, showing an initial drop with concentration, then a stabilising at 100–125 Ω cm2. c Dapp, observable was a decrease in Dapp with concentration. d \({t}_{+}^{0}\) showing an increase at low concentrations, then generally plateauing, and increasing again at 2 m. e (dc/dz)z=0,L, which was quite constant at low concentrations but increased rapidly after 1 m. This was concluded to be a result of a dramatic decrease in Dapp with concentration. f χM, which had values below 1 from 0 to 0.5 m, indicating association is dominating the thermodynamics and then begins to increase rapidly as solvation effects start to dominate, with ion-solvent effects out-competing ion-ion effects (χM = 1) at ~0.72 M.
As noted in Fig. 4b, there was an evident decrease in Rct going from 0.25 m to 1 m, but a flattening as one moved to higher concentrations. The decrease in Rct at lower concentrations is due to the dependence of concentration on interfacial kinetics, as is described by the exchange current density in electrochemical kinetics.37 The plateauing at higher concentrations could be a result of an increased resistivity of the SEI or an increased charge-transfer resistance from an increase in solvation energy. Structurally, an increased concentration leads to the formation of more CIP and AGG-type structures (see Fig. 2b) which inform the SEI composition more than at lower concentrations. Furthermore, the change in solvation structure may lead to an increase in activation overpotential if the solvation energy increases.
Diffusion coefficient
Figure 4c shows how Dapp magnitude was affected by changes in LiFSI concentration. Generally, we observed a decrease in Dapp with increasing concentration, which is common for electrolyte solutions. Grundy et al. reported the same trend with LiTFSI in G4.41 The absolute values appeared to agree with Grundy’s findings, although their chosen salt was LiTFSI, so would expect to have a slightly lower Dapp. Compared to other lithium-ion electrolytes, Dapp was quite low, with 1 M PC and EMC-based electrolytes exhibiting values 2–6 times higher.7,11 Decreasing Dapp with concentration is a result of an increasing association of ions and increasing complexation of Li+ with G4; an increasing frictional interaction between ions and solvent, as described by Stefan and Maxwell.42
Transference number
Figure 4d shows how \({t}_{+}^{0}\) was affected by concentration. As explicitly stated by Bazak et al., to measure \({t}_{+}^{0}\) with accuracy, a very precise measurement of local interfacial concentration gradients is required, due to the high sensitivity of \({t}_{+}^{0}\) with small changes in dcs/dz∣z=0,L. This, along with error propagation from calculating Dapp, could lead to poor reliability and large error, explaining the range of error in Fig. 4d, especially at high concentrations. That said, after multiple measurements, we noticed a trend, where \({t}_{+}^{0}\) generally increased with concentration, although it was quite constant at moderate concentrations. One should note that if the solvent velocity factor was not included (i.e., to calculate t+), it would appear the transference number has an even more pronounced increase with concentration. This underlines the importance of including this factor in transference number calculations. Within this concentration range, Grundy noticed a similar \({t}_{+}^{0}\) trend. A physical explanation for this shape remains contentious. We speculate that at lower concentrations the Li+ ion is more solvated than FSI−, which remains free. With increasing concentration, the FSI− becomes partially solvated, and so \({t}_{+}^{0}\) increases.
Perhaps most importantly, and so to reiterate, dcs/dz∣z = 0,L is a function of electrolyte properties Dapp and \({t}_{+}^{0}\), and current density. This interfacial gradient is not easily or readily characterised but is of primary importance for understanding poor electrolyte performance in LIBs, and also in understanding the likelihood of dendrite growth in alkali metal batteries.5 Fig. 4e shows how dcs/dz∣z = 0,L changed with concentration. Although fairly constant at lower concentrations, it increased very dramatically at higher concentrations. With a constant current applied to all concentrations, this was only due to changes in Dapp and \({t}_{+}^{0}\), which have been characterised. With a fivefold drop in Dapp over the concentration range, the large increase in dcs/dz∣z = 0,L at high concentrations was primarily due to the drop in Dapp.
Thermodynamic factor
Illustrated in Fig. 4f, the electrolyte behaved according to extended Debye–Huckel theory described in Supplementary Note 7; χM is plotted against the square root of concentration.38 Similar to Hou7 and Wang’s11 approach, the data were fitted with an extended Debye–Huckel Guggenheim equation; an x1/2 power series.43 This shape is akin to those of other organic-based electrolytes;7,11,13,14at low concentrations, a drop in χM suggests long-range ion-ion association dominates, but at higher concentrations, it is shorter range solvation effects that dominate. With increasing concentration, the solvent becomes increasingly bound, which decreases its vapour pressure, leading to an increase in salt activity and therefore χM. The extent to whether association dominates χM values is primarily influenced by solvent physicochemical properties, like relative dielectric constant (ϵr). For instance, a high ϵr will allow for more salt dissociation, as it stabilises isolated ions, and therefore the effects of association do not appear. Wang et al. showed this by comparing a PC-based electrolyte with an EMC-based electrolyte.11 G4 has a ϵr that lies between PC and EMC (7.91 vs. 64.92 and 2.96, respectively), and its χM dependence on concentration agrees with this. The concentration at which the curve crosses χM = 1 is indicative of when ion-solvent effects out-compete ion-ion effects. For EMC and PC, it was 1.01 M and 0.12 M respectively, and for this system, it was ~0.72 M.
Using Raman, the extent of associated species forming is shown in Fig. 2c: the ~ 717 cm−1 peak begins to shift, and shoulder peaks start to emerge, demonstrating increased Li+–FSI− interaction. Also, Bockris suggests triple-ion formation occurs when ϵr < 15, indicating triplets and perhaps clusters are likely to form in G4.38 Supplementary Figure 8c shows the free FSI− ion becoming a minor FSI− species at ~0.5 m as more aggregated species are dominating. As mentioned above, this evidence would suggest a decrease in χM with concentration.
However, the decreasing number of free solvent molecules available to bind and stabilise Li+, shown in Fig. 2b, leads to an increase in ion-solvent interaction and therefore an increase in χM. The emergence and increasing intensity of the 868 cm−1 peaks correlate with increasing χM. As an analysis in Supplementary Note 7 shows, at concentrations 1.5-2 m, there is more bound solvent than free.
In summary, the introduction of solvent structures like [Li(G4)]+ and the formation of SSIPs, CIPs and AGGs have competing effects on the observed χM value. The fairly low G4 ϵr leads to SSIPs and CIPs at low concentrations resulting in a decrease in χM; with increasing concentration more [Li(G4)]+-like solvent structures form, resulting in an increase in χM.
By measuring parameters κ, Dapp, \({t}_{+}^{0}\) and χM one can implement the values into a Doyle–Fuller–Newman (DFN) model and simulate symmetric and full cell performance. We performed these simulations using the Batteries and Fuel Cells Module in COMSOL Multiphysics 5.5. Firstly, a 1 m LiFSI in G4 concentration gradient in a symmetric cell was modelled at 15 μm, 50 μm and 100 μm, at 5 mA cm−2. Then, we simulated a LIB cell using LiFSI in G4 with a thickness of 20 μm to understand how electrolyte concentration and properties, and C-rate affects LIB cell performance. It was evident that using 1 m LiFSI in G4 led to the lowest overpotential in the LIB simulation and the highest final capacity at a 3 V cut-off. For details on this study, refer to Supplementary Discussion 1.
Stefan–Maxwell diffusion coefficients
For a more in-depth understanding of the diffusional behaviour of each individual species and their interactions with the other species in solution, the Stefan–Maxwell coefficients were calculated using concentrated-solution theory, developed by Newman and Thomas-Alyea.21 Stefan–Maxwell diffusion theory provides information on ion-solvent and ion-ion frictional interactions, which is an important consideration when describing diffusion in multicomponent systems. Using Supplementary Eqs. (S28)–(32), \({\mathfrak{D}}\) and the other Stefan–Maxwell coefficients, \({{\mathfrak{D}}}_{0+}\), \({{\mathfrak{D}}}_{0-}\) and \({{\mathfrak{D}}}_{+-}\) are plotted. \({\mathfrak{D}}\) is the thermodynamic diffusion coefficient, which is affected by salt chemical potential gradients rather than concentration gradients; \({{\mathfrak{D}}}_{0+}\) and \({{\mathfrak{D}}}_{0-}\) are the Stefan–Maxwell intermolecular diffusion coefficients of the cation (+) and anion (−) respectively, and their interaction with the solvent; and \({{\mathfrak{D}}}_{+-}\) is the coefficient that describes the interaction between cation and anion.
\({\mathfrak{D}}\) followed an exponential decay with concentration, see Fig. 5a. \({{\mathfrak{D}}}_{0+}\) and \({{\mathfrak{D}}}_{0-}\) were very large at low concentrations, with \({{\mathfrak{D}}}_{0-}\) generally higher than \({{\mathfrak{D}}}_{0+}\). This is a result of increased movement of FSI− due to weaker interaction with the solvent compared to Li+, which is known to bind to G4 strongly, as evidenced by \({t}_{+}^{0}\) < 0.5. The general decreasing trend of both \({{\mathfrak{D}}}_{0+}\) and \({{\mathfrak{D}}}_{0-}\) is due to the increasing drag on the solvated complexes. \({{\mathfrak{D}}}_{+-}\) was the lowest of each of the Stefan–Maxwell coefficients at low concentrations because of the poor movement of paired species. Interestingly at 2 m, each of the coefficients was of similar magnitude, within error. As free solvent is depleted, aggregates and/or even domains of ions begin to form, and we speculate the mechanism of transport begins to transition from vehicular movement to ion-hopping. Imide-based salts in G4 are sometimes described as “solvate” ionic liquids at high concentrations.36,44 The strong [Li(G4)]+ complexes forming and their weak interaction with FSI− the solution could be described as a “quasi” ionic liquid. As solvent molecules begin to deplete in solution, this description becomes apt.
a Exponential decay of LiFSI thermodynamic diffusion coefficient (\({\mathfrak{D}}\)) with concentration. b Stefan–Maxwell coefficients \({{\mathfrak{D}}}_{0+}\), \({{\mathfrak{D}}}_{0-}\) and \({{\mathfrak{D}}}_{+-}\), all decreasing with concentration. \({{\mathfrak{D}}}_{0-}\) was generally the highest value across concentrations, indicating FSI− had the least frictional interaction with G4, while FSI−’s frictional interaction Li+ was high. At 2 m, each Stefan–Maxwell coefficient was very similar, within error, which could illustrate a change in transport mechanism, from vehicular to ion-hopping. The error bars in (a) and (b) represent the standard error and propagation from previous calculations, see Supplementary Note 8.
Discussion
A method for the full characterisation of electrolyte systems has been presented using operando Raman microspectroscopy in tandem with PEIS. The Fickian diffusion coefficient, transference number, thermodynamic factor, ionic conductivity, the resistance of charge-transfer and Stefan–Maxwell coefficients of LiFSI in G4 have been studied through the formation and analysis of concentration gradients. An understanding of how each listed property is affected by bulk concentration was described, with structural information from Raman also providing insight into how solvent and electrolyte structure affects electrolyte properties. Specifically, we noted the interfacial concentration gradient increased with increasing bulk concentration, which was primarily due to decreasing Dapp. So, although much attention is placed on increasing \({t}_{+}^{0}\) to reduce ηc, focusing on increasing Dapp could be a more valuable pursuit for future work. Also, this was the first time χM was measured using concentration gradient visualisation; we hope our description will be a useful tool for more frequent χM characterisation. The full significance of interfacial concentration gradients and χM on LMB performance and its influence on lithium plating morphology could be compelling further work.
For explicit context, the measurement of κ, Rct, Dapp, \({t}_{+}^{0}\) and χM provides a full description of the electrolyte, which can be used in the theoretical modelling of battery systems, and also provides an explanation of potential shortcomings of measured electrolytes in Li-ion and “beyond Li-ion” systems. We showed that at discharge rates of 1C and 4C in our full-cell simulations, the 1m electrolyte exhibited the least overpotential and attained the highest average SOC.
Indeed, to successfully measure concentration gradients with Raman microspectroscopy, an isolatable and concentration-sensitive Raman band is required. Furthermore, if the required Raman band(s) are present, our described method could be extended to electrolyte systems with multiple ions. Evidence from the few other studies that have used Raman spectroscopy to monitor electrolyte concentration differences shows that many commonly used salts (e.g., LiClO427, LiBOB28, LiTFSI29) and solvents (e.g., DMC27 and G428) can successfully be studied via the presented method. The most popular salt in LIBs, LiPF6, has been studied using Raman for structural analysis, although, to the best of our knowledge, not been used to test concentration changes in the solution. Although LiPF6 has been shown to induce a fluorescence background in Raman spectroscopy experiments, its strong PF\({}_{6}^{-}\) Raman-active band would make it an ideal candidate for further studies.45 There is little doubt, therefore, that many current and future electrolyte mixtures benefit from measuring electrolyte properties in this manner. To increase the viability of the presented method further, more advanced Raman techniques such as stimulated Raman spectroscopy (SRS) could be employed. Its utilisation would increase the sensitivity of the method and reduce the acquisition time per spectrum46.
Overall, we hope this work will provide an alternative method for electrolyte characterisation and a tool for progressing our communal understanding of how these properties affect Li-ion battery performance and Li+ electrodeposition morphology.
Methods
Electrolyte description
Lithium bis(fluorosulfonyl)imide (LiFSI) (Battery Grade—99%) was purchased from Fluorochem Ltd. Tetraethylene glycol dimethyl ether (G4) (anhydrous, 99%+) was purchased from Sigma Aldrich. Handling of LiFSI and G4 was always performed in an argon-filled glovebox (MBraun) with low H2O content (<1 ppm) and low O2 content (<1 ppm). LiFSI was dried further under a high vacuum at 70 °C for 48 h. G4 has dried over 3 Å molecular sieves, which were washed and then dried for one week. All glassware was dried at 80 °C under vacuum before being used and brought into the glovebox. The H2O content of the electrolyte solutions was determined by Karl Fischer titration, also performed in an argon-filled glovebox, and recorded to be below 15 ppm of H2O. Experimental information describing density measurements and partial molar volume calculations are available in Supplementary Method 1 and 2.
Concentration gradient calibration with Raman spectroscopy
A Renishaw inVia Reflex laser confocal Raman microscope equipped with a near-IR 785 nm laser, a 5× magnification objective (Leica, 0.12 NA, 14 mm WD), providing a 4.8 μm spot size, and a 90° mirror was used to collect Raman spectra of the prepared calibration solutions. Specifically, we recorded spectra with a centre at 1200 cm−1, at 5% laser power, with a 1 s exposure time for each calibration sample. Measurements were repeated 20 times. Following the acquisition, we removed the background, using the Renishaw WiRE 5.5 software, and normalised all spectra against the intensity of the 1471 cm−1 band. The latter representing the CH2 bending/scissoring mode of G4. We further used this feature to normalise the line scan spectra. The Raman band at 717 cm−1, corresponding to S–N–S vibrations of the FSI− anion, was finally integrated to produce the calibration curve shown in Fig. 2c of the main text.
Cell construction
The operando cell was constructed in an Ar-filled glovebox. First, two stainless steel pistons were designed to fit inside a quartz glass tube 20 mm in length, with an inner diameter (ID) of 8 mm and an outer diameter (OD) of 10 mm. An interelectrode distance of 15 mm was chosen because it was sufficiently large to detect a concentration gradient with good spectral resolution and the diffusion layer not to progress too quickly into the centre of the cell, which would make the fitting equation invalid. If it were longer the diffusion layer would not progress quickly enough, and the measurement would take substantially longer than 36 h. Each piston was further equipped with an O-ring made of FFKM for increased chemical resistance against ethers. The lithium metal foil (99.9%, 750 μm thickness, Alfa-Aesar) acting as electrodes for the symmetric cell, was prepared by scraping off the native oxide layer of the foils and calendaring to 300 μm in thickness. From here, circular lithium discs were prepared with a diameter of 8 mm and placed onto each of the stainless steel pistons. One piston was then placed inside the quartz tube, ~1 mL of electrolyte was added, and then the second piston was introduced on the opposite side cell, sealing the cell. Care was taken not to introduce any gas bubbles into the system. Before any tests were run, the cell was set up inside the Raman microscope and connected to a Biologic SP150 potentiostat (Supplementary Fig. 2). Important to note, the cell was vertically placed on the sample stage to avoid natural convection (Supplementary Fig. 3a).
PEIS
Before any line scan or current was applied, PEIS was performed on the cell. First, a PEIS scan with voltage amplitude (Va) 100 mV and frequencies from 100 kHz to 1 Hz, was performed every hour, to monitor the stability of the interface. The large voltage amplitude was chosen for a reasonable signal-to-noise ratio. Linearity was still maintained. The ionic conductivity (κ), from Rbulk, and resistance of charge transfer (Rct) were collected after 4 h. The data were then fitted using Biologic EC-lab V11.26 software with the equivalent circuit (Qbulk/Rbulk)+(Qdl/Rct), with Rbulk and Rct representing the bulk resistance of the electrolyte and charge transfer respectively, and Qbulk and Qdl are the constant phase element of electrolyte and double layer respectively.
CP and operando Raman line scan measurements
A constant current was applied to the operando cell for 24–48 h, allowing a concentration gradient to form. We chose 100 μA cm−2 as the operating current to avoid dendrite formation, and also to allow a concentration gradient of sufficient magnitude to form. Both visually, and there is no drop in Rct with time, provided evidence that there was no dendrite growth at 100 μA cm−2. Supplementary Fig. 3c shows how the current density affected the concentration gradient. Supplementary Fig. 3d shows that mossy dendritic structures formed at 400 μA cm−2. In Supplementary Fig. 3c, the gradient that formed at this current density was very steep, with dendrites blocking the signal close to the plating electrode.
As the current was applied, a 1D line scan in the z-direction was started, with the same laser settings as the calibration curve. A laser power of 5% was deemed optimal as it provided good spectral resolution, whilst showing no evidence of thermal heating or oxidation of the solvent. This is illustrated in Supplementary Fig. 3e, which shows no change in the solvent peak with time, and therefore no evidence of decomposition products. Moreover, there was no emergence of additional peaks in the spectra after repeated line scans. Also, there was no decrease in the overpotential with time, indicating no thermal heating. For the starting point of each line scan, we focused as close to the electrode surface as possible, at a defined depth. Confocal microscopy uses a pinhole aperture to block out-of-focus light, measuring spectra in a precise plane of focus. This led us to gather spectra at defined depths (the centre point of the cell) with accurate spot size. The gradient evolution during a line scan acquisition, under the selected operating conditions of the cell, was determined to be within the signal-to-noise error for the acquired Raman spectra. For quantifying χM, a PEIS measurement was performed before each line scan acquisition. These measurements were performed with a Va = 100 mV and frequency range of 100 kHz to 1 Hz, resulting in each run taking ~30 s. To make sure that these PEIS measurements and the associated CP interruption did not negatively affect the Dapp and \({t}_{+}^{0}\) measurements determined with the Raman line scans, a second set of experiments was performed without PEIS interruption. No visible difference between these experiments could be determined. Using Renishaw’s WiRE5.5 software, each spectra had its background removed, then using a Python script each spectra was compared to the calibration curve to extract the electrolyte concentration at each point along with each line scan.
Data availability
The authors declare that all data supporting the findings of this study are included within the paper and its Supplementary Information. Source data are available from the corresponding author upon reasonable request.
References
Blomgren, G. E. The development and future of lithium ion batteries. J. Electrochem. Soc. 164, A5019–A5025 (2017).
Quartarone, E. & Mustarelli, P. Review-emerging trends in the design of electrolytes for lithium and post-lithium batteries. J. Electrochem. Soc. 167, 050508 (2020).
Li, M., Wang, C., Chen, Z., Xu, K. & Lu, J. New concepts in electrolytes. Chem. Rev. 120, 6783–6819 (2020).
Cheng, X. B., Zhang, R., Zhao, C. Z. & Zhang, Q. Toward safe lithium metal anode in rechargeable batteries: a review. Chem. Rev. 117, 10403–10473 (2017).
Jana, A., Woo, S. I., Vikrant, K. S. N. & García, R. E. Electrochemomechanics of lithium dendrite growth. Energy Environ. Sci. 12, 3595–3607 (2019).
Xu, K. Nonaqueous liquid electrolytes for lithium-based rechargeable batteries. Chem. Rev. 104, 4303–4418 (2004).
Hou, T. & Monroe, C. W. Composition-dependent thermodynamic and mass-transport characterization of lithium hexafluorophosphate in propylene carbonate. Electrochim. Acta 332, 135085 (2020).
Xu, K. Electrolytes and interphases in Li-ion batteries and beyond. Chem. Rev. 114, 11503–11618 (2014).
Diederichsen, K. M., McShane, E. J. & McCloskey, B. D. The most promising routes to a high Li+ transference number electrolyte for lithium ion batteries. ACS Energy Lett. 2, 2563–2575 (2017).
Chen, K. H. et al. Dead lithium: mass transport effects on voltage, capacity, and failure of lithium metal anodes. J. Mater. Chem. A 5, 11671–11681 (2017).
Wang, A. A., Hou, T., Karanjavala, M. & Monroe, C. W. Shifting-reference concentration cells to refine composition-dependent transport characterization of binary lithium-ion electrolytes. Electrochim. Acta 358, 136688 (2020).
Newman, J. & Chapman, T. W. Restricted diffusion in binary solutions. AIChE J. 19, 343–348 (1973).
Nyman, A., Behm, M. & Lindbergh, G. Electrochemical characterisation and modelling of the mass transport phenomena in LiPF6-EC-EMC electrolyte. Electrochim. Acta 53, 6356–6365 (2008).
Valoen, L. O. & Reimers, J. N. Transport properties of LiPF6-based Li-ion battery electrolytes. J. Electrochem. Soc. 152, A882 (2005).
Ehrl, A., Landesfeind, J., Wall, W. A. & Gasteiger, H. A. Determination of transport parameters in liquid binary lithium ion battery electrolytes: part I. Diffusion coefficient. J. Electrochem. Soc. 164, A826–A836 (2017).
Stejskal, E. O. & Tanner, J. E. Spin diffusion measurements: spin echoes in the presence of a time-dependent field gradient. J. Chem. Phys. 42, 288–292 (1965).
Bruce, P. G. & Vincent, C. A. Steady state current flow in solid binary electrolyte cells. J. Electroanal. Chem. 225, 1–17 (1987).
Hiller, M. M., Joost, M., Gores, H. J., Passerini, S. & Wiemhöfer, H. D. The influence of interface polarization on the determination of lithium transference numbers of salt in polyethylene oxide electrolytes. Electrochim. Acta 114, 21–29 (2013).
Zugmann, S. et al. Measurement of transference numbers for lithium ion electrolytes via four different methods, a comparative study. Electrochim. Acta 56, 3926–3933 (2011).
Doyle, M. & Newman, J. Analysis of transference number measurements based on the potentiostatic polarization of solid polymer electrolytes. J. Electrochem. Soc. 142, 3465 (1995).
Newman, J. & Thomas-Alyea, K. E. Electrochemical systems 3rd edition (Wiley & Sons, 2004).
Doyle, M., Fuller, T. F. & Newman, J. The importance of the lithium ion transference number in lithium/polymer cells. Electrochim. Acta 39, 2073–2081 (1994).
Landesfeind, J., Ehrl, A., Graf, M., Wall, W. A. & Gasteiger, H. A. Direct electrochemical determination of thermodynamic factors in aprotic binary electrolytes. J. Electrochem. Soc. 163, A1254–A1264 (2016).
Zheng, J. et al. Regulating electrodeposition morphology of lithium: towards commercially relevant secondary Li metal batteries. Chem. Soc. Rev. 49, 2701–2750 (2020).
Wang, M. et al. Effect of LiFSI concentrations to form thickness-and modulus-controlled SEI layers on lithium metal anodes. J. Phys. Chem. C 122, 9825–9834 (2018).
Rey, I., Bruneel, J.-L., Grondin, J., Servant, L. & Lassègues, J.-C. Raman spectroelectrochemistry of a lithium/polymer electrolyte symmetric cell. J. Electrochem. Soc. 145, 3034 (1998).
Forster, J. D., Harris, S. J. & Urban, J. J. Mapping Li+ concentration and transport via in situ confocal Raman microscopy. J. Phys. Chem. Lett. 5, 2007–2011 (2014).
Cheng, Q. et al. Operando and three-dimensional visualization of anion depletion and lithium growth by stimulated Raman scattering microscopy. Nat. Commun. 9, 1–10 (2018).
Georén, P., Adebahr, J., Jacobsson, P. & Lindbergh, G. Concentration polarization of a polymer electrolyte. J. Electrochem. Soc. 149, A1015 (2002).
Steinrück, H.-G. et al. Concentration and velocity profiles in a polymeric lithium-ion battery electrolyte. Energy Environ. Sci. 13, 4312 (2020).
Bazak, J. D. et al. Mapping of lithium-ion battery electrolyte transport properties and limiting currents with in situ MRI mapping of lithium-ion battery electrolyte transport properties and limiting currents with in situ MRI. J. Electrochem. Soc. 167, 140518 (2020).
Sethurajan, A. K., Krachkovskiy, S. A., Halalay, I. C., Goward, G. R. & Protas, B. Accurate characterization of ion transport properties in binary symmetric electrolytes using in situ NMR imaging and inverse modeling. J. Phys. Chem. B 119, 12238–12248 (2015).
Chandrashekar, S., Oparaji, O., Yang, G. & Hallinan, D. Communication-7 Li MRI unveils concentration dependent diffusion in polymer electrolyte batteries. J. Electrochem. Soc. 163, A2988–A2990 (2016).
Ko, J. & Yoon, Y. S. Recent progress in LiF materials for safe lithium metal anode of rechargeable batteries: Is LiF the key to commercializing Li metal batteries? Ceram. Int. 45, 30–49 (2019).
Liu, Z. et al. Interfacial study on solid electrolyte interphase at Li metal anode: implication for li dendrite growth. J. Electrochem. Soc. 163, A592–A598 (2016).
Terada, S., Ikeda, K., Ueno, K., Dokko, K. & Watanabe, M. Liquid structures and transport properties of lithium bis(fluorosulfonyl)amide/glyme solvate ionic liquids for lithium batteries. Aust. J. Chem. 72, 70–80 (2019).
Bard, A. J. & Faulkner, L. R. Electrochemical Methods 2nd edn (Wiley & Sons, 2001).
Bockris, J. O. & Reddy, A. K. N. Modern Electrochemistry Volume 1 Ionics 2nd edn (Kluwer Academic Publishers, 2002).
Andre, D. et al. Characterization of high-power lithium-ion batteries by electrochemical impedance spectroscopy. I. Experimental investigation. J. Power Sources 196, 5334–5341 (2011).
Casteel, J. F. & Amis, E. S. Specific conductance of concentrated solutions of magnesium salts in water-ethanol system. J. Chem. Eng. Data 17, 55–59 (1972).
Grundy, L. S. et al. Impact of frictional interactions on conductivity, diffusion, and transference number in ether- and perfluoroether-based electrolytes. J. Electrochem. Soc. 167, 120540 (2020).
Newman, J., Bennion, D. & Tobias, C. W. Mass transfer in concentrated binary electrolytes. Ber. Bunsenges. Phys. Chem. 69, 608–612 (1965).
Guggenheim, E. Thermodynamics: An Advanced Treatment for Chemists and Physicists 5th edn (North-Holland Publishing Company, 1950).
Ueno, K. et al. Glyme-lithium salt equimolar molten mixtures: concentrated solutions or solvate ionic liquids? J. Phys. Chem. B 116, 11323–11331 (2012).
Cabo-Fernandez, L. et al. Kerr gated Raman spectroscopy of LiPF6 salt and LiPF6-based organic carbonate electrolyte for Li-ion batteries. Phys. Chem. Chem. Phys. 21, 23833–23842 (2019).
Prince, R. C., Frontiera, R. R. & Potma, E. O. Stimulated Raman scattering: from bulk to nano. Chem. Rev. 117, 5070–5094 (2017).
Acknowledgements
The authors would like to acknowledge the ISCF Faraday Challenge projects SOLBAT [grant number FIRG007] and LiSTAR [grant number FIRG014] as well as the Henry Royce Institute (through UK Engineering and Physical Science Research Council grant EP/R010145/1) for capital equipment. Also, we would like to thank Andrew A. Wang for his assistance with the density measurements, and many fruitful discussions; Shobhan Dhir for insightful conversations and constructive comments; Giulia Galatolo for her Fig. 1 design, and Claire Halloran for some great earlier concentration gradient analysis work.
Author information
Authors and Affiliations
Contributions
J.F. and M.P. conceived the idea and designed the experiments. J.F. performed all the experiments, measurements, simulations, analysis and wrote the manuscript with input from all authors. J.I. helped with the initial operando Raman microspectroscopy experiments and provided clarity and helpful discussion on the interpretation of spectroscopic data. F.L.M. provided expertise relating to the electrochemical data. M.P. supervised the design of the project and provided frequent input in the interpretation of all results.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Erik J. Berg, Vinayan Bhaghavathi Parambath Andrew S Westover and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fawdon, J., Ihli, J., Mantia, F.L. et al. Characterising lithium-ion electrolytes via operando Raman microspectroscopy. Nat Commun 12, 4053 (2021). https://doi.org/10.1038/s41467-021-24297-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-021-24297-0
This article is cited by
-
Unraveling the energy storage mechanism in graphene-based nonaqueous electrochemical capacitors by gap-enhanced Raman spectroscopy
Nature Communications (2024)
-
Molecular anchoring of free solvents for high-voltage and high-safety lithium metal batteries
Nature Communications (2024)
-
Operando monitoring of dendrite formation in lithium metal batteries via ultrasensitive tilted fiber Bragg grating sensors
Light: Science & Applications (2024)
-
Three-dimensional operando optical imaging of particle and electrolyte heterogeneities inside Li-ion batteries
Nature Nanotechnology (2023)
-
Fundamental investigations on the ionic transport and thermodynamic properties of non-aqueous potassium-ion electrolytes
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.