Abstract
Graphene integrated photonics provides several advantages over conventional Si photonics. Single layer graphene (SLG) enables fast, broadband, and energy-efficient electro-optic modulators, optical switches and photodetectors (GPDs), and is compatible with any optical waveguide. The last major barrier to SLG-based optical receivers lies in the current GPDs’ low responsivity when compared to conventional PDs. Here we overcome this by integrating a photo-thermoelectric GPD with a Si microring resonator. Under critical coupling, we achieve >90% light absorption in a ~6 μm SLG channel along a Si waveguide. Cavity-enhanced light-matter interactions cause carriers in SLG to reach ~400 K for an input power ~0.6 mW, resulting in a voltage responsivity ~90 V/W, with a receiver sensitivity enabling our GPDs to operate at a 10−9 bit-error rate, on par with mature semiconductor technology, but with a natural generation of a voltage, rather than a current, thus removing the need for transimpedance amplification, with a reduction of energy-per-bit, cost, and foot-print.
Similar content being viewed by others
Introduction
The same-chip integration1 of active and passive optical components with electronics offers a cost- and energy-efficient solution for short- and long-reach optical interconnects2,3. Single layer graphene (SLG) is an ideal material for integrated photonics4,5, promising e.g. high-speed (>200 GHz)6,7 and broadband (ultraviolet to far-infrared)8,9 operation that could lift bandwidth (BW) (~100 GHz)10,11 and spectral (<1600 nm)12 limitations of existing technologies, such as Ge/Si13,14 and InGaAsP/InP15,16. A variety of waveguide (WG)-integrated SLG-based photonic devices have been reported17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34, including electro-absorption (EAMs)17,18,19 and electro-refraction modulators (ERMs)20, optical switches4,21, and photodetectors (GPDs)22,23,24,25,26,27,28,29,30,31,32,33. SLG and layered materials can be integrated with passive Si photonic WGs22,23,24,25,26,27 or any other passive WG technology4, including Si3N429,34,35, sapphire36, Ge37, and polymers38,39, extending the spectral range and scope of possible applications37,40.
SLG’s optical absorption is ~2.3% under normal incidence41, which limits the photoresponse in top-illuminated GPDs8. This can be increased in a WG configuration through the interaction with the evanescent field of the optical WG mode42. However, since the mode-overlap with SLG’s monatomic cross-section typically restricts absorption to ~0.01–0.1 dB/μm (~0.2–2%/μm)4, device lengths ~100 μm are needed for near-complete (>90%) absorption, with adverse effects on foot-print and capacitance7. The resulting trade-off between length and absorption has implications for GPDs that operate via the photo-thermoelectric effect (PTE)43,44,45: Due to slow (~ps46) heat dissipation to the lattice via phonon mediated cooling46,47, photo-excitation leads to the formation of a hot-carrier distribution in SLG8,43,44. The associated electron temperature, Te, can be substantially above the lattice temperature, T048, and leads to a photovoltage43,44,45:
if both a Te gradient and a spatially varying Seebeck coefficient, S, (controlled by the chemical potential, μc) are present43. In order to achieve a high (>mV) VPTE, it is better to absorb the incident electromagnetic energy over small (<10 μm) lengths, leading to localised electronic heating for a higher (~tens K) Te and ∇ Te(x).
Different approaches have been explored to increase and confine light absorption in free-space-coupled49,50,51 and WG-integrated GPDs26,27,28,29, e.g. by embedding SLG into optical cavities50,51, slot WGs26, plasmonic structures28,29,31,49, or by enhancing the light-matter interaction using sub-wavelength structures27, but these have coupling and propagation losses31, limitations in field enhancement25,30, or in carrier mobility μ26,32, fabrication flows incompatible with complementary metal-oxide-semiconductor (CMOS) processing25,31,32, bias-induced dark currents30,31, or a combination thereof25,31,32. Thus, the demonstration of GPDs on photonic integrated circuits (PICs) that leverage SLG’s unique hot-carrier dynamics and maximise the voltage responsivity R[V/W] = VPTE/Pin, with Pin the incident optical power in the WG, is challenging.
Here, we report GPDs integrated on looped WGs, known as microring resonators52, which act as PIC-embedded resonant cavities. The conversion of incident light into an electrical signal occurs via the PTE effect. The GPDs directly generate a voltage, which allows us to operate them without bias and dark currents, limiting the GPD noise to thermal Johnson-noise, due to fluctuations of the carrier density53. Other sources of noise, in particular low (~Hz-kHz) frequency contributions, such as 1/f and generation-recombination54, are not relevant for bias-free high-speed PTE-GPDs operating in the GHz regime33. This removes the need of transimpedance amplifiers (TIA) in the read-out electronics, with a reduction of the energy-per-bit cost and system foot-print. With R[V/W] ~ 90 V/W, our GPDs pave the way towards SLG integration on Si photonic receivers, overcoming the limitation of photocurrent (Iph) generating GPDs with current responsivities R[A/W] = Iph/Pin lower than mature Ge PDs25,30,31. We attribute this to our high (>104 cm2/Vs) μ, and the combination with the Si microring resonator giving a ~10-fold enhancement of electric field strength and >90% light absorption in just ~6 μm SLG on Si WGs.
Results
Device concept
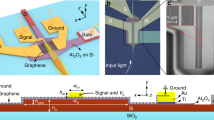
Figure 1 a is a scheme of our GPDs, which comprise a layered materials heterostructure (LHM) of SLG and hexagonal boron nitride (hBN). To increase the generated VPTE upon optical illumination according to Eq. (1), encapsulation of the SLG channel in hBN ensures a high (>104 cm2/Vs) μ55 for large (~200 μV/K) peak S29, according to Mott’s formula43,44:
where kB is the Boltzmann constant, e the electron charge, σ = nμe the conductivity, and n the carrier concentration. Dual-gate SLG electrodes, separated from the LMH by an Al2O3 layer, are employed to tune S in adjacent regions of the device26. The LMH is contacted on opposite sides and centrally aligned to the WG of a microring resonator fabricated on a Si-on-insulator (SOI) wafer. The resonator serves a two-fold purpose. First, the higher (compared to the bus WG) intra-cavity energy density52 results in ~10-fold enhanced light-matter interaction56 and can enable near-complete light absorption in the SLG channel if its coverage of the resonator is optimised. Second, the wavelength, λ, selectivity of the resonator56,57, makes the GPD suitable for wavelength division multiplexing (WDM)14, whereby the data rate of a single optical channel is increased by combining signals of different λ at the transmitter, and separating them at the receiver58,59,60.
a Sketch of device. b Transmission spectra of a ring cavity with SLG on top, indicating the effects of varying W on ER and Q. For clarity, the spectra are aligned at the resonance wavelength closest to 1553.55 nm. c Corresponding transmission at resonance. The black line is the calculated transmission for κ = 10%. The coloured dots mark the transmission for various loss coefficients.
To find the SLG length, W, over the ring that enables maximum absorption inside the resonator, we perform an initial experiment on a reference microring cavity with identical parameters (WG thickness tWG = 220 nm, WG width wWG = 480 nm, ring radius R = 40 μm). Coupling to the resonator occurs through a 200 nm gap via a single bus WG, Fig. 1a, which has grating couplers (GCs) on either end, with coupling efficiency14 \(\eta ={P}_{{\rm{in}}}/{P}_{{\rm{fibre}}} \sim\)0.28, with \({P}_{{\rm{fibre}}}\) the optical power in the fibre connecting source and SOI chip, determined from transmission measurements on reference WGs on the same chip. The power coupling between these two structures depends on the coupling and transmission coefficients, i.e. the scattering matrix elements relating incoming and outgoing electric fields from the coupling region56,57. The choice of the power coupling coefficient, κ, affects both the optical (frequency) bandwidth fFWHM and the quality factor Q = fFWHM/fres, with fres the resonance frequency59 of the resonator, resulting in a trade-off between achievable extinction ratio (ER, defined as the ratio of minimum (at resonance) and maximum transmitted optical power50), thus R[V/W], and the maximum achievable electrical bandwidth, f3dB. For our GPD, we select κ = 10% (with a measured optical (wavelength) bandwidth λFWHM ~ 150 pm at λres ~ 1.55 μm, corresponding to fFWHM ~ 18.7 GHz. This, according to61:
allows for f3dB ~ 12 GHz in our design, sufficient for applications in data centre optical interconnects2.
The wavelength-dependent transmitted power, Ptrans, of a ring resonator can be written as52:
where θ = 4π2Rneff/λ is the round-trip phase shift of the circulating mode and the effective mode index neff = βm/k0, with βm the propagation constant of the mode, defined as the wavevector component along the WG, and k0 the free-space wavevector60,62. Omitting negligible losses caused by coupling between bus and ring, the term:
describes the round-trip propagation loss in the ring, with αSLG and αWG, in dB/μm, the power attenuation coefficients in SLG and Si WG, respectively. When θ = 2πm (m = 1, 2, 3…), the light in the ring constructively interferes with itself and the cavity is in resonance52. From Eq. (4), the transmission drops to zero if ξ = 1 − κ. Under this so-called critical coupling57, as the transmission approaches zero, maximum absorption inside the ring resonator is achieved. With all other parameters fixed in Eq. (5), changing the SLG-induced losses by changing W can therefore be used to tune ξ and achieve critical coupling.
Coupling and absorption optimisation
To find the optimum W, we first measure the transmission of an unloaded (no SLG, i.e. W = 0 μm) resonator by coupling light (continuous-wave (CW), TE-polarised) from a tunable laser (Newport TLB6700) into the bus WG, using an optical single-mode fibre, and measuring the transmitted power at the output GC as a function of λ, around one of the resonance peaks close to main Telecom wavelength at 1.55 μm, Fig. 1b. Due to SLG’s broadband absorption8, there will be identical behaviour for the other resonances, apart from a shift in Pin with GC response envelope14. The results, after calibration for the coupling losses, are shown by the dark-blue line and symbols in Figs. 1b, c, respectively. The microring resonator is not critically coupled at resonance for λ ~ 1553.55 μm, as Ptrans does not vanish, but only part of the incident power is dissipated in the WG. From Eqs. (4), (5), αWG ~ 1.4 dB/cm.
We then proceed to study the effect of SLG with varying W on the power dissipated in the resonator. We first place a W = 20 μm SLG flake, prepared by micro-mechanical cleavage (MC)63 of bulk graphite, transferred using a micro-manipulator and a stamp consisting of polycarbonate (PC) and polydimethylsiloxane (PDMS), and cleaned by immersion in chloroform, over the ring, and measure the transmission as before. Using successive electron beam lithography (EBL, Raith e-LINE) runs to define a poly(methyl methacrylate) (PMMA) etch mask and reactive ion etching in O2 to remove excess material, we then reduce W further in several steps down to 2.5 μm, with transmission measurements in between. The results, Figs. 1b, c, show an initial transmission decrease at resonance with decreasing W, before the trend is inverted as W tends to zero. The minimum transmission, indicating critical coupling, is for W = 6 μm. From Eq. (5) we extract αG ~ 0.07 dB/μm, in agreement with measured17 and simulated4 values from literature. Using these and the comparison of the transmission curves for W = 6 μm, we estimate the fraction of absorbed light in the SLG channel to be ~92% under critical coupling. Figure 1b can also be used to monitor the effects of changing W on Q, as discussed in Supplementary Note 1. Supplementary Fig. 1 plots the degradation of Q as losses are increased with W. We further use Q56,64 to confirm the absorption in our devices.
LMH characterisation
Based on these findings, we fabricate the GPD in Fig. 1a with W = 6 μm from a LMH (hBN encapsulated SLG as channel layer) on top of the ring resonator, as shown in Fig. 2 and described in Methods. A microscope image of hBN/SLG/hBN on the WG is in Fig. 3a. We perform Raman spectroscopy (Renishaw inVia at 514.5 nm, power <0.5 mW) and atomic force microscopy (AFM, Bruker Dimension Icon) to monitor the SLG quality. A typical Raman spectrum before further processing of the stack is in Fig. 3b. The position of the combined hBN E2g peaks65 from top and bottom flakes is Pos(E2g) ~ 1366 cm−1 with full-width half maximum, FWHM(E2g) ~ 9.5 cm−1, as expected considering the top flake is bulk and that the planar domain size in MC-produced hBN crystals is limited by the flake size55,66. Pos(2D) ~ 2693 cm−1, FWHM(2D) ~ 18 cm−1, Pos(G) ~ 1583 cm−1, FWHM(G) ~ 14 cm−1, confirming the presence of SLG and low n < 1012 cm−267. The area (A(2D)/A(G) ~ 10.7) and intensity (I(2D)/I(G) ~ 7.6) ratios indicate a Fermi level EF < 100 meV67,68,69.
a Assembly of hBN/SLG/hBN. b Stack placement on photonic circuit and interface cleaning. c hBN etching in SF6 plasma. d SLG etching in O2 plasma to define channel geometry. e Metallization (Cr/Au) for drain-source contacts. f Al seed layer evaporation and ALD of Al2O3. g Wet transfer of CVD SLG. h Split-gate fabrication. i Metallization (Cr/Au) for gate contacts.
a Microscope image of hBN/SLG/hBN on ring resonator. The black dashed line indicates the area over which the Raman map in d is measured. Scale bar, 10 μm. b Raman spectrum measured at the position of the final device. c AFM image of LMH. The yellow dashed line indicates the area of top and bottom hBN. The blue line indicates the SLG area. Scale bar, 10 μm. d Raman map of FWHM(2D). The red box marks the position of the final device in a, c, d.
The AFM scan of the overlap region between LMH and microring in Fig. 3c shows blister-free SLG/hBN interfaces, confirming successful cleaning55, apart from a bubble trapped in a cladding trench above the WG. The FWHM(2D) map in Fig. 3d, taken from a 20 × 30 μm2 area in the centre of the LMH, shows a region with homogeneous (spread < 1 cm−1) and narrow (≤18 cm−1) FWHM(2D) and spots of increased (>21 cm−1) FWHM(2D) that coincide with the blister position, as revealed by AFM. Based on these findings, we then select the channel position (marked red in Figs. 3a, c, d) to be in a blister-free region. The final device has an active area L × W ~ 2.5 × 6 μm2. We use L ~ 2.5 μm, of the order of twice the cooling length Lcooling in SLG (~1 μm25,70, related to electron thermal conductivity κe (see Methods) and interfacial heat conductivity Γ ~ 0.5–5 MWm−2K−1 71,72, via \({L}_{{\rm{cooling}}}=\sqrt{{\kappa }_{e}/{{\Gamma }}}\)44), to fully exploit the Te profile with expected maximum at L/226,29, i.e. the WG centre.
Electrical characterisation
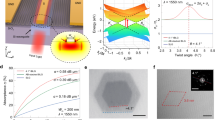
An image of the full GPD after fabrication, obtained by SEM, is in Fig. 4a, revealing a well-aligned WG, LMH, and split-gate structure. We first verify gate tunability of the SLG channel by measuring the drain-source current (IDS) at a fixed drain-source voltage (VDS) while varying the two gate-voltages. The resulting resistance map (Fig. 4b) shows a cross pattern, which confirms that four junction constellations (p-n, n-p, n-n, p-p) can be generated in the channel26. In order to extract the contact resistance, Rcontact, and μ from the GPD directly (rather than from a four-probe reference structure made from a second LMH), then used to estimate S, we utilize the measured transfer curve at homogenous channel doping in Fig. 4c and plot the device resistance as function of the inverse carrier concentration (1/n) for electron (Fig. 4e) and hole (Fig. 4f) doping. By fitting the linear part (as 1/n → 0) of these plots, as for ref. 73, Rcontact can be obtained from the intersection of the fit curve and y-axis, while the residual carrier concentration, n0, is found from the intersection between the fit curve and a horizontal line through the maximum. Using these values, we then model the total device resistance as for ref. 26: Rtotal = Rcontact + \(\frac{L}{W}\frac{1}{e\mu n}\), with \(n=\sqrt{{n}_{0}^{2}+{\left[{C}_{{\rm{ox}}}/e\left({V}_{{\rm{G}}}-{V}_{{\rm{CNP}}}\right)\right]}^{2}}\), where Rcontact includes the contacts and the contribution from the ungated region, VCNP is the gate voltage corresponding to the charge neutrality point (CNP, EF = 0 meV), Cox is the gate capacitance, and μ is used as a fit parameter. The original data (solid line) and the model (dashed line) are compared in Fig. 4c. We get Rcontact ~ 400 Ω and ~530 Ω, as well as μe ~ 17, 700 cm2/Vs and μh ~ 11, 800 cm2/Vs for electrons (red lines) and holes (blue lines), respectively. This demonstrates a PIC-integrated, LMH-based PD with high (>104 cm2/Vs) μ, while refs. 25,74 used hBN encapsulation for alternative detection concepts.
a False-colour SEM image of our GPD, showing Cr/Au contacts (yellow), Si WG (green), contacted hBN/SLG/hBN (blue, dashed line under contacts), and SLG gates (red). Scale bar: 2 μm. b Resistance map demonstrating independent tunability of charge carrier concentration in the SLG channel via VG1 and VG2. c Electrical characterization at homogeneous channel doping (solid lines, measured data; dashed lines, model). d Calculated S based on the electrical data in c. e, f) Resistance vs. inverse carrier concentration for e electron and f hole doping. g Photoresponse at zero bias on resonance (λ = 1555.87 nm). h Frequency response. The 3-dB cutoff frequency, marked by intersecting dashed lines, is ~12 GHz.
Steady-state photoresponse
For optical characterisation, we first couple modulated light (ON-OFF) with a duty cycle of 50% from a tuneable laser source (Agilent 81680A) into the bus WG using an optical single-mode fibre. While varying the potential at the two gate electrodes (VG1, VG2), the photoresponse of the unbiased GPD (VDS = 0 mV, to avoid dark currents impairing the noise performance) is recorded using a lock-in amplifier. Since the PTE effect as electromotive force is intrinsically best read-out as open circuit potential difference4,75, we record the response as VPTE, rather than measuring the resulting short-circuit photocurrent, which depends on external factors, such as Rcontact. Figure 4g shows a photoresponsivity map measured on resonance at 1555.87 nm, from which we extract a maximum R[V/W] ~ 90 V/W. The six-fold pattern, with the highest photoresponse for bipolar (p-n, n-p) junctions, and a sign-change across the diagonal (VG1 = VG2) for unipolar (n-n, p-p) junctions in the SLG channel, confirms that the PTE effect dominates the conversion of photons into electrical signal (rather than a photovoltaic conversion with a two-fold pattern in photovoltage over the same measurement range)43,44. Our R[V/W] outperforms the current state-of-the-art for waveguide-integrated PTE-GPDs, R[V/W] ~ 3–12 V/W25,29,33,76, by around one order of magnitude.
High-speed photoresponse
To determine the BW, we modulate CW light at 1555.87 nm from the same source using a commercial (Thorlabs LN05S-FC) intensity modulator (lithium niobate, f3dB = 40 GHz) and couple it into the device. While tuning the modulation frequency of the external modulator, we monitor the GPD response with an electrical spectrum analyzer (Agilent PSX N9030A), while the gate bias (VG1 = −0.5 V, VG2 = −2.1 V) is set at an operating point where R[V/W] is largest. This gives a 3-dB bandwidth ~12 GHz, Fig. 4h, as expected from the design of the passive photonic structure and the cavity-imposed limit calculated via Eq. (3).
Power and wavelength dependence
Figures 5a, b plot the wavelength dependence of optical transmission and photovoltage for VG1 = 1 V, VG2 = −1 V and various Pin. The maxima of the VPTE traces match the resonance minima in Ptrans, confirming the proportionality between the two, as SLG dominates absorption for our resonator-based PDs. This is also shown in Supplementary Note 2 and Supplementary Fig. 2, where we plot the estimated absorption and resulting VPTE at low (<0.1 mW) Pin on a linear scale. The shift of the resonance and its asymmetry for higher Pin (>0.2 mW) are attributed to the power-dependent change of the effective refractive index of the Si WG through a thermo-optic effect52,77. Extracting the power-dependent maxima in VPTE allows us to estimate Te at resonance, and plot the R[V/W] power dependence.
a Transmitted power for various Pin. b Photovoltage for a fixed gate voltage combination (VG1 = 1 V, VG2 = − 1 V) for various input powers (same color code as for the transmission in a). c Te calculated from the photoresponse in b and S in Fig. 4d. d Power-dependent R[V/W].
The junction carrier temperature, Te,j, can be written as (see Methods):
where T0 = 294 K is the room temperature and \({\zeta }_{1,2}=\frac{{\pi }^{2}{k}_{{\rm{B}}}^{2}}{3e\sigma }\frac{{\rm{d}}\sigma }{{\rm{d}}\epsilon }\) at ϵ = EF, in analogy to Eq. (2). In order to estimate ζ1,2, following the same method used to determine S in Fig. 4d, we use Rcontact and μ as obtained from the electrical measurements at homogeneous channel doping. The resulting Te extracted for different Pin is in Fig. 5c. The carriers reach Te ~ 400 K for Pin ~ 0.6 mW, due to cavity-enhanced light-matter interaction. The Te power dependence can be fitted by the heat equation44,70, neglecting diffusive cooling through the contacts (see Methods):
with δ ~ 378 and β a fitting parameter.
The associated, power-dependent, R[V/W] is in Fig. 5d. For small Pin (<0.2 mW), we get a constant R[V/W]. For Pin > 0.2 mW we have sublinear scaling between VPTE and Pin, giving a R[V/W] drop according to \({R}_{[{\rm{V}}/{\rm{W}}]}\propto {P}_{{\rm{in}}}^{-1/3}\) due to the Te dependence of the electronic heat capacity78,79.
Discussion
In order to assess our GPD performance against non-SLG-based ones, where typically a photocurrent Iph is generated14, we compare two representative optical receiver implementations: a conventional (i.e. non-SLG) system based on a wafer-scale, commercial, high-speed (>50 GHz) Ge photodiode with R[A/W] ~ 0.5 A/W80, and a receiver based on our GPD. In both systems the same amplifier is employed to obtain a >200 mV output voltage swing (VOUT), as required for driving the subsequent clock and data recovery CMOS circuit. For simplicity we assume that the amplifier represents a capacitive load.
Our GPDs are based on the PTE effect, where an electromotive force directly provides a voltage, rather than a current8,79. In case of Ge, an additional TIA is needed to convert the photocurrent into a voltage for further signal processing81. In the TIA we consider a feedback resistor RF = (90 V/W)/(0.5 A/W) = 180 Ω, which assures the same VOUT for same optical input power in both cases. Neglecting any noise other than thermal noise produced by RF, we estimate for the conventional receiver a lower limit for the sensitivity \({\bar{P}}_{{\rm{sens}}}=Q{i}_{{\rm{n}}}/{R}_{{\rm{[A/W]}}}=12.6\,\mu\)W ~ −19 dBm at a bit-error-rate (i.e. probability of false identification of a bit by the receiver decision circuit82) BER = 10−9. We calculate the thermal noise current as in = \(\sqrt{4{k}_{{\rm{B}}}\cdot T\cdot BW/{R}_{{\rm{F}}}}\) with BW = 12 GHz, as in our GPDs, and a Q factor (i.e. required signal-to-noise ratio to get a specific BER83) ~6 from82 BER = \(\frac{1}{2}{\rm{erfc}}(Q/\sqrt{2})\). For our GPDs, we estimate \({\bar{P}}_{{\rm{sens}}}\)=Qvn/R[V/W] ~ −16 dBm for same BER and BW, where vn=\(\sqrt{4{k}_{{\rm{B}}}\cdot T\cdot BW\cdot {R}_{{\rm{G}}}}\), and RG ~ 800 Ω is the total device resistance. Thus, in contrast to previous reports of both PTE25,26,27,29,33,76 and non-PTE30,31,32 GPDs for integrated photonics, \({\bar{P}}_{{\rm{sens}}}\) of our GPD-based receiver is on par with mature semiconductor technology, and could be further improved by reducing Rcontact, which dominates the total device resistance, thus being the primary source of thermal noise. The natural generation of a voltage makes the need for a TIA obsolete, with a reduction of energy-per-bit cost and system foot-print.
In summary, we reported photo-thermoelectric GPDs, integrated on Si microring resonators. By tuning the SLG coverage on top of the resonator, we optimised the round-trip propagation losses inside the cavity to get critical coupling, achieving >90% light absorption in ~6 μm SLG. The resulting carrier heating on such compact lengths enables high peak Te ~ 400 K in the GPDs. In combination with high (>104 cm2/Vs) mobility, obtained by encapsulating the SLG channel in hBN, this allowed us to get R[V/W] ~ 90 V/W. Our bias-free, Johnson-noise limited GPDs, with voltage output, are a more power-efficient alternative to state of the art commercial PDs used in optical interconnects. Hot-carrier effects in SLG can be exploited for receiver architectures where current-to-voltage conversion, traditionally performed by transimpedance amplifiers, can be bypassed for a reduction in energy-per-bit cost and system foot-print.
Methods
Sample fabrication
The LMH is made as follows55: SLG and hBN flakes of different thicknesses (tbottom ~ 3 nm, ttop ~ 20 nm) are prepared on Si/SiO2 (\({t}_{{{\rm{SiO}}}_{2}}\) = 285 nm) by MC of bulk graphite (Graphenium) and hBN single crystals grown at high pressure and temperature as detailed in ref. 84. The thickness of the bottom hBN, tbottom, is chosen with the following trade-off: sufficiently thin (<5 nm) to ensure αSLG (thus ξ) comparable to the initial experiment used to find W, but sufficiently thick (~nm) that high (>104 cm2/Vs) μ is achieved, due to reduced (in comparison to SiO2) carrier inhomogeneities, roughness, and charge impurities55,85,86. A micro-manipulator and a PC/PDMS stamp are then used to pick up and stack the flakes at 50 °C (Fig. 2a). In order to clean the LMH interfaces, the target photonic chip is then heated to 180 °C55, while we align the LMH to the Si WG. We then laminate the PC film onto the target substrate, pushing contamination blisters, formed at the SLG/hBN interfaces, out of the GPD channel region and placing the LMH on the WG, Fig. 2b.
After the PC film is dissolved in chloroform, we perform EBL (Raith EBPG 5200) to define the GPD channel geometry via a PMMA etch mask. To transfer this pattern to the LMH, we use two dry etching steps. First, to achieve etch selectivity between LMH and underlying photonic circuit, we use a reactive ion etcher (RIE, Plasma-Therm) with a forward radio frequency power ~80 W and an SF6 flow ~80 sccm. As reported by ref. 87, these conditions allow fast (>200 nm/min) etching of hBN, slow (<7 nm/min) etching of SiO2, while SLG is not etched, serving as etch stop on the bottom hBN flake (Fig. 2c). We then expose the LMH to low power (3W) O2 plasma to remove all excess SLG, leaving behind the fully shaped GPD channel (Fig. 2d). A second EBL step, electron beam evaporation (5nm Cr/50nm Au), and lift-off in acetone are then used to contact the exposed SLG channel edges (Fig. 2e). To fabricate the split-gate structure on top of the LMH, required to create a p-n juntion in the GPD channel, a transparent (at λ ~ 1.55 μm) conductor that does not affect ξ (thus W) is needed. A second layer of SLG, sufficiently high (~tens nm) above the WG to leave αSLG unaltered, can be used for this. We therefore thermally evaporate 1nm Al as seed layer on the top hBN, and atomic layer deposit (ALD, Savannah) tox ~ 20 nm Al2O3 as additional gate dielectric and spacer between channel and gate electrodes (Fig. 2f). The combined thickness of the top-gate dielectric (ttop + tox) ensures both low (~2 V or less) gate biases at the operating point of the GPD and, from eigenmode Lumerical simulations, a change in αSLG < 25%.
To ensure alignment between LMH and gate SLG, we transfer a continuous film of SLG, grown by chemical vapor deposition (CVD) on Cu, following the process described in ref. 88, using a PMMA support membrane89 on the SLG/Cu substrate. We etch Cu in ammonium persulfate, transfer the PMMA/SLG stack onto the photonic chip (Fig. 2g), and remove the PMMA by immersion in acetone. We then use two additional EBL steps, O2 plasma etching, and electron beam evaporation, to define the SLG split-gate geometry (Fig. 2h) and fabricate metal contacts to these gates (Fig. 2i). Finally, we perform optical lithography on a laser writer (MicroTECH LW405) and wet etching in HF to get access to drain and source contact pads.
Temperature estimation
The junction Te can be extracted from power-dependent photovoltage measurements. Rewriting Eq. (2) as S = ζTe, where \(\zeta =-({\pi }^{2}{k}_{{\rm{B}}}^{2})/3e\sigma {\rm{d}}\sigma /{\rm{d}}\epsilon\) at ϵ = EF, and using this in Eq. (1), we get VPTE = ∫S(x) ∇ Te(x)dx = ∫ζ(x)Te(x) ∇ Te(x)dx. Integration over the p-n-junction gives \({V}_{{\rm{PTE}}}={\zeta }_{1}\mathop{\int}\nolimits_{-\frac{L}{2}}^{0}{T}_{{\rm{e}}}(x)\frac{{\rm{d}}{T}_{{\rm{e}}}}{{\rm{d}}x}{\rm{d}}x+{\zeta }_{2}\mathop{\int}\nolimits_{0}^{\frac{L}{2}}{T}_{{\rm{e}}}(x)\frac{{\rm{d}}{T}_{{\rm{e}}}}{{\rm{d}}x}{\rm{d}}x=\frac{{\zeta }_{1}-{\zeta }_{2}}{2}\left({T}_{{\rm{e,j}}}^{2}-{T}_{0}^{2}\right)\). From this, we extract the junction Te from the measured photovoltage as Te,j=\(\sqrt{2\left|\frac{{V}_{{\rm{PTE}}}}{{\zeta }_{1}-{\zeta }_{2}}\right|+{T}_{0}^{2}}\). In the most general case, the Te profile can be calculated from the heat equation44,70, including diffusive cooling through contacts and cooling through the phonon bath: \(\frac{{\rm{d}}q}{{\rm{d}}x}=-\frac{{\rm{d}}}{{\rm{d}}x}\left({\kappa }_{{\rm{e}}}\frac{{\rm{d}}}{{\rm{d}}x}{T}_{{\rm{e}}}\right)+\frac{{\kappa }_{{\rm{e}}}}{{L}_{{\rm{cooling}}}^{2}}\left({T}_{{\rm{e}}}^{\delta }-{T}_{{\rm{0}}}^{\delta }\right)\), where \(\frac{{\rm{d}}q}{{\rm{d}}x}\) describes the heating of the system. The electronic thermal conductivity is given by \({\kappa }_{{\rm{e}}}=\sigma {{\mathcal{L}}}_{0}{T}_{{\rm{e}}}\)90, with Lorenz number \({{\mathcal{L}}}_{0}\), while a \({T}_{e}^{\delta }\) dependence with δ ~ 3 is characteristic for SLG70,91. Assuming the distance from the heat source to the heat sink larger than the cooling length (Lchannel > 2Lcooling), the heat equation becomes \(\frac{{\rm{d}}q}{{\rm{d}}x}=\frac{{\kappa }_{{\rm{e}}}}{{L}_{{\rm{cooling}}}^{2}}\left({T}_{{\rm{e}}}^{\delta }-{T}_{{\rm{0}}}^{\delta }\right)\), with \(\frac{{\rm{d}}q}{{\rm{d}}x}=\alpha {P}_{{\rm{in}}}/A\), αPin the fraction of the absorbed power, and A the heated area. We thus get \({T}_{{\rm{e,j}}}={\left(\beta {P}_{{\rm{in}}}+{T}_{0}^{\delta }\right)}^{\frac{1}{\delta }}\), with β a fit parameter.
Data availability
Data supporting the findings of this study are available from the corresponding authors upon reasonable request.
References
Atabaki, A. H. et al. Integrating photonics with silicon nanoelectronics for the next generation of systems on a chip. Nature 556, 349–354 (2018).
Cheng, Q., Bahadori, M., Glick, M., Rumley, S. & Bergman, K. Recent advances in optical technologies for data centers: a review. Optica 5, 1354–1370 (2018).
Subbaraman, H. et al. Recent advances in silicon-based passive and active optical interconnects. Opt. Express 23, 2487–2511 (2015).
Romagnoli, M. et al. Graphene-based integrated photonics for next-generation datacom and telecom. Nat. Rev. Mater. 3, 392–414 (2018).
Bonaccorso, F., Sun, Z., Hasan, T. & Ferrari, A. C. Graphene photonics and optoelectronics. Nat. Photonics 4, 611–622 (2010).
Urich, A., Unterrainer, K. & Mueller, T. Intrinsic response time of graphene photodetectors. Nano Lett. 11, 2804–2808 (2011).
Xia, F., Mueller, T., Lin, Y., Valdes-Garcia, A. & Avouris, P. Ultrafast graphene photodetector. Nat. Nanotechnol. 4, 839–843 (2009).
Koppens, F. H. et al. Photodetectors based on graphene, other two-dimensional materials and hybrid systems. Nat. Nanotechnol. 9, 780–793 (2014).
Cai, X. et al. Sensitive room-temperature terahertz detection via the photothermoelectric effect in graphene. Nat. Nanotechnol. 9, 814–819 (2014).
Vivien, L. et al. Zero-bias 40Gbit/s germanium waveguide photodetector on silicon. Opt. Express 20, 1096–1101 (2012).
Salamin, Y. et al. 100 GHz plasmonic photodetector. ACS Photonics 5, 3291–3297 (2018).
Michel, J., Liu, J. & Kimerling, L. C. High-performance Ge-on-Si photodetectors. Nat. Photonics 4, 527–534 (2010).
Thomson, D. et al. Roadmap on silicon photonics. J. Opt. 18, 073003 (2016).
Chrostowski, L. & Hochberg, M. Silicon Photonics Design: From Devices to Systems (Cambridge University Press, 2015).
Arafin, S. & Coldren, L. A. Advanced InP photonic integrated circuits for communication and sensing. IEEE J. Sel. Top. Quantum Electron. 24, 1–12 (2018).
Nagarajan, R. et al. InP photonic integrated circuits. IEEE J. Sel. Top. Quantum Electron. 16, 1113–1125 (2010).
Liu, M. et al. A graphene-based broadband optical modulator. Nature 474, 64–67 (2011).
Phare, C. T., Daniel Lee, Y., Cardenas, J. & Lipson, M. Graphene electro-optic modulator with 30 GHz bandwidth. Nat. Photonics 9, 511–514 (2015).
Giambra, M. A. et al. High-speed double layer graphene electro-absorption modulator on SOI waveguide. Opt. Express 27, 20145–20155 (2019).
Sorianello, V. et al. Graphene–silicon phase modulators with gigahertz bandwidth. Nat. Photonics 12, 40–44 (2018).
Cassese, T. et al. Capacitive actuation and switching of add-drop graphene-silicon micro-ring filters. Photonics Res. 5, 762–766 (2017).
Pospischil, A. et al. CMOS-compatible graphene photodetector covering all optical communication bands. Nat. Photonics 7, 892–896 (2013).
Gan, X. et al. Chip-integrated ultrafast graphene photodetector with high responsivity. Nat. Photonics 7, 883–887 (2013).
Wang, X., Cheng, Z., Xu, K., Tsang, H. K. & Xu, J. High-responsivity graphene/silicon-heterostructure waveguide photodetectors. Nat. Photonics 7, 888–891 (2013).
Shiue, R. J. et al. High-responsivity graphene-boron nitride photodetector and autocorrelator in a silicon photonic integrated circuit. Nano Lett. 15, 7288–7293 (2015).
Schuler, S. et al. Controlled generation of a p-n junction in a waveguide integrated graphene photodetector. Nano Lett. 16, 7107–7112 (2016).
Schuler, S. et al. Graphene photodetector integrated on a photonic crystal defect waveguide. ACS Photonics 5, 4758–4763 (2018).
Goykhman, I. et al. On-chip integrated, silicon-graphene plasmonic schottky photodetector with high responsivity and avalanche photogain. Nano Lett. 16, 3005–3013 (2016).
Muench, J. E. et al. Waveguide-integrated, plasmonic enhanced graphene photodetectors. Nano Lett. 19, 7632–7644 (2019).
Schall, D. et al. In Optical Fiber Communication Conference, M2I.4 (Optical Society of America, 2018).
Ma, P. et al. Plasmonically enhanced graphene photodetector featuring 100 Gbit/s data reception, high responsivity, and compact size. ACS Photonics 6, 154–161 (2019).
Ding, Y. et al. Ultra-compact integrated graphene plasmonic photodetector with bandwidth above 110 GHz. Nanophotonics 9, 317–325 (2020).
Mišeikis, V. et al. Ultrafast, zero-bias, graphene photodetectors with polymeric gate dielectric on passive photonic waveguides. ACS Nano 14, 11190–11204 (2020).
Giambra, M. A. et al. Wafer-scale integration of graphene-based photonic devices. ACS Nano 15, 3171–3187 (2021).
Gao, Y., Zhou, G., Zhao, N., Tsang, H. K. & Shu, C. High-performance chemical vapor deposited graphene-on-silicon nitride waveguide photodetectors. Opt. Lett. 43, 1399–1402 (2018).
Cheng, Z., Wang, J., Xu, K., Tsang, H. K. & Shu, C., In CLEO: Science and Innovations, STh1I–5 (Optical Society of America, 2015).
Wang, J. et al. Design of graphene-on-germanium waveguide electro-optic modulators at the 2μm wavelength. OSA Contin. 2, 749–758 (2019).
Kim, J. T. & Choi, C. Graphene-based polymer waveguide polarizer. Opt. Express 20, 3556–3562 (2012).
Kleinert, M. et al. Graphene-based electro-absorption modulator integrated in a passive polymer waveguide platform. Optical Mater. Express 6, 1800–1807 (2016).
Qu, Z. et al. In Silicon Photonics XIII, 105371N, (International Society for Optics and Photonics, 2018).
Nair, R. R. et al. Fine structure constant defines visual transparency of graphene. Science 320, 1308–1308 (2008).
Youngblood, N. & Li, M. Integration of 2D materials on a silicon photonics platform for optoelectronics applications. Nanophotonics 6, 1205–1218 (2017).
Gabor, N. M. et al. Hot carrier–assisted intrinsic photoresponse in graphene. Science 334, 648–652 (2011).
Song, J. C. W., Rudner, M. S., Marcus, C. M. & Levitov, L. S. Hot carrier transport and photocurrent response in graphene. Nano Lett. 11, 4688–4692 (2011).
Xu, X., Gabor, N. M., Alden, J. S., van der Zande, A. M. & McEuen, P. L. Photo-thermoelectric effect at a graphene interface junction. Nano Lett. 10, 562–566 (2010).
Brida, D. et al. Ultrafast collinear scattering and carrier multiplication in graphene. Nat. Commun. 4, 1987 (2013).
Tomadin, A., Brida, D., Cerullo, G., Ferrari, A. C. & Polini, M. Nonequilibrium dynamics of photoexcited electrons in graphene: Collinear scattering, Auger processes, and the impact of screening. Phys. Rev. B 88, 035430 (2013).
Soavi, G. et al. Broadband, electrically tunable third-harmonic generation in graphene. Nat. Nanotechnol. 13, 583–588 (2018).
Echtermeyer, T. J. et al. Strong plasmonic enhancement of photovoltage in graphene. Nat. Commun. 2, 455–458 (2011).
Engel, M. et al. Light-matter interaction in a microcavity-controlled graphene transistor. Nat. Commun. 3, 906 (2012).
Furchi, M. et al. Microcavity-integrated graphene photodetector. Nano Lett. 12, 2773–2777 (2012).
Bogaerts, W. et al. Silicon microring resonators. Laser Photonics Rev. 6, 47–73 (2012).
Fang, Y., Armin, A., Meredith, P. & Huang, J. Accurate characterization of next-generation thin-film photodetectors. Nat. Photonics 13, 1–4 (2019).
Balandin, A. A. Low-frequency 1/f noise in graphene devices. Nat. Nanotechnol. 8, 549–555 (2013).
Purdie, D. G. et al. Cleaning interfaces in layered materials heterostructures. Nat. Commun. 9, 5387 (2018).
Rabus, D. G. Integrated ring resonators (Springer, 2007).
Yariv, A. Critical coupling and its control in optical waveguide-ring resonator systems. IEEE Photonics Technol. Lett. 14, 483–485 (2002).
Xu, Q., Schmidt, B., Shakya, J. & Lipson, M. Cascaded silicon micro-ring modulators for WDM optical interconnection. Opt. Express 14, 9431–9436 (2006).
Zheng, X. et al. A tunable 1x4 silicon CMOS photonic wavelength multiplexer/demultiplexer for dense optical interconnects. Opt. Express 18, 5151–5160 (2010).
Paschotta, R. Encyclopedia of laser physics and technology (Wiley-VCH, 2008).
Timurdogan, E. et al. An ultralow power athermal silicon modulator. Nat. Commun. 5, 4008 (2014).
Reed, G. T. & Knights, A. P. Silicon Photonics: An Introduction (John Wiley & Sons, 2004).
Novoselov, K. S. et al. Two-dimensional atomic crystals. Proc. Natl Acad. Sci. USA 102, 10451–10453 (2005).
Gan, X. et al. Strong enhancement of light–matter interaction in graphene coupled to a photonic crystal nanocavity. Nano Lett. 12, 5626–5631 (2012).
Reich, S. et al. Resonant Raman scattering in cubic and hexagonal boron nitride. Phys. Rev. B 71, 12 (2005).
Nemanich, R. J., Solin, S. A. & Martin, R. M. Light scattering study of boron nitride microcrystals. Phys. Rev. B 23, 0 (1981).
Das, A. et al. Monitoring dopants by Raman scattering in an electrochemically top-gated graphene transistor. Nat. Nanotechnol. 3, 210–215 (2008).
Basko, D. M., Piscanec, S. & Ferrari, A. C. Electron-electron interactions and doping dependence of the two-phonon Raman intensity in graphene. Phys. Rev. B 80, 165413 (2009).
Ferrari, A. C. & Basko, D. M. Raman spectroscopy as a versatile tool for studying the properties of graphene. Nat. Nanotechnol. 8, 235–246 (2013).
Ma, Q. et al. Competing channels for hot-electron cooling in graphene. Phys. Rev. Lett. 112, 247401 (2014).
Freitag, M., Low, T. & Avouris, P. Increased responsivity of suspended graphene photodetectors. Nano Lett. 13, 1644–1648 (2013).
Tielrooij, K. et al. Out-of-plane heat transfer in van der Waals stacks through electron–hyperbolic phonon coupling. Nat. Nanotechnol. 13, 41 (2018).
Zhang, Z., Xu, H., Zhong, H. & Peng, L. Direct extraction of carrier mobility in graphene field-effect transistor using current-voltage and capacitance-voltage measurements. Appl. Phys. Lett. 101, 213103 (2012).
Bie, Y. et al. A MoTe2-based light-emitting diode and photodetector for silicon photonic integrated circuits. Nat. Nanotechnol. 12, 1124–1129 (2017).
Song, J. C. W. & Levitov, L. S. Energy flows in graphene: hot carrier dynamics and cooling. J. Phys. Condens. Matter 27, 164201 (2015).
Marconi, S. et al. Photo thermal effect graphene detector featuring 105 Gbit s-1 NRZ and 120 Gbit s-1 PAM4 direct detection. Nat. Commun. 12, 806 (2021).
Fainman, Y. et al. Silicon nanophotonic devices for chip-scale optical communication applications. Appl. Opt. 52, 613–624 (2013).
Graham, M. W., Shi, S., Ralph, D. C., Park, J. & McEuen, P. L. Photocurrent measurements of supercollision cooling in graphene. Nat. Phys. 9, 103 (2013).
Tielrooij, K. et al. Generation of photovoltage in graphene on a femtosecond timescale through efficient carrier heating. Nat. Nanotechnol. 10, 437–443 (2015).
Absil, P. P. et al. Silicon photonics integrated circuits: a manufacturing platform for high density, low power optical I/O’s. Opt. Express 23, 9369–9378 (2015).
Okamoto, D. et al. A 25-Gb/s 5 × 5 mm 2 chip-scale silicon-photonic receiver integrated with 28-nm CMOS transimpedance amplifier. J. Lightwave Technol. 34, 2988–2995 (2016).
Agrawal, G. P. Fiber-optic communication systems (John Wiley & Sons, 2012).
Bergano, N. S., Kerfoot, F. & Davidsion, C. Margin measurements in optical amplifier system. IEEE Photonics Technol. Lett. 5, 304–306 (1993).
Taniguchi, T. & Watanabe, K. Synthesis of high-purity boron nitride single crystals under high pressure by using Ba-BN solvent. J. Cryst. Growth 303, 525–529 (2007).
Dean, C. R. et al. Boron nitride substrates for high-quality graphene electronics. Nat. Nanotechnol. 5, 722 (2010).
Wang, L. et al. One-dimensional electrical contact to a two-dimensional material. Science 342, 614–617 (2013).
Jessen, B. S. et al. Lithographic band structure engineering of graphene. Nat. Nanotechnol. 14, 340 (2019).
Li, X. et al. Large-area synthesis of high-quality and uniform graphene films on copper foils. Science 324, 1312–1314 (2009).
Bonaccorso, F. et al. Production and processing of graphene and 2d crystals. Mater. Today 15, 564–589 (2012).
Kittel, C. Introduction to solid state physics (Wiley New York, 1996).
Song, J. C. W., Reizer, M. Y. & Levitov, L. S. Disorder-assisted electron-phonon scattering and cooling pathways in graphene. Phys. Rev. Lett. 109, 5 (2012).
Acknowledgements
We thank S. Wachter, D. Schall, A. Tomadin, J. Marcellino for useful discussions. We acknowledge funding from the EU Graphene Flagship, ERC grant Hetero2D, DSTL, EPSRC grants EP/L016087/1, EP/K01711X/1, EP/K017144/1, EP/N010345/1.
Author information
Authors and Affiliations
Contributions
S.S., J.E.M., A.C.F. and T.M. conceived the device. A.C.F. and T.M. supervised the work. S.S. and J.E.M. fabricated the devices and performed the experiments. S.S., J.E.M., T.M. and A.C.F. analysed and discussed the data. J.E.M. and A.R. built the measurement setup. O.B. prepared CVD SLG. T.T. and K.W. prepared hBN. D.V.T. and V.S. designed and provided the SOI waveguide substrates. S.S., J.E.M., T.M. and A.C.F. wrote the paper, with input from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Schuler, S., Muench, J.E., Ruocco, A. et al. High-responsivity graphene photodetectors integrated on silicon microring resonators. Nat Commun 12, 3733 (2021). https://doi.org/10.1038/s41467-021-23436-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-021-23436-x
This article is cited by
-
Optimal design of graphene-based plasmonic enhanced photodetector using PSO
Scientific Reports (2024)
-
Emerging single-photon detection technique for high-performance photodetector
Frontiers of Physics (2024)
-
Two-dimensional materials for future information technology: status and prospects
Science China Information Sciences (2024)
-
On-chip optical sources of 3D photonic integration based on active fluorescent polymer waveguide microdisks for light display application
PhotoniX (2023)
-
Two-dimensional materials-based integrated hardware
Science China Information Sciences (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.