Abstract
As quantum coherence times of superconducting circuits have increased from nanoseconds to hundreds of microseconds, they are currently one of the leading platforms for quantum information processing. However, coherence needs to further improve by orders of magnitude to reduce the prohibitive hardware overhead of current error correction schemes. Reaching this goal hinges on reducing the density of broken Cooper pairs, so-called quasiparticles. Here, we show that environmental radioactivity is a significant source of nonequilibrium quasiparticles. Moreover, ionizing radiation introduces time-correlated quasiparticle bursts in resonators on the same chip, further complicating quantum error correction. Operating in a deep-underground lead-shielded cryostat decreases the quasiparticle burst rate by a factor thirty and reduces dissipation up to a factor four, showcasing the importance of radiation abatement in future solid-state quantum hardware.
Similar content being viewed by others
Introduction
Quantum technologies based on solid-state devices are attracting a growing interest in both academic and industrial research communities, because they offer the tantalizing prospect of engineering quantum mechanical effects by using superconducting and semiconducting building blocks reminiscent of classical integrated circuits1,2,3. Although a daunting technological challenge, macroscopic components, such as capacitors, inductors, and Josephson junctions can be interconnected and assembled in complex quantum circuits, as recently proven by the operation of processors consisting of tens of quantum bits (qubits)4,5,6,7. While these pioneering implementations showcase the advantages of solid-state platforms, one of their main challenges for future development, increasing quantum coherence, stems from the difficulty in decoupling from various noisy environments2; be that dielectric defects, magnetic moments, trapped charges and vortices, spurious electromagnetic modes, or excess quasiparticles (QPs).
QPs, which can be viewed as broken Cooper pairs, degrade the performance of superconducting circuits in two ways8: their presence introduces dissipation, and fluctuations in their numbers give rise to noise. Although QPs are particularly damaging in circuits employing the high kinetic inductance of Cooper pairs9,10,11, often constituting the dominant source of decoherence, we will argue below that QPs can be an indicator of a more generally damaging pair-breaking mechanism for solid-state hardware, namely radioactivity.
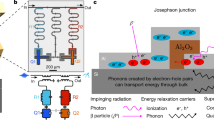
High-energy particles are a routinely observed source of noise in low-temperature circuits, such as microcalorimeters12,13, bolometers14, and MKIDs15. In particular, the latter ref. reports time-correlated glitches in the resonant frequency of an array of several hundreds same-chip resonators. Moreover, ref. 16 has also provided a clear evidence that radioactivity induces errors correlated both in space and time in qubits, undermining many algorithms for quantum error correction17, and ref. 18 has recently shown that the coherence limit imposed by ionizing radiation for transmon type qubits is in the millisecond range, only one order of magnitude above the state-of-the-art. As dielectric losses are steadily decreased19,20, further improving the coherence of solid-state devices will soon hinge on the reduction of QPs, and more generally on ionizing radiation abatement. In thermal equilibrium, at typical operational temperatures of 20–50 mK, QPs should be an extremely rare occurrence in commonly used materials such as Al and Nb, with critical temperatures well >1 K: e.g., one would need to wait a time comparable to the age of the universe to observe a single thermal QP in a 10 μm3 volume of Al at 100 mK. However, the detrimental effects of nonequilibrium QPs are routinely observed in a variety of devices9,21,22,23,24,25,26,27,28,29,30,31,32, including the microwave resonators used in this work (cf. Fig. 1). The multifarious QP sources include stray infrared radiation24,32, high-power microwave drive33, and pair-breaking phonons in the device substrate34,35, resulting from environmental or cosmic radioactivity. The latter is potentially damaging for any solid-state quantum hardware, not only superconducting, as it can give rise to correlated energy bursts in devices on the same chip. In the case of superconducting resonators, for instance, phonons generated by particle impacts in the device substrate produce correlated QP spikes orders of magnitude above the baseline36,37, visible as abrupt frequency drops (see Fig. 1b, c). The correlation among events can be mitigated by using so-called phonon traps15,35. On the contrary, their absolute rate (today of the order of one every few seconds9,10,36) can only be reduced by a careful selection of radio-pure materials and shielding protocols. Without a mitigation strategy, the ensuing relatively long-lasting38 and correlated36,37 effects of radioactive interactions can hinder quantum error correction protocols.
a False-colored photograph of the central part of the sapphire chip, supporting three 20 nm thick grAl resonators, labeled A, B, and C. b Overlay of ten measured time traces for the resonant frequency shift δf0 of resonator A. Similarly to refs. 10,21,36, quasiparticle (QP) bursts appear as sudden drops, given by the sharp rise in kinetic inductance, followed by a relaxation tail. The y-axis on the right-hand side shows the corresponding fractional quasiparticle density shift δxQP = −4δf0/f0. We identify a QP burst by applying a derivative filter, triggering only on sharp rises in the baseline. For clarity, the shown traces are selected to contain a QP burst; on average, only one trace in ten contains a QP burst. To highlight the fact that QP bursts are correlated in time, in c, we plot the measured frequency shifts of resonator B (upward triangles) and C (downward triangles) versus the frequency shift of resonator A. Colored markers correspond to values above threshold, with the threshold defined as two standard deviations of the baseline fluctuations (cf. Supplementary Information). Therefore, each colored marker depicts a time-correlated QP burst between resonators A–B (orange) and A–C (green). d Estimated distribution of the energy absorbed in the resonators δE = δxQPΔgrAlnCPV, calculated from the measured δxQP shown in the inset, where ΔgrAl ≃ 300 μeV is the grAl superconducting gap, and nCP = 4 × 106 μm−3 is the volume density of Cooper pairs, and V is the volume of each resonator. For each burst, the energy deposited in the substrate is estimated to be 103–104 times greater than δE (cf. Supplementary Information). The total QP burst rate ΓB is obtained by counting all bursts above the common threshold δxQP = 5 × 10−5.
Superconducting circuits can be sensitive to a variety of radioactive sources, depending, among others, on the distance from the device, penetrating power, spectral distribution, and shielding. So-called far sources consist of cosmic rays, mainly sea-level muons at a rate of ~1 cm−2 min−1 (refs. 39,40), as well as decay products of location-specific contaminants. Even when far sources can be shielded, using, e.g., Pb screens or underground facilities, near sources, such as residues from handling and machining, or radioactive isotopes in the sample holder and the sample itself might need to be mitigated by material selection and decontamination. In this work, we demonstrate that by reducing radioactivity we lower the internal dissipation in superconducting microwave resonators by factors two to four, and the QP burst rate by a factor 30. This was achieved by a combination of material selection and cleaning, and by shielding under the 1.4 km granite layer at the Gran Sasso National Laboratory (L’Aquila, Italy), corresponding to a 3.6 km water equivalent.
Results and discussion
We use high kinetic inductance granular aluminum (grAl) superconducting resonators (see Fig. 1a) as a sensitive QP probe, following the principle of kinetic inductance detectors (KIDs)41. Shifts in their resonant frequency \({f}_{0}^{-1}=2\pi \sqrt{LC}\), where C is the capacitance of the mode, directly reflect changes in the inductance δL/L = −(2/α)δf0/f0, where α is the ratio of kinetic inductance over the total inductance. In the case of high kinetic inductance materials, such as grAl, where the geometric inductance can be neglected10, the measured relative frequency shift informs on the corresponding change in the number of QPs with respect to the number of Cooper pairs: δxQP = 2δL/L = −4δf0/f0. Both KIDs and qubits are sensitive to pair-breaking phonons produced by radioactive deposits in the chip. The major difference between these devices is the phonon absorption probability in a region of the device susceptible to QPs, which depends on the supercurrent mode volume. We decided to rely on KIDs because, apart from the ease in operation, they enable a real-time monitoring of the QPs bursts due to phonon absorption, and they are sensitive over a much wider energy range compared to qubits.
The resonators were fabricated using optical lithography on a 1.2 cm2 and 330 μm thick sapphire substrate, following the stripline design of ref. 10. Their dimensions and corresponding resonant frequencies f0 are listed in Fig. 1a. We performed quality factor measurements in the range of \(\bar{n}=1\) circulating photons, which are the typical conditions for quantum circuits, and time domain evolution measurements of the resonant frequency at the highest available power before bifurcation. Furthermore, we used a 3D waveguide sample holder42 in order to minimize the electric field density at the interfaces and reduce coupling to dielectric losses43. In this setup, losses in grAl resonators are dominated by nonequilibrium QPs and dielectric losses contribute to up to ~20% (refs. 10,35). In Fig. 1b, we show typical time traces for the frequency shift δf0 of resonator A, measured in a cryostat above ground. We observe abrupt drops of f0, indicative of a QP burst in the resonator film, followed by a relaxation tail, associated with QP recombination and diffusion, similarly to refs. 10,21,36,37, one every ~10 s. We interpret them as the aftermath of ionizing events in the substrate, causing an energy release in the form of pair-breaking phonons, which in turn produce QPs. Indeed, as shown in Fig. 1c and in Supplementary Information, most QP bursts in resonator A are correlated with those in resonators B and C, proving the key role played by substrate phonons37. Notice that although resonator C is twice as far from resonator A compared to B, the correlation plot does not appear qualitatively different, indicating that in our present geometry QP bursts are time-correlated over at least 10 mm2 areas of the chip, similarly to refs. 36,37. The histogram of the QP burst rate as a function of the energy absorbed in the resonators is shown in Fig. 1d. We estimate the efficiency of phonon absorption from the substrate into the resonators to be 10−3–10−4, placing the energy deposited in the substrate by each ionizing impact in the keV–MeV range (cf. Supplementary Information).
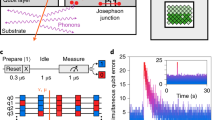
In the following, we will use the QP burst rate as an indicator of the ionizing radiation flux, while we perform various combinations of material selection, cleaning, and shielding. The three setups, located in Karlsruhe, Rome, and Gran Sasso, denoted by K, R, and G, are schematized in Fig. 2, and the dates of the four measurement runs are indicated by the top labels. The corresponding measured QP burst rates and internal quality factors of the resonators are listed in Fig. 3.
Schematic half-sections of the setups, in Karlsruhe, Rome, and Gran Sasso, denoted K, R, and G, respectively. The measurement dates for each setup are indicated in the top labels. The sapphire chip is glued to a copper waveguide using either silver paste (K and R, magenta) or vacuum grease (G and R, blue). A circulator routes the attenuated input signal to the sample holder, and the reflected output signal to an isolator and an amplification chain (cf. Supplementary Information). In the R and G setups, the waveguide is etched with citric acid to remove possibly radioactive contaminants. The G setup, located under 1.4 km of granite (3.6 km water equivalent) is operated in three configurations. First, the cryostat is surrounded by a 10 cm thick wall of lead bricks. Two days later, the bricks were removed. Finally, we added a ThO2 radioactive source next to the cryostat body (cf. red arrow).
a Quasiparticle burst rate ΓB and b internal quality factor at single photon drive Qi for all resonators and setups. When the sample is cleaned and tested in the R setup, the measured ΓB and Qi values are comparable to those obtained in K. Measurements in the G setup show a reduction in QP burst rate ΓB (factor 30) and dissipation (up to a factor 4). In G, removing the lead shielding increases ΓB by a factor two. Adding a ThO2 radioactive source next to the cryostat body yields a ΓB greater than the one measured above ground, and decreases the internal quality factor Qi by 18 ± 3%. Error bars are \(\sqrt{N}\) for ΓB (Poissonian error) and standard deviations of all data points in the \(\bar{n}=0.1{-}10\) range for Qi when available, and are not shown when smaller than the marker size. The chronological order of measurements in the three different setups is indicated by the dotted gray arrows.
Both the K and R setups are located above ground. The K setup is typical for superconducting circuit experiments and features additional magnetic shielding compared to the G and R setup, consisting of a superconducting and a μ-metal barrel encasing the waveguide. In the K and R facilities we expect muons (and their secondary products) to hit the substrate with a rate of ~0.6 mHz. These interactions release an average energy of 0.8 MeV, with tails extending up to few MeV. In the G setup, the 1.4 km of rock overburden reduces the cosmic ray flux by six orders of magnitude and thus to a completely negligible rate in the chip. However, according to our simulations (cf. Supplementary Information), an important contribution to the measured rate comes from radioactive contamination in the laboratory environment. According to measurements performed with a NaI commercial spectrometer, we predict a rate of 16 mHz in K, 48 mHz in R, and 4 mHz in G. The average energy deposit due to environmental radioactivity is 0.1 MeV.
The burst rate and the internal quality factors measured for all resonators in the three sites are shown in Fig. 3. The first set of data was collected in K, where we measured a burst rate (averaged over the three resonators) of ~76 mHz. In the K setup, no specific radio-purification measures have been taken. Therefore, the factor four larger burst rate compared to the expected value from the NaI spectrometer is likely due to residual radioactive contamination of the sample holder and its immediate environment. For the next data sets, we cleaned the sample enclosure and its mounting parts with citric acid and hydrogen peroxide to reduce surface contamination, removed the potentially radioactive indium wire used to seal the copper cap, substituted lead soldering with araldite glue, and replaced silver paste with more radio-pure44 cryogenic grease to attach the chip to the copper holder. The sample placed in this radio-cleaned holder was measured deep underground in a cryostat surrounded by a wall of 10 cm thick Pb bricks. The rate induced by muons in the underground setup is very small compared to the one induced by environmental radioactivity; however, the effectiveness of lead shielding against the environmental radioactivity increases when going underground. Cosmic rays, indeed, produce gamma showers in the materials surrounding the sample (including the lead shield itself) that are hard to suppress above ground. Thus, the same lead shield offers a stronger reduction against gamma’s when used deep underground. According to our simulations, the lead shield suppresses the contribution of environmental radioactivity to the counting rate down to 0.5 mHz.
We measured an average QP burst rate of 2.6 mHz, pointing to a small residual contribution due to contamination of the dilution refrigerator, and of the materials of the sample holder and assembly. The cleaning protocols and the cryostat shielding could be largely improved; nevertheless, we observed a reduction in the burst rate by a factor 30.
We performed two additional measurements by first removing the bricks, and then exposing the cryostat to a 232Th source in the form of ThO2. Removing the lead shielding increases the burst rate by a factor two, and adding the ThO2 source increases the rate beyond above ground levels, confirming the radioactive origin of the bursts. The internal quality factors (cf. Fig. 3, bottom) are anticorrelated with the burst rates between above and underground measurements, achieving up to a fourfold increase in the G setup. The measurement of single photon quality factors consists of averaging multiple frequency domain traces over a time span of tens of minutes, during which the resonator is averaging over QP-induced losses.
To confirm that such improvement in the internal quality factor was not due to the chip ageing, or to the electronics or magnetic shielding used in the G site, we moved the “cleaned” assembly with the entire readout and magnetic shield to the above ground cryostat in R. As expected, we observed an increase in the burst rate and a corresponding worsening in the quality factor. We also investigated if using vacuum grease instead of silver paste to attach the chip to the copper holder could affect the thermalization of the substrate and thus the quality factor. We replaced the vacuum grease with silver paste and repeated the measurements obtaining consistent results; a small excess in the burst rate was observed, probably related to contamination in the silver paste.
Notice that the burst rate is not simply a proxy for the quality factor, as indicated by the fact that the quality factor in the G setup only decreased by ~20% when the QP burst rate was increased by two orders of magnitude by using the ThO2 source. This is not surprising, given the fact that the ThO2 source alone is not a good proxy for the radioactive contributions that we would expect above ground, where we have to account for muons, releasing an average energy seven to eight times larger than the average energy released by the ThO2 source, and for neutrons. Therefore, a survey of various sources is needed in order to quantitatively understand the QP generation, and the influence on the quality factors of superconducting devices. We would like to mention that, during the editing stages of our work, in ref. 45 the authors report QP bursts with orders of magnitude higher rate, which decays over time scales of several weeks, and of undetermined origin, showcasing the challenges that lie ahead for the community.
In conclusion, we showed that the performance of superconducting circuits at the current level of coherence can be significantly degraded by environmental radioactivity in a typical above ground setting, in particular due to ionizing interactions in the device substrate. We demonstrated that the rate of correlated QP bursts is reduced by up to a factor 30 by shielding in a deep-underground facility and by a radioactive decontamination in the near environment of the sample. Furthermore, the quality factors of high kinetic inductance superconducting resonators improved up to a factor four with respect to above ground values.
These observations highlight the need for a systematic assessment of radioactive sources, which can produce energy bursts in solid-state quantum hardware, as well as for a better understanding of the relevant chains of mechanisms, such as the creation of electron–hole pairs, and the excitation of high-energy phonons, which potentially limit the performance of superconducting and semiconducting devices. The effectiveness of radiation abatement and phonon damping solutions, such as phonon traps15,35, will determine whether the next generation of solid-state quantum processors will need to be operated in deep-underground facilities.
Data availability
All relevant data are available from the authors upon request.
References
Gu, X. et al. Microwave photonics with superconducting quantum circuits. Phys. Rep. 718–719, 1–102 (2017).
Krantz, P. et al. A quantum engineer’s guide to superconducting qubits. Appl. Phys. Rev. 6, 021318 (2019).
Burkard, G. et al. Superconductor-semiconductor hybrid-circuit quantum electrodynamics. Nat. Rev. Phys. 2, 129–140 (2020).
Otterbach, J. S. et al. Unsupervised machine learning on a hybrid quantum computer. Preprint at http://arxiv.org/abs/1712.05771 (2017).
Song, C. et al. 10-qubit entanglement and parallel logic operations with a superconducting circuit. Phys. Rev. Lett. 119, 180511 (2017).
Wang, Y. et al. 16-qubit IBM universal quantum computer can be fully entangled. npj Quantum Inf. 4, 46 (2018).
Arute, F. et al. Quantum supremacy using a programmable superconducting processor. Nature 574, 505–510 (2019).
Catelani, G. et al. Relaxation and frequency shifts induced by quasiparticles in superconducting qubits. Phys. Rev. B 84, 064517 (2011).
De Visser, P. J. et al. Number fluctuations of sparse quasiparticles in a superconductor. Phys. Rev. Lett. 106, 167004 (2011).
Grünhaupt, L. et al. Loss mechanisms and quasiparticle dynamics in superconducting microwave resonators made of thin-film granular aluminum. Phys. Rev. Lett. 121, 117001 (2018).
Grünhaupt, L. et al. Granular aluminium as a superconducting material for high-impedance quantum circuits. Nat. Mater. 18, 816–819 (2019).
Stahle, C. et al. Cosmic ray effects in microcalorimeter arrays. Nucl. Instrum. Methods Phys. Res. A 520, 472–474 (2004).
Kilbourne, C. A. et al. In-flight calibration of Hitomi Soft X-ray Spectrometer. (1) Background. Publ. the Astron. Soc. Jpn 70, 20 (2018).
Catalano, A. et al. Impact of particles on the planck hfi detectors: ground-based measurements and physical interpretation. Astron. Astrophys. 569, A88 (2014).
Karatsu, K. et al. Mitigation of cosmic ray effect on microwave kinetic inductance detector arrays. Appl. Phys. Lett. 114, 032601 (2019).
Wilen, C. D. et al. Correlated charge noise and relaxation errors in superconducting qubits. Preprint at http://arxiv.org/abs/2012.06029 (2020).
Martinis, J. Saving superconducting quantum processors from qubit decay and correlated errors generated by gamma and cosmic rays. Preprint at http://arxiv.org/abs/2012.06137 (2020).
Vepsäläinen, A. et al. Impact of ionizing radiation on superconducting qubit coherence. Nature 584, 551–556 (2020).
Gambetta, J. M. et al. Investigating surface loss effects in superconducting transmon qubits. IEEE Trans. Appl. Supercond. 27, 1–5 (2017).
Place, A. P. M. et al. New material platform for superconducting transmon qubits with coherence times exceeding 0.3 milliseconds. Nat. Commun. 12, 1779 (2021).
Wang, C. et al. Measurement and control of quasiparticle dynamics in a superconducting qubit. Nat. Commun. 5, 5836 (2014).
Aumentado, J. et al. Nonequilibrium quasiparticles and 2e periodicity in single-cooper-pair transistors. Phys. Rev. Lett. 92, 066802 (2004).
Shaw, M. D. et al. Kinetics of nonequilibrium quasiparticle tunneling in superconducting charge qubits. Phys. Rev. B 78, 024503 (2008).
Barends, R. et al. Minimizing quasiparticle generation from stray infrared light in superconducting quantum circuits. Appl. Phys. Lett. 99, 113507 (2011).
Zgirski, M. et al. Evidence for long-lived quasiparticles trapped in superconducting point contacts. Phys. Rev. Lett. 106, 257003 (2011).
Ristè, D. et al. Millisecond charge-parity fluctuations and induced decoherence in a superconducting transmon qubit. Nat. Commun. 4, 1913 (2013).
Levenson-Falk, E. M. et al. Single-quasiparticle trapping in aluminum nanobridge josephson junctions. Phys. Rev. Lett. 112, 047002 (2014).
Janvier, C. et al. Coherent manipulation of andreev states in superconducting atomic contacts. Science 349, 1199–1202 (2015).
Van Woerkom, D. J. et al. One minute parity lifetime of a NbTiN Cooper-pair transistor. Nat. Phys. 11, 547–550 (2015).
Gustavsson, S. et al. Suppressing relaxation in superconducting qubits by quasiparticle pumping. Science 354, 1573–1577 (2016).
Hays, M. et al. Direct microwave measurement of andreev-bound-state dynamics in a semiconductor-nanowire josephson junction. Phys. Rev. Lett. 121, 047001 (2018).
Serniak, K. et al. Hot nonequilibrium quasiparticles in transmon qubits. Phys. Rev. Lett. 121, 157701 (2018).
De Visser, P. J. et al. Evidence of a nonequilibrium distribution of quasiparticles in the microwave response of a superconducting aluminum resonator. Phys. Rev. Lett. 112, 047004 (2014).
Patel, U. et al. Phonon-mediated quasiparticle poisoning of superconducting microwave resonators. Phys. Rev. B 96, 220501 (2017).
Henriques, F. et al. Phonon traps reduce the quasiparticle density in superconducting circuits. Appl. Phys. Lett. 115, 212601 (2019).
Swenson, L. J. et al. High-speed phonon imaging using frequency-multiplexed kinetic inductance detectors. Appl. Phys. Lett. 96, 263511 (2010).
Moore, D. C. et al. Position and energy-resolved particle detection using phonon-mediated microwave kinetic inductance detectors. Appl. Phys. Lett. 100, 232601 (2012).
Bespalov, A. et al. Theoretical model to explain excess of quasiparticles in superconductors. Phys. Rev. Lett. 117, 117002 (2016).
Barnett, R. M. et al. Review of particle physics. Phys. Rev. D. 54, 1–708 (1996).
Tsuji, S. et al. Measurements of muons at sea level. J. Phys. G Nucl. Part. Phys. 24, 1805–1822 (1998).
Day, P. K. et al. A broadband superconducting detector suitable for use in large arrays. Nature 425, 817–821 (2003).
Kou, A. et al. Simultaneous monitoring of fluxonium qubits in a waveguide. Phys. Rev. Appl. 9, 064022 (2018).
Calusine, G. et al. Analysis and mitigation of interface losses in trenched superconducting coplanar waveguide resonators. Appl. Phys. Lett. 112, 062601 (2018).
Busto, J. et al. Radioactivity measurements of a large number of adhesives. Nucl. Instrum. Methods Phys. Res. A 492, 35–42 (2002).
Mannila, E. T. et al. A superconductor free of quasiparticles for seconds. Preprint at http://arxiv.org/abs/2102.00484 (2021).
Acknowledgements
We are grateful to M. Devoret, M. Hays, R. McDermott, A. Monfardini, and M. Calvo for insightful discussions. We thank the directors and staff of the Laboratori Nazionali del Gran Sasso, and the technical coordinator of the Ieti facility M. Junker. We acknowledge M. Iannone for his help in designing and fabricating the components for the microwave readout, and M. Guetti for the installation of the microwave cables and for the assistance in the cryogenic operations. We thank M. Perego, E. Tatananni, A. Rotilio, A. Corsi, B. Romualdi, L. Radtke, S. Diewald, and A. Lukashenko for technical support. This work makes use of the Arby software for Geant4-based Monte Carlo simulations, that has been developed in the framework of the Milano-Bicocca R&D activities, maintained by O. Cremonesi and S. Pozzi. This work was funded by INFN under Grant73-Demetra, by the European Research Council (FP7/2007-2013) under contract CALDER no. 335359, by the Alexander von Humboldt foundation in the framework of a Sofja Kovalevskaja award endowed by the German Federal Ministry of Education and Research, and by the Initiative and Networking Fund of the Helmholtz Association, within the Helmholtz future project scalable solid-state quantum computing. A.V.U. acknowledges partial support from the Ministry of Education and Science of Russian Federation in the framework of the Increase Competitiveness Program of the National University of Science and Technology MISIS (Grant No. K2-2020-022).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
F.V. performed the measurements with the help of F.H., D.G., N.C., I.C., A.C., and M.V., and he analyzed the data. L.Gr. designed the resonators and waveguide, which were fabricated by F.H., T.C., M.L., and F.V. C.R. and S.P. cleaned and assembled the prototype in the radio-pure sample holder, and made the measurements with the NaI spectrometer. G.D., L.Gi., and C.T. performed the GEANT4 simulations. L.C., F.V., N.C., G.C., T.C., M.C., I.C., A.C., G.D., L.Gi., L.Gr., D.G., F.H., M.L., M.M., G.P., C.R., O.S., C.T., A.V.U., M.W., W.W., M.V., S.P., and I.M.P. all contributed to the text and to the scientific discussions. L.C. and I.M.P. supervised and coordinated the project.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cardani, L., Valenti, F., Casali, N. et al. Reducing the impact of radioactivity on quantum circuits in a deep-underground facility. Nat Commun 12, 2733 (2021). https://doi.org/10.1038/s41467-021-23032-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-021-23032-z
This article is cited by
-
Charge-parity switching effects and optimisation of transmon-qubit design parameters
npj Quantum Information (2024)
-
Mechanically induced correlated errors on superconducting qubits with relaxation times exceeding 0.4 ms
Nature Communications (2024)
-
QUEST-DMC: Background Modelling and Resulting Heat Deposit for a Superfluid Helium-3 Bolometer
Journal of Low Temperature Physics (2024)
-
A stress-induced source of phonon bursts and quasiparticle poisoning
Nature Communications (2024)
-
Quantum bath suppression in a superconducting circuit by immersion cooling
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.