Abstract
The Permian–Triassic mass extinction was marked by a massive release of carbon into the ocean-atmosphere system, evidenced by a sharp negative carbon isotope excursion. Large carbon emissions would have increased atmospheric pCO2 and caused global warming. However, the magnitude of pCO2 changes during the PTME has not yet been estimated. Here, we present a continuous pCO2 record across the PTME reconstructed from high-resolution δ13C of C3 plants from southwestern China. We show that pCO2 increased from 426 +133/−96 ppmv in the latest Permian to 2507 +4764/−1193 ppmv at the PTME within about 75 kyr, and that the reconstructed pCO2 significantly correlates with sea surface temperatures. Mass balance modelling suggests that volcanic CO2 is probably not the only trigger of the carbon cycle perturbation, and that large quantities of 13C-depleted carbon emission from organic matter and methane were likely required during complex interactions with the Siberian Traps volcanism.
Similar content being viewed by others
Introduction
The Permian–Triassic mass extinction (PTME; ca. 252 Ma) coincided with rapid global warming that produced one of the hottest intervals of the Phanerozoic1,2,3,4,5, which was likely triggered by a massive release of greenhouse gases6,7. The emplacement of the Siberian Traps large igneous province has been widely suggested as the ultimate trigger for the extinction of ~90% of marine species and ~70% of terrestrial vertebrate species at the Permian–Triassic boundary8, with major losses amongst plants (e.g. refs. 9,10). Alongside volcanic degassing, CO2, SO2, and halogen volatiles were likely released due to thermal metamorphism by Siberian Traps’ intrusions into organic-rich sediments6,7,11. The global negative carbon isotope excursion (CIE) found in both marine and terrestrial settings at the PTME (for a review, ref. 12) indicates a major carbon cycle perturbation in the ocean-atmosphere system, which implies a rise in the atmospheric CO2 levels (pCO2). However, pCO2 changes during the PTME still remain poorly constrained.
On the one hand, records of pCO2 from proxies (stomata index, palaeosol carbonates, and biomarkers) are mainly focused on the late Permian and/or Phanerozoic long-term trends without detailed pCO2 data for the earliest Triassic (refs. 13,14,15,16,17). On the other hand, various models show large variability of peak pCO2 estimates, because of the different assumed background pCO2 levels (e.g. refs. 18,19,20). Hence, there is a pressing need for a continuous proxy-based and high-resolution record of pCO2 during the PTME. Understanding the magnitude of pCO2 changes during past hyperthermals is indeed crucial to understand the possible imminent environmental effects of today’s CO2 increase: pCO2 has risen from 280 to more than 400 ppmv in the last 150 years and is projected to go higher21.
Experiments on living C3 plants (in the field and in growth chambers) suggest that carbon isotope fractionation (∆13C) during photosynthesis increases with increasing CO2 levels, lowering the carbon isotope signature of C3 plants (δ13Cp)22. Based on this relationship, ∆13C calculated from δ13Cp measured in fossil C3 plants remains can be used as a proxy for past pCO223. This proxy successfully reproduced ice-core records of pCO2 for the Last Glacial Maximum23, and has been applied to reconstruct pCO2 during Early Eocene hyperthermals24, the Cretaceous Period25, and the Toarcian Oceanic Anoxic Event26.
Here, we present high-resolution δ13C records of fossil C3 plant remains from sedimentary successions of southwestern China. Using the δ13C data of C3 plants, we calculated a six-fold increase of atmospheric pCO2 during the PTME, from 426 +133/−96 ppmv to 2507 +4764/−1193 ppmv. Furthermore, the pCO2 estimates are compared with carbon isotope mass balance calculations showing that in addition to volcanic CO2, large quantities of 13C-depleted carbon emission from organic matter and methane were likely required to trigger the observed global negative CIE in the exogenic carbon pool.
Results and discussion
High-resolution terrestrial carbon isotope records
We present high-resolution terrestrial organic carbon isotope records (δ13Corg) from plant cuticles, wood and bulk organic matter (OM) together with our previous work10 from four terrestrial Permian–Triassic boundary sections (Chahe, Jiucaichong, core ZK4703 and Chinahe) in southwestern China (Supplementary Fig. 1; Supplementary Fig. 2). The δ13C of bulk OM and C3 plant remains from the four study sections exhibit nearly identical secular trends (Fig. 1). Each profile can be divided into four stages: (1) a pre-CIE stage, (2) an onset of the negative CIE (onset of CIE) stage, (3) a prolonged CIE body stage and (4) a post-CIE stage. In the pre-CIE stage, δ13Corg records from the Xuanwei Formation are characterized by steady values around −25.0% (Fig. 1). The synchronous, prominent onset of CIEs with peak values of −32% occurs at the bottom of the Kayitou Formation. Subsequently, the onset of the CIE stage is followed by a prolonged interval with sustained low values (ca. −30%) through the whole Kayitou Formation, interrupted by a slight positive shift immediately after the onset of CIE. A recovery to slightly higher δ13Corg values (−28% to −26%) starts in the uppermost part of the Kayitou Formation and the Dongchuan Formation. Previously published terrestrial δ13Corg profiles in southwestern China (e.g. refs. 27,28) all belong to mixed organic carbon source in bulk OM. Few unusually negative values (< −34%) observed in the upper Kayitou Formation, e.g., in a published record from Chahe27, are statistical outliers and local signals, as such negative values are not observed in our high-resolution study. These outliers may be caused by local 13C-depleted samples possibly containing an algal and/or bacterial component29.
The secular carbon isotope excursion (CIE) trend can be divided into four stages (i.e. pre-CIE, onset of CIE, CIE body and post-CIE) in terrestrial bulk organic matter, C3 plants and marine carbonates, and are shown as different color fields. The last appearance datum (LAD) of coal beds and Gigantopteris flora distributions represent the coal gap and collapse of tropical peatlands respectively10,45. Carbon isotope (δ13C) data source: Chahe (δ13C of bulk organic matter from ref. 27; δ13C of plants data from this study), Jiucaichong (this study), ZK4703 core and Chinahe (δ13C data in this study together with our previous work10), Amb (Pakistan)32 and global marine carbonate δ13C (Methods). The locations of marine and terrestrial carbon isotope profiles are shown in the late Permian palaeogeographic map.
The four-stage terrestrial δ13Corg trend is also seen in the marine carbonate carbon isotope (δ13Ccarb) records (Fig. 1). A total of 10 global-distributed marine Permian–Triassic boundary sections with both high-resolution δ13Ccarb and conodont biostratigraphy were integrated as a global marine δ13Ccarb profile, using the age model from the Meishan Global Stratotype Section and Point (GSSP)30 (Supplementary Fig. 3; Supplementary Fig. 4). These newly compiled global δ13Ccarb records are nearly identical to those published previously (e.g. ref. 12).
pCO2 estimates based on ∆13C of fossil plants
Constraining the magnitude of the CIE is crucial to estimate accurate mass, rate, and source of the 13C-depleted carbon released during the PTME20. CIE magnitudes show large variations between different localities and substrates because they can be affected by multiple factors31. δ13Cp profiles from southwestern China (low latitude) and Pakistan32 (middle latitude) exhibit CIE magnitudes of ca. −7% and ca. −5.5% respectively, which are significantly larger than the ca. −3.5% marine CIE magnitude estimated from global marine δ13Ccarb records (Fig. 1). Data compilation confirms this discrepancy: terrestrial CIE magnitudes range from −3.6% to −6.1% (bulk OM, 25th percentile to 75th percentile, n = 29), and from −5.2% to −7.1% (C3 plants, n = 9), whereas marine CIE magnitudes range from −3.0% to −4.7% (n = 69) (Fig. 2; Supplementary Table 1). As shown both in modern and fossil plants, elevated atmospheric pCO2 was likely responsible for amplifying the magnitude of the CIE in the terrestrial δ13Cp record due to an increase of ∆13C22,33. Therefore, following the relationship between ∆13C and pCO2 developed by Cui and Schubert24 (Methods), we could calculate the pCO2 across the PTME. The ∆13C was calculated using the δ13Cp records of four study sections from southwestern China, and the δ13CCO2 (the δ13C of atmospheric CO2; Supplementary Fig. 5) calculated from the global marine δ13Ccarb compiled in this study. As explained above, this is possible because the marine and terrestrial δ13C records are closely comparable and can be readily correlated (Fig. 1), the correlation being supported also by biostratigraphy (flora and conchostracans), and radioisotope dating (Supplementary Fig. 6; Supplementary Information). The initial, background late Permian pCO2(t = 0) is set in our calculations at 425 ± 68 ppmv based on the late Changhsingian pCO2 estimates calculated by Li et al.16 using stomatal ratio method and mechanistic gas exchange model for fossil conifers from the Dalong Formation in South China, with good age control and reliable taxonomy.
Carbon isotope excursion (CIE) magnitudes of marine carbonate, terrestrial bulk organic matter (OM), and terrestrial C3 plant compiled from the literature and this study. The magnitude of the terrestrial CIE is larger compared to the marine CIE magnitude. The Wilcoxon test suggests that the CIE magnitude between marine and terrestrial substrate is statistically different (Supplementary Table 1, p < 0.001). A Kruskal-Wallis test further shows the significant difference of CIE among marine carbonate, terrestrial bulk organic matter and C3 plant groups (p < 0.001). The “n” value represents the number of δ13C profiles.
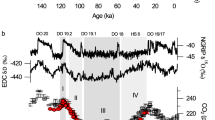
Our estimates (Fig. 3) show that pCO2 was moderately low (426 +133/−96 ppmv) at 252.1 Ma within the pre-CIE stage (upper part of conodont Clarkina changxingensis zone). Subsequently, the pCO2 began to increase rapidly in the Clarkina yini zone, reaching a maximum level (2507 +4764/−1193 ppmv), immediately after the Permian–Triassic boundary (Hindeodus parvus zone). This near six-fold increase of atmospheric pCO2 occurred within ~75 kyr and coincided with the onset of the global CIE. The pCO2 remained high (ca. 1500 to 2500 ppmv) immediately after the onset of the CIE, with only one transient drop (down to ca. 1300 ppmv). Coupled to the recovery of δ13C, pCO2 drops to ca. 700 ppmv at the top of Isarcicella isarcica zone. Atmospheric CO2 levels show a close coupling with estimated sea surface temperatures (r = + 0.60, p < 0.001, n = 173; Supplementary Fig. 7), implying that CO2 was likely the dominant greenhouse gas across the PTME, although the contribution of other greenhouse gases such as methane and water vapor cannot be excluded here. The six-fold increase of atmospheric pCO2, together with a 10 °C increase in sea surface temperatures estimated from low latitude conodont oxygen isotope (Fig. 3) implies Earth system sensitivity (ESS) of 3.9 °C per doubling of CO2 if we assume ESS equals to ∆T/log2[pCO2(peak)/pCO2(background)]34. This is consistent with a previous estimate of the Permian–Triassic ESS35 and the IPCC equilibrium climate sensitivity range of 1.5 to 4.5 with a median of 3.036, suggesting slow feedbacks operated in the geologic past. However, climate model simulations reveal that the increase of SST in high latitude should be higher than low latitude37. As a result, the 10 °C SST increase in low latitude might underestimate the global SST increase, which leads to an underestimate of the Earth system sensitivity during the PTME.
The radiometric ages are from the Meishan section30. Conodont zones are those of the Meishan section. Global marine carbonate carbon isotope (δ13Ccarb) compiled from ten sections (Methods). Land C3 plant carbon isotopes profile (δ13Cp) is from the four study sections in southwestern China (Fig. 1). Sea surface temperature (SST) was calculated based on conodont δ18O values from South China (Meishan and Shangsi)1,2,3, Iran (Kuh-e-Ali Bashi and Zal)4 and Armenia (Chanakchi)5. The blue, green and red lines represent the LOESS fit curve for δ13Ccarb, δ13Cp and SST, respectively, while light blue, green, and red shaded area represent 68% confidence intervals (standard errors calculated from LOESS). Reconstruction of atmospheric pCO2 based on carbon isotope fractionation in C3 land plant (on a log scale). Median values of the 10,000 re-samplings determined by Monte Carlo uncertainty propagation are shown as dark gray line. The 68% confidence intervals for pCO2 are showed as light gray shaded area (lower limit and upper limit represent the 16th and 84th percentiles respectively). Previous reported pCO2 estimates based on stomata16,17, palaeosol carbonates13,14 and phytane15 are shown as points with error bar (Supplementary Table 2). Marine species richness data show the two pulse mass extinction8. I.―Isarcicella; C. c―Clarkina changxingensis; C. y―Clarkina yini; C. m―Clarkina meishanensis; H. c―Hindeodus changxingensis; C. t―Clarkina taylorae; H. p―Hindeodus parvus.
Comparison with previous studies and uncertainty
Previous pCO2 estimates around the Permian–Triassic boundary (Fig. 3; Supplementary Table 2) come from stomatal proxies16,17, palaeosol carbonates13,14, phytane15 and carbon cycle modelling (e.g. refs. 18,19,20). Published proxy-based pCO2 reconstructions are mostly for the late Permian, within long-term and very low-resolution Phanerozoic records. Stomata-based estimates from modified fossil Ginkgo stomatal index method17 gave pCO2 around 400–800 ppmv in the latest Permian, but with poor age constraint and high taxonomic uncertainty16. Latest Permian pCO2 from δ13C of palaeosol carbonates from Texas, US13, was calculated at 400 ppmv38,39 (re-calculated by ref. 38 correcting the assumed soil respired CO2 concentration), but latest Permian palaeosol carbonate record from the Karoo Basin14 shows higher values (883–1325 ppmv). Similarly, the δ13Cphytane-based pCO2 estimates show that CO2 levels during Changhsingian could have ranged from 873 to 1085 ppmv15. The few earliest Triassic peak pCO2 estimates from stomatal17 and phytane15 proxies show significant variation (600–2100 ppmv). Simulations with various climate models (e.g. carbon cycle box modelling18,19 and cGENIE20) show major variability of peak pCO2 values (1000–9380 ppmv; Supplementary Table 3), using a large range of assumed background pCO2.
Several effects, especially diagenesis40, chemical treatment41, plant taxonomic changes42 and precipitation43,44 can influence the δ13Cp and consequently affect pCO2 estimates. The original signals of δ13Cp values can potentially be altered by diagenesis during burial40 and chemical treatment during sample preparation41. However, the method we use to calculate palaeo-pCO2 considers a relative change of the ∆13C that minimizes these biases (Methods). A dramatic plants turnover occurred in southwestern China during the PTME, with a Gigantopteris flora (spore plant) in the Xuanwei and basal Kayitou formations replaced by an Tomiostrobus (spore plant) and Peltaspermum (seed plant) dominated flora45. Experiments on modern plants indicate lower ∆13C in seed plants than in spore plants42. Using a plant assemblage including a mixture of different taxa and plant tissues is better than using single species and plant remains when using δ13Cp as pCO2 proxy33. In this study we used a mixture of different plant tissues (i.e. cuticle, charred wood and non-charred wood), which very likely includes different plant taxa.
An increase of the mean annual precipitation (MAP) can also increase ∆13C44,46. This effect is negligible in sites experiencing high precipitation (>1500 mm/yr)47, such as the studied area in southwestern China, which was a humid, equatorial peatland during the PTME45. The plant community changed from Gigantopteris flora-dominated rainforest ecosystem to isoetalean-dominated (lycophyte) herbaceous vegetation that inhabited the surrounding margins of coastal oligotrophic lakes, which indicate fairly constant precipitation regimes during the PTME interval48,49. The sedimentology of the Xuanwei and Kayitou formations suggests there was no significant precipitation change across the mass extinction (Supplementary Fig. 8; ref. 50). In contrast, low MAP can explain the smaller magnitude of the CIE (<3%) recorded at the PTME in the semi-arid locations of Karoo Basin and North China31. In summary, the persistently humid condition in southwestern China was unlikely to have affected plant ∆13C, thus the pCO2 estimates are considered robust. A Monte Carlo method has been applied to evaluate the uncertainties (Supplementary Information; Supplementary Fig. 9), which reveals that the uncertainty in the pCO2 increases with increasing pCO2, as seen in the previous studies51.
Potential source of 13C-depleted carbon during the PTME
The ultimate source of 13C-depleted carbon capable to trigger the observed negative CIE, is widely debated. Several climate models of varying complexities (e.g. simple box models18,19 and cGENIE20) use different light carbon sources to fit the δ13C of marine carbonates (Supplementary Table 3). Proposed 13C-depleted carbon sources include biotic or thermogenic methane (δ13C ≈ −60% to −40%; e.g. ref. 18), CO2 from thermal metamorphism or rapid oxidation of organic-rich rock (δ13C ≈ −25%; e.g. ref. 6,19,52,53), and volcanic CO2 (δ13C ≈ −6%; e.g. ref. 54) or a combination of these sources20. We performed a simple carbon isotope mass balance to evaluate the most likely 13C-depleted carbon source55,56. Under the assumption of four possible 13C-depleted carbon sources (i.e. volcanic CO2, organic matter, thermogenic methane, and biogenic methane), the mass of released carbon was calculated (Fig. 4) and compared with our pCO2 rise estimates (2081 +4764/−1193 ppmv). Our calculated pCO2 mostly falls within the range of model results for organic matter and methane release scenarios (Fig. 4), supporting the hypothesis that these more 13C-depleted sources than volcanic CO2 are required to contribute to the global carbon cycle perturbation. There are some U-Pb dating7 and field evidence6,57 show that the organic-rich sediment intruded by Siberian Traps sill likely provided massive 13C-depleted CO2 and thermogenic methane, which may have been the ultimate trigger of the global CIE and significant increase in atmospheric CO2. However, due to the limitation of the C3 plant proxy, the uncertainty of pCO2 is significantly larger at high CO2 levels (Supplementary Fig. 9). Therefore, volcanic CO2 source could still have made a contribution to the global carbon cycle perturbation.
Four different scenarios including volcanic CO2 (δ13C = −6%), organic matter (δ13C = −25%), thermogenic methane (δ13C = −40%) and biogenic methane hydrate (δ13C = −60%). Second y-axis converts the mass of added carbon to an increase in atmospheric pCO2 based on the earth system model (1 Gt C = 0.3 ppmv CO2)55,56. Gray shaded area represents the 68% confidence intervals of pCO2 increase (2081 +4764/−1193 ppmv) estimated from the C3 plant proxy.
The best estimates for mass of added carbon based on a 3.5% carbonate CIE magnitude and a source with δ13C of −25% to −60%, suggest that at least 3900~12,000 Gt carbon were added into the ocean-atmosphere system during the PTME. Previous estimates (15,000–20,000 Gt C) were based on an assumed ca. 5.5% negative shift of C3 plant in simple mass balance calculations32 and might therefore have overstated the amount of added carbon. The ca. 7% CIE in C3 plants, amplified by pCO2 increase, also produces an over-estimate in the mass balance calculation (Fig. 4). Our estimates of the amount of injected carbon are also smaller than those calculated by the cGENIE climate model (7,000~22,400 Gt C)20, because the ~5% magnitude of δ13Ccarb from Meishan used in the calculations is too large compared to the global carbonate records. However, simple mass balance calculations don’t consider global carbon cycle fundamental processes and changes through time, like carbon weathering and burial rates during the studied interval. In addition, the size of the DIC reservoir is usually assumed to be the size of the background surface carbon reservoir, because of poor understanding of atmosphere carbon reservoir size58. These limitations might lead to an underestimate of the total mass of added CO2.
Carbon emission caused prolonged high pCO2 and high temperature (ca. 35 °C) during the earliest Triassic (H. parvus and I. isarcica zones) and may have lasted for > 500 kyr (Fig. 3). This lengthy phase of extreme warmth likely implies prolonged carbon emissions into ocean-atmosphere system from continued eruption of the Siberian Traps volcanism, and/or reduced carbon sequestration rate, potentially due to lower consumption of atmospheric CO2 through reduced organic carbon burial and the possible failure of the silicate weathering thermostat59.
Methods
Sample treatment and analysis
In total, 68 samples from Chinahe, 41 samples from ZK4703 and 40 samples from Jiucaichong were analyzed for bulk organic carbon isotopes. Samples were crushed to fine powder (<200 mesh), and ∼2 g powder were weighed, placed into a centrifuge tube and treated with 3 mol/L HCl for 24 h to remove the carbonate. Then the treated samples were rinsed with ultrapure water repeatedly until neutralized and finally dried at 35 °C. For C3 plants δ13C analysis, 45 samples from Chinahe, 26 samples from ZK4703, 30 samples from Jiucaichong and 13 samples from Chahe were treated with concentrated HCl and HF, then sieved over 500 μm and a 100 μm mesh screen to get the 100~500 μm particles. C3 plant fragments, including cuticle, non-charred wood and charred wood (charcoal), were picked under the microscope. The δ13Corg analyses were performed by using an elemental analyzer (EA) coupled to an isotope ratio mass spectrometer (Thermo Delta V Advantage) at the State Key Laboratory of Biogeology and Environmental Geology of the China University of Geosciences (Wuhan). The results were calibrated using certified secondary references standards: USGS40 (δ13C = −26.39%) and UREA (δ13C = −37.32%) and given in per mil (%) relative to Vienna Pee Dee Belemnite (VPDB) with analytical precision better than ± 0.2%. A Multi EA 4000-analyzer was used for TOC at China University of Geosciences (Wuhan), yielding an analytical precision of 1.5%.
Carbon isotope compilation and estimate of CIE magnitude
In order to estimate a reliable magnitude of the CIE, the carbon isotope profiles that record a roughly complete CIE shape with pre-CIE and CIE body are selected in our study. The compilation consists of 69 marine carbonate carbon isotope (δ13Ccarb) profiles and 38 terrestrial δ13Corg profiles. The δ13Ccarb profiles recording complete negative CIE are from Eastern Palaeotethys (n = 29), Western Palaeotethys (n = 19), Central Palaeotethys (n = 4), Northern Neotethys (n = 4), Southern Neotethys (n = 10) and Panthalassa (n = 3). Bulk marine organic matter δ13C records were not included, because they often represent a mix of various organic components (both marine and terrestrial). The sedimentary facies belong to a range of shallow shelf, deep shelf, and slope environments. The few reported δ13Ccarb profiles from deep basins are ignored in this compilation (e.g. Shangsi section), because the elevated water stratification and large vertical δ13C DIC gradients at deep basin sites during Permian–Triassic crisis could cause large CIE magnitudes60. A total of 38 terrestrial δ13Corg records are reviewed from eight terrestrial basins including western Guizhou and eastern Yunnan in southwestern China (n = 14), Junggar Basin (n = 3), Turpan Basin (n = 1), North China (n = 3), Central European Basin (n = 1), Bowen Basin (n = 2), Sydney Basin (n = 7), Karoo Basin (n = 1) and three oceanic regions where organic matter (OM) in samples are C3 plants or a mix of organic matter dominated by C3 plants including South China (n = 1), Boreal realm (n = 2) and South Neotethys (n = 3). Among these terrestrial δ13Corg profiles, there are nine records of δ13C records from C3 plant (5 δ13Cwood and 4 δ13Ccuticle) from Meishan section, Amb section in South Neotethys, southwestern China, and others are all bulk δ13Corg profiles.
In order to demonstrate the difference of marine and terrestrial CIE magnitudes, carbon isotope values immediately before the CIE (δ13Cbackground) and peak values (δ13Cpeak) are used to calculate the magnitude of the CIE (δ13Cpeak − δ13Cbackground). Note that 31 pairs of δ13Cbackground and δ13Cpeak values are from marine sections that are well constrained by latest Permian conodont occurrences (e.g. C. changxingensis, H. praeparvus, H. latidentatus zones) and earliest Triassic conodont (H. parvus and I. isarcica zones) occurrences. To test if the discrepancy of the CIE magnitude in different substrates (marine carbonate, terrestrial bulk OM, terrestrial C3 plant tissues) is statistically significant, we used a non-parameter Kruskal-Wallis test (function kruskal.test), using R software. The Wilcoxon (function wilcox.test) test was performed in R software to determine whether means of two independent groups (marine vs. terrestrial) are equal or not. Boxplots were drawn to visualize discrepancy in CIE magnitude of different substrates. All statistical analyses and graphing functions were undertaken using R.
C3 plant proxy
The carbon isotope fractionation in C3 plants (∆13C) and atmospheric pCO2 is described as a hyperbolic relationship22,23,24,61:
The original δ13C signals in C3 plant can be altered by several effects (e.g. diagenesis40, chemical treatments41), that potentially influence pCO2 calculations. In order to minimize this effect, the data set is analyzed by a relative change in the ∆13C value between the time of interest (t) and a reference time (t = 0), designated as ∆ (∆13C):
which can be expanded as:
By rearranging Eq. (3), pCO2(t) at any given time can be calculated by
where A, B, C are curve fitting parameters. Values for A and B are 28.26 ± 0 and 0.22 ± 0.028, respectively51, which could produce more robust pCO2 estimates compared with other parameter values in subsequent research33. The C is the function of the A and B values [C =A×4.4/((A − 4.4) × B)]. The pCO2(t = 0) is equal to the pCO2 level before the negative CIE, determined from independent stomatal proxies based on fossil conifers from the Dalong Formation in South China16. Because of the good age control (Clarkina changxingensis conodont zone), reliable taxonomy and calculation method, these stomatal estimates are considered as robust pCO2 estimates before CIE. The mean value for the stomatal estimates is 425 ± 68 ppmv set as pCO2(t = 0). The ∆13C is the carbon isotope fractionation between atmospheric CO2 and plant organic carbon (\({\Delta}^{{\mathrm{13}}}{\mathrm{C}} = ( {{\delta}^{{\mathrm{13}}}{\mathrm{C}}_{{\mathrm{CO}}_2} - {\delta}^{{\mathrm{13}}}{\mathrm{C}}_{{\mathrm{p}}}} ){\mathrm{/}}( {{\mathrm{1}} +{\delta}^{{\mathrm{13}}}{\mathrm{C}}_{{\mathrm{p}}}/{\mathrm{1000}}} )\)). Thus, the ∆(∆13C) can be calculated by
where \({\delta}^{{\mathrm{13}}}{\mathrm{C}}_{{\mathrm{p}}(t = {\mathrm{0}})}\) and δ13Cp(t) are δ13C values in C3 plant at reference time (t = 0) and the time of interest (t). The values for \({\delta}^{{\mathrm{13}}}{\mathrm{C}}_{{\mathrm{p}}(t = {\mathrm{0}})}\) is determined as −24.42 ± 0.5%, whose age equals to Clarkina changxingensis conodont zone that occurred slightly earlier than the onset of the CIE16. We suggest that a mixture of δ13C in C3 plant cuticle, charred wood and non-charred wood from southwestern China (without δ13C of bulk OM) provides the best choice as δ13Cp(t) input data for three reasons. Firstly, using the δ13C values of C3 plant tissues (e.g. cuticle, wood) can minimize the influence of varying OM sources from mixed soils and sediments. Several previous reports on terrestrial δ13Corg in western Guizhou and eastern Yunnan, South China have recorded the negative CIE27,28,62,63, but all the data are not δ13C from C3 plants and not suitable for pCO2 calculation. Secondly, Eq. (1) is based on the combination of carbon isotope from stem and leaf tissues of chamber plants. Thirdly, the mixture of different micro plant tissues (i.e. cuticle, charred wood and non-charred wood) would contain different plant fossils species that is suggested to be better than a single species approach when applying this proxy33.
The \({\delta}^{{\mathrm{13}}}{\mathrm{C}}_{{\mathrm{CO}}_2(t = 0)}\) and \({\delta}^{{\mathrm{13}}}{\mathrm{C}}_{{\mathrm{CO}}_2(t)}\) are δ13C values in atmospheric CO2 at reference time (t = 0) and the time of interest (t). The temperature (T) dependent carbon isotope fractionation between dissolved inorganic carbon (DIC) and atmospheric CO264 can be used to calculate \({\delta}^{{\mathrm{13}}}{\mathrm{C}}_{{\mathrm{CO}}_2}\).
where T is the sea surface temperature determined from oxygen isotopes of conodont fossils1,2,3,4,5. δ13CDIC can be estimated from marine δ13Ccarb (δ13CDIC = δ13Ccarb − 1%), because the carbon isotope fractionation between marine carbonate (δ13Ccarb) and dissolved inorganic carbon (δ13CDIC) is constant and independent of temperature (~1%)65. Among the global CIE compilations, 10 marine, high-resolution, non-basinal δ13Ccarb profiles are well constrained by detail conodont zones including Meishan30, Nhi Tao66, Yangou67 in eastern Palaeotethys; Zal3, Kuh-e-Ali Bashi3 in central Palaeotethys; Bálvány North68 in western Paloetethys; Shahreza12, Abadeh12 in northern Neotethys; Wadi Shahha69, Wenbudangsang70 in Southern Neotethys. Thus, we integrated these 10 δ13Ccarb profiles together as a global marine δ13Ccarb profile combined with a U-Pb age model30 and high-resolution conodont zones (conodont zones from Meishan are selected as standard71,72). LOESS curves with 0.002 Myr spacing were fitted to the integration of global marine δ13Ccarb. At each 0.002 Myr time step, the probability maximum value and standard error are identified and served as δ13Ccarb input parameters in calculations. The best degree of smoothing for LOESS fitting was determined using cross-validation method in package fANCOVA. To eliminate the potential for an uneven distribution of δ13Ccarb data, we also applied a LOESS fitting based on an 80% subsample of all data. In addition, the δ13Ccarb data from Meishan (n = 199) is the most abundant of all the δ13Ccarb data (n = 707), thus, we performed a LOESS fitting based on δ13Ccarb data without Meishan data (Supplementary Fig. 4).
In order to calculate pCO2(t), we need to align global marine δ13Ccarb profiles and δ13Cp based on same age model. The nearly same CIE curves were divided into four stages in carbonate and C3 plants records to ensure the correlation between marine and terrestrial carbon isotope profiles. The age model for four sections is showed in Supplementary Information. In addition, the LOESS method with 0.002 Myr spacing was also performed in δ13Cp and temperature data to get the probability maximum value and standard error at each 0.002 Myr time step. The Monte Carlo method was employed to propagate input error51 by the propagate package in R. All the input parameters were assumed to be Gaussian distributed with mean and standard deviations listed in Supplementary Table 4. 10,000 values for each input parameters were randomly sampled to calculate 10,000 values for each pCO2(t). The invalid pCO2(t) values (i.e., pCO2(t) < 0 or >106 ppmv) were excluded. The 16th and 84th percentiles of the remaining estimates were determined to construct the 68% confidence interval. The positive error of the reconstructed pCO2(t) value represents the difference between the 84th percentile value and the median, and the negative error represents the difference between the 16th percentile value and the median. The sensitivity analysis of C3 plant proxy is discussed in Supplementary information and Supplementary Fig. 9.
Carbon isotope mass balance
This model used to evaluate the light carbon source, following mass balance equation is modified from McInerney and Wing55:
where Madded is the mass of carbon added into atmosphere-ocean system carbon emission. The Mbackground represents initial carbon reservoir size during Permian–Triassic including ocean and atmosphere carbon inventory, but dominated by the ocean reservoir. Thus, the Mbackground is assumed to be the initial marine DIC reservoir size ranging from 66,000 to 82,000 Gt58,73. CIE represents the global magnitude of CIE controlled only by release of light carbon effect, which is set as a series values from −1% to −8%. The peak δ13C value (δ13Cpeak) at the event is calculated by initial isotopic composition of global carbon reservoir (δ13Cbackground) and CIE (δ13Cpeak = δ13Cbackground + CIE). The δ13Cbackground is assumed to be the initial isotopic composition of DIC reservoir 2.2% that is estimated from global marine δ13Ccarb profiles (age >252.104 Ma). The δ13Cadded is the δ13C value of the carbon source causing the CIE. Four kinds of carbon sources are involved including biogenic methane buried in permafrost or seafloor (δ13C = −60%), thermogenic methane (δ13C = −40%), thermal metamorphism or rapid oxidation of organic-rich rock (δ13C = −25%) and CO2 released from direct volcanic eruption (−6%). Finally, the increased pCO2 is estimated from Madded (1 Gt C = 0.3 ppmv; ref. 56), and compared with reconstructed atmospheric CO2 levels from C3 plant proxy.
Data availability
The authors declare that all data supporting the findings of this study are available within the paper and its supplementary file.
Code availability
R code to run the model is available from D.L. Chu on request.
References
Joachimski, M. M. et al. Climate warming in the latest Permian and the Permian-Triassic mass extinction. Geology 40, 195–198 (2012).
Sun, Y. et al. Lethally hot temperatures during the Early Triassic greenhouse. Science 338, 366–370 (2012).
Chen, B. et al. Permian ice volume and palaeoclimate history: oxygen isotope proxies revisited. Gondwana Reso 24, 77–89 (2013).
Schobben, M., Joachimski, M. M., Korn, D., Leda, L. & Korte, C. Palaeotethys seawater temperature rise and an intensified hydrological cycle following the end-Permian mass extinction. Gondwana Reso 26, 675–683 (2014).
Joachimski, M. M., Alekseev, A. S., Grigoryan, A. & Gatovsky, Y. A. Siberian Trap volcanism, global warming and the Permian-Triassic mass extinction: new insights from Armenian Permian-Triassic sections. Geol. Soc. Am. Bull. 132, 427–443 (2020).
Svensen, H. et al. Siberian gas venting and the end-Permian environmental crisis. Earth Planet. Sci. Lett. 277, 490–500 (2009).
Burgess, S. D., Muirhead, J. D. & Bowring, S. A. Initial pulse of Siberian Traps sills as the trigger of the end-Permian mass extinction. Nat. Commun. 8, 164 (2017).
Song, H. J., Wignall, P. B., Tong, J. & Yin, H. Two pulses of extinction during the Permian-Triassic crisis. Nat. Geosci. 6, 52–56 (2013).
Fielding, C. R. et al. Age and pattern of the southern high-latitude continental end-Permian extinction constrained by multiproxy analysis. Nat. Commun. 10, 385 (2019).
Chu, D. et al. Ecological disturbance in tropical peatlands prior to marine Permian-Triassic mass extinction. Geology 48, 288–292 (2020).
Black, B. A. et al. Systemic swings in end-Permian climate from Siberian Traps carbon and sulfur outgassing. Nat. Geosci. 11, 949–954 (2018).
Korte, C. & Kozur, H. W. Carbon-isotope stratigraphy across the Permian-Triassic boundary: a review. J. Asian Earth Sci 39, 215–235 (2010).
Ekart, D. D., Cerling, T. E., Montanez, I. P. & Tabor, N. J. A 400 million year carbon isotope record of pedogenic carbonate: Implications for paleoatmospheric carbon dioxide. Am. J. Sci. 299, 805–827 (1999).
Gastaldo, R. A., Knight, C. L., Neveling, J. & Tabor, N. J. Latest Permian paleosols from Wapadsberg Pass, South Africa: implications for Changhsingian climate. Geol. Soc. Am. Bull. 126, 665 (2014).
Witkowski, C. R., Weijers, J. W. H., Blais, B., Schouten, S. & Sinninghe Damsté, J. S. Molecular fossils from phytoplankton reveal secular Pco2 trend over the Phanerozoic. Sci. Adv. 4, eaat4556 (2018).
Li, H., Yu, J., McElwain, J. C., Yiotis, C. & Chen, Z. Reconstruction of atmospheric CO2 concentration during the late Changhsingian based on fossil conifers from the Dalong Formation in South China. Palaeogeogr. Palaeoclimatol. Palaeoecol. 519, 37–48 (2019).
Retallack, G. J. & Conde, G. D. Deep time perspective on rising atmospheric CO2. Global Planet. Change 189, 103177 (2020).
Berner, R. A. Examination of hypotheses for the Permo-Triassic boundary extinction by carbon cycle modeling. Proc. Natl. Acad. Sci. U.S.A. 99, 4172–4177 (2002).
Payne, J. L. & Kump, L. R. Evidence for recurrent Early Triassic massive volcanism from quantitative interpretation of carbon isotope fluctuations. Earth Planet. Sci. Lett. 256, 264–277 (2007).
Cui, Y., Kump, L. R. & Ridgwell, A. Initial assessment of the carbon emission rate and climatic consequences during the end-Permian mass extinction. Palaeogeogr. Palaeoclimatol. Palaeoecol. 389, 128–136 (2013).
Keeling, R. F. & Keeling, C. D. Atmospheric Monthly In Situ CO2 Data-Mauna Loa observatory, Hawaii. Scripps CO2 Program Data (UC San Diego, Library Digital Collections, 2017).
Schubert, B. A. & Jahren, A. H. The effect of atmospheric CO2 concentration on carbon isotope fractionation in C3 land plants. Geochim. Cosmochim. Acta 96, 29–43 (2012).
Schubert, B. A. & Jahren, A. H. Global increase in plant carbon isotope fractionation following the Last Glacial Maximum caused by increase in atmospheric pCO2. Geology 43, 435–438 (2015).
Cui, Y. & Schubert, B. A. Towards determination of the source and magnitude of atmospheric pCO2 change across the early Paleogene hyperthermals. Global Planet. Change 170, 120–125 (2018).
Barral, A., Gomez, B., Fourel, F., Daviero-Gomez, V. & Lécuyer, C. CO2 and temperature decoupling at the million-year scale during the Cretaceous Greenhouse. Sci. Rep. 7, 8310 (2017).
Ruebsam, W., Reolid, M. & Schwark, L. δ13C of terrestrial vegetation records Toarcian CO2 and climate gradients. Sci. Rep. 10, 117 (2020).
Shen, S. Z. et al. Calibrating the End-Permian Mass Extinction. Science 334, 1367–1372 (2011).
Cui, Y. et al. Carbon cycle perturbation expressed in terrestrial Permian-Triassic boundary sections in South China. Global Planet. Change 148, 272–285 (2017).
Hermann, E. et al. A close-up view of the Permian-Triassic boundary based on expanded organic carbon isotope records from Norway (Trøndelag and Finnmark Platform). Global Planet. Change 74, 156–167 (2010).
Burgess, S. D., Bowring, S. & Shen, S. High-precision timeline for Earth’s most severe extinction. Proc. Natl Acad. Sci. USA 111, 3316–3321 (2014).
Wu, Y. et al. Organic carbon isotopes in terrestrial Permian-Triassic boundary sections of North China: Implications for global carbon cycle perturbations. Geol. Soc. Am. Bull. 132, 1106–1118 (2020).
Schneebeli-Hermann, E. et al. Evidence for atmospheric carbon injection during the end-Permian extinction. Geology 41, 579–582 (2013).
Porter, A. S. et al. Testing the accuracy of new paleoatmospheric CO2 proxies based on plant stable carbon isotopic composition and stomatal traits in a range of simulated paleoatmospheric O2:CO2 ratios. Geochim. Cosmochim. Acta 259, 69–90 (2019).
Knobbe, T. K. & Schaller, M. F. A tight coupling between atmospheric pCO2 and sea-surface temperature in the Late Triassic. Geology 46, 43 (2017).
Cui, Y. & Kump, L. R. Global warming and the end-Permian extinction event: Proxy and modeling perspectives. Earth-Sci. Rev. 149, 5–22 (2015).
Stocker, T. F. et al. Climate change 2013: The physical science basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change 1535 (2013).
Penn, J. L., Deutsch, C., Payne, J. L. & Sperling, E. A. Temperature-dependent hypoxia explains biogeography and severity of end-Permian marine mass extinction. Science 362, eaat1327 (2018).
Foster, G. L., Royer, D. L. & Lunt, D. J. Future climate forcing potentially without precedent in the last 420 million years. Nat. Commun. 8, 14845 (2017).
Breecker, D. O., Sharp, Z. D. & McFadden, L. D. Atmospheric CO2 concentrations during ancient greenhouse climates were similar to those predicted for A.D. 2100. Proc. Natl Acad. Sci. USA 107, 576–580 (2010).
Lukens, W. E., Eze, P. & Schubert, B. A. The effect of diagenesis on carbon isotope values of fossil wood. Geology 47, 987–991 (2019).
Barral, A., Lécuyer, C., Gomez, B., Fourel, F. & Daviero-Gomez, V. Effects of chemical preparation protocols on δ13C values of plant fossil samples. Palaeogeogr. Palaeoclimatol. Palaeoecol. 438, 267–276 (2015).
Porter, A. S., Yiotis, C., Montañez, I. P. & McElwain, J. C. Evolutionary differences in Δ13C detected between spore and seed bearing plants following exposure to a range of atmospheric O2:CO2 ratios; implications for paleoatmosphere reconstruction. Geochim. Cosmochim. Acta 213, 517–533 (2017).
Lomax, B. H., Lake, J. A., Leng, M. J. & Jardine, P. E. An experimental evaluation of the use of Δ13C as a proxy for palaeoatmospheric CO2. Geochim. Cosmochim. Acta 247, 162–174 (2019).
Schlanser, K. et al. On geologic timescales, plant carbon isotope fractionation responds to precipitation similarly to modern plants and has a small negative correlation with pCO2. Geochim. Cosmochim. Acta 270, 264–281 (2020).
Chu, D. et al. Biostratigraphic correlation and mass extinction during the Permian-Triassic transition in terrestrial-marine siliciclastic settings of South China. Global Planet. Change 146, 67–88 (2016).
Diefendorf, A. F., Mueller, K. E., Wing, S. L., Koch, P. L. & Freeman, K. H. Global patterns in leaf 13C discrimination and implications for studies of past and future climate. Proc. Natl. Acad. Sci. U.S.A. 107, 5738–5743 (2010).
Basu, S., Ghosh, S. & Sanyal, P. Spatial heterogeneity in the relationship between precipitation and carbon isotopic discrimination in C3 plants: Inferences from a global compilation. Global Planet. Change 176, 123–131 (2019).
Yu, J. et al. Vegetation changeover across the Permian–Triassic Boundary in Southwest China: Extinction, survival, recovery and palaeoclimate: a critical review. Earth-Sci. Rev. 149, 203–224 (2015).
Feng, Z. et al. From rainforest to herbland: New insights into land plant responses to the end-Permian mass extinction. Earth-Sci. Rev. 204, 103153 (2020).
Wignall, P. B. et al. Death in the shallows: the record of Permo-Triassic mass extinction in paralic settings, southwest China. Global Planet. Change 189, 103176 (2020).
Cui, Y. & Schubert, B. A. Quantifying uncertainty of past pCO2 determined from changes in C3 plant carbon isotope fractionation. Geochim. Cosmochim. Acta 172, 127–138 (2016).
Dal Corso, J. et al. Permo–Triassic boundary carbon and mercury cycling linked to terrestrial ecosystem collapse. Nat. Commun. 11, 2962 (2020).
Jurikova, H. et al. Permian–Triassic mass extinction pulses driven by major marine carbon cycle perturbations. Nat. Geosci. 13, 745–750 (2020).
Gales, E., Black, B. & Elkins-Tanton, L. T. Carbonatites as a record of the carbon isotope composition of large igneous province outgassing. Earth Planet. Sci. Lett. 535, 116076 (2020).
McInerney, F. A. & Wing, S. L. The Paleocene-Eocene Thermal Maximum: a perturbation of carbon cycle, climate, and biosphere with implications for the future. Annu. Rev. Earth Planet. Sci. 39, 489–516 (2011).
Panchuk, K., Ridgwell, A. & Kump, L. R. Sedimentary response to Paleocene-Eocene Thermal Maximum carbon release: a model-data comparison. Geology 36, 315–318 (2008).
Elkins-Tanton, L. T. et al. Field evidence for coal combustion links the 252 Ma Siberian Traps with global carbon disruption. Geology 48, 986–991 (2020).
Payne, J. L. et al. Calcium isotope constraints on the end-Permian mass extinction. Proc. Natl. Acad. Sci. USA 107, 8543–8548 (2010).
Kump, L. R. Prolonged Late Permian–Early Triassic hyperthermal: failure of climate regulation? Phil. Trans. R. Soc. A: Math. Phys. Eng. Sci. 376, 20170078 (2018).
Song, H. Y. et al. Large vertical δ13C DIC gradients in Early Triassic seas of the South China craton: implications for oceanographic changes related to Siberian Traps volcanism. Global Planet. Change 105, 7–20 (2013).
Schubert, B. A. & Jahren, A. H. Incorporating the effects of photorespiration into terrestrial paleoclimate reconstruction. Earth-Sci. Rev. 177, 637–642 (2018).
Zhang, H. et al. The terrestrial end-Permian mass extinction in South China. Palaeogeogr. Palaeoclimatol. Palaeoecol. 448, 108–124 (2016).
Shen, J. et al. Mercury evidence of intense volcanic effects on land during the Permian-Triassic transition. Geology 47, 1117–1121 (2019).
Tipple, B. J., Meyers, S. R. & Pagani, M. Carbon isotope ratio of Cenozoic CO2: a comparative evaluation of available geochemical proxies. Paleoceanography 25, PA3202 (2010).
Romanek, C. S., Grossman, E. L. & Morse, J. W. Carbon isotopic fractionation in synthetic aragonite and calcite: Effects of temperature and precipitation rate. Geochim. Cosmochim. Acta 56, 419–430 (1992).
Algeo, T. J., Ellwood, B., Nguyen, T. K. T., Rowe, H. & Maynard, J. B. The Permian–Triassic boundary at Nhi Tao, Vietnam: Evidence for recurrent influx of sulfidic watermasses to a shallow-marine carbonate platform. Palaeogeogr. Palaeoclimatol. Palaeoecol. 252, 304–327 (2007).
Song, H. et al. The large increase of 13Ccarb-depth gradient and the end-Permian mass extinction. Sci. China Earth Sci 55, 1101–1109 (2012).
Schobben, M. et al. Volatile earliest Triassic sulfur cycle: a consequence of persistent low seawater sulfate concentrations and a high sulfur cycle turnover rate? Palaeogeogr. Palaeoclimatol. Palaeoecol. 486, 74–85 (2017).
Clarkson, M. O. et al. A new high-resolution δ13C record for the Early Triassic: Insights from the Arabian Platform. Gondwana Res. 24, 233–242 (2013).
Ji, C. et al. 13C-18O Isotopic anomalous study of the carbonate rock at the Wenbudangsang PTB Section,Tibet. Acta Geologica Sin. 92, 2018–2027 (2018).
Yin, H. et al. The end-Permian regression in South China and its implication on mass extinction. Earth-Sci. Rev. 137, 19–33 (2014).
Yuan, D. et al. Revised conodont-based integrated high-resolution timescale for the Changhsingian Stage and end-Permian extinction interval at the Meishan sections, South China. Lithos 204, 220–245 (2014).
Ridgwell, A. & Zeebe, R. E. The role of the global carbonate cycle in the regulation and evolution of the Earth system. Earth Planet. Sci. Lett. 234, 299–315 (2005).
Acknowledgements
Many thanks to Linhao Fang for the help of sample treatment method. We thank Wenchao Shu and Yao Wang for sample treatment. This study was supported by the National Natural Science Foundation of China (42030513, 41821001, 41530104, 42072025, 41888101), the US National Science Foundation grant no. EAR-1603051 and EAR-2026877, and also benefited from Natural Environment Research Council (UK) grant, ‘Ecosystem resilience and recovery from the Permo-Triassic crisis’ (grant NE/P013724/1), which is a part of the Biosphere Evolution, Transitions and Resilience (BETR) Program. This is Center for Computational & Modeling Geosciences (BGEG) publication number 2.
Author information
Authors and Affiliations
Contributions
D.L.C., Y.C., and Y.Y.W. designed this study with in-depth inputs from H.J.S., P.B.W., J.D.C., and J.N.T. Y.Y.W. and D.L.C completed the data preparation and analysis with the help from H.Y.S., Y.D., and J.D.C. Y.Y.W. and Y.C. performed the calculations. Y.Y.W and D.L.C wrote the main text and supplementary materials with inputs from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Christopher Fielding and the other, anonymous reviewer(s) for their contribution to the peer review of this work. Peer review reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wu, Y., Chu, D., Tong, J. et al. Six-fold increase of atmospheric pCO2 during the Permian–Triassic mass extinction. Nat Commun 12, 2137 (2021). https://doi.org/10.1038/s41467-021-22298-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-021-22298-7
This article is cited by
-
Plant response to decreasing soil moisture under rising atmospheric CO2 levels
Communications Earth & Environment (2024)
-
Carbon cycle perturbations and environmental change of the middle permian and Late Triassic Paleo-Antarctic circle
Scientific Reports (2024)
-
Shifts in magnetic mineral assemblages support ocean deoxygenation before the end-Permian mass extinction
Communications Earth & Environment (2024)
-
High temperature methane emissions from Large Igneous Provinces as contributors to late Permian mass extinctions
Nature Communications (2022)
-
Environmental crises at the Permian–Triassic mass extinction
Nature Reviews Earth & Environment (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.