Abstract
The electro-optical properties of most semiconductors and insulators of technological interest are dominated by the presence of electron-hole quasi-particles, called excitons. The manipulation of excitons in dielectrics has recently received great attention, with possible applications in different fields including optoelectronics and photonics. Here, we apply attosecond transient reflection spectroscopy in a sequential two-foci geometry and observe sub-femtosecond dynamics of a core-level exciton in bulk MgF2 single crystals. Furthermore, we access absolute phase delays, which allow for an unambiguous comparison with theoretical calculations. Our results show that excitons surprisingly exhibit a dual atomic- and solid-like character, which manifests itself on different time scales. While the former is responsible for a femtosecond optical Stark effect, the latter dominates the attosecond excitonic response. Further theoretical investigation reveals a link with the exciton sub-femtosecond nanometric motion and allows us to envision a new route to control exciton dynamics in the close-to-petahertz regime.
Similar content being viewed by others
Introduction
The quest for new devices capable of surpassing the current technological limits1 has pushed the scientific community to explore solutions beyond classical electronics as done in excitonics, spintronics and valleytronics2. Therefore, studying the dynamics of excitons in solids3,4,5 becomes a priority task not only to widen our knowledge of fundamental solid-state dynamical phenomena, but also to explore the ultimate limits of these novel technologies6,7,8,9,10,11. While the development of attosecond spectroscopy12 has proven the possibility to study sub-femtosecond (fs) electron dynamics in solids13, shedding light onto strong-field phenomena and light-carrier manipulation14,15,16, a clear observation of attosecond exciton dynamics was missing. Besides more conventional femtosecond techniques17, attosecond transient absorption and reflectivity spectroscopy have been employed to study the ultrafast decay processes (few-fs) of core-excitons18,19, but failed in recording the sub-cycle dynamics unfolding during light–matter interaction. Here we used attosecond transient reflection spectroscopy (ATRS)20 to study attosecond dynamics of a core-level exciton in bulk MgF2 single crystals, a widely used material in optics, characterised by a clear core21 and valence22 exciton signal which make it an optimal target to investigate exciton dynamics with attosecond techniques. Thanks to the employment of simultaneous and independent calibration experiments, we achieved direct comparison with theoretical simulations, which in turn allowed us to make a clear link between the observed transient features of the system optical response and the nanometric and attosecond motion of the excitons. Holding in general for Wannier-Mott excitons, including valence excitons, our results provide a description of the ultrafast exciton–crystal interaction on sub-fs time scales and move an important step towards a more complete understanding of attosecond light-excitonic dynamics.
Results
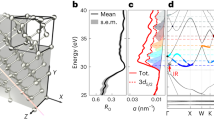
Figure 1a shows a schematic picture of the experimental setup characterised by a sequential two-foci geometry, used to perform simultaneous attosecond photoelectron and ATRS measurements23 (see Methods). The static reflectivity for a MgF2 (001) crystal, R0, close to the Mg L2,3 edge is probed by an extreme-ultraviolet (XUV) attosecond (as) pulse (Fig. 1b). In this energy region R0 is characterised by a peak (labelled with A), which has been attributed to the formation of excitons after excitation of a Mg2+ 2p core electron24 (Fig. 1c). The weaker satellite peak at about 54 eV (A′ in Fig. 1b) originates instead from the spin–orbit splitting of the Mg2+ 2p core state25. In our experiment we use a 5 -fs infrared (IR) pulse (centre wavelength 750 nm, peak intensity 1012–1013 W/cm2) to drive the crystal out of equilibrium (Fig. 1c). The induced ultrafast exciton dynamics are probed with 250-as pulses by monitoring the sample differential reflectivity ΔR/R in the XUV range, defined as the difference between pumped and unpumped reflectivity, divided by the latter: [RIR − R0] /R0. The results as a function of photon energy E and pump-probe delay t, are shown in Fig. 1d. At small values of t, we observe rich transient features which unfold either on few-fs or attosecond time scales (hereafter referred to as slow and a fast component, respectively). While the former is mainly located around the excitonic features A and A′, the latter oscillates at twice the IR frequency and extends over the full energy range under consideration, becoming more evident in the conduction band (CB) region. The weak differential signal already present at negative delays around 54.4 eV originates from a non-vanishing IR electric field. It goes below the experimental noise level for delays smaller than −15 fs and does not influence our analysis (see Supplementary Note 6). The upper panel in Fig. 1d shows the square of the IR vector potential, AIR2, as retrieved from the simultaneous streaking trace (see Supplementary Note 7). Knowing the associated pump field time evolution, we calibrated the pump-probe delay axis in order to have the zero delay coinciding with the maximum of the IR electric field squared (equivalently, a zero of AIR2). This allowed us to set an absolute reference for our measurements and study the precise timing of the system dynamics.
a Scheme of double-foci the experimental setup composed by the Ne gas target to perform an attosecond streaking experiment, the MgF2 crystal and the XUV spectrometer. The inset shows the attosecond pulse spectrum as reflected by the MgF2 sample. b Experimental (black solid) and calculated (red dotted) MgF2 reflectivity for an incidence angle of 73.5°. The grey shaded area represents twice the standard deviation over repeated experimental measurements, while the green dashed curve is the reflectivity extracted from Hanson et al.24. The horizontal dash-dotted lines mark the vertical transitions from the Mg2+ 2p core level to the conduction band (CB) and the bright exciton21, accounting for the spin–orbit splitting of the Mg2+ 2p state. c MgF2 band structure around its CB. While XUV photons can promote electrons from the Mg-2p state directly into the CB, or to an electron–hole pair state (exciton), the IR field perturbs the crystal, causing phenomena like intra-band motion or dressing of dark excitonic states. The false colours represent the density of states for the excitons. d Experimental and e calculated transient reflection spectrograms (main panels) as a function of the delay between the XUV and IR pulses, together with the square of the IR vector potential, AIR2, as extracted from the simultaneous streaking measurement (upper panels). The delay zero (vertical dashed line) has been chosen in order to coincide with a maximum of the IR electric field squared. The experimental IR peak fluence is 0.08 J/cm2.
To reach a complete understanding, we calculated the quantum dynamics with a Wannier-Mott (WM) exciton model26,27 (see Methods) and chose the same reference for the delay zero, such that we could directly compare experimental and theoretical results. The calculated ΔR/R reported in Fig. 1e accurately reproduces the experimental data of Fig. 1d, suggesting dynamics which go beyond the optical Stark effect28. While the calculated and experimental ΔR/R fall in the same order of magnitude, there are appreciable differences in their absolute values which may originate mainly from an underestimation of the pump intensity. In addition, we observe that the calculations overestimate the oscillatory part in the CB with respect to the slow component. This may originate from a combination of unavoidable experimental imperfections (any instability will reduce the contrast of the fast oscillation) and the approximations made in our theoretical model. The observed discrepancies have anyway no effect over the Results and Discussion reported in this paper.
Discussion
The slow component of the experimental ΔR/R (Fig. 2a) is characterised by a series of positive (red) and negative (blue) features, which develop around delay zero and fully disappear within 10–15 fs. These features originate mainly from IR-induced optical Stark effect of the excitonic transitions, and the presence of dark excitonic states which become optically active around zero pump-probe delay19. The exciton optical Stark effect is the analogous of the well-known optical Stark effect in atoms where absorption or emission of non-resonant photons can lead to a shift of the atomic energy levels29. In analogy with a photon-dressed two-level system, the optical Stark effect originates from the coupling between the bright and dark excitonic states. Since the photon energy (~1.6 eV) is bigger than the spacing between the two states (~1.3 eV), the associated transition is red-shifted, which translates in a blue shift of the Mg 2p—bright exciton transition.
a Slow component of the experimental ΔR/R reported in Fig. 1d. b, c Calculated slow component of ΔR/R considering solely the two excitonic states or only the crystal CB, respectively. d Measured (dots) and calculated (orange dotted and grey dashed curves) ΔR/R profiles for four representative delays marked by the dash-dotted vertical lines in (a).
Figure 2b, c shows the calculated slow component of ΔR/R considering only the excitonic states reported in Fig. 1c (“pure excitonic” contribution) or only the crystal CB (“pure crystal” contribution) (see Methods). We find that “pure exciton” calculations qualitatively reproduce the main experimental features while the crystal response does not (Fig. 2d).
Since in our pure-exciton model the exciton is described with atomic-like states, solid-like interactions with the IR field (e.g. intra-band motion) are not possible. Therefore, the good agreement between the calculations of Fig. 2b and the experimental data of Fig. 2a supports the attribution of the origin of the slow component of ΔR/R to the optical Stark effect and shows that the few-fs dynamics of the optical response can be understood, on first approximation, by considering only the atomic-like character of the exciton quasi-particle.
From the delay-dependent optical Stark shift, it is possible to study the exciton decay process19. We found the bright exciton to decay rather quickly with an effective time constant of 2.35 ± 0.3 fs (see Methods), comparable to what observed for other insulators like SiO218 and MgO19. A deeper analysis, which could reveal the interplay between Auger decay and phonon coupling, needs either measurements with a shorter IR pulse, or more complex reconstruction procedures, both of which go beyond the scope of this work.
While the fact that some optical properties can be described by the exciton atomic character is typical for a quasi-particle characterised by a binding energy of 1.4 eV21, the analysis of the sub-fs dynamics reveals an unexpected result. The fast component of the transient reflectivity spectrogram is reported in Fig. 3a, showing clear oscillations at twice the IR frequency, which are fully reproduced by our simulations (Fig. 3b). Both the amplitude and the tilt of the oscillations cannot be reproduced considering solely the exciton contribution (Fig. 3c). These oscillations have a V-shaped dispersion which resembles what is found for the dynamical Franz-Keldysh effect (DFKE) high into the CB of diamond30,31, suggesting a clear link with intra-band motion of virtual charges. We note that the interaction regime significantly differs from DFKE in valence excitons exposed to THz pulses32,33 where the pump field evolves on a much slower time scale. Furthermore, even if the lower 2p state is non-dispersive, the energy of the electron–hole particle follows the upper CB state and exhibits a parabolic profile. This explains why a V-shaped structure is observed even when the initial state is not a dispersive valence state, but an atomic-like core level.
a Fast component of the experimental ΔR/R. The phase delay, τ, between the oscillations and EIR2 is displayed in black. The solid curve represents the mean over four independent measurements and the shaded area twice its standard deviation. b, c Same as (a) but for the full or the pure exciton calculation results, respectively. d Comparison between the experimental (black solid) and calculated τ, considering the full system response (red solid), or addressing separately the crystal (grey dashed) and excitonic (orange dotted) contributions. .
Thanks to our independent pump-probe delay calibration, we can make a further step towards a complete comprehension of such a rich exciton dynamics and study the phase delay τ between the oscillations in the transient signal and the square of the IR electric field EIR2 (see Methods). Figure 3d presents the experimental τ obtained as a weighted average over four independent measurements (black solid curve) compared with the calculated phase delay in case of full model (red solid curve), pure exciton (orange dotted curve) or pure-crystal response (dashed grey curve). In all cases, the shaded area represents twice the standard deviation originating from the measurement error or from the uncertainty of the phase extraction method. The full model accurately reproduces the experiment both on a qualitative and quantitative level. However, in contrast to what we observed for the slow component of ΔR/R, now the pure excitonic contribution alone fails in capturing the measured τ, even qualitatively. This strongly indicates that the fast component of the differential reflectivity is dominated by the solid nature of the exciton, despite its localised character and in stark contrast to its slower atomic-like response. Indeed, the oscillations found in the pure exciton model (Fig. 3c) originate from an atomic effect: the instantaneous optical Stark shift. On the contrary, the oscillations observed in the pure-crystal model arise from the intra-band motion of virtual carriers (DFKE). In principle, real carrier motion at the CB bottom cannot be neglected31. Nevertheless, as observed in GaAs crystals21, while the total carrier injection rate into the CB is considerably affected by the interplay of inter- and intra-band transitions, the phase of the ultrafast optical response is mainly dictated by the motion of the virtual carriers. Therefore, we conclude that the latter plays a major role in sculpting the energy dispersion of the oscillation phase reported in Fig. 3a. The fact that the full system response (red curve in Fig. 3d) resembles the bare crystal case (dashed grey curve in Fig. 3d) but shifted in energy, suggests the following physical interpretation. The few-cycle IR pulse dresses the crystal CB inducing virtual charges intra-band motion (DFKE). In turn, this alters the exciton dynamical properties causing the quasi-particle to oscillate in the IR field with a phase relation similar to that of the bare crystal.
If the proposed picture is correct, we expect the observed transient features in the optical response to correspond to an actual movement of the exciton on attosecond (as) and nanometric scales. To tackle this, we calculated the excitonic dipole in real time and found that it oscillates almost at the same frequency of the IR field during interaction. The results are shown in Fig. 4a for the case of the full system (red curve) or considering only the quasi-particle (orange curve). By evaluating the phase delay for the dipole with respect to the IR field (black dotted curve), we found the oscillations of the pure exciton dipole to be delayed by 252 ± 69 as with respect to the full system response (square marks in Fig. 4b). Remarkably, a similar shift of 272 ± 57 as is observed between the oscillations of ΔR/R evaluated at the energy of the excitonic transition and calculated with the full model or considering only the excitonic contribution (full circles in Fig. 4b). Therefore, our findings suggest a strong correlation between the sub-nm exciton motion in real space and the sub-fs transient features observed in the differential reflectivity. This not only proves that localised excitons can show properties beyond atomic model, but also opens the possibility to investigate separately the optical Stark effect (atomic-like) and the DFKE (solid-like), which were previously found to compete in time-averaged measurements32, widening our comprehension of the ultrafast solid-state physics34.
a Exciton dipole oscillations in real time computed with the full (red) or pure exciton (orange) model. The black-dotted curve represents the IR electric field. b Comparison of the phase delay extracted from ΔR/R (circles) or from the dipole moment (squares) for the full calculations (red) or considering only the excitonic response (orange). c Behaviour of the calculated phase delay τ as a function of the exciton binding energy Eb. The vertical dash-dotted lines mark the exciton position. d Difference between the phase delay of the full system and the pure-crystal response, Δτ, for the data reported in (c). e Energy shift ΔE which minimises Δτ as a function of Eb (Bohr radius a0). The vertical blue dashed line marks the minimum inter-nuclear distance in the MgF2 crystal unit cell equal to 1.98 Å. f Value of the phase delay τ evaluated at the exciton vertical transition (τex, open circles), or at the bottom of the CB (τCB, full squares) for the different values of Eb (a0) considered.
So far we have proven that exciton–crystal interaction can transfer bulk properties to atomic-like core excitons on attosecond time scale. All the more reason, the same is expected to happen for Wannier-Mott valence excitons which, being more delocalised, have a stronger solid-like behaviour (see Supplementary Note 19). The question remains whether the attosecond response will qualitatively change, deviating by the solid-like response, if more localised excitons are taken into considerations. In order to further investigate the role of real space dynamics and exciton localisation we computed the reflectivity phase delay τ for different exciton binding energies Eb or, equivalently, Bohr radii a0, which provides a reference for the actual size of excitonic devices10,35. With increasing Eb and thus the degree of localisation, τ preserves its V shape whose centre appears to move towards lower photon energies (Fig. 4c), resulting in an overall bigger phase delay difference, Δτ, between the bare crystal and full system responses (Fig. 4d). The energy shift ΔE which minimises Δτ is not exactly equal to Eb (Fig. 4e), indicating that τ does not simply experience a rigid shift following the exciton transition. On the one hand this further confirms that the central role of exciton–crystal interaction, on the other hand it opens a way to sculpt and control the excitonic response in the petahertz regime. While the optical response of delocalised electron–hole pairs will react almost in phase with the pump electric field (as underlined by the phase delay τ evaluated at the exciton vertical transition, τex in Fig. 4f), more localised excitons will have a slower response, almost out of phase. Due to the exciton–crystal interaction, the CB response will also be significantly affected (see the phase delay τ evaluated at the CB bottom, τCB in Fig. 4f). Since the exciton binding energy can be continuously tuned around its natural value by an external field, modifying the dielectric screening or inducing a strain36,37,38, one can control the phase delay between the quasi-particle and an optical field on an attosecond level. In particular, for values of Eb ≈ 1 eV where a0 becomes comparable with the minimum inter-nuclear distance in the MgF2 unit cell, it is possible to control the attosecond timing between the exciton and the CB signal, realising a condition when the first is advanced with respect to the IR field while the second is delayed.
As the attosecond response of valence excitons behaves qualitatively in the same fashion (see Supplementary Note 19), our findings point to a possible route for the realisation of a different class of devices where a control over the degree of Coulomb screening39 can be used to tune the system response timing with attosecond resolution.
It is worth noticing that we expect intra-band motion to be less important for Frenkel excitons like charge-transfer excitons in molecular crystals8 or interlayer excitons in layered solids7. Therefore, the sub-fs optical response of these excitons could qualitatively differ from what is reported here.
To conclude, we investigated ultrafast core-exciton dynamics around the L2,3 edge in MgF2 single crystal with ATRS. Simultaneous calibration measurements allowed us to perform a direct and unambiguous comparison with theoretical results, addressing the dual nature of the excitonic quasi-particle from a different perspective. In particular, we found that while the exciton dynamics unfolding on the first few femtoseconds originate from the optical Stark effect and can be understood invoking just the atomic character of the quasi-particle, the physical processes happening on an attosecond time scale during light–matter interaction (i.e. intra-band motion and DFKE) are typical of the condensed state of matter. Moreover, our theoretical simulations and analysis revealed that the atom-solid duality is general and exists for strongly bound excitons and also for delocalised valence excitons where the absolute timing of the system optical response can be controlled on attosecond time scale by tuning the exciton binding energy. Since these findings are not limited to the chosen target but hold, in general, for excitons originated by dispersive bands in solids, they set a new lever for the coherent control of excitonic properties in the close-to-petahertz regime.
Methods
Experimental setup
The setup used for the experiment reported in the main manuscript is described in detail in ref. 23. Single attosecond pulses (SAPs), centred around 42 eV photon energy, and 5 fs IR pulses (central wavelength 750 nm) are first focused onto a Ne gas target. The XUV pulses have a time duration of about 250 as while the IR peak intensity is set between 1012 and 1013 W/cm2. A time-of-flight (TOF) spectrometer records the photoelectron spectra as a function of the delay, t, between the IR and XUV pulses to perform an attosecond streaking experiment40. This allows us to retrieve the temporal characteristics of the two pulses and to obtain a precise calibration of the relative delay t by extracting the exact shape of the IR vector potential. A gold-plated toroidal mirror then focuses both beams onto the MgF2 crystal, where a thin gold layer deposited on a portion of the sample is used to calibrate the incident XUV photon flux and extract the energy-dependent sample reflectivity, R0(E). For more details, see the Supplementary Notes 1–5.
Data analysis
To study the different mechanisms underlying the transient features observed in ΔR/R, we decompose the pump-probe spectrogram in a slow and a fast component. To extract the slow component, we apply a low-pass frequency filter to the reflectivity spectrogram which is constant for frequencies below a cut-off frequency fc and decays with a super-Gaussian a profile \(e^{\left( {\frac{{f - f_c}}{{2\sigma _f}}} \right)^n}\)with coefficient n = 16 and width σf = 0.01 PHz. Since the fastest feature observed oscillates at twice the IR frequency 2fIR ≈ 0.75 PHz, we decided to set fc to 1.5fIR = 0.5621 PHz. Once the slow component has been extracted, the fast component of ΔR/R is simply obtained by subtracting the slow component from the total spectrogram. In the case of the experimental data, a high-frequency filter centred at 5fIR = 1.8737 PHz is used to remove the fast noise from the data prior to slow and fast decomposition.
As discussed in the main manuscript, the femtosecond transient features of ΔR/R originate from the optical Stark effect (OSE) induced by the IR electric field. To extract the Stark shift ε from the experimental data, at each delay t, we fitted the sample reflectivity at the presence of the IR pump, RIR(E, t) with six Gaussian bells. Two Gaussians describe the background. Their parameters are derived from the static reflectivity R0(E). The other four Gaussians are used to fit the bright and dark exciton features, doubled because of the Mg2+ 2p spin–orbit splitting. As observed for MgO19, the dark excitonic state is responsible for an increase of RIR(E, t) around t = 0 fs, which appears next to the bright excitonic peak, on the low-energy side, thus overlapping with the bright exciton signal which originates from 2p3/2 state. Due to the energy overlap, it is not possible to fit accurately the contribution of the 2p1/2-dark state transition as well as all the transitions involving the 2p3/2 state. Therefore, we can obtain a reliable estimation of ε(t) only for the bright-exciton-2p1/2 transition which is found to follow the delay-dependent energy position of the maximum of ΔR/R around the A feature. The excitonic dipole d(t) is obtained by deconvoluting the delay-dependent Stark shift ε(t) with the envelope of the IR electric field19, directly extracted from the simultaneous streaking trace. The Auger decay rate γ and the phonon coupling ϕ can then be evaluated by modelling the excitonic dipole with the function \({\it{d}}({\it{t}})\sim e^{ - \gamma t}e^{\phi ({\it{t}})}\)18,19. For more details see Supplementary Note 9.
The absolute phase delay between the fast transient feature of ΔR/R and the IR electric field is evaluated following the approach reported in15,31. First the IR vector potential is extracted from the simultaneous streaking trace by means of a 2D fitting procedure based on the analytical model reported in41. Then the phase difference between the transient features in the differential reflectivity and EIR2 is directly evaluated by multiplying the energy-dependent Fourier transform of the first with the complex conjugate of the Fourier transform of the latter. The product thus constructed automatically peaks at the common frequency between the signals and has a phase equal to their phase difference Δφ. As Δφ could be frequency-dependent, we evaluate the average value around 2fIR using the local intensity of the Fourier transform product as weight. The standard deviation is obtained calculating the second momentum of this distribution. Finally, the phase delay τ is given by the ratio between Δφ and the beating frequency 2fIR. The main results reported in Fig. 3c represent an average over four independent transient reflection measurements conducted under similar conditions and weighted by the inverse of their individual experimental uncertainty. The final error accounts both for the mean measurement error and for the statistical deviation between the independent measurements. For further details, see Supplementary Note 7. We note that τ has the opposite sign of the pump-probe delay modulations (compare the black curves in Fig. 3a, c). This originates from the fact that a positive pump-probe delay t means that the IR pulse is coming later (IR behaving as a probe), but for the sake of an easier interpretation, we chose a positive τ to mean that the system has a delayed response with respect to the IR field in real time (IR behaving as a pump).
Theoretical model
To investigate the microscopic mechanism of the experimental observation, we describe the dynamical system under the intense IR pulse and the weak XUV pulse based on the following ansatz:
where \(\left| \right.\Psi\left(t\right) \left\rangle\right.\) is the wave-function of the dynamical system, \(\left| \right.{{\mathrm{{\Phi}}}_{{\mathrm{GS}}}} \left\rangle\right.\) is the ground state wave-function of the matter, \(\hat {a}_{c,k}^\dagger \left( \hat {a}_{v,k} \right)\) is a creation (annihilation) operator for the conduction (valence) state at the Bloch wavenumber k, and ck(t) is an expansion coefficient. Here, the vector potential of the IR field is denoted as AIR(t). Note that the ansatz in Eq. (1) is a linear combination of single-particle single-hole states and is in line with the Tamm-Dancoff approximation. Treating the excitation from the ground state to electron–hole states by the XUV field perturbatively, the equation of motion for the coefficient ck(t) is given by
where EXUV (t) is the electric field of the XUV pulse, Dk is the transition dipole moment between the ground state and the electron–hole state at the Bloch wavevector k, and Hkk′ (t) is the electron–hole Hamiltonian. We employ the Wannier-Mott model26,27, and the electron–hole Hamiltonian is given by
where Eg is the direct gap of the matter, μ is the effective electron–hole mass, and Vkk′ is the Coulomb interaction, which we model with the one-dimensional soft Coulomb interaction. Note that, by diagonalizing Hkk′ (t = 0), one obtains exciton states as bound states of electrons and holes as shown in Fig. 1c.
We solve the Schrödinger equation, Eq. (2), with an open-source code42 and evaluate physical observables with the time-evolving wave-function \(\left| {{\Psi}\left( {\it{t}} \right)} \right\rangle\), For example, the induced electric current density can be computed as \(J_{{\mathrm{XUV}}}\left( t \right) = \left\langle {{\Psi}\left( {\it{t}} \right)\left| {\hat J} \right|{\Psi}\left( {\it{t}} \right)} \right\rangle /{\Omega}\), where Ĵ is the current operator and Ω is the crystal volume. Furthermore, the linear susceptibility χexc (ω) can be evaluated as
where \(\sigma _{{\mathrm{exc}}}\left( \omega \right)\) is the optical conductivity evaluated as the ratio of the current and the electric field in the frequency domain. We model the dielectric function of MgF2 by combining the core-exciton susceptibility χexc (ω) and the valence contribution as
where \({\it{\epsilon }}_{{\mathrm{valence}}}\left( \omega \right)\) is the valence contribution, c is a fitting parameter and ΔSO is the spin–orbit split. By optimising \({\it{\epsilon }}_{{\mathrm{valence}}}\left( \omega \right)\) and c, the dielectric function and the reflectivity of MgF2 can be well reproduced by the above model (see Fig. 1b).
With the final goal being to investigate the transient reflectivity of the XUV pulse under the presence of the IR pulse, we compute the electron dynamics by solving Eq. (2) with both the IR and XUV fields. Then, we further compute the current with the time-dependent wave-function \(\left. {|{\mathrm{{\Psi}}}\left( t \right)} \right\rangle\). Following the above procedure, Eqs. (4) and (5), the transient dielectric function under the presence of the IR field and the corresponding transient reflectivity can be evaluated. The computed transient reflectivity by the Wannier-Mott model is shown in Fig. 1e.
In order to obtain further insight into the phenomena, we construct two idealised models. One is the pure-exciton model, and it is designed to exclude the crystalline nature of the dynamics. The other is the pure-crystal model, and it is designed to exclude the atomic nature. The pure-exciton model is a three-level model constructed by the following three states; the ground state \(\left. {|{\Phi}_{{\it{{\mathrm{GS}}}}}} \right\rangle\), the bright exciton state and the dark exciton state (see Fig. 1c). Hence the pure-exciton model allows us to extract the nature of the discrete energy levels (atomic nature). Note that the pure-exciton model is constructed by the subspace of the above Wannier-Mott model because the bright exciton state is the ground state of Hkk′ (t = 0) and the dark exciton state is the first excited state. The pure-crystal model, instead, consists of the conduction band (CB) but excludes the exciton states (see Fig. 1c). Such a model can be realised by setting the electron–hole attraction Vkk′ to zero, and it is identical to the parabolic two-band model used to discuss the dynamical Franz-Keldysh effect30. Therefore, the pure-crystal model allows us to extract the contribution purely from the intra-band motion (crystal nature) accelerated by the IR field. For a detailed discussion of the theoretical model42, see Supplementary Notes 10–19.
Data availability
All data generated and analysed during this study are available from the corresponding author upon reasonable request.
Code availability
All the custom codes used in this study are available from the corresponding author upon reasonable request.
References
Markov, I. L. Limits on fundamental limits to computation. Nature 512, 147–154 (2014).
Langer, F. et al. Lightwave valleytronics in a monolayer of tungsten diselenide. Nature 557, 76–80 (2018).
Tan, C. et al. Recent advances in ultrathin two-dimensional nanomaterials. Chem. Rev. 117, 6225–6331 (2017).
Liu, Y., Huang, Y. & Duan, X. van der Waals integration before and beyond two-dimensional materials. Nature 567, 323–333 (2019).
Koch, S. W., Kira, M., Khitrova, G. & Gibbs, H. M. Semiconductor excitons in new light. Nat. Mater. 5, 523–531 (2006).
Krausz, F. & Stockman, M. I. Attosecond metrology: from electron capture to future signal processing. Nat. Photonics 8, 205–213 (2014).
Karni, O. et al. Infrared interlayer exciton emission in MoS2/WSe2 heterostructures. Phys. Rev. Lett. 123, 247402 (2019).
Scholes, G. D. & Rumbles, G. Excitons in nanoscale systems. Nat. Mater. 5, 683–696 (2006).
Novoselov, K. S., Mishchenko, A., Carvalho, A. & Castro Neto, A. H. 2D materials and van der Waals heterostructures. Science 353, aac9439 (2016).
Butov, L. V. Excitonic devices. Superlattices Microstruct. 108, 2–26 (2017).
Unuchek, D. et al. Room-temperature electrical control of exciton flux in a van der Waals heterostructure. Nature 560, 340–344 (2018).
Krausz, F. & Ivanov, M. Attosecond physics. Rev. Mod. Phys. 81, 163–234 (2009).
Geneaux, R., Marroux, H. J. B., Guggenmos, A., Neumark, D. M. & Leone, S. R. Transient absorption spectroscopy using high harmonic generation: a review of ultrafast X-ray dynamics in molecules and solids. Philos. Trans. R. Soc. A 377, 20170463 (2019).
Schultze, M. et al. Attosecond band-gap dynamics in silicon. Science 346, 1348–1352 (2014).
Schlaepfer, F. et al. Attosecond optical-field-enhanced carrier injection into the gaas conduction band. Nat. Phys. 14, 560–564 (2018).
Volkov, M. et al. Attosecond screening dynamics mediated by electron localization in transition metals. Nat. Phys. 15, 1145–1149 (2019).
Merkl, P. et al. Ultrafast transition between exciton phases in van der Waals heterostructures. Nat. Mater. 18, 25–28 (2019).
Moulet, A., Bertrand, J. B., Klostermann, T., Guggenmos, A. & Karpowicz, N. Soft X-ray excitonics. Science 1138, 1134–1138 (2017).
Géneaux, R. et al. Attosecond time-domain measurement of core-level-exciton decay in magnesium oxide. Phys. Rev. Lett. 124, 207401 (2020).
Kaplan, C. J. et al. Femtosecond tracking of carrier relaxation in germanium with extreme ultraviolet transient reflectivity. Phys. Rev. B 97, 1–9 (2018).
Jouanin, C., Albert, J. P. & Gout, C. Band structure and optical properties of magnesium fluoride. J. Phys. 37, 595–602 (1976).
Yi, Z. & Jia, R. Quasiparticle band structures and optical properties of magnesium fluoride. J. Phys. Condens. Matter 24, 085602 (2012).
Lucarelli, G. D. et al. Novel beamline for attosecond transient reflection spectroscopy in a sequential two-foci geometry. Rev. Sci. Instrum. 91, 053002 (2020).
Hanson, W. F., Arakawa, E. T. & Williams, M. W. Optical properties of MgO and MgF2 in the extreme ultraviolet region. J. Appl. Phys. 43, 1661–1665 (1972).
Rabe, P., Sonntag, B., Sagawa, T. & Haensel, R. The optical absorption of MgF2, MgCl2, and MgBr2 in the vicinity of the Mg L‐shell transitions. Phys. Status Solidi 50, 559–569 (1972).
Wannier, G. H. The structure of electronic excitation levels in insulating crystals. Phys. Rev. 52, 191–197 (1937).
Mott, N. F. Conduction in polar crystals. II. The conduction band and ultra-violet absorption of alkali-halide crystals. Trans. Faraday Soc. 34, 500 (1938).
Mysyrowicz, A. et al. ‘Dressed excitons’ in a multiple-quantum-well structure: evidence for an optical stark effect with femtosecond response time. Phys. Rev. Lett. 56, 2748–2751 (1986).
Combescot, M. Semiconductors in strong laser fields: from polariton to exciton optical Stark effect. Phys. Rep. 221, 167–249 (1992).
Lucchini, M. et al. Attosecond dynamical Franz-Keldysh effect in polycrystalline diamond. Science 353, 916–919 (2016).
Lucchini, M. et al. Attosecond timing of the dynamical Franz–Keldysh effect. J. Phys. Photonics 2, 025001 (2020).
Nordstrom, K. B. et al. Excitonic dynamical Franz-Keldysh effect. Phys. Rev. Lett. 81, 457–460 (1998).
Shinokita, K. et al. Dynamical Franz-Keldysh effect in GaAs/AlGaAs multiple quantum wells induced by single-cycle terahertz pulses. Appl. Phys. Lett. 97, 1–4 (2010).
Sato, S. A. et al. Role of intraband transitions in photocarrier generation. Phys. Rev. B 98, 1–10 (2018).
La Rocca, G. Wannier–Mott excitons in semiconductors. In Electronic Excitations in Organic Nanostructures (eds. Agranovich, V. M. & Bassani, G. F.) Vol. 31, 97–128 (Elsevier, 2003).
Chernikov, A. et al. Electrical tuning of exciton binding energies in monolayer WS2. Phys. Rev. Lett. 115, 126802 (2015).
Ju, L. et al. Tunable excitons in bilayer graphene.Science 358, 907–910 (2017).
Aslan, O. B., Deng, M. & Heinz, T. F. Strain tuning of excitons in monolayer WSe2. Phys. Rev. B 98, 115308 (2018).
Prada, E., Alvarez, J. V., Bailen, F. J. & Palacios, J. J. Effective-mass theory for the anisotropic exciton in two-dimensional crystals: application to phosphorene. Phys. Rev. B 91, 245421 (2015).
Itatani, J. et al. Attosecond streak camera. Phys. Rev. Lett. 88, 4 (2002).
Gagnon, J. & Yakovlev, V. S. The direct evaluation of attosecond chirp from a streaking measurement. Appl. Phys. B 103, 303–309 (2011).
Sato, S. A. WM1D: solver for 1D Wannier-Mott model. https://github.com/shunsuke-sato/wannier_motto_model. Accessed 24 April 2020.
Acknowledgements
This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant Agreement No. 848411 title AuDACE). M.L., G.I. and L.P. further acknowledge funding from MIUR PRIN aSTAR, Grant No. 2017RKWTMY. S.S., H.H., U.D.G. and A.R. were supported by the European Research Council (ERC-2015-AdG-694097) and Grupos Consolidados UPV/EHU (IT1249-19).
Author information
Authors and Affiliations
Contributions
G.D.L, B.M. and G.I. performed the measurements. Together with R.B.V., M.N. and M.L., they also evaluated and analysed the results. G.D.L., B.M., G.I., M.L., F.F. and L.P. designed and built the reflectometer. S.A.S., H.H., U.D.G. and A.R. developed the theoretical models and performed the calculations. M.L. wrote the manuscript. All authors contributed to the analysis and interpretation of the experimental and theoretical results and writing of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Marcelo Ciappina and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Lucchini, M., Sato, S.A., Lucarelli, G.D. et al. Unravelling the intertwined atomic and bulk nature of localised excitons by attosecond spectroscopy. Nat Commun 12, 1021 (2021). https://doi.org/10.1038/s41467-021-21345-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-021-21345-7
This article is cited by
-
Exciton migration in two-dimensional materials
Communications Physics (2024)
-
Field-driven attosecond charge dynamics in germanium
Nature Photonics (2023)
-
Attosecond electron motion control in dielectric
Nature Photonics (2022)
-
Controlling Floquet states on ultrashort time scales
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.