Abstract
Stochastic processes govern the time evolution of a huge variety of realistic systems throughout the sciences. A minimal description of noisy many-particle systems within a Markovian picture and with a notion of spatial dimension is given by probabilistic cellular automata, which typically feature time-independent and short-ranged update rules. Here, we propose a simple cellular automaton with power-law interactions that gives rise to a bistable phase of long-ranged directed percolation whose long-time behaviour is not only dictated by the system dynamics, but also by the initial conditions. In the presence of a periodic modulation of the update rules, we find that the system responds with a period larger than that of the modulation for an exponentially (in system size) long time. This breaking of discrete time translation symmetry of the underlying dynamics is enabled by a self-correcting mechanism of the long-ranged interactions which compensates noise-induced imperfections. Our work thus provides a firm example of a classical discrete time crystal phase of matter and paves the way for the study of novel non-equilibrium phases in the unexplored field of driven probabilistic cellular automata.
Similar content being viewed by others
Introduction
Percolation theory describes the connectivity of networks, with applications pervading virtually any branch of science1, including economics2, engineering3, neurosciences4, social sciences5, geoscience6, food science7 and, most prominently, epidemiology8. Among the multitude of phenomena described by percolation, of predominant importance are spreading processes, in which time plays a crucial role and that can be studied within models of directed percolation (DP)9. Characterized by universal scalings in time10, in their discretized versions these models are probabilistic cellular automata (PCA), that is, dynamical systems with a state evolving in discrete time according to a set of stochastic and generally short-ranged update rules. To account for certain realistic situations, e.g. of long-distance travels in epidemic spreading, DP has been extended to long-ranged updates11,12 leading to a change of the universal scaling exponents13.
Despite their wide applicability, PCAs have surprisingly remained an outlier in a branch of non-equilibrium physics that has recently experienced a tremendous amount of excitement—that of discrete time crystals (DTCs)14,15,16,17,18,19,20. In essence, DTCs are systems that, under the action of a time-periodic modulation with period T, exhibit a periodic response at a different period \(T^{\prime} \ne T\), thus breaking the discrete time-translational symmetry of the drive and of the equations of motion. DTCs thus extend the fundamental idea of symmetry breaking21 to non-equilibrium phases of matter. Following the pioneering proposals in the context of many-body-localized (MBL) systems17,18, DTCs have been observed experimentally22,23, and their notion has been extended beyond MBL24,25,26,27.
More recently, Yao and collaborators have fleshed out the essential ingredients of a classical DTC phase of matter28. Namely, in a classical DTC, many-body interactions should allow for an infinite autocorrelation time, which should be stable in the presence of a noisy environment at finite temperature, a subtle requirement that rules out the vast class of long-known deterministic dynamical systems. Despite various efforts28,29,30,31, an example of such a classical DTC has mostly remained elusive, and proving an infinite autocorrelation time robust to noise and perturbations for this phase of matter is an outstanding problem. The general expectation is in fact that PCAs and other minimal models for noisy systems in one spatial dimension can only show a transient subharmonic response because noise-induced imperfections generically nucleate and spread, destroying true infinite-range symmetry breaking in time28,32.
Here we overcome these difficulties by introducing a simple and natural generalization of DP in which the dynamical rules are governed by power–law correlations. This leads to qualitative changes of the system behaviour and, crucially, the emergence of a bistable phase of long-ranged DP, enabled by the ability of long-range interactions to counteract the dynamic proliferation of defects. By adding a periodic modulation to the update rules, we then study a version of periodically driven DP and show that the underlying bistable phase intimately connects to a stable DTC. In this non-equilibrium phase, the system is able to self-correct noise-induced errors and the autocorrelation time grows exponentially with the system size, thus becoming infinite in the thermodynamic limit. In analogy to the one-dimensional Ising model for which, at equilibrium, long-range interactions enable a normally forbidden finite-temperature magnetic phase33,34, in our model, out of equilibrium, the long-range interactions lead to a classical time-crystalline phase. Crucially, our results appear naturally in a minimal model of long-ranged DP but are expected to find applications in many different contexts of dynamical many-body systems.
Basic understanding of new concepts has historically been built around the study of minimal models, such as the Ising model for magnetism at equilibrium33,34, the kicked transverse field Ising chain for DTCs17,18, or the prototypical Domany–Kinzel (DK) PCA for DP35. In this paper, we start our discussion with a brief review of the DK model and then generalize it to include power–law interactions. We characterize its phase diagram and show that its long-range nature is the key ingredient for the emergence of a bistable phase. Finally, we include a periodic drive for the long-ranged DP process and show with a careful scaling analysis that the autocorrelation time of the subharmonic response is exponential in system size. In the thermodynamic limit, our model provides therefore the first example of a PCA behaving as a classical DTC, which is persistent and stable to the continuous presence of noise. Lastly, we conclude with a summary of our findings and an outlook for future research.
Results
Review of DP
We consider a triangular lattice in which one dimension can be interpreted as discrete space i and the other one as discrete time t = 1, 2, 3, … , see Fig. 1. To implicitly account for the triangular nature of the lattice, i runs over integers and half-integers at odd and even times t, respectively. We denote L the spatial system size and are interested in the thermodynamic limit L → ∞. The site i at time t can be either occupied or empty, si,t = 0,1. For a given time t, we call generation the collection of variables \({\{{s}_{i,t}\}}_{i}\) specifying the system state. Initially, the sites are occupied with uniform probability p1 > 0. A DP process is defined by a stochastic Markovian update rule with which, starting from the initial generation \({\{{s}_{i,1}\}}_{i}\), all subsequent generations \({\{{s}_{i,t}\}}_{i}\) are obtained one by one. The main observable we will focus on is the global density n(t) (henceforth just referred to as density for brevity) defined as
where the inner and outer brackets denote average over the L sites and over R independent runs, respectively. Since n(1) = p1, we will often refer to p1 as initial density.
a The probability pi,t of site i to be occupied at time t depends on the occupation of its nearest-neighbours \(i\pm \frac{1}{2}\) at time t − 1 and can take discrete values 0, q1 and q2. b Flowchart representation of the DK model. The initial occupation probability is uniform pi,t = 1 = p1. At time t, each site i is either occupied (si,t = 1) or empty (si,t = 0) with probability pi,t and 1 − pi,t, respectively. Time is advanced and local densities \({\{{n}_{i,t}\}}_{i}\) are computed for each site i as averages of the nearest-neighbour occupations at previous time, and these densities determine the occupation probabilities for the next generation, see Eq. (3). The generations at all subsequent times are obtained by iteration. c, d The density n at late times can be used to discern the active and inactive phases, in which n(t = 103) >0 and ≈0, respectively. The dashed lines serve as a reference to locate the phase boundary and are the same for initial densities p1 = 1 (c) and p1 = 0.01 (d). The insets show representative single instances of the DP for the points in the (q1, q2) plane marked with a cross. Here L = 100 and R = 103.
The simplest, and yet already remarkably rich, example of the above setting of DP is the DK model35. Here, we briefly review it adopting an unconventional notation that, making explicit use of a local density, will prove very convenient for a straightforward generalization to a model of long-ranged DP.
In the DK model, the probability of site i to be occupied at time t depends on the state of its neighbours i ± 1/2 at previous time t − 1. More specifically, as summarized in Fig. 1a, site i is: (i) empty if both its neighbours were empty, (ii) occupied with probability q1 if one and just one of its neighbours was occupied, and (iii) occupied with probability q2 if both its neighbours were occupied. To account for these possibilities in a compact fashion, we define a local density ni,t as
and say that site i at time t is occupied with a probability pi,t given by
In other words, the probability pi,t is a nonlinear function \({f}_{{q}_{1},{q}_{2}}({n}_{i,t})\) of the local density ni,t, with domain {0, 0.5, 1}. Since ni,t only involves the nearest neighbours of site i, the DK model of DP is obviously ‘short-ranged’. In essence, si,t is a Bernoullian random variable of parameter pi,t, which we compactly denote \({s}_{i,t} \sim \,\text{Bernoulli}\,({p}_{i,t})\). The complexity of this model arises from the fact that the value of the parameter pi,t is not known a priori, as it depends on the actual state of the system at previous time t − 1. Equipped with a random number generator, one can obtain all the generations one by one according to the above procedure, as schematically illustrated in the flowchart of Fig. 1b. Reiterating for several independent runs, one finally obtains the time series of the density n in Eq. (1).
The DK model features two dynamical phases, shown in Fig. 1c, d. In the inactive phase, for small enough probabilities q1 and q2, the system eventually reaches the completely unoccupied absorbing state, that is, no percolation occurs. In the active phase instead, for large enough probabilities q1 and q2, a finite fraction of sites remains occupied up to infinite time, that is, the system percolates. For small initial probability p1 ≪ 1, the critical line separating the two phases is characterized by a power–law growth of the density36, n ~ tθ, with exponent θ ≈ 0.31. As conjectured by Grassberger37, this exponent is universal for all systems in the DP universality class. Indeed, DP exemplifies how the unifying concept of universality pertaining to quantum and classical many-body systems38 can be extended to non-equilibrium phenomena.
Important for our work is that, in the DK model, whether the system percolates or not depends on the parameters q1 and q2 but not on the initial density p1, at least as long as p1 > 0. Indeed, the phase boundaries for initial densities p1 = 0.01 and p1 = 1 in Fig. 1c, d, respectively, coincide.
Long-ranged percolation and bistability
As the vast majority of PCA, the DK model features short-ranged update rules9. In realistic systems, however, it is often the case that the occupation of a site i is influenced not only by the neighbouring sites but also by farther sites j, with an effect decreasing with the distance ri,j between the sites. Building on an analogy with the DK model, we propose here a model for such a ‘long-ranged’ DP, whose protocol is explained in the flowchart of Fig. 2a. Specifically, we consider as a local density ni,t a power–law-weighted average of the previous generation \({\{{s}_{j,t-1}\}}_{j}\) centred around site i
where the normalization factor \({{\mathcal{N}}}_{\alpha ,L}\) ensures ni,t = 1 if all sites j are occupied and the adjective ‘local’ emphasizes the site dependence. The occupation probability pi,t then depends on the local density ni,t through some nonlinear function fμ that for concreteness we consider to be
with μ ∈ (0, 1) a control parameter. The whole DP dynamics is determined via the occupations \({s}_{i,t} \sim \,\text{Bernoulli}\,({p}_{i,t})\) and reiterating from one generation to the next. Note, our findings are not contingent on the specific choice of Eqs. (4) and (5) but are rather expected to hold generally for a broad class of long-ranged forms of the densities ni,t and of functions fμ—see ‘Methods’ section for details.
a Flowchart representation of the long-ranged DP. Starting from an initial condition pi,t=1 = p1, site i at time t is occupied (si,t = 1) with probability pi,t. Local densities \({\{{n}_{i,t}\}}_{i}\) are computed as power–law-weighted averages of the previous generation \({\{{s}_{i,t-1}\}}_{i}\), and the occupation probabilities are updated as \({p}_{i,t}={f}_{\mu }\left({n}_{i,t}\right)\), see Eqs. (4) and (5). b, c Time evolution of the density n for p1 = 1 (b) and p1 = 0.01 (c) for various representative values of the power–law exponent α and control parameter μ. Three dynamical phases can be distinguished: (i) inactive—the density n decays to 0 (blue); (ii) active—n does not decay to 0 (yellow); (iii) bistable—n either decays to 0 or not depending on whether the initial density p1 is small or large (red). d, e Long-time density n(t = 103) in the plane of α and μ for p1 = 1 (d) and p1 = 0.01 (e). With the criterion used in b, c, we discern the three phases: inactive (light), active (dark), and bistable (light or dark depending on p1). The dashed lines help locating the phases and coincide in d and e, and critical values \({\mu }_{c}^{0}\) and \({\mu }_{c}^{\infty }\) of μ in the limits α → 0 and α → ∞, respectively, are reported (the offset of \({\mu }_{c}^{0}\) from the dashed line, as well as the softening of the dashed line for α ≈ 1, are due to finite-size effects). Crucially, the bistable phase is present only for small enough α ≾ 2, that is, for a sufficiently long-ranged DP. Single instances of the DP for the three phases are shown in the insets, as obtained for the α and μ indicated with coloured dots, and corresponding to the parameters used in b, c. Here R = 104 and 102 in b, c and d, e, respectively, and L = 500.
We emphasize that Eqs. (4) and (5) and the flowchart in Fig. 2a are a natural generalization of Eqs. (2) and (3) and Fig. 1b, respectively. Furthermore, whereas in the DK model the control parameters are the probabilities q1 and q2, the control parameter is now μ. As an important difference, now the domain of fμ accounts for several (and α-dependent) values of ni,t, for which the piecewise definition of pi,t as in Eq. (3) would have been unpractical, and the compact form of Eq. (5) was necessary instead.
The introduction of a long-ranged local density ni,t in Eq. (4) has profound implications. Arguably, the most dramatic is the appearance of a bistable phase, in addition to the standard active and inactive ones. In the bistable phase, the ability of the system to percolate depends on the initial density p1, see the red lines in Fig. 2b, c. That is, the bistable phase features two basins of attraction, resulting into an asymptotically vanishing or finite n, respectively, and separated by some critical initial density p1,c > 0. To characterize systematically the dynamical phases of our model, we plot in Fig. 2d, e the long-time density n(t = 103) as a suitable order parameter in the plane of the power–law exponent α and control parameter μ. Comparing the results obtained for a large and a small initial density p1, it is possible to sketch a phase diagram composed of three phases: (i) inactive—n decays to 0 at long times; (ii) active—n does not decay at long times; (iii) bistable—n either decays or not depending on p1 being small or large. The existence of this bistable phase is in striking contrast with short-ranged models of DP such as the DK model and in fact appears only for α ⪅ 2, that is, when the local densities \({\{{n}_{i,t}\}}_{i}\) are correlated over a sufficiently long range. To understand the origin of this rich phenomenology, we study the short- and infinite-range limits of our DP process.
In the short-range limit α → ∞, the local densities ni,t reduce to the averages of the nearest-neighbour occupations \({s}_{i-\frac{1}{2},t-1}\) and \({s}_{i+\frac{1}{2},t-1}\), that is, Eq. (4) recasts into Eq. (2) and the DK model is recovered. In the notation of Eq. (3), the DK parameters are q1 = fμ(0.5) and q2 = fμ(1). Therefore, we can move across the DK parameter space (q1,q2) varying μ, going from the inactive phase (\(\mu \;<\;{\mu }_{{\rm{c}}}^{\infty }\)) to the active one (\(\mu \;> \;{\mu }_{{\rm{c}}}^{\infty }\)), and no bistable phase is possible. We find that the transition happens at a critical \({\mu }_{{\rm{c}}}^{\infty }=0.85(7)\). Note that, in the active phase, a completely empty state (p1 = 0) remains trivially empty at all times. This behaviour is, however, unstable, because any p1 > 0 leads to percolation (i.e. p1,c = 0), and we therefore do not classify the active phase as bistable. At criticality, and for p1 ≪ 1, the density grows as n ~ tθ with θ = 0.3(0), as expected for the DP universality class9. See Supplementary Fig. 2 for details.
In the infinite-range limit α → 0, and more generally for α ≤ 1, the factor \({{\mathcal{N}}}_{\alpha ,L}\) in Eq. (4) diverges as L → ∞. Correspondingly, spatial stochastic fluctuations are suppressed, that is, all sites i share the same occupation probability pi,t+1 = pt and density ni,t = n(t) = pt. Therefore, in this limit the dynamics reduces to the deterministic 0-dimensional recurrence relation
The system asymptotic behaviour can then be understood from the analysis of the fixed points (FPs) of the equation x = fμ(x), which is detailed in the ‘Methods’ section.
Driven percolation and time crystals
We have established that long-range correlated local densities \({\{{n}_{i,t}\}}_{i}\) give rise to a bistable phase. We now show how, in a driven DP with periodically modulated update rules, this phase intimately relates to the emergence of a classical DTC. In this phase, as we shall see, the density n displays oscillations over a period larger than that of the drive and up to a time that, thanks to the long-range interactions and despite the presence of multiple sources of noise, is exponentially large in the system size, a feature that would generally be forbidden in short-ranged PCA28. In the thermodynamic limit L → ∞, these subharmonic oscillations are therefore persistent, that is, the system autocorrelation time diverges to infinity, breaking the time-translational symmetry and proving a classical DTC in a periodically driven PCA.
In the spirit of keeping the model as simple as possible, we consider a minimal drive in which, after every T iterations of the DP in Eqs. (4) and (5), empty sites are turned into occupied ones and vice versa, making the full equations of motion periodic with period T. As a further source of imperfections, adding to the underlying noisy DP, we also account for faulty swaps with probability pd. More explicitly, the periodic drive consists of the following transformation
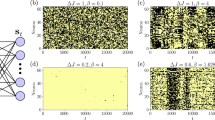
In Fig. 3a, b, we show the spatio-temporal pattern of single instances of the driven DP, alongside with the density n averaged over several independent runs. If the DP is short-ranged enough, the spatio-temporal pattern at long times looks similar from one period to the next, that is, the density n synchronizes with the drive and eventually picks a periodicity T. On the contrary, for a long-ranged enough DP, the system keeps alternating at every period between a densely occupied regime and a sparsely occupied one, and n oscillates with period 2T, that is, the system breaks the discrete time-translation symmetry of the equations of motion.
a, b Single instances of the periodically driven DP, alongside with the density n averaged over multiple independent runs, for L = 500 sites. a For a power–law exponent α = 1.4, n oscillates subharmonically with a period that is twice that of the drive, whereas, for α = 1.8, n eventually picks the periodicity T enforced by the drive. c For finite system sizes L, the subharmonicity Φ(t) decays as \({{\Phi }}(t) \sim \exp (-\frac{t-1}{\tau T})\) due to the accumulation of phase slips, and, after a few time scales τT, the density n synchronizes with the drive and oscillates with period T. Exponential fits (dotted lines) can be used to extrapolate the lifetime τ of the subharmonic response, on which a scaling analysis is performed in d. For α = 1.4 (blue), the lifetime τ scales exponentially with the system size, τ ~ eβL, whereas no such a scaling is found for α = 1.8. The scaling coefficient is again found from an exponential fit (dotted line) and plotted in e versus the power–law exponent α. For small α, that is, long-ranged enough DP, the scaling coefficient β is finite, indicating that in the thermodynamic limit L → ∞ the subharmonic response is persistent and a DTC with infinite autocorrelation time emerges. On the contrary, β ≈ 0 for large α, indicating a trivial dynamical phase in which no stable subharmonic dynamics is established. Here we considered p1 = 1, μ = 0.9, pd = 0.02, T = 20 and R = 2000.
When using the tag ‘classical DTC’, special care should be reserved for showing the defining features of this phase, namely, its rigidity and persistence28. Our system is rigid in the sense that it does not rely on fine-tuned model parameters, e.g. μ, α or the initial density p1, and that noise, either in the form of the inherently stochastic underlying DP or of a small but non-zero drive defect density pd, does not qualitatively change the results. Moreover, in the limit L → ∞, our DTC is truly persistent. Indeed, one might expect that the accumulation of stochastic mistakes introduces phase slips and eventually leads to the (possibly slow but unavoidable) destruction of the subharmonic response. Although this expectation is generally correct for short-ranged DP models, including our model at large α, it can fail for long-ranged DP models.
To show that, in the limit L → ∞, the lifetime of our DTC is infinite, we perform a scaling analysis comparing results for increasing system sizes L. First, we introduce an order parameter Φ(t), henceforth called subharmonicity, that is defined at stroboscopic times t = 1, 1 + T, 1 + 2T, … as
If the density n oscillates with the same period T as the drive, then n(t) = n(t + T) and Φ(t) = 0. On the contrary, if n oscillates with a doubled period 2T, then n(t = 1 + kT) is positive and negative for even and odd k, respectively, and Φ(t) is finite and maintains a constant sign. Therefore, Φ(t) is a suitable diagnostics to track the degree of subharmonicity of n in time and to perform the scaling analysis.
In Fig. 3c, we show Φ(t) for various system sizes L. For both α = 1.4 and α = 1.8, the subharmonicity decays exponentially in time, \({{\Phi }}(t) \sim \exp (-\frac{t-1}{\tau T})\). As shown in Fig. 3d, these two values of α are, however, crucially different in how the lifetime τT scales with the system size. In fact, τT is approximately independent of L for α = 1.8, whereas it scales exponentially as \(\tau \sim \exp (\beta L)\) for α = 1.4, for which the decay of the subharmonicity is therefore just a finite-size effect. The scaling coefficient β quantifies the time crystallinity of the system and can thus be used to obtain a full phase diagram as a function of the power–law exponent α, in Fig. 3e. We observe a phase transition between a DTC and a trivial phase at α ≈ 1.7. That is, if the DP is sufficiently long-ranged (α ⪅ 1.7), β is finite and in the thermodynamic limit L → ∞ the subharmonic response extends up to infinite time, as required for a true DTC. In contrast, for a shorter-range DP (α ⪆ 1.7), β ≈ 0 independently of L and the subharmonic response is always dynamically destroyed.
Discussion
We have shown that long-range DP and its periodically driven variant can give rise to a bistable phase and a DTC, respectively. At the core of our model in Eqs. (4) and (5) is the idea that the occupation of a given site depends on the state of all the other sites at the previous time. In this sense, our model is reminiscent of some SIR-type models of epidemic spreading in which not only a sick site can infect a susceptible site, but several infected sites can also cooperate to weaken a susceptible site and finally infect it39,40. This cooperation mechanism among an infinite number of parent sites, rather than a finite one as considered in previous works on long-ranged DP13,41, is the key feature allowing the emergence of the bistable phase that finds a transparent explanation in the infinite-range limit α → 0, where it corresponds to the equation x = fμ(x) having two stable FPs. Bistability also provides intuition on the origin of the DTC, to which it is deeply connected. Indeed, the drive in Eq. (7) switches the system from a densely occupied regime to a sparsely occupied one (and vice versa). If the underlying DP is bistable, these regimes fall each within different basins of attraction and can therefore be both stabilized by the contractive dynamics25,29. Ultimately, this double stabilization facilitates the establishment of the DTC with infinite autocorrelation time. Remarkably, this mechanism does not rely on the equations of motion being perfectly periodic, as required for DTCs in closed MBL systems42, and we expect that infinite autocorrelation times could be maintained even in the presence of aperiodic variations of the drive (although the nomenclature should be revised in this case, since the underlying discrete time symmetry would only be present on average but not for individual realizations). This is in contrast to DTCs in closed MBL systems42, in which the non-ergodic dynamics hinges on the peculiar mathematical structure of the Floquet operator, which, in turns, relies on the underlying equations being perfectly periodic.
The intimate connection between bistability and DTC is, however, not a strict duality, and the boundaries of the two phases, in the equilibrium and non-equilibrium phase diagrams, respectively, do not coincide. For instance, in our analysis we found that for μ = 0.9 the bistable phase extends up to α ≈ 1.6, whereas the DTC stretches slightly farther, up to α ≈ 1.7. The origins of this imperfect correspondence can be traced back to two competing effects. On the one hand, bistability may not be sufficient to stabilize a DTC. This can already be understood in the limit α → 0, in which the asymmetry of fμ and of its FPs does not guarantee the drive to switch the density n from one basin of attraction to the other, that is, across the critical probability p1,c. This issue becomes even more relevant for larger α, for which the asymmetry is possibly accentuated and p1,c can approach 0 (see for instance Supplementary Fig. 1). On the other hand, a perfect bistability may not even be necessary for a DTC to exist. In fact, for the stabilization of a DTC, it may be sufficient that, of the densely and sparsely occupied regimes of the underlying DP, only one is stable, and the other is just weakly unstable (that is, metastable), meaning that the time scales of the dynamics of the density n in the two regimes are very different. Loosely speaking, the stability of one regime might be able to compensate for the weaker instability of the other, resulting in an overall stable DTC. The asymmetry of the underlying DP and the mismatch between the bistable phase and the DTC highlight the purely dynamical nature of the latter, that cannot ‘piggy-back’ on any underlying symmetry.
While these considerations are model and parameters dependent, and it is ultimately up to numerics to find the bistable and the DTC phases, what is universal and far reaching here is the concept that long-ranged DP, and PCA more generally, can host novel dynamical phases, such as DTCs. As Yao and collaborators recently pointed out28, long autocorrelation times are in fact generally unexpected in 1 + 1-dimensional PCA, because imperfections and phase slips can nucleate, spread and destroy the order. Our work proves that this fate can be avoided, and time-crystalline order established, in long-ranged PCA. These systems enable in fact an error correction mechanism, in our case intimately related to the bistability, that would be impossible if correlations were limited to a finite radius. We may speculate that, in the physical picture of a Hamiltonian system coupled to a bath, this defect suppression would correspond to the cooling rate being larger than the heating rate.
In conclusion, we have studied the effects of long-range correlated update rules in a model of DP, which we built from an analogy with the prototypical (but short-ranged) DK PCA. First, we proved that, beyond the standard active and inactive phases, a new bistable phase emerges in which the system at long times is either empty or finitely occupied depending on whether it was initially sparsely or densely occupied. Second, in a driven DP with periodic modulation of the update rules, we showed that this bistable phase intimately connects with a DTC phase, in which the density oscillates with a period twice that of the drive. In this DTC phase, the autocorrelation time scales exponentially with the system size, and in the thermodynamic limit a robust and persistent breaking of the discrete time-translation symmetry is established.
As an outlook for future research, further work on the driven DP should better assess the nature of the transition between the DTC and the trivial phase, characterize more systematically the phase diagram in other directions of the parameter space, and, most interestingly, address the role of dimensionality. Indeed, it is well known that dimensionality can facilitate the establishment of ordered phases of matter at equilibrium, and the question whether this is the case also out of equilibrium remains open. A positive answer to this question is suggested by the fact that, in D + 1-dimension with D ≥ 2, bistability can emerge even in short-ranged models of DP40,43,44. Another interesting question regards the fate of chaos and damage spreading in long-ranged DP 45. Further research should then aim to gain analytical intuition into the problem. For instance, the critical α separating the various phases may be located using a field theoretical approach, which has been successful in similar contexts in the past41. Finally, on a broader perspective, our work paves the way towards the study of non-equilibrium phases of matter in the uncharted territory of driven PCA, with a potentially very broad range of applications throughout different branches of science. As a timely example, Floquet PCA may provide new insights into the understanding of seasonal epidemic spreading and periodic intervention efficacy.
Methods
Here we provide further technical details on our work. In Eq. (4), we considered as distance ri,j between sites i and j
where the tangent accounts for periodic boundary conditions and makes the distance of the farthest sites with ∣i − j∣ = L/2 artificially diverge. This divergence is expected to reduce finite-size effects without changing the underlying physics, that is, in fact dominated by sites with ∣i − j∣ ≪ L, for which we get a natural ri,j ≈ ∣i − j∣. Indeed, as we checked, similar results are obtained with \({r}_{i,j}=\min (| i-j| ,L-| i-j| )\). The Kac-like normalization factor \({{\mathcal{N}}}_{\alpha ,L}\) reads instead
The phenomenology of the bistable phase can be understood from a graphical FP analysis of the equation fμ(x) = x illustrated in Fig. 4, which explains the dynamics for α < 1. Three scenarios are possible and interpreted in terms of the ways the graph of the function fμ intersects with the bisect. (i) Inactive—if \(\mu \;<\;{\mu }_{{\rm{c}}}^{0}\), the only FP is x0 = 0, which is stable and corresponds to a completely empty state. The system moves towards this FP and \({p}_{t}\underset{\,}{\overset{t\to \infty }{\to }}0\). (ii) Critical—if \(\mu ={\mu }_{{\rm{c}}}^{0}\), a new semi-stable FP emerges at xc, which is attractive from its right and repulsive on its left. (iii) Bistable—if \(\mu \;> \;{\mu }_{{\rm{c}}}^{0}\), the semi-stable FP splits into an unstable FP x1 > x0 and a stable FP x2 > x1. In this case, the system will reach either the unoccupied FP x0 = 0 or the finitely occupied FP x2 > 0 depending whether p1 < x1 or p1 > x1, respectively. That is, the system is bistable, and the critical initial probability separating its two basins of attraction is p1,c = x1 (see also Supplementary Fig. 1). The critical value \({\mu }_{{\rm{c}}}^{0}\) is obtained numerically solving for the condition of tangency between the graph of fμ and the bisect and gives \({\mu }_{{\rm{c}}}^{0}=0.6550(8)\) and xc = 0.5216(9). For \(\mu \;> \;{\mu }_{{\rm{c}}}^{0}\), the FPs x1 and x2 are found solving for fμ(x) = x, and, for instance, we find x1 = 0.3326(5) and x2 = 0.7890(9) for μ = 0.8.
For a power–law exponent α < 1, the dynamics of Eq. (6) is understood from the FP analysis of the equation x = fμ(x). a For a control parameter \(\mu <{\mu }_{{\rm{c}}}^{0}=0.6550(8)\), the system is inactive, corresponding to a single FP x0 = 0: at long times, the system ends up in the empty, absorbing state with state variables si = 0 for all sites i. b At the critical point \(\mu ={\mu }_{{\rm{c}}}^{0}\), a new semi-stable FP emerges at xc = 0.5216(9), that is, unstable from his left and stable on his right. c Increasing μ above \({\mu }_{{\rm{c}}}^{0}\), the semi-stable FP splits into an unstable FP x1 < xc and a stable FP x2 > xc. Depending on whether the initial density p1 is <x1 or >x1, the system flows towards density n = x0 = 0 or n = x2 > 0, respectively, indicating bistability.
The FP analysis also clarifies the general features of fμ that allow for the emergence of bistability, that is, in fact not contingent on the choice of fμ made in Eq. (5). Indeed, the only requirement is that, for some parameter(s) μ, the equation fμ(x) = x has three FPs x0 < x1 < x2, of which x0 and x2 are stable, whereas x1 is unstable. Put simply, fμ should be a nonlinear function with a graph looking qualitatively as that of Fig. 4c. This condition guarantees a bistable phase for α < 1, which can then possibly extend to α ≥ 1 and, in the presence of a periodic drive, facilitate the establishment of a DTC.
Finally, note that higher resolution and smaller fluctuations could be achieved in the figures throughout the paper if simulating larger system sizes L and/or considering a larger number of independent runs R. This could, for instance, allow a more accurate characterization of both the equilibrium and the non-equilibrium phase diagrams of our model, which could be explored in other directions of the parameter space for varying α, μ, pd and T. This would, however, require a formidable numerical effort and goes therefore beyond the scope of this work. As a reference, for instance, the generation of Fig. 3e for the parameters considered therein requires a computing time of approximately 4 × 103 h per 3 GHz core.
Data availability
No data sets were generated or analysed during the current study.
Code availability
The codes that support the findings of this study are available at https://figshare.com/articles/software/Code/13468836.
References
Stauffer, D. & Aharony, A. Introduction to Percolation Theory (CRC, 2018).
Stauffer, D. Percolation models of financial market dynamics. Adv. Complex Syst. 4, 19 (2001).
Lee, S. et al. Trap-limited and percolation conduction mechanisms in amorphous oxide semiconductor thin film transistors. Appl. Phys. Lett. 98, 203508 (2011).
Breskin, I., Soriano, J., Moses, E. & Tlusty, T. Percolation in living neural networks. Phys. Rev. Lett. 97, 188102 (2006).
Morone, F. & Makse, H. A. Influence maximization in complex networks through optimal percolation. Nature 524, 65 (2015).
King, P. et al. Predicting oil recovery using percolation theory. Petroleum Geosci. 7, S105 (2001).
Illy, A. & Viani, R. Espresso Coffee: The Science of Quality (Academic, 2005).
Moore, C. & Newman, M. E. Epidemics and percolation in small-world networks. Phys. Rev. E 61, 5678 (2000).
Hinrichsen, H. Non-equilibrium critical phenomena and phase transitions into absorbing states. Adv. Phys. 49, 815 (2000).
Ódor, G. Universality classes in nonequilibrium lattice systems. Rev. Mod. Phys. 76, 663 (2004).
Mollison, D. Spatial contact models for ecological and epidemic spread. J. R. Stat. Soc. Ser. B (Methodol.) 39, 283 (1977).
Cannas, S. A. Phase diagram of a stochastic cellular automaton with long-range interactions. Phys. A Stat. Mech. Appl. 258, 32 (1998).
Janssen, H., Oerding, K., Van Wijland, F. & Hilhorst, H. Lévy-flight spreading of epidemic processes leading to percolating clusters. Eur. Phys. J. B Condens. Matter Complex Syst. 7, 137 (1999).
Wilczek, F. Quantum time crystals. Phys. Rev. Lett. 109, 160401 (2012).
Shapere, A. & Wilczek, F. Classical time crystals. Phys. Rev. Lett. 109, 160402 (2012).
Sacha, K. Modeling spontaneous breaking of time-translation symmetry. Phys. Rev. A 91, 033617 (2015).
Khemani, V., Lazarides, A., Moessner, R. & Sondhi, S. L. Phase structure of driven quantum systems. Phys. Rev. Lett. 116, 250401 (2016).
Else, D. V., Bauer, B. & Nayak, C. Floquet time crystals. Phys. Rev. Lett. 117, 090402 (2016).
Yao, N. Y., Potter, A. C., Potirniche, I.-D. & Vishwanath, A. Discrete time crystals: rigidity, criticality, and realizations. Phys. Rev. Lett. 118, 030401 (2017).
Moessner, R. & Sondhi, S. L. Equilibration and order in quantum floquet matter. Nat. Phys. 13, 424 (2017).
Sachdev, S. Quantum Phase Transitions, Handbook of Magnetism and Advanced Magnetic Materials (Wiley, 2007).
Choi, S. et al. Observation of discrete time-crystalline order in a disordered dipolar many-body system. Nature 543, 221 (2017).
Zhang, J. et al. Observation of a discrete time crystal. Nature 543, 217 (2017).
Gong, Z., Hamazaki, R. & Ueda, M. Discrete time-crystalline order in cavity and circuit qed systems. Phys. Rev. Lett. 120, 040404 (2018).
Gambetta, F., Carollo, F., Marcuzzi, M., Garrahan, J. & Lesanovsky, I. Discrete time crystals in the absence of manifest symmetries or disorder in open quantum systems. Phys. Rev. Lett. 122, 015701 (2019).
Pizzi, A., Knolle, J., & Nunnenkamp, A. Higher-order and fractional discrete time crystals in clean long-range interacting systems. Preprint at arXiv https://arxiv.org/abs/1910.07539 (2019).
Machado, F., Else, D. V., Kahanamoku-Meyer, G. D., Nayak, C. & Yao, N. Y. Long-range prethermal phases of nonequilibrium matter. Phys. Rev. X 10, 011043 (2020).
Yao, N. Y., Nayak, C., Balents, L. & Zaletel, M. P. Classical discrete time crystals. Nat. Phys. 16, 438–447 (2020).
Gambetta, F. M., Carollo, F., Lazarides, A., Lesanovsky, I. & Garrahan, J. P. Classical stochastic discrete time crystals. Phys. Rev. E 100, 060105 (2019).
Khasseh, R., Fazio, R., Ruffo, S. & Russomanno, A. Many-body synchronization in a classical hamiltonian system. Phys. Rev. Lett. 123, 184301 (2019).
Heugel, T. L., Oscity, M., Eichler, A., Zilberberg, O. & Chitra, R. Classical many-body time crystals. Phys. Rev. Lett. 123, 124301 (2019).
Bušić, A., Fatès, N., Mairesse, J. & Marcovici, I. Density classification on infinite lattices and trees. In Latin American Symposium on Theoretical Informatics (ed. Fernández-Baca, D.) 109–120 (Springer, 2012).
Dyson, F. J. Existence of a phase-transition in a one-dimensional ising ferromagnet. Commun. Math. Phys. 12, 91 (1969).
Thouless, D. Long-range order in one-dimensional ising systems. Phys. Rev. 187, 732 (1969).
Domany, E. & Kinzel, W. Equivalence of cellular automata to ising models and directed percolation. Phys. Rev. Lett. 53, 311 (1984).
Ódor, G. Universality classes in nonequilibrium lattice systems. Rev. Mod. Phys. 76, 663 (2004).
Grassberger, P. Are damage spreading transitions generically in the universality class of directed percolation? J. Stat. Phys. 79, 13 (1995).
Stanley, H. E. Scaling, universality, and renormalization: three pillars of modern critical phenomena. Rev. Mod. Phys. 71, S358 (1999).
Bizhani, G., Paczuski, M. & Grassberger, P. Discontinuous percolation transitions in epidemic processes, surface depinning in random media, and hamiltonian random graphs. Phys. Rev. E 86, 011128 (2012).
Janssen, H.-K., Müller, M. & Stenull, O. Generalized epidemic process and tricritical dynamic percolation. Phys. Rev. E 70, 026114 (2004).
Hinrichsen, H. & Howard, M. A model for anomalous directed percolation. Eur. Phys. J. B Condens. Matter Complex Syst. 7, 635 (1999).
von Keyserlingk, C. W., Khemani, V. & Sondhi, S. L. Absolute stability and spatiotemporal long-range order in floquet systems. Phys. Rev. B 94, 085112 (2016).
Lübeck, S. Tricritical directed percolation. J. Stat. Phys. 123, 193 (2006).
Grassberger, P. Tricritical directed percolation in 2+ 1 dimensions. J. Stat. Mech. Theory Exp. 2006, P01004 (2006).
Martins, M. L., Verona de Resende, H. F., Tsallis, C. & de Magalhes, A. C. N. Evidence for a new phase in the Domany-Kinzel cellular automaton. Phys. Rev. Lett. 66, 2045 (1991).
Acknowledgements
We are very thankful to P. Grassberger for insightful comments on the manuscript. J.K. thanks Kim Christensen for introducing him to the theory of percolation. We acknowledge support from the Imperial-TUM flagship partnership. A.P. acknowledges support from the Royal Society and hospitality at TUM. A.N. holds a University Research Fellowship from the Royal Society and acknowledges additional support from the Winton Programme for the Physics of Sustainability.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
J.K. initiated the project suggesting to investigate DTCs in long-ranged DP models and to take inspiration from the DK model. A.P. proposed the model and performed the computations. A.N. made critical contributions to the analysis of the results and the preparation of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Pizzi, A., Nunnenkamp, A. & Knolle, J. Bistability and time crystals in long-ranged directed percolation. Nat Commun 12, 1061 (2021). https://doi.org/10.1038/s41467-021-21259-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-021-21259-4
This article is cited by
-
Time crystal dynamics in a weakly modulated stochastic time delayed system
Scientific Reports (2022)
-
Exact multistability and dissipative time crystals in interacting fermionic lattices
Communications Physics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.