Abstract
Plasmons in two-dimensional (2D) materials beyond graphene have recently gained much attention. However, the experimental investigation is limited due to the lack of suitable materials. Here, we experimentally demonstrate localized plasmons in a correlated 2D charge-density-wave (CDW) material: 2H-TaSe2. The plasmon resonance can cover a broad spectral range from the terahertz (40 μm) to the telecom (1.55 μm) region, which is further tunable by changing thickness and dielectric environments. The plasmon dispersion flattens at large wave vectors, resulted from the universal screening effect of interband transitions. More interestingly, anomalous temperature dependence of plasmon resonances associated with CDW excitations is observed. In the CDW phase, the plasmon peak close to the CDW excitation frequency becomes wider and asymmetric, mimicking two coupled oscillators. Our study not only reveals the universal role of the intrinsic screening on 2D plasmons, but also opens an avenue for tunable plasmons in 2D correlated materials.
Similar content being viewed by others
Introduction
With strong tunability and extraordinary light field confinement, plasmons in 2D materials show great promise in reconfigurable photonics1,2,3,4,5,6,7,8,9,10,11. In the long wavelength limit, the plasmon frequency of 2D free electron gas is proportional to \(\sqrt q\)4,12, with q as the wave vector. Such dispersion may give us an illusion that the plasmon frequency can go as high as one wishes. However, recent theoretical studies suggest that the plasmon dispersion in real 2D materials flattens universally due to the intrinsic dielectric screening from interband transitions13,14,15, which is inevitable for almost every crystal. The flattened dispersion renders slow plasmon group velocity and facilitates plasmon localization15. Though with importance, the experimental verification of such flattened dispersion remains elusive up to date.
2H-TaSe2 belongs to a transition metal dichalcogenide (TMDC), which attracts much attention due to the appearance of CDW orders16. It exhibits a normal-incommensurate charge-density-wave (CDW) phase transition at about TC1 = 122 K, followed by an incommensurate–commensurate CDW phase transition at TC2 = 90 K16,17. Previously, the bulk plasmon of metallic TMDCs was studied by electron energy-loss spectroscopy (EELS) and the anomalous negative plasmon dispersion was observed18,19. The interactions between CDW and plasmons were proposed as the physics origin of the negative dispersion19,20,21. In contrast, some later theoretical calculations and doping experiments revealed that the narrow d bands near the Fermi level may account for the negative dispersion22,23,24. All these studies based on EELS are for bulk plasmons, while the coupling between 2D plasmons and CDW excitations in TaSe2 thin films is still unclear.
Here, we report the experimental studies of localized 2D plasmons in 2H-TaSe2 van der Waals (vdW) thin films. We patterned the vdW thin films of 2H-TaSe2 into ribbon arrays and measured the plasmon resonances by Fourier-transform infrared spectroscopy (FTIR). The plasmonic excitations correspond to the collective oscillations of carriers with the moving direction perpendicular to the ribbon1, analogous to localized plasmons in traditional metallic nanostructures. Of course, propagating surface plasmons can be expected to show up in TaSe2 thin films through momentum compensation techniques, such as an atomic force microscopy (AFM) tip in near field imaging experiments2,3. We find that the resonance frequency of the plasmon in TaSe2 thin films covers a broad spectra range and extends to the telecom region, which is unattainable for graphene plasmons6. In addition, TaSe2 plasmons sensitively depend on the layer thickness and dielectric environments. Particularly, we reveal that the plasmon dispersion becomes flat at large wave vectors due to the screening of interband transitions, fully consistent with theoretical predictions15. More interestingly, we find that the CDW phase has profound influence on the plasmon resonance. In our study, we observe the coupling effects between TaSe2 plasmons and CDW excitations, which causes non-monotonic change of the peak height and linewidth when the temperature decreases. For comparison, thin films of 2H-NbSe2 were fabricated into ribbon arrays as well. On the contrary to TaSe2, the plasmon peak of NbSe2 continually becomes sharper with decreasing temperature.
Results
The 2D plasmon dispersion of 2H-TaSe2
2H-TaSe2 exhibits hexagonal structures as illustrated in Fig. 1a. Thin films of TaSe2 were mechanically exfoliated from bulk crystals onto diamond substrates, as displayed in Fig. 1b. In one uniform TaSe2 film, we fabricated more than 10 plasmonic arrays with various ribbon widths. The extinction spectra, which are directly determined by the optical conductivity, were measured by FTIR as illustrated in Fig. 1c. When the polarization of incident light is along the ribbon direction, the extinction spectrum is dominated by free carrier response (Drude scattering rate 2000 cm−1), as shown in Fig. 1d (sample T1, thickness d = 40 nm, ribbon width W = 500 nm), whereas plasmon resonances are observed with perpendicular polarization. The optical conductivity of plasmons is fitted by a Lorentz oscillator model (Eqs. (4) and (5) in the “Methods” section).
a The crystal structures of 2H-TaSe2 viewed along c-axis (monolayer) and b-axis directions (bilayer). The gray and red atoms represent tantalum (Ta) and selenium (Se) atoms, respectively, and the cyan rectangle denotes the unit cell. b The optical image of a typical exfoliated TaSe2 thin film with thickness of 40 nm. The scale bar is 100 μm. c The schematic of the setup for transmission measurements. The yellow stripes represent TaSe2 ribbon arrays, T0 and T correspond to the transmission light of the bare diamond substrate and a ribbon array on the diamond substrate, respectively. d The extinction spectra 1−T/T0 for a plasmonic device (sample T1, d = 40 nm, W = 500 nm), the blue and gray solid lines correspond to the light polarization parallel (∥) and perpendicular (⊥) to the ribbon direction respectively. The red dashed line is the fitted curve of the plasmon peak. The first-order (P1) and the second-order (P2) plasmon peaks are denoted. The inset shows the scanning electron microscopy (SEM) image of the ribbon array.
Figure 2a shows the extinction spectra of TaSe2 plasmons for ribbon arrays with different widths. The first-order and the second-order plasmon peaks are simultaneously observed for plasmonic devices with ribbon width larger than 500 nm. The resonance frequency of the first-order plasmon increases significantly from 1035 to 6133 cm−1 as the ribbon width decreases from 2 μm to 60 nm, which corresponds to the light wavelength λ changes from 9.6 to 1.6 μm. Moreover, the plasmon resonance of TaSe2 can cover terahertz and far-infrared (far-IR) regions as well, with the resonance light wavelength readily beyond 40 μm (see Supplementary Fig. 1). The relatively broad spectral range of TaSe2 plasmons is originated from its high carrier density and the absence of Landau damping channels within this spectral range at room temperature. The effective sheet carrier density of the TaSe2 film with thickness of 40 nm is estimated to be 3.8 × 1017 cm−2 at room temperature (see the Hall resistance measurement in Supplementary note 11), much larger than that of graphene (2.5 × 1013 cm−2 for highly doped graphene5) and comparable to that of ultrathin gold films (1.8 × 1016 cm−2 for d = 3 nm25).
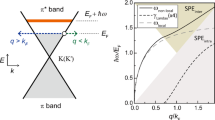
a The extinction spectra of plasmonic devices with ribbon width ranging from 60 nm to 2 μm, the spectra are vertically shifted for clarity. b The plasmon dispersion of a 2H-TaSe2 thin film (sample T1, d = 40 nm). The black squares denote the frequencies of the first-order plasmon, and the error bar represents the uncertainty from the inhomogeneity of ribbon width. The green solid line is the fitted dispersion based on Eq. (2). The blue dashed line is the \(\sqrt q\) scaling to fit data points with small wave vectors (<1.5 × 107 m−1). The pseudo-color map shows the calculated plasmon loss function \(- {\mathrm{{{Im}}}} (1/\varepsilon )\). c The peak width and d the spectral weight of plasmon resonances. The orange dashed line is the fitted spectral weight at large wave vectors which follows the \(S_{\mathrm{P}} \propto (1 + \alpha q)^{ - 1}\) relation.
In the long-wavelength limit, the plasmon dispersion of a 2D free electron system is given by4,12
where ε0 is the vacuum permittivity, εe is the relative dielectric constant of the surrounding environment, ns is the sheet carrier density, and m is the effective mass of carriers. The wave vector q is \(\pi /W\) for the ribbon with width W6. As shown in Fig. 2b, the plasmon dispersion follows the \(\sqrt q\) dependence at small wave vectors, whereas it becomes almost dispersionless when the wave vector is larger than 3 × 107 m−1. As suggested by Jornada et al.15, the deviation from the ideal 2D plasmon dispersion is originated from the screening effect of interband transitions, and the flattening of plasmon dispersion at large q appears to be universal for 2D metals. For metallic TMDCs, there are multiple interband transitions between bands near the Fermi level, namely, the occupied (unoccupied) bands just below (above) the Femi level, whose onset energy is around 1–2 eV according to optical measurements26,27,28 and first-principles calculations14,15,22,23. The plasmon dispersion can be modified by introducing screening effects of interband transitions into the effective dielectric constant εe15, which becomes q-dependent in Keldysh model29. In the long-wavelength limit, the effective dielectric constant is approximately expressed as \(\varepsilon _{\mathrm{{e}}} = \frac{{1 + \varepsilon _{\mathrm{{s}}}}}{2} + \rho _0q\), where εs is the dielectric constant of the substrate, ρ0 is the screening length of the 2D film. For thin films with finite thickness d, the screening length is \(\rho _0 \approx d\varepsilon /2\), and ε is the intrinsic dielectric constant due to interband transitions29. By incorporating the q-dependent dielectric constant εe(q) into Eq. (1), the plasmon dispersion of 2D materials with interband screening reads:15
The plasmon dispersion as well as the saturation behavior at large wave vectors are well fitted by Eq. (2), as displayed in Fig. 2b. The fitted screening length ρ0 is (710 ± 260) Å and the intrinsic dielectric constant ε is about 3.5 ± 1.3 for 2H-TaSe2 with thickness of 40 nm. The plasmon dispersion can also be simulated by the loss function11 \(- {\mathrm{{{Im}}}} (\frac{1}{{\varepsilon (q,\omega )}})\), as illustrated by the pseudo-color map in Fig. 2b, and more details can be found in Supplementary note 2. Plasmons at the flat dispersion region can exhibit low group velocity, strong light confinement and considerably large field enhancement15, which holds promise for highly sensitive detection of local and non-local electronic structures.
As shown in Fig. 2c, the peak width of the first-order plasmon is 552 cm−1 at 1.6 × 106 m−1 and increases to 3200 cm−1 at 5.2 × 107 m−1. Due to the retardation effect30,31, the plasmon peak width at small wave vectors is less than its Drude scattering rate. At relatively large wave vectors, where the retardation effect is already negligible, the plasmon width gradually increases with the wave vector increases. We attribute such peak width enhancement to the more pronounced edge scattering of carriers6 and the inevitable nanofabrication imperfections and inhomogeneities.
In addition to the dispersion, the spectral weight of TaSe2 plasmons is also strongly influenced by the interband screening. For the relatively wide ribbons, the spectral weight of the first-order plasmon is less than that of the second-order plasmon (see Fig. 2d), which is presumably transferred to the second-order plasmon due to the retardation effect30,31. Therefore, we focus on the relatively narrow ribbons whose the second-order plasmon peak is nearly diminishing. That is the region with wave vector larger than 1 × 107 m−1 where the plasmon spectral weight depends on the wave vector as follows: \(S_{\mathrm{P}} \propto (1 + \alpha q)^{ - 1}\), where α is a coefficient associated to the intrinsic screening of interband transitions. This relation can be derived and generalized from the analytical solution of plasmons in metal disks32,33 (see Supplementary note 2). As shown in Fig. 2c, the spectral weight closely follows such scaling rule for q > 1 × 107 m−1. In contrast, for the ideal 2D free electron gas the plasmon spectral weight is independent of q. Thus, the decrease of plasmon spectral weights at large wave vectors is also a manifestation of the interband screening for real 2D materials.
Tunable plasmons by thickness and dielectric environments
The plasmon resonance of 2D materials is tunable by changing thickness. For example, the intensity of graphene plasmons and the resonance frequency were effectively modified by stacking multiple layers of graphene5. To explore the thickness dependence of TaSe2 plasmons, we fabricated plasmonic devices in TaSe2 films with different thickness ranging from 10 to 40 nm. The intensity of the plasmon peak can be largely tuned by the thickness, as illustrated in Fig. 3a. In addition, when it is far away from the saturation frequency, the plasmon frequency is proportional to \(\sqrt d\) according to Eq. (1), provided that \(n_{\mathrm{{s}}} \propto d\) and other material properties remain the same. This relation fits the plasmon frequency well, as shown in Fig. 3b. More details about the thickness dependence of TaSe2 plasmons are shown in Supplementary Fig. 3.
a The extinction spectra of plasmonic devices with film thickness of 10 nm (an isolated sample), 15 nm (sample T3), 25 nm (sample T2), and 40 nm (sample T1), respectively. The ribbon width is fixed at 500 nm. b The thickness dependence of the plasmon frequency, the blue solid line shows the fitted plasmon frequency as a function of \(\sqrt d\), the gray solid line in the inset also shows this relation. c The extinction spectra of plasmonic devices on BaF2 (sample T5), diamond (sample T1), and Si (sample T6) εs substrates, respectively, with the same thickness and ribbon width (d = 40 nm, W = 500 nm). d The plasmon frequency as a function of substrate dielectric constants, the gray dashed line represents the fitted plasmon frequency which is proportional to \(((1 + \varepsilon _{\mathrm{{s}}})/2 + \rho _0q)^{ - 1/2}\). The inset illustrates the screening effect of the substrate. The TaSe2 thin film (yellow film) is surrounded by the substrate (blue region) and air (gray region) with dielectric constants of εs and εa, respectively. The gray solid lines denote the electric field lines caused by the spatial distribution of positive charges (+) and negative charges (−) in the film.
TaSe2 plasmons are also extremely sensitive to the surrounding dielectric environment. We fabricated TaSe2 plasmonic devices on BaF2 (εs = 2.1, sample T5) and Si substrates (εs = 11.8, sample T6), in addition to diamond substrates (εs = 5.7). Low dielectric constant substrates facilitate the observation of higher energy plasmon in experiments. The plasmon frequency of the sample on BaF2 substrates is about twice as high as that on Si, as illustrated in Fig. 3c. It perfectly follows Eq. (2), as indicated by the dashed curve in Fig. 3d. The fitted screening length ρ0 for the film with thickness of 40 nm is (700 ± 280) Å and thus the intrinsic dielectric constant ε is 3.5 ± 1.4, which agrees with the value fitted from the plasmon dispersion. The maximal plasmon frequency we observed is 6580 cm−1 (λ = 1.52 μm) for a plasmonic device on BaF2 substrates (sample T5, d = 40 nm, W = 130 nm). Therefore, the plasmon in TaSe2 films covers the terahertz to the telecom range, which promises broad applications in photonics and optoelectronics. Note that, according to Eq. (2), the achievable maximal plasmon frequency is still limited by the intrinsic screening. More details on the substrate effect are displayed in Supplementary Fig. 4.
Plasmons and the CDW phase transition
In general, the carrier scattering in metals is suppressed as the temperature decreases. As a consequence, the linewidth of the plasmon resonance reduces. For example, the WTe2 plasmon peak becomes much sharper at cryogenic temperatures11. However, the plasmon of 2H-TaSe2 exhibits anomalous temperature dependence. As shown in Fig. 4a and b, the TaSe2 plasmon peak (sample T4, W = 700 nm, d = 20 nm) firstly becomes sharper and the peak height increases when the temperature decreases from 300 to 120 K. Then, on the contrary, as the temperature drops below the CDW phase transition temperature TC1, the plasmon peak becomes wider and asymmetric, and the peak height decreases. This is in sharp contrast to 2H-NbSe2, the plasmon peak of which (sample N1, W = 700 nm, d = 25 nm) continually becomes sharper as the temperature decreases, as shown in Fig. 4c. The plasmon properties of 2H-NbSe2 are generally similar to those of 2H-TaSe2 except for the temperature dependence. The detailed study for NbSe2 plasmons is presented in Supplementary note 6.
a The temperature evolution of the plasmon spectra of 2H-TaSe2 (sample T4, W = 700 nm, d = 20 nm) above TC1. b Same as a but below TC1. c The temperature-dependent plasmon spectra of 2H-NbSe2 (sample N1, W = 700 nm, d = 25 nm). The arrows in a–c beside the main peaks indicate the peak height evolution with decreasing temperature, P1 and P2 denote the first-order and the second-order plasmons, respectively. d The extinction spectra of 2H-TaSe2 with light polarized along the ribbon direction at various temperatures. The CDW excitation appears with temperature below TC1. The inset shows the normalized temperature-dependent resistivity of a TaSe2 thin film (d ≈ 20 nm). e The fitted temperature-dependent peak widths of TaSe2 and NbSe2 plasmons (the first order), the error bars show the uncertainty of spectral fitting. The pink and blue backgrounds denote the normal metal and CDW phases of 2H-TaSe2, respectively.
To understand the underlying mechanism of the abnormal temperature dependence of TaSe2 plasmons, we measured its intrinsic optical response with incident light polarized along the ribbon direction. As shown in Fig. 4d, an absorption peak emerges as the temperature decreases below TC1, while only Drude response is observed at higher temperature. The frequency of the absorption peak is 2180 cm−1 (270 meV) and the peak width is ~1000 cm−1 (124 meV) at 15 K, as determined from a Lorentz fitting (see Supplementary Fig. 5). Meanwhile, the spectral weight of Drude response at this spectral range is suppressed and shifts to lower frequency range26, which is a typical consequence of opening a partial gap34. Based on the above analysis, we attribute the excitation peak to the opening of a partial CDW gap, whose size is comparable to that of bulk TaSe2, which is 150–250 meV determined by different techniques such as infrared reflection spectroscopy26,27,35, angle-resolved photoemission spectroscopy (ARPES)36,37,38,39, and scanning tunneling microscopy (STM)40. Furthermore, our electrical transport measurements on a TaSe2 thin film also corroborate the appearance of CDW phase transition: the slope of the resistivity changes at TC1 = 122 K as illustrated in the inset of Fig. 4d. Note that the CDW order preserves for monolayer and few-layer metallic TMDCs41,42, and for flakes thicker than 10 nm the phase transition temperature remains almost the same as that of the bulk43, which is the case in our study. For 2H-NbSe2, no clear CDW excitation is observed in previous reflection measurements28, presumably due to the competition between the superconductivity (TS = 7.2 K) and CDW orders (TC = 33 K)16,17. This is consistent with our measurements on the intrinsic optical response of 2H-NbSe2, as detailed in Supplementary note 7.
After identification of the CDW excitation, now we can attribute the anomalous plasmon behavior to the coupling between plasmonic and CDW excitations, since the plasmon frequency is in the vicinity of the CDW resonance frequency. A phenomenological coupled-oscillator model is applied to describe the interplay between them44 (more details are presented in Supplementary note 8). The optical conductivity of the plasmon resonance coupled with a CDW excitation can be expressed as follows:
Here ω1, ω2, γ1, γ2 correspond to the frequencies and the damping rates of oscillator 1 and 2 respectively, and Ω is the coupling rate between the two oscillators. Oscillator 1 represents the TaSe2 plasmonic excitation, which can be directly excited by the driving electric field \(E(t) = E_0{\mathrm{{e}}}^{ - {\mathrm{{i}}}\omega t}\), while oscillator 2 represents the CDW excitation. The CDW excitation is much weaker than the plasmonic excitation (see Supplementary Fig. 5), hence we treat it as a quasi “dark” mode in the model, which can be excited only indirectly through the coupling with the bright plasmon mode45.
The first-order plasmon of TaSe2 below TC1 is fitted by Eq. (3). While for simplicity, the second-order plasmon is still fitted by the uncoupled oscillator model as shown in Eq. (5), because it is relatively weak and far away from the frequency of the CDW excitation. Figure 4e shows the temperature evolution of the peak width of TaSe2 and NbSe2 plasmons (W = 700 nm). Above TC1, the peak width of the first-order TaSe2 plasmons decreases from 1500 cm−1 (300 K) to 1280 cm−1 (120 K). However, when the temperature drops below TC1, the linewidth of the plasmon peak increases as the temperature decreases and eventually reaches 1620 cm−1 at 15 K, in sharp contrast to the behavior of NbSe2 plasmons. The temperature dependence of the peak width of 2H-TaSe2 plasmons deviates from that of its Drude scattering rate, which continually reduces as the temperature decreases26.
To reveal the coupling effect further, we fabricated multiple plasmonic devices with plasmon resonance frequency sweeping across the CDW excitation (sample T4, W = 900–400 nm, d = 20 nm). Figure 5a shows the extinction spectra of them at 120 and 15 K. The detailed temperature evolution of the plasmon peak is displayed in Supplementary Fig. 5. For extinction spectra at 15 K, as ribbon width decreases, the shape of the resonance peak continuously evolves due to the coupling to the CDW excitation. More prominent coupling effect is observed when the frequency of the plasmon and the CDW excitation is closer, such as the plasmonic devices with ribbon width of 800–600 nm. When the plasmon frequency is away from the CDW excitation, the broadening and asymmetry of plasmon peaks are less pronounced. The coupling effect becomes negligible at the far-IR region (see Supplementary Fig. 1), where the plasmon peak continually sharpens as the temperature drops, similar to that of 2H-NbSe2 in uncoupled situations.
a The extinction spectra of TaSe2 plasmons with ribbon width of 900–400 nm. The blue dashed and the gray solid lines correspond to the measured spectra at 120 and 15 K, respectively. The colored lines represent the fitted spectra at 15 K by the coupled-oscillator model. P1 and P2 denote the first-order and the second-order plasmons, respectively. b A sketch for the coupling effect in a prototype three-level system. The gray, orange, and green solid lines illustrate the energy level of the ground state \(\left| 0 \right\rangle\), the bright excited state \(\left| 1 \right\rangle\), and the dark state \(\left| 2 \right\rangle\), respectively. The gray arrow denotes transition 1 (\(\left| 0 \right\rangle \to \left| 1 \right\rangle\)) with frequency of ω1. The gray dashed line is plotted to define the energy detuning \(\delta = \omega _1 - \omega _2\), where ω2 is the transition frequency between state \(\left| 2 \right\rangle\) and \(\left| 0 \right\rangle\). The red arrows near the state \(\left| 1 \right\rangle\) and \(\left| 2 \right\rangle\) represent the damping rates of the corresponding transitions, which are γ1 and γ2, respectively. The black arrow defines the coupling rate Ω between state \(\left| 1 \right\rangle\) and \(\left| 2 \right\rangle\). The left inset illustrates the modulation of charge density (ρ) and ion positions (x) in the CDW phase. The right inset denotes the positive (orange circle) and negative charge (green circle) in the ribbon when the localized plasmon is excited. c The fitted damping/coupling rates as a function of energy detuning (the unit is wave number) at 15 K. The uncoupled plasmon damping rate γ1 is estimated by the extrapolation from the temperature evolution of the plasmon peak width above TC1, which generally follows linear relations (see Supplementary Fig. 5).
Discussion
Depending on the coupling strength, the coupling effects between plasmons and other excitations can behave in different forms such as Purcell effect46, Fano resonance47,48, plasmonic analog of electromagnetically induced transparency (EIT)45,49,50,51,52,53, and Rabi splitting54,55,56,57,58. The coupling between two subsystems can enhance light–matter interactions and play an important role in applications, such as nanolasers59, sensors60, and quantum information processing61. The coupling effect between TaSe2 plasmonic and CDW excitations is originated from the interference effect between two different excitation pathways. Figure 5b shows the scheme for the coupling effect in a prototype three-level system. The transition between the energy level \(\left| 1 \right\rangle\) and \(\left| 0 \right\rangle\) with resonance frequency ω1 can be directly excited, which corresponds to the plasmon excitation. Whereas the transition between energy level \(\left| 2 \right\rangle\) and \(\left| 0 \right\rangle\) is forbidden or extremely weak, which represents the quasi-“dark” CDW excitation45. The energy detuning between the two transitions is \(\delta = \omega _1 - \omega _2\). There are two different excitation pathways contributing to the occupation of the energy level \(\left| 1 \right\rangle\), i.e., \(\left| 0 \right\rangle \to \left| 1 \right\rangle\) and \(\left| 0 \right\rangle \to \left| 1 \right\rangle \to \left| 2 \right\rangle \to \left| 1 \right\rangle\). The two excitation pathways interfere with each other, leading to a modification of the extinction spectrum. The fitted frequencies of the plasmonic (ω1) and the CDW excitations (ω2) as a function of wave vectors (sample T4, W = 900–400 nm, d = 20 nm, T = 15 K) are depicted in Supplementary Fig. 8b. Generally, their dispersions are approximately close to those in uncoupled situations. Figure 5c presents the damping/coupling rates fitted by the coupled-oscillator model as a function of energy detuning. The plasmon damping rate γ1 is enhanced compared to the uncoupled conditions. Meanwhile, the damping rate of the CDW excitation γ2 is also enhanced from 1000 cm−1 in the uncoupled case to 1300–1400 cm−1. The coupling rate Ω increases as the energy detuning increases from negative to positive. It presumably suggests an increase of the effective density of CDW excitations62 coupled to the plasmonic field as the size of nanostructures decreases.
The minimal energy detuning is realized for the plasmonic device with ribbon width of 700 nm. In that case, γ1, γ2, and Ω are 1618, 1375, and 1114 cm−1, respectively. With these parameters in hand, we can make a comparison between the coupling effect in 2H-TaSe2 and two typical coupling phenomena in plasmonic systems. The first is the classical analog of EIT45,49,50,51. In plasmonic EIT systems, the damping rate of the dark mode γ2 is significantly smaller than that of the bright mode γ1, such as the non-radiative quadrupole mode versus radiative dipole mode in metamaterials45,49,50 and the plasmon–phonon coupled systems51,52. In our case, γ2 of the quasi-“dark” CDW excitation is comparatively large. Consequently, only modification of the lineshape instead of a sharp dip is observed in extinction spectra. However, if we can effectively reduce γ2, a dip can emerge, as simulated in Supplementary Fig. 8. It implies that the coupling effects in TaSe2 and EIT plasmonic systems share the same physics origin. The second is the strong Rabi splitting in exciton–plasmon systems55,56,57,58. In those systems, the coupling rate Ω is larger than the damping rates of the two excitations, which results in the formation of half-matter, half-light exciton–plasmon polaritons. Meanwhile, the hybridized polariton dispersion typically exhibits pronounced anti-crossing behavior, with large splitting in the dispersion intersection area. Here, the coupling rate Ω between TaSe2 plasmonic and CDW excitations is less than their damping rates and no clear anti-crossing scenario can be observed.
In light of the coupling effects, plasmons can be utilized in probing and manipulating other polaritons like excitons63,64, phonons51,52, excitations in correlated materials65, and non-local quantum response of neighboring metals66. However, the coupling effect in 2H-TaSe2 have something unique. Plasmonic and CDW excitations are both internal excitations, while in many other coupled plasmonic systems, the coupling depends on excitations in different materials or structures, such as excitons in semiconductor layers and plasmons in metal nanostructures55,56,57,58. Therefore, TaSe2 plasmons can in return effectively manifest its intrinsic excitations. Once the plasmon peak becomes damped or asymmetric, it indicates there might exist intrinsic excitations at nearby frequency. This can open an avenue in probing weak excitations in other phase transition or correlated systems67.
In summary, we experimentally demonstrated plasmons in 2H-TaSe2 thin films, which covers a broad spectral range from the terahertz to the near-infrared region. The plasmon dispersion flattens at large wave vectors due to the screening of interband transitions. TaSe2 plasmons are tunable by varying the film thickness and dielectric environments. In addition, the coupling effect between TaSe2 plasmonic and CDW excitations is observed. The interplay between them is well interpreted by the coupled-oscillator model. 2H-TaSe2, along with other metallic TMDCs, has been demonstrated as a competitive building block in photonics. Our study can stimulate further endeavors on the plasmon in atomically thin TMDCs, given that the CDW phase transition temperature of monolayer and few-layer metallic TMDCs are dramatically different than that of their relatively thick or bulk counterparts41. Moreover, large-scale atomically thin TMDCs are available from controllable synthesis by chemical vapor deposition (CVD)68,69 or molecular beam epitaxy (MBE)42 methods, which can render more tunabilities such as electrical gating1 or chemical doping5.
Methods
Sample preparation and nanofabrication
The bulk single crystals of 2H-TaSe2 were grown by a chemical vapor transport (CVT) method18. The 2H-NbSe2 single crystals were bought from 2D Semiconductors Inc. We checked the crystal quality by Raman spectroscopy41,70 (see Supplementary Fig. 9). The thin films were mechanically exfoliated onto polydimethylsiloxane (PDMS) substrates from bulk crystals and then transferred to diamond or other substrates11. Diamond substrates are used in this work unless otherwise stated. The film thickness was determined by a stylus profiler (Bruker DektakXT). The lateral size of one thin film with uniform thickness is at most 200–300 μm. For mid-infrared (mid-IR) measurements, we can fabricate 6–12 plasmonic arrays with different ribbon widths in one homogeneous thin film. As such, the thickness uncertainty can be excluded in the determination of the plasmon dispersion. For far-IR measurements, one thin film is only large enough for one plasmonic array, because the beam size of the focused far-IR light is larger. We used electron beam lithography and reactive ion etching (the reaction gas is CF4) to fabricate ribbon arrays. Scanning electron microscope (Zeiss Sigma SEM) was used to finally determine the ribbon width. In general, the lateral etching is on the same order of magnitude of film thickness. No notable oxidation and degradation were found during the process of device fabrications and optical measurements, for the relatively thick TMDC films studied in this work (see Supplementary Fig. 10).
Optical measurements and the fitting of extinction spectra
We used a Bruker FTIR spectrometer (Bruker Vertex 70v) in conjunction with a Hyperion 2000 microscope to measure the extinction spectra. The incident light was focused on samples with a ×15 IR objective. A liquid-nitrogen-cooled Mercury–Cadmium–Telluride (MCT) detector and a ZnSe grid polarizer were used for mid-IR measurements, while a liquid-helium-cooled silicon bolometer and a terahertz polarizer were applied in far-IR measurements. The low-temperature measurements were carried out with a helium-flow cryostat (Janis Research ST-300).
The relation between the extinction spectrum and the sheet optical conductivity \(\sigma (\omega )\) is given by5
where Z0 is the vacuum impedance, nsub is the refractive index of the substrate, which is 2.38 for diamond substrates in the mid-IR range (1.46 for BaF2 and 3.44 for Si substrates), and ω is the light frequency. The optical conductivity contributed from the plasmon (without coupling to other excitations, such as CDW) is5
where Sp, ωp, and γp are the spectral weight, the frequency, and the damping rate of plasmon resonance, respectively, and f is the filling factor (the area of nanoribbons/all areas). The designed filling factor of our plasmonic devices is 0.4–0.5, but the lateral etching in fabrication process usually reduces the actual filling factor. Therefore, it is determined by the real ribbon width measured by SEM.
Electrical transport measurements
The TaSe2 and NbSe2 flakes were mechanically exfoliated onto Si/SiO2 substrates. The electrical devices were fabricated by electron-beam lithography technique and wet-etched by standard buffered HF solution for 5 s in the electrode regime. We deposited 5 nm-thick Cr and 80 nm-thick Au electrodes using magnetic sputtering. Four-terminal temperature-dependent transport measurements were carried out in a physical property measurement system (PPMS, Quantum Design) which achieved a base temperature of 1.8 K, in conjunction with lock-in amplifiers (SR830).
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
References
Ju, L. et al. Graphene plasmonics for tunable terahertz metamaterials. Nat. Nanotechnol. 6, 630–634 (2011).
Chen, J. et al. Optical nano-imaging of gate-tunable graphene plasmons. Nature 487, 77–81 (2012).
Fei, Z. et al. Gate-tuning of graphene plasmons revealed by infrared nano-imaging. Nature 487, 82–85 (2012).
Grigorenko, A. N., Polini, M. & Novoselov, K. S. Graphene plasmonics. Nat. Photonics 6, 749–758 (2012).
Yan, H. et al. Tunable infrared plasmonic devices using graphene/insulator stacks. Nat. Nanotechnol. 7, 330–334 (2012).
Yan, H. et al. Damping pathways of mid-infrared plasmons in graphene nanostructures. Nat. Photonics 7, 394–399 (2013).
Brar, V. W., Jang, M. S., Sherrott, M., Lopez, J. J. & Atwater, H. A. Highly confined tunable mid-infrared plasmonics in graphene nanoresonators. Nano Lett. 13, 2541–2547 (2013).
Di Pietro, P. et al. Observation of Dirac plasmons in a topological insulator. Nat. Nanotechnol. 8, 556–560 (2013).
Low, T. et al. Polaritons in layered two-dimensional materials. Nat. Mater. 16, 182–194 (2017).
Gjerding, M. N., Pandey, M. & Thygesen, K. S. Band structure engineered layered metals for low-loss plasmonics. Nat. Commun. 8, 15133 (2017).
Wang, C. et al. Van der Waals thin films of WTe2 for natural hyperbolic plasmonic surfaces. Nat. Commun. 11, 1158 (2020).
Stern, F. Polarizability of a two-dimensional electron gas. Phys. Rev. Lett. 18, 546–548 (1967).
Cudazzo, P., Gatti, M. & Rubio, A. Local-field effects on the plasmon dispersion of two-dimensional transition metal dichalcogenides. New J. Phys. 15, 125005 (2013).
Andersen, K. & Thygesen, K. S. Plasmons in metallic monolayer and bilayer transition metal dichalcogenides. Phys. Rev. B 88, 155128 (2013).
da Jornada, F. H., Xian, L., Rubio, A. & Louie, S. G. Universal slow plasmons and giant field enhancement in atomically thin quasi-two-dimensional metals. Nat. Commun. 11, 1013 (2020).
Wilson, J. A., Disalvo, F. J. & Mahajan, S. Charge-density waves and superlattices in the metallic layered transition metal dichalcogenides. Adv. Phys. 24, 117–201 (1975).
Naito, M. & Tanaka, S. Electrical transport properties in 2H-NbS2, -NbSe2, -TaS2 and -TaSe2. J. Phys. Soc. Jpn. 51, 219–227 (1982).
Schuster, R., Kraus, R., Knupfer, M., Berger, H. & Büchner, B. Negative plasmon dispersion in the transition-metal dichalcogenide 2H-TaSe2. Phys. Rev. B 79, 045134 (2009).
van Wezel, J. et al. Effect of charge order on the plasmon dispersion in transition-metal dichalcogenides. Phys. Rev. Lett. 107, 176404 (2011).
König, A. et al. Plasmon evolution and charge-density wave suppression in potassium intercalated 2H-TaSe2. Europhys. Lett. 100, 27002 (2012).
König, A., Schuster, R., Knupfer, M., Büchner, B. & Berger, H. Doping dependence of the plasmon dispersion in 2H-TaSe2. Phys. Rev. B 87, 195119 (2013).
Cudazzo, P., Gatti, M. & Rubio, A. Plasmon dispersion in layered transition-metal dichalcogenides. Phys. Rev. B 86, 075121 (2012).
Faraggi, M. N., Arnau, A. & Silkin, V. M. Role of band structure and local-field effects in the low-energy collective electronic excitation spectra of 2H-NbSe2. Phys. Rev. B 86, 035115 (2012).
Müller, E. et al. Doping dependent plasmon dispersion in 2H-transition metal dichalcogenides. Phys. Rev. B 94, 035110 (2016).
Maniyara, R. A. et al. Tunable plasmons in ultrathin metal films. Nat. Photonics 13, 328–333 (2019).
Vescoli, V., Degiorgi, L., Berger, H. & Forró, L. Dynamics of correlated two-dimensional materials: the 2H-TaSe2 case. Phys. Rev. Lett. 81, 453–456 (1998).
Ruzicka, B., Degiorgi, L., Berger, H., Gaál, R. & Forró, L. Charge dynamics of 2H-TaSe2 along the less-conducting c-axis. Phys. Rev. Lett. 86, 4136–4139 (2001).
Dordevic, S. V., Basov, D. N., Dynes, R. C. & Bucher, E. Anisotropic electrodynamics of layered metal 2H-NbSe2. Phys. Rev. B 64, 161103 (2001).
Keldysh, L. V. Coulomb interaction in thin semiconductor and semimetal films. JETP Lett. 29, 658–661 (1979).
Gusikhin, P. A., Muravev, V. M., Zagitova, A. A. & Kukushkin, I. V. Drastic reduction of plasmon damping in two-dimensional electron disks. Phys. Rev. Lett. 121, 176804 (2018).
Oriekhov, D. O. & Levitov, L. S. Plasmon resonances and tachyon ghost modes in highly conducting sheets. Phys. Rev. B 101, 6 (2020).
Allen, S. J., Störmer, H. L. & Hwang, J. C. M. Dimensional resonance of the two-dimensional electron gas in selectively doped GaAs/AlGaAs heterostructures. Phys. Rev. B 28, 4875–4877 (1983).
Leavitt, R. P. & Little, J. W. Absorption and emission of radiation by plasmons in two-dimensional electron-gas disks. Phys. Rev. B 34, 2450–2457 (1986).
Hu, W. Z. et al. Optical study of the charge-density-wave mechanism in 2H-TaS2 and 2H-NaxTaS2. Phys. Rev. B 76, 045103 (2007).
Barker, A. S., Ditzenberger, J. A. & DiSalvo, F. J. Infrared study of the electronic instabilities in tantalum disulfide and tantalum diselenide. Phys. Rev. B 12, 2049–2054 (1975).
Valla, T. et al. Charge-density-wave-induced modifications to the quasiparticle self-energy in 2H-TaSe2. Phys. Rev. Lett. 85, 4759–4762 (2000).
Rossnagel, K., Rotenberg, E., Koh, H., Smith, N. V. & Kipp, L. Fermi surface, charge-density-wave gap, and kinks in 2H-TaSe2. Phys. Rev. B 72, 121103 (2005).
Borisenko, S. V. et al. Pseudogap and charge density waves in two dimensions. Phys. Rev. Lett. 100, 196402 (2008).
Li, Y. W. et al. Folded superstructure and degeneracy-enhanced band gap in the weak-coupling charge density wave system 2H-TaSe2. Phys. Rev. B 97, 115118 (2018).
Wang, C., Giambattista, B., Slough, C. G., Coleman, R. V. & Subramanian, M. A. Energy gaps measured by scanning tunneling microscopy. Phys. Rev. B 42, 8890–8906 (1990).
Xi, X. et al. Strongly enhanced charge-density-wave order in monolayer NbSe2. Nat. Nanotechnol. 10, 765–769 (2015).
Ryu, H. et al. Persistent charge-density-wave order in single-layer TaSe2. Nano Lett. 18, 689–694 (2018).
Wu, Y. et al. Dimensional reduction and ionic gating induced enhancement of superconductivity in atomically thin crystals of 2H-TaSe2. Nanotechnology 30, 035702 (2018).
Alzar, C. L. G., Martinez, M. A. G. & Nussenzveig, P. Classical analog of electromagnetically induced transparency. Am. J. Phys. 70, 37–41 (2002).
Liu, N. et al. Plasmonic analogue of electromagnetically induced transparency at the Drude damping limit. Nat. Mater. 8, 758–762 (2009).
Pelton, M. Modified spontaneous emission in nanophotonic structures. Nat. Photonics 9, 427–435 (2015).
Luk’yanchuk, B. et al. The Fano resonance in plasmonic nanostructures and metamaterials. Nat. Mater. 9, 707–715 (2010).
Limonov, M. F., Rybin, M. V., Poddubny, A. N. & Kivshar, Y. S. Fano resonances in photonics. Nat. Photonics 11, 543–554 (2017).
Gu, J. et al. Active control of electromagnetically induced transparency analogue in terahertz metamaterials. Nat. Commun. 3, 1151 (2012).
Yang, Y. M., Kravchenko, I. I., Briggs, D. P. & Valentine, J. All-dielectric metasurface analogue of electromagnetically induced transparency. Nat. Commun. 5, 5753 (2014).
Yan, H., Low, T., Guinea, F., Xia, F. & Avouris, P. Tunable phonon-induced transparency in bilayer graphene nanoribbons. Nano Lett. 14, 4581–4586 (2014).
Brar, V. W. et al. Hybrid surface-phonon-plasmon polariton modes in graphene/monolayer h-BN heterostructures. Nano Lett. 14, 3876–3880 (2014).
Pelton, M., Storm, S. D. & Leng, H. Strong coupling of emitters to single plasmonic nanoparticles: exciton-induced transparency and Rabi splitting. Nanoscale 11, 14540–14552 (2019).
Törmä, P. & Barnes, W. L. Strong coupling between surface plasmon polaritons and emitters: a review. Rep. Prog. Phys. 78, 013901 (2014).
Liu, X. et al. Strong light–matter coupling in two-dimensional atomic crystals. Nat. Photonics 9, 30–34 (2015).
Wen, J. et al. Room-temperature strong light–matter interaction with active control in single plasmonic nanorod coupled with two-dimensional atomic crystals. Nano Lett. 17, 4689–4697 (2017).
Zheng, D. et al. Manipulating coherent plasmon–exciton interaction in a single silver nanorod on monolayer WSe2. Nano Lett. 17, 3809–3814 (2017).
Stührenberg, M. et al. Strong light–matter coupling between plasmons in individual gold bi-pyramids and excitons in mono- and multilayer WSe2. Nano Lett. 18, 5938–5945 (2018).
Ye, Y. et al. Monolayer excitonic laser. Nat. Photonics 9, 733–737 (2015).
Krivenkov, V., Goncharov, S., Nabiev, I. & Rakovich, Y. P. Induced transparency in plasmon–exciton nanostructures for sensing applications. Laser Photonics Rev. 13, 1800176 (2019).
Sillanpää, M. A., Park, J. I. & Simmonds, R. W. Coherent quantum state storage and transfer between two phase qubits via a resonant cavity. Nature 449, 438–442 (2007).
Tserkezis, C. et al. On the applicability of quantum-optical concepts in strong-coupling nanophotonics. Rep. Prog. Phys. 83, 082401 (2020).
Lo, T. W. et al. Thermal redistribution of exciton population in monolayer transition metal dichalcogenides probed with plasmon–exciton coupling spectroscopy. ACS Photonics 6, 411–421 (2019).
Qi, X. et al. Effects of gap thickness and emitter location on the photoluminescence enhancement of monolayer MoS2 in a plasmonic nanoparticle-film coupled system. Nanophotonics 9, 2097–2105 (2020).
Costa, A. T. et al. Harnessing ultra-confined graphene plasmons to probe the electrodynamics of superconductors. Preprint at https://arxiv.org/abs/2006.00748 (2020).
Gonçalves, P. A. D. et al. Quantum surface-response of metals revealed by acoustic graphene plasmons. Preprint at https://arxiv.org/abs/2008.07613 (2020).
Basov, D. N., Averitt, R. D., van der Marel, D., Dressel, M. & Haule, K. Electrodynamics of correlated electron materials. Rev. Mod. Phys. 83, 471–541 (2011).
Shi, J. P. et al. Chemical vapor deposition grown wafer-scale 2D tantalum diselenide with robust charge-density-wave order. Adv. Mater. 30, 1804616 (2018).
Zhou, J. et al. A library of atomically thin metal chalcogenides. Nature 556, 355–359 (2018).
Hajiyev, P., Cong, C., Qiu, C. & Yu, T. Contrast and Raman spectroscopy study of single- and few-layered charge density wave material: 2H-TaSe2. Sci. Rep. 3, 2593 (2013).
Acknowledgements
H.Y. is grateful to the financial support from the National Key Research and Development Program of China (Grant Nos. 2016YFA0203900 and 2017YFA0303504), the National Natural Science Foundation of China (Grant Nos. 12074085 and 11734007), the Natural Science Foundation of Shanghai (Grant No. 20JC1414601) and the Strategic Priority Research Program of Chinese Academy of Sciences (No. XDB30000000). F.X. is grateful to the financial support from the National Natural Science Foundation of China (Grant Nos. 11934005, 61322407 and 11874116), the Science and Technology Commission of Shanghai (Grant No. 19511120500) and the Program of Shanghai Academic/Technology Research Leader (Grant No. 20XD1400200). X.Y. acknowledges the financial support from the Science and Technology Commission of Shanghai (Grant Nos. 20YF1411700 and 20520710900). C.W. is grateful to the financial support from the National Natural Science Foundation of China (Grant No. 11704075). The authors thank L.J. Wang, W. Li, Z.Z. Sun and J.M. Luo for the help in experiments. Part of the experimental work was carried out in Fudan Nanofabrication Lab.
Author information
Authors and Affiliations
Contributions
H.Y. conceived the research. C.S. performed sample preparation, optical measurements and data analysis with assistance from S.H., Q.X., C.W., Y.X., Y.L., F.W., L.M., and J.Z.; F.X., X.Y., and C.Z. grew and characterized the bulk single crystals of 2H-TaSe2; C.H. performed electrical measurements; H.Y. and C.S. cowrote the paper; all authors commented on the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Song, C., Yuan, X., Huang, C. et al. Plasmons in the van der Waals charge-density-wave material 2H-TaSe2. Nat Commun 12, 386 (2021). https://doi.org/10.1038/s41467-020-20720-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-20720-0
This article is cited by
-
Vanadium Dichalcogenides Triangular Nanoflakes: A Comparative Study of Optical and Electronic Properties
Plasmonics (2024)
-
Molecular beam epitaxy growth of topological insulator Bi4Br4 on silicon for the infrared applications
Quantum Frontiers (2024)
-
Detection of tuberculosis using palladium -tantalum diselenide (Pd-TaSe2) bases SPR biosensor
Journal of Optics (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.