Abstract
Density-functional theory (DFT) is a rigorous and (in principle) exact framework for the description of the ground state properties of atoms, molecules and solids based on their electron density. While computationally efficient density-functional approximations (DFAs) have become essential tools in computational chemistry, their (semi-)local treatment of electron correlation has a number of well-known pathologies, e.g. related to electron self-interaction. Here, we present a type of machine-learning (ML) based DFA (termed Kernel Density Functional Approximation, KDFA) that is pure, non-local and transferable, and can be efficiently trained with fully quantitative reference methods. The functionals retain the mean-field computational cost of common DFAs and are shown to be applicable to non-covalent, ionic and covalent interactions, as well as across different system sizes. We demonstrate their remarkable possibilities by computing the free energy surface for the protonated water dimer at hitherto unfeasible gold-standard coupled cluster quality on a single commodity workstation.
Similar content being viewed by others
Introduction
In their seminal 1964 paper, Hohenberg and Kohn proved that there exists a universal functional F[ρ] of the electron density ρ, that captures all electronic contributions to the total energy of a system of interacting electrons1. This universal functional has since become something of a holy grail for chemistry, physics, and materials science, as its knowledge would allow determining the exact ground-state energy and electron density for any molecule or solid2. Unfortunately, the concrete form of F[ρ] itself has remained elusive. Indeed, it has been shown that the universal functional likely has the same prohibitive computational complexity as solving the Schrödinger equation directly3.
Nevertheless, Hohenberg and Kohn’s density functional theory (DFT) has become an essential method in the toolkits of computational chemistry, condensed matter physics, or surface science. This is mostly owing to the formulation of Kohn and Sham (KS), which reduces the problem to finding a density functional Exc[ρ] for electronic exchange and correlation4. Again, the exact form of Exc[ρ] is unknown, but many useful density functional approximations (DFAs) exist, which are generally considered to offer a good trade-off between computational complexity and accuracy.
The large zoo of DFAs that has been developed over the years is often organized in the hierarchy of Jacob’s ladder, where approximations are grouped according to the ingredients that are used in their functional form5. At the lower rungs of this ladder, (semi-)local DFAs are found, which only require information about the local density and its derivatives. Such functionals are sometimes called pure, because they can be computed from the electron density alone. At higher-rungs, information about the occupied and/or unoccupied KS orbitals is also included6,7,8. These so-called (double) hybrid DFAs are therefore no longer pure in the sense described above. This increases their computational complexity, but also makes them more accurate, because they incorporate non-local information.
In spite of their known limitations (e.g., regarding electron self-interaction)9, the pure functionals at the bottom of Jacob’s latter are a widely used state-of-the-art, e.g., in practical calculations of large systems or with extensive sampling. This reveals a crucial dilemma of Jacob’s ladder, namely that very often it is not possible to use a higher-rung functional due to computational constraints, even if the nature of the system of interest would in principle require a more accurate description.
Recently, machine-learning (ML)-based DFAs have been shown to break the constraints of Jacob’s ladder, offering highly accurate, pure, and non-local density functionals for different one-dimensional model systems10,11,12,13. Although these approaches show that it is possible to learn the highly non-linear mapping from the electron density to the energy from data, they cannot be directly transferred to real systems. A straightforward real-space representation of the electron density (e.g., on a grid) is extremely inefficient in three dimensions. Even for a small molecule, a single reference energy value would have to be fitted as a function of on the order of one hundred thousand input values. Furthermore, grid-based models are not in general size-extensive, particularly if they require the grid to be of constant size. Very recently, Burke and co-workers developed ML-based DFT models, which represent the density in a plane-wave basis14,15. These models have successfully been applied to real molecules, though they are still not size-extensive.
These issues can be circumvented if the reference energy is projected onto the grid in the form of an energy density16,17,18. This brings the number of target values to the same order of magnitude as the number of input values, leading to a much better defined fitting problem. On the other hand, this also makes the resulting ML-DFAs more like the traditional functionals in Jacob’s ladder. For instance, if a semilocal Ansatz is chosen to fit a reference energy density, the resulting functional will display electron self-interaction, even if the reference method does not17. Developing correlation functionals in this manner is particularly challenging. Correlation energy densities based on high-level wavefunction methods can, e.g., display significant positive values at the centers of stretched bonds, where the electron density is vanishingly small19.
In this paper, we therefore propose a new route to pure ML-based DFAs, using a density-fitting representation of the electron density. This representation is much more compact than a real-space grid, and allows decomposing the density into atomic contributions. As a consequence, the presented ML-DFAs can readily be applied to real molecules and are by construction size-extensive. At the same time, any reference method can be used for training without the need for real-space projection or energy decomposition.
Results
Density representation
In KS-DFT, the electron density is computed from the occupied KS orbitals ψi(r). These are in turn expanded as a linear combination of basis functions χμ(r):
with the density matrix elements Dμν. A noteworthy aspect of eq. (1) is that the density is expanded in terms of products of basis functions, which are not in general atom-centered, even if the basis functions themselves are (see Fig. 1, left). This leads to the appearance of memory intensive four-index integrals in the computation of Coulomb and exchange contributions to the KS matrix.
Left: In a conventional Kohn–Sham DFT calculation, the electron density (solid black line) is expanded in terms of density matrix elements Dμν and products of basis functions χμχν. Right: Density-fitting (DF) allows expanding the density in terms of fitting coefficients \({C}_{Q}^{A}\) and atom-centered basis functions ϕQ (dotted black line). The DF expansion can unambiguously be decomposed into atomic contributions. Note that higher angular momentum functions are needed in the DF basis to correctly describe the overlap region between the atoms. This is illustrated in the schematic figure by the use of only s-type basis functions for the Kohn–Sham expansion and s- and p-type basis functions for the DF expansion.
In many electronic structure codes it is therefore common practice to use additional density-fitting (DF) basis functions ϕQ(r − rA), which allow an atom-centered expansion of the density (see Supplementary Note 1):
Here, the first sum is over all atoms A, and \({C}_{Q}^{A}\) is the expansion coefficient of basis function Q on atom A. Unlike eq. (1), the DF expansion can readily (and unambiguously) be decomposed into atomic densities ρA (see Fig. 1, right)20,21.
It should be noted that the accurate DF representation of ρ(r) requires significantly larger basis sets than those used for the expansion of the KS orbitals. Nonetheless, the density can typically be precisely represented with the knowledge of ca. 100 coefficients per atom and a set of DF basis functions that only depend on the element of the atom. This is in contrast to eq. (1), where the product basis is dependent on the geometry (i.e. on the relative position of pairs of atoms) of the molecule in question.
The DF basis thus offers a highly compressed and transferable representation of ρ, both of which are desirable properties for ML. However, there is also a significant downside to this representation, namely that the coefficients \({C}_{Q}^{A}\) are not in general rotationally invariant. In other words, rotating a molecule and its density will lead to a different set of coefficients \({C}_{Q}^{A}\), even though the target energy remains unchanged. Although this invariance could in principle be learned from data, this would require significantly more training data and only lead to an approximately invariant model.
This issue can be circumvented by borrowing a trick from the Smooth Overlap of Atomic Positions (SOAP) representation of atomic environments22: Instead of using the coefficients directly, we use their rotationally invariant power spectrum pA (see Supplementary Note 2), which has the added benefit of further compressing the representation. In the following, we will refer to this as the rotationally invariant density representation (RIDR).
Correlation functionals from ML
We can now proceed to construct a ML-DFA based on the RIDR. Herein, we will focus on learning correlation energy functionals from calculated Hartree-Fock (HF) densities. Although exchange is treated exactly within HF, the combination of full HF exchange with conventional pure DFT correlation functionals leads to poor results23. This is because the non-local exchange in HF is incompatible with (semi-)local correlation5. We therefore train our model on non-local correlation energies obtained from many-body wavefunction methods. Specifically, we will consider second-order Møller-Plesset theory (MP2) and gold-standard Coupled Cluster theory with single, double, and perturbative triple excitations (CCSD(T)), to illustrate the approach for both an efficient and a fully quantitative treatment of electron correlation, respectively24,25,26. In addition to being non-local, both these methods also provide much improved fractional charge behavior, overcoming one of the main pathologies of conventional DFAs9,27,28,29.
Because wavefunction-based reference calculations are computationally expensive, it is critical to choose an ML approach that is as data-efficient as possible. In chemistry applications, Kernel Ridge Regression (KRR) has been found to be a good choice in this respect30,31,32,33. We can write a generic KRR correlation functional as:
where the sum runs over N training densities, αi are regression coefficients and K(ρ, ρi) is a kernel function that measures the similarity between the target and training densities. To ensure size-extensivity of the functional, we construct K(ρ, ρi) from the atomic densities provided by the DF representation (see eq. (2)):
Now a kernel k(ρA, ρB) that measures the similarity of atomic densities can be defined using the RIDR. A wide range of kernel functions are possible, but we found that a simple polynomial Ansatz (as used for the SOAP kernel) already displays very promising performance, as discussed below:
Having defined the kernel function, the regression coefficients αi (in eq. (3)) can be determined in closed form, for a given training set (see Supplementary Note 3). In the following these functionals are referred to as kernel density functional approximations (KDFA).
Performance and applications
KDFAs need to be trained on data, and are consequently always to some extent system specific. Nonetheless, a useful ML-DFA methodology should be general in the sense that it can easily be trained for different chemistries and system sizes34. Herein, three types of systems are considered, namely water clusters, microsolvated protons and linear alkanes of different sizes. In all cases, training and test structures are randomly drawn from molecular dynamics (MD) simulations at 350 K (see Methods section for details). For this part, we will concentrate on the results obtained with MP2 reference data. As also further commented below, CCSD(T) energies can be learned with the same accuracy and a full account of these results is provided in the SI.
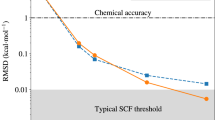
In Fig. 2, learning curves of ML correlation functionals for the three types of systems are shown. In all cases, mean absolute errors (MAEs) below 25 meV (roughly corresponding to kBT at 300 K) are reached with 100 training examples. Indeed, in many cases so-called chemical accuracy (1 kcal mol−1 ≈ 43 meV) is already achieved with only 10 training structures. Within each class, the MAEs generally increase for larger systems. However, the errors for pure and protonated water clusters with three and four molecules are nearly identical. This is readily understood, as the intermolecular interactions are approximately additive in these systems. In contrast, the interactions in longer alkane chains are harder to learn, e.g., owing to more pronounced interactions between the molecular termini in butane (C4H10) than in propane (C3H8).
Shown is the mean absolute error (MAE) vs number of training densities (Ntrain) for the correlation energy in water clusters (left), protonated water clusters (center) and alkane configurations (right). For reference, the dashed line denotes an error of 1 kcal mol−1 ≈ 43 meV and the dash-dotted one an error of kBT ≈ 25 meV (at 300 K).
Overall, these results show that highly accurate, non-local correlation functionals can be learned from easily tractable reference data sets. In fact, the similarity of the learning curves obtained for the three systems suggests that high-level energies for a large ensemble of configurations can already be obtained with only 10–100 reference calculations. In many applications, even such a limited number of high-level reference calculations may not be feasible, however, owing to the prohibitive scaling of wavefunction methods with system size35,36.
Here, the size-extensivity of our approach becomes important, as it enables us to train on small systems and predict the energies of larger ones34,37. In Fig. 3, this is highlighted for the water octamer and octane, with the corresponding KDFAs trained exclusively on the systems with up to four monomers (i.e., at most half the size of the predicted systems). Clearly, this is a challenging test for the transferability of the functionals. The observed MAEs are indeed somewhat larger than for models validated on configurations of the same size as the training set (74 and 48 meV for (H2O)8 and octane, respectively). A larger error should be expected for larger systems, however, precisely owing to the extensive nature of the correlation energy38,39. Furthermore, the prediction errors are somewhat systematic, in particular for (H2O)8. Consequently, the MAE for relative energies of water octamer configurations is further reduced to 42 meV (46 meV for octane).
Shown are error histograms for predicted correlation energies \({E}_{{\rm{C}}}^{{\rm{ML}}}\) of water octamer (left) and octane configurations (right) relative to MP2 reference energies \({E}_{{\rm{C}}}^{{\rm{MP2}}}\). The corresponding models were exclusively trained on systems with up to four monomers, exploiting the size-extensivity of the ML correlation functional.
Of comparable computational cost as conventional low-rung functionals, the transferable KDFA approach provides access to quantitative CCSD(T) simulations for systems that before were on the brink of largest-scale supercomputing studies or simply not tractable at all. We demonstrate this for the shared proton in a protonated water dimer, as an intensely studied testbed for the role of electron correlation and nuclear quantum effects in hydrated excess protons40,41,42,43,44,45,46,47,48,49. An ensemble of 100,000 uncorrelated configurations of the protonated water dimer was drawn from a 5 ns MD trajectory generated at the semiempirical GFN2-XTB level of theory50. From this ensemble, 100 structures were randomly sampled and their energies computed at the CCSD(T)/def2-TZVP level. These configurations were used to train a KDFA, which was used to predict the energies of all 100,000 configurations. These KDFA energies were then used to generate a CCSD(T)-level ensemble, via the Monte Carlo resampling (RSM) approach of Essex and co-workers (see Supplementary Note 4)51.
The two dominant reaction coordinates for this system are the oxygen–oxygen distance (rOO) and the proton transfer coordinate ν40. The latter is defined as the difference between the O-H distances of the shared proton and each oxygen atom, with a value of ν = 0 meaning that the proton is equidistant to both oxygens, whereas positive or negative values indicate that the proton is closer to one of the oxygen atoms. In Fig. 4 (left) the free-energy surface derived from the semiempirical MD trajectory is shown with respect to these coordinates. This reveals a fairly broad single-well potential with a minimum around rOO ≈ 2.45 Å and ν = 0. The location of the minimum and the overall shape of the well are in good agreement with previously reported probability distributions obtained from MD simulations with dispersion-corrected (semilocal) DFT52.
Left: original surface from the semiempirical molecular dynamics simulation. Right: resampled free-energy surface from the machine-learned coupled cluster functional. Histograms of the underlying distributions along both coordinates are also shown. Free energies are given in meV as a function of the proton reaction coordinate (ν) and the O–O distance (rOO). Note the different topology of the two surfaces discussed in the text, but also the largely different energy range obtained at the two levels of theory.
In contrast, the free-energy surface for the CCSD(T)-quality KDFA displays some strikingly different features. Here, the minimum is more narrow and at shorter rOO. Furthermore, the potential well has a distinct heart-shape, meaning that at larger values of rOO, the proton is no longer equidistant to both oxygen atoms but preferentially located closer to one or the other. Finally, the energy range of both free-energy plots differs by over 100 meV, indicating that the minimum is much deeper and narrower at the CCSD(T) level. The comparison with the semiempirical surface (and analogous semilocal DFT surfaces)40,52 shows that the electron delocalization errors of these methods also leads to proton over-delocalization. Interestingly, the inclusion of nuclear quantum effects actually does delocalize the proton more strongly40,41. However, to obtain good agreement with the experimental properties of water both an explicit treatment of nuclear quantum effects (i.e., via path-integral MD) and a quantitatively correct classical potential energy surface (as provided by our CCSD(T)-quality KDFA) are required53,54.
Overall, the features of the presented CCSD(T) surface are in good agreement with the one recently reported by Kühne and co-workers, which was based on tour-de-force MD simulations requiring millions of CCSD/cc-pVDZ calculations41, i.e., in comparison with our work without perturbative triples in the coupled cluster ansatz and using an inferior basis set. In contrast, our combined KDFA/RSM approach only required 100 CCSD(T) reference calculations and was quickly performed in a matter of hours on a single workstation, even though we chose to employ a much larger ensemble to arrive at a better free-energy sampling.
Discussion
Given the large variety of ML approaches reported in recent years, it is important to discuss the proposed KDFA method in a broader context. Most prominently, kernel and neural network regression has been very successfully used to directly learn the relationship between atomic coordinates and ground-state energies, i.e., the potential energy surface (PES)22,30,31,33,48,55,56,57,58,59,60,61,62,63,64,65,66. The main advantage of this direct approach is that electronic structure calculations are only required for training, whereas predictions can be performed using just the atomic coordinates as input. On the other hand, this also means that the complex physics underlying the PES has to be learned completely from data, which often translates to very large training sets from tens of thousands to millions of configurations, depending on the system (see Supplementary Note 5)67,68. Another downside is that most such ML forcefields are by construction short-ranged, meaning that long-range Coulomb and dispersion interactions are not included.
Von Lilienfeld and co-workers proposed the so-called Δ-ML approach to mitigate these downsides69. Here, the idea is to use an inexpensive semiempirical method as a baseline and learn the energy difference to a higher-level method like DFT or CC. They showed that this requires much less training data to reach a given accuracy than for a pure ML model. Broadly speaking, the KDFA approach proposed here also falls into this category. However, rather than learning the total energy differences between different approximations wholesale, we exclusively focus on the correlation energy, which is generally much smoother (and therefore easier to learn) than the total PES32,70. Furthermore, unlike the original Δ-ML approach, we use the electron density as input, rather than geometric information. Our ML models are thus genuine density functionals.
The presented approach is closest in spirit to the work of Miller and co-workers, where pair-correlation energies are learned from molecular orbital based descriptors (MOB-ML)34,37. As in their work, our models are based on a rigorous physical theory of electron correlation and are by construction size-extensive. The main difference is that in our case no previous energy decomposition or orbital localization is required. This enables us to choose arbitrary reference methods, for which pair-correlation energies may not be available or implemented (i.e., the random phase approximation, RPA, or quantum Monte Carlo methods). Furthermore, the requirement of orbital localization makes the application of MOB-ML to metallic or small band-gap systems fundamentally difficult.
Of course, the work of Burke, Müller, Tuckermann, and co-workers on ML-based DFT is also highly pertinent10,11,13,14,15. Their most recent method focuses on the integrated prediction of both the valence electron density and the exchange-correlation energy14. This work was originally aimed at accelerating the computation of established DFAs, but has very recently been extended to also learn corrections to higher-level methods like CCSD(T)15. The main difference to our work is their choice of density representation. Specifically, they work in a plane-wave basis instead of the atom-centered Gaussians used herein. This makes learning the density much easier, since all basis functions are orthogonal. As a consequence of this choice, their models are not size-extensive, however. Furthermore, molecular symmetry can only be included in an approximate form, i.e., through data-augmentation. Consequently, these models can only be applied if at least some number of high-level CC calculations are affordable for the complete system, and if the predictions are done on fairly similar configurations (i.e., within an MD trajectory). It should also be noted that Ceriotti, Corminbeauf, and co-workers have recently developed a method for learning electron densities in atom-centered basis sets20,21,71. In future work, integrated, size-extensive KDFAs could thus be developed that can predict both densities and energies.
Finally, a note on self-consistency is in order. KS-DFT calculations are commonly carried out self-consistently. One could therefore argue that the presented approach is more closely related to post-HF methods like Coupled Cluster theory. Nonetheless, we feel that our models are more accurately described as DFAs, as they exclusively depend on the electron density. In particular, no information related to virtual orbitals is required. The models therefore share the favorable computational scaling of pure DFAs. We also note that higher-rung DFAs (i.e., double hybrids or RPA-based functionals) are still commonly used non-self-consistently6,8. Indeed, even classic semilocal functionals like Becke’s B88 were developed in a non-self-consistent framework72. In the same vein, a self-consistent extension of the proposed method is clearly possible and will be the subject of future work. This will, however, likely require significantly more training data.
To conclude, we have presented a novel method to learn pure, non-local and transferable density functionals for the correlation energy from data. The high accuracy and data-efficiency of the method was demonstrated for a range of non-covalent, ionic and covalent systems of different sizes. In all cases, MAEs below 25 meV could be achieved with <100 training structures. We also demonstrated the transferability and size-extensivity of the approach by training and predicting on differently sized systems. As an exemplary application of the new method, a highly accurate free-energy surface for the shared proton in a protonated water dimer was obtained by resampling a semiempirical MD trajectrory with a CCSD(T)-based KDFA at mean-field computational cost.
Methods
Computational details
Most electronic structure calculations were performed with the Psi4 package73. The KDFA method was implemented as an external plugin to Psi4 via the Psi4numpy interface74. CCSD(T) and MP2 calculations were performed with ORCA75. The Karlsruhe def2-TZVP basis set and corresponding DF basis were used throughout76,77.
Molecular dynamics
NVT MD simulations were performed with the semiempirical GFN2-XTB method and the atomic simulation environment50,78. All simulations were run with a timestep of 0.5 fs and a Langevin thermostat with a coupling constant of 0.1 atomic units. For the learning curves in Fig. 2, decorrelated snapshots from 50 ps trajectories at 350 K were used. For the free-energy surfaces in Fig. 4, a trajectory of 5 ns at 300 K was calculated.
Data availability
All data sets used in this paper are available in the supplementary information (Supplementary Data 1).
Code availability
The code used to fit the ML models is available at https://gitlab.com/jmargraf/kdf.
References
Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. Phys. Rev. 136, B864–B871 (1964).
Peverati, R. & Truhlar, D. G. Quest for a universal density functional: the accuracy of density functionals across a broad spectrum of databases in chemistry and physics. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 372, 20120476 (2014).
Schuch, N. & Verstraete, F. Computational complexity of interacting electrons and fundamental limitations of density functional theory. Nat. Phys. 5, 8 (2007).
Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133–A1138 (1965).
Perdew, J. P. & Schmidt, K. Jacob’s ladder of density functional approximations for the exchange-correlation energy. In AIP Conf. Proc., vol. 577, 1–20 (AIP, 2001).
Grimme, S. Semiempirical hybrid density functional with perturbative second-order correlation. J. Chem. Phys. 124, 034108 (2006).
Becke, A. D. Density functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 98, 5648–5652 (1993).
Zhang, I. Y., Rinke, P., Perdew, J. P. & Scheffler, M. Towards efficient orbital-dependent density functionals for weak and strong correlation. Phys. Rev. Lett. 117, 133002 (2016).
Cohen, A. J., Mori-Sanchez, P. & Yang, W. Insights into current limitations of density functional theory. Science 321, 792–794 (2008).
Wagner, L. O., Stoudenmire, E. M., Burke, K. & White, S. R. Reference electronic structure calculations in one dimension. Phys. Chem. Chem. Phys. 14, 8581–8590 (2012).
Li, L., Baker, T. E., White, S. R. & Burke, K. Pure density functional for strong correlation and the thermodynamic limit from machine learning. Phys. Rev. B 94, 245129 (2016).
Schmidt, J., Benavides-Riveros, C. L. & Marques, M. A. L. Machine learning the physical nonlocal exchange-correlation functional of density-functional theory. J. Phys. Chem. Lett. 10, 6425–6431 (2019).
Snyder, J. C., Rupp, M., Hansen, K., Müller, K.-R. & Burke, K. Finding density functionals with machine learning. Phys. Rev. Lett. 108, 253002 (2012).
Brockherde, F. et al. Bypassing the Kohn-Sham equations with machine learning. Nat. Commun. 8, 872 (2017).
Bogojeski, M., Vogt-Maranto, L., Tuckerman, M. E., Müller, K.-R. & Burke, K. Quantum chemical accuracy from density functional approximations via machine learning. Nat. Commun. 11, 5223 (2020).
Nudejima, T., Ikabata, Y., Seino, J., Yoshikawa, T. & Nakai, H. Machine-learned electron correlation model based on correlation energy density at complete basis set limit. J. Chem. Phys. 151, 024104 (2019).
Margraf, J. T., Kunkel, C. & Reuter, K. Towards density functional approximations from coupled cluster correlation energy densities. J. Chem. Phys. 150, 244116 (2019).
Vyboishchikov, S. F. A simple local correlation energy functional for spherically confined atoms from ab initio correlation energy density. ChemPhysChem 18, 3478–3484 (2017).
Baerends, E. J. & Gritsenko, O. V. Quantum chemical view of density functional theory. J. Phys. Chem. A 101, 5383–5403 (1997).
Grisafi, A. et al. Transferable machine-learning model of the electron density. ACS Cent. Sci. 5, 57–64 (2019).
Fabrizio, A., Grisafi, A., Meyer, B., Ceriotti, M. & Corminboeuf, C. Electron density learning of non-covalent systems. Chem. Sci. 10, 9424–9432 (2019).
Bartók, A. P., Kondor, R. & Csányi, G. On representing chemical environments. Phys. Rev. B 87, 184115 (2013).
Oliphant, N. & Bartlett, R. J. A systematic comparison of molecular properties obtained using Hartree-Fock, a hybrid Hartree-Fock density-functional-theory, and coupled-cluster methods. J. Chem. Phys. 100, 6550–6561 (1994).
Urban, M., Noga, J., Cole, S. J. & Bartlett, R. J. Towards a full CCSDT model for electron correlation. J. Chem. Phys. 83, 4041–4046 (1985).
Raghavachari, K., Trucks, G. W., Pople, J. A. & Head-Gordon, M. A fifth-order perturbation comparison of electron correlation theories. Chem. Phys. Lett. 157, 479–483 (1989).
Bartlett, R. J. Many-body perturbation theory and coupled cluster theory for electron correlation in molecules. Annu. Rev. Phys. Chem. 32, 359–401 (1981).
Cohen, A. J., Mori-Sánchez, P. & Yang, W. Second-order perturbation theory with fractional charges and fractional spins. J. Chem. Theory Comput. 5, 786–792 (2009).
Steinmann, S. N. & Yang, W. Wave function methods for fractional electrons. J. Chem. Phys. 139, 074107 (2013).
Margraf, J. T. & Bartlett, R. Coupled cluster and many-body perturbation theory for fractional charges and spins. J. Chem. Phys. 148, 221103 (2018).
von Lilienfeld, O. A. Quantum machine learning in chemical compound space. Angew. Chem. Int. Ed. 57, 4164–4169 (2018).
Bartók, A. P. et al. Machine learning unifies the modeling of materials and molecules. Sci. Adv. 3, e1701816 (2017).
Margraf, J. T. & Reuter, K. Making the coupled cluster correlation energy machine-learnable. J. Phys. Chem. A 122, 6343–6348 (2018).
Rupp, M. Machine learning for quantum mechanics in a nutshell. Int. J. Quantum Chem. 115, 1058–1073 (2015).
Welborn, M., Cheng, L. & Miller, T. F. Transferability in machine learning for electronic structure via the molecular orbital basis. J. Chem. Theory Comput. 14, 4772–4779 (2018).
Bartlett, R. J. & Musiał, M. Coupled-cluster theory in quantum chemistry. Rev. Mod. Phys. 79, 291–352 (2007).
Crawford, T. D. & Schaefer, H. F. An introduction to coupled cluster theory for computational chemists. Rev. Comput. Chem. 14, 33–136 (2000).
Cheng, L., Kovachki, N. B., Welborn, M. & Miller, T. F. Regression clustering for improved accuracy and training costs with molecular-orbital-based machine learning. J. Chem. Theory Comput. 15, 6668–6677 (2019).
Perdew, J. P., Sun, J., Garza, A. J. & Scuseria, G. E. Intensive atomization energy: re-thinking a metric for electronic structure theory methods. Z. f.ür. Phys. Chem. 230, 737–742 (2016).
Margraf, J. T., Ranasinghe, D. S. & Bartlett, R. J. Automatic generation of reaction energy databases from highly accurate atomization energy benchmark sets. Phys. Chem. Chem. Phys. 19, 9798–9805 (2017).
Tuckerman, M. E., Marx, D., Klein, M. L. & Parrinello, M. On the quantum nature of the shared proton in hydrogen bonds. Science 275, 817 (1997).
Spura, T., Elgabarty, H. & Kühne, T. D. On-the-fly coupled cluster path-integral molecular dynamics: impact of nuclear quantum effects on the protonated water dimer. Phys. Chem. Chem. Phys. 17, 14355–14359 (2015).
Clark, T., Heske, J. & Kühne, T. D. Opposing electronic and nuclear quantum effects on hydrogen bonds in H2O and D2O. ChemPhysChem 20, 2461–2465 (2019).
Dagrada, M., Casula, M., Saitta, A. M., Sorella, S. & Mauri, F. Quantum Monte Carlo study of the protonated water dimer. J. Chem. Theory Comput. 10, 1980–1993 (2014).
Marx, D., Tuckerman, M. E., Hutter, J. & Parrinello, M. The nature of the hydrated excess proton in water. Nature 397, 601–604 (1999).
Auer, A. A., Helgaker, T. & Klopper, W. Accurate molecular geometries of the protonated water dimer. Phys. Chem. Chem. Phys. 2, 2235–2238 (2000).
Cheng, H. P. & Krause, J. L. The dynamics of proton transfer in H5O2+. J. Chem. Phys. 107, 8461–8468 (1997).
Valeev, E. F. & Schaefer, H. F. The protonated water dimer: Brueckner methods remove the spurious C1 symmetry minimum. J. Chem. Phys. 108, 7197–7201 (1998).
Schran, C., Behler, J. & Marx, D. Automated fitting of neural network potentials at coupled cluster accuracy: protonated water clusters as testing ground. J. Chem. Theory Comput. 16, 88–99 (2020).
Kapil, V., VandeVondele, J. & Ceriotti, M. Accurate molecular dynamics and nuclear quantum effects at low cost by multiple steps in real and imaginary time: Using density functional theory to accelerate wavefunction methods. J. Chem. Phys. 144, 054111 (2016).
Bannwarth, C., Ehlert, S. & Grimme, S. GFN2-xTB - an accurate and broadly parametrized self-consistent tight-binding quantum chemical method with multipole electrostatics and density-dependent dispersion contributions. J. Chem. Theory Comput. 15, 1652–1671 (2019).
Cave-Ayland, C., Skylaris, C. K. & Essex, J. W. A Monte Carlo resampling approach for the calculation of hybrid classical and quantum free energies. J. Chem. Theory Comput. 13, 415–424 (2017).
Marsalek, O. & Markland, T. E. Ab initio molecular dynamics with nuclear quantum effects at classical cost: ring polymer contraction for density functional theory. J. Chem. Phys. 144, 054112 (2016).
Naserifar, S. & Goddard, W. A. Liquid water is a dynamic polydisperse branched polymer. Proc. Natl Acad. Sci. 116, 1998–2003 (2019).
Head-Gordon, T. & Paesani, F. Water is not a dynamic polydisperse branched polymer. Proc. Natl Acad. Sci. 116, 13169–13170 (2019).
Dral, P. O. Quantum chemistry in the age of machine learning. J. Phys. Chem. Lett. 11, 2336–2347 (2020).
Jung, H. et al. Size-extensive molecular machine learning with global representations. ChemSystemsChem 1900052, syst.201900052 (2020).
Dragoni, D., Daff, T. D., Csányi, G. & Marzari, N. Achieving DFT accuracy with a machine-learning interatomic potential: Thermomechanics and defects in bcc ferromagnetic iron. Phys. Rev. Mater. 2, 013808 (2018).
Butler, K. T., Davies, D. W., Cartwright, H., Isayev, O. & Walsh, A. Machine learning for molecular and materials science. Nature 559, 547–555 (2018).
Huo, H. & Rupp, M. Unified representation of molecules and crystals for machine learning https://arxiv.org/abs/1704.06439 (2017).
Faber, F. A. et al. Prediction errors of molecular machine learning models lower than Hybrid DFT error. J. Chem. Theory Comput. 13, 5255–5264 (2017).
Deringer, V. L. & Csányi, G. Machine learning based interatomic potential for amorphous carbon. Phys. Rev. B 95, 094203 (2017).
Rupp, M., Tkatchenko, A., Müller, K.-R. & von Lilienfeld, O. A. Fast and accurate modeling of molecular atomization energies with machine learning. Phys. Rev. Lett. 108, 058301 (2012).
Bartók, A. P., Payne, M. C., Kondor, R. & Csányi, G. Gaussian approximation potentials: the accuracy of quantum mechanics, without the electrons. Phys. Rev. Lett. 104, 136403 (2010).
Artrith, N., Morawietz, T. & Behler, J. High-dimensional neural-network potentials for multicomponent systems: applications to zinc oxide. Phys. Rev. B 83, 153101 (2011).
Morawietz, T., Sharma, V. & Behler, J. A neural network potential-energy surface for the water dimer based on environment-dependent atomic energies and charges. J. Chem. Phys. 136, 064103 (2012).
Behler, J. & Parrinello, M. Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys. Rev. Lett. 98, 146401 (2007).
Smith, J. S., Isayev, O. & Roitberg, A. E. ANI-1: an extensible neural network potential with DFT accuracy at force field computational cost. Chem. Sci. 8, 3192–3203 (2017).
Smith, J. S. et al. Approaching coupled cluster accuracy with a general-purpose neural network potential through transfer learning. Nat. Commun. 10, 2903 (2019).
Ramakrishnan, R., Dral, P. O., Rupp, M. & von Lilienfeld, O. A. Big data meets quantum chemistry approximations: the δ-machine learning approach. J. Chem. Theory Comput. 11, 2087–2096 (2015).
Peyton, B., Briggs, C., D’Cunha, R., Margraf, J. T. & Crawford, T. Machine-learning coupled cluster properties through a density tensor representation. J. Phys. Chem. A 124, 4861–4871 (2020).
Grisafi, A., Wilkins, D. M., Csányi, G. & Ceriotti, M. Symmetry-adapted machine learning for tensorial properties of atomistic systems. Phys. Rev. Lett. 120, 36002 (2018).
Becke, A. D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 38, 3098–3100 (1988).
Smith, D. G. A. et al. Psi4Numpy: an interactive quantum chemistry programming environment for reference implementations and rapid development. J. Chem. Theory Comput. 14, 3504–3511 (2018).
Parrish, R. M. et al. Psi4 1.1: an open-source electronic structure program emphasizing automation, advanced libraries, and interoperability. J. Chem. Theory Comput. 13, 3185–3197 (2017).
Neese, F. Software update: the ORCA program system, version 4.0. WIREs Comput. Mol. Sci. 8, e1327 (2018).
Weigend, F. & Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 7, 3297–305 (2005).
Weigend, F. Hartree-fock exchange fitting basis sets for H to Rn. J. Comput. Chem. 29, 167–175 (2008).
Hjorth Larsen, A. et al. The atomic simulation environment - a Python library for working with atoms. J. Phys. Condens. Matter 29, 273002 (2017).
Acknowledgements
We acknowledge funding from the German Research Foundation (DFG) through its Cluster of Excellence e-conversion EXC 2089/1.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
J.T.M. and K.R. devised the project. J.T.M. wrote the KDFT code and performed all calculations. All authors contributed to writing the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Margraf, J.T., Reuter, K. Pure non-local machine-learned density functional theory for electron correlation. Nat Commun 12, 344 (2021). https://doi.org/10.1038/s41467-020-20471-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-20471-y
This article is cited by
-
Human- and machine-centred designs of molecules and materials for sustainability and decarbonization
Nature Reviews Materials (2022)
-
A transferable recommender approach for selecting the best density functional approximations in chemical discovery
Nature Computational Science (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.