Abstract
Nano-lamellar materials with ultrahigh strengths and unusual physical properties are of technological importance for structural applications. However, these materials generally suffer from low tensile ductility, which severely limits their practical utility. Here we show that markedly enhanced tensile ductility can be achieved in coherent nano-lamellar alloys, which exhibit an unprecedented combination of over 2 GPa yield strength and 16% uniform tensile ductility. The ultrahigh strength originates mainly from the lamellar boundary strengthening, whereas the large ductility correlates to a progressive work-hardening mechanism regulated by the unique nano-lamellar architecture. The coherent lamellar boundaries facilitate the dislocation transmission, which eliminates the stress concentrations at the boundaries. Meanwhile, deformation-induced hierarchical stacking-fault networks and associated high-density Lomer-Cottrell locks enhance the work hardening response, leading to unusually large tensile ductilities. The coherent nano-lamellar strategy can potentially be applied to many other alloys and open new avenues for designing ultrastrong yet ductile materials for technological applications.
Similar content being viewed by others
Introduction
Advanced structural materials with ultrahigh strengths and excellent ductilities are highly desirable for a wide variety of technological applications, including aerospace, transportation, and energy sectors. Nanolamellar alloys containing high-density interfaces are of particular interest owing to their unusual interface-driven properties, such as extremely high strengths1,2,3,4,5,6,7,8. Unfortunately, these materials typically suffer from a severe limitation—lack of tensile ductility, typically <5% elongation, and the region of the uniform deformation is even more limited9,10,11,12. This makes them difficult to be fabricated and prone to catastrophic failure in load-bearing applications. The strength-ductility trade-off has been a long-standing dilemma, which has attracted great attention in materials science13,14,15,16,17. Recently, several engineered heterogeneous nanostructures, such as gradient, bimodal, harmonic, and hierarchical structures, have been demonstrated to have the potential to enhance tensile ductility of nanostructured materials, leading to improved strength-ductility synergy18,19,20,21,22,23. However, these approaches usually produce materials with limited strengths (on the order of 1 GPa) because the creation of microstructural heterogeneity requires the incorporation of some coarse-scale microstructures that sacrifice the strength. By contrast, for nanolamellar alloys with extremely high strengths on the order of 2 GPa, brittleness remains their Achilles’ heel, which can be ascribed to the absence of work-hardening and serious strain localization at incoherent lamellar boundaries. Furthermore, most nanolamellar alloys are fabricated in the form of thin films/sheets by such methods as electrodeposition and severe plastic deformation1, which are not readily applicable to the large volume components necessary for practical applications. Consequently, developing ultrahigh strength, ductile, and scalable nanolamellar alloys are highly desirable but extremely challenging.
Here we overcome these critical challenges and present the development of new nanolamellar alloys featuring in situ-formed coherent nanolamellar (CNL) architectures, which exhibit an unprecedented combination of ultrahigh strength and tensile ductility and can be produced through conventional casting and thermomechanical treatments. Our design philosophy is to create nanometer-thick lamellae for an extremely high strengthening purpose while maintaining coherent lamellar boundaries that can suppress stress concentration and accommodate plastic strain, thereby promoting work hardening together with tensile ductility for nanostructured materials. In particular, we chose Ni-Fe-Co-Cr-Al-Ti multicomponent alloys as our model system, because they provide a large dual-phase region consisting of disordered face-centered cubic (FCC) and ordered FCC (L12) phases (Supplementary Fig. 1) with a small lattice mismatch, satisfying the requirement for the formation of coherent boundaries. The CNL architectures were controlled through a solid-state phase separation involving the process of “supersaturated FCC solid solution → L12 + FCC lamellae” within ultrafine grains at a relatively low temperature of 600 °C. At this temperature, the bulk diffusion is significantly inhibited, which kinetically suppresses the continuous precipitation of spheroidal nanoparticles. In contrast, the ultrafine grain structure promotes the discontinuous precipitation of nano-lamellae, because the high-density grain boundaries not only provide numerous nucleation sites but also promote their growth through grain boundary diffusion, which leads to the formation of unique FCC/L12 CNL architecture across the whole grains.
Results
Tensile properties
We performed tensile tests at room temperature to quantitatively measure the mechanical properties of a representative CNL alloy, Ni32.8Fe21.9Co21.9Cr10.9Al7.5Ti5.0 (at.%), which can also be written as (Ni1.5FeCoCr0.5)87.5Al7.5Ti5.0. To emphasize the substantial improvement in mechanical property upon the formation of the CNL architecture, the curves of two other samples having the same composition as the CNL alloy but without any CNL architectures are presented for comparison. The two reference materials are, respectively, a conventionally processed alloy and a severely deformed alloy (see Methods). From these curves, we see that our CNL alloy exhibits an extraordinary combination of ultrahigh strength and large uniform ductility (Fig. 1). The yield strength reaches as high as 2026 ± 20 MPa, and the ultimate tensile strength to 2118 ± 34 MPa; these values are more than quadruple of those for the conventionally processed alloy without such CNL architectures. More intriguingly, the ultrahigh strength CNL alloy also shows a large tensile ductility, with a uniform elongation of 16%, which is an order of magnitude larger than that of the severe deformed alloy with high dislocation densities (~1% uniform elongation). In addition, from the true stress–strain curve (Supplementary Fig. 2a), an obvious work hardening appears in the major plastic deformation stage, indicative of considerable dislocation accumulation during the plastic straining before failure. The work-hardening rate curve (Supplementary Fig. 2b) reveals a multi-stage work-hardening response. After a precipitous initial drop associated with the elastic to plastic transition, the work-hardening rate increases rapidly to a peak at the 2% strain and then drops gradually till a strain of 5%. Beyond that strain, the work-hardening rate increases again till the 6% strain, followed by a monotonic decrease. The fracture surface has two regions, i.e., the peripheral shear lip and central flat fracture regions (Supplementary Fig. 3). Both regions reveal a microvoid coalescence fracture mode with a plenty of fine dimples, indicating a characteristic mode of a ductile fracture at room temperature. The large area of shear lips indicates that the plane stress state prevails during the fracture, which is related to the small thickness of the tensile specimens. The specimen thickness can influence the post-necking elongation, but it has a negligible impact on the uniform elongation. Thus, our CNL alloy achieves an unprecedented synergy of both ultrahigh strength and large uniform ductility, which are inaccessible to conventional lamellar materials.
The curves of the conventionally processed alloy (black) and severely deformed alloy (blue), which have the same composition as the CNL alloy but without the CNL architectures, are presented for comparison. The CNL alloy (red) reveals an extraordinary combination of ultrahigh strength and large ductility.
Microstructural characterization
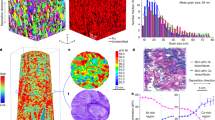
To understand the observed superb mechanical properties of the CNL alloy, we studied the underlying microstructures in detail down to the atomic scale. Electron backscatter diffraction (EBSD) reveals that the grain structure exhibits a uniform distribution of ultrafine equiaxed grains with an average size of 390 nm and random orientations along the rolling, transverse, and normal directions (Supplementary Fig. 4), indicating a full recrystallized and uniform microstructure. Each grain contains a high density of alternating lamellae of the order-L12 and disorder-FCC phases with thicknesses in the nanometer range, as observed in bright-field (Fig. 2a) and dark-field (Fig. 2b) transmission electron microscopy (TEM). All the grains have the FCC/L12 nanolamellar structure without any spheroidal L12 nanoparticles. The average thickness for the FCC and L12 lamellae was measured to be ~37 ± 18 and 30 ± 16 nm, respectively (Fig. 2c). From high-resolution TEM (Fig. 2d), we observed a coherent FCC/L12 interface with continuous crystal lattices, where the crystal lattice of the ordered L12 phase is very close to that of the disordered FCC phase. This agrees with the X-ray diffraction (XRD) results that the lattice mismatch between the two phases is only ~0.13% (Supplementary Fig. 5), the small value of which effectively stabilizes the CNL structure without any heterogeneous coarsening. We further analyzed the phase composition and elemental distribution of the FCC/L12 CNL structure by three-dimensional atom probe tomography (3D-APT) (Fig. 2e) and energy-dispersive X-ray spectroscopy mapping in the scanning-TEM mode (STEM-EDS) (Supplementary Fig. 6). We observed that Ni (green), Ti (blue), and Al (cyan) partition to the L12 lamellae, whereas Co (purple), Cr (pink), and Fe (orange) partition to the FCC lamellae. The 12% (Al + Ti) concentration isosurfaces were used to visualize the boundary between the FCC and L12 lamellae, and the corresponding proximity histogram showing the concentration profiles across the boundary is also displayed in Fig. 2e. Data points within the flat region of the profiles at the left and right sides of the interface delineate the composition of the FCC and L12 nano-lamellae, respectively. The composition of the FCC lamellae is 36.4Fe-28.1Co-14.6Ni-18.2Cr-2.3Al-0.4Ti (at.%), whereas that the L12 lamellae can be regarded as 59.7Ni-10.6Co-3.5Fe-1.5Cr-13.5Al-11.2Ti (at.%), yielding a (Ni + Co + Fe + Cr):(Al + Ti) ratio of ~3:1 (A3B-type). By using the lever rule analysis, the volume fraction of the FCC and L12 phases are determined to be ~56% and 44%, respectively (Supplementary Fig. 7). From the aforementioned observations, we can see that our newly developed CNL alloy exhibits a unique lamellar architecture consisting of alternating order-L12 and disorder-FCC lamellae with nanometer thicknesses and coherent boundaries, which is significantly distinctive to conventional lamellar alloys with coarse lamellar thickness and/or incoherent boundaries.
a, b Bright-field and dark-field TEM microstructure of the FCC and L12 nano-lamellae within ultrafine grains. c Statistical distributions for thicknesses of the FCC and L12 nano-lamellae. d High-resolution TEM image illustrating the interfacial coherency of the FCC/L12 lamellar boundary. e APT characterization of the elemental partitioning and composition of the FCC and L12 nano-lamellae.
Microstructures of the conventionally processed and severely deformed alloys were examined for comparison (Supplementary Fig. 8). The conventionally processed alloy exhibits a mixed microstructure containing spheroidal nanoparticles in grain interiors and nano-lamellae near grain boundaries, which is similar to that reported in the literature. The severely deformed alloy exhibits a typical cellular microstructure containing elongated sub-grains.
Discussion
We attribute the ultrahigh yield strength of the CNL alloy mainly to the lamellar boundary strengthening associated with nanometer-thick order/disorder lamellae. In this material, the ordered L12 lamellae are much stronger than the FCC solid solution lamellae, because the ordered L12 superlattice structure has high anti-phase boundary energy (~200 mJ m-2)24, requiring high stresses for dislocations to cut through. Thus, the FCC/L12 lamellar boundaries are strong barriers to the dislocation motion. It was documented that a Hall–Petch relationship also describes the yield strength of dual-phase nanolamellar structures25. In the FCC/L12 CNL architecture, initial plastic deformation occurs in the soft FCC lamellae; thus, the parameter controlling the yield strength is the thickness of FCC lamellae. Based on the Hall–Petch modeling, we estimated that the contribution of nanolamellar boundaries to the yield strength is ~1.0 GPa (see Methods), which provides the dominant contribution to the macroscopic yield strength. In addition, the ultrafine grains with an average size of 390 nm also contributes to a large component of the yield strength (0.8 GPa), as estimated from the Hall–Petch relation for grain boundary strengthening. Overall, the collective strengthening contributions from the FCC/L12 nano-lamellae, ultrafine grain sizes, together with other strengthening from solid solution and dislocations, elevate the yield strength of the CNL alloy beyond 2 GPa.
To understand the underlying mechanisms for the unusual work hardening and large tensile ductility of the ultrahigh-strength CNL alloy, we investigated the dynamic evolution of deformation microstructures at different strains of plastic deformation (Fig. 3). At the strain of ~2% (Fig. 3a), the dislocation slipping is activated in the appearance of extended stacking faults (SFs, red arrow) on the primary {111} planes, which cuts across the FCC/L12 nano-lamellae, indicating an early stage of planar dislocation slip across the coherent lamellar boundaries. With further increasing strain to ~5% (Fig. 3b), the SFs (red arrow) are activated in more grains and with a much higher density as compared with those in the 2% strain state. Further increasing the strain to 16% results in the planar SF-dominated deformation mode with an extremely high-density of SFs on two {111} slip systems (red and yellow arrows) and extensive SF intersections (Fig. 3c). The enlarged view (Fig. 3d) shows that numerous intersected SFs activated on two {111} slip systems, leading to the formation of hierarchical nano-spaced SF networks.
a Deformation microstructure at the 2% strain revealing the activation of parallel SFs (red arrow). b Activations of more planar SFs (red arrow) at the 5% strain. c High-density hierarchical SFs on two {111} slip planes (red and yellow arrows) at the 16% strain. d High-resolution TEM image showing the hierarchical SF network (white dash line) and Lomer-Cottrell (LC) locks (red dot) in different intersecting {111} slip systems. The FFT image with crossing diffraction fringes (yellow arrow) reveals the presence of intersected SFs, and an enlarged view of a representative SF is marked by the BCABABCA-stacking sequence.
On the basis of these observations, we now discuss the structural origins responsible for the unusual deformation behavior and large ductility of the CNL alloy. First, the presence of extensive SFs suggests that the CNL matrix might have an intrinsically low SF energy. To understand the generation of SFs during plastic deformation, we calculated the SF energy of the CNL matrix using ab initio calculations (Supplementary Fig. 9), where the supercell composition (17Fe-14Co-7Ni-9Cr-1Al) was based on the matrix composition determined by APT. The average SF energy of the FCC lamellar matrix is ~25 mJ m−2. This value is in the range of 20–45 mJ m−2, within which partial dislocations separation with SF bonds are thermodynamically preferred26, thereby making the activation of SFs easy under plastic deformation. For FCC-type materials with low SF energy, a perfect a/2 < 110> unit dislocation tends to dissociate into a pair of a/6 < 112> Shockley partials bonded with the SF during plastic deformation, in contrast to materials with high SF energies in which the dislocation cross-slip and micro-banding are the preferred deformation mode27. Therefore, the unusual SF-dominated deformation in the nanolamellar alloys should originate from the low SF energy of the CNL matrix (25 mJ m−2), which results in a high propensity of dislocation dissociation into wide SFs in our material, thereby hindering the cross-slip process. Second, the coherent boundaries in the CNL alloy are characterized by continuous crystal lattices, and the orientation of the ordered L12 phase is very close to that of the disordered FCC phase. These structural features facilitate continuous dislocation transmissions across the lamellar boundaries, with no need to change the slip direction25. When an applied stress is higher than the yield strength, dislocations can easily transmit across the coherent boundaries, rather than being localized at the boundaries, thereby suppressing the stress concentration due to dislocation accumulations. In addition, the dislocation transmission across the boundaries facilitates long-range dislocation gliding through different L12 and FCC lamellae, which results in the microscopic homogeneous plastic deformation, thereby enhancing the plastic deformation stability and averting an early stage of crack initiation of the CNL alloy. Third, the interaction of the two leading partial dislocations results in the formation of a sessile stair-rod dislocations on a non-slipping {100} plane (Fig. 3d), known as the immobile Lomer-Cottrell (LC) locks. The formation of those high-density LC locks not only act as strong obstacles to effectively pin the dislocation motion, but can also be served as Frank-Read sources for dislocation multiplication27, leading to a steady and progressive work hardening of the CNL alloy. Because the formation of SF networks and LC locks is a dynamic process, their density may not be very high at the early stage of the plastic deformation, which may result in a low work-hardening capacity at the early stage of plastic strain. As the deformation proceeds, the density of SF networks and LC locks increases. The LC locks derive their effectiveness in strain hardening from their capability to accumulate dislocations from the two aspects: on the one hand, LC locks serve to stabilize the SF network by pinning lock-forming dislocation segments, because when two dislocations meet to produce an LC lock, four dislocation segments are pinned28, and on the other hand, the sessile nature of the stair-rod dislocation in the LC locks enables them to exhibit high structural stability resistant to dissociations and to block other dislocation motion as a barrier, which consequently presents a strong hindering effect on dislocation motion29. In addition, the hierarchical SF networks dynamically subdivide the ultrafine grains into even finer sub-grains during deformation (with sizes of ~20 nm at the 16% strain) (Fig. 3d), which can pin the motion of dislocations by decreasing their mean free path (i.e., the dynamic Hall–Petch effect)30, thereby further enhancing the work hardening of the CNL alloy. Fourth, APT reveals that the L12 phase in the CNL alloy has a multicomponent composition, which can be regarded as (Ni,Co,Cr,Fe)3(Al,Ti). Previous research indicates that the incorporation of Co and Fe in the L12 phase improves its intrinsic ductility31,32, whereas the partial substitution of Al by Ti alleviates the environment embrittlement33. Furthermore, it has been demonstrated that the multicomponent L12 phase is much stronger and more ductile than binary Ni3Al34. Therefore, the multicomponent L12 lamellae effectively enhance the strength of the CNL alloys while maintaining high ductilities. Consequently, the combination of the coherent nanolamellar boundaries, high-density immobile LC locks, hierarchical SF networks, and ductile nature of the L12 lamellae substantially enhances the plastic deformation stability and work-hardening capability of the CNL alloy, leading to the large uniform tensile ductility at an ultrahigh-strength level. Upon fracture, the high-density SF interactions and LC locks may act as preferred nucleation sites for microvoids, leading to a homogeneous microvoid coalescence with fine dimples and ductile fracture (cf. Supplementary Fig. 3).
To illustrate the unusual properties of our CNL alloy, we compare its tensile properties with those of other lamellar materials and high-performance nanostructured materials35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57 (Fig. 4). We see that our CNL alloy exhibits an order of magnitude larger uniform elongation than lamellar pearlitic steels while maintaining a tantamount strength44,45. Meanwhile, our CNL alloy shows a twofold strength and uniform elongation advantage over lamellar titanium alloys35,36. Even when compared with the recently reported lamellar high-entropy alloys (HEAs)41,42, our CNL alloy displays a simultaneous 50% increase in both yield strength and uniform ductility. Therefore, our CNL alloy exhibits an unprecedented combination of ultrahigh yield strength and large uniform ductility, which outperforms from other lamellar materials and high-performance nanostructured materials, thereby overcoming the long-standing dilemma of the strength-ductility trade-off. Several major contributions from the unique lamellar architectures account for the superior mechanical properties of the CNL alloy. First, the unique processing approach for tailoring architectures with nanometer-thick lamellae and strong order/disorder lamellar boundaries effectively elevates the yield strength over 2 GPa, reaching to the ultrahigh strength level. Second, the coherent lamellar boundaries eliminate the stress concentration that normally occur in incoherent lamellar materials, thereby enhancing the plastic deformation stability and avoiding an early stage of crack initiation of the CNL alloy. Third, the intrinsically low SF energy (25 mJ m−2) of the FCC lamellae promotes the dynamic formation of hierarchical SF networks and high densities of LC locks during plastic deformation, which substantially increases the work-hardening capacity, leading to the superior tensile ductility even at the ultrahigh strength level. Fourth, the fully recrystallized and uniform microstructure promotes the homogeneous deformation, leading to stable mechanical properties of the CNL alloy. This contrasts with non-uniform structured materials, which usually induce inhomogeneous deformation, resulting in large variations of mechanical properties58. In addition, the delicate composition design endows our materials with extra advantages compared with other existing ultrahigh-strength materials. For instance, the Cr and Al additions provide a good oxidation resistance of the materials, making them potentially attractive for applications in harsh environments such as in aerospace and aeronautic applications. Furthermore, unlike most conventional nanolamellar materials that are fabricated in the form of thin films/sheets in the micron scale, such as magnetron sputtered and electrodeposited films59,60, our CNL materials produced by casting and thermomechanical treatments can potentially be produced in relatively large dimensions (in the mm scale), thus offering a great potential for structural applications in industries.
The reference materials include lamellar-structured alloys (Ti alloy35,36, Fe alloy37, Co alloy38, Ni alloy39, Zr alloy40, HEA41,42, TiAl alloy43, pearlitic steel44,45, bainitic steel46, and twinning-induced plasticity (TWIP) steel47), laminated metal composites (Al/Ti48, Ti/Ta49, Fe/Cu50, Cu/Zr51, Cu/Nb52, and steel/steel53), and nanostructured metals (Al54, Ni55, Mo56, and W57). Our CNL alloy (red dot) clearly outperforms other high-performance materials and overcomes the long-standing dilemma of the strength-ductility trade-off.
In summary, we presented an innovative design concept for high-performance materials by engineering nanolamellar architectures, which leads to the development of new bulk nanostructured materials with the unprecedented combination of over 2 GPa yield strength and 16% uniform tensile ductility at ambient temperature. The extraordinary mechanical properties of the CNL materials offer tremendous potential for structural applications in aerospace, automotive, and energy industries. In addition, the fundamental concept of lamellar architecture engineering can be applied to many other metallic materials, including new-generation superalloys, titanium alloys, advanced steels, and HEAs, to achieve enhanced properties for specific applications.
Methods
Material preparation
Alloy with nominal composition of Ni32.8Fe21.9Co21.9Cr10.9Al7.5Ti5.0 (at.%), which can also be written as (Ni1.5FeCoCr0.5)87.5Al7.5Ti5.0, was prepared by arc-melting a mixture of the constituent elements with purity higher than 99.9 wt.% under a Ti-gettered argon atmosphere. Repeated melting was carried out at least four times to ensure the chemical homogeneity. The melted alloys were then drop-cast into copper molds with dimensions of 6 × 15 × 50 mm and 10 × 15 × 50 mm and then homogenized for 2 h at 1150 °C, followed by water quenching. The CNL architecture was produced through controlled thermomechanical treatments consisting of a cold-rolling process for a reduction of 90% and a subsequent tempering treatment for 8 h at 600 °C (referred to as the “CNL alloy”). For comparison, two samples with the same composition as the CNL alloy but different treatment histories were prepared; one was fabricated by cold-rolling the homogenized ingot to a reduction of 90% (referred to as the “severely deformed alloy”), and the other was fabricated by recrystallizing the cold-rolled sample for 3 min at 1150 °C and subsequent tempering for 8 h at 600 °C (referred to as the “conventionally processed alloy”).
Microstructural characterization. TEM and STEM observations were conducted on a JEM-2100F microscope operated at 200 kV. The TEM is equipped with EDS for elemental analysis and SAED for structural analysis. TEM specimens were mechanically thinned to ~40 μm, punched to Ф3 mm circle sheets, and then thinned by twin-jet electro-polishing in a solution consisting of 5 vol.% perchloric acid and 95 vol.% alcohol at a temperature of −30 °C with a potential of 24 V. To quantify the observed lamellar thicknesses, TEM images were analyzed by an Image-J software. At least 800 lamellae were measured to obtain a reliable determination. EBSD measurements were performed to characterize the grain structure and orientation distribution using a FEI-SEM with an Oxford detector operated at 30 kV and 0.8 nA. The specimens were prepared by mechanical polishing down to 0.05 μm, followed by electro-polishing in a solution of HNO3 (25%) and C2H5OH (75%) with a voltage of 20 V at −40 °C. Crystal structures were examined by a Rigaku XRD instrument with Cu-Kα irradiation. XRD samples were polished using standard mechanical polishing procedures. The θ-2θ scanning was conducted in the range of 20–100° with a scanning speed of 4°/min. A slow scan in the range of 88–92° with a speed of 0.05°/min was performed to calculate the lattice mismatch (δ) at the (311) diffraction peak. The equation can be described as: δ = 2(αL12–αFCC)/(αL12 + αFCC), where α refers to the lattice constant for a specific phase. APT characterizations were performed in a CAMECA Instruments LEAP 5000XR local electrode atom probe. The specimens were analyzed in a voltage mode, at a specimen temperature of 70 K, a pulse repetition rate of 200 kHz, a pulse fraction of 0.2, and an ion collection rate of 0.5% ions per field evaporation pulse. Needle-shaped specimens required for APT were fabricated by lift-outs and annular milled in an FEI Scios focused ion beam/scanning electron microscope (FIB/SEM). Imago Visualization and Analysis Software version 3.8 was used for three-dimensional reconstructions and data analysis. The obtained compositions were used to evaluate the volume fraction of the FCC and L12 lamellae by using the level rule. The equation can be described as: ƒL12 = (cnominali–cFCCi)/(cL12i–cFCCi), where cnominali, cL12i, and cFCCi refers to the atomic ratio of element i in the nominal alloy composition, L12, and FCC phases, respectively. Plotting the concentration for each element species, and fitting the data to a linear relationship yields a slope, which is equal to the volume fraction of the L12 phase.
Mechanical tests. Room temperature tensile properties were evaluated using an MTS mechanical testing system with a strain rate of 10−3 s−1. Dog-bone shaped tensile specimens with a gauge length of 12.5 mm and a cross-section area of 3.2 × 0.7 mm2 were prepared using electrical-discharge machining. During tensile testing, a high-resolution strain extensometer was attached to the gauge length section, which ensures an accurate measurement of the yielding behavior and tensile ductility. At least three tensile samples for each condition were tested to obtain statistically valid results. In addition, larger-sized tensile samples with a gauge length of 25 mm and a gauge width of 5 mm were tested to verify the initial results, and the resulted mechanical properties are displayed in Supplementary Fig. 10. Fracture surfaces of tensile samples were examined by the FEI-SEM.
Thermodynamic and ab initio calculations
Thermodynamic calculations were performed by the Thermo-Calc 3.0.1 software with a Ni-based database (TTNi8). Ab initio calculation was performed using the Vienna ab initio simulation package (VASP)61,62 with the projector augmented wave63,64 method and the Perdew–Becke–Erzenhof65 exchange-correlation functional. A plane wave cutoff energy of 400 eV and a k-point mesh of 9 × 3 × 1 were used, and magnetism was considered. A vacuum layer of 25 Å was set in the 48 atoms FCC supercell, which was built by special quasirandom structure method66. The supercell composition was 17Fe-14Co-7Ni-9Cr-1Al, which is based on the matrix composition determined by APT. Supplementary Fig. 9 shows the method to build a SF in the FCC supercell, which has 12 different atomic layers in the direction perpendicular to the SF plane. Because the arrangements of atoms are disordered in the FCC phase, each atomic layer in the supercell was moved to build 12 derivative supercells containing different SF planes. The mean value of the 12 calculated results was taken as the average SF energy of the FCC phase.
Theoretical calculations of strengthening responses. It was documented that a Hall–Petch relationship also describes the yield strength of dual-phase nanolamellar materials25. In these materials, dislocations initially start to propagate inside the soft phase and pile-up at interphase boundaries. The yield occurs when the leading dislocation in a pile-up can overcome the barrier strength and transmit slip across the boundary. Thus, the parameters controlling the strength are the thickness and physical properties of the soft lamellae25. In the FCC/L12 CNL architecture, initial plastic deformation occurs in the soft FCC lamellae; thus, the parameters controlling the yield strength is the thickness and physical properties of the FCC lamellae. The strengthening contributed by the FCC/L12 boundaries can be described by \(\Delta \sigma _l = k_l(\lambda )^{ - 0.5}\), where kl is the Hall–Petch coefficient and λ is the average thickness of the FCC lamellae. The Hall–Petch coefficient kl can be calculated by67:
where n = ~4.5 is the number of dislocations crossing the same lamellae (obtained through TEM analysis of the 2% and 5% strained samples), G = 84 GPa is the shear modulus of the FCC phase68, \(b = \sqrt 2 a/2\) = 0.255 nm is the magnitude of the Burgers vector of the FCC phase, a = 0.3585 nm is the lattice constant of the FCC phase obtained from XRD, d = ~37 nm is the average lamellar thickness of the FCC lamellae. Using these data, the strengthening contribution by the nanolamellar boundaries was estimated to be ~1.0 GPa, which accounts for approximately a half of the total yield strength, providing the dominant contribution to the macroscopic yield strength.
The ultrafine grain structure also contributes considerably to the yield strength. The grain boundary strengthening can be described using the well-known Hall–Petch relationship \(\Delta \sigma _g = k_g(d)^{ - 0.5}\), where kg = ~516 MPa μm0.5 is the Hall–Petch coefficient, measured from an alloy having the composition of the FCC lamellae in the CNL alloy (Supplementary Fig. 11), and d = ~390 nm is the average grain size of the CNL alloy. The strengthening due to the ultrafine grains was calculated to be 0.8 GPa. Therefore, the total strengthening contributed by the lamellar and grain boundaries is ~1.8 GPa, accounting for as high as 90% of the total yield strength.
Data availability
The data that support the findings of this study are available from the corresponding authors on reasonable request.
Code availability
The VASP is a proprietary software available for purchase at https://www.vasp.at/.
References
Vecchio, K. S. Synthetic multifunctional metallic-intermetallic laminate composites. JOM 57, 25–31 (2005).
Liu, X. C., Zhang, H. W. & Lu, K. Strain-induced ultrahard and ultrastable nanolaminated structure in nickel. Science 342, 337–340 (2013).
Koyama, M. et al. Bone-like crack resistance in hierarchical metastable nanolaminate steels. Science 355, 1055–1057 (2017).
Wat, A. et al. Bioinspired nacre-like alumina with a bulk-metallic glass-forming alloy as a compliant phase. Nat. Commun. 10, 1–12 (2019).
Li, X., Wei, Y., Lu, L., Lu, K. & Gao, H. Dislocation nucleation governed softening and maximum strength in nano-twinned metals. Nature 464, 877–880 (2010).
Huang, C. X. et al. Interface affected zone for optimal strength and ductility in heterogeneous laminate. Mater. Today 21, 713–719 (2018).
An, X. H. et al. Atomic-scale investigation of interface-facilitated deformation twinning in severely deformed Ag-Cu nanolamellar composites. Appl. Phys. Lett. 107, 011901 (2015).
Zheng, S. et al. High-strength and thermally stable bulk nanolayered composites due to twin-induced interfaces. Nat. Commun. 4, 1–8 (2013).
Gleiter, H. Nanostructured materials: state of the art and perspectives. Nanostruct. Mater. 6, 3–14 (1995).
Koch, C. C., Morris, D. G., Lu, K. & Inoue, A. Ductility of nanostructured materials. MRS Bull. 24, 54–58 (1999).
Lu, Y. & Liaw, P. K. The mechanical properties of nanostructured materials. JOM 53, 31–35 (2001).
Kumar, K. S., Van Swygenhoven, H. & Suresh, S. Mechanical behavior of nanocrystalline metals and alloys. Acta Mater. 51, 5743–5774 (2003).
Wei, Y. et al. Evading the strength-ductility trade-off dilemma in steel through gradient hierarchical nanotwins. Nat. Commun. 5, 1–8 (2014).
Li, Z., Pradeep, K. G., Deng, Y., Raabe, D. & Tasan, C. C. Metastable high-entropy dual-phase alloys overcome the strength–ductility trade-off. Nature 534, 227–230 (2016).
Lei, Z. et al. Enhanced strength and ductility in a high-entropy alloy via ordered oxygen complexes. Nature 563, 546–550 (2018).
Gludovatz, B. et al. A fracture-resistant high-entropy alloy for cryogenic applications. Science 345, 1153–1158 (2014).
Ding, Q. et al. Tuning element distribution, structure and properties by composition in high-entropy alloys. Nature 574, 223–227 (2019).
Olson, G. B. Computational design of hierarchically structured materials. Science 277, 1237–1242 (1997).
Lu, K. Making strong nanomaterials ductile with gradients. Science 345, 1455–1456 (2014).
Wang, Y., Chen, M., Zhou, F. & Ma, E. High tensile ductility in a nanostructured metal. Nature 419, 912–915 (2002).
Orlov, D., Fujiwara, H. & Ameyama, K. Obtaining copper with harmonic structure for the optimal balance of structure-performance relationship. Mater. Trans. 54, 1549–1553 (2013).
Ma, E. & Zhu, T. Towards strength–ductility synergy through the design of heterogeneous nanostructures in metals. Mater. Today 20, 323–331 (2017).
Ovid’Ko, I. A., Valiev, R. Z. & Zhu, Y. T. Review on superior strength and enhanced ductility of metallic nanomaterials. Prog. Mater. Sci. 94, 462–540 (2018).
Vittori, M. & Mignone, A. On the antiphase boundary energy of Ni3(Al, Ti) particles. Mater. Sci. Eng. 74, 29–37 (1985).
Misra, A. Mechanical behavior of metallic nanolaminates. In Nanostructure control of materials (Woodhead, Cambridge, 2006).
Lu, J. et al. Stacking fault energies in austenitic stainless steels. Acta Mater. 111, 39–46 (2016).
Hirth, J. & Lothe, J. Theory of Dislocations (Wiley, New York, 1982).
Wu, X. L., Zhu, Y. T., Wei, Y. G. & Wei, Q. Strong strain hardening in nanocrystalline nickel. Phys. Rev. Lett. 103, 205504 (2009).
Chen, S. et al. Real-time observations of TRIP-induced ultrahigh strain hardening in a dual-phase CrMnFeCoNi high-entropy alloy. Nat. Commun. 11, 1–8 (2020).
Laplanche, G., Kostka, A., Horst, O. M., Eggeler, G. & George, E. P. Microstructure evolution and critical stress for twinning in the CrMnFeCoNi high-entropy alloy. Acta Mater. 118, 152–163 (2016).
Chiba, A., Hanada, S. & Watanabe, S. Improvement in ductility of Ni3Al by γ former doping. Mater. Sci. Eng. A 152, 108–113 (1992).
Stoloff, N. S. Physical and mechanical metallurgy of Ni3Al and its alloys. Int. Mater. Rev. 34, 153–184 (1989).
Yang, T. et al. Multicomponent intermetallic nanoparticles and superb mechanical behaviors of complex alloys. Science 362, 933–937 (2018).
Yang, T. et al. Ultrahigh-strength and ductile superlattice alloys with nanoscale disordered interfaces. Science 369, 427–432 (2020).
Chong, Y. & Tsuji, N. The Effect of Initial Microstructure on the Mechanical Properties of Bi-lamellar Ti-6Al-4V. In TMS 2016 145th Annual Meeting & Exhibition 633-640 (Springer, Cham. 2016).
Shin, S., Zhu, C., Zhang, C. & Vecchio, K. S. Extraordinary strength-ductility synergy in a heterogeneous-structured β-Ti alloy through microstructural optimization. Mater. Res. Lett. 7, 467–473 (2019).
Baker, I. & Meng, F. Lamellar coarsening in Fe28Ni18Mn33Al21 and its influence on room temperature tensile behavior. Acta Mater. 95, 124–131 (2015).
Nakamoto, Y., Yuasa, M., Chen, Y., Kusuda, H. & Mabuchi, M. Mechanical properties of a nanocrystalline Co–Cu alloy with a high-density fine nanoscale lamellar structure. Scr. Mater. 58, 731–734 (2008).
Guha, S., Munroe, P. R. & Baker, I. Room temperature deformation behavior of multiphase Ni-20at.%Al-30at.% Fe and its constituent phases. Mater. Sci. Eng. A 131, 27–37 (1991).
Yang, Z. N., Zhang, F. C., Liu, F. C., Yan, Z. G. & Xiao, Y. Y. Achieving high strength and toughness in a Zr–2.3 Nb alloy by the formation of duplex microstructure. Mater. Des. 40, 400–406 (2012).
Shi, P. et al. Enhanced strength–ductility synergy in ultrafine-grained eutectic high-entropy alloys by inheriting microstructural lamellae. Nat. Commun. 10, 1–8 (2019).
Reddy, S. R. et al. Nanostructuring with structural-compositional dual heterogeneities enhances strength-ductility synergy in eutectic high entropy alloy. Sci. Rep. 9, 1–9 (2019).
Chen, G. et al. Polysynthetic twinned TiAl single crystals for high-temperature applications. Nat. Mater. 15, 876–881 (2016).
Liu, Y. et al. Effects of microstructure and crystallography on mechanical properties of cold-rolled SAE1078 pearlitic steel. Mater. Sci. Eng. A 709, 115–124 (2018).
Zhou, L., Wang, L., Chen, H., Xie, Z. & Fang, F. Effects of chromium additions upon microstructure and mechanical properties of cold drawn pearlitic steel wires. J. Mater. Eng. Perform. 27, 3619–3628 (2018).
García-Mateo, C. & Caballero, F. G. The role of retained austenite on tensile properties of steels with bainitic microstructures. Mater. Trans. 46, 1839–1846 (2005).
Bouaziz, O., Barbier, D., Cugy, P. & Petigand, G. Effect of process parameters on a metallurgical route providing nano-structured single phase steel with high work-hardening. Adv. Eng. Mater. 14, 49–51 (2012).
Lyu, S., Sun, Y., Ren, L., Xiao, W. & Ma, C. Simultaneously achieving high tensile strength and fracture toughness of Ti/Ti-Al multilayered composites. Intermetallics 90, 16–22 (2017).
Xu, S. et al. Compositionally gradient Ti-Ta metal-metal composite with ultra-high strength. Mater. Sci. Eng. A 712, 386–393 (2018).
Shingu, P. H., Ishihara, K. N., Otsuki, A. & Daigo, I. Nano-scaled multi-layered bulk materials manufactured by repeated pressing and rolling in the Cu–Fe system. Mater. Sci. Eng. A 304, 399–402 (2001).
Wang, Y., Li, J., Hamza, A. V. & Barbee, T. W. Ductile crystalline-amorphous nanolaminates. Proc. Natl Acad. Sci. 104, 11155–11160 (2007).
Nizolek, T., Beyerlein, I. J., Mara, N. A., Avallone, J. T. & Pollock, T. M. Tensile behavior and flow stress anisotropy of accumulative roll bonded Cu-Nb nanolaminates. Appl. Phys. Lett. 108, 051903 (2016).
Inoue, J., Nambu, S., Ishimoto, Y. & Koseki, T. Fracture elongation of brittle/ductile multilayered steel composites with a strong interface. Scr. Mater. 59, 1055–1058 (2008).
Liddicoat, P. V. et al. Nanostructural hierarchy increases the strength of aluminium alloys. Nat. Commun. 1, 1–7 (2010).
Dalla Torre, F., Van Swygenhoven, H. & Victoria, M. Nanocrystalline electrodeposited Ni: microstructure and tensile properties. Acta Mater. 50, 3957–3970 (2002).
Liu, G. et al. Nanostructured high-strength molybdenum alloys with unprecedented tensile ductility. Nat. Mater. 12, 344–350 (2013).
Wei, Q. & Kecskes, L. Effect of low-temperature rolling on the tensile behavior of commercially pure tungsten. Mater. Sci. Eng. A 491, 62–69 (2008).
Du, X. H. et al. Dual heterogeneous structures lead to ultrahigh strength and uniform ductility in a Co-Cr-Ni medium-entropy alloy. Nat. Commun. 11, 1–7 (2020).
Ross, C. A. Electrodeposited multilayer thin films. Annu. Rev. Mater. Sci. 24, 159–188 (1994).
Jankowski, A. F. Vapor deposition and characterization of nanocrystalline nanolaminates. Surf. Coat. Tech. 203, 484–489 (2008).
Kresse, G. & Hafner, J. Ab initio molecular-dynamics simulation of the liquid-metal–amorphous-semiconductor transition in germanium. Phys. Rev. B 49, 14251 (1994).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Zunger, A., Wei, S. H., Ferreira, L. G. & Bernard, J. E. Special quasirandom structures. Phys. Rev. Lett. 65, 353 (1990).
Caillard, D. & Couret, A. The Hall-Petch law investigated by means of in situ straining experiments in lamellar TiAl and deformed Al. Microsc. Res. Tech. 72, 261–269 (2009).
Wu, Z., Bei, H., Pharr, G. M. & George, E. P. Temperature dependence of the mechanical properties of equiatomic solid solution alloys with face-centered cubic crystal structures. Acta Mater. 81, 428–441 (2014).
Acknowledgements
This research was supported by the Early Career Scheme from the Research Grants Council (RGC) of Hong Kong (no. 25202719) and the National Natural Science Foundation of China (no. 51801169), and internal research fund from PolyU (nos. P0009738 and P0013994). C.T.L. is grateful for the financial support from Hong Kong RGC with grant nos. 11213319 and 11202718. The ab initio calculation was supported by Advanced Computing East China Sub-center. We thank M.C. Niu from The Hong Kong Polytechnic University and H.J. Kong from City University of Hong Kong for technical assistance with mechanical tests and TEM characterization.
Author information
Authors and Affiliations
Contributions
Z.B.J. and C.T.L. designed the research. L.F. prepared materials and conducted mechanical testing. L.F., T.Y., and Y.L.Z. carried out XRD, EBSD, and TEM. J.H.L. conducted 3D-APT. G.Z. and H.W. performed ab initio calculations. L.F., T.Y., Z.B.J., and C.T.L. analyzed the data and discussed the results. L.F., Z.B.J., and C.T.L. wrote the manuscript. All authors reviewed and contributed to the final manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no conflict of interest.
Additional information
Peer review information Nature Communications thanks Hyoung Seop Kim, Robert Ritchie and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Fan, L., Yang, T., Zhao, Y. et al. Ultrahigh strength and ductility in newly developed materials with coherent nanolamellar architectures. Nat Commun 11, 6240 (2020). https://doi.org/10.1038/s41467-020-20109-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-20109-z
This article is cited by
-
An order-disorder core-shell strategy for enhanced work-hardening capability and ductility in nanostructured alloys
Nature Communications (2024)
-
Harnessing instability for work hardening in multi-principal element alloys
Nature Materials (2024)
-
Simultaneous enhancement of strength and conductivity via self-assembled lamellar architecture
Nature Communications (2024)
-
Effect of Nb-content on the corrosion resistance of Co-free high entropy alloys in chloride environment
Tungsten (2024)
-
Effect of Al on the microstructure, mechanical properties, and wear resistance of TiVZrNbAlx alloys
Journal of Materials Science (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.