Abstract
A defining characteristic of the recent geomagnetic field is its dominant axial dipole which provides its navigational utility and dictates the shape of the magnetosphere. Going back through time, much less is known about the degree of axial dipole dominance. Here we use a substantial and diverse set of 3D numerical dynamo simulations and recent observation-based field models to derive a power law relationship between the angular dispersion of virtual geomagnetic poles at the equator and the median axial dipole dominance measured at Earth’s surface. Applying this relation to published estimates of equatorial angular dispersion implies that geomagnetic axial dipole dominance averaged over 107–109 years has remained moderately high and stable through large parts of geological time. This provides an observational constraint to future studies of the geodynamo and palaeomagnetosphere. It also provides some reassurance as to the reliability of palaeogeographical reconstructions provided by palaeomagnetism.
Similar content being viewed by others
Introduction
A primary feature of the geomagnetic field today is its strong axial dipole (AD) component which provides an effective shield against the solar wind1,2 helping to make the planet habitable3. The field is highly variable in time however and our knowledge of its morphology declines rapidly as we go back in geological history. At a given instance, the degree of AD dominance over the remaining non-axial dipole (NAD) components at Earth’s surface may be expressed, here, in terms of the Lowes power4 for the magnetic field energy (W) as5
where
and
Here \(g_n^m\) and \(h_n^m\) are the Gauss coefficients of degree n and order m for the spherical harmonic expansion of the geomagnetic potential6; \(g_1^0\) is the AD component.
The current geomagnetic field has AD/NAD of ~10 (Fig. 1) but, according to time-dependent global magnetic field models7,8,9,10,11, this has varied by more than one order of magnitude on timescales of kyr (Supplementary Fig. 1) over the last 100 kyr. By definition, AD/NAD must briefly fall to zero during a polarity reversal and can also fall far below unity during excursions7. To avoid biasing by brief extreme events, we will take the median of the instantaneous AD/NAD ratios which we call AD/NADmedian as our measure of average AD dominance. We note that this value is a first-order description of the average, time-instantaneous field morphology and is not intended as a direct measure of the validity of the geocentric axial dipole (GAD12) hypothesis, which rather would rely on the morphology of the time-average field (TAF). The TAF is defined by time-averaging all Gauss coefficients independently before using their ratios to define its properties, which may be very different to the properties of the instantaneous field at any and all times. For example AD/NADTAF is, by definition, infinite for a GAD field whereas the associated AD/NADmedian value may be finite and even small. In this sense, AD/NADmedian is more relevant to those using palaeomagnetic records to understand geomagnetic behaviour, core dynamics and the magnetospheric shielding it confers than to those interested in making tectonic reconstructions. The implications of this study for palaeogeographical reconstructions is nevertheless explored later.
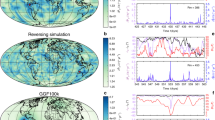
The dynamo simulations (first three columns) show the tendency of AD/NADmedian to increase as VGP dispersion decreases. The first row is a snapshot of radial field at the Earth’s surface taken from a timestep with AD/NAD close to its median for the time series shown in the second row (median shown as red line; note the semi-log scale). The third row represents palaeosecular variation as presented in studies of ancient time periods (but with far more data); the red line represents the best Model G fit (parameters a and b provided) to the entire data set of 500 randomly drawn timesteps (blue circles) sampled at each of 324 regularly placed locations (see the “Methods” section). Final column: equivalent plots for observational geomagnetic models11,63 and a palaeosecular variation dataset from last 10 Myr19. Note that AD/NAD for IGRF2015 is 9.6 and AD/NADmedian for gufm1 is 16.4. The red shaded area around the Model G fit to the empirical data represents 95% confidence bounds.
Direct estimates of AD/NADmedian and other useful ratios are possible from statistical field models based on the Giant Gaussian Process13,14,15,16,17 spanning back to 10 Ma (Supplementary Table 1). Previous efforts to assess the average morphology of the palaeomagnetic field prior to 10 Ma have been forced to rely on the Model G approach18 to analysing palaeomagnetic secular variation data. This relies on measurements of the angular dispersion (S; see the “Methods” section) of virtual geomagnetic poles (VGPs) recovered from collections of palaeomagnetic recorders (normally lavas). Model G has the form of a second-order polynomial:
where a and b are constants that define the value of S at the equator and the rate of its increase with palaeolatitude (λ), respectively. Using PSV10, a recent compilation of palaeomagnetic secular variation data from rocks formed within the last 10 Myr19, these Model G constants, given together with their 95% confidence limits, were recently calculated20 as \(a = 11.3_{ - 1.1}^{ + 1.3^\circ }\) and \(b = 0.27_{ - 0.08}^{ + 0.04}\). For older datasets, the palaeolatitude must be estimated using the palaeomagnetic data themselves and this approach was simulated here (see “Methods” section).
Using insights from mean-field kinematic dynamo theory and the modern field, McFadden et al. 18 made the case that Model G could be used to represent the relative importance of two independent dynamo “families”. The constant a denoted the magnitude of the secular variation in the “quadrupole family” comprising those spherical harmonic terms which are symmetric with respect to the equator (and include the equatorial dipole terms). Likewise, b did the same for anti-symmetric terms (including the AD) comprising the “dipole family”. In the context of this approach, intervals of time whereby the AD and related antisymmetric terms were particularly dominant over the symmetric terms should be recognisable through increased values of b relative to a in Model G fits to PSV datasets. Such intervals have previously been argued to include the Cretaceous Normal Superchron21,22,23 and much of Precambrian time5,24,25,26,27 but these claims are difficult to verify since the premise on which Model G fits are interpreted is oversimplified28.
Here we develop and apply a more robust approach to ascertaining information regarding the morphology of the ancient geomagnetic field using palaeosecular variation data. The power law that we derive is used to obtain quantitative estimates of ancient AD dominance showing that this has been maintained at near-present-day values for much of Earth history.
Results and discussion
Model G relationships from dynamo simulations
For the purposes of this study, we use the outputs of 61 numerical dynamo simulations (see “Methods” section; Supplementary Data 1) which were required to be run for a sufficient amount of time (>100 kyr) to obtain a reasonable temporal sampling of the simulated magnetic field behaviour at the Earth’s surface. Each model was distinct in terms of its input parameters and diverse physical ingredients were represented. These included homogeneous and heterogeneous outer boundary heat flux conditions and small and present-day inner core sizes. Models with internal heating sources derived from radiogenic heating, with a stably stratified layer at the top of the core, as well as models where convection is purely chemically driven were also employed (see “Methods” section). The resulting field behaviour ranges from exhibiting S and AD/NADmedian values much greater than the Earth’s values for recent times to much lower values (Fig. 1). In most cases, Model G (after applying a variable cutoff29 for outliers in VGP distributions) provided a good, though not perfect, fit to VGP dispersion data across the apparent latitudes (Supplementary Data 1) yielding root mean square error (RMSE) values with a median across all models of 1.2°. Model G a and b parameters are positively correlated as are the powers of the Gauss coefficients (except \(g_1^0\)) with degree and order that sum to odd values (WODD) and even values (WEVEN) (Supplementary Fig. 2). As VGP dispersion increases, so does its latitudinal dependence and this reflects increases in the nonaxial-dipole field being partitioned similarly into antisymmetric (given by WODD) and symmetric (given by WEVEN) terms. We also note in passing that less dipolar simulations in particular tended to produce more complicated curves with an equatorial peak in VGP dispersion (see e.g. LEDA001 in Fig. 1). This implies that a reasonable latitudinal distribution of observations is required to obtain both Model G parameters to a good degree of accuracy.
Having ascertained that the structure of Model G (Eq. (4)) provides efficient two-parameter descriptions for a wide range of simulated PSV behaviour, we explored the potential of these simple quadratic fits to predict average morphological characteristics of the generated fields defined as both the median instantaneous and the TAF (Supplementary Fig. 3). The most striking observation is a strong power-law relation between Model G a parameter (average VGP dispersion at the equator; Eq. (4)) and AD/NADmedian (Fig. 2) that in log–log space reads
where the constants and their 95% confidence limits were obtained from standard linear regression: k1 = −2.26 ± 0.13; k2 = 3.44 ± 0.16. We also observe the following: (1) since Model G a and b parameters co-vary (Supplementary Fig. 2a), the latter is also correlated with AD/NADmedian but here the relationship is not quite so strong (Supplementary Fig. 3c); (2) the relatively weak relationship between b/a and O/E implies that the original morphological interpretation of Model G parameters in terms of independent families of equatorially symmetric and antisymmetric spherical harmonic terms5,18,22 is only moderately supported by our dynamo simulations (Supplementary Fig. 3a, d); (3) intuitively, Model G parameters provide much stronger constraints on the average instantaneous field morphology (Supplementary Fig. 3a–c) than the morphology of the time-averaged field (Supplementary Fig. 3d–f).
The power law (5) presents a potentially powerful new tool linking geomagnetic secular variation and morphology. While the broad observation that enhancing AD dominance suppresses VGP dispersion may be considered intuitive28, the correlation and significance of the power law (Adj. R2 = 0.955, P < 10−5, number of data, N = 61, Spearman rank coefficient ρ = 0.971) is remarkably and unexpectedly high. We note that a power-law relationship with similar parameters may also be predicted from simple theoretical arguments (see Supplementary Note 1).
Testing the correlation using observation-based field models
To ascertain whether time-varying and statistical field models of PSV derived from palaeo-magnetic and geo-magnetic observations yield estimates of AD/NADmedian and Model G a values which are consistent with the power law in Fig. 2, we apply the same analytical approach (see “Methods” section) to a selection of these (Supplementary Table 1)7,8,10,11,13,14,15. Although similarly represented by sets of Gauss coefficients, the methods of generating these field descriptions are fundamentally distinct to those used to obtain the outputs of the dynamo simulations. While dynamo simulations model field behaviour by numerically solving equations governing the outer core magnetohydrodynamic processes responsible for it, observational models are defined by fitting spatially and temporally restricted datasets of palaeomagnetic, archaeomagnetic and geomagnetic measurements and their associated age estimates. Another important difference is that three of these observational models are restricted to intervals of 9–20 kyr which may be too short to capture time-averaged field behaviour30. The statistical models, on the other hand, assume that the statistical properties of palaeosecular variation can be modelled by a “Giant Gaussian Process”, whereby the Gauss coefficients are randomly drawn from normal distributions with means and variances set to produce the desired characteristics of palaeosecular variation and the time-averaged field13,14,15,16,17 (all models assume independently distributed Gauss coefficients except those of ref. 16, which assumes a covariance among a select set of Gauss coefficients).
Given the above and the varied AD/NADmedian values produced by these observational models (red circles in Fig. 2) it is remarkable to observe the Model G parameters are all found close to the power law derived from the dynamo simulations. Indeed, they all fall within an interval (dashed lines) where 95% of future models are predicted to fall according to a t-distribution (see “Methods” section). We note that we are not overly concerned here with the relative realism of any of the outputs shown by these models, merely the ability of their output palaeosecular variation to predict their average morphology.
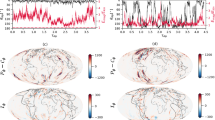
The robust nature of this geometric relationship is also supported by the results of an analysis summarised in Fig. 3a and Supplementary Fig. 3. Here, the \(g_1^0\) term produced at each timestep (or realisation) from three dynamo simulations and one Giant Gaussian Process was rescaled to produce values of AD/NADmedian that were radically different from that which the model originally produced (see Supplementary Note 2 for more details). Doing so simultaneously affected the angular dispersion of VGPs such that the resulting a parameter of the Model G fit fell within the prediction bounds of the earlier derived power law (Fig. 3a). This demonstrates that, so long as the power spectrum of the nondipole field is consistent with any of these models, the relationship is robust to a large range of AD/NADmedian values.
a Effects of arbitrarily rescaling the axial dipole term at every realisation using four models shown in Fig. 1 (see Supplementary Note 2 for details and Supplementary Fig. 3 for individual Model G fits). Original model outputs (large symbols) are diverse; rescaled models (small symbols) can have entirely different values of AD/NADmedian to the original but the corresponding Model G fit adjusts simultaneously such that each point remains within the 95% prediction bounds derived from Fig. 2. b Results of a sliding window analysis using time series from the same four models as in Fig. 1. In each case, the sliding window of length given by the x-axis was moved from the start of the time series through to the end in window steps of 1−20 kyr (adjusted for the total time series length) drawing 15 random timesteps from each of 19 random locations on the surface of the Earth. Estimates of AD/NADmedian made using the power law in Fig. 2 were defined as accurate if they were within calculated uncertainties of the actual value of AD/NADmedian for that specific time window. See Supplementary Fig. 5 for individual plots of the AD/NADmedian time series and estimates from windows sliding along it. c Effects of down-sampling (15 timesteps at each of 19 locations) on 61 dynamo models and 12 observational models on their adherence to the power law shown in Fig. 2. Model G a parameters were calculated from the downsampled dataset whereas AD/NADmedian values were calculated directly from the models using every timestep. The overlaps of the majority of calculated uncertainties on Model G a parameters with the prediction bounds ascertained from Fig. 2 indicates that this method of estimating AD/NADmedian values from the Model G fit is reliable for palaeomagnetically feasible datasets.
Based on the evidence presented in Figs. 2 and 3a, Eq. (5) and its associated prediction bounds appear consistent with all available empirical and synthetic datasets. We therefore consider it to provide a robust description of the relationship between geomagnetic variability and morphology allowing reliable estimates of one to act as a proxy for the other.
Estimating the ancient geomagnetic AD dominance
Figure 3b, c and Supplementary Fig. 4 demonstrate two further useful properties of the power-law relation outlined above. Firstly, although AD/NADmedian may change significantly for subintervals within a single model time series, the associated Model G a parameter from the same subinterval also shifts according to the power law. This implies that selections of palaeomagnetic datasets from any interval duration may be useful for estimating the average AD dominance for that same interval. A caveat is that the interval must be sufficiently long such that significant serial correlation of VGP positions is avoided. Based on our sliding window analysis of both observational models and dynamo simulations (Fig. 3b, Supplementary Fig. 4), 50–100 kyr appears to be sufficient for this purpose; this duration is similar to earlier estimates of the time necessary to sample the time-averaged field30.
The second useful property of the power-law relation is that it remains capable of accurately estimating AD/NADmedian even when the number of locations and time steps used to construct the Model G curve are reduced to values that are well within the bounds of palaeomagnetic datasets available for ancient intervals. Table 1 presents a selection of recent published estimates of Model G a parameters for intervals extending back into the Archaean19,20,27. The smallest number of locations comprising any single one of these datasets is 19, while the smallest median number of sampling sites per location (representative of time steps) is 15. These values were used as conservative inputs for the downsampling of models (see “Methods“ section) whose results are summarised in Fig. 3c (see also Supplementary Fig. 4). So long as the interval is sufficiently long (>50 kyr), the estimates of AD/NADmedian were found to be nearly always reliable (accurate, if not necessarily precise).
Figure 4a presents estimates of AD/NADmedian calculated using the Model G a parameter for the five studied intervals listed in Table 1. In each case, the Model G parameters were taken directly from the publications and required application of the Vandamme cutoff29 as used for all models here. These intervals are far longer than the time spanned by any one of the individual estimates of VGP angular dispersion from which the Model G fits were constructed. Furthermore, in the earlier intervals in particular, there are large gaps in the age distribution of the rocks used to obtain the estimate. Therefore, values of AD/NADmedian cited for each period should be considered as weighted towards sub-intervals with denser data coverage (Fig. 4a) and may not be representative of sub-intervals (of which 600–1100 Ma is the most striking) where no or very little data currently exists. A further point to note is that AD/NADmedian values will also be more heavily influenced by those rock units with low apparent palaeolatitudes since they exert more influence on the a parameter of the Model G fit.
a Application of the power law in Fig. 2 to ascertain the first quantitative estimates of axial dipole dominance in deep time (see Table 1). Horizontal range of boxes indicates nominal time range; vertical range indicates 95% uncertainties with numerical bounds provided. Crosses relate to age of one or more rock units comprising the estimate within the box. Reversal frequency was calculated using 10 Myr bins38. b Relationship between palaeosecular variation and time-averaged inclination anomaly in outputs of dynamo models (blue circles). Shaded area represents 95% confidence bounds. Dataset from the last 10 Myr19 (purple square) is shown to fit the linear trend well. Extrapolations of inclination anomalies (ΔInc) are made using median a parameters for four earlier datasets shown in panel a.
The above caveats notwithstanding, the degree of stationarity displayed by our obtained estimates of AD/NADmedian is remarkable (Fig. 4a). Uncertainty limits on AD/NADmedian, calculated by combining uncertainties associated with the Model G a parameters with the power-law prediction bounds, render each time interval indistinguishable from the rest. Furthermore, the total range observed in estimated AD/NADmedian values (including 95% uncertainty limits) from 3.5 to 45.0 encompasses the values derived from observation-based field models covering intervals in more recent geological time (Fig. 2).
While AD dominance apparently changes rapidly on short timescales (Supplementary Fig. 1) and is prone to collapse during geomagnetic excursions and reversal transitions, we presently find no evidence that its average over 107–109 year timescales is subject to significant variations. Given that AD/NAD must instantaneously reach zero for a reversal to take place, a particularly surprising insight is that intervals with substantially different reversal frequencies (e.g. the last 10 Myr, the Cretaceous Normal Superchron, and the early Cretaceous–Jurassic) apparently yield nearly identical values of AD/NADmedian (Fig. 4a). This implies that, regardless of how frequently AD/NAD undergoes brief collapse, the field recovers to spend most of its time in a similarly dipole dominated state. Intervals of stable average AD dominance also apparently coincided with significant variations in long-term average field intensity31,32,33. This further suggests that the magnitude of the AD and NAD field are correlated on long-timescales such that the degree of AD dominance remains approximately constant. These coupled observations may be used as constraints for future geodynamo modelling studies seeking to capture long-term variations in geomagnetic field behaviour.
Changes in aspects of geodynamo behaviour are thought likely to result from secular changes in core cooling modulated by mantle convection over the last several billion years33,34,35,36,37,38,39. Indeed the changing nature of the forcing of outer core convection from both above and below implies that it is already a challenge to explain how the geomagnetic field has been continuously sustained over Earth history40. Here we add the further constraint that models should produce a similar average geomagnetic field morphology for much of a time period where the Earth has seen its liquid core nucleate and grow an inner core41 and the mantle undergo several supercontinent cycles42 with consequences expected for core-mantle heat flow and its pattern43.
Almost all of the numerical dynamo simulations performed in a study44 aiming to elucidate the magnetic signature of inner core nucleation gave values of AD dominance within the range implied by the palaeomagnetic datasets used here. This suggests that diverse core geometries, control parameters, forcing conditions, etc., are capable of giving rise to field morphologies similar to those associated with Earth in the past. Nevertheless, it is important to highlight that our analysis of palaeomagnetic datasets does not rule out exotic field morphologies (e.g. extreme multipolar or equatorial dipole dominated45) existing for some times in the past. These could be missed either because of insufficient palaeomagnetic data coverage (Fig. 4) or because their behaviour (and especially their power spectra) is outside the range of models used to constrain the power-law tested here.
Our findings also have implications for Earth’s palaeo-magnetosphere and the long-term shielding of Earth’s atmosphere from solar wind. The strong and dominantly axial dipolar morphology of the present-day geomagnetic field is an efficient one for reducing fluxes of energetic particles into Earth’s upper and middle atmosphere and restricting these to high latitudes46. Large reductions in AD dominance, even while maintaining the same dipole moment (e.g. in a pure dipole rotation scenario) are expected to cause polar caps, auroral zones and atmospheric impacts of solar energetic particles to migrate to lower latitudes1,47. For the time periods considered, our results suggest that such major decreases in AD dominance are relatively rare, being restricted to the extremes of reversals and excursions.
A primary application of palaeomagnetism is to produce palaeogeographic reconstructions, making use of the GAD assumption to relate changes in mean inclination to inferred shifts in palaeolatitude. Values of AD/NADmedian cannot be interpreted directly as measures of the validity of the GAD approximation of the time-averaged field because they are constructed using different averaging processes (specifically, the former is the average of multiple instantaneous global field morphologies, whereas the latter is the field produced by the average of multiple directional measurements, i.e. the time-averaged power spectrum, and yields AD/NADTAF values in these models of approximately one order of magnitude higher). Nevertheless, our dynamo simulations do show correlations between their Model G parameters and AD/NADTAF (Supplementary Fig. 3) and, most usefully, exhibit a statistically significant relationship between the Model G a parameter, used here to estimate the AD/NADmedian values, and the maximum absolute inclination anomaly, a direct and commonly used (e.g. ref. 18) measurement of the validity of GAD (Fig. 4b; see “Methods” section). Furthermore, our actual measurements of these two parameters using rocks from the last 10 million years19 also fit this trend very well. We point out that while the peak inclination anomalies in both the dynamo models and the PSV10 dataset tend to produce shallower than expected directions, the peak in the models is nearly always observed at latitudes of 25–30° (north or south; Appendix 1) whereas in the data it is within 10° of the equator19. If we nevertheless take the relationship in Fig. 4b at face value, the range of published Model G a parameters from much older datasets suggest that its violations for the time periods studied here are unlikely to be much more severe than that measured for the last 10 Myr. A recent study48 claimed that the model underlying the inclination anomalies measured for the past 10 Myr may be GAD; if this is true, then we cannot discount GAD for any of the periods examined here.
The overall picture emerging from this study is of a geomagnetic field whose average morphology has been extraordinarily uniformitarian in the face of substantial changes in geodynamo forcing that impacted on its strength and tendency to reverse polarity. It should be emphasised that this does not preclude the past occurrence of intervals of sustained highly anomalous field behaviour that also presented distinctive morphological characteristics (e.g. the mid-Palaeozoic49,50 and Ediacaran33,51 are both potential candidates for such times). It would, however, seem to require that such intervals are relatively rare and do not include the most recent superchron.
Methods
Calculation of virtual geomagnetic pole dispersion and Model G fits
Outputs of magnetic field at Earth’s surface were extracted from numerical dynamo and observational models in the form of 120 Gauss coefficients (i.e. up to degree and order 10) for each regularly spaced time realisation. We truncate the numerical dynamo simulation results to degree and order 10 in order to make them compatible with the highest resolution available in the observational models considered here.
In all analyses, except for those employing “down sampling” (Fig. 3b, c and Supplementary Fig. 4), 324 locations spaced 20° apart in longitude (between 0° and 340°) and 10° apart in latitude (between −85° and 85°) were analysed and 500 different sets of random timesteps were chosen at each of these. Note that this geographical sampling was deliberately chosen to be far from uniform (being very heavily concentrated at high latitudes) in order to define Model G equally well at all latitudes.
From each set of Gauss coefficients, we synthesised a magnetic field vector at the specified location and used its direction (expressed by declination and inclination) to represent an independent palaeomagnetic direction. Conversion to VGPs followed standard palaeomagnetic convention52. VGPs were then grouped by location, flipped to give a common polarity (i.e., the VGPs falling into the southern hemisphere were replaced by antipodal locations in the northern hemisphere), and used to produce 324 estimates of apparent palaeolatitude (λ) and VGP dispersion (S). λ was calculated using the great-circle distance between the mean VGP position and the site location. S was initially defined from the root mean square angular distances (Δi) between the ith VGP and the mean VGP position according to
where N is the total number of VGPs (500 in this case). This approach has been applied to all palaeomagnetic datasets used in our study, except for the 0–10 Ma dataset, and was therefore simulated here.
An iterative procedure was then used to exclude outliers at each location caused by reversal transitions and excursions following the well-established variable cut-off approach of Vandamme29.
Model G (Eq. (4)) was fit to curves comprising the 324 λ–S pairs calculated above using a least-squares minimisation algorithm within the optimisation toolbox of Matlab using a bounded search, where the limits are conservatively set for Model G a and b parameters (1–90° and 0–1, respectively). With the exception of the lower bound for b, all Model G fits fall far from the boundaries used in the minimisation.
The procedure for obtaining Model G parameters from down-sampled models was identical to the above except that N at each location was reduced from 500 to 15 and the number of locations was reduced from 324 to 19 which were randomly drawn from a uniform distribution on a sphere.
Numerical dynamo simulations
Most of the numerical geodynamo models employed in this study have been extensively described elsewhere53,54,55,56,57 and we thus outline only the essentials here. An electrically conducting and convecting Boussinesq fluid is confined in a spherical shell of thickness d = ro − ri, where ri and ro denote the inner and outer boundary radii, respectively. The spherical shell rotates about the vertical direction with angular frequency Ω. As detailed in ref. 56, we solve numerically the momentum equation for the fluid velocity u in the co-rotating frame of reference, the induction equation for the magnetic field B, and an equation of evolution for the temperature perturbations T. The equations are non-dimensionalised using the shell thickness d as length scale, the core magnetic diffusion time \(\tau _\eta = d^2/\eta\) as time scale, while \(\left( {2{\Omega}\rho \mu _0\eta } \right)^{1/2}\) serves to rescale the magnetic field. Here η denotes the outer core magnetic diffusivity, ρ the core fluid density, and μ0 the vacuum permeability. Five dimensionless parameters control the system: the shell aspect ratio
the Ekman number
the Prandtl number
the magnetic Prandtl number
and the modified Rayleigh number
Here ν, κ, and α are the fluid kinematic viscosity, thermal diffusivity, and thermal expansivity respectively; go is gravity at the outer boundary and δT is a temperature scale that depends on the temperature boundary conditions and on the internal heating mode (see refs. 53,55 for further details).
Supplementary Data 1 provides values of the above input parameters for all the numerical simulations employed in this study. All simulations have Pr = 1. With the exception of three models with smaller inner core sizes, we consider a present-day outer core aspect ratio of χ = 0.35. All simulations employ no-slip flow boundary conditions and consider an electrically insulating mantle. The inner core can be either electrically insulating or conducting. As for the thermal boundary conditions, fixed heat flux (FF) is imposed at ro in all simulations. FF or fixed temperature (FT) conditions are used at ri. Some simulations employ spatial variations in the outer boundary heat flux. In most of these cases, the imposed heat flux heterogeneity pattern is a recumbent spherical harmonic of degree 2 and order 0 (recumbent \(Y_2^0\)) that approximates the large-scale structure of the observed lower mantle seismic shear-wave anomalies57,58. Three models are instead based on the lower mantle tomographic model of shear-wave velocity of ref. 59. The heterogeneity amplitude is defined by the parameter
where qmin and qmax are the minimum and maximum values of the outer boundary heat flux, respectively, and 〈q〉 is its surface mean value. Values of \({\it{\epsilon }}\) range from 0.3 to 1.5 in our numerical simulations (see Supplementary Data 1).
In the suite of simulations considered in this study, 37 have been reported in ref. 55 (a subset of these are previously published models; see Supplementary Table 1) and we thus do not describe them in detail here. We additionally employed 24 new simulations here. Among these, three include a uniform internal heat source term in the temperature equation modelling the presence of radiogenic heating (or secular cooling of the core). In several of these new models convection is purely chemically driven, that is the source of buoyancy is the release of light elements at the inner core boundary as the inner core freezes. Finally, some models allow for the presence of a stably stratified layer at the top of the core. We now briefly describe the formulation employed to model these different physical characteristics of the core. The equation of evolution for the temperature perturbations T around the background (adiabatic) reference state is
Here \(q = \kappa /\eta\) is the Roberts number, which is related to the input model parameters by \(q = {\rm{{Pm}}}/{\rm{{Pr}}}\), and γ is a uniform volumetric sink (γ < 0) or source (γ > 0) term. The stationary background temperature profile is given by
with \(\gamma = \gamma \prime d^2/\kappa \delta T\), where γ′ denotes the dimensional heat source/sink amplitude. A volumetric sink term and a zero heat flux condition at the outer boundary are appropriate for modelling purely chemical convection60,61. In this case, the variable T here is interpreted as the relative concentration of light elements in the core that are released at the inner core boundary. From Eq. (M9), a zero flux condition at ro sets the value of the sink term to \(\gamma = - 3\left( {1 - \chi } \right)^3\). For χ = 0.35, the present-day outer core aspect ratio, then \(\gamma \approx - 0.824 = \gamma _0\). For values γ < γ0, the neutrally buoyant radius r∗ falls within the fluid interior. Convection thus occurs for r < r∗, while the region r > r∗ is sub-adiabatic and mimics the presence of a stably stratified layer at the top of the core. In our numerical simulations, we used either γ = −1.14 or γ = −1.44 (see Supplementary Data 1), which correspond to a stably stratified layer at the top of the core of thickness of about δ/d = 0.16 and δ/d = 0.26, respectively. In one case we explored the effect of an extreme stably stratified layer thickness of δ/d = 0.54 (γ = −3).
Time is rescaled to physical units based on the electrical conductivity estimates provided by ref. 62 which suggests τη = 200 kyr. All models were truncated such that transient effects associated with initialisation were excluded. The individual Gauss coefficients were then temporally resampled using a cubic spline fit in order to yield regularly spaced time steps.
Regression and calculation of uncertainties
Uncertainties for the estimates of AD/NADmedian calculated for the palaeomagnetic datasets (Table 1, Fig. 4a) and the downsampled models (Fig. 3b, c) combined errors in the prediction of the power law (Fig. 2) and in the Model G a parameter. The former were 95% prediction bounds on the power law displayed in Fig. 2 calculated using standard linear regression analysis and a t-distribution (Matlab curve-fitting toolbox and predint function using default settings) performed on the datasets in log-space. Although these techniques strictly assume Gaussian bivariate distributions, they are demonstrably effective here in encompassing the majority of the data. The latter consisted of 95% confidence bounds calculated using 1000 or 10,000 bootstraps resampling with replacement. Combining these two errors into a single uncertainty for estimated AD/NADmedian allowed for the full overlap of error bars and the shaded region in Fig. 3c producing a conservative range whose usefulness is supported by the down-sampling results displayed in Fig. 3b, c and Supplementary Fig. 4.
Data availability
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
Code availability
The code used to perform these analyses are available from the corresponding author on reasonable request.
References
Zossi, B., Fagre, M., Amit, H. & Elias, A. G. Polar caps during geomagnetic polarity reversals. Geophys. J. Int. 216, 1334–1343 (2019).
Siscoe, G. L. & Sibeck, D. G. Effects of nondipole components on auroral zone configurations during weak dipole field epochs. J. Geophys. Res. 87, 3549–3556 (1980).
Tarduno, J. A. et al. Geodynamo, solar wind, and magnetopause 3.4 to 3.45 billion years ago. Science 327, 1238–1240 (2010).
Lowes, F. J. Spatial power spectrum of the main geomagnetic field, and extrapolation to the core. Geophys. J. R. Astron. Soc. 36, 717–730 (1974).
Coe, R. S. & Glatzmaier, G. A. Symmetry and stability of the geomagnetic field. Geophys. Res. Lett. 33, GL027903 (2006).
Langel R. A. The main field. In Geomagnetism, Vol. 1 (ed. Jacobs, J. A.) 249–512 (Academic Press, London, 1987).
Brown, M. C., Korte, M., Holme, R., Wardinski, I. & Gunnarson, S. Earth’s magnetic field is probably not reversing. Proc. Natl Acad. Sci. USA 115, 5111–5116 (2018).
Constable, C., Korte, M. & Panovska, S. Persistent high paleosecular variation activity in southern hemisphere for at least 10000 years. Earth Planet. Sci. Lett. 453, 78–86 (2016).
Jackson, A., Jonkers, A. R. T. & Walker, M. R. Four centuries of geomagnetic secular variation from historical records. Philos. Trans. R. Soc. Lond. Ser. a 358, 957–990 (2000).
Nilsson, A., Holme, R., Korte, M., Suttie, N. & Hill, M. Reconstructing Holocene geomagnetic field variation: new methods, models and implications. Geophys. J. Int. 198, 229–248 (2014).
Panovska, S., Constable, C. & Korte, M. Extending global continuous geomagnetic field reconstructions on timescales beyond human civilization. Geochem. Geophys. Geosyst. 19, 4757–4772. (2018).
Creer, K. M., Irving, J. & Runcorn, S. K. The direction of the geomagnetic field in remote epochs in Great Britain. J. Geomagn. Geoelectr. 6, 163–168 (1954).
Constable, C. & Johnson, C. Anisotropic paleosecular variation models: implications for geomagnetic field observables. Phys. Earth Planet. Inter. 115, 35–51 (1999).
Constable, C. G. & Parker, R. L. Statistics of the geomagnetic secular variation for the past 5-My. J. Geophys. Res.—Solid 93, 11569–11581 (1988).
Tauxe, L. & Kent, D. V. A simplified statistical model for the geomagnetic field and the detection of shallow bias in paleomagnetic inclinations: was the ancient magnetic field dipolar? AGU Geophys. Monogr. Ser. 145, 101–115 (2004).
Bono, R. K. et al. Covariant giant Gaussian process models with improved reproduction of Palaeosecular variation. Geochem. Geophys. Geosyst. 21, e2020GC008960 (2020).
Brandt, D., Constable, C. & Ernesto, M. Giant Gaussian process models of geomagnetic palaeosecular variation: a directional outlook. Geophys. J. Int 222, 1526–1541 (2020).
McFadden, P. L., Merrill, R. T. & McElhinny, M. W. Dipole quadrupole family modeling of paleosecular variation. J. Geophys. Res.—Solid 93, 11583–11588 (1988).
Cromwell, G., Johnson, C. L., Tauxe, L., Constable, C. & Jarboe, N. PSV10: a global data set for 0–10 Ma time-averaged field and paleosecular variation studies. Geochem. Geophys. Geosyst. https://doi.org/10.1002/2017GC007318 (2018).
Doubrovine, P. V. et al. Latitude dependence of geomagnetic paleosecular variation and its relation to the frequency of magnetic reversals: observations from the Cretaceous and Jurassic. Geochem. Geophys. Geosyst. 20, 1240–1279 (2019).
Biggin, A. J., van Hinsbergen, D., Langereis, C. G. & Deenen, G. B. S. MHL. Geomagnetic Secular variation in the Cretaceous Normal Superchron and in the Jurassic. Phys. Earth Planet. Inter. 169, 3–19 (2008).
McFadden, P. L., Merrill, R. T., McElhinny, M. W. & Lee, S. H. Reversals of the earths magnetic-field and temporal variations of the dynamo families. J. Geophys. Res.—Solid 96, 3923–3933 (1991).
Tarduno, J. A., Cottrell, R. D. & Smirnov, A. V. The Cretaceous superchron geodynamo: observations near the tangent cylinder. Proc. Natl Acad. Sci. USA 99, 14020–14025 (2002).
Biggin, A. J., Strik, G. H. M. A. & Langereis, C. G. Evidence for a very-long-term trend in geomagnetic secular variation. Nat. Geosci. 1, 395–398 (2008).
Smirnov, A. V., Tarduno, J. A. Secular variation of the Late Archean Early Proterozoic geodynamo. Geophys. Res. Lett. 31, (2004) https://doi.org/10.1029/2004GL020333.
Smirnov, A. V., Tarduno, J. A. & Evans, D. A. D. Evolving core conditions ca. 2 billion years ago detected by paleosecular variation. Phys. Earth Planet. Inter. 187, 225–231 (2011).
Veikkolainen, T. & Pesonen, L. J. Palaeosecular variation, field reversals and the stability of the geodynamo in the Precambrian. Geophys. J. Int. 199, 1515–1526 (2014).
Hulot, G. & Gallet, Y. On the interpretation of virtual geomagnetic pole (VGP) scatter curves. Phys. Earth Planet. Inter. 95, 37–53 (1996).
Vandamme, D. A new method to determine Paleosecular variation. Phys. Earth Planet. Inter. 85, 131–142 (1994).
Merrill, R. T. & McFadden, P. L. The geomagnetic axial dipole field assumption. Phys. Earth Planet. Inter. 139, 171–185 (2003).
Biggin, A. J. et al. Palaeomagnetic field intensity variations suggest Mesoproterozoic inner-core nucleation. Nature 526, 245–248 (2015).
Kulakov, E. V. et al. Analysis of an updated paleointensity database (QPI-PINT) for 65–200 Ma: implications for the long-term history of dipole moment through the Mesozoic. J. Geophys. Res. 124, (2019) https://doi.org/10.1029/2018JB017287.
Bono, R. K., Tarduno, J. A., Nimmo, F. & Cottrell, R. D. Young inner core inferred from Ediacaran ultra-low geomagnetic field intensity. Nat. Geosci. 12, 143–147 (2019).
Aubert, J., Labrosse, S. & Poitou, C. Modelling the palaeo-evolution of the geodynamo. Geophys. J. Int. 179, 1414–1428 (2009).
Driscoll, P. Simulating 2 Ga of geodynamo history. Geophys. Res. Lett. 43, 5680–5687 (2016).
Biggin, A. J. et al. Possible links between long-term geomagnetic variations and whole-mantle convection processes. Nat. Geosci. 5, 526–533 (2012).
Buffett, B. A. Core–mantle interactions. In Core Dynamics, Vol. 8 (ed. Olson, P.) 213–224 (Elsevier: Amsterdam, 2015).
Hounslow, M., Domeier, M. & Biggin, A. J. Subduction flux modulates the geomagnetic polarity reversal rate. Tectonophysics 742–743, 34–49 (2018).
Olson, P. L., Deguen, R., Hinnov, L. A. & Zhong, S. J. Controls on geomagnetic reversals and core evolution by mantle convection in the Phanerozoic. Phys. Earth Planet. Inter. 214, 87–103 (2013).
Olson, P. The new core paradox. Science 342, 431–432 (2013).
Davies, C., Pozzo, M., Gubbins, D. & Alfe, D. Constraints from material properties on the dynamics and evolution of Earth’s core. Nat. Geosci. 8, 678–685 (2015).
Li, Z. X. et al. Decoding Earth’s rhythms: modulation of supercontinent cycles by longer superocean episodes. Precambr. Res. 323, 1–5 (2019).
Zhang, N. & Zhong, S. J. Heat fluxes at the Earth’s surface and core–mantle boundary since Pangea formation and their implications for the geomagnetic superchrons. Earth Planet. Sci. Lett. 306, 205–216 (2011).
Landeau, M., Aubert, J. & Olson, P. The signature of inner-core nucleation on the geodynamo. Earth Planet. Sci. Lett. 465, 193–204 (2017).
Abrajevitch, A., Van & der Voo, R. Incompatible Ediacaran paleomagnetic directions suggest an equatorial geomagnetic dipole hypothesis. Earth Planet. Sci. Lett. 293, 164–170 (2010).
Vogt, J. et al. Energetic particles in the paleomagnetosphere: reduced dipole configurations and quadrupolar contributions. J. Geophys. Res. 112, A06216 (2007).
Winkler, H. et al. Modeling impacts of geomagnetic field variations on middle atmospheric ozone responses to solar proton events on long timescales. J. Geophys. Res. 113, D02302 (2008).
Behar, N. et al. Paleomagnetism and paleosecular variations from the Plio‐Pleistocene Golan heights Volcanic Plateau, Israel. Geochem. Geophys. Geosyst. 20, (2019) https://doi.org/10.1029/2019GC008479.
Hawkins, L. et al. An exceptionally weak Devonian geomagnetic field recorded by the Viluy Traps. Sib. Earth Planet. Sci. Lett. 506, 134–145 (2019).
Shcherbakova, V. V. et al. Was the Devonian geomagnetic field dipolar or multipolar? Palaeointensity studies of Devonian igneous rocks from the Minusa Basin (Siberia) and the Kola Peninsula dykes, Russia. Geophys. J. Int. 209, 1265–1286 (2017).
Meert, J. G., Levashova, N. M., Bazhenov, M. L. & Landing, E. Rapid changes in magnetic field polarity during the Late Ediacaran: trigger for the agronomic revolution and demise of the Ediacaran fauna? Gondwana Res. 34, 149–157 (2016).
Butler, R. F. Paleomagnetism: Magnetic Domains to Geologic Terranes. (Blackwell Scientific Publications, Oxford, 1992).
Davies, C. & Constable, C. Insights from geodynamo simulations into long-term geomagnetic field behaviour. Earth Planet. Sci. Lett. 404, 238–249 (2014).
Davies, C. & Gubbins, D. A buoyancy profile for Earth’s core. Geophys. J. Int. 187, 549–563 (2011).
Sprain, C. J., Biggin, A. J., Davies, C. J., Bono, R. K. & Meduri, D. G. An assessment of long duration geodynamo simulations using new paleomagnetic modeling criteria (QPM). Earth Planet. Sci. Lett. 526, 115758 (2019).
Willis, A. P., Sreenivasan, B. & Gubbins, D. Thermal core–mantle interaction: exploring regimes for ‘locked’ dynamo action. Phys. Earth Planet. Inter. 165, 83–92 (2007).
Davies, C., Gubbins, D., Willis, A. & Jimack, P. Time-averaged paleomagnetic field and secular variation: predictions from dynamo solutions based on lower mantle seismic tomography. Phys. Earth Planet. Inter. 169, 194–203 (2008).
Dziewonski, A. M., Lekic, V. & Romanowicz, B. A. Mantle anchor structure: an argument for bottom up tectonics. Earth Planet. Sci. Lett. 299, 69–79 (2010).
Masters, G., Johnson, S., Laske, G. & Bolton, H. A shear-velocity model of the mantle. Philos. Trans. R. Soc. A354, 1385–1411 (1996).
Braginsky, S. & Roberts, P. Equations governing convection in Earth’s core and the geodynamo. Geophys. Astrophys. Fluid Dyn. 79, 1–97 (1995).
Kutzner, C. & Christensen, U. R. Effects of driving mechanisms in geodynamo models. Geophys. Res. Lett. 27, 29–32 (2000).
Pozzo, M., Davies, C., Gubbins, D. & Alfè, D. Thermal and electrical conductivity of iron at Earth’s core conditions. Nature 485, 355–358 (2012).
Thébault, E. International geomagnetic reference field: the 12th generation. Earth Planets Space 67, 79 (2015).
Acknowledgements
A.J.B., C.J.S. and C.J.D. acknowledge support from the Natural Environment Research Council (standard grant, NE/P00170X/1); A.J.B., R.K.B. and D.G.M. acknowledge support from The Leverhulme Trust (Research Leadership Award, RL-2016-080); P.V.D. acknowledges support from the Research Council of Norway through its Centres of Excellence funding scheme, project 646 number 223272 (CEED).
Author information
Authors and Affiliations
Contributions
A.J.B. designed the study and performed the analyses. R.K.B., D.G.M., C.J.S. and C.J.D. performed new dynamo simulations and analyses. P.V.D. derived the theoretical power law. All above authors and R.H. contributed to writing the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Julien Aubert and the other anonymous reviewer for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Biggin, A.J., Bono, R.K., Meduri, D.G. et al. Quantitative estimates of average geomagnetic axial dipole dominance in deep geological time. Nat Commun 11, 6100 (2020). https://doi.org/10.1038/s41467-020-19794-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-19794-7
This article is cited by
-
Geomagnetic secular variation consequences on the trajectories of radiation belt trapped particles
Astrophysics and Space Science (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.