Abstract
Bloch oscillations (BOs) are a fundamental phenomenon by which a wave packet undergoes a periodic motion in a lattice when subjected to a force. Observed in a wide range of synthetic systems, BOs are intrinsically related to geometric and topological properties of the underlying band structure. This has established BOs as a prominent tool for the detection of Berry-phase effects, including those described by non-Abelian gauge fields. In this work, we unveil a unique topological effect that manifests in the BOs of higher-order topological insulators through the interplay of non-Abelian Berry curvature and quantized Wilson loops. It is characterized by an oscillating Hall drift synchronized with a topologically-protected inter-band beating and a multiplied Bloch period. We elucidate that the origin of this synchronization mechanism relies on the periodic quantum dynamics of Wannier centers. Our work paves the way to the experimental detection of non-Abelian topological properties through the measurement of Berry phases and center-of-mass displacements.
Similar content being viewed by others
Introduction
The quest for topological quantization laws has been a central theme in the exploration of topological quantum matter1,2, which originated from the discovery of the quantum Hall effect3. In the last decade, the development of topological materials has led to the observation of fascinating quantized effects, including the half-integer quantum Hall effect4 and the quantization of Faraday and Kerr rotations5 in topological insulators6,7, as well as half-integer thermal Hall conductance in spin liquids8 and quantum Hall states9. In parallel, the engineering of synthetic topological systems has allowed for the realization of quantized pumps10,11, and revealed quantized Hall drifts12,13,14, circular dichroism15, and linking numbers16.
In this context, Bloch oscillations (BOs)17,18,19,20,21,22 have emerged as a powerful tool for the detection of geometric and topological properties in synthetic lattice systems23,24,25,26, hence providing access to quantized observables. Indeed, transporting a wavepacket across the Brillouin zone (BZ) can be used to explore various geometric features of Bloch bands, including the local Berry curvature23 and the Wilson loop of non-Abelian connections25. This strategy has been exploited to extract the Berry phase27,28, the Berry curvature29,30, the Chern number12,13,14, and quantized Wilson loops31 in ultracold matter and photonics.
The Wilson loop measurement of ref. 31 highlighted a fundamental relation between two intriguing properties of multi-band systems: the quantization of Wilson loops, a topological property related to the Wilczek-Zee connection32, and the existence of “multiple Bloch oscillations”, which are characterized by a multiplied Bloch period31,33,34,35,36,37,38,39. The effect investigated in ref. 31 was eventually identified as an instance of “topological Bloch oscillations”, whose general framework was proposed in ref. 40 based on the space groups of crystals and its implications on the quantization of geometric quantities (Zak phases differences). The Bloch period multiplier appears as a topological invariant, protected by crystalline symmetries, thus making multiple BOs genuinely topological. Furthermore, when a Wannier representation of the bands is possible, Zak phases correspond to the positions of charges within the unit cell, namely the Wannier centers. As a consequence, a Zak-Wannier duality allows to connect BOs to the relative phases acquired by charges within a classical point-charge picture. More recently, BOs displaying topologically protected sub-oscillations have also been found in periodically driven systems in the context of quantum walks41.
In this work, we identify a distinct topological effect that manifests in the BOs of higher-order topological insulators (HOTIs). These newly discovered systems belong to the family of topological crystalline insulators42,43,44,45,46, i.e., gapped quantum systems characterized by crystal symmetries; they are characterized by quantized multipole moments in the bulk and unusual topologically protected states (e.g., corner or hinge modes) on their boundaries; see refs. 47,48,49,50,51,52,53,54,55,56,57,58,59,60. Considering the prototypical Benalcazar-Bernevig-Hughes (BBH) model47,48, we unveil a phenomenon by which multiple BOs take the form of an oscillating Hall drift, accompanied with a synchronized inter-band beating, for special directions of the applied force, as summarized in Fig. 1a. Although the Hall motion is attributed to the finite non-Abelian Berry curvature of the degenerate band structure, the inter-band beating captured by the Wilson loop is shown to be topologically protected by winding numbers. The synchronization of real-space motion and inter-band dynamics is elucidated through a quantum Rabi oscillation of Wannier centers. Finally, we observe that detached helical edge states are present on specific boundaries, compatible with the special symmetry axes associated with the topological BOs. A topological transition signaled by the sign change of the identified winding numbers and by the corresponding appearence/disapperance of these states is identified.
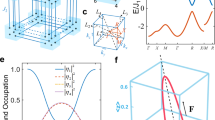
a The center-of-mass position \(\left\langle {\bf{r}}\right\rangle\) of a gaussian wavepacket experiences a sign-changing Hall drift under the applied force F, while displaying a synchronized beating within two occupied bands. This synchronized effect, represented by the metronome, is topologically protected by the winding number w. b BBH model: a square lattice with π flux and staggered hopping amplitudes J1 and J2. Vertical bonds with arrows correspond to a Peierls phase π in the hopping amplitudes. c Band structure of the model. Each band is twofold degenerate. d Brillouin zones and paths \({\mathcal{C}}\) and \(\bar{{\mathcal{C}}}\) exhibiting topological BOs.
Overall, our results demonstrate the rich interplay of non-Abelian gauge structures and winding numbers in the topological BOs of HOTI’s, but also establish BOs as a powerful probe for non-Abelian topological properties in quantum matter.
Results
Model and symmetries
We consider the BBH model, as introduced in refs. 47,48. It consists of a square lattice with alternating hopping amplitudes J1 and J2 in the two spatial directions and a π flux per plaquette, as depicted in Fig. 1b. We have introduced the flux by Peierls phases on the vertical links but other conventions can be used without affecting the results of this work. The model is represented by a chiral-symmetric Hamiltonian of the form
where the 4 × 4 Dirac matrices are written in the chiral basis Γi = −σ2 ⊗ σi for i = 1, …, 3 and \({\Gamma }^{4}={\sigma }_{1}\otimes {\mathcal{I}}\). This model has twofold degenerate energy bands E(k) = ±ϵ(k) with \(\epsilon ({\bf{k}})=\sqrt{{\left|{\bf{d}}({\bf{k}})\right|}^{2}}\). The eigenfunctions of the lowest two bands read \(\left|{u}_{{\bf{k}}}^{1}\right\rangle =\frac{1}{\sqrt{2}\epsilon }{\left({d}_{1}-i{d}_{2},-{d}_{3}-i{d}_{4},0,i\epsilon \right)}^{T}\) and \(\left|{u}_{{\bf{k}}}^{2}\right\rangle =\frac{1}{\sqrt{2}\epsilon }{\left({d}_{3}-i{d}_{4},{d}_{1}+\, i{d}_{2},i\epsilon ,0\right)}^{T}\).
The full expressions of the di(k)’s for the isotropic BBH model is \({d}_{1}({\bf{k}})=({J}_{1}-{J}_{2})\sin ({k}_{y}/2)\), \({d}_{2}({\bf{k}})=-({J}_{1}+{J}_{2})\cos ({k}_{y}/2)\), \({d}_{3}({\bf{k}})=({J}_{1}-{J}_{2})\sin ({k}_{x}/2)\) and \({d}_{4}({\bf{k}})=-({J}_{1}+{J}_{2})\cos ({k}_{x}/2)\) and the corresponding energy dispersion is displayed in Fig. 1c. Here, we take the periodicity d = 2a = 1, where a is the lattice spacing. The ordering of the unit cell sites chosen to represent the model in Eq. (1) is indicated in Fig. 1b. Notice that the chosen basis takes into account the geometric shape of the unit cell. As a consequence, the Hamiltonian is not Bloch invariant, namely H(k + G) ≠ H(k), with G a reciprocal lattice vector.
The presence of time-reversal symmetry \(\hat{T}\), with \({\hat{T}}^{2}=1\) and chiral symmetry \(\hat{S}\), represented by \({\Gamma }^{0}={\sigma }_{3}\ \otimes \ {\mathcal{I}}\), sets the model into the BDI class1. Moreover, several crystalline symmetries are also present: two non-commuting mirror symmetries with respect to the x and y axis, namely \({\hat{M}}_{x}={\sigma }_{1}\otimes {\sigma }_{3}\) and \({\hat{M}}_{y}={\sigma }_{1}\otimes {\sigma }_{1}\), respectively; and a π/2 rotation symmetry \({C}_{4}=\left(\begin{array}{ll}0&{\mathcal{I}}\\ -i{\sigma }_{2}&0\end{array}\right)\). The two mirror symmetries guarantee that inversion (C2) is also a symmetry of the model, with \({\hat{C}}_{2}={\hat{M}}_{x}{\hat{M}}_{y}\). Moreover, the presence of mirror and rotation symmetries allows us to define a pair of mirror symmetries with respect to the diagonal axes of the lattice, \({\hat{M}}_{xy}={\hat{M}}_{y}{\hat{C}}_{4}\) and \({\hat{M}}_{x\bar{y}}=-{\hat{M}}_{x}{\hat{C}}_{4}\). This is one of the central ingredients allowing for topologically protected BOs, as we will show below.
Owing to the two non-commuting mirror symmetries \({\hat{M}}_{x}\) and \({\hat{M}}_{y}\), the BBH model is a quadrupole insulator that has a quantized quadrupole moment in the bulk, vanishing bulk polarization and corner charges47. The non-commutation of the mirror symmetries also provides a non-vanishing non-Abelian Berry curvature \({\Omega }_{xy}({\bf{k}})={\partial }_{{k}_{x}}{A}_{y}-{\partial }_{{k}_{y}}{A}_{x}-i[{A}_{x},{A}_{y}]\) of the twofold degenerate lowest (or highest) bands61,62, where A is the non-Abelian Berry connection32. However, the total Chern number of the degenerate bands remains zero due to time-reversal. It is then possible to define Wannier functions \(|{\nu }_{x,{k}_{y}}^{\alpha }\rangle\) and \(|{\nu }_{y,{k}_{x}}^{\alpha }\rangle\), with α = 1, 2 numbering the bands below the energy gap, which are eigenstates of the position operators \(\hat{P}\hat{x}\hat{P}\) and \(\hat{P}\hat{y}\hat{P}\) projected onto the lowest two bands, respectively47,48. The non-commutation of the mirror symmetries (and therefore of the projected position operators) forces the use of hybrid Wannier functions, namely Wannier states that can only be maximally localized in one direction63,64. Furthermore, it provides a necessary condition to have gapped Wannier bands, namely Wannier centers that are displaced from each other at every momentum kx or ky. In ref. 47,48, the Wannier gap has been exploited to define a winding of the Wannier states (nested Wilson loop) as a condition to have a quantized quadrupole moment in the bulk, which can be revealed from the Wannier-Stark spectrum65.
Winding numbers
We now prove that a nontrivial topological structure captured by novel winding numbers characterizes the BBH model along the diagonal paths of the BZ, \({\mathcal{C}}\) and \(\bar{{\mathcal{C}}}\), which are shown in Fig. 1d. In order to emphasize the generality of these results, we hereby consider a generic Dirac-like model [Eq. (1)] without specifying the components of the d(k) vector. We assume that all previously discussed symmetries are satisfied with the additional constraint that each di function only depends on one component of the momentum k, namely we assume that d1 = d1(ky), d2 = d2(ky), d3 = d3(kx), d4 = d4(kx). Such constraint is satisfied by the BBH model. Mirror symmetries impose that d1 and d3 are odd functions whereas d2 and d4 are even. We then find that along \({\mathcal{C}}\) (i.e., for k = kx = ky), the diagonal mirror symmetry represented by the operator \({\hat{M}}_{xy}\) requires d3(k) = d1(k) and d4(k) = d2(k), while along \(\bar{{\mathcal{C}}}\) (i.e., for k = kx = −ky), the symmetry operator \({\hat{M}}_{x\bar{y}}\) requires d3(k) = −d1(k) and d4(k) = d2(k). We then conclude that only two components of d are independent and we therefore define the vector \(\tilde{{\bf{d}}}(k)\equiv ({d}_{1}(k),{d}_{2}(k))\). After writing the Hamiltonian in its chiral representation \(\hat{H}({\bf{k}})=\left(\!\!\begin{array}{ll}0&Q({\bf{k}})\\ Q{({\bf{k}})}^{\dagger}&0\end{array}\!\!\right)\), where \(Q({\bf{k}})={d}_{4}({\bf{k}}){\mathcal{I}}+i{d}_{i}({\bf{k}}){\sigma}^{i}\), we obtain the following result
where ε12 = −ε21 = 1, and where we used the \(\tilde{{\bf{d}}}\) vector of the BBH model in the last step.
We therefore conclude that the quantities \({w}_{{\mathcal{C}}}\) and \({w}_{\bar{{\mathcal{C}}}}\) count how many times the vector \(\tilde{{\bf{d}}}\) winds over the closed paths \({\mathcal{C}}\) and \(\bar{{\mathcal{C}}}\), respectively. The quantized windings \({w}_{{\mathcal{C}}}\) and \({w}_{\bar{{\mathcal{C}}}}\) are here protected by the crystalline symmetries \({\hat{M}}_{x}\), \({\hat{M}}_{y}\), and \({\hat{C}}_{4}\), as shown in Supplementary Note 1. These symmetries also imply that the two topological invariants are not independent. We point out that similar winding numbers have been introduced in chiral-symmetric one-dimensional topological superconductors66.
Finally, the sign change of the winding numbers at the gap closing point J1 = J2 signals a phase transition. We will show below that the transition corresponds to the appearance of detached helical edge states. Let us now focus on the BOs of the BBH model and the role played by the quantized winding numbers discussed above.
Topological BOs: band-population dynamics
We consider a wavepacket obtained as a superposition of the lowest two bands and centered at k, which we write as \(\left|{u}_{{\bf{k}}}(t)\right\rangle ={\eta }_{1}(t)\left|{u}_{{\bf{k}}}^{1}\right\rangle +{\eta }_{2}(t)\left|{u}_{{\bf{k}}}^{2}\right\rangle\) with \(\eta ={({\eta }_{1},{\eta }_{2})}^{T}\). Owing to the degeneracy of the states \(\left|{u}_{{\bf{k}}}^{1,2}\right\rangle\), other parametrizations can be chosen. As shown in Supplementary Note 2, this gauge ambiguity can be removed by weakly breaking time-reversal symmetry, thus splitting the two states in energy. Under an applied homogeneous and constant force F, which makes the crystal momentum change linearly in time, \(\dot{{\bf{k}}}={\bf{F}}\), the bands occupation evolves according to67
where the matrix elements of the Berry connection are defined as \({A}_{i}^{\alpha \beta }=i\langle {u}_{{\bf{k}}}^{\alpha }| {\partial }_{{k}_{i}}| {u}_{{\bf{k}}}^{\beta }\rangle\). Here, the force is assumed to be weak enough so that transitions to upper bands are neglected.
We can formally solve Eq. (3) as \(\eta (t)=\exp (-i\mathop{\int}\nolimits_{0}^{t}{\rm{d}}t\ {\epsilon }_{{\bf{k}}})W\ \eta (0)\). The Wilson line operator W is defined as \(W={\mathcal{T}}\exp (i\mathop{\int}\nolimits_{0}^{t}{\rm{d}}t\ {\bf{F}}\cdot {\bf{A}})={\mathcal{P}}\exp (i\mathop{\int}\nolimits_{{{\bf{k}}}_{i}}^{{{\bf{k}}}_{f}}{\bf{A}}\cdot {\rm{d}}{\bf{k}})\), where we have denoted as ki and kf the initial and final momenta of the BO, respectively. For a closed path \({{\mathcal{C}}}_{0}\) with kf = ki + G, where G is a reciprocal lattice vector, the bands population dynamics is determined by the Wilson loop matrix \({W}_{{{\mathcal{C}}}_{0}}={\mathcal{P}}\exp (i{\int}_{{{\mathcal{C}}}_{0}}{\bf{A}}\cdot {\rm{d}}{\bf{k}})\).
Importantly, the winding numbers \({w}_{{\mathcal{C}}(\bar{{\mathcal{C}}})}\) that we have previously introduced appear in the Wilson loops defined along the diagonal paths \({\mathcal{C}}\) and \(\bar{{\mathcal{C}}}\), as \({W}_{{\mathcal{C}}(\bar{{\mathcal{C}}})}=\exp (i(2\pi /4){w}_{{\mathcal{C}}(\bar{{\mathcal{C}}})}{\sigma }_{1(3)})\), with \({w}_{{\mathcal{C}}(\bar{{\mathcal{C}}})}=\pm\! 1\). From this, we obtain that BOs require four loops in momentum space in order to map the wavefunction back to itself, namely \({[{W}_{{\mathcal{C}}(\bar{{\mathcal{C}}})}]}^{4}={\mathcal{I}}\). Notice that the degeneracy of the bands brings a trivial dynamical phase that does not influence the internal band-population dynamics.
According to the classification of topological BOs discussed in ref. 40, rotational symmetries \({\hat{C}}_{n}\) can quantize BOs with a force applied orthogonal to the rotational symmetry axis. This is (partially) the case here, with \({\hat{C}}_{4}\) providing period-four BOs. However, \({\hat{C}}_{4}\) symmetry alone is not sufficient to quantize the BOs. Additional symmetries, namely \({\hat{M}}_{x}\) and \({\hat{M}}_{y}\), are required in order to have a protected winding number along the paths \({\mathcal{C}}\) and \(\bar{{\mathcal{C}}}\), see Supplementary Note 1. In the general framework presented in ref. 40, a “Wannier-Zak” relation is demonstrated when mirror symmetries commute. As a consequence, the Zak phase winding that appears in the Wilson loop has a one-to-one correspondence with the position of the Wannier centers. This is well described by independently evolving point charges within a classical picture. In our case, such a direct correspondence is not possible owing to the non-vanishing Berry curvature and we will see below that the physical consequences of this feature appear on the real-space motion of the wavepacket.
Topological BOs: real-space dynamics
Let us now consider the real-space motion of the wavepacket’s center-of mass, which satisfies the following semiclassical equations67
Here, Ωxy denotes the SU(2) Berry curvature, whose components are shown in Fig. 2a for the BBH model; they satisfy the following conditions: \({\Omega }_{xy}^{11}=-{\Omega }_{xy}^{22}\), \({\rm{Re}}\ {\Omega }_{xy}^{12}={\rm{Re}}\ {\Omega }_{xy}^{21}\) and \({\rm{Im}}\ {\Omega }_{xy}^{12}=-{\rm{Im}}\ {\Omega }_{xy}^{21}\). One anticipates from the accumulation of Berry curvature near the M point of the BZ that the paths \({\mathcal{C}}\) and \(\bar{{\mathcal{C}}}\) may display nontrivial features also in the real-space dynamics and not only in the band population beating discussed above. As we shall explain in detail below, the wavepacket experiences a transverse Hall drift that changes sign after each BO, thus bringing the center-of mass position back to its initial point after two BOs. This behavior is synchronized and tightly connected with the band-population dynamics captured by the Wilson loop.
a Non-Abelian Berry curvature Ωxy(k) for the BBH model. b Band occupation dynamics along the \({\mathcal{C}}\) path for θ(0) = 0 and ϕ(0) = 0. Here J2 = 0.3J1 and \(| F| =0.2\sqrt{2}{J}_{1}\). c Real-space wavepacket trajectory. d Comparison of the wavepacket \(\left\langle x\right\rangle\) position for (solid line) numerical real-space evolution of a wavepacket with width σ = 0.15a−1 and momentum grid-spacing kpts = 20, (dashed line) exact evolution, (dots) semiclassical evolution. e Orthogonal displacement Δr⊥ after one BO along the paths \({\mathcal{C}}\) and \(\bar{{\mathcal{C}}}\).
The twofold degeneracy of the bands allows us to parametrize the evolving state \(\left|{u}_{{\bf{k}}}(t)\right\rangle\) on the Bloch sphere as \({\eta }_{1}(t)=\cos \theta (t)\) and \({\eta }_{2}(t)=\sin \theta (t){e}^{i\phi (t)}\). We can therefore rewrite the anomalous velocity as
On the \({\mathcal{C}}\) path, the angle ϕ is a constant of motion, namely \(\dot{\phi }=0\). This means that the Bloch vector is confined to a meridian of the Bloch sphere. Moreover, since \({\rm{Re}}\ {\Omega }_{xy}^{12}=0\) on \({\mathcal{C}}\), only the first and the last term of Eq. (5) are relevant. After one BO, the two bands populations exchange, symmetrically with respect to the M point, as displayed in Fig. 2b [i.e., \({W}_{{\mathcal{C}}}\propto {\sigma }_{1}\)]. Let us consider the case with ϕ = 0 and θ(0) = 0, where only the first term in Eq. (5) matters. The Berry curvature has a node and the band population starts with η1(0) = 1. Near the M point and before crossing it, the occupation of band 1 is larger than the occupation of band 2. The Berry curvature \({\Omega }_{xy}^{11}\) is positive and the Hall displacement in the x direction is therefore negative (see the minus sign in the first of Eq. (4)). Once the path has crossed the M point, the occupations are flipped but so is also the sign of the Berry curvature, thus the Hall displacement continues with the same sign until the wavepacket reaches the Γ point. As the bands occupations have exchanged, a second BO will experience an opposite Hall drift and bring back the wavepacket to its initial position, as shown in Fig. 2c, d. From this, we obtain that the real-space motion is a witness of the non-Abelian band dynamics. For θ(0) ≠ 0, the off-diagonal component of the Berry curvature also contributes, and it fully suppresses the Hall displacement when θ(0) = π/4 since the anomalous Hall velocity vanishes identically: the two bands are equally populated, no band exchange takes place and therefore the positive and negative deflections compensate each other.
On the \(\bar{{\mathcal{C}}}\) path, the Berry curvature has only off-diagonal components and the Hall dynamics is determined by the relative phase ϕ, whereas θ is a constant of motion. In this case, the populations of the two bands do not exchange over time but the relative phase does by an angle π. The transverse displacement as a function of θ(0) and ϕ(0) for the two paths is shown in Fig. 2e.
We have thus found that the center-of mass of the wavepacket displays a period-two BO instead of a period-four one. This difference with respect to the Wilson loop analysis occurs because after two BOs, the wavefunction has picked up an overall phase 2 × (π/2), which does not appear in observables \(\left\langle \hat{O}\right\rangle\), such as for the center-of mass position.
Atomic limit: single-plaquette dynamics
In order to elucidate the role of Wannier functions in the BOs analyzed here and the synchronization between real-space and band-population dynamics, we consider the instructive atomic limit with J2 = 0, where we can study the time dynamics of a single plaquette. The lowest energy eigenstates read \(\left|{u}^{1}\right\rangle ={(1/2,1/2,0,1/\sqrt{2})}^{T}\) and \(\left|{u}^{2}\right\rangle ={(1/2,-1/2,1/\sqrt{2},0)}^{T}\).
We construct the position operator \(\hat{{\bf{r}}}={\sum }_{i}({{\bf{r}}}_{i}-{{\bf{r}}}_{0})\left|{{\bf{r}}}_{i}\right\rangle \left\langle {{\bf{r}}}_{i}\right|\) by setting the spatial origin at the plaquette center. We obtain the matrices \(\hat{x}/a={\rm{diag}}(1/2,-1/2,-1/2,1/2)\) and \(\hat{y}/a={\rm{diag}}(1/2,-1/2,1/2,-1/2)\). Let us now call \(\hat{P}\) the projector operator on the states \(\left|{u}^{1}\right\rangle\) and \(\left|{u}^{2}\right\rangle\), from which we can construct the projected position operators \(\hat{P}\hat{x}\hat{P}\equiv {\hat{x}}_{P}={\sum }_{\alpha ,\beta = 1,2}\left|{u}^{\alpha }\right\rangle \left\langle {u}^{\alpha }| \hat{x}| {u}^{\beta }\right\rangle \left\langle {u}^{\beta }\right|\) and \(\hat{P}\hat{y}\hat{P}\equiv {\hat{y}}_{P}={\sum }_{\alpha ,\beta = 1,2}\left|{u}^{\alpha }\right\rangle \left\langle {u}^{\alpha }| \hat{y}| {u}^{\beta }\right\rangle \left\langle {u}^{\beta }\right|\). It follows that \([{\hat{x}}_{P},{\hat{y}}_{P}]\,\ne\, 0\), whereas \(\{{\hat{x}}_{P},{\hat{y}}_{P}\}=0\). The eigenfunctions of the projected position operators are the Wannier functions \(|{\nu }_{x,y}\rangle\) and the corresponding eigenvalues are the Wannier centers48,61,68, which read here νx = νy = ±a/4.
In the presence of an external tilt (or electric field), the perturbative Hamiltonian governing the dynamics for small values of the force F reads
The projected Hamiltonian reveals how the external force induces a quantum dynamics between the eigenstates of non-commuting position operators, in the form of a Rabi oscillation. This result is in sharp contrast with the classical point-charge picture introduced in ref. 40, which is valid for commuting position operators. We can now diagonalize \({\hat{H}}_{F}\) and we find the spectrum \(E=\pm\! Fa/2\sqrt{2}\), with \(F=\sqrt{{F}_{x}^{2}+{F}_{y}^{2}}\) . The Rabi period can be easily obtained as \({T}_{R}=2\pi /(Fa/\sqrt{2})\). This solution is general and it does not depend on the direction of the force. Besides, we can always rotate the coordinate system in order to have one axis parallel to the force and one axis orthogonal to it, r∥ and r⊥, and reduce the Hamiltonian to \({\hat{H}}_{F}={F}^{\parallel }\ {\hat{r}}_{P}^{\parallel }\). Then, the corresponding time dynamics can be represented by the eigenstates of \({\hat{r}}_{P}^{\perp }\), namely the Wannier functions obtained by diagonalizing \({\hat{r}}_{P}^{\perp }\). As a consequence, we observe a transverse dynamics compared with the direction of the applied force F, as shown in Fig. 3a, b.
a Comparison between (solid line) the exact dynamics and (dashed line) the projected model. b Full real-space evolution. c Hybrid Wannier centers obtained from diagonalizing the Wilson loops orthogonal to the \({\mathcal{C}}\) path away from the atomic limit for J1 = 0.3J2. Here the force is aligned along the diagonal Fx = Fy.
However, the Wannier centers dynamics is not directly connected to the BOs and its period does not have to be the same as the Rabi period of the Wannier centers. For example, let us consider a BO with Fy = 0. The periodicity of the BO occurs at the discrete times TB = 2πn/dFx, for \(n\in {{\mathbb{Z}}}_{+}\) where d = 2a. There is no solution that satisfies TB = TR. However, if we take Fx =±Fy we find that n = 2 provides TB = TR. Therefore, a force oriented along the diagonal axes allows to synchronize the Wannier centers dynamics with the BOs, whereas the other directions yield out-of-sync oscillations that does not bring the wavepacket back to its initial position at integer multiples of the fundamental Bloch period.
Away from the atomic limit, we can still use Wannier functions as a complete basis to express the wavepacket. A direct calculation (see Fig. 3c) shows that along the paths \({\mathcal{C}}\) and \(\bar{{\mathcal{C}}}\), the Wannier centers remain gapped and their spectrum flat, namely they are equispaced along the entire path. We interpret this fact as a witness that the Wannier centers can be thought as oscillators with the same oscillation frequency (i.e., displacement), as in the atomic limit represented by Eq. (6), thus keeping the same oscillatory motion while changing the momentum \({k}_{{\mathcal{C}}}\) or \({k}_{\bar{{\mathcal{C}}}}\). In conclusion, Wannier centers perform a quantum periodic dynamics where their transverse motion with respect to the applied force is periodic and synchronized with the BO period.
Edge states
The quantized winding numbers \({w}_{{\mathcal{C}}}\) and \({w}_{\bar{{\mathcal{C}}}}\), which we have previously identified along the paths \({\mathcal{C}}\) and \(\bar{{\mathcal{C}}}\), indicate that a topological transition takes place when J1 = J2. Here, we show that an open system with edges along the diagonals x ± y displays detached helical edge states. From Fig. 4a, we notice that near the atomic limit J2 → 0, the bulk has gapped states at energies \({E}_{b} \sim \pm\! \sqrt{2}{J}_{1}\). The edge displays disconnected single sites at energy Es ~ 0 and trimers, with energies Et1 ~ 0 and \({E}_{t2}=\pm\! \sqrt{2}{J}_{1}\). Thus, a pair of zero energy (Es and Et1) modes exists at the edge.
a Open lattice in the atomic limit respecting mirror Mx,y and C4 symmetries. Highlighted in blue the edge sites displaying zero modes and in red the unit cell for the stripe geometry. b Energy spectrum obtained by imposing periodic boundary conditions along \(\hat{y}^{\prime}\) and J1 = 0.8J2. Each edge hosts a pair of detached helical edge modes. c Positive energy edge state for \({k}_{y^{\prime} }={k}_{{\mathcal{C}}}=\pi /2\).
Near the gap closing point, J2 = (1 + m)J1 with ∣m∣ ≪ 1, we construct an effective continuum theory69 for two (pseudo)-spins satisfying
These equations provide two independent zero-energy solutions
where σ2χη = ηχη and η = ±1, which are localized at \(x^{\prime} =0\) and exist only for m > 0, namely when J1 < J2 (see Methods section). To compute the dispersion relation of the edge modes, it is convenient to consider a cylindrical geometry. In this case, we find that the edge modes become helical, see Fig. 4b. An example of such states is shown in Fig. 4c.
Discussion
In this work, we have shown a new type of multiple BOs that is connected to the quantum beating of Wannier centers and we have identified HOTIs as a model where this effect can be observed. By studying the BBH model, we have shown that the Wilson loop imposes period-four oscillations and the center-of-mass motion displays an anomalous Hall displacement over one period of oscillation. We have connected these features to the crystalline symmetries of the model and we have identified quantized winding numbers that protect the topological BOs. Moreover, we have shown that detached helical edge states emerge in an open system with the required symmetries.
Our results can be observed with cold atoms70,71, where flux engineering can be achieved through time-dependent protocols72,73 and where the staggered hopping amplitudes requires a bipartite lattice27,74. Interferometric and tomographic methods can be exploited to measure the Wilson loop winding25,31,75 and real-space cloud imaging makes possible to measure the center-of-mass displacement76. A fundamental question concerns the preparation of the initial state, owing to the degenerate nature of the bands. As shown in Supplementary Note 2 the bands can be split by slightly breaking time-reversal symmetry. In this case, it is possible to prepare a non-degenerate Bose-Einstein condensate (BEC) at the Γ point. When projected onto the eigenstates of the BBH model, this state is peaked at specific values of θ and ϕ. One can then obtain the desired superposition of the two zero-momentum modes (the BEC and the gapped mode) by a coherent coupling through an external driving. The subsequent BOs require that the applied force has a magnitude that is larger than the band separation to effectively recover the band degeneracy during the BOs.
In the context of photonics, our results can be investigated by using optical waveguides77, where it has been recently possible to realize synthetic π flux78,79. In this platform, the input laser profile can be inprinted in order to map the degenerate manifold of states at the Γ point that are parametrized by the angles θ and ϕ. It is then possible to reconstruct the Wilson loop dynamics by measuring the output field phase profile, whereas the Hall displacement is obtained from the spatial profile of the field intensity.
As a perspective of our work, it would be interesting to generalize our results to other two- and three-dimensional topological crystalline insulators and consider corrections to the semiclassical equations, e.g., involving the quantum metric once an inhomogeneous electric field or a harmonic trap potential are introduced80,81. Finally, given the role played by the initial state in the observation of the anomalous Hall displacement, BOs can be thought as a tool to witness the phenomenology of symmetry-broken condensates where the ground state degeneracy has been removed by interactions (Di Liberto et al., in prepration).
Methods
Berry connection and curvature
For the BBH model introduced in the main text, the corresponding matrix elements of the non-Abelian Berry connection, defined as \({A}_{i}^{\alpha \beta }=i\left\langle {u}_{{\bf{k}}}^{\alpha }| {\partial }_{{k}_{i}}| {u}_{{\bf{k}}}^{\beta }\right\rangle\), read
The SU(2) Berry curvature, defined as \({\Omega }_{xy}({\bf{k}})={\partial }_{{k}_{x}}{A}_{y}-{\partial }_{{k}_{y}}{A}_{x}-i[{A}_{x},{A}_{y}]\), reads
Real-space wavepacket dynamics
To validate the semiclassical real-space dynamics, we have numerically simulated the evolution of a real-space wavepacket using a finite size Lx × Ly lattice. We start by constructing a Gaussian wavepacket centered at k0 = Γ = (0, 0) of the form
where μ indicates the sublattice degree of freedom in the unit cell and rμ is its spatial position. In the simulations we take a grid of kpts × kpts points in k space within an interval k ∈ [−3σ, 3σ] × [−3σ, 3σ]. We evolve the state with the real-space Hamiltonian \(\hat{H}\) and calculate the observable \({{\bf{r}}}^{{\rm{num}}}(t)=\left\langle \psi (t)| \hat{{\bf{r}}}| \psi (t)\right\rangle\), with \(\hat{{\bf{r}}}\equiv {\sum }_{{\bf{r}}}({\bf{r}}-{{\bf{r}}}_{0})\ \left|{\bf{r}}\right\rangle \left\langle {\bf{r}}\right|\).
We also study the exact evolution of the Bloch wave vector, by considering the velocity operator \(\hat{{\bf{v}}}({\bf{k}})=\partial \hat{H}({\bf{k}})/\partial {\bf{k}}={\sum }_{i}{\partial }_{{\bf{k}}}{d}_{i}({\bf{k}}){\Gamma }^{i}\). At each time t the velocity reads \({\bf{v}}({\bf{k}}(t))=\left\langle \psi ({\bf{k}}(t))| \hat{{\bf{v}}}| \psi ({\bf{k}}(t))\right\rangle\), where \(\left|\psi ({\bf{k}}(t))\right\rangle ={\mathcal{T}}\exp [-i\mathop{\int}\nolimits_{0}^{t}{\rm{d}}t\ \hat{H}({\bf{k}}(t))]\left|{u}_{\Gamma }(0)\right\rangle\) and k(t) = k(0) + Ft. This method corresponds to solving the Schrödinger equation in k space. We find the displacement by integration \({{\bf{r}}}^{{\rm{exact}}}(t)=\mathop{\int}\nolimits_{0}^{t}{\rm{d}}t\ {\bf{v}}(t)+{{\bf{r}}}_{0}\).
Edge states
Here we derive the effective theory at the edge by considering periodic boundary conditions along the \(y^{\prime}\) direction (see Fig. 5) for J1 ≈ J2. In this stripe geometry, we have to double the unit cell to correctly represent the lattice periodicity, which reads \(d^{\prime} =2\sqrt{2}a\). In chiral form, the Hamiltonian reads
where
Here, we are taking units \(d^{\prime} =1\) and we are also using the convention that the lattice points within the unit cell are all sitting in the center of the unit cell. The Hamiltonian Hs(k) is therefore in Bloch form.
In order to build an effective theory near zero energy69, let us take J2 = (1 + m)J1, with ∣m∣ ≪ 1. We can then split the Hamiltonian into \({\hat{H}}_{{\rm{s}}}({\bf{k}})={\hat{H}}_{{\rm{s}}}({\bf{k}}=0)+{\hat{V}}_{{\rm{s}}}({\bf{k}})\), where \({\hat{V}}_{{\rm{s}}}({\bf{k}})\) is expanded to lowest order in k. The zeroth order term \({\hat{H}}_{{\rm{s}}}({\bf{k}}=0)\) can be diagonalized and we find four eigenvectors \(\left|{v}_{0}^{i}\right\rangle\) with energy \(E=\pm\! \sqrt{2}m{J}_{1}\), which we use as a basis for the effective theory, and four high-energy states \(\left|{v}_{e}^{i}\right\rangle\) that we neglect. We can then construct the projection operator \({\hat{P}}_{s}={\sum }_{i}\left|{v}_{0}^{i}\right\rangle \left\langle {v}_{0}^{i}\right|\) to obtain at lowest order
where we have rearranged the order of the components to have the Hamiltonian in block-diagonal form and we have defined
in units where J1 = 1.
We can now substitute \({k}_{x^{\prime} }\to -i{\partial }_{x^{\prime} }\) and use m ≪ 1 to obtain the coupled equations
We use standard procedures to solve these equations, namely we take \(\psi (x^{\prime} )\) as an eigenstate of σ2, i.e., we decompose it as \(\psi (x^{\prime} )=\varphi (x^{\prime} ){\chi }_{\eta }\), where σ2χη = ηχη with η = ±1. After taking the ansatz \(\varphi (x^{\prime} )\propto {e}^{-tx^{\prime} }\), we find that the following algebraic equations must be satisfied
for \({H}_{\uparrow }({k}_{x^{\prime} })\) and \({H}_{\downarrow }({k}_{x^{\prime} })\), respectively. Let us focus on the solution for \({H}_{\uparrow }({k}_{x^{\prime} })\), namely the one with plus sign. We find \({t}_{\uparrow }=-\eta \pm \sqrt{1-4m}\approx -\eta \pm (1-2m)\). For η = −1, we can construct a solution \(\varphi (x^{\prime} )={c}_{1}{e}^{-{t}_{\uparrow }^{+}x^{\prime} }+{c}_{2}{e}^{-{t}_{\uparrow }^{-}x^{\prime} }\) that is exponentially localized for m > 0 and that vanishes at \(x^{\prime} =0\), namely c1 = −c2. The solution constructed for η = 1 does not satisfy these requirements for any value of m. A similar reasoning can be repeated for \({H}_{\downarrow }({k}_{x^{\prime} })\), where we have to take the solution with η = 1 in this case and the solution only exists for m > 0. We end up with the two zero-energy solutions
that are localized at the edge \(x^{\prime} =0\) and that exist for m > 0, namely for J2 > J1.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Code availability
The code that supports the plots within this paper are available from the corresponding author upon reasonable request.
References
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045 (2010).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057 (2011).
Klitzing, K. V., Dorda, G. & Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance. Phys. Rev. Lett. 45, 494 (1980).
Xu, Y. et al. Observation of topological surface state quantum Hall effect in an intrinsic three-dimensional topological insulator. Nat. Phys. 10, 956 (2014).
Wu, L. et al. Quantized Faraday and Kerr rotation and axion electrodynamics of a 3d topological insulator. Science 354, 1124 (2016).
Fu, L. & Kane, C. L. Topological insulators with inversion symmetry. Phys. Rev. B 76, 045302 (2007).
Qi, X.-L., Hughes, T. L. & Zhang, S.-C. Topological field theory of time-reversal invariant insulators. Phys. Rev. B 78, 195424 (2008).
Kasahara, Y. et al. Majorana quantization and half-integer thermal quantum Hall effect in a Kitaev spin liquid. Nature 559, 227 (2018).
Banerjee, M. et al. Observation of half-integer thermal Hall conductance. Nature 559, 205 (2018).
Lohse, M., Schweizer, C., Zilberberg, O., Aidelsburger, M. & Bloch, I. A Thouless quantum pump with ultracold bosonic atoms in an optical superlattice. Nat. Phys. 12, 350 (2015).
Nakajima, S. et al. Topological Thouless pumping of ultracold fermions. Nat. Phys. 12, 296 (2016).
Aidelsburger, M. et al. Measuring the Chern number of Hofstadter bands with ultracold bosonic atoms. Nat. Phys. 11, 162 (2015).
Genkina, D. et al. Imaging topology of Hofstadter ribbons. N. J. Phys. 21, 053021 (2019).
Chalopin, T. et al. Probing chiral edge dynamics and bulk topology of a synthetic Hall system. Nat. Phys. 515, 237–240 (2020).
Asteria, L. et al. Measuring quantized circular dichroism in ultracold topological matter. Nat. Phys. 15, 449 (2019).
Tarnowski, M. et al. Measuring topology from dynamics by obtaining the Chern number from a linking number. Nat. Commun. 10, 1728 (2019).
Waschke, C. et al. Coherent submillimeter-wave emission from Bloch oscillations in a semiconductor superlattice. Phys. Rev. Lett. 70, 3319 (1993).
Ben Dahan, M., Peik, E., Reichel, J., Castin, Y. & Salomon, C. Bloch oscillations of atoms in an optical potential. Phys. Rev. Lett. 76, 4508 (1996).
Pertsch, T., Zentgraf, T., Peschel, U., Bräuer, A. & Lederer, F. Anomalous refraction and diffraction in discrete optical systems. Phys. Rev. Lett. 88, 939011 (2002).
Corrielli, G., Crespi, A., Della Valle, G., Longhi, S. & Osellame, R. Fractional Bloch oscillations in photonic lattices. Nat. Commun. 4, 1555 (2013).
Block, A. et al. Bloch oscillations in plasmonic waveguide arrays. Nat. Commun. 5, 3843 (2014).
Meinert, F. et al. Bloch oscillations in the absence of a lattice. Science 356, 945 (2017).
Price, H. M. & Cooper, N. R. Mapping the Berry curvature from semiclassical dynamics in optical lattices. Phys. Rev. A 85, 1 (2012).
Liu, X.-J., Law, K. T., Ng, T. K. & Lee, P. A. Detecting topological phases in cold atoms. Phys. Rev. Lett. 111, 120402 (2013).
Grusdt, F., Abanin, D. & Demler, E. Measuring Z2 topological invariants in optical lattices using interferometry. Phys. Rev. A 89, 043621 (2014).
Flurin, E. et al. Observing topological invariants using quantum walks in superconducting circuits. Phys. Rev. X 7, 031023 (2017).
Atala, M. et al. Direct measurement of the Zak phase in topological Bloch bands. Nat. Phys. 9, 795 (2013).
Duca, L. et al. An Aharonov-Bohm interferometer for determining Bloch band topology. Science 347, 288 (2015).
Jotzu, G. et al. Experimental realization of the topological Haldane model with ultracold fermions. Nature 515, 237 (2014).
Wimmer, M., Price, H. M., Carusotto, I. & Peschel, U. Experimental measurement of the Berry curvature from anomalous transport. Nat. Phys. 13, 545 (2017).
Li, T. et al. Bloch state tomography using Wilson lines. Science 352, 1094 (2016).
Wilczek, F. & Zee, A. Appearance of gauge structure in simple dynamical systems. Phys. Rev. Lett. 52, 2111 (1984).
Zheng, Y., Feng, S. & Yang, S.-J. Chiral Bloch oscillation and nontrivial topology in a ladder lattice with magnetic flux. Phys. Rev. A 96, 063613 (2017).
Zhang, S.-L. & Zhou, Q. Two-leg Su-Schrieffer-Heeger chain with glide reflection symmetry. Phys. Rev. A 95, 061601 (2017).
Lang, L.-J., Zhang, S.-L. & Zhou, Q. Nodal Brillouin-zone boundary from folding a Chern insulator. Phys. Rev. A 95, 053615 (2017).
Yan, Y., Zhang, S.-L., Choudhury, S. & Zhou, Q. Emergent periodic and quasiperiodic lattices on surfaces of synthetic Hall tori and synthetic Hall cylinders. Phys. Rev. Lett. 123, 260405 (2019).
Li, C.-H. et al. A Bose-Einstein condensate on a synthetic Hall cylinder. http://arxiv.org/abs/1809.02122 (2018).
Li, C., Zhang, W., Kartashov, Y. V., Skryabin, D. V. & Ye, F. Bloch oscillations of topological edge modes. Phys. Rev. A 99, 053814 (2019).
Anderson, R. P. et al. Realization of a deeply subwavelength adiabatic optical lattice. Phys. Rev. Res. 2, 013149 (2020).
Höller, J. & Alexandradinata, A. Topological Bloch oscillations. Phys. Rev. B 98, 024310 (2018).
Upreti, L. K. et al. Topological Swing of Bloch Oscillations in Quantum Walks. Phys. Rev. Lett. 125, 186804 (2020).
Fu, L. Topological crystalline insulators. Phys. Rev. Lett. 106, 106802 (2011).
Morimoto, T. & Furusaki, A. Topological classification with additional symmetries from Clifford algebras. Phys. Rev. B 88, 125129 (2013).
Slager, R.-J., Mesaros, A., Juricic, V. & Zaanen, J. The space group classification of topological band-insulators. Nat. Phys. 9, 98 (2013).
Shiozaki, K. & Sato, M. Topology of crystalline insulators and superconductors. Phys. Rev. B 90, 165114 (2014).
Alexandradinata, A. & Bernevig, B. A. Berry-phase description of topological crystalline insulators. Phys. Rev. B 93, 205104 (2016).
Benalcazar, W. A., Bernevig, B. A. & Hughes, T. L. Quantized electric multipole insulators. Science 357, 61 (2017a).
Benalcazar, W. A., Bernevig, B. A. & Hughes, T. L. Electric multipole moments, topological multipole moment pumping, and chiral hinge states in crystalline insulators. Phys. Rev. B 96, 245115 (2017b).
Schindler, F. et al. Higher-order topological insulators. Sci. Adv. 4 eaat0346 (2018).
Langbehn, J., Peng, Y., Trifunovic, L., von Oppen, F. & Brouwer, P. W. Reflection-symmetric second-order topological insulators and superconductors. Phys. Rev. Lett. 119, 246401 (2017).
Song, Z., Fang, Z. & Fang, C. d-dimensional edge states of rotation symmetry protected topological states. Phys. Rev. Lett. 119, 246402 (2017).
Ezawa, M. Higher-order topological insulators and semimetals on the breathing kagome and pyrochlore lattices. Phys. Rev. Lett. 120, 026801 (2018).
Imhof, S. et al. Topolectrical-circuit realization of topological corner modes. Nat. Phys. 14, 925 (2018).
Serra-Garcia, M. et al. Observation of a phononic quadrupole topological insulator. Nature 555, 342 (2018).
Mittal, S. et al. Photonic quadrupole topological phases. Nat. Photonics 13, 692 (2019).
Chen, X.-D. et al. Direct observation of corner states in second-order topological photonic crystal slabs. Phys. Rev. Lett. 122, 233902 (2019).
Kempkes, S. N. et al. Robust zero-energy modes in an electronic higher-order topological insulator. Nat. Mater. 18, 1292 (2019).
Zhang, X. et al. Second-order topology and multidimensional topological transitions in sonic crystals. Nat. Phys. 15, 582 (2019).
Dutt, A., Minkov, M., Williamson, I. A. D. & Fan, S. Higher-order topological insulators in synthetic dimensions. Light. Sci. Appl. 9, 131 (2020).
He, L., Addison, Z., Mele, E. J. & Zhen, B. Quadrupole topological photonic crystals. Nat. Commun. 11, 3119 (2020).
Marzari, N. & Vanderbilt, D. Maximally localized generalized Wannier functions for composite energy bands. Phys. Rev. B 56, 12847 (1997).
Nagaosa, N., Sinova, J., Onoda, S., MacDonald, A. H. & Ong, N. P. Anomalous Hall effect. Rev. Mod. Phys. 82, 1539 (2010).
Marzari, N., Mostofi, A. A., Yates, J. R., Souza, I. & Vanderbilt, D. Maximally localized Wannier functions: theory and applications. Rev. Mod. Phys. 84, 1419 (2012).
Taherinejad, M., Garrity, K. F. & Vanderbilt, D. Wannier center sheets in topological insulators. Phys. Rev. B 89, 115102 (2014).
Poddubny, A. N. Distinguishing trivial and topological quadrupolar insulators by Wannier-Stark ladders. Phys. Rev. B 100, 075418 (2019).
Daido, A. & Yanase, Y. Chirality polarizations and spectral bulk-boundary correspondence. Phys. Rev. B 100, 174512 (2019).
Xiao, D., Chang, M. C. & Niu, Q. Berry phase effects on electronic properties. Rev. Mod. Phys. 82, 1959 (2010).
Alexandradinata, A., Dai, X. & Bernevig, B. A. Wilson-loop characterization of inversion-symmetric topological insulators. Phys. Rev. B 89, 1 (2014).
Zhang, H. et al. Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface. Nat. Phys. 5, 438 (2009).
Goldman, N., Budich, J. C. & Zoller, P. Topological quantum matter with ultracold gases in optical lattices. Nat. Phys. 12, 639 (2016).
Cooper, N. R., Dalibard, J. & Spielman, I. B. Topological bands for ultracold atoms. Rev. Mod. Phys. 91, 015005 (2019).
Aidelsburger, M. et al. Experimental realization of strong effective magnetic fields in an optical lattice. Phys. Rev. Lett. 107, 255301 (2011).
Aidelsburger, M. et al. Realization of the Hofstadter hamiltonian with ultracold atoms in optical lattices. Phys. Rev. Lett. 111, 185301 (2013).
Di Liberto, M. et al. Controlling coherence via tuning of the population imbalance in a bipartite optical lattice. Nat. Commun. 5, 5735 (2014).
Sugawa, S., Salces-Carcoba, F., Yue, Y., Putra, A. & Spielman, I. Observation and characterization of a non-Abelian gauge field’s wilczek-zee phase by the Wilson loop. https://arxiv.org/abs/1910.13991 (2019).
Wintersperger, K. et al. Realization of an anomalous Floquet topological system with ultracold atoms. Nat. Phys. 16, 1058–1063 (2020).
Ozawa, T. et al. Topological photonics. Rev. Mod. Phys. 91, 015006 (2018).
Mukherjee, S., Di Liberto, M., Öhberg, P., Thomson, R. R. & Goldman, N. Experimental observation of Aharonov-Bohm cages in photonic lattices. Phys. Rev. Lett. 121, 075502 (2018).
Kremer, M. et al. A square-root topological insulator with non-quantized indices realized with photonic Aharonov-Bohm cages. Nat. Commun. 11, 907 (2020).
Bleu, O., Malpuech, G., Gao, Y. & Solnyshkov, D. D. Effective theory of nonadiabatic quantum evolution based on the quantum geometric tensor. Phys. Rev. Lett. 121, 020401 (2018).
Lapa, M. F. & Hughes, T. L. Semiclassical wave packet dynamics in nonuniform electric fields. Phys. Rev. B 99, 121111 (2019).
Acknowledgements
We acknowledge M. Aidelsburger, W. Benalcazar, F. Grusdt, H. M. Price, G. Salerno for fruitful discussions. This work is supported by the ERC Starting Grant TopoCold, and the Fonds De La Recherche Scientifique (FRS-FNRS, Belgium).
Author information
Authors and Affiliations
Contributions
G.P. and M.D. initiated the project. M.D. and G.P. performed the analytical calculations with inputs from N.G. M.D. performed the numerical analysis with inputs from N.G. All the authors discussed the results and prepared the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Di Liberto, M., Goldman, N. & Palumbo, G. Non-Abelian Bloch oscillations in higher-order topological insulators. Nat Commun 11, 5942 (2020). https://doi.org/10.1038/s41467-020-19518-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-19518-x
This article is cited by
-
Bloch oscillations of coherently driven dissipative solitons in a synthetic dimension
Nature Physics (2023)
-
Three-dimensional non-Abelian Bloch oscillations and higher-order topological states
Communications Physics (2023)
-
Higher-order band topology
Nature Reviews Physics (2021)
-
Wilson loop and Wilczek-Zee phase from a non-Abelian gauge field
npj Quantum Information (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.