Abstract
An enduring geological mystery concerns the missing xenon problem, referring to the abnormally low concentration of xenon compared to other noble gases in Earth’s atmosphere. Identifying mantle minerals that can capture and stabilize xenon has been a great challenge in materials physics and xenon chemistry. Here, using an advanced crystal structure search algorithm in conjunction with first-principles calculations we find reactions of xenon with recently discovered iron peroxide FeO2, forming robust xenon-iron oxides Xe2FeO2 and XeFe3O6 with significant Xe-O bonding in a wide range of pressure-temperature conditions corresponding to vast regions in Earth’s lower mantle. Calculated mass density and sound velocities validate Xe-Fe oxides as viable lower-mantle constituents. Meanwhile, Fe oxides do not react with Kr, Ar and Ne. It means that if Xe exists in the lower mantle at the same pressures as FeO2, xenon-iron oxides are predicted as potential Xe hosts in Earth’s lower mantle and could provide the repository for the atmosphere’s missing Xe. These findings establish robust materials basis, formation mechanism, and geological viability of these Xe-Fe oxides, which advance fundamental knowledge for understanding xenon chemistry and physics mechanisms for the possible deep-Earth Xe reservoir.
Similar content being viewed by others
Introduction
The chemical reaction of inert xenon (Xe), a quintessential full-shell element, was earliest predicted by Pauling in 1933 and the first xenon compound was experimentally produced in 19621. Then, more xenon compounds were experimentally synthesized at ambient pressure, containing some most electronegative atoms like fluorine2,3,4,5 or oxygen6,7,8,9. Subsequently, scientists found that pressure can effectively improve the chemical reactivity of Xe10,11,12,13,14,15,16,17. At moderate pressures, solid xenon forms weakly bonded compounds with other species, e.g., with H2O10 and O211,12 at 1 and 3 GPa, respectively. Strikingly, several novel Xe compounds with unusual stoichiometries are found to be thermodynamically stable at high pressures, e.g., Xe oxides13,14, Xe nitrides15, xenon-hydrogen16, and Xe–Mg compounds17.
At ultra-high-pressure conditions, the high volatility, relative chemical inertia, and abundant isotopes of xenon make it a valuable tracer in the study of evolutionary dynamics and history of Earth. However, 99% of Earth’s primordial Xe is mysteriously missing as characterized by its very low abundance compared to other noble gases in Earth’s atmosphere18, which is known as the missing Xe problem19. Early hypotheses proposed that Xe might have escaped from the atmosphere after ionization20,21,22, or that it might be stored in the interior of Earth23,24,25,26,27,28,29. Attempts to incorporate Xe into ices, clathrates and sediments in the Earth’s crust were not successful27,28,29. Laboratory experiments have succeeded in trapping Xe in quartz30,31 and observing predicted stable xenon oxides13,14,32; but these results cannot explain the missing Xe mystery, because xenon oxides are unstable in equilibrium with metallic iron in lower mantle while xenon silicates decompose spontaneously at mantle pressures13. Reactions of Xe with iron and nickel in Earth’s core were predicted as a viable scenario33 and the predicted compounds were synthesized under core pressure and temperature conditions32,34. However, it remains highly intriguing and challenging to explore possible capture and stabilization of Xe by suitable minerals in Earth’s mantle, which is of special significance because it was estimated that the loss of atmospheric Xe occurred about 100 million years from accretion, corresponding to the time of mantle differentiation event30.
Extensive past searches were unable to find chemical reactions of Xe with known mantle minerals. Recently discovered FeO2 synthesized at lower mantle conditions35 and stablized above 74 GPa in theoretical calculation36, offer an intriguing new possibility. This newly identified iron peroxide is able to react with helium to form a rare helium-bearing compound that explains deep-Earth primordial helium deposits revealed by geochemical evidences37. This finding raises exciting prospects that FeO2 may be able to react with Xe (actually P–T stability range of FeO2 has not been completely established in experiments) at mantle conditions, thereby forming compounds capable of trapping Xe in Earth’s interior. In this work, we have explored possible reactions of Xe with FeO2 in contrast with known mantle constituents FeO, SiO2, MgO, CaO, and Al2O3. We find that FeO2 has unique ability to react with Xe and form robust Xe-Fe oxides Xe2FeO2 and XeFe3O6 with surprisingly strong Xe–O bonding, while other mantle oxides do not react with Xe. We have further examined mass density and sound velocities of these Xe-Fe oxides, and the results support their viability in vast lower mantle region. These findings establish robust materials basis, formation mechanism, and geological viability of these Xe-Fe oxides, which advance fundamental knowledge for understanding xenon chemistry and physics mechanisms for the possible deep-Earth Xe reservoir.
Results
Crystal structures
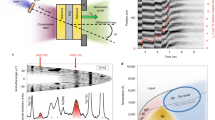
We take the crystal phases identified by the structure search process at various FeO2: Xe ratios and compute their enthalpy to determine the most viable structure at each composition, and based on the obtained results we construct the convex hull, as shown in Fig. 1a, which indicates stable products from reactions of FeO2 and Xe. This exercise has led to the discovery of two Xe-Fe oxides, Xe2FeO2 and XeFe3O6, that are stable against decomposition at 150 GPa and 200 GPa. The pressure–volume terms, associated with packing efficiency, make the major contribution to guarantee the thermodynamical stability of Xe2FeO2 and XeFe3O6 with formation enthalpies lying on the convex hull (Supplementary Fig. 1). These two Xe-Fe oxides are both still stable relative to all possible binary phases or pure simple substances of Xe-Fe-O2, which can be seen in Supplementary Information (Supplementary Figs. 2 and 3). The details Phonon dispersions calculated at 150 GPa (Fig. 1b, c) show that these compounds are dynamically stable and, as will be shown below, thermal effects further stabilize both oxides over a wider range of pressure at elevated temperatures at deep-Earth conditions. Here we first present a full analysis of structural and bonding characters of these two oxides at 150 GPa as a representative case study. The compound Xe2FeO2 is crystalized in a monoclinic structure with P21/c symmetry (Fig. 1d); its structural motif consists of stacked layers of corner-sharing octahedron with each Fe atom surrounded by six O atoms and the Fe atom is centered in a slightly distorted octahedron containing Fe–O bond lengths in a narrow range of 1.79–1.82 Å at 150 GPa. Each Xe atom in this structure has a coordination number of 3, bonding at the corners of FeO6 octahedra with the Xe–O bond lengths in the range of 2.40–2.42 Å at 150 GPa, which are similar to those found in Xe2O3 (~2.50 Å) and Xe2O5 (~2.37 Å) at the same pressure38. Meanwhile, XeFe3O6 is stabilized in a triclinic structure with P-1 symmetry, containing two formula units per cell (Fig. 1e); its corner-sharing FeO6 octahedra host Fe–O bonds with lengths of 1.73–1.81 Å at 150 GPa, forming a tubular structure, and each Xe atom has a coordination number of 6, located in the Fe-O tube with the nearest Xe-O distance of 2.08 Å, resulting in the vibrational mode of the lowest-frequency branch at F as shown in Fig. 1c. Further vibrational analyses are shown in Supplementary Fig. 4 and structural details of both Xe-Fe oxides at 150 GPa are listed in Supplementary Information (Supplementary Table 1).
a The ground-state convex hull with solid lines for the FeO2-Xe system constructed from calculated formation enthalpy (ΔH) data, identifying two stable Xe-Fe oxides, Xe2FeO2 and XeFe3O6, at 150 GPa and 200 GPa. The solid and open symbols represent the stable structures lying on the convex hull and the unstable structures above the convex hull, respectively. b Phonon dispersions of Xe2FeO2 at 150 GPa. c Phonon dispersions of Xe3FeO6 at 150 GPa. d The structure of Xe2FeO2 with a polyhedral and an enlarged view. e The structure of Xe3FeO6 with a polyhedral and an enlarged view. Xe, Fe, and O atoms are, respectively, shown in purple, gray, and red spheres.
Discussion
Chemical Bonding
To assess bonding characters in the two Xe-Fe oxides, we have calculated their electronic density of states (DOS) at 150 GPa. The results shown in Fig. 2a, c reveal metallic nature of these compounds; crucially, in both cases the DOS in the vicinity of the Fermi level contain significant contributions from the Fe 3d, Xe 5p and O 2p states, indicating considerable Fe–O and Xe–O bonding interactions. We further calculated projected crystal orbital Hamiltonian population (pCOHP) that evaluates weighted population of wavefunctions on two atomic orbitals of a pair of selected atoms39. The results in Fig. 2b, d reveal characteristic Fe–O and Xe–O covalent bonding as indicated by the prominent features of strong low-energy bonding states together with some occupied antibonding states near the Fermi level in each case. It is noted that the occupied bonding states in Xe2FeO2 occur deeper below the Fermi level compared to those in XeFe3O6, indicating higher stability of Xe2FeO2. Moreover, integrated COHP (ICOHP) provides an estimate of the overall bonding strength39. Calculated ICOHP values for the Fe–O and Xe–O bonds at 150 GPa are -1.45 eV/pair and −0.24 eV/pair in XeFe3O6 and −1.01 eV/pair and −0.12 eV/pair in Xe2FeO2, respectively. These results show considerable Xe–O bonding compared to the strong Fe–O bonding, in sharp contrast to recently discovered He-FeO2 compound where He atoms show little direct bonding37 but instead serve as a Coulomb shield in stabilizing the structure40. We also examined charge distribution in Xe2FeO2 and XeFe3O6 by a Bader charge analysis41, and the results reveal a considerable amount of highly unusual charge transfer from Fe and Xe to O atoms. At 150 GPa, the Bader partial charges in Xe2FeO2 are +0.30, +1.40, −1.00 for Xe, Fe, and O, respectively; meanwhile, Bader partial charges in XeFe3O6 are +1.35, +1.35, −0.90 for Xe, Fe, and O, respectively, at the same pressure. As a result, Xe atoms in XeFe3O6 can donate more electrons than in Xe2FeO2 and Xe atoms can display different valence states in FeO2–Xe compounds. These significant charge transfers once again indicate strong bonding formation involving Xe, which is rare among noble gases atoms.
a Projected density of states (PDOS) of Fe-d, O-p, and Xe-p orbitals in Xe2FeO2. b Projected crystal orbital Hamiltonian Population (-pCOHP) of the newly predicted Xe2FeO2 compound. The values of -pCOHP >0 signify bonding states and the values of -pCOHP <0 signify antibonding states. c PDOS of Fe-d, O-p, and Xe-p orbitals in XeFe3O6. d -pCOHP of the newly predicted XeFe3O6 compound. The Fermi energy is set to zero of the energy.
Thermal effect
Thermal effects play a crucial role in material stability at pertinent geophysical conditions, where temperatures reach 2000–4500 K. Here, we evaluate Gibbs free energy of Xe2FeO2 and XeFe3O6 by calculating lattice contributions to the entropic term using the quasiharmonic approximation to account for volume dependence of phonon frequencies due to temperature induced lattice expansion. In Fig. 3a we present relevant energetic terms affecting structure stability. It is seen that internal energy U values of the two Xe-Fe oxides are higher than those of their separate constituents, namely Xe and FeO2, but the PV terms are decisively favorable and dominant, producing the lower enthalpy H for the formation of both oxides. The temperature effect (i.e., thermal vibration of atomic positions) are favorable to reduce Gibbs free energy G of the Xe-Fe oxides even more relative to their separate constituents, further stabilizing the resulting crystal structures. Consequently, the threshold pressure above which these oxides are stable reduces considerably at increasing temperatures, thereby significantly expanding their stability field as will be seen in the phase diagram presented below.
a Various energetic term (ΔE) for the two Xe-Fe oxides, enthalpy (H), pressure–volume (PV) terms, internal energy (U), and Gibbs free energy (G) at 150 GPa, 2000 K. b Mean square deviations (MSD) of Xe, O, and Fe atomic positions in Xe2FeO2 at 150 GPa, 3000 K. c MSD of Xe, O, and Fe atomic positions in XeFe3O6 at 150 GPa, 3000 K.
Phase diagram
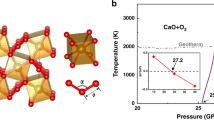
For a full assessment of temperature effects, we have performed extensive energetic and ab initio molecular dynamics (AIMD) simulations to evaluate structural stability and construct pressure–temperature (P–T) phase diagram for the Xe-Fe oxide system. We present in Fig. 3b, c the mean square deviations (MSD) of atomic positions in the Xe-Fe oxides at typical high P–T conditions of 150 GPa and 3000 K, and the results show that the Fe, O, and Xe atoms all remain near their lattice sites, indicating stability of the crystal structure. Similar AIMD simulations were performed systematically to probe each phase and determine the boundary where temperature-driven instability sets as indicated by deviating MSD from equilibrium positions; meanwhile Gibbs free energies were computed and compared to determine the boundaries between different solid phases in the P–T space. The resulting phase diagram (Fig. 4) spans a wide P–T range covering the lower mantle and higher P–T regions.
The dotted and dashed lines indicate phase boundaries and temperature-driven phase instability, which are determined by Gibbs free energy and ab initio molecular dynamics (AIMD) calculations, respectively. The square symbols show phase transition points based on relative Gibbs free energy, and the solid and open triangle symbols represent stable and temperature-driven unstable solid phases, respectively, determined by AIMD simulations. The P–T regions of stable Xe2FeO2 are covered by slash lines and the P–T regions of stable XeFe3O6 are filled by back-slash. The pressure boundary between the lower mantle and the core is shown at the top of the figure. Also shown is the geotherm of the Earth’s interior65.
We now analyze the stability fields of the predicted Xe-Fe oxides under the (P, T) conditions conforming to geological constraints dictated by the geotherm that is also shown in Fig. 4. It is seen that Xe2FeO2 is stable in the pressure range 110-120 GPa and temperatures around 2500 K inside the geotherm corresponding to the deep lower mantle region; meanwhile, both Xe2FeO2 and XeFe3O6 are stable between pressures 120–136 GPa and temperatures 2500–3600 K inside the geotherm corresponding to the lowest mantle to core-mantle boundary (CMB); finally, as pressure and temperature rise further, Xe2FeO2 becomes the sole stable phase.
The above results suggest stable Xe-Fe oxides under the (P, T) conditions in vast deep-Earth regions. It is, however, necessary to assess the viability of the predicted Xe-Fe oxides in geological environments by examining their key material characteristics. To this end, we have run AIMD simulations to determine crystal structures at selected (P, T) conditions and used an AIMD-based strain-stress method42,43 to calculate the elastic tensors, from which elastic-wave velocities were determined by solving the Christoffel equation det |Tik-δikρV2 | = 0, where δik is the Kronecker delta function, V is one of the seismic velocities, and Tik is the Christoffel stiffness44.
Mass density and sound velocities
We examine mass density and mean compressional (P-wave) and shear (S-wave) sound velocities, VP and VS, respectively, at two representative (P, T) points: (120 GPa, 2500 K) for lower mantle, and (135 GPa, 3500 K) for CMB, and compare with geological data. We first examine XeFe3O6, whose stability field compared to the geotherm indicates its stability in the lower mantle and CMB regions, but higher temperatures destabilize this compound. The calculated densities of XeFe3O6 are 8.86 and 9.06 g/cm3 at the selected lower mantle and CMB (P, T) points, respectively, which lie within or close to the range of 4.95–9.90 g/cm3 from the core rigidity zone (CRZ) model and the range of 5.57–8.91 g/cm3 from the ultralow velocity zone (ULVZ) model45. The calculated VP (VS) are 8.94(4.03) km/s and 9.20(4.26) km/s, respectively, which lie within the range of 8.20–10.70 km/s (1.00–5.00 km/s) for the ULVZs45. All these results indicate that XeFe3O6 is a viable constituent at the lower mantle and CMB (P, T) conditions.
The calculated densities of Xe2FeO2 are 9.78 and 9.87 g/cm3 at the lower mantle and CMB points, respectively, which lie outside the range of 5.57–8.91 g/cm3 from the ULVZ model and at the top of the range of 4.95–9.90 g/cm3 from the CRZ model45. The calculated VP (VS) are 7.83(4.21) km/s and 7.94(4.02) km/s at the lower mantle and CMB points, respectively. While these VS values lie within the range of 1.00–5.00 km/s from the CRZ model or the range 2.91–6.17 km/s from the ULVZ model45, the VP values are out of the range of 10.97–13.03 km/s from the ULVZ model or the range of 8.20–10.70 km/s from the CRZ model45. These results render Xe2FeO2 a marginal lower mantle or CMB constituent at best.
Reaction of noble gases and deep-Earth constituents
Finally, we highlight several significant aspects on the special role of FeO2 in trapping Xe in deep Earth. First, we have systematically examined possible reaction of Xe with major deep-Earth constituents FeO, SiO2, MgO, CaO, and Al2O3, and the resulting convex-hull data (Supplementary Fig. 5) show highly unfavorable energetics in all the cases, offering an underlying cause for unsuccessful past attempts to find Xe-bearing minerals in Earth’s mantle. Second, we have examined possible reactions of other noble gases Ne, Ar, and Kr with FeO2, and the results (Supplementary Fig. 6) indicate no tendency toward forming any stable noble-gas-Fe oxides up to 200 GPa. These results provide the possibility that Xe could be the sole inert element for reacting with deep-Earth constituents under mantle conditions. Moreover, while He-bearing compound FeO2He is found stable at CMB conditions, there is little direct bonding between He and Fe or O atoms in the compound37. Compared to Kr, Ar, Ne, and He, Xe has the lowest ionization energy and electronegativity, and consequently Xe is the easiest noble-gas atom to open up its outermost closed shell and form direct bonding as found in Xe2FeO2 and XeFe3O6.
In summary, we have identified two Xe-Fe oxides, Xe2FeO2 and XeFe3O6, that are the first viable Xe-bearing compound at Earth’s lower mantle conditions. These new compounds are predicted by extensive crystal structure search in conjunction with ab initio energetic calculations and molecular dynamics simulations. Mass densities and compressional and shear sound velocities calculated at deep-Earth conditions are compatible with pertinent ULVZ and PREM data, thus confirming viability of Xe2FeO2 in geological environments. These results provide compelling evidence for a distinct deep-Earth Xe reservoir beyond previously proposed Xe-Fe and Xe-Ni intermetallic compounds in Earth’s inner core, thereby greatly expanding the range and scope of Xe-bearing compounds in deep Earth. The Xe-Fe oxides may enrich the understanding of prominent geophysical and geochemical processes, such as seismic anomalies near the CMB and possibly new chemical reactions inside Earth’s lower mantle.
Methods
Structural predictions
Our structure search is based on a global optimization of free-energy surfaces using the CALYPSO methodology46,47, which has been successfully employed in predicting a large variety of crystal structures48,49,50,51,52. Evolutionary variable-cell calculations were performed at 120, 150, and 200 GPa with 1, 2, 3, and 4 formula units (f. u.) per cell. Most searches converge in 50 generations with about 2500 structures generated.
Ab initio calculations
First-principles total-energy and electronic property calculations were carried out using the density functional theory with the Perdew–Burke–Ernzerhof exchange-correlation functional in the generalized gradient approximation (GGA)53,54 as implemented in the VASP code55, adopting frozen-core all-electron projector-augmented wave method56 with 3s2 3p6 3d7 4s1, 2s2 2p4, and 4d10 5s2 5p6 treated as valence electrons for Fe, O, and Xe, respectively. Correlation effects among the Fe 3d electrons were treated in the GGA + U approach57,58, adopting the recently proposed on-site Coulomb interaction U = 5.0 eV and a Hund’s coupling J = 0.8 Ev36,59,60,61. The spin-polarized and magnetic states were considered in obtaining the total-energy of the compounds containing iron. Zero-point energy was included in all reported calculations. A cutoff energy of 1200 eV for the plane-wave expansion and fine Monkhorst-Pack k meshes62 were chosen to ensure enthalpy convergence of better than 1 meV/atom.
Phonon calculations
To determine the dynamical stability, we performed phonon calculations by the direct supercell method using the Hellmann-Feynman theorem, as implemented in Phonopy code63. The harmonic interatomic force constants are calculated by 3 × 3 × 3 and 3 × 2 × 2 supercells for P21/c-Xe2FeO2 and P−1-XeFe3O6, respectively. Forces were calculated for atomic displacements of 0.01 Å, with a convergence threshold of 1 × 10−5 eV/Å.
Van der Waals interaction
To examine the contribution of vdW interaction to the lattice energy, we have calculated the enthalpy of formation of Xe2FeO2 at high pressures using the vdW-DF2 density functional64. Our results show that the enthalpy of formation is less sensitive to the contribution of vdW correction at high-pressure conditions for Xe-FeO2 compounds, e.g., about 0.6 meV/atom for P21/c Xe2FeO2 at 135 GPa, thus vdW interaction is not considered in the calculations of lattice energy.
Data availability
The authors declare that the main data supporting the findings of this study are contained within the paper and its associated Supplementary Information. All other relevant data are available from the corresponding author upon reasonable request.
Code availability
CALYPSO code is free for academic use, by registering at http://www.calypso.cn. The other scripts are available from the authors upon reasonable request.
References
Bartlett, N. Xenon hexafluoroplatinate(v) Xe+[PtF6]−. Proc. Chem. Soc. 1, 218 (1962).
Chernick, C. L. et al. Fluorine compounds of xenon and radon. Science 138, 136–138 (1962).
Claassen, H. H., Selig, H. & Malm, J. G. Xenon tetrafluoride. J. Am. Chem. Soc. 84, 3593 (1962).
Gavin JR, R. M. & Bartell, L. S. Molecular structure of XeF6. I. Analysis of electron-diffraction intensities. J. Chem. Phys. 48, 2460–2465 (1968).
Hoppe, R., Daehne, W., Mattauch, H. & Roedder, K. Fluorination of xenon. Angew. Chem. Int. Ed. Engl. 1, 599 (1962).
Smith, D. F. Xenon trioxide. J. Am. Chem. Soc. 85, 816–817 (1963).
Templeton, D. H., Zalkin, A., Forrester, J. D. & Williamson, S. M. Crystal and molecular structure of xenon trioxide. J. Am. Chem. Soc. 85, 817 (1963).
Huston, J. L., Studier, M. H. & Sloth, E. N. Xenon tetroxide: mass spectrum. Science 143, 1161 (1964).
Selig, H., Claassen, H. H., Chernick, C. L., Malm, J. G. & Huston, J. L. Xenon tetroxide: preparation and some properties. Science 143, 1322–1323 (1964).
Sanloup, C., Mao, H.-K. & Hemley, R. J. High-pressure transformations in xenon hydrates. Proc. Natl Acad. Sci. USA 99, 25–28 (2002).
Dewaele, A., Loubeyre, P., Dumas, P. & Mezouar, M. Oxygen impurities reduce the metallization pressure of xenon. Phys. Rev. B 86, 014103 (2012).
Weck, G., Dewaele, A. & Loubeyre, P. Oxygen/noble gas binary phase diagrams at 296 K and high pressures. Phys. Rev. B 82, 014112 (2010).
Zhu, Q. et al. Stability of xenon oxides at high pressures. Nat. Chem. 5, 61–65 (2012).
Hermann, A. & Schwerdtfeger, P. Xenon suboxides stable under pressure. J. Phys. Chem. Lett. 5, 4336–4342 (2014).
Peng, F., Wang, Y., Wang, H., Zhang, Y. & Ma, Y. Stable xenon nitride at high pressures. Phys. Rev. B 92, 094104 (2015).
Somayazulu, M. et al. Pressure-induced bonding and compound formation in xenon–hydrogen solids. Nat. Chem. 2, 50–53 (2010).
Miao, M. S. et al. Anionic chemistry of noble gases: formation of Mg–NG (NG = Xe, Kr, Ar) compounds under pressure. J. Am. Chem. Soc. 137, 14122–14128 (2015).
Ozima, M. & Podosek, F. A. Formation age of Earth from 129I/127I an d 244Pu/238U systematics and the missing Xe. J. Geophys. Res. 104, 25493–25499 (1999).
Anders, E. & Owen, T. Mars and Earth: origin and abundance of volatiles. Science 198, 453–465 (1977).
Pepin, R. O. On the origin and early evolution of terrestrial planet atmospheres and meteoritic volatiles. Icarus 92, 2–79 (1991).
Pepin, R. O. & Porcelli, D. Origin of noble gases in the terrestrial planets. Rev. Mineral. Geochem. 47, 191–246 (2002).
Caldwell, W. A. et al. Structure, bonding, and geochemistry of xenon at high pressures. Science 277, 930–933 (1997).
Jephcoat, A. P. Rare-gas solids in the Earth’s deep interior. Nature 393, 355 (1998).
Lee, K. K. & Steinle Neumann, G. High‐pressure alloying of iron and xenon: ‘Missing’ Xe in the Earth’s core? J. Geophys. Res. 111, B02202 (2006).
Nishio-Hamane, D., Yagi, T., Sata, N., Fujita, T. & Okada, T. No reactions observed in Xe-Fe system even at Earth core pressures. Geophys. Res. Lett. 37, L04302 (2010).
Seoung, D. et al. Irreversible xenon insertion into a small-pore zeolite at moderate pressures and temperatures. Nat. Chem. 6, 835 (2014).
Sill, G. T. & Wilkening, L. L. Ice clathrate as a possible source of the atmospheres of the terrestrial planets. Icarus 33, 13–22 (1978).
Wacker, J. F. & Anders, E. Trapping of xenon in ice: implications for the origin of the Earth’s noble gases. Geochim. Cosmochim. Acta 48, 2373–2380 (1984).
Matsuda, J. I. & Matsubara, K. Noble gases in silica and their implication for the terrestrial ‘missing’ Xe. Geophys. Res. Lett. 16, 81–84 (1989).
Sanloup, C. et al. Retention of xenon in quartz and Earth’s missing xenon. Science 310, 1174–1177 (2005).
Probert, M. An ab initio study of xenon retention in α-quartz. J. Phys.: Condens. Matter 22, 025501 (2009).
Dewaele, A., Pépin, C. M., Geneste, G. & Garbarino, G. Reaction between nickel or iron and xenon under high pressure. High. Press. Res. 37, 137–146 (2017).
Zhu, L., Liu, H., Pickard, C. J., Zou, G. & Ma, Y. Reactions of xenon with iron and nickel are predicted in the Earth’s inner core. Nat. Chem. 6, 644–648 (2014).
Stavrou, E. et al. Synthesis of xenon and iron-nickel intermetallic compounds at Earth’s core thermodynamic conditions. Phys. Rev. Lett. 120, 096001 (2018).
Hu, Q. et al. FeO2 and FeOOH under deep lower-mantle conditions and Earth’s oxygen–hydrogen cycles. Nature 534, 241–244 (2016).
Lu, C., Amsler, M. & Chen, C. Unraveling the structure and bonding evolution of the newly discovered iron oxide FeO2. Phys. Rev. B 98, 054102 (2018).
Zhang, J. et al. Rare helium-bearing compound FeO2He stabilized at deep-Earth conditions. Phys. Rev. Lett. 121, 255703 (2018).
Dewaele, A. et al. Synthesis and stability of xenon oxides Xe2O5 and Xe3O2 under pressure. Nat. Chem. 8, 784 (2016).
Deringer, V. L., Tchougréeff, A. L. & Dronskowski, R. Crystal orbital Hamilton population (COHP) analysis as projected from plane-wave basis sets. J. Phys. Chem. A 115, 5461–5466 (2011).
Liu, Z. et al. Reactivity of He with ionic compounds under high pressure. Nat. Commun. 9, 951 (2018).
Bader, R. F. W. Atoms in Molecules: A Quantum Theory. (Clarendon, Oxford, UK, 1990).
Le Page, Y. & Saxe, P. Symmetry-general least-squares extraction of elastic data for strained materials from ab initio calculations of stress. Phys. Rev. B 65, 104104 (2002).
Martorell, B., Vočadlo, L., Brodholt, J. & Wood, I. G. Strong premelting effect in the elastic properties of hcp-Fe under inner-core conditions. Science 342, 466–468 (2013).
Mainprice, D. A FORTRAN program to calculate seismic anisotropy from the lattice preferred orientation of minerals. Computers Geosci. 16, 385–393 (1990).
Thorne, M. S. & Garnero, E. J. Inferences on ultralow-velocity zone structure from a global analysis of SPdKS waves. J. Geophys. Res. 109, B08301 (2004).
Wang, Y., Lv, J., Zhu, L. & Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 82, 094116 (2010).
Wang, Y., Lv, J., Zhu, L. & Ma, Y. CALYPSO: A method for crystal structure prediction. Comput. Phys. Commun. 183, 2063–2070 (2012).
Zhu, L. et al. Substitutional alloy of Bi and Te at high pressure. Phys. Rev. Lett. 106, 145501 (2011).
Li, Y., Hao, J., Liu, H., Li, Y. & Ma, Y. The metallization and superconductivity of dense hydrogen sulfide. J. Chem. Phys. 140, 174712 (2014).
Peng, F. et al. Hydrogen clathrate structures in rare earth hydrides at high pressures: possible route to room-temperature superconductivity. Phys. Rev. Lett. 119, 107001 (2017).
Lv, J., Wang, Y., Zhu, L. & Ma, Y. Predicted novel high-pressure phases of lithium. Phys. Rev. Lett. 106, 015503 (2011).
Gao, B. et al. Interface structure prediction via CALYPSO method. Sci. Bull. 64, 301 (2019).
Perdew, J. P. & Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 45, 13244 (1992).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953 (1994).
Anisimov, V. I., Solovyev, I. V., Korotin, M. A., Czyżyk, M. T. & Sawatzky, G. A. Density-functional theory and NiO photoemission spectra. Phys. Rev. B 48, 16929 (1993).
Wang, L., Maxisch, T. & Ceder, G. Oxidation energies of transition metal oxides within the GGA+U framework. Phys. Rev. B 73, 195107 (2006).
Liu, J. et al. Hydrogen-bearing iron peroxide and the origin of ultralow-velocity zones. Nature 551, 494 (2017).
Lu, C. & Chen, C. High-pressure evolution of crystal bonding structures and properties of FeOOH. J. Phys. Chem. Lett. 9, 2181–2185 (2018).
Hu, Q. et al. Dehydrogenation of goethite in Earth’s deep lower mantle. Proc. Natl Acad. Sci. USA 114, 1498–1501 (2017).
Monkhorst, H. J. & Pack, J. D. Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188–5192 (1976).
Togo, A., Oba, F. & Tanaka, I. First-principles calculations of the ferroelastic transition between rutile-type and CaCl2-type SiO2 at high pressures. Phys. Rev. B 78, 134106 (2008).
Lee, K., Murray, E. D., Kong, L., Lundqvist, B. I. & Langreth, D. C. Higher-accuracy van der Waals density functional. Phys. Rev. B 82, 081101 (2010).
Anzellini, S., Dewaele, A., Mezouar, M., Loubeyre, P. & Morard, G. Melting of iron at Earth’s inner core boundary based on fast X-ray diffraction. Science 340, 464–466 (2013).
Acknowledgements
We acknowledge funding from National Natural Science Foundation of China under Grant Nos. 11774140 and 11622432, China Postdoctoral Science Foundation under Grant No. 2016M590033, Natural Science Foundation of Henan Province under Grant No. 162300410199, Program for Science and Technology Innovation Talents in University of Henan Province under Grant No. 17HASTIT015, and Open Project of the State Key Laboratory of Superhard Materials, Jilin University under Grant No. 201602.
Author information
Authors and Affiliations
Contributions
Q.L., C.C., and Y.M. designed the research; F.P., and X.S. performed the calculations; F.P., X.S., C.L., Q.L., M.M., C.C., and Y.M. analyzed and interpreted the data, and contributed to the writing of the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Peng, F., Song, X., Liu, C. et al. Xenon iron oxides predicted as potential Xe hosts in Earth’s lower mantle. Nat Commun 11, 5227 (2020). https://doi.org/10.1038/s41467-020-19107-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-19107-y
This article is cited by
-
Open questions on the high-pressure chemistry of the noble gases
Communications Chemistry (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.