Abstract
Quantum engineering using photonic structures offer new capabilities for atom-photon interactions for quantum optics and atomic physics, which could eventually lead to integrated quantum devices. Despite the rapid progress in the variety of structures, coherent excitation of the motional states of atoms in a photonic waveguide using guided modes has yet to be demonstrated. Here, we use the waveguide mode of a hollow-core photonic crystal fibre to manipulate the mechanical Fock states of single atoms in a harmonic potential inside the fibre. We create a large array of Schrödinger cat states, a quintessential feature of quantum physics and a key element in quantum information processing and metrology, of approximately 15000 atoms along the fibre by entangling the electronic state with the coherent harmonic oscillator state of each individual atom. Our results provide a useful step for quantum information and simulation with a wide range of photonic waveguide systems.
Similar content being viewed by others
Introduction
The quantum engineering toolbox developed from free space atom–light interaction experiments over the decades has led to many exciting breakthroughs in the areas of quantum information, metrology and simulation. Departing from free space interactions towards photonic system interfaces could provide new paradigms1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17, such as increased interaction strength, scalability of the devices and novel design of functionalities. For instance, atoms trapped by the evanescent fields of nanofibres and photonic crystal slabs have been used to study long-range atom–atom interactions mediated by the coupling of superradiant emission into the structure4,14. In quantum communication applications, single collective excitation6 and light storage9,10,11 have been demonstrated in nanofibres and hollow-core fibres. Moreover, tight and diffraction-free confinement of atoms in photonic structures was used for optical switching7,17. In metrology, cold atoms in hollow-core fibres have also shown potential applications in timekeeping and sensing8,12,13. Regardless of these achievements, quantum control and manipulation of both external and internal degrees of freedom of atoms using photonic waveguide modes have not been realised.
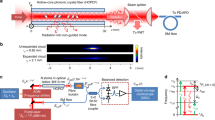
Here, we demonstrate coherent excitation of the Fock states of atoms in an optical harmonic potential formed by the fundamental LP01 mode of a hollow-core photonic crystal fibre. We implement an anti-Jaynes–Cummings-type Hamiltonian to excite the coherent harmonic oscillator states18 (denoted as a coherent state here) and create a Schrödinger cat (SC) state18,19 using the LP01 mode. Our realisation of the SC states is based on a 3-mm array of atoms trapped in an optical lattice potential inside a hollow-core fibre, as shown in Fig. 1. The diffraction-free optical waveguide allows us to prepare an array of harmonic potentials with nearly identical axial trapping frequency. The axial vibrational energy levels of the lattice form the Fock state basis |n> for our experiments.
Two 150-mm achromatic lenses are used to couple all the beams into the fibre with 70% coupling efficiency. The π-polarised optical pump beam incident from the side of the fibre can efficiently prepare atoms in the |F = 2, m = 0> state with >90% efficiency. Each lattice site in the fibre represents a harmonic oscillator potential for atoms (red filled circles). The coloured Gaussian wave packets in the potential illustrate the coherent harmonic oscillator states that are entangled with the spin states. The inset shows a near-field image of the waveguide mode. PBS: polarising beam splitter. NPBS nonpolarising beam splitter, NF notch filter, APD avalanche photodiode.
Results
Ground-state cooling to the Zeeman insensitive state
We first collect an ensemble of 85Rb atoms by Doppler and sub-Doppler cooling 5 mm above a 4-cm-long open-end hollow-core photonic crystal fibre. The fibre is a hypocycloid-shaped photonic crystal fibre with 1/e2 mode field radius of 22 μm11,12,13. Atoms are then transported into the fibre at a velocity of 2 cm s−1 by an optical conveyer belt using a moving optical lattice formed by a pair of counterpropagating beams13. The optical lattice has a period of 410.5 nm, with a power of 110 mW per beam. When atoms are in the fibre, we hold the atoms in a stationary lattice and optically pump them into the magnetic-field-insensitive |F = 2, m = 0> state to avoid the influence of inhomogeneous magnetic fields, where F denotes the hyperfine ground state of 85Rb and m is the Zeeman state. The vibrational frequency of the harmonic-like trap formed by each lattice site is ω = 2π × 400 kHz in the axial direction and ωr = 2π × 3.5 kHz in the radial direction.
To prepare atoms in the axial vibrational ground state of the optical harmonic potential, we implement Raman sideband cooling (RSC) to cool atoms to the |F = 2, m = 0, n = 0> state20. The cooling cycle starts with exciting atoms from |F = 2, m = 0, n> to |F = 3, m = 0, n − 1> with a pair of linearly and orthogonally polarised Raman lasers (RB1 and RB2) at 821 nm, as shown in Fig. 2a, where a magnetic field of 2 G is applied along the fibre axis to define the quantisation axis and break the Zeeman degeneracy. A linearly polarised depump beam is used to bring atoms back to the |F = 2, m, n − 1> state in the Lamb–Dicke regime, where the coupling between the internal spin states and motional states is strongly suppressed during spontaneous emission, to preserve the vibrational quantum number. Finally, a π-polarised optical pump beam is applied to accumulate atoms in the |F = 2, m = 0, n − 1> state to complete the cooling cycle. The cooling process continues until all the atoms are in the |F = 2, m = 0, n = 0> state, which is the dark state for all the laser beams. Figure 2b shows the vibrational spectroscopy before and after cooling. The mean vibrational quantum number <n> is determined by taking the ratio of the areas of the first red sideband Arsb and first blue sideband Absb as <n> = (Arsb/Absb)/(1 − (Arsb/Absb)). We achieve <n>0 = 0.25 after cooling from <n> = 3.3 before cooling. An optical depth (OD) of one corresponds to approximately 1.5 × 104 atoms, which gives an average of two atoms per lattice site12.
a Energy levels and timing sequence. The energy levels represent the vibrational energy splitting of the optical lattice potential in the axial direction. The wavy blue arrow denotes the spontaneous emission of atoms. Each cooling cycle consists of 250 μs of the Raman pulses (RB1 and RB2) and 25 μs of the depump and optical pump pulses. The overall duration for the best cooling performance is N = 120 cooling cycles. RB1 and RB2 are detuned by 3 GHz−ω/2π to reduce n by 1. b Vibrational spectra. We use RB1 and RB2 to excite atoms to the |F = 3, m = 0> state. The x axis is the detuning between the two Raman beams and is set at zero at the carrier transition frequency. We plot the OD for the |F = 3, m = 0> state as a function of the detuning with and without RSC. Most of the atoms are accumulated in the n = 0 state after RSC; therefore, the blue sidebands remain (mostly n = 0 to n = 1 transition), and the red sidebands are suppressed. Smaller OD after RSC is mainly due to atom loss during RSC. Error bars are the standard error of the mean of four experimental runs.
Study of the coherence between Fock states
To study the coherence of the spin Fock states in our system, we use RB1 and RB2 detuned by 3 GHz−ω/2π to excite a two-photon transition between |F = 2, m = 0, n> ≡ |↓, n> and |F = 3, m = 0, n − 1> ≡| ↑, n − 1> through a π/2–π–π/2 spin-echo sequence. We observe 37% and 22% contrasts at 0.1 ms and 0.9 ms separation times between the π/2 and π laser pulses, respectively, as shown in Fig. 3a. In our differential light shift compensated optical lattice potential13, the spin coherence time of the two spin states |↑> and |↓> measured by a microwave π/2–π–π/2 spin-echo sequence exceeds tens of milliseconds. The decay of the contrast is, thus, mostly due to the amplitude noise of the optical lattice and the radial motion of atoms.
a Coherence time measurements between |↓, n> and |↑, n − 1> states. A π/2–π–π/2 spin-echo sequence is implemented on the atoms before sideband cooling. The duration of the π/2 laser pulses is 7.5 μs. The OD of |↑, n − 1> is measured with the varying phase of the final π/2 laser pulse. Error bars are the standard error of the mean of four experimental runs. The curves are sinusoidal fits to the data. b Measurements of the amplitude of the coherent state as a function of driving lasers pulse duration, where atoms are initially prepared in |↓> state. We determine the amplitude of the coherent state by measuring <n> with vibrational spectroscopy, similar to Fig. 2b. Each data point corresponds to one vibrational spectroscopy measurement. Error bars are the standard error of mean of four experimental runs. The straight line is a linear fit to the data with a fixed intercept at zero. c Measurements of <n> of a coherent state after two consecutive driving lasers pulses with phase difference ϕ. The coherence of Fock states components in the coherent state is examined by applying two consecutive driving lasers pulses with phase difference ϕ. After the two driving lasers pulses, we measure <n> from the vibrational spectra and plot it for different phases between the first and second displacement pulses. Error bars are the standard error of the mean of four experimental runs. The curve is a sinusoidal fit to the data.
Preparation of a quantum coherent harmonic oscillator state
The oscillation amplitude of a classical harmonic oscillator increases when the oscillator is subject to an external sinusoidal force at its natural frequency. Similarly, for a quantum harmonic oscillator, resonant driving can be achieved when the oscillation frequency of the force is at the vibrational frequency of the quantum harmonic oscillator21. The oscillatory force in our experiment is created by the time-dependent dipole force from a pair of counterpropagating driving lasers whose relative frequency ω’ is tuned near the vibrational frequency ω of the oscillator. In the quantum mechanical formulation, this corresponds to an initial |n = 0> state displaced by displacement operator D̂(α) to a coherent state |α> . The coherent state created by applying the time-dependent dipole force for a time t can be written as α = (ηΩ/δ)sin(δt/2)e−iδt/2, where η = (ωR/ω)1/2 = 0.20 is the Lamb–Dicke parameter, ωR is the recoil frequency of the driving lasers, Ω is the Rabi frequency of the ac Stark shift arising from the driving lasers, and δ = ω–ω’ (see “Methods”).
The coherent state created by a harmonic oscillator can be written in the Fock state basis with a Poissonian distribution as |α> =exp(−|α|2/2)Σnαn/√n!|n> . Therefore, its amplitude can be determined by the mean phonon number <n> obtained from vibrational spectroscopy measurements. Figure 3b shows the amplitude of the coherent state |α| versus the laser driving time t, where atoms are initially prepared in |↓> state. The pair of driving lasers have wavelengths of 795 nm and are 3.78 GHz red-detuned from the |F = 2> to |F ’ = 2> transition, with ~13 μW per beam. They are linearly polarised and relatively detuned by frequency ω’. To avoid the effect of the radial motion while creating a coherent state, we operate the driving lasers in the short pulse regime t << 1/ωr. When δt is small, the amplitude of the coherent state is linear with the driving time t and independent of the detuning δ as α = ηΩt/2. The data show a linear trend confirming the approximation of our system.
However, this amplitude measurement does not reveal information about the coherence between the superposition of Fock states in the coherent state22. We demonstrate the coherence in the coherent state by applying two consecutive driving lasers pulses with phase difference ϕ. The mean phonon number after the application of two successive displacement operators D̂(α) and D̂(αeiϕ) is <n> = <n>0 + 2|α|2 + 2|α|2cosϕ, as shown in Fig. 3c. The mean phonon number returning to the initial value <n>0 when the phase ϕ is π indicates the coherence between different Fock states in the coherent state. The fitted data show the coherent state with an amplitude |α| = 0.36.
Creation of an array of the SC states
The SC state is a superposition of two spatially separated but localised classical states entangled with an auxiliary superposition state, where the projection measurement on the auxiliary state (or atomic decay) collapses the SC state into one or the other widely separated classical states (or live or dead cat)19. The SC state can be created by entangling a superposition of coherent states with the internal spin states of an atom. For trapped ions SC states, the coherent state α has been created in ions’ motional Fock states basis18,23,24,25,26,27 as large as |α| = 12. In SC states with neutral atoms28,29,30,31 and superconducting circuits32, the coherent states have been formed by the photonic Fock states in resonators with |α| around 1–3. These approaches, typically including one SC state in single apparatus, have been used for quantum-information processing and for testing the boundary between classical and quantum physics18,28. For neutral atoms’ motional Fock states, the coherent states have been demonstrated in a harmonic potential33,34. Here, we create the SC states in an optical lattice by entangling the coherent states and spin states in an optical waveguide.
The protocol of the SC state preparation is shown in Fig. 4a23. A microwave π/2 pulse of 7.5 μs brings the atoms from the vibrational ground state |↓, n = 0> into a superposition state of spin up |↑, n = 0> and spin down |↓, n = 0> . The coherent state |↑, α> is prepared by the driving lasers, whose beat frequency is resonant on the vibrational frequency. The internal spin states are then flipped by a microwave π pulse, followed by another driving lasers pulse with a different phase ϕ to create a coherent state. The resulting SC state can then be written as
Equation (1) is an entangled state between a superposition of coherent states and spin states. To confirm this, we measure the interference of the two separated coherent states by applying another microwave π/2 pulse with a phase shift δM relative to the first two microwave pulses, and the state becomes
The population of atoms in state |↑> is then determined by the overlap between the two coherent states in phase space. We detect the population of the atoms in state |↑> by absorption detection (OD) with varying phase ϕ. The probability of finding the atoms in |↑> is
Figure 4b shows the experimental data of SC state interference fringes for different driving lasers pulse durations. The population of the atoms in |↑> is normalised to 0.5 when the driving lasers are off, and the relative phase is set at δM = π/2. When the microwave phase is set to δM = 0 (π), the SC state is termed the odd (even) cat state. The odd (even) cat states only contain odd (even) Fock states, similarly to squeezed vacuum states. We use this approach to verify the validity of the SC state created in our experiment. Figure 4c shows a comparison of the SC states when δM = 0 and π, and it clearly confirms the trend of population change of Eq. (3) for odd (even) cat states.
a Protocol for creating the SC state in phase space representation. The top and bottom columns represent |↑> and |↓>, respectively. The circles in red indicate the uncertainty in the ground state and the coherent state. The microwave π/2 and π pulses are used to manipulate the internal spin states. The displacement operator D̂(α) and D̂(αeiϕ) are created by driving lasers pulses. b Interference fringes of the SC state interferometer. The population of atoms in |↑> state P↑ is measured with the relative phase ϕ of the two driving lasers pulses for different pulse durations. Error bars are the standard error of the mean of four experimental runs. c Even and odd SC states. The population of atoms in |↑> state P↑ is measured with the relative phase ϕ of the two driving lasers pulses for δM = 0 (odd SC state) and δM = π (even SC state). The driving lasers pulse duration is 0.45 μs. Error bars are the standard error of the mean of four experimental runs. d Fitting parameters of Eq. (4) for the experimental data in panel b is plotted against different driving lasers pulse duration. e Measurements of the |↑> state population P↑ in cat interferometer operation versus phase ϕ with additional free evolution time τ. The total free evolution time between the two driving lasers pulses for τ = 1 μs is 16 μs. Error bars are the standard error of the mean of four experimental runs. f Simulation of the temperature effect on the SC state interferometer. The simulation uses the fitted parameters for t = 0.45 μs in panel d. The 1/e Gaussian radius of the atomic cloud in the radial direction is 0.9 μm and 8 μm for 2 μK and 150 μK, respectively.
Our implementation of the generation of SC states deviates from the ideal case of Eq. (3) due to the imperfect conditions of our experiment. We modify Eq. (3) to fit the data in Fig. 4b by introducing the effects of the residual excitation of the driving lasers on the |↓> state, contrast C, and imperfect initial ground-state preparation as
where β = (1 + εeiϕ’)α, eiθ = (eiϕ’ + ε)/(1 + εeiϕ’), ϕ’ = ϕ − ϕf and ϕf = ω’Δt is the phase advance of the driving lasers due to the increase in the pulse time Δt. For the residual driving, the parameter ε = 0.19 is used to consider the off-resonant dipole force on |↓> (see “Methods”). The imperfect ground-state preparation is taken into account by adding a factor of 2<n>0+1 = 1.5 into the exponent of Eq. (3). The fitting parameters |α|, C and ϕf are displayed in Fig. 4d. The phase advance ϕf is linear in time, as expected, due to the free evolution of the phase of the beating of the driving lasers. For t = 0.45 μs, the amplitude of the coherent state is α = 1.42, which corresponds to a maximum separation of the two coherent wave packets of 2√2|α|z0 = 54 nm, where z02 = (ħ/2mω) is the variance in the ground-state wave packet size, ħ is the reduced Planck constant and m is the mass of 85Rb. The fidelity of the state can be estimated from the contrast27 as C1/2.The loss of contrast suggests phase noise during the operation23, which also widen the narrow interference feature. The increase of the interference width leads to the saturation of |α| after t = 0.45 μs for the fitting of Eq. (4).
We study the effect of radial motion during the free evolution between driving lasers pulses by inserting an additional free evolution time τ, as shown in Fig. 4e. The sequence follows π/2− D̂(α)–τ–π–D̂(αeiϕ)–π/2. The data show that the radial motion does not significantly degrade the contrast at our experimental timescale. We also numerically integrate Eq. (4) over the radial distribution of atoms with radial position-dependent parameters of η, Ω and δ, as shown in Fig. 4 f (see “Methods”). Our results indicate that the radial distribution of atoms is not the main loss mechanism for the interference contrast. The anharmonicity of the optical lattice also causes deviation of the vibrational energy splitting between |n> and |n + 1> from the pure harmonic potential as ωanh = ω − ωrec(1 + n), where ωrec is the recoil frequency of the lattice. This gives an approximately few percent deviations at the centre of the fibre35. Other decoherence mechanisms, such as single-photon scattering of the driving lasers and amplitude fluctuation of the lattice potential36, are 10 and 100 times slower than the coherent interaction between the driving lasers and the atoms.
Discussion
Our results show the coherent interaction of single quantum harmonic oscillator states of matter with the light guided in a fibre. We use the fundamental waveguide mode to create entanglement between coherent states and spin states inside a hollow-core fibre. Such a state can enable quantum simulation of a truly one-dimensional system with the assistance of ground-state cooling in the radial direction1,37. Other than the fundamental importance, the plethora of photonic structures of fibres38 provides fruitful ways for manipulating atoms. For example, the higher-order modes can be tailored to create multiple lattice sites and different polarisations in the transverse plane, creating a three-dimensional atom array in a cylindrically symmetric photonic structure39. Strong atom–light interactions can be achieved by trapping atoms in the cladding modes, which can be patterned by engineering the geometry and thickness of the cladding structure40. As silica fibreglass is transparent to light in the visible to near-infrared range, light propagating from the side into the fibre can also be used for controlling the internal and external degrees of freedom of atoms41. Other photonic crystal structures also possess similar degrees of freedom to control atoms at the single quantum state level. Our experiments pave the way for the realisation of quantum devices of photonic structures with the matter for promising applications in quantum-information science.
Methods
Experimental details
Cold atoms in this experiment are prepared by Doppler and sub-Doppler cooling of a magneto-optical trap (MOT) 5 mm above the fibre tip in 1 s. At this stage, the MOT contains ~108 atoms at 8 μK. After switching off the cooling lasers, a moving optical lattice is turned on to transport atoms into the fibre at a velocity of 2 cm s−1, where the velocity is determined by the frequency difference between the two counterpropagating laser beams. When atoms are a few mm inside the fibre after 200 ms of transport, the frequency difference of the lasers is ramped down to zero to form a stationary lattice. The lattice contains ~2 × 104 atoms. We subsequently apply a push beam in a cycling transition to blow away any atoms above the fibre tip to ensure that only the atoms inside the fibre will be probed. The population in the |F = 3, m = 0> state is measured by the transmission T of a 50 μs probe pulse in the F = 3 to F ’ = 4 D2 transition and represented by the optical depth (OD) as OD = − ln(T).
The two optical lattice beams are from an 821 nm Ti-sapphire laser. They separately pass through two independent acoustic–optical modulators (AOMs) to control their relative frequencies. RB1 is formed by sending part of the Ti-sapphire laser to a 3 GHz electro-optical modulator, followed by a temperature-stabilised solid-state etalon that selects the +1st order laser light. It then passes through an AOM for switching and frequency shifting. The driving lasers are from an extended cavity diode laser frequency locked at 0.744 GHz from F = 3 to F ’ = 2 on the D1 line. It is split into two paths with two independent AOMs before being coupled into the fibre from both ends.
Derivation of the displacement operator
The Hamiltonian of a forced harmonic oscillator in the interaction picture has a form similar to the classical harmonic oscillator
where f(t) is a time-dependent force, and â and ↠are the annihilation and creation operators, respectively. The state after some interaction time t can be characterised by the time-evolution operator
where we only consider the first term in the exponent and α is defined as
The time-dependent force f(t) in our experiment is provided by a moving standing wave resulting from a pair of counterpropagating lasers whose frequency difference ω’ is set to be near the vibrational frequency ω of the harmonic potential. The interaction Hamiltonian between the spin states |↑> of atoms and the lasers can be written as
where Ω is the Rabi frequency of the driving lasers, keff is the effective wave number of the lasers, ω’ is the relative frequency of the driving lasers, and ϕ is the relative phase between the two lasers. In the Lamb–Dicke regime, where keff∙z = keffz0(â†eiωt+ âe-iωt) <<1, exp[ikeff∙z]≈(1+iη(a†eiωt+ ae-iωt) − O(η2)), where η = keffz0. By detuning the driving lasers from the vibrational frequency, the corresponding Hamiltonian for the first blue sideband is
where δ = ω–ω’.
The anti-Jaynes–Cummings-type Hamiltonian has the same form as a forced quantum harmonic oscillator, and α(t) can now be written as
Schrödinger cat-state interferometer
In the preparation of the coherent harmonic state, ideally, the driving lasers should only excite atoms in |↑, n = 0> . However, off-resonant excitation of |↓, n = 0> also occurs. We model this residual excitation by the coefficient ε = Δs/(Δs+fhf), where Δs = 744 MHz is the single-photon detuning of the driving lasers from the |F = 3> to |F ’ = 2> D1 transition, and fhf = 3 GHz is the frequency splitting of |F = 3> and |F = 2> . After the first microwave π/2 pulse, the driving lasers pulse operates on |↓, n = 0> and |↑, n = 0> with εα and α, respectively, and the state becomes
A π microwave pulse flips the spin, and the second driving lasers pulse operates on |↓, α> and |↑, εα> with εαeiϕ’ and αeiϕ’, respectively, where ϕ’ = ϕ + ω’Δt, ϕ is the relative phase of the driving lasers and ω’Δt is the phase advance during the extra waiting time between driving lasers pulses. The state then becomes
The global phase term ε|α|2sinϕ can be ignored in our measurements. The final π/2 microwave pulse with phase δM relative to the first two microwave pulses creates the state
where we define β ≡ (1+εeiϕ’)α and eiθ ≡ (eiϕ’ + ε)/(1 + εeiϕ’). The population of atoms in the |↑> state P↑ is
Temperature effect in the Schrödinger cat-state interferometer
Due to the finite temperature of the atoms in the radial direction, atoms at different locations of the radial trap experience different axial trapping frequencies and therefore different Lamb–Dicke parameters and Rabi frequencies of the driving lasers. Assuming that the above parameters have a Gaussian distribution radially, we numerically integrate Eq. (3) over the position r-dependent coherent harmonic state α(r) = (η(r)Ω(r)/δ(r))sin(δ(r)t/2)e−iδ(r)t/2 weighted by the Gaussian distribution of the atoms as
where the centre of the fibre is defined as r = 0, wa2 = W2kBTr/2/U is the 1/e radius of the spatial distribution of the atomic cloud in the radial direction, W = 22 μm is the 1/e2 mode field radius, kB is the Boltzmann constant, Tr is the radial atom temperature and U is the radial trapping potential. The results for different temperatures are shown in Fig. 4f.
Reporting summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
Chang, D. E., Douglas, J. S., González-Tudela, A., Hung, C.-L. & Kimble, H. J. Colloquium: quantum matter built from nanoscopic lattices of atoms and photons. Rev. Mod. Phys. 90, 031002 (2018).
Solano, P. et al. Optical nanofibers: a new platform for quantum optics. Adv. Mol. Opt. Phys. 66, 439 (2017).
Debord, B., Amrani, F., Vincetti, L., Gérôme, F. & Benabid, F. Hollow-core fibre technology: the rising of gas photonics. Fibers 7, 16 (2019).
Solano, P., Barberis-Blostein, P., Fatemi, F. K., Orozco, L. A. & Rolston, S. L. Super-radiance reveals infinite-range dipole interactions through a nanofiber. Nat. Commun. 8, 1857 (2017).
Meng, Y., Dareau, A., Schneeweiss, P. & Rauschenbeutel, A. Near-ground-state cooling of atoms optically trapped 300 nm away from a hot surface. Phys. Rev. X 8, 031054 (2018).
Corzo, N. V. et al. Waveguide-coupled single collective excitation of atomic arrays. Nature 566, 359–362 (2019).
Bajcsy, M. et al. Efficient all-optical switching using slow light within a hollow fibre. Phys. Rev. Lett. 102, 203902 (2009).
Okaba, S. et al. Lamb-Dicke spectroscopy of atoms in a hollow-core photonic crystal fibre. Nat. Commun. 5, 4096 (2014).
Sprague, M. R. et al. Broadband single-photon-level memory in a hollow-core photonic crystal fibre. Nat. Photonics 8, 287 (2014).
Peters, T., Wang, T.-P., Neumann, A., Simeonov, L. S. & Halfmann, T. Single-photon-level narrowband memory in a hollow-core photonic bandgap fiber. Opt. Express 28, 5340–5354 (2020).
Leong, W. S., Xin, M., Huang, C., Chen, Z. & Lan, S.-Y. Long light storage time in an optical fibre. Phys. Rev. Res. 2, 033320 (2020).
Xin, M., Leong, W. S., Chen, Z. & Lan, S.-Y. An atom interferometer inside a hollow-core photonic crystal fibre. Sci. Adv. 4, e1701723 (2018).
Xin, M., Leong, W. S., Chen, Z. & Lan, S.-Y. Transporting long-lived quantum spin coherence in a photonic crystal fibre. Phys. Rev. Lett. 122, 163901 (2019).
Goban, A. et al. Superradiance for atoms trapped along a photonic crystal waveguide. Phys. Rev. Lett. 115, 063601 (2015).
Hood, J. D. et al. Atom–atom interactions around the band edge of a photonic crystal waveguide. Proc. Natl Acad. Sci. USA 113, 10507–10512 (2016).
Burgers, A. P. et al. Clocked atom delivery to a photonic crystal waveguide. Proc. Natl Acad. Sci. USA 116, 456–465 (2019).
Tiecke, T. G. et al. Nanophotonic quantum phase switch with a single atom. Nature 508, 241–244 (2014).
Wineland, D. J. Nobel lecture. Superposition, entanglement, and raising Schrödinger’s cat. Rev. Mod. Phys. 85, 1103–1114 (2013).
Schrödinger, E. Die gegenwärtige situation in der quantenmechanik. Naturwissenschaften 23, 807–812 (1935).
Sompet, P. et al. Zeeman-insensitive cooling of a single atom to its two-dimensional motional ground state in tightly focused optical tweezers. Phys. Rev. A 95, 031403(R) (2017).
Carruthers, F. & Nieto, M. M. Coherent states and the forced quantum oscillator. Am. J. Phys. 33, 537–544 (1965).
Meekhof, D. M., Monroe, C., King, B. E., Itano, W. M. & Wineland, D. J. Generation of nonclassical motional states of a trapped atom. Phys. Rev. Lett. 76, 1796–1799 (1996). Erratum. Phys. Rev. Lett. 77, 2346 (1996).
Monroe, C., Meekhof, D. M., King, B. E. & Wineland, D. J. A “Schrödinger cat” superposition state of an atom. Science 272, 1131–1136 (1996).
McDonnell, M. J. et al. Long-lived mesoscopic entanglement outside the Lamb-Dicke regime. Phys. Rev. Lett. 98, 063603 (2007).
Poschinger, U., Walther, A., Singer, K. & Schmidt-Kaler, F. Observing the phase space trajectory of an entangled matter wave packet. Phys. Rev. Lett. 105, 263602 (2010).
Lo, H.-Y. et al. Spin-motion entanglement and state diagnosis with squeezed oscillator wavepackets. Nature 521, 336–339 (2015).
Johnson, K. G., Wong-Campos, J. D., Neyenhuis, B., Mizrahi, J. & Monroe, C. Ultrafast creation of large Schrödinger cat states of an atom. Nat. Commun. 8, 697 (2017).
Haroche, S. Nobel lecture. Controlling photons in a box and exploring the quantum to classical boundary. Rev. Mod. Phys. 85, 1083–1102 (2013).
Brune, M. et al. Observing the progressive decoherence of the “meter” in a quantum measurement. Phys. Rev. Lett. 77, 4887–4890 (1996).
Deléglise, S. et al. Reconstruction of non-classical cavity field states with snapshots of their decoherence. Nature 455, 510–514 (2008).
Hacker, B. et al. Deterministic creation of entangled atom–light Schrödinger-cat states. Nat. Photonics 13, 110 (2019).
Vlastakis, B. et al. Deterministically encoding quantum information using 100-photon Schrödinger cat states. Science 342, 607–610 (2013).
Morinaga, M., Bouchoule, I., Karam, J. C. & Salomon, C. Manipulation of motional quantum states of neutral atoms. Phys. Rev. Lett. 83, 4037–4040 (1999).
Belmechri, N. et al. Microwave control of atomic motional states in a spin-dependent optical lattice. J. Phys. B . Mol. Opt. Phys. 46, 104006 (2013).
Blatt, S. et al. Rabi spectroscopy and excitation inhomogeneity in a one-dimensional optical lattice clock. Phys. Rev. A 80, 052703 (2009).
Turchette, Q. A. et al. Decoherence and decay of motional quantum states of a trapped atom coupled to engineered reservoirs. Phys. Rev. A 62, 053807 (2000).
Roy, D., Wilson, C. M. & Firstenberg, O. Strongly interacting photons in one-dimensional continuum. Rev. Mod. Phys. 89, 021001 (2017).
Markos, C., Travers, J. C., Abdolvand, A., Eggleton, B. J. & Bang, O. Hybrid photonic-crystal fiber. Rev. Mod. Phys. 89, 045003 (2017).
Osório, J. H. et al. Tailoring modal properties of inhibited-coupling guiding fibers by cladding modification. Sci. Rep. 9, 1376 (2019).
Couny, F., Benabid, F., Roberts, P. J., Light, P. S. & Raymer, M. G. Generation and photonic guidance of multi-octave optical-frequency combs. Science 318, 1118–1121 (2007).
Kim, M. E., Chang, T.-H., Fields, B.-M., Chen, C.-A. & Hung, C.-L. Trapping single atoms on a nanophotonic circuit with configurable tweezer lattices. Nat. Commun. 10, 1647 (2019).
Acknowledgements
We thank Dzmitry Matsukevich for fruitful discussion and Thomas Billotte on the fibre modal characterisation. This work is supported by the Singapore National Research Foundation under Grant No. NRFF2013-12 and Quantum Engineering Programme under Grant No. QEP-P4, and Singapore Ministry of Education under Grant No. MOE2017-T2-2-066.
Author information
Authors and Affiliations
Contributions
W.S.L., M.X., Z.C., S.C., Y.W. and S.-Y.L. contributed to designing the experiment, taking and analysing the data and preparing the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Barak Dayan, Michal Bajcsy and the other anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Leong, W.S., Xin, M., Chen, Z. et al. Large array of Schrödinger cat states facilitated by an optical waveguide. Nat Commun 11, 5295 (2020). https://doi.org/10.1038/s41467-020-19030-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-19030-2
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.