Abstract
Rotational invariance strongly constrains the viscosity tensor of classical fluids. When this symmetry is broken in anisotropic materials a wide array of novel phenomena become possible. We explore electron fluid behaviors arising from the most general viscosity tensors in two and three dimensions, constrained only thermodynamics and crystal symmetries. We find nontrivial behaviors in both two- and three-dimensional materials, including imprints of the crystal symmetry on the large-scale flow pattern. Breaking time-reversal symmetry introduces a non-dissipative Hall component to the viscosity tensor, and while this vanishes for 3D isotropic systems we show it need not for anisotropic materials. Further, for such systems we find that the electronic fluid stress can couple to the vorticity without breaking time-reversal symmetry. Our work demonstrates the anomalous landscape for electron hydrodynamics in systems beyond graphene, and presents experimental geometries to quantify the effects of electronic viscosity.
Similar content being viewed by others
Introduction
Theoretical and experimental studies have revealed that electrons in condensed matter can behave hydrodynamically, exhibiting fluid phenomena such as Stokes flow and vortices1,2,3,4,5,6,7,8,9. Unlike classical fluids, preferred directions inside crystals lift isotropic restrictions, necessitating a generalized treatment of electron hydrodynamics. While anisotropic viscous flows have been studied in geophysics10, their prominence in condensed matter has yet to be explored. This is of particular importance, given the recent demonstration of hydrodynamic behavior in three-dimensional materials such as Weyl semimetals11,12. Electron hydrodynamics is observed when microscopic scattering processes conserve momentum over time- and length scales that are large compared to those of the experimental probe. However, even as momentum is conserved, free energy may be dissipated from the electronic system, giving rise to a measurable viscosity in the electron flow12,13,14,15,16,17,18.
When momentum is conserved, a fluid obeys Cauchy’s laws of motion19
where u and ρ are the fluid velocity and density, f and l are body forces and couples, τ and m are the fluid stress and couple stress, and σ is the intrinsic angular momentum density (internal spin). The superscript dot denotes the material derivative, \(\dot{x}={\partial }_{t}x \, +{u}_{j}{\partial }_{j}x\), and ϵ is the rank-3 alternating tensor. We assume couple stresses and body couples to be zero, but allow for body forces of the form ρfi = −Rijuj, where R is a rank-2, positive–semidefinite tensor that is inversely proportional to a microscopic momentum-relaxing lifetime. In steady state and at experimentally accessible Reynolds numbers17,20, this implies that the stress tensor is symmetric19. In this limit, electron fluids obey the modified Navier–Stokes equation
where τ is symmetric. Note that in electron fluids, current density is analogous to the fluid velocity, and voltage drops are analogous to changes in pressure. Assuming that the fluid velocity is much smaller than the electronic speed of sound, u ≪ cs, the electron fluids are nearly incompressible, thus
In this limit, ρ is a constant, which we take to be unity. Since the fluid stress appears in a divergence, it is defined only up to a constant, which we choose to make τ vanish when u is uniformly zero21,22. We further assume that the fluid stress vanishes for uniform flow, so that it is only a function of the velocity gradient.
Without further loss of generality, the constitutive relation is written to the first order as21
where A is the fluid viscosity, a rank-4 tensor relating the fluid velocity gradient (∂jui) and the fluid stress. Since we take τ to be symmetric, A is invariant under permutation of its first two indices, i.e., Aijkl = Ajikl21,22. Viscosity is represented as the sum of three rank-4 tensor basis elements23, summarized in Table 1
Tensor α describes dissipative behavior respecting both stress symmetry and objectivity, i.e., αijkl = αjikl = αklij. Tensor β on the other hand, describes nondissipative Hall viscosity7,23,24,25,26,27, i.e., βijkl = −βklij, and is nonzero only when time-reversal symmetry is broken. Finally, γ breaks stress objectivity, i.e., γijkl = −γijlk, coupling fluid stress to the vorticity. The fifth column in Table 1 specifies whether the tensor is defined according to a handedness convention.
In classical fluids, the added consideration of rotational invariance requires A to be isotropic, reducing it to the form
where δ is the Kronecker delta, ϵ is the rank-2 alternating tensor, and the Lamé parameters λ and μ can be identified as the two independent components of the proper tensor α. In the incompressible case, λ does not contribute to the stress21. \({{\mathcal{B}}}_{1}\) and Γ1 are constants parameterizing terms with the symmetry of β and γ, respectively. Since β and γ are pseudotensors, the last three terms in Eq. (7) are only nonzero in two dimensions23,24.
In crystals, however, there exist preferred directions and we cannot assume rotational invariance. Instead, we must consider the effect of the crystal symmetry given by Neumann’s principle28,29, which requires that physical properties described by rank-4 tensors, such as viscosity, remain invariant under the transformation law
where s is the space representation of any given point group symmetry of the crystal, ∣s∣ = ±1 is the determinant of the symmetry operation, and η = 0 for proper tensors and η = 1 for pseudotensors.
Although Eq. (8) relates different components of the viscosity tensor, further constrains must be imposed to ensure that the viscosity tensor never does positive work in Eq. (3), so that for any velocity field u in d dimensions
Letting the Fourier transform of u be
in d dimensions, we find
This is satisfied when Aijkl has a positive definite biquadratic form in il and jk, so we impose this constraint in addition to ij symmetry and crystal symmetry.
Viscosity tensors are then randomly generated to satisfy the aforementioned constraints, allowing for normalized numerical deviations from isotropy lower than order unity. The viscosity tensor is assumed to be spatially uniform in all cases. To demonstrate the differences between these general viscosity tensors and those more strongly constrained by symmetry, we solve for the velocity and pressure of low Reynolds number flows in several geometries. The parameterization of the viscosity tensor in Eq. (6) allows us to explore the effects of breaking stress objectivity and time-reversal symmetry. We highlight the effects of symmetry in the last two indices (kl) because it implies that the stress only couples to the strain rate (∂kul + ∂luk) and not to the vorticity (∂kul − ∂luk). This is a property of classical fluids, which means that rigid–rotational flows are stress-free, and hence are only sensitive to rotation via weaker effects like the Coriolis force. Below, we demonstrate that with more general viscosity tensors, this is not the case, and that the resulting rotational stresses can be probed in experimentally accessible geometries.
Results
Effect of anisotropy
We first consider rotational flow in an annulus with inner radius Rinner = 1 and outer radius Router = 2 (Fig. 1). We apply a no-slip condition to the outer boundary, allow the inner boundary to rotate with unit angular velocity ω = 1, and solve for the steady-state flow at Reynolds number
where
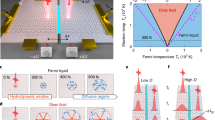
The zero-pressure point is fixed at the bottom of the annulus. Experimentally, such rotational flows can be achieved by threading a time-varying magnetic flux through a Corbino disk geometry30,31 (Fig. 1a). For a fluid with an isotropic viscosity, the steady-state velocity field rotates rigidly with the angular velocity set by the inner boundary condition (Fig. 1b).
a Corbino disk geometry schematic. The time-varying magnetic flux, Φ(t), acting on a voltage drop, ΔV, gives rise to a Lorentz force, inducing rotational electron flow. b Steady-state streamplot plot using an isotropic (SO(2)) viscosity tensor. Streamplots using c hexagonal (D6), and d square (D4) viscosity tensors. e Streamplot using square (D4) viscosity tensor, allowing for momentum-relaxing body force terms equal to ∣R∣L2/∣A∣ = 0.1. f Difference in steady-state streamplot between isotropic and D4 viscosity tensors, highlighting the emergence of steady-state vortices. Steady-state pressure plot using g D6 and h D4 viscosity tensors, illustrating the breaking of azimuthal symmetry in the latter. Color scales indicate the magnitude of the velocity vector field (b–f) and pressure field (g, h).
To investigate the effects of anisotropy in two-dimensional materials, we consider materials with D6 (hexagonal) and D4 (square) symmetry. Notably, D6 materials do not deviate from isotropic behavior (Fig. 1(c)), consistent with experimental observations for graphene9,17. We note that 2D materials with C3 (threefold), C6 (sixfold), and D3 (triangular) symmetry also exhibit isotropic viscosity tensors (see Supplementary Methods). By contrast, the flow deviates considerably from isotropic behavior in D4 materials (Fig. 1d). We repeat the calculation, allowing for a momentum-relaxing body force equal to ∣R∣L2/∣A∣ = 0.1, illustrating that the deviation from isotropy remains observable (Fig. 1e). We assume R → 0 for the rest of the paper, and investigate its effects and symmetry in Supplemenentary Figs. 1 and 2. Figure 1f shows the steady-state velocity flow difference between the isotropic case and D4 materials. We observe steady-state vortices emerging at ~15% of the bulk flow rate overlaid onto the isotropic velocity field. While the steady-state pressure field in D6 materials mirrors that of an isotropic fluid (Fig. 1g), the pressure field in D4 materials also exhibits four vortices (Fig. 1h), with orientation set by the underlying crystal axes.
Effect of asymmetry
We next examine the importance of symmetry in the last two indices of the viscosity tensor. We calculate the flow profile for the annulus in Fig. 1 scaled by a factor of two, equipped with a pressure gauge, as shown in Fig. 2a. The pressure gauge is a channel with no-slip boundary conditions, allowing us to measure the difference between the flow and a nearly stationary fluid. To isolate the effects of \({{\mathcal{B}}}_{1}\) and Γ1 in Eq. (7), Fig. 2a, b shows the flow and pressure fields in the annulus for a material with isotropic viscosity tensor where both \({{\mathcal{B}}}_{1}\) and Γ1 have been set to zero (SO(2){α}). These are nearly unchanged inside the annulus as compared to Fig. 1b, g, with a constant pressure in the gauge. Allowing for nonzero stress-breaking components, i.e., using a material with isotropic viscosity for \({{\mathcal{B}}}_{1}=0\) and Γ1 = 0.25 (SO(2){γ}), we observe a significant pressure buildup near the gauge. This is due to the shear stress between the rotating and stationary fluids, while the pressure within the gauge itself is nearly uniform, as shown in Fig. 2c.
Steady-state a streamplot and b pressure plot using viscosity tensor SO(2){α}. c Difference in steady-state pressure between viscosity tensor SO(2){α} and the same with additional stress objectivity-breaking terms (SO(2){γ}). The asymmetry introduces an additional pressure-like contribution, which can be directly measured. d Difference in steady-state pressure between the D2h and C2v viscosity tensors along the ab plane, showing a similar pressure drop in the gauge, despite the anisotropic behavior inside the annulus. Color scales indicate the magnitude of the velocity vector field (a) and pressure field (b–d).
To quantify the pressure difference between SO(2){α} and SO(2){γ}, note that the pressure is fixed to zero at a point p, the bottom of the annulus domain. The pressure in the gauge may be written as the path integral
where g is a point in the gauge. At low Reynolds numbers, we may neglect uj∂jui in Eq. (3), to find in the steady state
Taking into account Eq. (7) and noting that the changes in fluid flow are negligible, we find
where ωi = ϵijk∂juk is the vorticity of the flow. For the geometry used, we find Δpgauge = 0.15, vorticity in the gauge is zero, and that in the annulus is 0.6, so Δω = 0.6 (Fig. 2c). Since we chose Γ1 = 0.25, we see that in this setup, the pressure gauge (Δpgauge = Γ1Δω = 0.25 × 0.6 = 0.15) is directly sensitive to the asymmetry in the viscosity, which couples the rotation directly to the pressure field and the stress. We note that the same setup is sensitive to Hall viscosity coefficients for time-reversal broken systems, i.e., for the case where both \({{\mathcal{B}}}_{1}\) and Γ1 are nonzero, the pressure gauge generalizes to
While time-reversal and stress objectivity-breaking terms persist in two-dimensional isotropic materials, the handedness of the pseudotensor implies that mirror operations set them to zero in 3D. This can be directly observed by comparing low- and high-symmetry three-dimensional crystals. We consider the same rotational flow along the ab crystal plane of orthorhombic materials, such as the hydrodynamically reported Weyl semimetal WP211,12. Along this plane, the difference between the two viscosity tensors can be parameterized as follows:
where \({{\mathcal{B}}}_{2}\), \({{\mathcal{B}}}_{3}\), Γ2, and Γ3 are constants parameterizing terms with the symmetry of β and γ, respectively, σx and σz are Pauli matrices. Figure 2d shows the pressure difference between a material with D2h symmetry and one with C2v symmetry (for \({{\mathcal{B}}}_{2}={{\mathcal{B}}}_{3}={\Gamma }_{3}=0\) and Γ2 = 0.25), indicating the same pressure buildup as in Fig. 2c inside the gauge along with a nontrivial pressure structure in the annulus.
2D flows in 3D crystals
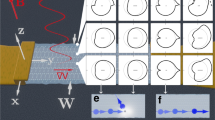
Finally, we consider flow through an expanding channel along high-symmetry planes in 3D. This geometry has been proposed as a diagnostic of electron hydrodynamics because it naturally generates vortices, not present in ordinary ohmic flow. The case with isotropic viscosity is shown in Fig. 3a, where the small vortices that form in the corners are clearly detached from the bulk of the flow. We consider the Td (tetrahedral) and Oh (cubic) point groups. In particular, we consider flows along the polar {111}, nonpolar {110}, and semipolar {001} family of planes (Fig. 3b)
Along these planes, the difference between the two viscosity tensors can be parameterized according to Eqs. (20a), (20b), (20c). We impose fully developed (parabolic) inlet and outlet flows with constant discharge, and solve for the steady-state flow at low Reynolds number. Figure 3c shows the difference between the flow in an isotropic material and the flow in a cubic material along a {111} close-packed plane, which exhibits rotational invariance. Along the nonpolar {110} planes, terms with β and γ symmetry vanish. However, \({{A}}^{{{O}}_{{\rm{h}}}^{(110)}}\) is anisotropic along this plane, with Fig. 3d showing the difference in flow between the isotropic case. Finally, along the semipolar {001} family of planes, the viscosity tensor is both anisotropic (Fig. 3e) and asymmetric. Figure 3f quantifies the additional vortices generated by the asymmetry at ~10%, for \({{\mathcal{B}}}_{5}=0\) and Γ5 = 0.25.
a Steady-state streamplot using an isotropic (SO(3)) viscosity tensor. b High-symmetry family of planes in cubic crystals. In crystals with Td (tetrahedral) symmetry, these are further identified as polar {111}, nonpolar {110}, and semipolar {001}. Difference in the steady-state streamplot between using an isotropic viscosity tensor and using c (111)-projected, d (110)-projected, and e (001)-projected viscosity tensors of cubic crystals with Td symmetry. Note that c shows no difference. f Effect of viscosity tensor asymmetry difference between Oh and Td crystals along a semipolar {001} plane. Color scales indicate the magnitude of the velocity vector field.
Discussion
We found that electron fluids in crystals with anisotropic and asymmetric viscosity tensors can exhibit steady-state fluid behaviors not observed in classical fluids. In 3D, discrete deviations from isotropy allow the fluid stress to couple to the fluid vorticity with or without breaking time-reversal symmetry, for the case of Hall viscosity and objectivity-breaking viscosity, respectively. Recent measurements of spatially resolved flows9,17,32 suggest that these effects can be directly observed in systems beyond graphene. Our findings further hint at potential applications. For instance, the pressure gauge in Fig. 2 could be used as a magnetometer, converting a time-varying magnetic flux through a modified Corbino disk geometry into current in the annulus, and ultimately into a voltage drop between it and the gauge. Our work highlights the importance of crystal symmetry on electronic flow, and invites further exploration of time-dependent flows in systems with internal spin degrees of freedom and asymmetric stress tensors.
Data availability
The authors declare that the main data supporting the findings of this study are available within the article and its Supplementary Information files.
Code availability
Code available upon request from the authors.
References
Andreev, A. V., Kivelson, S. A. & Spivak, B. Hydrodynamic description of transport in strongly correlated electron systems. Phys. Rev. Lett. 106, 256804 (2011).
Levitov, L. & Falkovich, G. Electron viscosity, current vortices and negative nonlocal resistance in graphene. Nat. Phys. 12, 672–676 (2016).
Scaffidi, T., Nandi, N., Schmidt, B., Mackenzie, A. P. & Moore, J. E. Hydrodynamic electron flow and hall viscosity. Phys. Rev. Lett. 118, 226601 (2017).
Lucas, A. & Fong, K. C. Hydrodynamics of electrons in graphene. J. Phys. 30, 053001 (2018).
Link, J. M., Narozhny, B. N., Kiselev, E. I. & Schmalian, J. Out-of-bounds hydrodynamics in anisotropic dirac fluids. Phys. Rev. Lett. 120, 196801 (2018).
Cook, C. Q. & Lucas, A. Electron hydrodynamics with a polygonal fermi surface. Phys. Rev. B 99, 235148 (2019).
Holder, T., Queiroz, R. & Stern, A. Unified description of the classical hall viscosity. Phys. Rev. Lett. 123, 106801 (2019).
Holder, T. et al. Ballistic and hydrodynamic magnetotransport in narrow channels. Phys. Rev. B 100, 245305 (2019).
Sulpizio, J. A. et al. Visualizing poiseuille flow of hydrodynamic electrons. Nature 576, 75–79 (2019).
Perry-Houts, J. & Karlstrom, L. Anisotropic viscosity and time-evolving lithospheric instabilities due to aligned igneous intrusions. Geophys. J. Int. 216, 794–802 (2018).
Coulter, J., Sundararaman, R. & Narang, P. Microscopic origins of hydrodynamic transport in the type-II weyl semimetal wp2. Phys. Rev. B 98, 115130 (2018).
Gooth, J. et al. Thermal and electrical signatures of a hydrodynamic electron fluid in tungsten diphosphide. Nat. Commun. 9, 4093 (2018).
Molenkamp, L. W. & de Jong, M. J. M. Observation of knudsen and gurzhi transport regimes in a two-dimensional wire. Solid-State Electron. 37, 551–553 (1994).
de Jong, M. J. M. & Molenkamp, L. W. Hydrodynamic electron flow in high-mobility wires. Phys. Rev. B 51, 13389–13402 (1995).
Bandurin, D. A. et al. Negative local resistance caused by viscous electron backflow in graphene. Science 351, 1055–1058 (2016).
Crossno, J. et al. Observation of the dirac fluid and the breakdown of the wiedemann-franz law in graphene. Science 351, 1058–1061 (2016).
Ku, M. J. H. et al. Imaging Viscous Flow of the Dirac Fluid in Graphene Using a Quantum Spin Magnetometer. http://arxiv.org/abs/1905.10791v1.
Moll, P. J. W., Kushwaha, P., Nandi, N., Schmidt, B. & Mackenzie, A. P. Evidence for hydrodynamic electron flow in PdCoO2. Science 351, 1061–1064 (2016).
Stokes, V. K. Couple stresses in fluids. Phys. Fluids 9, 1709 (1966).
Mendoza, M., Herrmann, H. J. & Succi, S. Hydrodynamic model for conductivity in graphene. Sci. Rep. 3, 1052 (2013).
Landau, L. D. & Lifshitz, E. M. Fluid Mechanics (London, Pergamon Press, 1959).
Steinberg, M. S. Viscosity of the electron gas in metals. Phys. Rev. 109, 1486–1492 (1958).
Epstein, J. M. & Mandadapu, K. K. Time Reversal Symmetry Breaking in Two-dimensional Non-equilibrium Viscous Fluids. http://arxiv.org/abs/1907.10041v1.
Avron, J. E. Odd Viscosity. J. Stat. Phys. 92, 543–557 (1998).
Banerjee, D., Souslov, A., Abanov, A. G. & Vitelli, V. Odd viscosity in chiral active fluids. Nat. Commun. 8, 1573 (2017).
Berdyugin, A. I. et al. Measuring Hall viscosity of graphene’s electron fluid. Science 364, 162–165 (2019).
Rao, P. & Bradlyn, B. Hall viscosity in quantum systems with discrete symmetry: point group and lattice anisotropy. Phys. Rev. X 10, 021005 (2020).
Neumann, F. E. Vorlesungen üBer die Theorie der Elastizität der Festen Körper und des Lichtäthers. (B. G. Teubner-Verlag, 1885).
Nye, J. F. Physical Properties of Crystals (Oxford University Press, 1985).
Tomadin, A., Vignale, G. & Polini, M. Corbino disk viscometer for 2d quantum electron liquids. Phys. Rev. Lett. 113, 235901 (2014).
Mumford, S., Paul, T., Lee, S. H., Yacoby, A. & Kapitulnik, A. A cantilever torque magnetometry method for the measurement of hall conductivity of highly resistive samples. Rev. Sci. Instrum. 91, 045001 (2020).
Ella, L. et al. Simultaneous voltage and current density imaging of flowing electrons in two dimensions. Nat. Nanotechnol. 14, 480–487 (2019).
Acknowledgements
The authors thank Prof. Andrew Lucas of the University of Colorado Boulder for fruitful discussions. The authors acknowledge funding from the Defense Advanced Research Projects Agency (DARPA), Defense Sciences Office (DSO) Driven, and Nonequilibrium Quantum Systems program Grant Number D18AC00014 and the STC Center for Integrated Quantum Materials, NSF Grant No. DMR-1231319. A.S.J. is supported by the Flatiron Institute of the Simons Foundation. P.N. is a Moore Inventor Fellow supported by the Gordon and Betty Moore Foundation Grant Number 8048.
Author information
Authors and Affiliations
Contributions
G.V. and A.S.J. jointly conceived the ideas and developed the framework. G.V., C.F., and P.N. identified the material systems and link with the transport measurements of topological systems. G.V., P.A., and P.N. jointly worked on introducing the effects of crystal symmetries. All authors discussed the findings and contributed to the writing of the paper.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Gregory Falkovich and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Varnavides, G., Jermyn, A.S., Anikeeva, P. et al. Electron hydrodynamics in anisotropic materials. Nat Commun 11, 4710 (2020). https://doi.org/10.1038/s41467-020-18553-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-18553-y
This article is cited by
-
Charge transport and hydrodynamics in materials
Nature Reviews Materials (2023)
-
Directional ballistic transport in the two-dimensional metal PdCoO2
Nature Physics (2022)
-
Hydrodynamic approach to two-dimensional electron systems
La Rivista del Nuovo Cimento (2022)
-
Hydrodynamic effective field theories with discrete rotational symmetry
Journal of High Energy Physics (2022)
-
Optical N-invariant of graphene’s topological viscous Hall fluid
Nature Communications (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.