Abstract
Understanding defect evolution and structural transformations constitutes a prominent research frontier for ultimately controlling the electrochemical properties of advanced battery materials. Herein, for the first time, we utilize in situ high-energy Kr ion irradiation with transmission electron microscopy to monitor how defects and microstructures evolve in Na- and Li-layered cathodes with 3d transition metals. Our experimental and theoretical analyses reveal that Li-layered cathodes are more resistant to radiation-induced structural transformations, such as amorphization than Na-layered cathodes. The underlying mechanism is the facile formation of Li-transition metal antisite defects in Li-layered cathodes. The quantitative mathematical analysis of the dynamic bright-field imaging shows that defect clusters preferentially align along the Na/Li ion diffusion channels (a-b planes), which is likely governed by the formation of dislocation loops. Our study provides critical insights into designing battery materials for extreme irradiation environments and understanding fundamental defect dynamics in layered oxides.
Similar content being viewed by others
Introduction
Crystal defects play a critical role in influencing the physicochemical properties of metal oxides1,2, such as catalytic activity3, optical absorption4, electronic5, and electromagnetic properties6. Thus, defect engineering has gained broad attention as a method of tailoring metal oxide characteristics7. Layered transition metal oxides are extensively utilized as cathodes for the state-of-the-art rechargeable batteries8,9. Defects in these materials can be induced by the high-temperature synthesis10 and electrochemical cycling11 and can broadly influence battery properties. For example, defect dynamics is related to capacity loss12, ion migration13,14, voltage hysteresis15, and structural transformations during cycling16. Voltage fade and oxygen loss in Li-rich layered cathodes are directly correlated to the defect evolution17. However, it has also been reported that defects can relieve the strain by acting as an interface between two phases during phase transformation18. Defect engineering can enhance electrochemical performance in certain cases19,20. Thus, a recent incentive is to control and monitor the defect evolution to enhance the electrochemical performance of battery electrodes. However, efficient monitoring of defect dynamics is still a challenging task. Researchers have been developing techniques that can track defects under operating conditions21,22. Ulvestad et al.23 and Singer et al.17 utilized Bragg coherent diffraction imaging to monitor dislocation dynamics in spinel LiNi0.5Mn1.5O4 and layered Li1.2Ni0.333Mn0.333Co0.333O2 cathodes, respectively. However, a limited resolution of the technique means that point defects or small defect clusters are difficult to characterize24. Transmission electron microscopy (TEM) with high spatial/temporal resolution may provide a solution in this regard22.
Defect and structural evolution can be accelerated in complex oxides through high-energy ion irradiation25,26. Ion irradiation in conjunction with TEM has been utilized to understand the irradiation damage in nuclear reactor materials and fuels27,28,29,30. Alkali-ion batteries have the potential to be utilized in extreme environments, such as outer space and nuclear power industries, where high-energy irradiation can impart significant damage to materials31,32. Accelerated degradation of cell components, such as cathode and electrolyte, has been observed under neutron and gamma irradiation31,33. Radiation-induced hardness is observed in perovskite tandem solar cells34. Structural transformation, for example, amorphization can take place in a crystalline material under extreme irradiation35. For the reliable performance of battery materials in extreme environments, these materials are required to be resistant to such structural damage. Under irradiation, high-energy particles, such as neutron or Kr ions, can displace atoms away from their lattice sites and form a locally disordered region, called cascade36,37,38. A cascade can recover in a few picoseconds (10−12 s), but some displaced atoms can form defects, such as interstitials and vacancies. The aggregation of these point defects can form extended defects, such as dislocation loops and voids39. Dislocation loop and void formation will require the diffusion of interstitials and vacancies at the temperature of irradiation, respectively. In comparison, interstitial-type defects are also formed during electrochemical cycling through transition metal migration in the interlayer space40,41. Such migration can lead to structural transformation42 and voltage fading43,44. Vacancy cluster formation in Na0.75Li0.25Mn0.75O2 is reported in as early as the first cycle15. Since vacancies and interstitials are also formed under ion irradiation, the material damage due to ion irradiation shares some similarities with the electrochemical cycling. Furthermore, the ability to create high-density defects in a short time through ion irradiation enables studying defect and structural evolution in situ45, thus overcoming the limitation of slow defect evolution through electrochemical cycling.
In this study, we explore the defect and structural evolution in layered cathodes with 3d transition metals (AxTMO2, where A is akali ion, TM is transition metal ion, and x is ≤1) under high-energy Kr ion irradiation. Kr ion irradiation can induce observable damage within a short period of time46. The cascade damage profile produced by Kr ion irradiation is similar to neutron irradiation in a nuclear reactor. Hence, efficient mirroring of the defect and structural evolution throughout the actual service life in extreme environments is possible within the timescale of a laboratory experiment. Layered P2-Na2/3Fe1/2Mn1/2O2 (space group: P63/mmc) and O3-LiNiO2 (space group: R\(\bar 3\)m) are utilized as the model materials for this study. P2-Na2/3Fe1/2Mn1/2O2 has received broad attention because it contains only earth-abundant elements and delivers high discharge capacity47. LiNiO2 has been revitalized recently because of the incentive to eliminate high cost and child labor-intensive Co from cathodes48. In situ TEM imaging, electron diffraction, and density functional theory (DFT)-based calculations have revealed that Li-layered oxides are more resistant to irradiation-induced structural transformation (e.g., amorphization) than Na-layered oxides. Our comprehensive mathematical analysis on the bright-field two-beam images of the irradiated materials shows that defect clusters tend to aggregate preferentially along the a–b planes of the irradiated materials. Electrochemically cycled cathodes also exhibit similar behavior as exemplified by the similarity between irradiated LiNiO2 and delithiated LiNiO2.
Results
Physical and electrochemical characterization of layered cathodes
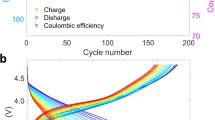
Na2/3Fe1/2Mn1/2O2 crystallizes into a layered structure with ABBA-type oxygen stacking (P2 type) and the Na ion in the interlayer space is in prismatic coordination with the oxygen ions (inset of Fig. 1a). All diffraction peaks in the X-ray powder diffraction (XRD) pattern can be indexed towards a pure hexagonal lattice with a P63/mmc space group (Fig. 1a), isostructural to P2-NaxCoO249. LiNiO2 crystallizes into a layered structure with ABCABC-type oxygen stacking (O3 type). Li ion is in octahedral coordination with oxygen ions (inset of Fig. 1b). The diffraction peaks in the XRD pattern can be indexed towards a pure rhombohedral lattice with R\(\bar 3\)m space group50, isostructural to α-NaFeO2 (Fig. 1b). The primary particles of both materials have random morphology (inset of Fig. 1a, b). Na2/3Fe1/2Mn1/2O2 delivers a specific discharge capacity of 185–190 mAh/g at C/10 rate (Fig. 1c) and 150–155 mAh/g at 1C rate (Fig. 1d) in Na half cells. LiNiO2 delivers 225 mAh/g capacity at C/5 rate (Fig. 1e) and 185 mAh/g at 1C rate (Fig. 1f) in Li half cells. The capacity and capacity retention (Supplementary Fig. 1) delivered by these materials are comparable to those reported in the literature47,48. In summary, the phase pure crystal structure along with the electrochemical performance shows that these materials are representative and can provide a good platform for studying the defect and structural evolution of Li- and Na-layered cathodes under extreme environments.
a XRD pattern of Na2/3Fe1/2Mn1/2O2. The inset shows the crystal structure and SEM image of the material. The scale bar in the SEM image corresponds to a length of 500 nm. b XRD pattern of LiNiO2. The inset shows the crystal structure and SEM image of the material. The scale bar in the SEM image corresponds to a length of 500 nm. c Charge and discharge curves of Na half cell containing the Na2/3Fe1/2Mn1/2O2 as the cathode material at a rate of C/10. d Charge and discharge curves of Na half cell containing the Na2/3Fe1/2Mn1/2O2 as the cathode material at a rate of 1C. e Charge and discharge curves of Li half cell containing the LiNiO2 as the cathode material at a rate of C/5. f Charge and discharge curves of Li half cell containing the LiNiO2 as the cathode material at a rate of 1C. The first cycle is at C/5 rate. The charge and discharge curves for both materials are plotted for up to 20 cycles.
Structural transformation under in situ Kr ion irradiation
Kr ion with an energy of 1 MeV at room temperature is used to irradiate Na2/3Fe1/2Mn1/2O2 and LiNiO2 to induce defects and structural transformations. SRIM (stopping and range of ions in the matter) simulation51 is performed to understand the Kr ion concentrations and damage profiles within the materials (Supplementary Fig. 2). The simulation shows that for a particle with a 1000 nm thickness, the maximum Kr ion concentration is at a depth of ~400 nm for both Na2/3Fe1/2Mn1/2O2 and LiNiO2 (Supplementary Fig. 2a, c). The maximum number of vacancies (peak damage) is produced within the depth of ~300 nm of both Na2/3Fe1/2Mn1/2O2 and LiNiO2 (Supplementary Fig. 2b, d).
Structural evolution is monitored in situ by electron diffraction (ED) with increasing fluence of Kr ion irradiation at room temperature (Fig. 2). The ED of Na2/3Fe1/2Mn1/2O2 can be indexed as lattice planes from a hexagonal lattice with P63/mmc space group when viewed from the [100] zone axis (Fig. 2b), in corroboration with the global crystal structure deciphered from the XRD pattern. The diffraction spots from the particle of LiNiO2 can be indexed as lattice planes from the rhombohedral lattice with the space group R\(\bar 3\)m when viewed from the [100] zone axis (Fig. 2g), in corroboration with the global XRD pattern of the material. The brightness of the diffraction spots can be a measure of the crystallinity of the materials. For irradiated Na2/3Fe1/2Mn1/2O2 and LiNiO2, the spots get dimmer with increasing fluence of Kr ion irradiation. We measured the brightness of the spots in terms of pixel values of a grayscale image (black being 0 and white being 255 in pixel value). Starting with a range of pixel values from 200 to 255 within the spot, the spots for the lattice plane (004) of Na2/3Fe1/2Mn1/2O2 and (006) plane of LiNiO2 contain increasingly less number of pixels within the same range (Supplementary Figs. 3 and 4), indicating that the materials are losing crystallinity with increasing fluence of Kr ion irradiation. However, a striking dissimilarity is observed when we compare the resistance to loss of crystallinity between Na2/3Fe1/2Mn1/2O2 and LiNiO2. At a fluence of 4.38 × 1014 Kr2+/cm2, many of the diffraction spots of Na2/3Fe1/2Mn1/2O2 disappear and only those from the (00l) lattice planes remain (Fig. 2d). At 6.25 × 1014 Kr2+/cm2, the particle of Na2/3Fe1/2Mn1/2O2 becomes completely amorphous since all the spots from the lattice planes disappear (Fig. 2e). However, the particle of LiNiO2 at that particular fluence still maintains some of its crystallinity since some of the spots from both (0kl) and (00l) are observable (Fig. 2j). In fact, even at 1.25 × 1015 Kr2+/cm2, that is, double the fluence of 6.25 × 1014 Kr2+/cm2, LiNiO2 still maintains some crystallinity (Supplementary Fig. 5b). Hence, LiNiO2 is more resistant to amorphization than Na2/3Fe1/2Mn1/2O2 when irradiated with high-energy ion beam to the same fluence. Similar to pristine LiNiO2, electrochemically delithiated LiNiO2 (charged to 4.5 V against Li+/Li) is also more resistant to radiation-induced structural damage than Na2/3Fe1/2Mn1/2O2 (Supplementary Fig. 6). It should be noted that, in some cases, the electron beam utilized for imaging has been reported to induce structural transformations in a material52,53. However, upon prolonged exposure to electron beam irradiation alone (up to 1 h), no significant microstructural evolution in Na2/3Fe1/2Mn1/2O2 is observed in this work (Supplementary Fig. 7a–f). In comparison, the structural damage induced by Kr ion irradiation is significantly larger and accounts for the most structural changes observed in the material (Fig. 2 and Supplementary Fig. 7g–l).
a The Na2/3Fe1/2Mn1/2O2 particle that is irradiated at room temperature. The scale bar corresponds to a length of 100 nm. Electron diffraction of Na2/3Fe1/2Mn1/2O2 at the fluence of b 6.25 × 1013 Kr2+/cm2, c 1.88 × 1014 Kr2+/cm2, d 4.38 × 1014 Kr2+/cm2, and e 6.25 × 1014 Kr2+/cm2. The scale bars in b–e are equivalent to 2 1/nm. f The LiNiO2 particle that is irradiated at room temperature. The scale bar corresponds to a length of 100 nm. Electron diffraction of LiNiO2 at the fluence of g 6.25 × 1013 Kr2+/cm2, h 1.25 × 1014 Kr2+/cm2, i 4.38 × 1014 Kr2+/cm2, and j 6.25 × 1014 Kr2+/cm2. The scale bars in g–j are equivalent to 2 1/nm.
Loss of crystallinity in Na2/3Fe1/2Mn1/2O2 under Kr ion irradiation (Fig. 2) is accompanied by the formation of amorphous regions on the particles (Fig. 3). Figure 3a–c and Supplementary Fig. 8 show the microstructural evolution of Na2/3Fe1/2Mn1/2O2 particle. The area of the amorphous region increases with irradiation (Fig. 3a–c, and Supplementary Fig. 9) until the particle becomes fully amorphous at the fluence of 6.25 × 1014 Kr2+/cm2 (Supplementary Fig. 10g), in corroboration with Fig. 2e. The area of the amorphous layer on the surface of LiNiO2 particle also seems to increase with irradiation (Fig. 3d–f and Supplementary Fig. 11), although complete amorphization is not observed. It must be noted that the amorphous layers on these two materials are fundamentally distinct from each other. The growth of the amorphous layer within the particle of Na2/3Fe1/2Mn1/2O2 indicates a transformation from the crystalline to the amorphous phase, which is supported by the ED results (Fig. 2a–e). Meanwhile, the transparent amorphous layer on the surface of LiNiO2 indicates that the growth of this layer is due to the entrapment of trace carbon by electrons inside the TEM column54,55.
a TEM image of Na2/3Fe1/2Mn1/2O2 before irradiation. TEM images of Na2/3Fe1/2Mn1/2O2 at the fluence of b 1.88 × 1014 Kr2+/cm2, and c 3.13 × 1014 Kr2+/cm2 at room temperature. The red dashed lines in (b–c) indicate the growth of the amorphous layer upon irradiation. d TEM image of LiNiO2 before irradiation. TEM images of LiNiO2 at the fluence of e 1.25 × 1014 Kr2+/cm2, and f 3.13 × 1014 Kr2+/cm2 at room temperature. All the scale bars correspond to a length of 20 nm.
The observed differences in structural transformations between the Na- and Li-layered cathode can possibly be explained based on the previous studies of other metal oxides29,30. These studies indicated that in pyrochlores (A2B2O7, where A and B indicate two different cations), the formation energy of the cationic antisite defect pair is inversely related to the resistance to radiation tolerance. The formation energy would depend on the difference in ionic radius between two types of cations in pyrochlores. A large difference in ionic radius will have a high energy for cationic antisite defect formation and vice versa. The difference in ionic radius between Li+ and Ni3+ in LiNiO2 is smaller than the difference in ionic radius between Na+ and the transition metal ions (Fe3+ and Mn4+) in Na2/3Fe1/2Mn1/2O2, using the ionic radii provided by Shannon and Prewitt56. Hence, LiNiO2 should be more radiation-resistant than Na2/3Fe1/2Mn1/2O2 based on this argument from an earlier study29, which is consistent with our experimental observations. However, it is yet to be determined if antisite formation energy can be directly correlated with the radiation tolerance in layered oxide materials. A detailed account of the relationship between the cationic antisite defect formation energy and resistance to radiation damage of layered oxides is provided later by DFT calculations.
Structural transformations also depend on the temperature. At a high temperature (e.g., 200 °C), Na2/3Fe1/2Mn1/2O2 displays more resistance to amorphization than at room temperature (Supplementary Fig. 12). At 200 °C, Na2/3Fe1/2Mn1/2O2 still maintains some crystallinity when irradiated at the fluence of 6.25 × 1014 Kr2+/cm2 (Supplementary Fig. 12d), which is the dose required for amorphization at room temperature (see Fig. 2e). However, instead of going through a direct layered to amorphous transformation observed at room temperature, an intermediate spinel phase (space group: Fd\(\bar 3m\)) is observed at 200 °C (Supplementary Fig. 12b). The spots for the spinel phase start to form partial rings at higher fluence (Supplementary Fig. 12c–f), indicating the development of a polycrystalline nature of the emerging spinel phase. In fact, from the TEM image, a number of small domains of the spinel phase are observed at the fluence of 3.13 × 1014 Kr2+/cm2 (Supplementary Fig. 13c). Formation of the spinel phase may indicate oxygen evolution in order to form a cation densified state, according to previously reported literature57. Meanwhile at a low temperature (−173 °C), the resistance to amorphization of Na2/3Fe1/2Mn1/2O2 decreases significantly (Supplementary Fig. 14). The material becomes completely amorphous even at a fluence as low as 1.25 × 1014 Kr2+/cm2 (Supplementary Fig. 14c). Thus, it is evident that the critical dose for complete amorphization of layered materials strongly depends on temperature and increases with the elevation of temperature, which is similar to other ceramics58,59. This is because defect annihilation typically accelerates as temperature increases, thus increasing the critical dose of amorphization60,61.
Dynamic defect evolution under in situ Kr ion irradiation
Defect evolutions in Na2/3Fe1/2Mn1/2O2 and LiNiO2 are monitored through bright-field two-beam imaging with increasing fluence of Kr ion irradiation. The defect clusters are manifested as black spots in the images since they diffract more beam away from the particle62. These grayscale images enable the mapping of defect clusters distribution and propagation under irradiation by performing statistical analysis through pixel by pixel gradient vector computation (Figs. 4 and 5). In a grayscale image, the pixels are composed of either black, white or various shades of gray colors. A number is assigned to the pixels with black color having a value of 0, white color having a value of 255, and different shades of gray colors being assigned values in between (color bar in Fig. 4a). A certain pixel will be surrounded by two pixels in each of the x- and y-direction (Fig. 4a). Each gradient vector is computed by the partial gradient vectors in both directions. The partial gradient vectors represent brightness changes (calculated in terms of pixel values) in either the x-direction or the y-direction. The final vector (\(\vec g\)) is the sum of the two partial vectors (Fig. 4a). This gradient vector represents the overall directional change in brightness from a certain pixel in consideration. The equations listed below define the partial gradient vectors, the final gradient vector, and the size of the final vector:
Here, \(\frac{{\partial \vec f}}{{\partial x}}\) and \(\frac{{\partial \vec f}}{{\partial y}}\) mean the change in pixel values in the x-direction and y-direction, respectively. The angle (θ) of the gradient vector is defined with respect to the Na/Li ion diffusion channel (along the y-direction in Fig. 4a). The angle of the gradient vector is defined in such a way that if any vector is along the Na/Li ion diffusion channel, the angle will be 0°. If the vector is perpendicular to the diffusion channel, the angle will be 90° (inset of Fig. 4g and Supplementary Fig. 15). The size of the gradient vectors depends on the magnitudes of the partial gradient vectors (Eq. 4).
Grayscale bright-field two-beam images are acquired to study the defect clusters distribution and evolution. a Scheme presenting the calculation of the gradient vector from a certain pixel of a bright-field two-beam image. The gradient vector points to the overall directional change in pixel value. Gradient vector calculated and superimposed on the bright-field two-beam image of a Na2/3Fe1/2Mn1/2O2 particle irradiated at the total fluence of b 6.25 × 1013 Kr2+/cm2, c 1.88 × 1014 Kr2+/cm2, d 4.38 × 1014 Kr2+/cm2, and e 5.0 × 1014 Kr2+/cm2 at room temperature. Bright-field two-beam image of a Na2/3Fe1/2Mn1/2O2 particle irradiated at the total fluence of f 6.25 × 1014 Kr2+/cm2 at room temperature. The bright-field images are taken from the [100] zone axis. All the scale bars in the image b–f correspond to a length of 100 nm. g Distribution of the gradient vectors of image b–e against the angle of the gradient vector. The inset shows the scheme of how the angle of the gradient vector is defined. Dynamic defect evolution in a Na2/3Fe1/2Mn1/2O2 particle with increasing fluence of Kr ion irradiation (h–j). The dynamic defect evolution is studied through the subtraction of the image acquired at higher irradiation dose from that of the lower irradiation dose (e.g., image c subtracted from image b). Defect evolution from h image b–c, i image c–d, and j image d–e. All the scale bars from images h–j correspond to a length of 100 nm. The color bar shows the corresponding values of the subtracted pixels after the subtracted grayscale image is converted to an RGB image. k Distribution of the gradient vectors of images h–j against the angle of the gradient vector.
Gradient vector calculated and superimposed on the bright-field two-beam image of a LiNiO2 particle irradiated at the fluence of a 1.25 × 1014 Kr2+/cm2, b 3.13 × 1014 Kr2+/cm2, c 4.38 × 1014 Kr2+/cm2, d 6.25 × 1014 Kr2+/cm2, and e 1.25 × 1015 Kr2+/cm2 at room temperature. The bright-field images are taken from the [100] zone axis. All the scale bars in the image a–e correspond to a length of 100 nm. f Distribution of the gradient vectors of images a–e against the angle of the gradient vector. The inset shows the scheme of how the angle of the gradient vector was defined. Dynamic defect evolution in a LiNiO2 particle with increasing fluence of Kr ion irradiation (g–j). The dynamic defect evolution is studied through the subtraction of the image acquired at higher irradiation dose from that of the lower irradiation dose (e.g., image b subtracted from image a). Defect evolution (g) from image a to image b, h from image b to image c, i from image c to image d, and j from image d to image e. All the scale bars from image g to image j correspond to a length of 100 nm. The color bar shows the corresponding values of the subtracted pixels after the subtracted grayscale image was converted to an RGB image. k Distribution of the gradient vector of images g–j against the angle of the gradient vector.
The physical meaning of the gradient vector is explained in more details in the Supplementary Discussion and Supplementary Figs. 16–21. In short, the gradient vector is pointing to the direction of non-defect to defect transition or defect to non-defect transition because it shows the direction of the most change in the pixel value, that is, the brightness. The angle of the gradient vector (θ) with respect to the Na ion diffusion channel (y-direction in Fig. 4a and along 0° in the inset of Fig. 4g) enables the statistical representation of the defect cluster distribution and propagation (Fig. 4g, k). Since every pixel has only two directions associated with it (x- and y-direction), an angle of the gradient vector of >45° (defined according to the inset in Fig. 4g) means that the larger partial gradient of the pixels is along the x-direction, causing the vector to lean closer to the x-direction than to the y-direction (see Supplementary Discussion and Supplementary Figs. 18 and 21 for more details). Then, it can be conferred that the defect clusters are more likely to terminate in the x-direction and align along the y-direction because the most change in brightness (calculated in terms of pixel values) is along the x-direction. For angles lesser than 45°, the alignment of the defect clusters will be the opposite.
First, we compute the gradient vectors on the bright-field two-beam images of a particle of Na2/3Fe1/2Mn1/2O2 (Fig. 4b–e) at various fluences of Kr ion irradiation at room temperature in order to understand the distribution of the defect clusters. Gradient analysis is not performed on the particle at the fluence of 6.25 × 1014 Kr2+/cm2 because the particle is fully amorphous at that irradiation dose (Fig. 4f). The population of the gradient vectors against the angle of the vectors shows if there is any preferential direction of the defect cluster distribution on the particle (Fig. 4g). Inspecting the population of the gradient vectors against the angle, one can notice that most of the vectors have an angle of >45°, with almost 90% of the vectors having an angle of 60° or higher (Supplementary Fig. 22a). This means that most of the defect clusters are more preferentially distributed in the direction of the Na ion diffusion channel (along the y-direction) because the larger gradient is in the other direction (Supplementary Figs. 17–21). The higher fluence of Kr ion irradiation can induce more defects and the defects can be diffusive in nature as well63,64. Hence, it is important to understand the propagation of the defect clusters under irradiation. We analyzed the defect cluster propagation by the subtraction of the image at a higher fluence from that of a lower fluence (e.g., Fig. 4c subtracted from Fig. 4b) according to the scheme shown in Supplementary Fig. 23. This is followed by similar gradient vector computation and conversion of the grayscale image to an RGB image (Fig. 4h–j). The distribution of the gradient vectors against the angle (Fig. 4k) shows that most of the vectors have an angle >45°, meaning the propagation of the defect clusters is also preferred on the direction of the Na ion diffusion channel (Supplementary Figs. 17–21). The size of the gradient vectors against the angle can provide further justification on the preferential distribution and propagation of the defect clusters. Supplementary Fig. 24a, b show the size of the gradient vectors against the angle from the gradient computation in Fig. 4b–e and h–j, respectively. The larger sized vectors in these distributions are at angles >45° and the largest vectors in size are at the angle of 90°. The largest vectors at 90° suggest that the biggest gradients among all the vectors are at this angle and the magnitude of the vectors is entirely because of the pixel difference along the x-direction (see Supplementary Fig. 18). Furthermore, comparing Fig. 4g, k with Supplementary Fig. 24a, b respectively, one can notice that the largest vectors in size at the angle 90° are also the most substantial in population. These facts combined indicate that many defect clusters prefer the distribution and propagation shown in Supplementary Fig. 18, further providing justification to the preferential alignment of the defect clusters in the direction of the Na ion diffusion channel.
Similar gradient analysis on the particle of LiNiO2 is performed at various fluences of Kr ion irradiation at room temperature (Fig. 5a–e). The angle of the gradient vector is defined similarly to that of Na2/3Fe1/2Mn1/2O2 (inset of Fig. 5f and Supplementary Fig. 15b). The population of the gradient vector against the angle shows that the majority of vectors have an angle >45°. Similar to Na2/3Fe1/2Mn1/2O2, such gradient vector distribution again points towards a preferential distribution of the defect clusters along the direction of the Li ion diffusion channel (Fig. 5f and Supplementary Fig. 22b). Delithiated LiNiO2 (charged to 4.5 V against Li+/Li) particles also have a similar trend of defect cluster distribution (Supplementary Fig. 25). The gradient analysis on the subtracted images (Fig. 5g–j) and the distribution of the vectors against the angle (Fig. 5k) reveal that the defect clusters tend to propagate preferably in the direction of the Li ion diffusion channel, similar to what we have observed for Na2/3Fe1/2Mn1/2O2. Size of the vectors against the angle (Supplementary Fig. 24c,d) shows that the larger sized vectors are distributed at angles >45°, with the largest sized vectors being at the angle of 90°. The largest vectors are also the most substantial in population (compare Fig. 5f,k with that of Supplementary Fig. 24c, d), further suggesting the preferential alignment of the defect clusters along the Li ion diffusion channel. This similar trend of preferential defect evolution in both layered materials points to the possible formation of interstitial-type defect clusters and potentially dislocation loops that are parallel to the Na ion or Li ion layers. Here the interstitial-type defect is broadly defined as TM occupying the interlayer space, similar to that reported for graphite65,66. The reason may be that in each material the interlayer space between two transition metal layers is large (Fig. 1a, b). The large space provides free volume to accommodate the radiation-induced interstitial atoms. When interstitials accumulate in the interlayer space, they can form interstitial-type clusters or even an extra plane (dislocation loop) (see schematic in Supplementary Fig. 26). This mechanism is similar to the dislocation loop formation mechanisms in some other layered materials, such as graphite under irradiation65,66. In graphite, accumulation of interstitials in between basal planes (graphene layers) can form prismatic dislocation loops that are parallel to the basal planes, leading to lattice expansion in c-direction and contraction in a-direction65,66. The defect clusters or loops can cause lattice distortion67, which will cause different contrast in the bright-field images. Therefore, we believe that the large interlayer space in the layered oxide cathodes provides the needed free volume for the growth of the defect clusters or dislocation loops along the Na/Li ion diffusion channel. Furthermore, our conclusion is consistent with the experimental observation of edge dislocations in alkali-ion-layered oxides68,69.
Theoretical explanation of the radiation damage behavior
In line with the earlier works on pyrochlores29,30, we attempt to understand the radiation damage behavior of layered oxide cathodes in terms of the antisite defect formation under irradiation. In complex oxides with two types of cations (A and B), antisite defects are formed by exchanging the cations30,
where the A and B in the normal text represent the two different cations and their subscripts represent the cation sites. The formation of antisite defects is also referred to as “cation disorder”30. In pyrochlores (A2B2O7), the lower the antisite defect formation energy, the better the resistance to radiation-induced amorphization29,30. This is because if the formation energy is low, the crystal lattice can effectively accommodate a substantial amount of cation disorders by still maintaining the crystallinity. Likewise, if the antisite formation energy is high, the system energy increases significantly with the increasing disorder, which can lead to amorphization. Interestingly, the use of antisite formation energy as a criterion for predicting the radiation tolerance of complex oxides may be materials dependent as exemplified by the opposite correlation of amorphization to antisite formation in MgAl2O470. For the layered oxide cathodes, it is unknown if such a correlation between the antisite formation energy and radiation tolerance exists.
To establish such case, DFT calculations are conducted to calculate the formation energy of an antisite pair in the layered cathodes. Four simulation systems are used: O3-LiNiO2, P2-NaFeO2, O3-NaFeO2, and P2-Na2/3Fe1/2Mn1/2O2. These materials are used as model systems for the two materials studied in our experiment. In addition, P2-NaFeO2 and O3-NaFeO2 are used to check if the antisite formation energy is sensitive to material polymorph.
We begin with examining the first three systems in which the alkali cations have the full occupancy. Table 1 shows the calculated lattice parameters in the three systems after structural optimization. For O3-LiNiO2 and O3-NaFeO2, both a and c lattice constants are in very good agreement with experimental values. For P2-NaFeO2, our DFT results are slightly larger than previous DFT results73. Although there are no experimental data of perfect P2-NaFeO2 for direct comparison, our DFT results are in reasonable agreement with the experimentally determined lattice parameters of P2-Na2/3Fe1/2M1/2O2 (a = 2.93 Å, c = 11.22 Å)47. To introduce a pair of antisite defects with a maximized distance between them (to minimize the interaction between the two antisite defects), a Li (or Na) atom near the bottom of each simulation system in the c-direction is swapped with a Ni (or Fe) atom at the center (Supplementary Fig. 27). The distance between the two antisite defects in each system is shown in Table 1. The formation energy of an antisite pair (or cation disorder energy) is defined as,
where Eantisite is the total energy of the simulation system containing one antisite pair and Eperfect is the total energy of the perfect system of the same system size. For O3-LiNiO2, the antisite pair formation energy is −0.54 eV, indicating a slightly favorable antisite pair formation in this 96-atom system (Table 1), in which the antisite defect concentration is 4.2% (=1/24). Note that the negative antisite formation energy (−0.54 eV in 96-atom system) indicates that a perfect LiNiO2 is difficult to obtain due to the spontaneous formation of Li-Ni antisite defects, even in the pristine state. In fact, a few percent of Ni sitting in the Li site is widely reported in the literature48,74. In some other LiNiO2-based materials, the antisite concentration can be as high as 11.8% (Table 2 in ref. 75). Therefore, our DFT results are consistent with these experimental observations. In a separate DFT calculation using a smaller O3-LiNiO2 with 48 total atoms, in which the concentration of antisite defects is doubled (i.e., 8.3%), the antisite pair formation energy is 0.23 eV, indicating that antisite defect formation is slightly unfavorable at high antisite concentrations. In either case, the formation of an antisite pair in O3-LiNiO2 does not change the system energy significantly, suggesting that O3-LiNiO2 can efficiently accommodate radiation-induced antisite defects. In comparison, the calculated formation energy of an antisite pair is much larger in O3-NaFeO2 (4.32 eV) and P2-NaFeO2 (4.52 eV) (Table 1), regardless of material polymorph. Therefore, from the energetics viewpoint, LiNiO2 can accommodate much more radiation-induced antisite defects than NaFeO2. In turn, O3-LiNiO2 should be more radiation tolerant than either O3 or P2-NaFeO2. As discussed below, if we assume P2-NaFeO2 can be used as a model system for P2-Na2/3Fe1/2Mn1/2O2, our DFT results can be used to explain our experimental observation (see Fig. 2).
Previously, it has been shown that the antisite formation energy (and thus, radiation tolerance) can be correlated with the ionic radius difference between A and B cations in pyrochlores30. If the difference is large, the antisite formation energy is high and thus the radiation tolerance is low. As shown below, such rationalization can be extended to layered oxides to predict the resistance to radiation damage and design layered oxide cathodes that are stable under irradiation. For the cations in our battery materials, the effective ionic radii are: Li+ (0.76 Å), Ni3+ (0.56 Å, 0.60 Å), Na+ (1.02 Å), and Fe3+ (0.55 Å, 0.645 Å), where the two values for each of Ni3+ and Fe3+ correspond to low spin and high spin states, respectively76. The much smaller ionic radius difference between Li+ and Ni3+ in LiNiO2 than that between Na+ and Fe3+ in NaFeO2 is indeed consistent with the difference in the antisite formation energy between the two systems.
As to Mn3+, its ionic radius (0.58 Å, 0.645 Å) is nearly identical as Fe3+ for each spin state76. In P2-Na2/3FexMn1 − xO2, Mn4+ and Fe4+ may also exist according to the X-ray absorption spectroscopy measurements77 and their ionic radii are also similar (0.585 vs. 0.53 Å) 76. Therefore, if the ionic radius difference between alkali and TM cations is the key factor for affecting the antisite formation energy (and thus the radiation tolerance), an Mn–Na antisite pair should also have a high antisite formation energy. To prove this hypothesis, Mn–Na and Fe–Na antisite formation energies are directly calculated in P2-Na2/3Fe1/2Mn1/2O2. More complex than the ideal P2-NaFeO2, the Na cations in Na2/3Fe1/2Mn1/2O2 do not have a full site occupancy and the TM layer consists of both Mn and Fe cations. Moreover, it has been shown experimentally that Na cations can stay in two different sites in Na2/3FexMn1 − xO2: 2b (0, 0, 1/4) and 2d (2/3, 1/3, 1/4)77, although it is unclear the exact arrangement of Na cations at the two sites. To predict the atomic configuration of P2-Na2/3Fe1/2Mn1/2O2, a P2-NaFeO2 consisting of 3 × 2 × 2 unit cells (96 atoms in total) is created initially. In each of four TM layers, three out of six Fe cations are replaced by Mn cations so that the Fe:Mn ratio is 1:1 in each TM layers (Fig. 6a). All Na cations are initially placed at the 2d sites. Then two out of six Na cations in each of four Na layers are removed. Now the system has 88 atoms in total (16 Na, 12 Fe, 12 Mn, 48 O), which has the same stoichiometry as Na2/3Fe1/2Mn1/2O2. After structural relaxation, interestingly, one Na cation in each of four Na layers moves from a 2d site to a 2b site. The moving directions of these Na cations are illustrated in Fig. 6a and the final configuration is shown in Fig. 6b. The final Na site occupancy factors are 0.5 for 2d site and 0.17 for 2b site in Na2/3Fe1/2Mn1/2O2, which are similar to 0.43 for 2d site and 0.26 for 2b site in Na2/3Fe1/3Mn2/3O2 as determined by experiments77. Therefore, our DFT calculation predicts reasonable Na site occupancy factors without any a priori assumptions. In addition, the predicted lattice parameters are also similar to the experimental values, as shown in Table 1.
a Before structural relaxation. All Na cations are placed at 2d sites initially. The blue arrows indicate the moving directions of some Na cations after relaxation. b After structural relaxation. The Na cations with an asterisk (*) are those moving to the new 2b sites. The labeled TM and Na cations are those used to create antisite pairs. The two figures show some additional atoms at simulation box boundaries for visualization purpose (based on periodic boundary conditions). Large yellow spheres: Na; medium brown spheres: Fe; medium purple spheres: Mn; small red spheres: O.
Due to the complex atomic configuration of P2-Na2/3Fe1/2Mn1/2O2, it is expected that the antisite pair formation energy depends on the local atomic environment of each antisite defect. To ensure that our conclusion is not specific to a certain antisite defect configuration, three Fe–Na antisite pairs (Fe1–Na1, Fe2–Na2, Fe3–Na2) and three Mn–Na antisite pairs (Mn1–Na1, Mn2–Na1, Mn3–Na2) are modeled and the original positions of these cations are shown in Fig. 6b. The calculated antisite pair formation energies are shown in Table 1. Similar to O3 or P2-NaFeO2, the formation energy of an Fe–Na antisite pair is still high: in the range of 2.73–3.22 eV; the formation energy of a Mn–Na antisite pair is even higher: in the range of 4.04–5.05 eV. The exact cause for the discrepancy between the two types of antisite pairs is unclear. It could be due to different charge states of Fe and Mn cations in P2-Na2/3Fe1/2Mn1/2O2, or different local atomic environment of these defects, or the actual ionic radii of Fe and Mn are slightly different from the theoretical predictions by Shannon76. Nevertheless, the formation energy of an antisite pair in P2-Na2/3Fe1/2Mn1/2O2 is significantly higher than in O3-LiNiO2, regardless of the antisite defect type (Table 1). Therefore, our DFT results of antisite pair formation energy as well as the ionic radius difference can be well applied to explain why O3-LiNiO2 has a better radiation tolerance than P2-Na2/3Fe1/2Mn1/2O2. The DFT results from the P2-Na2/3Fe1/2Mn1/2O2 are qualitatively similar as that from the ideal NaFeO2 (although the magnitudes are different), indicating the ionic radius difference between TM and alkali cations is a key factor for predicting the antisite formation energy and radiation tolerance. This justifies NaFeO2 can be used as a model system for Na2/3Fe1/2Mn1/2O2 in terms of radiation tolerance.
Bader charge analysis78 for both perfect and defective systems is performed to explain the charge transfer between an antisite defect and its surrounding atoms. Charge transfer takes place due to the antisite defect formation. Hence, it is important to understand whether there is a correlation between the charge transfer and radiation tolerance of a material. Note that in Bader charge analysis, the charge of each atom is represented by the effective amount of valence electrons. Here the charge of each atom in the perfect system is subtracted from its counterpart in the defective system. Such change in valence electrons is used as a qualitative measure to analyze the charge transfer due to the formation of an antisite pair. A positive value in our charge transfer analysis means that the atom gains extra electrons and thus its oxidation state is lowered and vice versa. The results of the first three model systems are shown in Supplementary Fig. 27. In O3-LiNiO2, when a Li+ replaces Ni3+ (LiNi, center of Supplementary Fig. 27a), some nearby Ni and O atoms lose electrons slightly to accommodate the charge difference at the antisite. However, it seems that the charge transfer around the LiNi antisite is not localized. Similarly, for the NiLi antisite (bottom of Supplementary Fig. 27a), the charge transfer is also delocalized. Here localized charge transfer means that the charge transfer is mainly concentrated at the antisite defect itself or its nearest neighbors; delocalized charge transfer means that the charge transfer spreads beyond this range. In O3-NaFeO2, the oxygen atoms around the NaFe (center of Supplementary Fig. 27b) lose electrons to accommodate the change from Fe3+ to Na+. The charge transfer is more localized than that near LiNi. The result suggests that the oxidation state of some oxygen atoms may change from O2− to O−. For the FeNa antisite (bottom of Supplementary Fig. 27b), the charge transfer is also localized and the Fe gains electrons. In addition, another nearby Fe atom also gains electrons. The result suggests that the oxidation state of Fe at or near the FeNa antisite may change from Fe3+ to Fe2+ to accommodate the antisite defect. In the P2-NaFeO2, interestingly, the charge transfer has a mixed behavior. Near the NaFe (center of Supplementary Fig. 27c), the charge transfer seems to be delocalized. At the FeNa (bottom of Supplementary Fig. 27c), the charge transfer seems to be localized at the antisite—Fe gains electrons and its oxidation state may change from Fe3+ to Fe2+. The charge transfer in P2-Na2/3Fe1/2Mn1/2O2 is more complex, as shown in Fig. 7. For the systems containing an Fe–Na antisite pair (Fig. 7a–c), some nearby oxygen anions around the NaFe (at the middle of each figure in the vertical direction) lose electrons. Interestingly, one nearby Mn cation also loses some electrons, as indicated by the red dashed circle in each figure. This suggests that the oxidation state of the nearby Mn cation may increase to accommodate the charge difference between Na+ and Fe3+. At the FeNa antisite (near the bottom of each figure), the FeNa antisite defect gains some electrons, suggesting the oxidation state of Fe at the antisite may decrease. For the systems containing an Mn–Na antisite pair (Fig. 7d–f), oxygen anions behave similarly as the cases with a Fe–Na antisite pair. Near the NaMn antisite (at the middle of each figure), a nearby Mn also tends to lose electrons, except in Fig. 7d. At the MnNa antisite (near the bottom of each figure), the MnNa antisite defect gains some electrons, indicating the Mn may lower the oxidation state. In two cases (bottom of Fig. 7d, f), a nearby Fe also gains some electrons. Overall, it seems that the oxidation state of Mn can either increase or decrease to accommodate antisite defects, while the oxidation state of Fe always tends to decrease. The different charge transfer behavior between Fe and Mn cations may shed a light on the experimental observation that Fe4+ is more difficult to form than Mn4+ in P2-Na2/3Fe1/2Mn1/2O2 during charging77. The above analysis shows that the detailed charge transfer/redistribution mechanism is material specific. We have not observed a clear correlation between the detailed charge transfer mechanism and antisite formation energy. If other electronic configurations are used in our DFT modeling, the details of the charge transfer process may change somewhat. However, the trend of the antisite formation energy should not change significantly because the difference in ionic radius between TM and alkali cations is the key factor for determining the antisite defect formation energy. Meanwhile, our density of states calculations suggest that the introduction of antisite defects might give all these defective materials more metallic-like characteristics as their bandgaps disappear (Supplementary Figs. 28 and 29). However, such a prediction needs further experimental validation, which is beyond the scope of this work.
Each atom is colored by the change of its valence electrons with respect to its counterpart in the pristine system. Red and magenta arrows indicate the NaTM and TMNa antisite defects, respectively. Red dashed circles indicate a significant loss of electrons of some nearby Mn cations. Magenta dashed circles indicate a large gain of electrons of some nearby Fe cations. Large spheres: Na; medium spheres: Fe; medium diamonds: Mn; small spheres: O. The antisite defect pairs are: a Fe1–Na1, b Fe2–Na2, c Fe3–Na2, d Mn1–Na1, e Mn2–Na1, and f Mn3–Na2.
Discussion
In summary, our work has unveiled the fundamental mechanisms of defect evolution and structural transformations in Na- and Li-layered cathodes, promoted by high-energy Kr ion irradiation. High-energy ion irradiation such as Kr ion is different from electron irradiation in TEM characterization. The structural damage due to electron irradiation on battery materials has been reported to mostly induce structural transformations on the surface and near-surface region of the particle53,79. As evidenced in our work, Kr ion irradiation can induce structural transformations within hundreds of nanometers of a cathode particle at a short duration of time. Moreover, electron irradiation mostly produces point defects or small defect clusters80,81. However, Kr ion irradiation can produce much larger dislocation loops and voids26. Hence, utilizing Kr ion irradiation allows us to truly compare the radiation tolerance of the Li- and Na-layered cathodes in extreme environments. Our experimental results suggest that Li-layered cathode, for example, LiNiO2 is more resistant to Kr ion irradiation-induced structural damage than Na-layered cathode, for example, Na2/3Fe1/2Mn1/2O2, which can be associated with the easiness of the cationic antisite defect formation in the former. Our theoretical analysis has revealed that the antisite defect formation energy is significantly smaller in LiNiO2 because of the much smaller difference in ionic radius between Li+ and Ni3+ than those between Na+ and Fe3+/Mn3+/Mn4+, allowing better accommodation of radiation damage than P2-Na2/3Fe1/2Mn1/2O2. The findings suggest that structural transformations in both Li- and Na-layered cathodes under irradiation follow the similar principle of cationic antisite defect formations, similar to pyrochlore oxides. Hence, our study provides a valuable guideline for designing stable layered cathodes under extreme conditions, such as outer space exploration and nuclear power industries. Between different layered oxides (AxTMO2, where A is alkali ion, and TM is transition metal ion), a material with a smaller difference in the ionic size between A and TM will have a smaller cationic antisite defect formation energy and will be more resistant to radiation damage. Resistance to radiation damage is also closely related to the temperature82,83. Like in many other oxide ceramics35, high temperature can lessen the severity of structural transformations of Na-layered oxide by accelerating the annihilation of radiation-induced defects through the recombination of vacancies and interstitials82. Enhanced defect annihilation at high temperature should enhance the structural stability of Li-layered oxide as well. Instead of a direct crystalline to amorphous transformation, our study shows that Na-layered oxide undergoes a phase transformation to a spinel-type structure at high temperature. Some irradiation-resistant pyrochlores, for example, Gd2Zr2O7 also undergoes a phase transformation to a fluorite-type structure25. Such phase transformation is indicative of an intermediate phase formation rather than full disordering to an amorphous phase. Our study informs the radiation damage of battery materials at a broad range of temperatures and establishes the fact that the resistance to radiation damage of layered cathodes increases with the elevation of temperature. Thus, our findings provide a comprehensive guideline for predicting radiation tolerance of layered cathodes. Meanwhile, our mathematical analysis on the bright-field images quantitatively mapped the distribution and propagation of defect clusters under irradiation and revealed that defect clusters tend to align along the direction of the Na/Li ion diffusion channels (a–b plane). The preferential defect alignment is likely due to the formation of interstitial-type dislocation loops in the interlayer space between transition metal layers, in which a large free volume is available to accommodate the accumulation of the interstitials. Such dynamics of defect evolution (e.g., the formation and accumulation of vacancies and interstitials) under ion irradiation shares similar attributes to that of defect evolution in layered cathodes on electrochemical cycling (e.g., vacancies and interstitials formation through oxygen evolution and ion migration)57,84,85. Point defects such as vacancies and interstitials can largely influence the electrochemical performance of layered cathodes. Interstitials resulting from the transition metal migration are reported to cause voltage decay in high-energy Li-rich layered cathode materials43. Voltage decay results in subpar energy efficiency, which hinders the commercialization of these promising cathode materials. A large quantity of interstitial defects can cause phase transformation from layered to spinel or rocksalt phase42, leading to transition metal dissolution, cathode particle cracking, and high electrochemical impedance development86. Extensive material damage due to phase transformation and oxygen evolution may induce amorphization, leading to accelerated electrochemical performance degradation87. The aforementioned structural and chemical stability issues can be alleviated to some degree through doping chemistry48. Radiation creates a high concentration of point defects. The impacts of irradiation-induced defects on the electrochemical performance of Li- and Na-layered cathodes and whether doping can play a role in the stability under irradiation deserve further studies in the future.
Methods
Materials synthesis
Na2/3Fe1/2Mn1/2O2 was synthesized by a simple solid-state synthesis method with the stoichiometric amount of precursors Na2CO3, Fe2O3, and Mn2O3 being ball milled at a rate of 35 Hz for 6 h. The precursor was calcined in a box furnace at 900 °C for 12 h, followed by rapid quenching and stored in the glovebox. The precursor of the LiNiO2 was synthesized by the precipitation of the salt solution of NiSO4·6H2O by a base solution of NaOH and NH4OH. The precipitated Ni(OH)2 was collected and dried in a vacuum oven overnight at 105 °C. The precursor powder was mixed with stoichiometric amount of LiOH and calcined in a tube furnace under airflow at 450 °C for 2 h, followed by 675 °C for 6 h to get the final LiNiO2 powder. The powder of LiNiO2 was stored in the glovebox for further usage.
Electrochemical characterization
Electrodes of Na2/3Fe1/2Mn1/2O2 were casted on a carbon-coated aluminum foil by making a slurry of 80% active material, 15% carbon black, and 5% poly(vinylidene difluoride) (PVDF). Discs of 10 mm diameter were cut from the casted slurry and dried in a vacuum oven overnight at 120 °C. Electrodes of LiNiO2 were casted in a similar way with a slurry of 90% active material, 5% carbon black, and 5% PVDF and discs of 10 mm diameter were cut and dried in a vacuum oven overnight at 120 °C. CR2032 coin cells with Na anode and Na2/3Fe1/2Mn1/2O2 cathode were assembled with 1.0 M NaClO4 in propylene carbonate as the electrolyte and Whatman glass fiber (1827-047934-AH) as the separator. A specific current density of 180 mA/g (defined as 1C) was used to calculate the charge and discharge current density. Li half cells were assembled from CR2032 coin cell parts with Li metal as the anode, LiNiO2 as the cathode, and the Whatman glass fiber as the separator. One mole of LiPF6 dissolved in ethylene carbonate and ethyl methyl carbonate with 2 wt% vinylene carbonate was utilized as the electrolyte. A specific current density of 200 mA/g was used to calculate the current density at 1 C. LANDT battery cycler was utilized to collect the electrochemical cycling data.
Materials irradiation and characterization
In situ Kr ion irradiation and simultaneous TEM observation was performed in an intermediate voltage electron microscope (IVEM-Tandem facility) at Argonne National Laboratory. A Kr ion energy of 1 MeV was utilized for irradiation and an electron beam energy of 300 keV (Hitachi-9000) was utilized for imaging. Na2/3Fe1/2Mn1/2O2 was irradiated at a total fluence of 6.25 × 1014 Kr2+/cm2 and LiNiO2 was irradiated at a total fluence of 1.25 × 1015 Kr2+/cm2 at room temperature. A total fluence of 1.25 × 1014 Kr2+/cm2 was utilized for irradiation at −173 °C and a total fluence of 1.25 × 1015 Kr2+/cm2 was utilized for irradiation at 200 °C. Electron irradiation for TEM imaging was in the direction “into the plane of the paper.” Kr ion irradiation was incident at an angle of 30° with respect to the electron irradiation. The fluence rate of Kr ion irradiation was 6.25 × 1010 Kr2+/cm2/s. The charge of Kr ion is marked with 2+ (++) but the charge number does not impact the material damage. Irradiation was stopped at various intermediate fluence for defect imaging and acquiring ED patterns. Morphology of the materials was acquired in a scanning electron microscope (LEO FESEM) operating with an accelerating voltage of 5 kV. The XRD patterns of the materials were collected in a benchtop Rigaku Miniflex II X-ray diffractometer utilizing a Cu Kα radiation at a wavelength of 1.54 Å. For acquiring the pattern, a step size of 0.02° and a scan rate of 1°/min were used.
Theoretical calculation
All DFT calculations were conducted in Vienna Ab initio Simulation Package (VASP) software. The projector-augmented-wave (PAW) pseudopotential88 was used to describe the electron-core interaction. The Perdew–Burke–Ernzerhof (PBE) functional89 of gradient approximation was used for the electron exchange-correlation energy. In this work, the standard PAW-PBE potentials for Li, Na, Ni, Fe, Mn, and O available in VASP were utilized. In all calculations, the plane wave cutoff energy was set to 520 eV, Gaussian smearing was used with a smear width of 0.05 eV, and the energy convergence criterion was set to 10−4 eV. Spin polarization effect is included and the initial magnetic moment is set to 2μB for Ni, 6μB for Fe, and 6μB for Mn. To treat the strongly correlated d electrons in Ni, Fe, and Mn, DFT + U method was used in which the Hubbard correction parameter (Ueff) was set to 5.96 eV for Ni89, 5.2 eV for Fe90, and 4.0 eV for Mn91. Each of the first three simulation systems consists of 2 × 2 × 2 unit cells and its number of total atoms was shown in Table 1. The P2-Na2/3Fe1/2Mn1/2O2 consists of 3 × 2 × 2 unit cells (88 atoms). The k-point mesh was a gamma-centered grid with 5 × 5 × 2 for O3-LiNiO2, 5 × 5 × 2 for O3-NaFeO2, and 4 × 4 × 2 for P2-NaFeO2 and P2-Na2/3Fe1/2Mn1/2O2.
The gradient vector calculation was performed in the commercial software package Avizo and the vector size and distribution against the angle histograms were calculated in MATLAB. The size of each pixel on the gradient vector computation was 1.124 nm × 1.124 nm.
Data availability
The data supporting the findings of the study are available from the corresponding authors upon reasonable request.
Code availability
The codes supporting the findings of the study are available in the following link: http://github.com/mrahman4179/Defect-Gradient-vector-analysis/blob/master/Gradient%20vector%20analysis.m.
References
Youssef, M., Van Vliet, K. J. & Yildiz, B. Polarizing oxygen vacancies in insulating metal oxides under a high electric field. Phys. Rev. Lett. 119, 126002 (2017).
Smyth, D. M. Effects of dopants on the properties of metal oxides. Solid State Ion 129, 5–12 (2000).
Jia, J. et al. Heterogeneous catalytic hydrogenation of CO2 by metal oxides: defect engineering-perfecting imperfection. Chem. Soc. Rev. 46, 4631–4644 (2017).
Sun, Q. et al. The formation of defect-pairs for highly efficient visible-light catalysts. Adv. Mater. 29, 1605123 (2017).
Giordano, F. et al. Enhanced electronic properties in mesoporous TiO2 via lithium doping for high-efficiency perovskite solar cells. Nat. Commun. 7, 10379 (2016).
Das, S. et al. Controlled manipulation of oxygen vacancies using nanoscale flexoelectricity. Nat. Commun. 8, 615 (2017).
Smith, K. A. et al. Effect of proton irradiation on anatase TiO2 nanotube anodes for lithium-ion batteries. J. Mater. Sci. 54, 13221–13235 (2019).
Li, M., Lu, J., Chen, Z. & Amine, K. 30 Years of lithium-ion batteries. Adv. Mater. 30, 1800561 (2018).
Li, L. et al. Recent progress on sodium ion batteries: potential high-performance anodes. Energy Environ. Sci. 11, 2310–2340 (2018).
Vu, N. H. et al. Effect of synthesis temperature on the structural defects of integrated spinel-layered Li1.2Mn0.75Ni0.25O2+: δ: a strategy to develop high-capacity cathode materials for Li-ion batteries. J. Mater. Chem. A 5, 15730–15742 (2017).
Li, Q. et al. Dynamic imaging of crystalline defects in lithium-manganese oxide electrodes during electrochemical activation to high voltage. Nat. Commun. 10, 1692 (2019).
Wang, H., Jang, Y. I. I., Huang, B., Sadoway, D. R. & Chiang, Y. M. TEM study of electrochemical cycling-induced damage and disorder in LiCoO 2 cathodes for rechargeable lithium batteries. J. Electrochem. Soc. 146, 473–480 (1999).
Clark, J. M., Barpanda, P., Yamada, A. & Islam, M. S. Sodium-ion battery cathodes Na2FeP2O7 and Na2MnP2O7: diffusion behaviour for high rate performance. J. Mater. Chem. A 2, 11807–11812 (2014).
Gardiner, G. R. & Islam, M. S. Anti-site defects and ion migration in the LiFe 0.5 Mn 0.5 PO 4 mixed-metal cathode material. Chem. Mater. 22, 1242–1248 (2010).
House, R. A. et al. Superstructure control of first-cycle voltage hysteresis in oxygen-redox cathodes. Nature 577, 502–508 (2020).
Jarvis, K. A., Deng, Z., Allard, L. F., Manthiram, A. & Ferreira, P. J. Understanding structural defects in lithium-rich layered oxide cathodes. J. Mater. Chem. 22, 11550–11555 (2012).
Singer, A. et al. Nucleation of dislocations and their dynamics in layered oxide cathode materials during battery charging. Nat. Energy 3, 641–647 (2018).
Van Der Ven, A., Marianetti, C., Morgan, D. & Ceder, G. Phase transformations and volume changes in spinel LixMn2O4. Solid State Ion 135, 21–32 (2000).
Guo, H. et al. Abundant nanoscale defects to eliminate voltage decay in Li-rich cathode materials. Energy Storage Mater. 16, 220–227 (2019).
Smith, K. A. et al. Effects of proton irradiation on structural and electrochemical charge storage properties of TiO2 nanotube electrodes for lithium-ion batteries. J. Mater. Chem. A 5, 11815–11824 (2017).
Yau, A., Cha, W., Kanan, M. W., Stephenson, G. B. & Ulvestad, A. Materials science: Bragg coherent diffractive imaging of single-grain defect dynamics in polycrystalline films. Science 356, 739–742 (2017).
Yuan, Y., Amine, K., Lu, J. & Shahbazian-Yassar, R. Understanding materials challenges for rechargeable ion batteries with in situ transmission electron microscopy. Nat. Commun. 8, 1–14 (2017).
Ulvestad, U. et al. Topological defect dynamics in operando battery nanoparticles. Science 348, 1344–1347 (2015).
Yang, W. et al. Coherent diffraction imaging of nanoscale strain evolution in a single crystal under high pressure. Nat. Commun. 4, 1680 (2013).
Lian, J., Wang, L. M., Haire, R. G., Helean, K. B. & Ewing, R. C. Ion beam irradiation in La2Zr2O7-Ce 2Zr2O7 pyrochlore. Nucl. Instrum. Methods Phys. Res. B 218, 236–243 (2004).
Chen, W. Y. et al. Characterization of dislocation loops in CeO2 irradiated with high energy Krypton and Xenon. Philos. Mag. 93, 4569–4581 (2013).
Matzke, H. Radiation damage effects in nuclear materials. Nucl. Inst. Methods Phys. Res. B 32, 455–470 (1988).
Matzke, H. Radiation damage in nuclear materials. Nucl. Inst. Methods Phys. Res. B 65, 30–39 (1992).
Sickafus, K. E. et al. Radiation-induced amorphization resistance and radiation tolerance in structurally related oxides. Nat. Mater. 6, 217–223 (2007).
Sickafus, K. E. et al. Radiation tolerance of complex oxides. Science 289, 748–751 (2000).
Qiu, J. et al. Effects of neutron and gamma radiation on lithium-ion batteries. Nucl. Instrum. Methods Phys. Res. B 345, 27–32 (2015).
Tan, C. et al. Radiation effects on the electrode and electrolyte of a lithium-ion battery. J. Power Sources 318, 242–250 (2016).
Ding, N., Zhu, J., Yao, Y. X. & Chen, C. H. The effects of gamma-radiation on lithium-ion cells. Electrochim. Acta 51, 6320–6324 (2006).
Lang, F. et al. Proton radiation hardness of perovskite tandem photovoltaics. Joule 4, 1054–1069 (2020).
Lian, J. et al. Ion-irradiation-induced amorphization of La2Zr2O7 pyrochlore. Phys. Rev. B 66, 541081–541085 (2002).
Bai, X. M., Voter, A. F., Hoagland, R. G., Nastasi, M. & Uberuaga, B. P. Efficient annealing of radiation damage near grain boundaries via interstitial emission. Science 327, 1631–1634 (2010).
Zhang, Y., Schwen, D., Zhang, Y. & Bai, X. M. Effects of oversized tungsten on the primary damage behavior in Fe-W alloys. J. Alloy. Compd. 794, 482–490 (2019).
Bai, X. M. & Uberuaga, B. P. Multi-timescale investigation of radiation damage near TiO2 rutile grain boundaries. Philos. Mag. 92, 1469–1498 (2012).
Was, G. S. In Fundamentals of Radiation Materials Science: Metals and Alloys 3–72 (Springer, Berlin, Heidelberg, 2007).
Boulineau, A., Simonin, L., Colin, J.-F., Bourbon, C. & Patoux, S. First evidence of manganese–nickel segregation and densification upon cycling in Li-rich layered oxides for lithium batteries. Nano Lett. 13, 3857–3863 (2013).
Gu, M. et al. Formation of the spinel phase in the layered composite cathode used in Li-Ion batteries. ACS Nano 7, 760–767 (2013).
Lin, F. et al. Surface reconstruction and chemical evolution of stoichiometric layered cathode materials for lithium-ion batteries. Nat. Commun. 5, 3529 (2014).
Sathiya, M. et al. Origin of voltage decay in high-capacity layered oxide electrodes. Nat. Mater. 14, 230–238 (2014).
Myeong, S. et al. Understanding voltage decay in lithium-excess layered cathode materials through oxygen-centred structural arrangement. Nat. Commun. 9, 1–10 (2018).
Krasheninnikov, A. V. & Nordlund, K. Ion and electron irradiation-induced effects in nanostructured materials. J. Appl. Phys. 107, 71301 (2010).
Abromeit, C. Aspects of simulation of neutron damage by ion irradiation. J. Nucl. Mater. 216, 78–96 (1994).
Yabuuchi, N. et al. P2-type Nax[Fe1/2Mn1/2]O2 made from earth-abundant elements for rechargeable Na batteries. Nat. Mater. 11, 512–517 (2012).
Mu, L. et al. Dopant distribution in Co-free high-energy layered cathode materials. Chem. Mater. 31, 9769–9776 (2019).
Delmas, C., Braconnier, J. J., Fouassier, C. & Hagenmuller, P. Electrochemical intercalation of sodium in NaxCoO2 bronzes. Solid State Ion 3–4, 165–169 (1981).
Laubach, S. et al. Changes in the crystal and electronic structure of LiCoO 2 and LiNiO 2 upon Li intercalation and de-intercalation. Phys. Chem. Chem. Phys. 11, 3278–3289 (2009).
Ziegler, J. F., Ziegler, M. D. & Biersack, J. P. SRIM—the stopping and range of ions in matter (2010). Nucl. Instrum. Methods Phys. Res. B 268, 1818–1823 (2010).
Jiang, N. Electron beam damage in oxides: a review. Rep. Prog. Phys. 79, 016501 (2016).
Lin, F., Markus, I. M., Doeff, M. M. & Xin, H. L. Chemical and structural stability of lithium-ion battery electrode materials under electron beam. Sci. Rep. 4, 1–6 (2014).
Ennos, A. E. The origin of specimen contamination in the electron microscope. Br. J. Appl. Phys. 4, 101 (1953).
Ennos, A. E. The sources of electron-induced contamination in kinetic vacuum systems. Br. J. Appl. Phys. 5, 27 (1954).
Shannon, R. D. & Prewitt, C. T. Effective ionic radii in oxides and fluorides. Acta Crystallogr. Sect. B 25, 925–946 (1969).
Zhang, H. et al. Layered oxide cathodes for Li-ion batteries: oxygen loss and vacancy evolution. Chem. Mater. 31, 7790–7798 (2019).
Weber, W. J. & Wang, L. M. The temperature dependence of ion-beam-induced amorphization in β-SiC. Nucl. Inst. Methods Phys. Res. B 106, 298–302 (1995).
Lu, F. et al. Ion beam irradiation-induced amorphization of nano-sized KxLnyTa2O7-v tantalate pyrochlore. Front. Energy Res. 2, 48 (2014).
Mori, H. & Fujita, H. Temperature dependence of electron-irradiation induced amorphization of niti alloys. Jpn. J. Appl. Phys. 21, L494–L496 (1982).
Jiang, W., Weber, W. J. & Thevuthasan, S. Ion implantation and thermal annealing in silicon carbide and gallium nitride. Nucl. Instrum. Methods Phys. Res. B 178, 204–208 (2001).
El-Atwani, O. et al. Loop and void damage during heavy ion irradiation on nanocrystalline and coarse grained tungsten: Microstructure, effect of dpa rate, temperature, and grain size. Acta Mater. 149, 206–219 (2018).
Lu, C. et al. Direct observation of defect range and evolution in ion-irradiated single crystalline Ni and Ni binary alloys. Sci. Rep. 6, 19994 (2016).
Wallace, J. B. et al. The role of Frenkel defect diffusion in dynamic annealing in ion-irradiated Si. Sci. Rep. 7, 17574 (2017).
Burchell, D. T. In Carbon Materials for Advanced Technologies 1st edn (ed. Burchell, D. T.), Ch. 13, 429–484 (Elsevier Science Ltd, 1999).
Karthik, C., Kane, J., Butt, D. P., Windes, W. E. & Ubic, R. In situ transmission electron microscopy of electron-beam induced damage process in nuclear grade graphite. J. Nucl. Mater. 412, 321–326 (2011).
Eapen, J., Krishna, R., Burchell, T. D. & Murty, K. L. Early damage mechanisms in nuclear grade graphite under irradiation. Mater. Res. Lett. 2, 43–50 (2014).
Mu, L. et al. Deciphering the cathode-electrolyte interfacial chemistry in sodium layered cathode materials. Adv. Energy Mater. 8, 1801975 (2018).
Yan, P. et al. Intragranular cracking as a critical barrier for high-voltage usage of layer-structured cathode for lithium-ion batteries. Nat. Commun. 8, 1–9 (2017).
Uberuaga, B. P. et al. Opposite correlations between cation disordering and amorphization resistance in spinels versus pyrochlores. Nat. Commun. 6, 1–8 (2015).
Dyer, L. D., Borie, B. S. & Smith, G. P. Alkali metal-nickel oxides of the type MNiO2. J. Am. Chem. Soc. 76, 1499–1503 (1954).
Li, Y. et al. Iron migration and oxygen oxidation during sodium extraction from NaFeO2. Nano Energy 47, 519–526 (2018).
Persson, K. Materials data on NaFeO2 (SG:194) by Materials Project. DOE Data Explorer https://doi.org/10.17188/1313534 (2016).
Bianchini, M., Roca-Ayats, M., Hartmann, P., Brezesinski, T. & Janek, J. There and back again—the journey of LiNiO2 as a cathode active material. Angew. Chem. Int. Ed. 58, 10434–10458 (2019).
Venkatraman, S. & Manthiram, A. Structural and chemical characterization of layered Li1-xNi 1-yMnyO2-δ (y = 0.25 and 0.5, and 0 ≤ (1 − x) ≤ 1) oxides. Chem. Mater. 15, 5003–5009 (2003).
Shannon, R. D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. Sect. A 32, 751–767 (1976).
Zhao, J. et al. Electrochemical and thermal properties of P2-type Na2/3Fe 1/3Mn2/3O2 for Na-ion batteries. J. Power Sources 264, 235–239 (2014).
Tang, W., Sanville, E. & Henkelman, G. A grid-based Bader analysis algorithm without lattice bias. J. Phys. Condens. Matter 21, 084204 (2009).
Lu, P. et al. Observation of electron-beam-induced phase evolution mimicking the effect of the charge-discharge cycle in Li-rich layered cathode materials used for Li ion batteries. Chem. Mater. 27, 1375–1380 (2015).
Stoddard, N., Karoui, A., Duscher, G., Kvit, A. & Rozgonyi, G. In situ point defect generation and agglomeration during electron-beam irradiation of nitrogen-doped czochralski silicon. Electrochem. Solid State Lett. 6, G134 (2003).
Radu, R. et al. Investigation of point and extended defects in electron irradiated silicon—dependence on the particle energy. J. Appl. Phys. 117, 164503 (2015).
Clark, D. W., Zinkle, S. J., Patel, M. K. & Parish, C. M. High temperature ion irradiation effects in MAX phase ceramics. Acta Mater. 105, 130–146 (2016).
Chu, F., Song, M., Mitsuishi, K., Yasuda, H. & Furuya, K. Temperature effect on ion irradiation‐induced phase transformation in 304 stainless steel. J. Electron Microsc. (Tokyo) 51, S231–S234 (2002).
Talaie, E., Duffort, V., Smith, H. L., Fultz, B. & Nazar, L. F. Structure of the high voltage phase of layered P2-Na2/3-z[Mn1/2Fe1/2]O2 and the positive effect of Ni substitution on its stability. Energy Environ. Sci. 8, 2512–2523 (2015).
Mu, L. et al. Surface transformation by a “cocktail” solvent enables stable cathode materials for sodium ion batteries. J. Mater. Chem. A 6, 2758–2766 (2018).
Steiner, J. D. et al. Targeted surface doping with reversible local environment improves oxygen stability at the electrochemical interfaces of nickel-rich cathode materials. ACS Appl. Mater. Interfaces 11, 37885–37891 (2019).
Cao, X. et al. Restraining oxygen loss and suppressing structural distortion in a newly ti-substituted layered oxide P2-Na0.66Li0.22Ti0.15Mn0.63O2. ACS Energy Lett. 4, 2409–2417 (2019).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Gao, Y., Wang, Z. & Lu, G. Atomistic understanding of structural evolution, ion transport and oxygen stability in layered NaFeO 2. J. Mater. Chem. A 7, 2619–2625 (2019).
Wang, L., Maxisch, T. & Ceder, G. Oxidation energies of transition metal oxides within the GGA+U framework. Phys. Rev. B 73, 195107 (2006).
Acknowledgements
This work is primarily supported by The Thomas F. and Kate Miller Jeffress Memorial Trust, Bank of America, Trustee, and the Jeffress Trust Awards Program in Interdisciplinary Research. F.L. and X.-M.B. also acknowledge their startup funds at Virginia Tech. The Na cathode was developed based on a project funded by the National Science Foundation (No. CBET-1912885). The Li cathode was developed based upon work supported by the U.S. Department of Energy’s Office of Energy Efficiency and Renewable Energy (EERE) under the Award Number: DE-EE0008444. The irradiation work at the IVEM User Facility at Argonne National Laboratory was supported by the U.S. Department of Energy, Office of Nuclear Energy under DOE Idaho Operations Office Contract DE-AC07-051D14517 as part of a Nuclear Science User Facilities experiment. X.-M.B. acknowledges the high-performance computing facilities at Virginia Tech’s Advanced Research Computing.
Author information
Authors and Affiliations
Contributions
F.L. and X.-M.B. conceived and designed the project. M.M.R. and L.M. synthesized the materials and performed the electrochemical analysis. M.M.R. performed the SEM and XRD characterizations. M.M.R. and W.-Y.C. conducted the ion irradiation and TEM imaging experiments. M.M.R., and Z.Xu. wrote the code for gradient vector analysis. X.-M.B. conducted the DFT calculations with the help from Z.Xiao. M.M.R and F.L. performed the experimental data analysis and organized the structure of the manuscript. M.M.R., F.L., and X.-M.B. wrote the manuscript with help from all the coauthors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Hui (Claire) Xiong, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rahman, M.M., Chen, WY., Mu, L. et al. Defect and structural evolution under high-energy ion irradiation informs battery materials design for extreme environments. Nat Commun 11, 4548 (2020). https://doi.org/10.1038/s41467-020-18345-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-18345-4
This article is cited by
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.