Abstract
The ocean is a sink for ~25% of the atmospheric CO2 emitted by human activities, an amount in excess of 2 petagrams of carbon per year (PgC yr−1). Time-resolved estimates of global ocean-atmosphere CO2 flux provide an important constraint on the global carbon budget. However, previous estimates of this flux, derived from surface ocean CO2 concentrations, have not corrected the data for temperature gradients between the surface and sampling at a few meters depth, or for the effect of the cool ocean surface skin. Here we calculate a time history of ocean-atmosphere CO2 fluxes from 1992 to 2018, corrected for these effects. These increase the calculated net flux into the oceans by 0.8–0.9 PgC yr−1, at times doubling uncorrected values. We estimate uncertainties using multiple interpolation methods, finding convergent results for fluxes globally after 2000, or over the Northern Hemisphere throughout the period. Our corrections reconcile surface uptake with independent estimates of the increase in ocean CO2 inventory, and suggest most ocean models underestimate uptake.
Similar content being viewed by others
Introduction
In recent years, an international effort has assembled a quality-controlled database of surface ocean carbon dioxide observations, the Surface Ocean Carbon Dioxide Atlas (SOCAT)1,2,3. SOCAT has enabled several recent studies evaluating air–sea CO2 flux from the observed partial pressure at the ocean surface4,5,6,7,8,9,10. In order to use the data to obtain accurate values of ocean-atmosphere CO2 fluxes, it is necessary to apply the gas exchange equation to the concentration difference of dissolved CO2 across the mass boundary layer (MBL) of the sea surface—the topmost ~100 µm within which molecular diffusion dominates vertical transport toward the interface (see Methods section). Calculation of the concentration at the base of this layer comes from the sea surface data. Previous studies using the SOCAT data have generated this concentration from the measurements specified at the temperature of the water inlet, at a depth usually several meters below the surface. However, there are typically temperature differences in the surface ocean layer11, which can materially affect the partial pressure, or fugacity of CO2 (fCO2). For this reason, a procedure was developed to recalculate the SOCAT data from the measurement temperature to the subskin temperature, a few millimeters below the surface11,12,13. This temperature is derived predominantly from satellite infrared observations and is available as an optimally interpolated gridded product14. Furthermore, the MBL is embedded within the ocean’s thermal skin, the uppermost ~1000 µm which is cooler than the underlying water because the ocean surface is a net emitter of heat, both via latent heat and longwave radiative fluxes, to the atmosphere15. The cooler skin temperature also affects the calculation of the CO2 flux since the CO2 concentration at the top of the MBL, at the air–water interface, is set by the product of the fCO2 in the atmosphere, and its solubility in the water there. The solubility is temperature dependent and increases at the lower temperature. It has long been known that this effect has a globally significant impact on calculated air–sea fluxes16, but most studies have ignored it. Recent work has however confirmed and clarified the theory11.
Here, we apply these corrections to a recent update of the SOCAT data, in combination with several different interpolation techniques. We derive a time history of corrected ocean-atmosphere fluxes and their associated uncertainties, for the period from 1992 to 2018, finding substantially increased net uptake of CO2 by the oceans. We then compare our results with a recently published analysis of the increase in ocean anthropogenic carbon dioxide calculated from global repeat hydrography programs17. In contrast to earlier surface flux estimates, our revision is consistent with this inventory increase. Comparison with the inventory suggests that the pre-industrial flux of CO2 from the open ocean to the atmosphere was ~0.5 PgC yr−1 and that it exhaled mostly from the Southern Hemisphere. The close agreement between two independent observationally based syntheses, one based on surface data and the other on interior measurements, suggests that most ocean carbon models are underestimating the net sink for atmospheric CO2 over recent decades.
Results and discussion
Effect of temperature corrections
Figure 1 illustrates the effect of the two adjustments described above on a calculation of annual global ocean-atmosphere fluxes for this period, with calculations starting from the SOCAT v2019 database. To interpolate the SOCAT surface water fCO2 data in space and time we adopt as our standard method the two-step neural network approach described by Landschützer et al.8,18, (see also description below and Methods section). The interpolation was applied to the SOCAT data without modification, after adjusting the data to a subskin temperature and regridding (as described in refs. 12,19, see also Methods section) then additionally after repeating the flux calculation assuming a ΔT across the cool skin of 0.17 K15 salinity increase of 0.1 unit11 and the conservative “rapid transport” scheme of Woolf et al.11 (see Methods section). Each adjustment increases the calculated flux by ~0.4 PgC yr−1 when integrated over the global ocean. For the period ~2000, this approximately doubles the calculated flux into the ocean. Over the 27 years 1992–2018 inclusive, the cumulative uptake is increased from 43 to 67 PgC.
Global air–sea flux calculated by interpolating SOCAT gridded data using a neural network technique8, followed by the gas exchange equation applied to the ocean mass boundary layer. The net flux into the ocean is shown as negative, following convention. The uncorrected curve uses the SOCAT fCO2 at inlet temperature as usually done. Correction of the data to a satellite-derived subskin temperature is shown, and the additional change in flux due to a thermal skin assumed to be cooler and saltier than the subskin by 0.17 K15 and 0.1 salinity units11. Excludes the Arctic and some regional seas—ocean regions included are shown in Supplementary Fig. 2.
Uncertainty estimates
Ocean-atmosphere fluxes calculated using the gas exchange equation are subject to two broad sources of uncertainty: (1) specification of the gas transfer velocity, which depends on the thickness of the MBL and is usually parameterized as a function of wind speed, and (2) specification of the CO2 concentration difference across the MBL. The recent study by Woolf et al.20 contains a detailed treatment of the uncertainties due to the gas transfer, concluding that a realistic estimate (approximately, a 90% confidence interval) is ±10% when applying this to global data.
The second source of uncertainty, due to the concentration difference, is dominated by that introduced by the interpolation in time and location of surface ocean CO2. This is relatively well constrained in the more densely observed regions such as the North and Equatorial Atlantic and North and Tropical Pacific. However, in more remote regions such as the Southern, South Pacific, and Indian Oceans, the observational coverage is patchier in space and time and often seasonally biased, with few winter measurements (see Supplementary Fig. 3). New sensors and designs of autonomous floats, as now being deployed in the Southern Ocean21, show promise to solve the problem of adequately observing surface CO2 in remote regions22, but for the gap-prone historical data, the interpolation method used can have a substantial influence on the results in these data-poor regions.
To evaluate the uncertainty in flux estimates introduced by the gap-filling procedure, we used three methods for interpolating in space and time, each applied to the global data divided according to three different spatial clustering schemes, for a total of nine mappings. The interpolation methods were as follows: (1) a time series (TS) of fCO2sw data, constructed by a least squares fit to all monthly averaged fCO2 values within the defined region. The model fitted was a seasonal cycle with three harmonics superimposed on a linear trend; (2) simple multilinear regression (MLR) of the fCO2 data on latitude, longitude, and four variables for which continuous comprehensive mappings are available, these being sea-surface temperature (SST), salinity (SSS), mixed layer depth (MLD), and atmospheric CO2 mixing ratio (XCO2); (3) the feed-forward neural network method of Landschützer et al.8,18 (FFN), which also seeks a regression on these four variables. The spatial clustering schemes applied to each of the techniques (shown in Supplementary Fig. 1) were as follows: (a) division into 14 regions along latitude–longitude lines; (b) division into the 17 biogeochemical divisions suggested by Fay and Mckinley23, and (c) division into 16 biomes using a self-organizing map technique employed by Landschützer et al.8.
Where the data are adequately distributed over space and time, the use of multiple mapping techniques and different clustering schemes to estimate uncertainty gives similar results to formal geostatistical techniques, such as kriging7,20. However, in regions of very sparse and uneven coverage, statistically based techniques can underestimate uncertainties because of the assumption that the available data are representative of the true data population over a region, which may not be the case if whole regions or seasons are poorly sampled. In this instance, different mapping techniques can give substantially different results. Altering the clustering of the data by changing the shape of the geographical divisions can also have a major effect, because unsampled areas are assumed to have the same statistical properties as the sampled regions with which they are grouped.
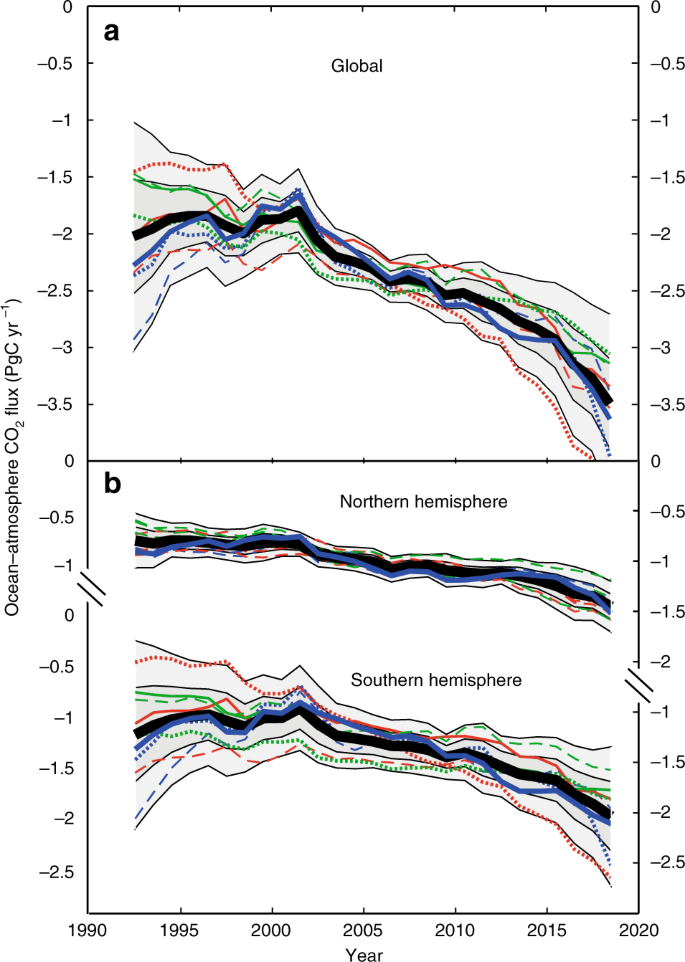
For each combined mapping-and-clustering technique, Table 1 shows the spread and mean of the residuals (the global set of predicted values minus observed values). The neural network FFN mapping method provides a much smaller spread of residuals, giving better agreement with data at a given location and time than do the other methods. This is to be expected given its much greater flexibility, with typically several hundred parameters being adjusted to provide a non-linear fit to each cluster, compared to only 8 and 11 fitted parameters for respectively the TS and MLR methods. Figure 2 shows estimates of global and hemispheric ocean-atmosphere CO2 flux over the period 1992–2018 by the nine interpolations (using a single parameterization of the gas transfer velocity). Despite the difference in the quality of the fits to the individual data as evidenced by Table 1, convergent results are obtained by all the calculations for the Northern Hemisphere over the whole period, and there is a good agreement in the Southern Hemisphere for much of the period after 2000. The average of all the methods is shown, with one and two standard deviations of the nine separate estimates. A few regions are excluded (see Supplementary Fig. 2) to ensure compatibility in the comparison between methods, but these affect the results by <0.05 PgC yr−1.
Fluxes are integrated a globally, and b for northern and southern hemispheres, calculated using a standard gas exchange formulation (see Methods section) with the nine interpolation schemes for fCO2 described in the text shown as colored lines: TS red, MLR green, FFN blue. The line styles indicate the spatial clustering schemes used (illustrated in Supplementary Fig. 1): solid, Landschützer SOM; dashed, latitudinal regions; dotted, Fay and Mckinley biomes. The standard method, SOM-FFN as described in Landschützer et al.8, is shown as a thicker blue line. Shading indicates one- and two-standard deviations of the nine methods around the mean (thick black line).
The wider uncertainties indicated pre-2000 arise from the divergence of fits in the Southern Hemisphere. The majority of studies using the historical surface CO2 data find that the Southern Ocean sink was static or weakening during the 1990s and strengthened considerably after 200024,25. The simpler, linearly constrained interpolation methods show something of this change, but it is less pronounced than in the more flexible FFN calculations. However, we retain the wider spread pre-2000 as a realistic estimate of uncertainty then, given the paucity of the data and its uneven, and decadally changing, spatial distribution in the Southern Ocean and South Pacific (see Supplementary Fig. 3, which shows the distribution of the data in the Southern Hemisphere).
New CO2 surface fluxes compared to interior observations
We now compare our estimates for global CO2 flux into the ocean, with a recent independent synthesis of observations estimating the increase in oceanic anthropogenic carbon from interior repeat hydrography measurements, over the period 1994–200717. This comparison requires accounting for pre-industrial ocean-atmosphere fluxes: the ocean was pre-industrially a source of CO2 to the atmosphere, with a net dissolved river flux usually estimated as 0.45–0.6 PgC yr−1 flowing down rivers to the ocean, from ocean to atmosphere and from the atmosphere to the land surface26,27. We also have to add a flux for the Arctic Ocean, not included in our study but estimated at 0.12 PgC yr−1 28. In Fig. 3, we show our standard case estimate of the anthropogenic sink, with the ocean-atmosphere flux increased by 0.57 PgC yr−1, (0.12 PgC yr−1 Arctic plus a pre-industrial flux of 0.45 PgC yr−1), and with the uncertainty bands now widened to include the Woolf et al. estimate for gas transfer velocity uncertainty20. This is compared to the recent estimate for the accumulation of anthropogenic carbon from interior ocean observations, over the period 1994–200717. Two previously published estimates of the sink calculated from the surface data are also shown for comparison8,10. In contrast to these earlier estimates, our revised surface flux is consistent with the interior anthropogenic accumulation and most previous estimates of the pre-industrial ocean-to-atmosphere source.
The black line is our standard case global ocean-atmosphere flux increased by −0.57 PgC Cyr−1 to account for pre-industrial and Arctic fluxes as described in the text. The shading gives one and two standard deviations of estimates around this value, including the uncertainty in gas transfer rates as assessed by Woolf et al.20. Red horizontal line and uncertainty is a recent estimate of the global inventory increase of anthropogenic carbon in the ocean between 1994 and 200717. Dashed lines: two previous estimates of global uptake based on surface data: blue dashed line from Landschützer et al.8, red dashed line from Rödenbeck et al.10, both as quoted in Le Quéré et al.31. Both are increased by the pre-industrial flux correction and Landschützer et al.8 also increased by Arctic correction.
In Table 2, we show uptake integrated over the 13 years from mid-1994 to mid-2007 in the northern and southern Pacific, Indian and Atlantic basins, and compare these with the inventory increases as given by Gruber et al.17. The inventory increase in each basin will not equal the flux through the surface of that basin, both because of the pre-industrial flux correction described above, and because subsurface ocean transport redistributes the CO2 away from the uptake regions. The comparison is revealing, however, because we should not expect a very large change in inter-hemispheric CO2 exchange in the ocean during this time. We expect some correspondence between these figures, therefore, at least at the hemispheric level. The global flux through the ocean surface is less than the inventory change by ~7 PgC over this period, an amount consistent with the expected pre-industrial ocean source. However, the Northern Hemisphere uptake, which is comparatively well constrained by the surface data, quite closely matches the inventory increase in the Northern Hemisphere. The majority of the difference between surface uptake and inventory increase is in the Southern Hemisphere, suggesting that excess river carbon that the natural cycle puts into the open ocean was pre-industrially compensated by net outgassing almost entirely in that hemisphere, and that its magnitude is ~0.5 PgC yr−1. A recent proposed upward revision of this flux to 0.78 Pg Cyr−1 29 was motivated in part by the clear mismatch between anthropogenic carbon uptake and the earlier, lower estimates of surface uptake, but our analysis is more consistent with the lower values of previous studies, which come from ocean inverse models26 and inventories of global dissolved riverine carbon27,30. We note also that the uncertainty on the South Pacific flux (including the Pacific sector of the Southern Ocean) is particularly large, reflecting the paucity of data there (Supplementary Fig. 3). However, over the entire Pacific basin, and globally, uncertainties are smaller, because there is inter-basin compensation with some mapping estimates that give high values in the southern Pacific giving lower values in the tropical and northern regions.
The agreement between the observational estimates of CO2 uptake by the oceans provides an important constraint on calculations of the global carbon budget and its rate of change. Supplementary Table 1 gives more detail on global fluxes calculated over decadal periods compared to those of earlier estimates, both of the net contemporary ocean-atmosphere flux and the ocean uptake of anthropogenic carbon. As indicated in Fig. 3, our best estimate of 2.5 ± 0.4 Pg yr−1 for anthropogenic carbon uptake during 1994–2007 agrees closely with that of Gruber et al. and has a similar uncertainty. This sink is stronger than most recent estimates and is ~0.5 PgCyr−1 larger than the central estimate of the Global Carbon Project31 for that period for example. That estimate is the average of a number of models, which however span a wide range, with a 2-σ uncertainty of ±0.6 PgC yr−1 for that period. The discrepancy between our value and that of the Global Carbon Project increases with time and approaches 1 PgC yr−1 after 2010.
We conclude that, when correctly applied, two data-led independent estimates for the ocean sink for CO2, based respectively on observations of the surface flux and the interior inventory of CO2, agree within relatively well-constrained uncertainties. The sink so determined is larger than most ocean carbon models predict, and suggests that some revision of the global carbon budget is required. Due weight should be given to the constraints that ocean interior and surface observations impose when calculating global carbon budgets, and near-surface temperature deviations need to be taken into account when using surface observations to calculate fluxes. Continued systematic observation of the surface and interior ocean carbon system remains essential to tracking how the global carbon cycle is changing in response to human activities.
Methods
Adjustments to surface CO2 data
The individual voyage surface CO2 data (v2019) were downloaded from the SOCAT website (www.socat.info1,2). We used only the data from 1992 onward, since the number of observations begins to increase substantially at around that time2. We used the surface fCO2 product, which is closely equivalent to the partial pressure of CO2 in equilibrium with seawater but is the more correct variable for concentration and flux calculations32.
The SOCAT database records fCO2 of surface seawater measured in an equilibrator, temperature-corrected to an inlet temperature using an empirical equation33. As described in Goddijn-Murphy et al.12, the SOCAT inlet temperature is not the same as the temperature measured at the base of the MBL, the topmost ~100 µm of the ocean, which is where the water-side concentration must be specified for the purposes of air–sea flux calculations11. We used the “FluxEngine” programs (http://www.oceanflux-ghg.org/Products/FluxEngine13,34) to correct the SOCAT data to a standard subskin temperature derived from satellite optimally interpolated sea-surface temperature data, implementing the method described by Goddijn-Murphy et al.12, and assuming an isochemical temperature correction. A new “cruise-weighted” gridded product following the SOCAT methodology was then created using the corrected cruise data3. This produces a 1° longitude and latitude by one-monthly time resolution data set3. This gridded product is publically available19.
Interpolation techniques for the global fCO2
These have typically involved two steps. First the full data set is divided into clusters (using location, time, or some other criteria), then an interpolation procedure is applied to each of these clusters. We used three different schemes for the initial division, and three methods of interpolating the fCO2 data within those clusters. The divisions used are described in the main text and illustrated in Supplementary Fig. 1. Permanently ice-covered regions, the Arctic ocean, coastal regions, and other areas unclassified in the Fay and Mckinley description of biomes23 were excluded from all techniques when comparing the output of different methods, (e.g., Fig. 2 and interpolation uncertainty estimates) to ensure a like-for-like comparison. Supplementary Figure 2 shows the regions excluded and included when making the comparisons and when calculating a best estimate using our standard method, e.g., for Fig. 3 and Table 2.
The three classes of method used to interpolate the fCO2 data within these clusters were as follows:
-
(1)
TS curves fitted to the mean of all data in the region binned into monthly time steps, using least squares. The curves were the sums of a linear trend and three sinusoidal cycles having frequencies of one, two, and three cycles per year. Each fit therefore had eight variable parameters: amplitude and phase for each sine curve, and slope and intercept for the inter-annual trend.
-
(2)
MLR of surface fCO2 with the co-located SST, SSS, MLD, and XCO2, latitude and longitude. The first four of these were each decomposed into two components: a climatology calculated as the averages over each month of the year for the period 1992–2018, and an anomaly from that climatology. In total, there were 10 variables therefore, which with a constant, yielded 11 parameters to be fitted by least squares. Table S1 in the supplementary information details the sources of these “driver” variables that we used. Surface chlorophyll derived from satellite ocean color is frequently used as a predictor variable for fCO2 interpolations25, but we preferred not to use this as it is not available before 1997, or in polar regions in the winter.
-
(3)
The FFN network method as described by Landschützer et al.8, implemented with the MATLAB neural net toolbox. The independent variables were again SST, SSS, MLD, and XCO2, decomposed as for the MLR into a seasonal climatology and anomalies from that climatology.
Calculation of air–sea fluxes
The gas exchange equation was used to calculate FCO2, the sea-to-air flux of CO2, (positive from sea to air):
where k is the appropriate gas transfer velocity, Csw is the concentration of dissolved CO2 at the base of the MBL and C′ is the concentration at the interface with the atmosphere. C′ was calculated as αskin.fCO2atm, the product of the solubility of CO2 at the surface skin temperature and salinity (αskin) and fCO2atm, the fugacity of atmospheric CO2. The gradient from the base to the top of the thermal skin was assumed to be 0.1 salinity units11 and −0.17 K15. Csw was calculated as αsubskin.fCO2subskin, the product of the seawater fCO2 corrected to the subskin temperature derived as described above, and the solubility at the subskin temperature and salinity. This treatment follows that by Woolf et al.11, implementing their “rapid transport” approximation for carbonate equilibration in the surface layers. In this approximation, the transport from the interior across the thermal boundary to the MBL is assumed to occur more rapidly than the time scale for reaction of CO2 with H2O molecules, so that the dissolved CO2 concentration does not change. This is a conservative assumption, in the sense that it gives a smaller adjustment due to skin effects than if change in the hydration state is assumed.
The gas transfer velocity was parameterized as a function of the wind speed at 10 m (we used the relation of Nightingale et al.35 based on a compilation of dual tracer experiments, which is one of several evaluated by Woolf et al.20 that give similar results to more recent parameterizations using the global 14C budget36,37). The wind used was the CCMP product at 0.25o and 6-h resolution38, with gas exchange rates subsequently averaged monthly over 1 × 1 degree tiles. Atmospheric fugacity was calculated from XCO2, the atmospheric mixing ratio of CO2, using the method outlined for the CO2—air mixture by Weiss32, and assuming air at 100% humidity at the sea surface39. The sources of data for winds, surface temperature, salinity, atmospheric pressure, ice cover, and XCO2 used are given in Supplementary Table 1. Ice cover was assumed to suppress air–sea exchange entirely, so that the calculated flux was reduced by a factor (1 − i) where i was the fractional ice cover.
Data availability
The gridded data set of sea surface fCO2 described in the Methods section above, based on SOCAT v2019 and adjusted to satellite-derived subskin surface temperature, is available at https://doi.org/10.1594/PANGAEA.905316. Ocean-atmosphere fluxes interpolated to monthly and 1 × 1 degree spatial resolution, and used to construct figures and tables in this publication, are available on request from the corresponding author. The mean annual fluxes used to draw the line graphs of Figs. 1–3 are included in the Supplementary Data file linked to this publication.
References
Bakker, D. C. E. et al. A multi-decade record of high-quality fCO2 data in version 3 of the Surface Ocean CO2 Atlas (SOCAT). Earth Syst. Sci. Data 8, 383–413 (2016).
Pfeil, B. et al. A uniform, quality controlled Surface Ocean CO2 Atlas (SOCAT). Earth Syst. Sci. Data 5, 125–143 (2013).
Sabine, C. L. et al. Surface Ocean CO2 Atlas (SOCAT) gridded data products. Earth Syst. Sci. Data 5, 145–153 (2013).
Denvil-Sommer, A., Gehlen, M., Vrac, M. & Mejia, C. LSCE-FFNN-v1: a two-step neural network model for the reconstruction of surface ocean pCO2 over the global ocean. Geosci. Model Dev. 12, 2091–2105 (2019).
Gregor, L., Kok, S. & Monteiro, P. M. S. Empirical methods for the estimation of Southern Ocean CO2: support vector and random forest regression. Biogeosciences 14, 5551–5569 (2017).
Iida, Y. et al. Trends in pCO2 and sea–air CO2 flux over the global open oceans for the last two decades. J. Oceanogr. 71, 637–661 (2015).
Jones, S. D., Le Quéré, C., Rödenbeck, C., Manning, A. C. & Olsen, A. A statistical gap-filling method to interpolate global monthly surface ocean carbon dioxide data. J. Adv. Model. Earth Syst. 7, 1554–1575 (2015).
Landschützer, P., Gruber, N., Bakker, D. C. E. & Schuster, U. Recent variability of the global ocean carbon sink. Glob. Biogeochem. Cycles 28, 927–949 (2014).
Rödenbeck, C. et al. Data-based estimates of the ocean carbon sink variability—first results of the Surface Ocean pCO2 Mapping intercomparison (SOCOM). Biogeosciences 12, 7251–7278 (2015).
Rodenbeck, C. et al. Global surface-ocean pCO2 and sea-air CO2 flux variability from an observation-driven ocean mixed-layer scheme. Ocean Sci. 9, 193–216 (2013).
Woolf, D. K., Land, P. E., Shutler, J. D., Goddijn-Murphy, L. M. & Donlon, C. J. On the calculation of air-sea fluxes of CO2 in the presence of temperature and salinity gradients. J. Geophys. Res. Oceans 121, 1229–1248 (2016).
Goddijn-Murphy, L. M., Woolf, D. K., Land, P. E., Shutler, J. D. & Donlon, C. The OceanFlux Greenhouse Gases methodology for deriving a sea surface climatology of CO2 fugacity in support of air-sea gas flux studies. Ocean Sci. 11, 519–541 (2015).
Shutler, J. D. et al. FluxEngine: a flexible processing system for calculating atmosphere-ocean carbon dioxide gas fluxes and climatologies. J. Atmos. Ocean. Technol. 33, 741–756 (2016).
Banzon, V., Smith, T. M., Chin, T. M., Liu, C. & Hankins, W. A long-term record of blended satellite and in situ sea-surface temperature for climate monitoring, modeling and environmental studies. Earth Syst. Sci. Data 8, 165–176 (2016).
Donlon, C. J. et al. Toward improved validation of satellite sea surface skin temperature measurements for climate research. J. Clim. 15, 353–369 (2002).
Robertson, J. E. & Watson, A. J. Thermal skin effect of the surface ocean and its implications for CO2 uptake. Nature 358, 738–740 (1992).
Gruber, N. et al. The oceanic sink for anthropogenic CO2 from 1994 to 2007. Science 363, 1193–1199 (2019).
Landschützer, P. et al. A neural network-based estimate of the seasonal to inter-annual variability of the Atlantic Ocean carbon sink. Biogeosciences 10, 7793–7815 (2013).
Holding, T., Ashton, I. G. C. & Shutler, J. D. Reanalysed (depth and temperature consistent) surface ocean CO2 atlas (SOCAT) version 2019. PANGAEA. https://doi.org/10.1594/PANGAEA.905316 (2019).
Woolf, D. K. et al. Key Uncertainties in the recent air-sea flux of CO2. Glob. Biogeochem. Cycles 33, 1548–1563 (2019).
Gray, A. R. et al. Autonomous biogeochemical floats detect significant carbon dioxide outgassing in the high-latitude Southern Ocean. Geophys. Res. Lett. 45, 9049–9057 (2018).
Bushinsky, S. M. et al. Reassessing Southern Ocean air-sea CO2 flux estimates with the addition of biogeochemical float observations. Glob. Biogeochem. Cycles 33, 1370–1388 (2019).
Fay, A. R. & McKinley, G. A. Global open-ocean biomes: Mean and temporal variability. Earth Syst. Sci. Data 6, 273–284 (2014).
Ritter, R. et al. Observation-based trends of the Southern Ocean Carbon Sink. Geophys. Res. Lett. 44, 339–312 (2017).
Landschützer, P. et al. The reinvigoration of the Southern Ocean carbon sink. Science 349, 1221–1224 (2015).
Jacobson, A. R., Fletcher, S. E. M., Gruber, N., Sarmiento, J. L. & Gloor, M. A joint atmosphere-ocean inversion for surface fluxes of carbon dioxide: 1. Methods and global-scale fluxes. Global Biogeochem. Cycles. https://doi.org/10.1029/2005gb002556 (2007).
Sarmiento, J. L. & Sundquist, E. T. Revised budget for the oceanic uptake of anthropogenic carbon-dioxide. Nature 356, 589–593 (1992).
Schuster, U. et al. An assessment of the Atlantic and Arctic sea–air CO2 fluxes, 1990–2009. Biogeosciences 10, 607–627 (2013).
Resplandy, L. et al. Revision of global carbon fluxes based on a reassessment of oceanic and riverine carbon transport. Nat. Geosci. 11, 504–509 (2018).
Dlugokencky, E. J., Thoning, K. W., Lang, P. M. & Tans, P. P. NOAA Greenhouse Gas Reference from Atmospheric Carbon Dioxide Dry Air Mole Fractions from the NOAA ESRL Carbon Cycle Cooperative Global Air Sampling Network. Data Path: ftp://aftp.cmdl.noaa.gov/data/trace_gases/co2/flask/surface/ (2017).
Le Quéré, C. et al. Global Carbon Budget 2017. Earth Syst. Sci. Data 10, 405–448 (2018).
Weiss, R. F. Carbon dioxide in water and seawater: the solubility of a non-ideal gas. Mar. Chem. 2, 201–215 (1974).
Takahashi, T., Olafsson, J., Goddard, J. G., Chipman, D. W. & Sutherland, S. C. Seasonal-variation of CO2 and nutrients in the high-latitude surface oceans—a comparative-study. Glob. Biogeochem. Cycles 7, 843–878 (1993).
Holding, T. et al. The fluxengine air-sea gas flux toolbox: simplified interface and extensions for in situ analyses and multiple sparingly soluble gases. Ocean Sci. 15, 1707–1728 (2019).
Nightingale, P. D. et al. In situ evaluation of air-sea gas exchange parameterizations using novel conservative and volatile tracers. Glob. Biogeochem. Cycles 14, 373–387 (2000).
Sweeney, C. et al. Constraining global air-sea gas exchange for CO2 with recent bomb C-14 measurements. Glob. Biogeochem. Cycles 21, Gb2015 (2007).
Wanninkhof, R. Relationship between wind speed and gas exchange over the ocean revisited. Limnol. Oceanogr. Methods 12, 351–362 (2014).
Wentz, F. J. et al. Remote Sensing Systems Cross-calibrated multi-platform (CCMP) 6-hourly ocean vector wind analysis product on 0.25 degree grid, version 2.0 Remote Sensing Systems, Santa Rosa CA. www.remss.com/measurements/ccmp (2015).
Cooper, D. J., Watson, A. J. & Ling, R. D. Variation of PCO2 along a North Atlantic shipping route (UK to the Caribbean): a year of automated observations. Mar. Chem. 60, 147–164 (1998).
Acknowledgements
A.J.W. was funded by a Royal Society Research Professorship. U.S. was funded by Natural Environment Research Council Sonata project, (NE/P021417/1); J.D.S., I.G.C.A., and T.H. were funded by European Union program “Ringo” and the joint Baltic Sea research and development program project “Integral”. P.L. received funding from the European Community’s Horizon 2020 Project under grant agreement no. 821003 (4C). The authors would like to acknowledge the European Space Agency OCEANFLUX Greenhouse Gases projects that enabled the early stages of this work (contract numbers 4000104762/11/I-AM and 4000112091/14/I-LG). The Surface Ocean CO2 Atlas (SOCAT) is an international effort, endorsed by the International Ocean Carbon Coordination Project (IOCCP), the Surface Ocean Lower Atmosphere Study (SOLAS), and the Integrated Marine Biosphere Research (IMBeR) program, to deliver a uniformly quality-controlled surface ocean CO2 database. The many researchers and funding agencies responsible for the collection of data and quality control are thanked for their contributions to SOCAT.
Author information
Authors and Affiliations
Contributions
The methods for correcting surface data to subskin temperatures and for skin effect were developed by J.D.S., D.K.W., L.G.-M., I.G.C.A., T.H., and A.J.W. The methods for time and space interpolation of surface data were developed by P.L., U.S., and A.J.W.; A.J.W. and U.S. performed the global calculations. A.J.W. wrote the first draft of the manuscript, and all authors contributed to subsequent drafts.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Seth Bushinsky and other, anonymous, reviewer(s) for their contributions to the peer review of this work. Peer review reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Watson, A.J., Schuster, U., Shutler, J.D. et al. Revised estimates of ocean-atmosphere CO2 flux are consistent with ocean carbon inventory. Nat Commun 11, 4422 (2020). https://doi.org/10.1038/s41467-020-18203-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-18203-3
This article is cited by
-
Impact of sampling depth on CO\(_{2}\) flux estimates
Scientific Reports (2024)
-
Microbial strategies driving low concentration substrate degradation for sustainable remediation solutions
npj Clean Water (2024)
-
Enhanced CO2 uptake of the coastal ocean is dominated by biological carbon fixation
Nature Climate Change (2024)
-
Diurnal warming rectification in the tropical Pacific linked to sea surface temperature front
Nature Geoscience (2024)
-
The Southern Ocean carbon sink has been overestimated in the past three decades
Communications Earth & Environment (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.