Abstract
Establishing new energy-saving systems for gas separation using porous materials is indispensable for ensuring a sustainable future. Herein, we show that ELM-11 ([Cu(BF4)2(4,4′-bipyridine)2]n), a member of flexible metal–organic frameworks (MOFs), exhibits rapid responsiveness to a gas feed and an ‘intrinsic thermal management’ capability originating from a structural deformation upon gas adsorption (gate-opening). These two characteristics are suitable for developing a pressure vacuum swing adsorption (PVSA) system with rapid operations. A combined experimental and theoretical study reveals that ELM-11 enables the high-throughput separation of CO2 from a CO2/CH4 gas mixture through adiabatic operations, which are extreme conditions in rapid pressure vacuum swing adsorption. We also propose an operational solution to the ‘slipping-off’ problem, which is that the flexible MOFs cannot adsorb target molecules when the partial pressure of the target gas decreases below the gate-opening pressure. Furthermore, the superiority of our proposed system over conventional systems is demonstrated.
Similar content being viewed by others
Introduction
Half of the USA’s industrial energy is consumed in separation processes, among which 49% of separation costs are for distillation1. To ensure a sustainable future, it is necessary to establish new-energy-saving purification systems, such as gas permeation with membranes and gas adsorption with porous materials. Pressure vacuum swing adsorption (PVSA) and temperature swing adsorption (TSA) processes are much more energy efficient than distillation. However, it is difficult for these techniques to achieve high-throughput separation, which requires system enlargement, because they cause pressure loss and crushing of adsorbents at the bottom of the adsorption column. One potential solution to this problem is to rapidly operate a PVSA process to increase the flow rate of the gas without enlarging the system size. This technique, so-called rapid PVSA, is currently widely investigated and recognized as a possible strategy2,3,4. However, the rapid PVSA process is also limited in that the short-term cycle makes the system more adiabatic; thus, the generation of heat of adsorption and resulting amount of the decrease in adsorption is more serious than in the case of the normal PVSA process. The coexistence of adsorbents and phase change materials as latent heat storage mediums in a column may solve this problem5, though such a coexistence requires system enlargement. Therefore, to achieve a high-throughput separation system, innovative adsorption materials that exhibit a large loading capacity, high selectivity, and minimal heat of adsorption are required. Such ground-breaking materials must have completely different characteristics than conventional materials because high affinity and low heat of adsorption are essentially conflicting.
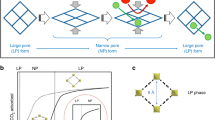
For a dozen years, metal–organic frameworks (MOFs) have been extensively studied as promising porous materials, as their designable framework structures can provide desirable adsorption properties. Moreover, flexible MOFs have attracted great attention as a result of their peculiar “gate-opening” and “breathing” behaviour, which is a structural transition phenomenon induced by guest adsorption6,7,8,9,10,11. The gate-opening and breathing effects induce stepwise change in the amount adsorbed at a specific gas pressure, which engenders larger working capacities and higher selectivities than the conventional adsorbents do. This is schematically illustrated in Fig. 1a,b; therein, the classical Langmuir-type adsorption isotherm is shown. Furthermore, it has been recently reported that flexible MOFs possess “intrinsic thermal management” capabilities12,13. Namely, the exothermic heat associated with guest adsorption is partially offset by the endothermic expansion of the host framework during gate-opening. The opposite phenomenon occurs during gate-closing based on the relationship between the endothermic heat of desorption of the guest and the exothermic shrinkage of the host. These effects are not observed for conventional adsorbents with rigid frameworks, but they are desired features for the rapid PVSA process: resulting from the suppressed heating impact owing to the adsorption and cooling from desorption, the CO2 loading and working capacities of flexible MOFs during the rapid PVSA cycle can be much larger than those of conventional adsorbents (Fig. 1c).
a Stepwise change in the amount adsorbed due to the gate-opening of the flexible MOF, X, can provide a larger working capacity when the same pressure swing is considered for the flexible MOF and the conventional adsorbent, Y. b For a gas mixture adsorption (components α and β), the flexible MOF can give higher selectivity for component α than the conventional adsorbent can give, because the gate-opening is a kind of molecular recognition; in this case, the flexible MOF can only accommodate component α and shows gate-opening. c When an adiabatic gas adsorption is considered, the temperature rise of the system for the flexible MOF, ΔTX, is smaller than that for the conventional adsorbent, ΔTY, and the resulting decrease in the adsorption amount can be suppressed because of the smaller net heat of adsorption of the flexible MOF owing to its intrinsic thermal management capability. d The flexible MOF cannot adsorb component α when the partial pressure of α in a gas mixture decreases below the inherent gate-opening pressure of the flexible MOF, Pαgate. Thus, a pure effluent gas (component β) cannot be obtained at the end of the adsorption column (“slipping-off” phenomenon).
To demonstrate that the flexible MOFs can be breakthrough materials for actual high-throughput separation processes, the following three issues require clarification. The first involves the time constant for the gate-opening; the duration of the feed operation of a rapid PVSA process should be short (i.e., a few tens of seconds). Namely, the gate-opening accompanying the structural deformation of the host framework must respond quickly to the gas feed and be accomplished considerably faster than the cycle time. Second, the separation properties must be retained for operations under non-isothermal conditions. To the best of our knowledge, the intrinsic thermal management capability of flexible MOFs for such a condition has not been discussed. The third issue involves solving the “slipping-off” phenomenon of the flexible MOFs; flexible MOFs cannot adsorb guest molecules when the partial pressure of the guest in a gas mixture flowing in an adsorption column decreases below its specific gate-opening pressure. This has not been recognized as a major challenge in the development of gas separation systems using flexible MOFs, as it was first reported by Horike et al.14. However, this is a crucial matter when considering the separation for a binary mixture (α and β): using a flexible MOF that exhibits gate-opening only for component α, the pure component β cannot be obtained at the outlet of an adsorption column because of the slipping-off of component α from the adsorption column (Fig. 1d).
Here, we focus on ELM-11 ([Cu(BF4)2(4,4′-bipyridine)2]n)15,16, which has a flexible framework and shows a typical gate adsorption for CO2 at ambient temperatures, as an adsorbent for CO2/CH4 gas mixture separation. The separation of CO2/CH4 gas mixtures such as those found in natural gas and landfill gas have gathered attention in the field of carbon capture and storage technologies17,18,19. First, we reveal that the gate-opening/closing behaviour of ELM-11 for CO2 is sufficiently fast in response to the increasing/decreasing of CO2 gas pressure by time-resolved in situ synchrotron X-ray powder diffraction (XRPD) measurements. Second, we compare the CO2 separation characteristics (uptake, selectivity, working capacity, and regenerability) of ELM-11 and HKUST-1 ([Cu3(1,3,5-benzenetricarboxylate)2]n)20 having a rigid framework that was reported as the most promising adsorbent for landfill gas separation17. We then illustrate the superiority of ELM-11, assuming a rapid PVSA process for landfill gas separation (CO2:CH4 = 50:50) composed of the following four elementary steps: (i) pressurization and adsorption of an equimolar CO2/CH4 mixture at 500 kPa, (ii) depressurization and rinsing with pure CO2 at 250 kPa, (iii) desorption at 15 kPa, and (iv) purging with pure CH4 at 15 kPa. We finally show that the issue of the slipping-off phenomenon can be solved by improving the adsorption column from an operational point of view, and we demonstrate that our proposed rapid PVSA process using flexible MOFs is an advanced adsorption system for CO2 separation.
Results
Pressure-aided fast gating of the flexible MOF
We investigated the rate of structural transition on gating of ELM-11 by time-resolved in situ synchrotron XRPD measurements. Figure 2a,b show that the structural transition of ELM-11 started immediately after the introduction of CO2 at 40.8 kPa and 273 K, and was accomplished in ~10 s. We also confirmed that ELM-11 accommodating CO2 responded quickly to the decrease in gas pressure at 273 K: the structural transition was completed in 5 s when the CO2 pressure was decreased at the rate of 2.4 kPa s−1 (Fig. 2c,d, and Supplementary Fig. 1). Time development of the fraction of the open phase by introducing ~41 kPa of CO2 at 273, 264, and 241 K is shown in Fig. 2e, and that of the closed phase is shown in Fig. 2f; it can be seen that the rate of phase transition increases as the temperature decreases under the same CO2 pressure. We also investigated the dependence of the rate of phase transition on the pressure at 227 K, as shown in Fig. 2g,h, and found that the rate of structural transition increased with increasing CO2 pressure, and the phase transition was completed within a few seconds at the highest gas pressure. Furthermore, these data were found to obey the Kolmogorov–Johnson–Mehl–Avrami (KJMA) equation21,22, as drawn with solid lines in Fig. 2e–h. The obtained parameters are summarized in Supplementary Table 1. The KJMA parameters for the open and closed phases under the same experimental conditions are in good agreement within the fitting errors, although the errors for the closed phase are mostly larger than those for the open phase because of the lower intensity of the 020 reflection of the closed phase. Figure 2i shows the relation between the rate constant of the KJMA equation and the pressure difference, P − Pgate, where P is the CO2 pressure introduced into the glass capillary with ELM-11 and Pgate is the gate-opening pressure. We found that a characteristic curve in proportion to P − Pgate could be drawn for all the rate constants of the open phase investigated. The constant of proportionality was determined to be 12.0 ± 0.5 s−1/n MPa−1 by least-squares fitting of Eq. (3). This suggests that the rate constant only depends on the CO2 gas pressure and the temperature, which controls the gate-opening pressure, and that the gate-opening rate is amplified by the CO2 pressure exerted on ELM-11. This equation tells us that it takes only 1.5 s for ELM-11 to achieve 95% structural transition when CO2 gas of 250 kPa is introduced at 298 K. This feature is particularly suitable for the rapid PVSA proposed in the later section.
a Colour map of XRPD patterns for CO2 adsorption on ELM-11 at 273 K and a constant pressure of 40.8 kPa. b Normalized peak intensities (fractions of the phase transformed) from the 002 reflection at 6.1° for the open phase and the 020 reflection at 10.2° for the closed phase shown in a. The two solid lines after 4.15 s were obtained by fitting of the Kolmogorov–Johnson–Mehl–Avrami (KJMA) equation. c Colour map of XRPD patterns for CO2 desorption at 273 K during pressure depression from 100 to 3.8 kPa (the change in CO2 pressure is shown in Supplementary Fig. 1). d Fractions of the phase transformed from the 002 reflection for the open phase and the 020 reflection for the closed phase shown in c. e Fractions of the phase transformed for the open phase and f for the closed phase at 40.8 kPa and 241 K, at 41.0 kPa and 264 K, and at 40.8 kPa and 273 K. The numbers in e and f denote the temperature. g Fractions of the phase transformed for the open phase and h for the closed phase at 227 K as a function of the CO2 pressure. The numbers in g and h denote the CO2 gas pressure in kPa introduced. The curves after 4.15 s in e–h were obtained by fitting of the KJMA equation. i Relationship between the rate coefficients and the pressure difference between the CO2 gas pressure, P, and the gate-opening pressure, Pgate. The error bar represents the standard deviation of the value obtained using the least-square fitting of the KJMA equation to the experimental data (n ≥ 3, n: number of experimental points used for fitting). The rate coefficients used in this plot are those for the open phase tabulated in Supplementary Table 1. The solid line in i was obtained from the least-squares fitting of Eq. (3).
It is also worth noting that the exponents of the KJMA equation, n, obtained from all the data for the open phase were 1.2−1.3, which indicates the quasi-one-dimensional growth of the open phase of ELM-1121. This is indeed consistent with the mechanism of gate-opening predicted in the previous study:23 one-dimensional channels composed of the stacked two-dimensional square grid layers are formed in ELM-11 once the interlayer distance is increased, and simultaneously, the CO2 molecules penetrate through the one-dimensional channels (Supplementary Fig. 2), i.e. the formation of the open phase encapsulating CO2 proceeds along the one-dimensional direction.
Adsorption properties under isothermal conditions
Figure 3a shows the experimental single-component adsorption isotherms for CO2 and CH4 on HKUST-1 at 298 K; the data were taken from the Virial–Langmuir equations experimentally determined by Chowdhury et al.24. The total and component adsorption isotherms of an equimolar CO2/CH4 mixture on HKUST-1 at 298 K, and the selectivity of CO2 over CH4, were evaluated by the ideal adsorbed solution theory25 using the experimentally obtained single-component adsorption isotherms; the obtained data are shown in Fig. 3b. Figure 3c depicts our experimentally obtained single-component adsorption isotherms for CO2 and CH4 on ELM-11 at 298 K together with their theoretical adsorption isotherms obtained by grand canonical Monte Carlo (GCMC) simulations using the quenched open framework structure of ELM-11, which was determined by the Rietveld method for pure CO2 gas adsorption at 298 K23,26. The plateau of the simulated adsorption isotherm for CO2 on the quenched open framework was in good agreement with that of the experimentally obtained one for CO2 on ELM-11, demonstrating the validity of our GCMC simulations. The fictitious GCMC isotherm for CH4 on the quenched open framework shows low adsorption, even though the framework has voids to accommodate CH4 molecules, which is due to the weak solid–fluid interactions. In contrast, the experimental isotherm of CH4 shows no adsorption, which is because the affinity of CH4 is too weak to pry open the framework of ELM-11. We also performed in situ XRPD measurements of ELM-11 in vacuo and after adsorption of CO2 gas (50 kPa), CH4 gas (50 kPa), and an equimolar mixture of CO2/CH4 gas (94 kPa) at 273 K, respectively, which are shown in Fig. 4a. The XRPD pattern of ELM-11 exposed to CH4 gas was the same as that in vacuo, and the XRPD pattern of ELM-11 after adsorption of the CO2/CH4 gas mixture perfectly coincided with that after gate adsorption of CO2. This strongly suggests that the open framework structure of ELM-11 after the adsorption of the equimolar CO2/CH4 gas mixture is the same as that after the adsorption of pure CO2. Hence, we computed the total and component adsorption isotherms of the equimolar CO2/CH4 gas mixture and the selectivity of CO2 over CH4 by GCMC simulations using the open framework structure of ELM-11 for pure CO2. The obtained results are shown in Fig. 3d.
Single-component adsorption isotherms of CO2 and CH4 at 298 K on a HKUST-1 from the experimentally determined Virial−Langmuir equations24 and c ELM-11 (filled symbols: experimental adsorption data, open symbols: experimental desorption data, lines: adsorption data simulated by grand canonical Monte Carlo (GCMC)). Total and component adsorption isotherms of an equimolar mixture of CO2 and CH4 at 298 K for b HKUST-1 evaluated by the ideal adsorbed solution theory25 and d ELM-11 simulated by GCMC. The abscissae of b and d correspond to the partial pressures of CO2. Black filled circles represent the points at which the corresponding pressures were applied in the four elementary steps of the rapid pressure vacuum swing adsorption (PVSA) process. e CO2 separation characteristics of HKUST-1 and ELM-11 assuming PVSA under isothermal conditions at 298 K.
a In situ X-ray powder diffraction patterns (Cu Kα) of ELM-11 in vacuo and after adsorption of CO2 gas (50 kPa), CH4 gas (50 kPa), and an equimolar CO2/CH4 gas mixture (94 kPa) at 273 K together with crystal structures of ELM-11 in closed and open states determined in our previous studies23,26. Pore structure and CO2 configuration of b ELM-11 and c HKUST-1.
The compatibility of the open framework structures of ELM-11 for pure CO2 adsorption and equimolar CO2/CH4 gas mixture adsorption can also provide insights into the slipping-off phenomenon of ELM-11. The gate-opening of ELM-11 under the flow of CO2/CH4 mixture gas should not occur when the CO2 partial pressure of mixture gas falls below the gate-opening pressure of ELM-11 for pure CO2 adsorption. Namely, the fraction of slipping-off CO2 in an effluent gas can be estimated as the ratio of the gate adsorption pressure for pure CO2 adsorption and the total gas pressure in the adsorption column. Indeed, by using our experimental gate-opening pressure of ELM-11 for pure CO2, we successfully predicted the effluent fraction of CO2 of the experimental breakthrough curve, as described in a later section.
The separation characteristics of HKUST-1 and ELM-11, evaluated by assuming that all steps of the PVSA process were operated under isothermal conditions at 298 K, are shown in Fig. 3e. The CO2 selectivity, Sads, of ELM-11 was 9.5 times higher than that of HKUST-1 (ELM-11: Sads = 82.3, HKUST-1: Sads = 8.67). Thus, the high CO2 selectivity of ELM-11 arises from the fact that the GCMC adsorption isotherms for the quenched open framework at low pressures (<50 kPa) show an overwhelmingly high affinity for CO2 over CH4, compared with HKUST-1. There has been an argument that the gate adsorption does not necessarily lead to high adsorption selectivity because guest molecules with low affinity should be adsorbed on the host framework pried open by other guest molecules with high affinity;27,28 however, this is not the case for ELM-11. Specifically, the adsorption amount of CH4 in the open framework is much less than that of CO2, as shown in Fig. 3c, even though the open framework of ELM-11 provides enough space for adsorption. This is because ELM-11 provides a purpose-built framework structure for CO2 in terms of size and intermolecular interactions as depicted in Fig. 4b. Owing to the large pore volume of HKUST-1 (Fig. 4c), its CO2 uptake, \(N_{{\mathrm{CO}}_2}^{{\mathrm{ads}}}\), reached 9.08 mmol g−1, which is 2.6 times the CO2 uptake of ELM-11. After the desorption process, the amount of adsorbed CO2, \(N_{{\mathrm{CO}}_2}^{{\mathrm{des}}}\), on HKUST-1 was 0.95 mmol g−1; hence, the CO2 working capacity of HKUST-1 decreased slightly to Δ\(N_{{\mathrm{CO}}_2}\) = 8.13 mmol g−1, which is still 2.3 times larger than that of ELM-11. The regenerability of ELM-11 (100%) is superior to that of HKUST-1 (89.6%), which arises from the fact that the amount of CO2 adsorbed on ELM-11 under desorption conditions (CO2 pressure of 15 kPa) is zero, as a result of gate-closing. It is worth noting that if the open framework structure of ELM-11 is rigid and does not transform to the closed state, the CO2 adsorption isotherm during the desorption process must be type I (depicted by the red dashed line in Fig. 3c) and the Δ\(N_{{\mathrm{CO}}_2}\) value is only 0.96 mmol g−1, which corresponds to a regenerability of 27%. In other words, for rigid adsorbents, the factors to improve regenerability and selectivity are essentially contradictory. In contrast, flexible MOFs can provide both perfect regenerability and high selectivity as long as the gate-opening and gate-closing pressures are compatible with the operating conditions of the PVSA process.
Adsorption properties under adiabatic conditions
We evaluated the “effective adsorption properties” of HKUST-1 and ELM-11 through adiabatic separation operations, which are extreme conditions in the rapid PVSA process: the values were obtained by considering the negative effects of temperature rise/drop caused by heats of adsorption/desorption under adiabatic conditions. In this case, all of the heat generated by guest adsorption is consumed to increase the system temperature. Namely, the changes in adsorption amount and temperature in response to the pressure swing are determined such that the heat generated by adsorption is commensurate with the heat required to change the system temperature. For simplicity, the specific heat of gas can be ignored because it is much smaller than that of the adsorbent. Figure 5a depicts the heats of adsorption for HKUST-1 as a function of temperature, represented as isobars for the equimolar CO2/CH4 mixture at 500 kPa, pure CO2 at 250 kPa, pure CO2 at 15 kPa, and pure CH4 at 15 kPa, corresponding to the operating pressures used for the rapid PVSA process (see also Supplementary Fig. 3). The heats of adsorption and specific heat of HKUST-1 were taken from the experimental data reported by Chowdhury et al.24, Kloutse et al.29, and Mu et al30. The green plane in Fig. 5a represents the adiabatic operating plane calculated by integrating the specific heat of HKUST-1 with respect to temperature. Starting from point a, the intersection point of the green plane and yellow line (298 K), we considered performing adiabatic pressurization and adsorption with the equimolar CO2/CH4 mixture at 500 kPa. The state should move from point a to the intersection of the red line and the green plane (point b), because the heat released by adsorption and the heat absorbed by the adsorbent are equal at point b. This means that the temperature of HKUST-1 changes from 298 to 370 K during the adiabatic pressurization and adsorption process. If we perform adiabatic depressurization and rinsing with pure CO2 at 250 kPa, the state moves to point c (366 K), where the purple line and the green plane intersect. The adiabatic desorption of CO2 from 250 to 15 kPa results in a significant decrease in the system temperature, as indicated by point d (313 K). Finally, the state moves back to point a on adiabatic purging of CO2 with a flow of a pure CH4 gas at 15 kPa. The adsorption amounts of CO2 and CH4 on HKUST-1 at corresponding points a−d are listed in Table 1.
Temperature dependence of heat of adsorption for a HKUST-1 and b ELM-11. Red line: adsorption of an equimolar CO2/CH4 gas mixture at 500 kPa, purple line: pure CO2 adsorption at 250 kPa, blue line: pure CO2 adsorption at 15 kPa, and yellow line: pure CH4 adsorption at 15 kPa. The green plane shows the heat required to change the temperature of the host framework. White arrows represent the four adiabatic operating processes of rapid pressure vacuum swing adsorption (PVSA). The starting temperature was set as 298 K. c CO2 separation characteristics of HKUST-1 and ELM-11 for PVSA assuming the adiabatic operations and the starting temperatures of 298, 283, and 263 K together with those assuming isothermal operations at 298 K. d Temperature dependence of net heat of adsorption for ELM-11 for adsorption of an equimolar CO2/CH4 gas mixture at 500 kPa (red), pure CO2 at 250 kPa (purple), pure CO2 at 15 kPa (blue), and pure CH4 at 15 kPa (yellow). Green lines are the heat balance curves when the adiabatic adsorption process starts from 298, 283, and 263 K. e Temperature dependence of the amount of CO2 adsorbed on ELM-11 for an equimolar CO2/CH4 mixture at 500 kPa (red) and that for pure CO2 at 15 kPa (blue).
To evaluate the adsorption properties of ELM-11 under adiabatic conditions, the temperature dependences of the enthalpy change of guest −ΔHguest, the net heat qnet, and the intrinsic thermal management capability e were evaluated. At 298 K, the exothermic heat ΔHguest during the adsorption of the equimolar CO2/CH4 gas mixture at 500 kPa was 135.3 J g−1; however, on considering the endothermic heat consumed by the host expansion (ΔHhost = 55.7 J g−1)13, the net heat qnet decreased to 79.6 J g−1, which means that e = 41.1% of the exothermic heat was offset. The e values were always ~40% over the temperature range of 248−335 K and showed a small dependence on the temperature, demonstrating the superior intrinsic thermal management capability of ELM-11 (Supplementary Fig. 4). Figure 5b shows the obtained heats of adsorption as a function of temperature for ELM-11. The isobars for the heats of adsorption for the equimolar CO2/CH4 mixture at 500 kPa and pure CO2 at 250 kPa show a sharp decrease at 335 K because of the gating of ELM-11. Starting from point s on the green plane at 298 K, the state moves to point t (335 K) on adiabatic pressurization and adsorption of the equimolar CO2/CH4 mixture at 500 kPa. The green plane divides the perpendicular segment of the red line at 335 K into two parts, suggesting that 54% of ELM-11 undergoes gate adsorption (Supplementary Note 1). The state moves to point u upon adiabatic depressurization and rinsing with pure CO2 at 250 kPa; however, this process does not affect the system temperature. Adiabatic desorption of CO2 from 250 to 15 kPa causes the system temperature to decrease to 298 K (point v) and results in evacuation of all the CO2 molecules adsorbed on ELM-11. Therefore, purging of CO2 is not required for ELM-11 (point v → point s); this is an advantage of flexible MOFs showing gate adsorption. The adsorption amounts of CO2 and CH4 on ELM-11 at corresponding points s−v are also listed in Table 1.
The four separation characteristics of HKUST-1 and ELM-11 under adiabatic conditions are depicted in Fig. 5c together with those under isothermal conditions. Three data sets are classified in accordance with the “starting temperature”, which should be set for point a for HKUST-1 and point s for ELM-11. If we set the starting temperature at 298 K, the CO2 uptake of HKUST-1 significantly decreases to 2.00 mmol g−1 in contrast to 9.08 mmol g−1 obtained for adsorption under isothermal conditions at 298 K, becoming comparable with that of ELM-11 (1.68 mmol g−1) for adiabatic adsorption. The CO2 selectivity, Sads, also decreases for both HKUST-1 and ELM-11 because of the temperature increase of the system (ΔT = 71.5 K for HKUST-1 and ΔT = 36.5 K for ELM-11, Table 1); however, the Sads value of ELM-11 still remains large. Furthermore, the CO2 working capacity of ELM-11 (1.68 mmol g−1) surpasses the record of HKUST-1 (1.41 mmol g−1).
The decrease in the starting temperature below 283 K can improve the CO2 uptake and working capacity of ELM-11, and all the separation characteristics of ELM-11 were found to be superior to those of HKUST-1 (Fig. 5c). This should be possible because the cyclic steady state of the PVSA process can be controlled by varying the initial temperature of the adsorption column31. Fig. 5d replots Fig. 5b together with the heat balance curves assuming the starting temperatures of 283 and 263 K. The PVSA cycle becomes s′→t′→u′→v′→s′ by setting the starting temperature as 283 K and crossing the perpendicular segment of the red line at point t′. The intersection point t′, at a higher heat of adsorption than point t, refers to the increase in the ratio of ELM-11 undergoing gate adsorption, wherein the CO2 uptake of ELM-11 is improved (Fig. 5e). If we can further lower the starting temperature to 263 K, the heat balance curve passes through the top of the perpendicular segment of the red line, and 100% of ELM-11 becomes available. This results in significant improvements in the CO2 uptake and working capacity of ELM-11. The starting temperature of 263 K may seem relatively low; however, some reports have shown that the temperature of adsorption columns attains values below 273 K in the cyclic steady state32,33. It should be also noted that, assuming that the system is completely adiabatic, the additional cost of cooling is unnecessary once the system cools down to the starting temperature and the cyclic steady state is established; hence, for a partially heat-insulated PVSA system, only a small amount of energy would be required for cooling to maintain the cyclic steady state.
In comparing the adsorption properties under the isothermal conditions and the adiabatic conditions for each adsorbent (Fig. 5c), the adsorption properties of ELM-11 are almost unaffected by the adsorption conditions, except for the CO2 selectivity. This fact suggests that flexible MOFs with the intrinsic thermal management capability are effective for improving the efficiency of the rapid PVSA system.
Strategy for preventing the slipping-off problem
ELM-11 can exhibit superior performance in the rapid PVSA system for landfill gas separation, as described in the previous section; however, pure CH4 gas cannot be obtained from the system unless the slipping-off problem is solved. To show it and demonstrate our strategy for preventing the slipping-off problem, we measured the breakthrough curve of CO2 on ELM-11 using the two systems shown in Fig. 6a,b.
Photographs of the column system used to measure the breakthrough curves: a a single-column system containing ELM-11 and b a sequential-column system containing ELM-11 and HKUST-1. c, d are breakthrough curves for an equimolar CO2/CH4 gas mixture in a and b, respectively. The flow rate of the gas mixture was 20 sccm, and the adsorption columns were kept at 273 K. The outlet pressure was maintained at 200 kPa.
An equimolar CO2/CH4 gas mixture at 200 kPa was flowed through a column containing ELM-11 at 273 K, which was previously heat-treated and purged with pure Ar (Fig. 6a), and the gas composition of the outlet flow from the column was determined using a quadrupole mass spectrometer. As shown in Fig. 6c, the CO2 fraction of the outlet stream became 0.16 after extruding the preloaded Ar ~1.5 min. This is the slipping-off phenomenon, and another step around 12 min comes from the essential breakthrough of ELM-11. The fraction of slipping-off CO2 obtained by the breakthrough experiment is in good agreement with Pgate/Pt = 0.165, where Pgate = 33.1 kPa is the gate adsorption pressure for pure CO2 adsorption on ELM-11 at 273 K, and Pt = 200 kPa is the total pressure of the feed gas. This result indicates that lowering the gate adsorption pressure and/or increasing the total pressure of the feed gas can reduce the molar percentage of slipping-off gas. In fact, Horike et al. performed breakthrough experiments for CO2/CH4 and CO2/C2H6 gas mixtures adsorbed on solid solutions of [Zn(5-nitroisophthalate)(4,4′-bipyridine)]n and [Zn(5-methoxyisophthalate)(4,4′-bipyridine)]n. Their results demonstrated that the gate-opening pressure and the fraction of slipping-off CO2 was reduced by controlling the ratio of 5-nitroisophthalate/5-methoxyisophthalate14. Although their method is effective, it is probably applicable to only a limited range of flexible MOFs. Moreover, reducing the gating pressure would undermine the large working capacity and perfect regenerability, which are advantages of the flexible MOFs. Although over-pressurization of the feed gas was also suggested by Sotomayor and Lastoskie34, this would consume considerable energy because, for example, to obtain pure CH4 gas (99.9%), the total pressure of the feed gas should be increased to 2.08 MPa by assuming the adsorption process for an equimolar CO2/CH4 gas mixture with the starting temperature of 263 K.
To prevent the CO2 slipping-off problem, we propose attaching a secondary column containing a conventional adsorbent that exhibits a Langmuir-type CO2 isotherm to a primary column filled with the flexible MOF. Although this system is similar to the one with multi-layered columns for separating a mixture of three or more components35, it is based on a new strategy using multiple items to improve the efficiency of the rapid PVSA system using the flexible MOF, as described in the following sections. To demonstrate the availability of our strategy, we set HKUST-1 in the secondary column downstream of the ELM-11 column (Fig. 6b), and we measured the breakthrough curve for the CO2/CH4 gas mixture at 200 kPa and 273 K. We successfully confirmed that no slipping-off CO2 was detected from the outlet of the secondary column, as shown in Fig. 6d. Note that to make the system cost-effective, the amount of conventional adsorbent for eliminating slipping-off CO2 can be determined, with two possible cases. Case I is to determine the amount of conventional adsorbent so that the secondary column’s breakthrough owing to the slipping-off CO2 matches the primary column’s breakthrough, as shown in Fig. 7a. Namely, the amount of conventional adsorbent should be the minimum quantity necessary for removing the slipping-off CO2, and in this case, the outlet flow from the secondary column exhibits a two-stage breakthrough, wherein the first breakpoint is related to the slipping-off CO2, and the second is related to the feed gas (Fig. 7b). However, it is clear that the conventional adsorbent installed in the secondary column, which was saturated by the slipping-off CO2, still has a redundant capacity to adsorb CO2. That is, after the CO2 fraction in the inlet flow for the secondary column was increased from the slipping-off concentration (Pgate/Pt) to that of the feed flow (yFeed) owing to the primary column’s breakthrough, the secondary column can be also available to remove CO2. Therefore, Case II should be designed to reduce the time lag between the first and second breakpoints to zero by installing a slightly larger amount of conventional adsorbent than that in Case I. This design is possible because the Langmuir-type adsorption isotherm of conventional adsorbent is convex upward (the slope of the isotherm decreases with an increasing concentration of CO2), and thus, the mass-transfer zone for reducing the CO2 fraction from yFeed to Pgate/Pt moves faster than that for reducing the CO2 fraction from Pgate/Pt to zero (Fig. 7a). The choice between Case I and Case II should depend on the operating conditions and the characteristics of the flexible and rigid adsorbents used.
a Movement of the mass-transfer zone in the primary and secondary columns containing a flexible MOF and a Langmuir-type adsorbent, respectively, where red and green lines show the CO2 fraction in the stream in the columns before and after the primary column breaks through, respectively. b Breakthrough curves at the three positions indicated by dashed lines in a, where “intermediate” is the outlet of the primary column, “case I“ is the front of the mass-transfer zone in the secondary column when the primary column breaks through, and “case II” is the front of the mass-transfer zone when the first breakpoint just merges with the second one.
Comparison between a conventional and our proposed system
To verify the effectiveness of our proposed system, we compared the performance of two rapid PVSA processes: a conventional system using a single column filled with HKUST-1 and our proposed system where ELM-11 and HKUST-1 are filled in the primary and secondary columns, respectively. These systems are schematically illustrated in Fig. 8a. We assumed that the adiabatic adsorption of equimolar CO2/CH4 mixture at 500 kPa (starting temperature of 263 K) was performed under the same conditions with the rapid PVSA process investigated in this study. We determined the column length and the molar flow rate of the feed gas required to obtain the same molar flow rate of CH4 (product gas), F, for both systems by conducting material balance calculations using the “effective adsorption properties” under adiabatic conditions obtained in the former section. Note that the basic concept of the calculation is analogous to the screening method for the PVSA systems developed by Maring and Webley, which can provide a good estimation36. The obtained results are shown in Fig. 8b. When we set the size of the column of the conventional system to L, our proposed system based on Case II only requires a primary column with a size of 0.224L and a secondary column with a size of 0.082L to accomplish the same molar flow rate of product gas, F. This means that our proposed system is, overall, 69% smaller than the conventional one, even though it consists of two columns. Moreover, the molar flow rate of the feed gas for our system (2.39F) was also found to be 62% less than that of the conventional one (6.24F). These results suggest that our proposed system, using the flexible MOFs, can be more efficient than the conventional system. In addition, if both systems are set to the same size, our system can process a much larger amount of gas and thus achieve a high-throughput CO2 separation. Note that the proposed system based on Case I is also superior to the conventional system, as demonstrated in detail in Supplementary Note 2.
Discussion
Time-resolved in situ synchrotron XRPD measurements revealed that the CO2 gate-opening of ELM-11 can be extremely fast when P–Pgate is large. This should be an inherent characteristics of ELM-11 originated from its framework structure because it has been reported that, conversely, other flexible MOFs exhibit slow transitions37. Moreover, it was found that ELM-11 accommodating CO2 responded quickly to the decrease in gas pressure; the gate-closing can be much faster than the gate-opening. This suggests that the desorption of CO2 is accelerated by the squeezing when the host framework shrinks and returns to the closed structure.
We also found that, owing to the intrinsic thermal management capability, ELM-11 has superior properties in terms of CO2 uptake, CO2 selectivity, CO2 working capacity, and regenerability under adiabatic operating conditions compared with those of HKUST-1, although HKUST-1 has a larger CO2 capacity under isothermal conditions. This suggests that the performance of flexible MOFs on a separation process operated under an adiabatic condition as a limit of the rapid PVSA process should be evaluated not only by the adsorption isotherms, but also by the net heat of adsorption, considering the intrinsic thermal management capability.
We proposed a sequential-column system to solve the problem of the slipping-off phenomenon with flexible MOFs and demonstrated the availability of it by measuring breakthrough curves. The proposed system with ELM-11 and HKUST-1, operating under adiabatic conditions, can produce the same amount of CH4 with much smaller columns and less feed than those of the conventional single-column system using HKUST-1. It is worth noting that our proposed sequential-column system is suitable for flexible MOFs showing pressure-aided fast gating because the primary column containing a flexible MOF can be designed to treat a gas mixture with a high concentration of CO2 or a large P − Pgate value. The secondary column should therefore be designed to process the slipping-off CO2 and to maximize the utilization of fast gating of the flexible MOFs. Further, note that filling a simple mixture of a flexible MOF and a rigid nanoporous material into one adsorption column cannot inherently solve the slipping-off problem. Mixing the materials only produces a type IV isotherm (IUPAC classification38) as a sum of the gate adsorption and Langmuir-type isotherms, which cannot avoid the two-stage breakthrough of CO2, although a modest amount of pure CH4 can be obtained before the first breakthrough of CO2 (see Supplementary Fig. 5 for more details). The efficiency of the sequential-column system can be further improved if the operations for the primary column filled with a flexible MOF and the secondary column filled with a conventional adsorbent are optimized and performed individually. This is technically feasible by installing a multi-way valve at the junction of the two columns, which enables simultaneous operations of the desorption process for the primary column and purging process for the secondary column, leading to a reduction in the total cycle time (Supplementary Fig. 6). Thus, our sequential-column system can provide a variety of options for the rapid PVSA operations. Our system is also highly customizable for other separation applications because the resolution of the slipping-off problem of flexible MOFs enables effective separation of a mixture of gases, one or both of which have high added value, such as C3H6/C3H8, C2H4/C2H6, and H2/CH4. Accordingly, we believe that our methodology provides a significant advance in the field of PVSA using solid adsorbents. Moreover, we anticipate that the intrinsic thermal management and the pressure-aided fast gating capabilities of flexible MOFs will also be useful for increasing the efficiency of TSA for CO2 capture, which has been comprehensively studied by Hefti et al.39.
It should be also noted that, to realize rapid PVSA using the flexible MOFs, some issues must be resolved, for example, the hindrance of gate-opening by the pelletization of flexible MOFs, pellets braking owing to the gate-opening, and a pressure drop owing to the volume expansion of the pellets induced by the gate-opening. We have already started addressing these concerns, and the results will be published elsewhere.
Methods
Rapid PVSA process for landfill gas separation
We considered the following four elementary steps for the rapid PVSA process: (i) co-current pressurization and adsorption of an equimolar CO2/CH4 mixture at 500 kPa, (ii) co-current depressurization and rinsing with pure CO2 at 250 kPa, (iii) counter-current desorption at 15 kPa (a bench-scale PVSA plant for CO2 separation using NaX zeolite is operated at 10 kPa40), and (iv) counter-current purging of remaining CO2 in the adsorbent with pure CH4 at 15 kPa.
For simplicity, we assumed that the heat transfer from the adsorbent to the mixture gas and the adsorption tower can be ignored, and that the heat transfer between the adsorbent crystals is sufficiently rapid, which should correspond to the conditions under rapid and adiabatic adsorption/desorption operations.
The following four factors were investigated to evaluate the CO2 separation characteristics of ELM-11 and HKUST-1:
- 1.
CO2 uptake: \(N_{{\mathrm{CO}}_2}^{{\mathrm{ads}}}\),
- 2.
CO2 selectivity: \(S^{{\mathrm{ads}}} = (N_{{\mathrm{CO}}_2}^{{\mathrm{ads}}}/N_{{\mathrm{CH}}_4}^{{\mathrm{ads}}})/(y_{{\mathrm{CO}}_2}/y_{{\mathrm{CH}}_4})\),
- 3.
CO2 working capacity: \({\mathrm{{\Delta}}}N_{{\mathrm{CO}}_2} = N_{{\mathrm{CO}}_2}^{{\mathrm{ads}}} - N_{{\mathrm{CO}}_2}^{{\mathrm{des}}}\), and
- 4.
regenerability:\(R_{\mathrm{e}} = {\mathrm{{\Delta}}}N_{{\mathrm{CO}}_2}/N_{{\mathrm{CO}}_2}^{{\mathrm{ads}}}\),
where Ni is the amount of component i adsorbed, yi is the mole fraction of component i in the gas phase, and superscripts ‘ads’ and ‘des’ denote adsorption and desorption operating conditions, respectively.
CO2 and CH4 adsorption measurements
Pre-ELM-11 was purchased from Tokyo Chemical Industry Co. and was transformed into ELM-11 by heating at 373 K for 10 h under a vacuum (< 0.1 mPa). The adsorption isotherms of CO2 over the temperature range of 195–298 K and CH4 at 298 K on ELM-11 were obtained using a BELSORP-max (MicrotracBEL Co.) and a cryostat equipped with a two-stage Gifford–McMahon (GM) refrigerator41. The sample cell temperature fluctuation was maintained within ±0.01 K during the adsorption measurements.
In situ XRPD measurements
The in situ XRPD patterns of ELM-11 in vacuo and after adsorption of CO2 gas (50 kPa), CH4 gas (50 kPa), and an equimolar CO2/CH4 mixture gas (94 kPa) at 273 K were obtained using a SmartLab instrument with Cu Kα radiation (Rigaku Co.), which has a cryostat equipped with a single-stage GM refrigerator connected to BELSORP-18 volumetric adsorption equipment (MicrotracBEL Co.). ELM-11 was transformed from pre-ELM-11 under the same conditions mentioned above, and the sample cell temperature was kept within ±0.01 K during the XRPD measurements.
Time-resolved in situ synchrotron XRPD measurements
The pre-ELM-11 sample was placed at the end of a 0.3-mm-diameter borosilicate glass capillary, which was attached to a stainless-steel tube with an epoxy adhesive. The sample was then evacuated for 10 h at 373 K to transform it into ELM-11. Time-resolved in situ synchrotron XRPD patterns of ELM-11 during gate adsorption of CO2 at 273 K were measured on the BL02B2 beamline of the SPring-8 synchrotron facility, Japan, using a large Debye-Scherrer-type diffractometer with a multi-modular system constructed with six MYTHEN detectors42,43. The temperature of the glass capillary was controlled by a nitrogen gas blower at 273 K, and the wavelength of the incident X-rays was 0.099899 nm. The in situ synchrotron XRPD patterns were continuously obtained by exposing the sample for 1 s at regular intervals of 50 ms. After 4.15 s from starting the XRPD measurements, CO2 gas at 103 kPa filled in a gas manifold of a remote gas handling system was automatically introduced into the glass capillary in which the ELM-11 sample was maintained in a vacuum. The CO2 gas pressure was decreased to 41 kPa within 1 s at the latest and the pressure was rigorously kept constant during the XRPD measurements. In the case of desorption measurement, the CO2 gas was rapidly depressed from 100 to 3.8 kPa through a needle valve; the XRPD measurements were performed under the same conditions for the adsorption measurement. Peak intensities of the 020 reflection at 10.2° for the closed phase of ELM-11 and the 002 reflection at 6.1° for the open phase of ELM-11 were obtained by nonlinear least-squares fitting of the pseudo-Voigt function. The fractions of each phase transformed as a function of time were determined by normalizing the peak intensities by those after completion of the transition for the open phase and before gas introduction for the closed phase. For the adsorption process, the following KJMA equation21,22 was fitted to the relation between the fraction transformed of the open phase and time:
where α is the fraction transformed at time t, k is the rate constant, and n is the number of dimensions in which the transition occurs. For the closed phase, the equation is arranged as
The fitting of the KJMA equation was performed for the data after the introduction of CO2 gas.
Time-resolved in situ synchrotron XRPD measurements for the adsorption process on ELM-11 were also performed at 264 K for the CO2 pressure of 41.0 kPa, at 256 K for 40.8 kPa, at 241 K for 40.8 kPa, and at 227 K for the five constant CO2 pressures of 7.74, 13.0, 16.9, 31.0, and 40.8 kPa. The pressure of CO2, P, introduced into the glass capillary was controlled by preliminarily adjusting the pressure of CO2 dosed in the gas manifold of the remote gas handling system. The correlation between k, and the pressure difference between P and the gate-opening pressure Pgate was investigated for all the open phase data. This is formulated as follows:
where k0 is a constant and the gate-opening pressure at the corresponding temperature T is evaluated by the relation obtained from the experimental adsorption isotherms over a wide temperature range of 195–298 K (Supplementary Fig. 7):
GCMC simulations
Adsorption isotherms of CO2 and CH4 on ELM-11 with the open framework structure were obtained using our own GCMC code. The Rietveld refined structure of ELM-11 at 298 K, as determined in our previous work23, was used as the open framework structure. The framework atoms were fixed, and four trial moves (displacement, rotation, creation, and deletion) for CO2 and three trial moves (displacement, creation, and deletion) for CH4 were performed with the equal probabilities. The system was equilibrated at 1 × 107 Monte Carlo steps, after which data were collected for another 1 × 107 steps. The length of the Markov chain of 1 × 107 steps corresponds to >6 × 104 trials per guest molecule. The simulation box was constructed with 3 × 3 × 2 unit cells and periodic boundary conditions were applied in the a, b, and c directions.
The guest–guest and guest–host interaction potential, Uguest, was assumed to be the sum of the Coulombic and Lennard-Jones (LJ) potentials:
where qi is the atomic charge, ε0 (8.8542 × 10–12 C2 N–1 m–2) is the permittivity in vacuum, rij is the interatomic distance, and σij and εij are the LJ parameters. The Ewald summation method was used to correct the long-range Coulombic interactions with a charge screening constant of 2.0 nm–1 and reciprocal space sum for k vectors of La/2π|k|, Lb/2π|k|, and Lc/2π|k|< 10 (where La, Lb, and Lc are the dimensions of the simulation box). The Lorentz-Berthelot mixing rules were applied to calculate the short-range interactions and were truncated at a cutoff distance of 1.6289 and 1.5557 nm for CO2 and CH4, respectively. The partial atomic charges of the host framework were obtained using periodic density functional theory (DFT) calculations at the GGA-PBE/DNP level and Mulliken population analysis using the DMol3 package44,45. The universal force field (UFF)46 was applied to calculate the LJ interaction term of the framework atoms by modifying the energy parameters as 0.74εUFF26. The atomic coordinates, charges, and LJ parameters of the host framework are listed in Supplementary Tables 2 and 3. The interaction parameters for CO247 and CH448 are listed in Supplementary Tables 4 and 5.
The adsorption isotherms for an equimolar CO2/CH4 gas mixture on ELM-11 were obtained by using the RASPA49 software. We used the same settings and force fields for ELM-11, CO2, and CH4, as mentioned above.
Specific heat of ELM-11 and HKUST-1
To evaluate the specific heat of ELM-11, we conducted phonon calculations for the closed and open states of ELM-11 according to the density functional perturbation theory using the VASP50,51 and PHONOPY52 codes. For the calculations using VASP, we implemented projector-augmented wave method pseudopotentials53 with the GGA-PBE exchange-correlation functional and 400 eV plane wave cutoffs. We used a 1 × 1 × 1 unit cell (two primitive cells) for both the states because of the large cell size (204 and 228 atoms for the closed and open structures, respectively). The Brillouin zone of the closed state was sampled using a 3 × 3 × 2 Gamma-centred Monkhorst-Pack k-point mesh, and that of the open state was sampled using a 2 × 3 × 2 k-point mesh.
When the lattice vibrations are described by the harmonic approximation, the specific heat at constant volume, Cv, can be represented as
where q is the wave vector, ν is the index for the phonon branch, kB is the Boltzmann factor, ħ is the reduced Planck constant, ω is the vibrational frequency, and T is the temperature. Here, the specific heat at constant pressure, Cp, was assumed to be equal to Cv because we assumed adsorption and desorption processes under moderate temperatures. The summation for q and ν implies the addition for all the vibrational frequencies in the phonon density of states. The obtained phonon density of states and specific heat of ELM-11 as a function of temperature are shown in Supplementary Figs 8 and 9, respectively. The regular specific heat of ELM-11 in the open state at 298 K, obtained using this calculation, was 0.94 J g−1 K−1.
We fitted a polynomial function to the experimental specific heats of HKUST-1 reported by Kloutse et al.29 (below 320 K) and Mu et al.30 (over 333 K), and the function was integrated with respect to temperature to evaluate the heat required to change the temperature of the host framework (green plane in Fig. 5a). The parameters of the polynomial function are listed in Supplementary Table 6, and the specific heat of HKUST-1 as a function of temperature is shown in Supplementary Fig. 9. The regular specific heat of HKUST-1 at 298 K was 0.78 J g−1 K−1.
Transition enthalpy and thermal management capability
The transition enthalpy during gate adsorption, required in order to assess the intrinsic thermal management capability, is expressed as:13
where ΔHhost and ΔHguest(Pgate) are the enthalpy changes of the host and guest during gate adsorption, and \(N_{{\mathrm{op}}}^{{\mathrm{guest}}}\left( {P^{{\mathrm{gate}}}} \right)\) and \(q_{{\mathrm{op}}}^{{\mathrm{int}}}\left( {P^{{\mathrm{gate}}}} \right)\) are the amount of gas adsorbed on the open framework and the molar integral heat at the gate pressure Pgate, respectively. Here, the enthalpies are given as values per weight of adsorbent. \(q_{{\mathrm{op}}}^{{\mathrm{int}}}\) is positive when heat is released from the system. When the pressure is increased to P after the gate-opening at Pgate and additional guest adsorption occurs without host deformation, the heat of adsorption, qadd, is released from the system:
Hence, the net heat, qnet, released by the adsorption through the gate-opening at P (>Pgate) is written as
\(q_{{\mathrm{op}}}^{{\mathrm{int}}}\left( P \right)\) can be evaluated using the following equation:
where \(H_{{\mathrm{op}}}^{{\mathrm{guest}}}\left( P \right) - H^{{\mathrm{gas}}}\left( P \right)\) is the enthalpy change when \(N_{{\mathrm{op}}}^{{\mathrm{guest}}}\left( P \right)\) of the gas molecules are encapsulated in the open framework, \(u_{{\mathrm{op}}}^{{\mathrm{guest}}}\left( P \right)\) is the molar interaction potential energy of the guest molecules, R is the gas constant, and T is the temperature. We performed GCMC simulations for the open framework to obtain the values of \(N_{{\mathrm{op}}}^{{\mathrm{guest}}}\left( P \right)\) and \(u_{{\mathrm{op}}}^{{\mathrm{guest}}}\left( P \right)\). We then assumed ΔHhost = ΔUhost + PΔV ≈ ΔUhost, where ΔV is the volume change of the host and ΔUhost is the internal energy change of the host because the PΔV term is negligible compared to ΔUhost in most cases. We define the intrinsic thermal management capability, e, as
which represents the ratio of the endothermic heat caused by host deformation to the total exothermic heat resulting from guest desorption.
Adsorption amounts and heat of adsorption on HKUST-1
The amounts of CO2 and CH4 adsorbed on HKUST-1 were evaluated using the Virial–Langmuir equation reported by Chowdhury et al.24:
where f is the fugacity, n is the amount adsorbed, and ηi, βi, bi, and ci (i = 0, 1) are parameters that are listed in Supplementary Table 7. We assumed that the fugacity can be replaced by the pressure of a real gas because we treat the adsorption and desorption processes only under moderate pressures and temperatures. The isosteric heat of adsorption, qst, can be obtained by substituting Eq. (14) into the Clausius–Clapeyron equation:
The total heat of adsorption Q, as depicted in Fig. 5a, was obtained using
Adsorption isobars and heat of adsorption on ELM-11
It has been reported that the logarithms of the gate opening and closing pressures of flexible MOFs should be proportional to the reciprocal temperature54, and we confirmed that the gate opening and closing pressures of CO2 on ELM-11 also followed the relationship shown in Supplementary Fig. 7. Therefore, by using the lnPgate vs reciprocal temperature plot, we evaluated the theoretical adsorption isobars and heats of adsorption on ELM-11 for an equimolar CO2/CH4 gas mixture at 500 kPa, pure CO2 at 250 kPa, pure CO2 at 15 kPa, and pure CH4 at 15 kPa, which correspond to the operating pressures used for the adsorption, rinsing, desorption, and purging processes, respectively. First, we determined the gate-opening/-closing temperatures of ELM-11 for pure CO2 as 335 K/341 K at 250 kPa and 256 K/262 K at 15 kPa, respectively, from Supplementary Fig. 7. Then, we assumed that the gate-opening/-closing temperatures for the equimolar CO2/CH4 gas mixture at 500 kPa were the same as those for pure CO2 at 250 kPa, which was based on the fact that the molar fraction of slipping-off CO2 could be predicted using the gate-opening pressure for pure CO2, as shown in Fig. 6c. Finally, we calculated the adsorption amounts of CO2 and CH4 on the open framework structure of ELM-11 and the corresponding heats of adsorption at temperatures below the gate-opening temperature using the GCMC simulations. The adsorption loadings of CO2 and CH4 and the corresponding heats of adsorption at temperatures above the gate-opening temperature were set to be zero because the closed framework structure showed no adsorption of CO2 and CH4.
Breakthrough curve measurement
Breakthrough curves were measured using lab-made equipment consisting of three mass-flow controllers (HORIBA STEC Co.), a static gas mixer, a ∅ 9 mm glass tube as the primary column, a ∅ 6 mm glass tube as the secondary column, a bypass flow path, a back-pressure regulator, and a quadrupole mass spectrometer (CANON ANELVA Co.). The flowsheet of the apparatus is illustrated in Supplementary Fig. 10. The pre-ELM-11 sample used in this experiment was synthesized using the protocol reported by Kondo et al.16 after modification: a methanol solution of 4,4′-bipyridine (1.60 m, 365 mL) was added to a water (200 mL)-methanol (92 mL) mixed solution of Cu(II) tetrafluoroborate (1.00 m) for 2 h with vigorous stirring at room temperature. After additional stirring (1 h), the reaction mixture was filtrated, and the filter cake was washed with water three times. The blue powder was dried at room temperature under a vacuum below 5 mPa for 12 h. HKUST-1 (BasoliteC 300) was purchased from Sigma-Aldrich. Pre-ELM-11 and HKUST-1 were placed in the adsorption columns and activated by heating at 393 K for 12 h under a vacuum (< 0.1 mPa). The adsorption columns were then purged with 200 kPa of pure Ar and kept at 273 K using a thermostatic bath. Next, an equimolar CO2/CH4 gas mixture was flowed through the bypass flow path. Its flow rate was controlled to be 20 sccm (standard cm3 min−1) by the mass-flow controllers, and the system pressure was maintained at 200 kPa by the back-pressure regulator. Then, the feed stream was switched from the bypass channel to the adsorption columns side, and the gas composition downstream of the back-pressure regulator was measured using the mass spectrometer, which was calibrated using certified CO2/CH4/Ar gas mixtures before measuring the breakthrough curves.
Material balance calculations for column systems
We evaluated the column length and molar flow rate of the feed gas required to obtain the same molar flow rate of CH4 for conventional and sequential-column systems, including case I and case II, via material balance calculations. The details of the material balance calculations are provided in the Supplementary Method.
Data availability
The data that support the findings of this study are provided in Supplementary Information and the online repository at https://github.com/2koza/slipping-off. They can also be available from the corresponding author upon request.
Code availability
The codes used in this study are available from the corresponding author upon reasonable request.
References
Sholl, D. S. & Lively, R. P. Seven chemical separations to change the world. Nature 532, 435–437 (2016).
Lopes, F. V. S., Grande, C. A. & Rodrigues, A. E. Fast-cycling VPSA for hydrogen purification. Fuel 93, 510–523 (2012).
Sircar, S. & Hanley, B. F. Production of oxygen enriched air by rapid pressure swing adsorption. Adsorption 1, 313–320 (1995).
Chai, S. W., Kothare, M. V. & Sircar, S. Rapid pressure swing adsorption for reduction of bed size factor of a medical oxygen concentrator. Ind. Eng. Chem. Res. 50, 8703–8710 (2011).
Horstmeier, J. F., Gomez Lopez, A. & Agar, D. W. Performance improvement of vacuum swing adsorption processes for CO2 removal with integrated phase change material. Int. J. Greenh. Gas. Con. 47, 364–375 (2016).
Schneemann, A. et al. Flexible metal–organic frameworks. Chem. Soc. Rev. 43, 6062–6096 (2014).
Horike, S., Shimomura, S. & Kitagawa, S. Soft porous crystals. Nat. Chem. 1, 695–704 (2009).
Fairen-Jimenez, D. et al. Opening the gate: framework flexibility in ZIF-8 explored by experiments and simulations. J. Am. Chem. Soc. 133, 8900–8902 (2011).
Coudert, F.-X., Boutin, A., Fuchs, A. H. & Neimark, A. V. Adsorption deformation and structural transitions in metal–organic frameworks: from the unit cell to the crystal. J. Phys. Chem. Lett. 4, 3198–3205 (2013).
Krause, S. et al. A pressure-amplifying framework material with negative gas adsorption transitions. Nature 532, 348–352 (2016).
Verploegh, R. J., Nair, S. & Sholl, D. S. Temperature and loading-dependent diffusion of light hydrocarbons in ZIF-8 as predicted through fully flexible molecular simulations. J. Am. Chem. Soc. 137, 15760–15771 (2015).
Mason, J. A. et al. Methane storage in flexible metal–organic frameworks with intrinsic thermal management. Nature 527, 357–361 (2015).
Hiraide, S., Tanaka, H., Ishikawa, N. & Miyahara, M. T. Intrinsic thermal management capabilities of flexible metal–organic frameworks for carbon dioxide separation and capture. ACS Appl. Mater. Interfaces 9, 41066–41077 (2017).
Horike, S., Inubushi, Y., Hori, T., Fukushima, T. & Kitagawa, S. A solid solution approach to 2D coordination polymers for CH4/CO2 and CH4/C2H6 gas separation: equilibrium and kinetic studies. Chem. Sci. 3, 116–120 (2012).
Li, D. & Kaneko, K. Hydrogen bond-regulated microporous nature of copper complex-assembled microcrystals. Chem. Phys. Lett. 335, 50–56 (2001).
Kondo, A. et al. Novel expansion/shrinkage modulation of 2D layered MOF triggered by clathrate formation with CO2 molecules. Nano Lett. 6, 2581–2584 (2006).
Bae, Y. S. & Snurr, R. Q. Development and evaluation of porous materials for carbon dioxide separation and capture. Angew. Chem. Int. Ed. 50, 11586–11596 (2011).
Kenarsari, S. D. et al. Review of recent advances in carbon dioxide separation and capture. RSC Adv. 3, 22739 (2013).
Choi, S., Drese, J. H. & Jones, C. W. Adsorbent materials for carbon dioxide capture from large anthropogenic point sources. ChemSusChem 2, 796–854 (2009).
Chui, S. S. A chemically functionalizable nanoporous material [Cu3(TMA)2(H2O)3]n. Science 283, 1148–1150 (1999).
De Bruijn, T. J. W., De Jong, W. A. & Van Den Berg, P. J. Kinetic parameters in Avrami—Erofeev type reactions from isothermal and non-isothermal experiments. Thermochim. Acta 45, 315–325 (1981).
Krüger, P. On the relation between non-isothermal and isothermal Kolmogorov-Johnson-Mehl-Avrami crystallization kinetics. J. Phys. Chem. Solids 54, 1549–1555 (1993).
Hiraide, S., Tanaka, H. & Miyahara, M. T. Understanding gate adsorption behaviour of CO2 on elastic layer-structured metal–organic framework-11. Dalton Trans. 45, 4193–4202 (2016).
Chowdhury, P., Mekala, S., Dreisbach, F. & Gumma, S. Adsorption of CO, CO2 and CH4 on Cu-BTC and MIL-101 metal organic frameworks: Effect of open metal sites and adsorbate polarity. Micropor. Mesopor. Mater. 152, 246–252 (2012).
Myers, A. L. & Prausnitz, J. M. Thermodynamics of mixed-gas adsorption. AlChE J. 11, 121–127 (1965).
Tanaka, H., Hiraide, S., Kondo, A. & Miyahara, M. T. Modeling and visualization of CO2 adsorption on elastic layer-structured metal–organic framework-11: Toward a better understanding of gate adsorption behavior. J. Phys. Chem. C. 119, 11533–11543 (2015).
D’Alessandro, D. M., Smit, B. & Long, J. R. Carbon dioxide capture: prospects for new materials. Angew. Chem. Int. Ed. 49, 6058–6082 (2010).
Pirngruber, G. D. et al. A method for screening the potential of MOFs as CO2 adsorbents in pressure swing adsorption processes. ChemSusChem 5, 762–776 (2012).
Kloutse, F. A., Zacharia, R., Cossement, D. & Chahine, R. Specific heat capacities of MOF-5, Cu-BTC, Fe-BTC, MOF-177 and MIL-53 (Al) over wide temperature ranges: Measurements and application of empirical group contribution method. Micropor. Mesopor. Mater. 217, 1–5 (2015).
Mu, B. & Walton, K. S. Thermal analysis and heat capacity study of metal-organic frameworks. J. Phys. Chem. C. 115, 22748–22754 (2011).
Farooq, S., Hassan, M. M. & Ruthven, D. M. Heat effects in pressure swing adsorption systems. Chem. Eng. Sci. 43, 1017–1031 (1988).
Tomomura, M., Nogita, S. & Someya, K. Carbon dioxide removal from compressed air by pressure swing adsorption. Kagaku Kogaku Ronbunshu 13, 139–144 (1987).
Wilson, S. J. & Webley, P. A. Cyclic steady-state axial temperature profiles in multilayer, bulk gas PSA—the case of oxygen VSA. Ind. Eng. Chem. Res. 41, 2753–2765 (2002).
Sotomayor, F. J. & Lastoskie, C. M. Predicting the breakthrough performance of gating adsorbents using osmotic framework-adsorbed solution theory. Langmuir 33, 11670–11678 (2017).
Yang, S.-I., Choi, D.-Y., Jang, S.-C., Kim, S.-H. & Choi, D.-K. Hydrogen separation by multi-bed pressure swing adsorption of synthesis gas. Adsorption 14, 583–590 (2008).
Maring, B. J. & Webley, P. A. A new simplified pressure/vacuum swing adsorption model for rapid adsorbent screening for CO2 capture applications. Int. J. Greenh. Gas. Con 15, 16–31 (2013).
Yamazaki, T., Takahashi, Y. & Yoshida, D. Adsorption of several gases on flexible metal organic framework [Cu(dhbc)2(4,4′-bpy)]·H2O. J. Colloid Interface Sci. 362, 463–469 (2013).
Thommes, M. et al. Physisorption of gases, with special reference to the evaluation of surface area and pore size distribution (IUPAC technical report). Pure Appl. Chem. 87, 1051 (2015).
Hefti, M., Joss, L., Bjelobrk, Z. & Mazzotti, M. On the potential of phase-change adsorbents for CO2 capture by temperature swing adsorption. Faraday Discuss. 192, 153–179 (2016).
Saima, W. H., Mogi, Y. & Haraoka, T. Development of PSA system for the recovery of carbon dioxide and carbon monoxide from blast furnace gas in steel works. Energy Procedia 37, 7152–7159 (2013).
Tanaka, H. et al. Adsorption-induced structural transition of ZIF-8: a combined experimental and simulation study. J. Phys. Chem. C. 118, 8445–8454 (2014).
Kawaguchi, S. et al. High-throughput powder diffraction measurement system consisting of multiple MYTHEN detectors at beamline BL02B2 of SPring-8. Rev. Sci. Instrum. 88, 085111 (2017).
Kawaguchi, S. et al. Fast continuous measurement of synchrotron powder diffraction synchronized with controlling gas and vapour pressures at beamline BL02B2 of SPring-8. J. Synchrotron Rad. 27, 616–624 (2020).
Delley, B. An all-electron numerical method for solving the local density functional for polyatomic molecules. J. Chem. Phys. 92, 508–517 (1990).
Delley, B. From molecules to solids with the DMol3 approach. J. Chem. Phys. 113, 7756–7764 (2000).
Rappé, A. K., Casewit, C. J., Colwell, K. S., Goddard, W. A. III & Skiff, W. M. UFF, a full periodic table force field for momechanics and molecular dynamics simulations. J. Am. Chem. Soc. 114, 10024–10035 (1992).
Chen, Y. F., Lee, J. Y., Babarao, R., Li, J. & Jiang, J. W. A highly hydrophobic metal−organic framework Zn(BDC)(TED)0.5 for adsorption and separation of CH3OH/H2O and CO2/CH4: an integrated experimental and simulation study. J. Phys. Chem. C. 114, 6602–6609 (2010).
Cracknell, R. F. & Nicholson, D. Adsorption and selectivity of carbon dioxide with methane and nitrogen in slit-shaped carbonaceous micropores: simulation and experiment. Adsorption 2, 193–203 (1996).
Dubbeldam, D., Calero, S., Ellis, D. E. & Snurr, R. Q. RASPA: molecular simulation software for adsorption and diffusion in flexible nanoporous materials. Mol. Simul. 42, 81–101 (2016).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Togo, A. & Tanaka, I. First principles phonon calculations in materials science. Scr. Mater. 108, 1–5 (2015).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Numaguchi, R., Tanaka, H., Watanabe, S. & Miyahara, M. T. Simulation study for adsorption-induced structural transition in stacked-layer porous coordination polymers: equilibrium and hysteretic adsorption behaviors. J. Chem. Phys. 138, 054708 (2013).
Acknowledgements
This work was financially supported by a Grant-in-Aid for JSPS fellows no. 15J05846, a Grant-in-Aid for Research Activity Start-up no. 19K23574, a Grant-in-Aid for Scientific Research (B) no. 17H03097 and no. 20H04466, a Challenging Research (Exploratory) no. 18K18975, the ENEOS Hydrogen Trust Fund, JST CREST grant no. JPMJCR1324, Japan and “Five-star Alliance” in “NJRC Mater. & Dev.”. For this work, we used the supercomputer at ACCMS, Kyoto University. We thank Dr. Atsushi Kondo and professor Hirofumi Kanoh for fruitful discussions. The synchrotron radiation experiments were performed at the BL02B2 beamline of SPring-8 with the approval of the Japan Synchrotron Radiation Research Institute (JASRI) (proposal no. 2017B1210, 2018A1082, 2018B1539, 2019B1290).
Author information
Authors and Affiliations
Contributions
S.H., H.T., H.K., and M.T.M. designed this study and wrote the paper. S.H. performed the in situ XRPD experiments, the adsorption measurements, and the calculations. H.T., S.K., and Y.S. performed time-resolved in situ synchrotron XRPD measurements. H.K. synthesized ELM-11 to measure the breakthrough curves, and S.H. and Y.S. performed these measurements. All authors discussed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks François-Xavier Coudert, Carlos Grande, and Krishna Chandran Jayachandrababu for their contributions to the peer review of this work. Peer review reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hiraide, S., Sakanaka, Y., Kajiro, H. et al. High-throughput gas separation by flexible metal–organic frameworks with fast gating and thermal management capabilities. Nat Commun 11, 3867 (2020). https://doi.org/10.1038/s41467-020-17625-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-17625-3
This article is cited by
-
Selective sorting of hexane isomers by anion-functionalized metal-organic frameworks with optimal energy regulation
Nature Communications (2024)
-
Logic and symbolism of switchable porous framework materials
Communications Materials (2024)
-
CO2 photocatalytic reduction with robust and stable metal–organic framework: a review
Materials for Renewable and Sustainable Energy (2024)
-
Investigating the mechanical stability of flexible metal–organic frameworks
Communications Chemistry (2023)
-
Bayesian framework for analyzing adsorption processes observed via time-resolved X-ray diffraction
Scientific Reports (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.