Abstract
The complexity of an ecological community can be distilled into a network, where diverse interactions connect species in a web of dependencies. Species interact directly with each other and indirectly through environmental effects, however to our knowledge the role of these ecosystem engineers has not been considered in ecological network models. Here we explore the dynamics of ecosystem assembly, where species colonization and extinction depends on the constraints imposed by trophic, service, and engineering dependencies. We show that our assembly model reproduces many key features of ecological systems, such as the role of generalists during assembly, realistic maximum trophic levels, and increased nestedness with mutualistic interactions. We find that ecosystem engineering has large and nonlinear effects on extinction rates. While small numbers of engineers reduce stability by increasing primary extinctions, larger numbers of engineers increase stability by reducing primary extinctions and extinction cascade magnitude. Our results suggest that ecological engineers may enhance community diversity while increasing persistence by facilitating colonization and limiting competitive exclusion.
Similar content being viewed by others
Introduction
To unravel nature’s secrets we must simplify its abundant complexities and idiosyncrasies. The layers of natural history giving rise to an ecological community can be distilled—among many forms—into a network, where nodes represent species and links represent interactions between them. Networks are generally constructed for one type of interaction, such as food webs capturing predation1,2,3 or pollination networks capturing a specific mutualistic interaction4, and continue to lead to significant breakthroughs in our understanding of the dynamical consequences of community structure5,6,7. This perspective has also been used to shed light on the generative processes driving the assembly of complex ecological communities8,9.
To what extent assembly leaves its fingerprint on the structure and function of ecological communities is a source of considerable debate10,11,12. There is strong evidence that functional traits constrain assembly12,13,14, while differences in species’ trophic niche15,16, coupled with early establishment of fast/slow energy channels17, appear to significantly impact long-term community dynamics. There has been growing interest in understanding the combined role of trophic and mutualistic interactions in driving assembly18,19, where the establishment of species from a source pool19,20,21 and the plasticity of species interactions22,23,24,25 constrain colonization and extinction dynamics. While recent interest in “multilayer networks” comprising multiple interaction types (multitype interactions) may provide additional insight into these processes26,27, there is not yet a well-defined theory for the assembly of communities that incorporates multitype interactions, as well as both biotic and abiotic components from which functioning ecosystems are composed (cf. ref. 28).
Diverse interactions occur not only between species but indirectly through the effects that species have on the abiotic environment29,30,31. Elephants root out large saplings and small trees, enabling the formation and maintenance of grasslands32,33 and creating habitat for smaller vertebrates34. Burrowing rodents such as gophers and African mole rats create shelter and promote primary production by aerating the soil35,36, salmon, and aquatic invertebrates create freshwater habitats by changing stream morphology37, and leaf-cutter ants alter microclimates, influencing seedling survival and plant growth38. These examples illustrate ecosystem engineering, where the engineering organism alters the environment on timescales longer than its own39. Engineers are widely acknowledged to have impacts on both small and large spatial scales40, and likely serve as important keystone species in many habitats41.
Ecosystem engineering not only impacts communities on ecological timescales, but has profoundly shaped the evolution of life on Earth42. For example, the emergence of multicellular cyanobacteria fundamentally altered the atmosphere during the Great Oxidation Event of the Proterozoic roughly 2.5 Byrs BP42,43, paving the way for the biological invasion of terrestrial habitats. In the oceans it is thought that ribosomal RNA (rRNA) and protein biogenesis of aquatic photoautotrophs drove the nitrogen:phosphorous ratio (the Redfield Ratio) to ca. 16:1 matching that of plankton44, illustrating that engineering clades can have much larger, sometimes global-scale effects.
The effect of abiotic environmental conditions on species is commonly included in models of ecological dynamics45,46,47 due to its acknowledged importance and because it can—to first approximation—be easily systematized. By comparison the way in which species engineer the environment defies easy systemization due to the multitude of mechanisms by which engineering occurs. While interactions between species and the abiotic environment have been conceptually described30,48, the absence of engineered effects in network models was detailed by Odling-Smee et al.31, where they outlined a conceptual framework that included both species and abiotic compartments as nodes of a network, with links denoting both biotic and abiotic interactions.
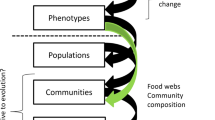
How does the assembly of species constrained by multitype interactions impact community structure and stability? How are these processes altered when the presence of engineers modifies species’ dependencies within the community? Here, we model the assembly of an ecological network where nodes represent ecological entities, including engineering species, non-engineering species, and the effects of the former on the environment, which we call abiotic “modifiers.” The links of the network that connect both species and modifiers represent trophic (“eat” interactions), service (“need” interactions), and engineering dependencies, respectively (Fig. 1; see “Methods” for a full description). Trophic interactions represent both predation and parasitism, whereas service interactions account for non-trophic interactions associated with reproductive facilitation such as pollination or seed dispersal. In our framework, a traditional mutualism (such as a plant-pollinator interaction) consists of a service (need) interaction in one direction and a trophic (eat) interaction in the other. These multitype interactions between species and modifiers thus embed multiple dependent ecological sub-systems into a single network (Fig. 1). Modifiers in our framework overlap conceptually with the “abiotic compartments” described in Odling-Smee et al.31. Following Pillai et al.49, we do not track the abundances of biotic or abiotic entities but track only their presence or absence. We use this framework to explore the dynamics of ecosystem assembly, where the colonization and extinction of species within a community depends on the constraints imposed by the trophic, service, and engineering dependencies. We then show how observed network structures emerge from the process of assembly, compare their attributes with those of empirical systems, and examine the effects of ecosystem engineers.
a Multitype interactions between species (colored nodes) and abiotic modifiers (black nodes). Trophic and mutualistic relationships define both species–species (S–S) and species–modifier (S–M) interactions; an engineering interaction is denoted by an engineer that makes a modifier, such that the modifier needs the engineer to persist. b An assembling food web with species (color denotes trophic level) and modifiers. The basal resource is the white node at the bottom of the network. c The corresponding adjacency matrix with colors denoting interactions between species and modifiers. d A species (*) can colonize a community when a single trophic and all service requirements are met. e Greater vulnerability increases the risk of primary extinction via competitive exclusion (competition denoted by dashed line) to species (†). The extinction of species (†) will cascade to affect those connected by trophic (††) and service (†††) dependencies.
Our results offer four key insights into the roles of multitype interactions and ecosystem engineering in driving community assembly. First, we show that the assembly of communities in the absence of engineering reproduces many features observed in empirical systems. These include changes in the proportion of generalists over the course of assembly that accord with measured data and trophic diversity similar to empirical observations. Second, we show that increasing the frequency of mutualistic interactions leads to the assembly of ecological networks that are more nested, a common feature of diverse mutualistic systems50, but that are also prone to extinction cascades. Our third key result shows that increasing the proportion of ecosystem engineers within a community has nonlinear effects on observed extinction rates. While we find that a low amount of engineering increases extinction rates, a high amount of engineering has the opposite effect. Finally we show that redundancies in engineered effects promote community diversity by lowering the barriers to colonization.
Results and discussion
Assembly without ecosystem engineering
Our framework assumes that communities assemble by random colonization from a source pool. A species from the source pool can colonize if it finds at least one resource that it can consume (one eat interaction is satisfied; cf. ref. 51) and all of its non-trophic needs are met (all need interactions are satisfied; see Fig. 1). As such, service interactions are assumed to be obligate, whereas trophic interactions are flexible—except in the case of a consumer with just a single resource. While an abiotic basal resource is always assumed to be present (white node in Fig. 1b), following the establishment of an autotrophic base, the arrival of mixotrophs (i.e., mixing auto- and heterotrophy) and lower-trophic heterotrophs create opportunities for organisms occupying higher trophic levels to invade. This expanding niche space initially serves as an accelerator for community growth.
Following the initial colonization phase, extinctions begin to slow the rate of community growth. Primary extinctions occur if a given species is not the strongest competitor for at least one of its resources. A species’ competition strength is determined by its interactions: competition strength is enhanced by the number of need interactions (where the number of potential and realized interactions are equivalent) and penalized by the number of its realized resources (i.e., those resources present in the local community, favoring functional trophic specialists) and realized predators (i.e., those predators present in the local community). This encodes three key assumptions: that mutualisms provide a fitness benefit52, specialists are stronger competitors than generalists53,54,55,56, and having many predators entails an energetic cost57. Secondary extinctions occur when a species loses its last trophic or any of its service requirements. As the colonization and extinction rates converge, the community reaches a steady state around which it oscillates (Fig. 2a). See Fig. 1d, e for an illustration of the assembly process, and the “Methods” and Supplementary Note 1 for a complete description. Specific model parameterizations are described in Supplementary Note 2.
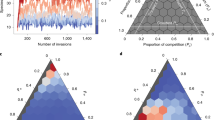
a Assembling communities over time from a pool of 200 non-engineering species. Steady state species richness is reached by t = 250. b The proportion of specialists as a function of assembly time (iterations). Diamonds denote expected values for functional (realized) trophic interactions at each point in time, and triangles denote expected values for potential trophic interactions (as if all trophic interactions with all species in the pool were realized), where the expectation is taken across replicates. Individual replicate results are shown for functional trophic interactions (small points). c The frequency distribution of trophic levels as a function of assembly time (iterations). Autotrophs occupy TL = 1. Measures were evaluated across 104 replicates; see “Methods” for parameter values.
Assembly of ecological communities in the absence of engineering results in interaction networks with structures consistent with empirical observations. As the community reaches steady state (Fig. 2a), we find that the connectance of trophic interactions (C(t) = L(t)/S(t)2, where S(t) is species richness and L(t) is the number of links at time t) decays to a constant value (Supplementary Fig. 1). Decaying connectance followed by stabilization around a constant value has been documented in the assembly of mangrove communities16 and experimental aquatic mesocosms17. The initial decay is likely inevitable in sparse webs as early in the assembly process the small set of tightly interacting species will have a high link density from which it will decline as the number of species increases. In Supplementary Note 3 we include a brief comparison of assembly model food webs with those produced by the Niche model58. While the aims of these approaches are quite distinct, we provide this comparison as a reference point to traditional food web models, and to emphasize that both approaches result in food webs with similar structures (Supplementary Figs. 2 and 3).
Recent empirical work has suggested that generalist species may dominate early in assembly, whereas specialists colonize after a diverse resource base has accumulated16,51. Here, the trophic generality of species i is defined as \({G}_{i}(t)={k}_{i}^{{\rm{in}}}(t)/({L}^{* }/{S}^{* })\)58, where \({k}_{i}^{{\rm{in}}}(t)\) is the number of resource species linked to consumer i at simulation time-step t, which is scaled by the steady state link density L*/S*, as is typically performed in empirical investigations16. Only trophic links between species are considered here, such that we ignore links to the abiotic basal resource in our evaluation of trophic generality. A species is classified as a generalist if Gi > 1 and a specialist if Gi < 1. If generality is evaluated with respect to the steady state link density, we find that species with many potential trophic interactions realize only a subset of them, thereby functioning as specialists early in the assembly process (Fig. 2b). As the community grows, more potential interactions become realized, and functional specialists become functional generalists. Moreover, as species assemble, the available niche space expands, and the proportion of potential trophic specialists grows (Fig. 2b). This latter observation confirms expectations from the trophic theory of island biogeography51, where communities with lower richness (i.e., early assembly) are less likely to support specialist consumers than species-rich communities (late assembly). At steady state the proportion of functional specialists is ca. 48%, which is similar to empirical observations of assembling mangrove island food webs16.
The dominance of functional specialists following the initial assembly of autotrophs is due to the colonization of lower-trophic consumers with few resources, where the observed trophic level (TL) distribution early in assembly (t = 5) has an average TL = 1.659. Four trophic levels are typically established by t = 50, where colonization is still dominant, and by the time communities reach steady state the interaction networks are characterized by an average \({\mathrm{TL}}_{\max }\) (±standard deviation) = 11 ± 2.8 (Fig. 2c). While the maximum trophic level is higher than that measured in most consumer-resource systems60, it is not unreasonable if parasitic interactions (which we do not differentiate from other consumers) are included61. Overall, the most common trophic level among species at steady state is ca. TL = 4.75.
The distribution of trophic levels changes shape over the course of assembly. Early in assembly, we observe a skewed pyramidal structure, where most species feed from the base of the food web. At steady state, we observe that intermediate trophic levels dominate, with frequencies taking on an hourglass structure (purple bars, Fig. 2c). Compellingly, the trophic richness pyramids that we observe at steady state follow closely the hourglass distribution observed for empirical food webs and are less top-heavy than those produced by static food web models62.
Structure and dynamics of mutualisms
Nested interactions, where specialist interactions are subsets of generalist interactions, are a distinguishing feature of mutualistic networks50,63,64,65. Nestedness has been shown to maximize the structural stability of mutualistic networks66, emerge naturally via adaptive foraging behaviors24,67 and neutral processes68, and promote the influence of indirect effects on coevolutionary dynamics69. While models and experiments of trophic networks suggest that compartmentalization confers greater stabilizing properties70,71, interaction asymmetry among species may promote nestedness in both trophic65 and mutualistic systems72. Processes that operate on different temporal and spatial scales may have a significant influence on these observations73. For example, over evolutionary time, coevolution and speciation may degrade nested structures in favor of modularity25, and there is some evidence from Pleistocene food webs that geographic insularity may reinforce this process74.
Does the assembly of ecological networks favor nestedness when mutualistic interactions are frequent? In the absence of mutualisms, the trade-offs in our model preclude high levels of nestedness because we assume that generalists are at a competitive disadvantage when they share the same resources with a specialist consumer. Yet, we find that as we increase the frequency of service interactions (holding constant trophic interaction frequency; see Supplementary Note 2), the assembled community at steady state becomes more nested (Fig. 3a). More service interactions increase a species’ competition strength, lowering its primary extinction risk. Participation in a mutualism thus delivers a fitness advantage to the species receiving the service, compensating for the lower competitive strength of generalists and allowing generalists to share subsets of resources with specialists, promoting nestedness. However, increases in mutualisms also increase inter-species dependencies, which raises the potential risk associated with losing mutualistic partners75,76. While this shifting landscape of extinction risks lowers the steady state species richness of highly mutualistic communities, we do not observe a direct relationship between nestedness and richness (Supplementary Fig. 4).
a Structural nestedness of communities, measured as UNODF (Unipartite Nestedness based on Overlap and Decreasing Fill; measured using the R package UNODF v.1.2)100. The value reported is the mean value taken across the rows and columns of the adjacency matrix accounting for both trophic and service interactions. b Mean rate of primary extinction (where primary extinctions occur from competitive exclusion of consumers over shared resources) and c secondary extinction (which cascade from primary extinctions) as a function of service interaction frequency. d Species persistence as a function of service interaction frequency. Primary and secondary extinction rates were evaluated at the community level, whereas persistence was determined for each species and averaged across the community. Measures were evaluated for 104 replicates; see “Methods” and Supplementary Note 2 for parameter values.
When we examine the dynamics of the community as a function of service interaction frequency, we observe that mutualistic interactions have different effects on primary versus secondary extinction rates. As service dependencies bolster the competitive strength of otherwise susceptible species such as trophic generalists and species with multiple predators, the rate of primary extinctions is lowered, though this effect is weak (Fig. 3b). However, because mutualisms build rigid dependencies between species, more service interactions result in higher frequencies of secondary extinctions (Fig. 3c). In communities with many mutualistic interactions, this combined influence yields extinctions that are less likely to occur, but that lead to larger cascades when they do.
An increased rate of secondary extinctions means that the network is less robust to perturbation, which may impact community turnover, or persistence. If we measure persistence in terms of the proportion of time species are established in the community, we find that higher frequencies of service interactions lower average persistence (increased species turnover; Fig. 3d). Analysis of species-specific interactions reveals that it is the species that require more services that have lower persistence (Supplementary Fig. 5). Some empirical systems appear to support model predictions. For example, long-term observations of ant-plant mutualistic systems have demonstrated high rates of turnover among service-receivers (plants) relative to service-donors (ants)77.
We emphasize that we have restricted ourselves to examining the effects of obligate mutualisms, although the importance of non-obligate mutualisms has long been recognized23,24,67,78,79. We expect that the increased rate of secondary extinctions attributable to the loss of obligate mutualistic partners to have greater impact on system stability than the potential loss of non-obligate mutualistic partners. As such, we do not expect inclusion of non-obligate mutualisms to alter the qualitative nature of our findings.
Assembly with ecosystem engineering
The concept of ecosystem engineering, or more generally niche construction, has both encouraged an extended evolutionary synthesis80 while also garnering considerable controversy81,82. Models that explore the effects of ecosystem engineering are relatively few, but have covered important ground31,39. For example, engineering has been shown to promote invasion83, alter primary productivity84, and change the selective environment over eco-evolutionary timescales85,86, which can lead to unexpected outcomes such as the fixation of deleterious alleles87. On smaller scales, microbiota construct shared metabolitic resources that have a significant influence on microbial communities88, the dynamics of which may even serve as the missing ingredient stabilizing some complex ecological systems89. Soil is one place where these macro- and microbiotic systems intersect90. Many microbes and detritivores transform and deliver organic matter into the macrobiotic food web, themselves hosting a complex network of trophic and service dependencies between species and abiotic entities91,92.
We next explore the effects of ecosystem engineering by allowing species to produce abiotic modifiers as additional nodes in the ecological network (Fig. 1). These modifier nodes produced by engineers can serve to fulfill resource or service requirements for other species. The parameter η defines the mean number of modifiers produced per species in the pool, drawn from a Poisson distribution (see “Methods” and Supplementary Note 1 for details). If a species makes ≥1 modifier, we label it an engineer. As the mean number of modifiers/species η increases, both the number of engineers in the pool, as well as the number of modifiers made per engineer increases. As detailed in Supplementary Note 1, multiple engineers can make the same modifier, such that engineering redundancies are introduced when η is large. When an engineer colonizes the community, so do its modifiers, which other species in the system may interact with. When engineers are lost, their modifiers will also be lost, though can linger in the community for a period of time inversely proportional to the density of disconnected modifiers in the community (see Supplementary Note 1).
While the inclusion of engineering does not significantly impact the structure of species–species interactions within assembling food webs (see Supplementary Note 4 and Supplementary Fig. 6), it does have significant consequences for community stability. Importantly, these effects also are sensitive to the frequency of service interactions within the community, and we find that their combined influence can be complex.
As the number of engineers increases, mean rates of primary extinction are first elevated and then decline (Fig. 4a). At the same time, the mean rates of secondary extinction systematically decline and persistence systematically increases (Fig. 4b, c). When engineered modifiers are rare (0 < η ≤ 0.5), higher rates of primary extinction coupled with lower rates of secondary extinction mean that extinctions are common, but of limited magnitude such that disturbances are compartmentalized. As modifiers become more common both primary and secondary extinction rates decline, which corresponds to increased persistence. We suggest two mechanisms that may produce the observed results. First, when engineers and modifiers are present but rare, they provide additional resources for consumers. This stabilization of consumers ultimately results in increased vulnerability of prey, such that the cumulative effect is increased competitive exclusion of prey and higher rates of primary extinction (Fig. 4a). Second, when engineers and their modifiers are common (η > 0.5) the available niche space expands, lowering competitive overlap and suppressing both primary and secondary extinctions. Notably the presence of even a small number of engineers serves to limit the magnitude of secondary extinction cascades (Fig. 4b). Assessment of species persistence as a function of trophic in-degree (number of resources) and out-degree (number of consumers) generally supports this proposed dynamic (Supplementary Fig. 7).
a Mean rates of primary extinction, where primary extinctions occur from competitive exclusion of consumers over shared resources. b Mean rates of secondary extinction, which cascade from primary extinctions. c Mean species persistence. d The ratio \({S}^{* }/{S}_{{\rm{u}}}^{* }\), where \({S}_{{\rm{u}}}^{* }\) denotes steady states for systems where all engineered modifiers are unique to each engineer, and S* denote steady states for systems with redundant engineering. Higher values of \({S}^{* }/{S}_{{\rm{u}}}^{* }\) mean that systems with redundant engineers have higher richness at the steady state than those without redundancies. Primary and secondary extinction rates were evaluated at the community level, whereas persistence was determined for each species and averaged across the community. Each measure reports the expectation taken across 50 replicates. See “Methods” and Supplementary Note 2 for parameter values.
Increasing the frequency of service interactions promotes service interactions between species and engineered modifiers (Fig. 1). A topical example of the latter is the habitat provided to invertebrates by the recently discovered rock-boring teredinid shipworm (Lithoredo abatanica)93. Here, freshwater invertebrates are serviced by the habitat modifications engineered by the shipworm, linking species indirectly via an abiotic effect (in our framework via a modifier node). As the frequency of service interactions increases, the negative effects associated with rare engineers is diminished (Fig. 4a). Increasing service interactions both elevates the competitive strength of species receiving services (from species and/or modifiers), while creating more inter-dependencies between and among species. As trophic interactions are replaced by service interactions, previously vulnerable species gain a competitive foothold and persist, lowering rates of primary extinctions (Fig. 4a). The cost of these added services to the community is an increased rate of secondary extinctions (Fig. 4b) and higher species turnover (Fig. 4c), such that extinctions are less common but lead to larger cascades.
While the importance of engineering timescales has been emphasized previously39, redundant engineering has been assumed to be unimportant94. We argue that redundancy may be an important component of highly engineered systems, and particularly relevant when the effects of engineers increase their own fitness83 as is generally assumed to be the case with niche construction86. If ecosystem engineering also includes, for example, biogeochemical processes such as nitrogen-fixing among plants and mycorrhizal fungi, redundancy may be perceived as the rule rather than the exception. Moreover, the vast majority of contemporary ecosystem engineering case studies focus on single taxa, such that redundant engineers appear rare94. If we consider longer timescales, diversification of engineering clades may promote redundancy, and in some cases this may feed back to accelerate diversification95. Such positive feedback mechanisms likely facilitated the global changes induced by cyanobacteria in the Proterozoic42,43 among other large-scale engineering events in the history of life42. Engineering redundancies are likely important on shorter timescales as well. For example, diverse sessile epifauna on shelled gravels in shallow marine environments are facilitated by the engineering of their ancestors, such that the engineered effects of the clade determine the future fitness of descendants96. In the microbiome, redundant engineering may be very common due to the influence of horizontal gene transfer in structuring metabolite production97. In these systems, redundancy in the production of shared metabolitic resources may play a key role in community structure and dynamics88,89.
When there are few engineers, each modifier in the community tends to be unique to a particular engineering species. Engineering redundancies increase linearly with η (Supplementary Note 1 and Supplementary Fig. 8), such that the loss of an engineer will not necessarily lead to the loss of engineered modifiers. We examine the effects of this redundancy by comparing our results to those produced by the same model, but where each modifier is uniquely produced by a single species. Surprisingly, the lack of engineering redundancies does not alter the general relationship between engineering and measures of community stability (Supplementary Fig. 9). However, we find that redundancies play a central role in maintaining species diversity. When engineering redundancies are allowed, steady state community richness S* does not vary considerably with increasing service interactions and engineering (Supplementary Fig. 10a). In contrast, when redundant engineering is not allowed (each modifier is unique to an engineer, denoted by the subscript “u”), steady state community richness \({S}_{{\rm{u}}}^{* }\) declines sharply (Fig. 4d and Supplementary Fig. 10b).
Communities lacking redundant engineering have lower species richness because species’ trophic and service dependencies are unlikely to be fulfilled within a given assemblage (Supplementary Fig. 10c, d). Colonization occurs only when trophic and service dependencies are fulfilled. A species requiring multiple engineered modifiers, each uniquely produced, means that each required entity must precede colonization. This magnifies the role of priority effects in constraining assembly order12, precluding many species from colonizing. In contrast, redundant engineering increases the temporal stability of species’ niches while minimizing priority effects by allowing multiple engineers to fulfill the dependencies of a particular species. Our results thus suggest that redundant engineers may play important roles in assembling ecosystems by lowering the barriers to colonization, promoting community diversity.
Conclusions
We have shown that simple process-based rules governing the assembly of species with multitype interactions can produce communities with realistic structures and dynamics. Moreover, the inclusion of ecosystem engineering by way of modifier nodes reveals that low levels of engineering may be expected to produce higher rates of extinction while limiting the size of extinction cascades, and that engineering redundancy—whether it is common or rare—serves to promote colonization and by extension community diversity. We suggest that including the effects of engineers, either explicitly as we have done here, or otherwise, is vital for understanding the inter-dependencies that define ecological systems. As past ecosystems have fundamentally altered the landscape on which contemporary communities interact, future ecosystems will be defined by the influence of engineering today. Given the rate and magnitude with which humans are currently engineering environments98, understanding the role of ecosystem engineers is thus tantamount to understanding our own effects on the assembly of natural communities.
Methods
Assembly model framework
We model an ecological system with a network where nodes represent “ecological entities” such as populations of species and or the presence of abiotic modifiers affecting species. Following Pilai et al.49, we do not track the abundances of entities but track only their presence or absence (see also refs. 19,20). The links of the network represent interactions between pairs of entities (x, y). We distinguish three types of such interactions: x eats y, x needs y to be present, x makes modifier y.
The assembly process entails two steps: first a source pool of species is created, followed by colonization/extinction into/from a local community. The model is initialized by creating S species and M = ηS modifiers, such that N = S + M is the expected total number of entities (before considering engineering redundancies) and η is the expected number of modifiers made per species in the community, where the expectation is taken across independent replicates. For each pair of species (x, y) there is a probability pe that x eats y and probability pn that x needs y. For each pair of species x and modifier m, there is a probability qe that species x eats modifier m and a probability qn that species x needs modifier m. Throughout we assume that pe = qe and pn = qn for simplicity. Each species i makes a number of modifiers Mi ~ Poiss(η). If engineering redundancies are allowed, once the number of modifiers per species is determined each modifier is assigned to a species independently to match its assigned number of modifiers. This means that multiple species may make the same modifier, and that there may be some modifiers that are not assigned to any species, which are eliminated from the pool. Accounting for engineering redundancies, the number of modifiers in the pool becomes \({M}^{\prime}=\eta S(e-1)/e\) where e is Euler’s number. If engineering redundancies are not allowed, each modifier is made by a single engineer and \({M}^{\prime}=M\).
In addition to interactions with ecosystem entities, there can be interactions with a basal resource, which is always present. The first species always eats this resource, such that there is always a primary producer in the pool. Other species eat the basal resource with probability pe. Species with zero assigned trophic interactions are assumed to be primary producers. See Supplementary Note 1 for additional details on defining the source pool.
We then consider the assembly of a community, which at any time will contain a subset of entities in the pool and always the basal resource. In time, the entities in the community are updated following a set of rules. A species from the pool can colonize the community if the following conditions are met: (1) all entities that a species needs are present in the community, and (2) at least one entity that a species eats is present in the community. If a colonization event is possible, it occurs stochastically in time with rate rc.
An established species is at risk of extinction if it is not the strongest competitor at least one of its resources that it eats. We compute the competitive strength of species i as
where ni is the number of entities that species i needs, ei is the number of entities from the pool that species i can eat, and vi is the number of species in the community that eat species i. This captures the ecological intuition that mutualisms provide a fitness benefit52, specialists are stronger competitors than generalists55, and many predators entail an energetic cost57. The coefficients cn, ce, cv describe the relative effects of these contributions to competition strength. In the following, we use the relationship cn > ce > cv, such that the competitive benefit of adding an additional mutualism is greater than the detriment incurred by adding another resource or predator. A species at risk of extinction leaves the community stochastically in time at rate re.
A modifier is present in the community whenever at least one species that makes the modifier is present. If a species that makes a modifier colonizes a community, the modifier is introduced as well; however; modifiers may persist for some time after the last species that makes the modifier goes extinct. Any modifier that has lost all of its makers disappears stochastically in time at rate rm.
The model described here can be simulated efficiently with an event-driven simulation utilizing a Gillespie algorithm. In these types of simulations, one computes the rates rj of all possible events j in a given step. One then selects the time at which the next event happens by drawing a random number from an exponential distribution with mean 1/∑jrj. At this time, an event occurs that is randomly selected from the set of possible events such that the probability of event a is ra/∑jrj. The effect of the event is then realized and the list of possible events is updated for the next step. This algorithm is known to offer a much better approximation to the true stochastic continuous time process than a simulation in discrete time steps, while providing a much higher numerical efficiency99. Simulations described in the main text have default parameterizations of S = 200, pe = 0.01, cn = π, \({c}_{{\rm{e}}}=\sqrt{2}\), cv = 1, and 4000 iterations. Replicates are defined as the independent assembly of independently drawn source pools with a given parameterization.
Reporting summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
Simulation data to reproduce the findings of this study can be generated from the code available for download at https://github.com/jdyeakel/Lego.
Code availability
The custom simulation code supporting this work is available for download at https://github.com/jdyeakel/Lego.
References
Paine, R. T. Food web complexity and species diversity. Am. Nat. 100, 65–75 (1966).
Dunne, J. A., Williams, R. J. & Martinez, N. D. Food-web structure and network theory: the role of connectance and size. Proc. Natl Acad. Sci. USA 99, 12917–12922 (2002).
Pascual, M. & Dunne, J. Ecological Networks: Linking Structure to Dynamics in Food Webs. (Oxford University Press, Oxford, UK, 2006).
Bascompte, J. & Jordano, P. Mutualistic Networks. (Princeton University Press, Princeton, NJ, 2013).
May, R. M. Will a large complex system be stable? Nature 238, 413–414 (1972).
Gross, T., Levin, S. A. & Dieckmann, U. Generalized models reveal stabilizing factors in food webs. Science 325, 747–750 (2009).
Allesina, S. & Tang, S. Stability criteria for complex ecosystems. Nature 483, 205–208 (2012).
Montoya, J. M. & Solé, R. V. Topological properties of food webs: from real data to community assembly models. Oikos 102, 614–622 (2003).
Bascompte, J. & Stouffer, D. The assembly and disassembly of ecological networks. Philos. T. Roy. Soc. B 364, 1781 (2009).
Hubbell, S. The Unified Neutral Theory of Biodiversity and Biogeography. (Princeton Univ Press, Princeton, USA, 2001).
Tilman, D. Niche tradeoffs, neutrality, and community structure: a stochastic theory of resource competition, invasion, and community assembly. Proc. Natl Acad. Sci. USA 101, 10854–10861 (2004).
Fukami, T. Historical contingency in community assembly: integrating niches, species pools, and priority effects. Annu. Rev. Ecol. Evol. Syst. 46, 1–23 (2015).
Kraft, N. J. B., Valencia, R. & Ackerly, D. D. Functional traits and niche-based tree community assembly in an Amazonian forest. Science 322, 580–582 (2008).
O’Dwyer, J. P., Lake, J., Ostling, A., Savage, V. M. & Green, J. An integrative framework for stochastic, size-structured community assembly. Proc. Natl Acad. Sci. USA 106, 6170 (2009).
Brown, J. H., Kelt, D. A. & Fox, B. J. Assembly rules and competition in desert rodents. Am. Nat. 160, 815–818 (2002).
Piechnik, D. A., Lawler, S. P. & Martinez, N. D. Food-web assembly during a classic biogeographic study: species’ “trophic breadth” corresponds to colonization order. Oikos 117, 665–674 (2008).
Fahimipour, A. K. & Hein, A. M. The dynamics of assembling food webs. Ecol. Lett. 17, 606–613 (2014).
Barbier, M., Arnoldi, J.-F., Bunin, G. & Loreau, M. Generic assembly patterns in complex ecological communities. Proc. Natl Acad. Sci. USA 115, 2156–2161 (2018).
Campbell, C., Yang, S., Albert, R. & Shea, K. A network model for plant-pollinator community assembly. Proc. Natl Acad. Sci. USA 108, 197–202 (2011).
Hang-Kwang, L. & Pimm, S. L. The assembly of ecological communities: a minimalist approach. J. Anim. Ecol. 62, 749–765 (1993).
Law, R. & Morton, R. D. Permanence and the assembly of ecological communities. Ecology 77, 762–775 (1996).
Valdovinos, F. S., Ramos-Jiliberto, R., Garay-Narváez, L., Urbani, P. & Dunne, J. A. Consequences of adaptive behaviour for the structure and dynamics of food webs. Ecol. Lett. 13, 1546–1559 (2010).
Ramos-Jiliberto, R., Valdovinos, F. S., Moisset de Espanés, P. & Flores, J. D. Topological plasticity increases robustness of mutualistic networks. J. Anim. Ecol. 81, 896–904 (2012).
Valdovinos, F. S. et al. Niche partitioning due to adaptive foraging reverses effects of nestedness and connectance on pollination network stability. Ecol. Lett. 19, 1277–1286 (2016).
Ponisio, L. C. et al. A network perspective for community assembly. Front. Ecol. Evol. 7, 103 (2019).
Kéfi, S., Miele, V., Wieters, E. A., Navarrete, S. A. & Berlow, E. L. How structured is the entangled bank? the surprisingly simple organization of multiplex ecological networks leads to increased persistence and resilience. PLoS Biol. 14, e1002527 (2016).
Pilosof, S., Porter, M. A., Pascual, M. & Kéfi, S. The multilayer nature of ecological networks. Nat. Ecol. Evol. 1, 1–9 (2017).
Odum, E. P. The strategy of ecosystem development. Science 164, 262–270 (1969).
Jones, C. G., Lawton, J. H. & Shachak, M. Organisms as ecosystem engineers. Oikos 69, 373–386 (1994).
Olff, H. et al. Parallel ecological networks in ecosystems. Philos. T. Roy. Soc. B 364, 1755–1779 (2009).
Odling-Smee, J., Erwin, D. H., Palkovacs, E. P., Feldman, M. W. & Laland, K. N. Niche construction theory: a practical guide for ecologists. Q. Rev. Biol. 88, 4–28 (2013).
Leuthold, W. Recovery of woody vegetation in Tsavo National Park, Kenya, 1970-94. Afr. J. Ecol. 34, 101–112 (1996).
Haynes, G. Elephants (and extinct relatives) as earth-movers and ecosystem engineers. Geomorphology 157-158, 99–107 (2012).
Pringle, R. M. Elephants as agents of habitat creation for small vertebrates at the patch scale. Ecology 89, 26–33 (2008).
Reichman, O. & Seabloom, E. W. The role of pocket gophers as subterranean ecosystem engineers. Trends Ecol. Evol. 17, 44–49 (2002).
Hagenah, N. & Bennett, N. C. Mole rats act as ecosystem engineers within a biodiversity hotspot, the cape fynbos. J. Zool. 289, 19–26 (2013).
Moore, J. W. Animal ecosystem engineers in streams. BioScience 56, 237–246 (2006).
Meyer, S. T., Leal, I. R., Tabarelli, M. & Wirth, R. Ecosystem engineering by leaf-cutting ants: nests of atta cephalotes drastically alter forest structure and microclimate. Ecol. Entomol. 36, 14–24 (2011).
Hastings, A. et al. Ecosystem engineering in space and time. Ecol. Lett. 10, 153–164 (2007).
Wright, J. P., Jones, C. G., Boeken, B. & Shachak, M. Predictability of ecosystem engineering effects on species richness across environmental variability and spatial scales. J. Ecol. 94, 815–824 (2006).
Jones, C. & Lawton, J. Linking Species & Ecosystems. (Springer, New York City, USA, 2012).
Erwin, D. H. Macroevolution of ecosystem engineering, niche construction and diversity. Trends Ecol. Evol. 23, 304–310 (2008).
Schirrmeister, B. E., de Vos, J. M., Antonelli, A. & Bagheri, H. C. Evolution of multicellularity coincided with increased diversification of cyanobacteria and the great oxidation event. Proc. Natl Acad. Sci. USA 110, 1791–1796 (2013).
Loladze, I. & Elser, J. J. The origins of the Redfield nitrogen-to-phosphorus ratio are in a homoeostatic protein-to-rRNA ratio. Ecol. Lett. 14, 244–250 (2011).
Woodward, G., Perkins, D. M. & Brown, L. E. Climate change and freshwater ecosystems: impacts across multiple levels of organization. Philos. T. Roy. Soc. B 365, 2093–2106 (2010).
Brose, U. et al. Climate change in size-structured ecosystems. Philos. T. Roy. Soc. B 367, 2903–2912 (2012).
Gibert, J. P. Temperature directly and indirectly influences food web structure. Sci. Rep.-UK 9, 5312 (2019).
Getz, W. M. Biomass transformation webs provide a unified approach to consumer-resource modelling. Ecol. Lett. 14, 113–124 (2011).
Pillai, P., Gonzalez, A. & Loreau, M. Metacommunity theory explains the emergence of food web complexity. Proc. Natl Acad. Sci. USA 108, 19293–19298 (2011).
Bascompte, J., Jordano, P., Melián, C. J. & Olesen, J. M. The nested assembly of plant-animal mutualistic networks. Proc. Natl Acad. Sci. USA 100, 9383–9387 (2003).
Gravel, D., Massol, F., Canard, E., Mouillot, D. & Mouquet, N. Trophic theory of island biogeography. Ecol. Lett. 14, 1010–1016 (2011).
Bronstein, J. L. Conditional outcomes in mutualistic interactions. Trends Ecol. Evol. 9, 214–217 (1994).
MacArthur, R. & Levins, R. Competition, habitat selection, and character displacement in a patchy environment. Proc. Natl Acad. Sci. USA 51, 1207 (1964).
Dykhuizen, D. & Davies, M. An experimental model: bacterial specialists and generalists competing in chemostats. Ecology 61, 1213–1227 (1980).
Futuyma, D. J. & Moreno, G. The evolution of ecological specialization. Annu. Rev. Ecol. Syst. 19, 207–233 (1988).
Costa, A. et al. Generalisation within specialization: inter-individual diet variation in the only specialized salamander in the world. Sci. Rep. 5, 1–10 (2015).
Brown, J. S., Kotler, B. P. & Valone, T. J. Foraging under predation-a comparison of energetic and predation costs in rodent communities of the negev and sonoran deserts. Aust. J. Zool. 42, 435–448 (1994).
Williams, R. J. & Martinez, N. D. Simple rules yield complex food webs. Nature 404, 180–183 (2000).
Kones, J. K., Soetaert, K., van Oevelen, D. & Owino, J. O. Are network indices robust indicators of food web functioning? A monte carlo approach. Ecol. Model. 220, 370–382 (2009).
Williams, R. & Martinez, N. Limits to trophic levels and omnivory in complex food webs: Theory and data. Am. Nat. 163, 458–468 (2004).
Lafferty, K. D., Dobson, A. P. & Kuris, A. M. Parasites dominate food web links. Proc. Natl Acad. Sci. USA 103, 11211–11216 (2006).
Turney, S. & Buddle, C. M. Pyramids of species richness: the determinants and distribution of species diversity across trophic levels. Oikos 125, 1224–1232 (2016).
Bascompte, J., Jordano, P. & Olesen, J. M. Asymmetric coevolutionary networks facilitate biodiversity maintenance. Science 312, 431–433 (2006).
Guimarães Jr., P. R., Rico-Gray, V., Furtado dos Reis, S. & Thompson, J. N. Asymmetries in specialization in ant–plant mutualistic networks. Proc. Roy. Soc. B 273, 2041 (2006).
Araújo, M. S. et al. Nested diets: a novel pattern of individual-level resource use. Oikos 119, 81–88 (2010).
Rohr, R. P., Saavedra, S. & Bascompte, J. On the structural stability of mutualistic systems. Science 345, 1253497–1253497 (2014).
Valdovinos, F. S. Mutualistic networks: moving closer to a predictive theory. Ecol. Lett. 22, 1517–1534 (2019).
Krishna, A., Guimarães Jr., P. R., Jordano, P. & Bascompte, J. A neutral-niche theory of nestedness in mutualistic networks. Oikos 117, 1609–1618 (2008).
Guimarães Jr., P. R., Pires, M. M., Jordano, P., Bascompte, J. & Thompson, J. N. Indirect effects drive coevolution in mutualistic networks. Nature 18, 586 (2017).
Stouffer, D. B. Compartmentalization increases food-web persistence. Proc. Natl Acad. Sci. USA 108, 3648–3652 (2011).
Gilarranz, L. J., Rayfield, B., Liñán-Cembrano, G., Bascompte, J. & Gonzalez, A. Effects of network modularity on the spread of perturbation impact in experimental metapopulations. Science 357, 199–201 (2017).
Pires, M. M., Prado, P. I. & Guimarães Jr., P. R. Do food web models reproduce the structure of mutualistic networks? PLoS ONE 6, e27280 (2011).
Massol, F. et al. Linking community and ecosystem dynamics through spatial ecology. Ecol. Lett. 14, 313–323 (2011).
Yeakel, J. D., Guimarães Jr., P. R., Bocherens, H. & Koch, P. L. The impact of climate change on the structure of Pleistocene food webs across the mammoth steppe. Proc. Roy. Soc. B 280, 20130239 (2013).
Bond, W. J., Lawton, J. H. & May, R. M. Do mutualisms matter? Assessing the impact of pollinator and disperser disruption on plant extinction. Philos. Trans. Roy. Soc. B 344, 83–90 (1994).
Colwell, R. K., Dunn, R. R. & Harris, N. C. Coextinction and persistence of dependent species in a changing world. Ann. Rev. Ecol. Evol. Sys. 43, 183–203 (2012).
Díaz-Castelazo, C., Sánchez-Galván, I. R., Guimarães, J., Paulo, R., Raimundo, R. L. G. & Rico-Gray, V. Long-term temporal variation in the organization of an ant-plant network. Ann. Bot. -Lond. 111, 1285–1293 (2013).
Vieira, M. C. & Almeida Neto, M. A simple stochastic model for complex coextinctions in mutualistic networks: robustness decreases with connectance. Ecol. Lett. 18, 144–152 (2015).
Ponisio, L. C., Gaiarsa, M. P. & Kremen, C. Opportunistic attachment assembles plant-pollinator networks. Ecol. Lett. 20, 1261–1272 (2017).
Laland, K. N. et al. The extended evolutionary synthesis: its structure, assumptions and predictions. Proc. Roy. Soc. B 282, 20151019 (2015).
Gupta, M., Prasad, N., Dey, S., Joshi, A. & Vidya, T. Niche construction in evolutionary theory: the construction of an academic niche? J. Gen. 96, 491–504 (2017).
Feldman, M. W., Odling-Smee, J. & Laland, K. N. Why Gupta et al.’s critique of niche construction theory is off target. J. Gen. 96, 505–508 (2017).
Cuddington, K. Invasive engineers. Ecol. Model. 178, 335–347 (2004).
Wright, J. P. & Jones, C. G. Predicting effects of ecosystem engineers on patch-scale species richness from primary productivity. Ecology 85, 2071–2081 (2004).
Kylafis, G. & Loreau, M. Ecological and evolutionary consequences of niche construction for its agent. Ecol. Lett. 11, 1072–1081 (2008).
Krakauer, D. C., Page, K. M. & Erwin, D. H. Diversity, dilemmas, and monopolies of niche construction. Am. Nat. 173, 26–40 (2009).
Laland, K. N., Odling-Smee, F. J. & Feldman, M. W. Evolutionary consequences of niche construction and their implications for ecology. Proc. Natl Acad. Sci. USA 96, 10242–10247 (1999).
Kallus, Y., Miller, J. H. & Libby, E. Paradoxes in leaky microbial trade. Nat. Commun. 8, 1361 (2017).
Butler, S. & O’Dwyer, J. P. Stability criteria for complex microbial communities. Nat. Comm. 9, 2970 (2018).
Amundson, R. et al. Soil and human security in the 21st century. Science 348, 1261071 (2015).
Gutérrez, J. L. & Jones, C. G. Physical ecosystem engineers as agents of biogeochemical heterogeneity. BioScience 56, 227–236 (2006).
Jouquet, P., Dauber, J., Lagerlöf, J., Lavelle, P. & Lepage, M. Soil invertebrates as ecosystem engineers: Intended and accidental effects on soil and feedback loops. Appl. Soil Ecol. 32, 153–164 (2006).
Shipway, J. R. et al. A rock-boring and rock-ingesting freshwater bivalve (shipworm) from the Philippines. Proc. Roy. Soc. B 286, 20190434 (2019).
Lawton, J. H. What do species do in ecosystems? Oikos 71, 367–374 (1994).
Odling-Smee, F., Laland, K. & Feldman, M. Niche Construction: The Neglected Process in Evolution. (Princeton University Press, Princeton, NJ, 2013).
Kidwell, S. M. Taphonomic feedback in Miocene assemblages: testing the role of dead hardparts in benthic communities. Palaios 1, 239–255 (1986).
Polz, M. F., Alm, E. J. & Hanage, W. P. Horizontal gene transfer and the evolution of bacterial and archaeal population structure. Trends Genet. 29, 170–175 (2013).
Corlett, R. T. The anthropocene concept in ecology and conservation. Trends Ecol. Evol. 30, 36–41 (2015).
Gillespie, D. T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81, 2340–2361 (1977).
Cantor, M. et al. Nestedness across biological scales. PLoS ONE 12, e0171691 (2017).
Acknowledgements
We would like to thank Uttam Bhat, Irina Birskis Barros, Emmet Brickowski, Jennifer A. Dunne, Ashkaan Fahimipour, Marilia P. Gaiarsa, Jean Philippe Gibert, Christopher P Kempes, Eric Libby, Lauren C. Ponisio, Taran Rallings, Samuel V. Scarpino, Megha Suswaram, and Ritwika VPS for insightful discussions and comments throughout the lengthy gestation of this manuscript. The original idea was conceived at the Networks on Networks Working Group in Göttingen, Germany (2014) and the Santa Fe Institute (2015). This work was formerly prepared as a part of the Ecological Network Dynamics Working Group at the National Institute for Mathematical and Biological Synthesis (2015–2019), sponsored by the National Science Foundation through NSF Award DBI-1300426, with additional support from The University of Tennessee, Knoxville. Infinite revisions were conducted at the Santa Fe Institute made possible by travel awards to J.D.Y. and T.G. Additional support came from UC Merced startup funds to J.D.Y., the International Center for Theoretical Physics ICTP-SAIFR, FAPESP (2016/01343-7 and 2019/20271-5) and CNPq (302049/2015-0) to M.A.M.d.A., CNPq and FAPESP (2018/14809-0) to P.R.G., and DFG research unit 1748 and EPSRC (EP/N034384/1) to T.G.
Author information
Authors and Affiliations
Contributions
J.D.Y. and T.G. conceived of the model framework. J.D.Y., M.M.P., M.A.M.d. A., and T.G. designed the analyses. J.D.Y., M.M.P., M.A.M.d.A., J.L.O.D., P.R.G., D.G., and T.G. analyzed the results and contributed to multiple versions of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Alva Curtsdotter and Dirk Sanders for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Yeakel, J.D., Pires, M.M., de Aguiar, M.A.M. et al. Diverse interactions and ecosystem engineering can stabilize community assembly. Nat Commun 11, 3307 (2020). https://doi.org/10.1038/s41467-020-17164-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-17164-x
This article is cited by
-
Ecosystem engineering and food web stability
Scientific Reports (2024)
-
Net-spinning caddisflies create denitrifier-enriched niches in the stream microbiome
ISME Communications (2023)
-
Environmental connectivity controls diversity in soil microbial communities
Communications Biology (2021)
-
Species diversity and food web structure jointly shape natural biological control in agricultural landscapes
Communications Biology (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.