Abstract
Polar van der Waals chalcogenophosphates exhibit unique properties, such as negative electrostriction and multi-well ferrielectricity, and enable combining dielectric and 2D electronic materials. Using low temperature piezoresponse force microscopy, we revealed coexistence of piezoelectric and non-piezoelectric phases in CuInP2Se6, forming unusual domain walls with enhanced piezoelectric response. From systematic imaging experiments we have inferred the formation of a partially polarized antiferroelectric state, with inclusions of structurally distinct ferrielectric domains enclosed by the corresponding phase boundaries. The assignment is strongly supported by optical spectroscopies and density-functional-theory calculations. Enhanced piezoresponse at the ferrielectric/antiferroelectric phase boundary and the ability to manipulate this entity with electric field on the nanoscale expand the existing phenomenology of functional domain walls. At the same time, phase-coexistence in chalcogenophosphates may lead to rational strategies for incorporation of ferroic functionality into van der Waals heterostructures, with stronger resilience toward detrimental size-effects.
Similar content being viewed by others
Introduction
Layered thiophosphates, with a general composition of CuInP2Q6 (Q = S, Se)1, have recently gained attention as candidate materials for two-dimensional2,3,4 (2D) or few-layered ferroelectrics2,5. The sulfur6,7 and selenium8,9,10 compounds have similar structure of individual layers and a concomitant ferrielectric (FE) ordering, with Cu+ and In3+ ions counter-displaced within individual layers, against the backbone of P2Q4-6 anions. The spontaneous polarization of the sulfide can range from ~5 μC/cm2 to ~12 μC/cm2 11 vs ~2.5 μC/cm2 12 in the selenide, in part due to larger off-centric Cu displacement in the sulfide. Despite the structural similarity, the reported properties of their phase transitions are quite different10. Other than the difference in the transition temperatures (~230 K8,9 in the selenide vs ~305 K in the sulfide6,10), CuInP2Se6 exhibits a broader transition window compared to CuInP2S6, as evidenced by macroscopic dielectric, caloric and thermal characterization9,10. It was proposed that this anomaly is evidence for the coexistence of ferrielectric and antiferroelectric (AFE) ordering, and an incommensurate phase that precedes ferroelectric ordering9. The properties of the intermixed S–Se compound are even more interesting, possibly involving a Lifshitz transition as well as polar glassy phases13. The apparent compatibility of chalcogenophosphates with a variety of polar orderings signifies comparatively weak dipolar correlations in the lattice. This property may be particularly pertinent toward prospective application of these materials as functional components of van der Waals heterostructures.
Indeed, recently, Song et al.12 proposed that ultrathin films of CuInP2Se6 develop an antiferroelectric ground state, with the ferrielectric-antiferroelectric crossover occurring at a thickness of ~6–8 layers. The primary driving force for the crossover is the depolarizing field that favors the antiferroelectric with net zero polarization. This feature is in contrast to perovskite oxides, such as the canonical BaTiO3, which become non-polar in the ultrathin limit14. However, at present, most nanoscale polar properties in both CuInP2S6 and CuInP2Se6 remain to be understood, with respect to the mechanisms that screen spontaneous polarization at the interfaces, polarization switching, and the structure of the domains and their domain walls1 as well as the scalability down to the single-layer limit. Understanding these behaviors will also help to identify the possible mechanisms by which these materials can be functional in van der Waals heterostructures.
Here, we report the structure of polarization domains in bulk CuInP2Se6 utilizing quantitative imaging of nanoscale piezoelectric properties. Contrary to the expectation of ferrielectric ordering analogous to CuInP2S6, we reveal a fundamentally different domain structure, with two markedly different values of piezoresponse. Moreover, the domain boundaries exhibit the strongest piezoelectric response, with up to fourfold enhancement compared to domain surfaces. CuInP2S6, on the other hand, features an expected domain structure, with nearly uniform value of piezoresponse within domains, alternating polarization orientation and domain walls with vanishing piezoresponse15,16,17. Despite the more complex polar structure of CuInP2Se6, the domains can be flexibly manipulated with applied fields. We explain the phenomena observed in CuInP2Se6 by considering the real-space domain structure of an antiferroelectric that is partially polarized in finite electric field. Our arguments are supported by Raman spectroscopy and DFT calculations indicating the possible coexistence of ferrielectric and antiferroelectric states. FE/AFE coexistence presents an intriguing opportunity for few-unit-cell thiophosphates, particularly within van der Waals heterostructures. At the same time, piezoelectric domain walls, which are polar phase boundaries in this case and can be readily manipulated by applied electric fields, present a new functional element for the domain-wall electronics paradigm18,19.
Results and discussion
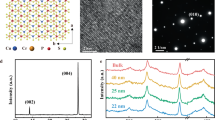
Piezoresponse force microscopy does not exhibit any significant signal on the surface of CuInP2Se6 at room temperature in the paraelectric state, as expected. On a crystal cooled below 200 K, the piezoresponse phase and amplitude images (Fig. 1a, b) reveal domains of various forms and sizes (the measured response is defined by the normal components of the piezoelectric coefficient \(d_{3j} = 2\varepsilon _0\varepsilon _{33}Q_{j3}P_3\), where the Qj3 are components of electrostriction tensor, P3 is the normal polarization component, and ε33 is the normal component of the dielectric constant). Despite structural similarity, however, there is a stark contrast between CuInP2Se6 and Cu0.4In1.2P2S6 as shown in Fig. 1. In Cu0.4In1.2P2S6, the contrast of the piezoelectric signal.
CuInP2Se6 surfaces were measured at 140 K in ultrahigh vacuum and that of CuInP2S6—at room temperature in controlled environment: a, b piezoresponse signals Acos(θ) (where A is the amplitude and θ the phase of piezoresponse)—revealing at least three distinct magnitudes of piezoresponse for both materials, and c, d line-profiles of piezoresponse along the white dashed lines, crossing domain boundaries in a, b, respectively. Orange arrows point to the regions of the domain walls.
comprises the non-polar dielectric phase In4/3P2S6, with negligible piezoresponse, and the ferrielectric phase CuInP2S6, whose piezoresponse is comparable to a ferroelectric: domains of opposite polarization have opposite signs of piezoresponse, with nearly zero signal at the domain wall in between (Fig. 1b, d)20,21. Cancellation of piezoresponse at the domain wall is a mutual consequence of nearly zero polarization at the wall, and possibly the mechanical cancellation effect due to opposite direction of surface deformation in the adjacent domains separated by the domain wall.
In CuInP2Se6, extended regions of negligible piezoresponse and extended regions of uniform piezoresponse also exist. However, in contrast to Cu0.4In1.2P2S6, CuInP2Se6 crystals studied here are nearly stoichiometric, excluding the existence of a non-ferroelectric phase, such as In4/3P2S6 in Cu0.4In1.2P2S6. Moreover, the regions of finite piezoresponse appear only below the transition and can be flexibly manipulated with applied fields (shown below in Fig. 2j). At the same time, the piezoresponse signal across a boundary separating the two distinct regions in CuInP2Se6 has maximum rather than minimum piezoresponse signal. These observations imply that CuInP2Se6 below the ferroic transition intrinsically exhibits at least two distinct structural phases. The imaging results are reproduced for a variety of tips, cleaved surfaces and are also observed irrespective of the underlying topography (Supplementary Fig. 1). By using PFM in ultrahigh vacuum on freshly cleaved and nearly atomically flat surfaces, as well as invoking the band-excitation methodology for piezoresponse22, we have further ruled out simple experimental artifacts such as the underlying topography23, electrochemistry24, or mechanical properties of the contact25.
a–e CuInP2S6 imaged (image size 1.5 µm x 1.5 μm) at room temperature in a controlled environment and f–j CuInP2Se6 imaged (image size 2.0 µm x 2.0 μm) at 140 K in ultrahigh vacuum. Dotted white lines indicate line profile locations for Fig. 3(a, b). The bias applied to the tip is specified in the top row.
Further insight as well as confirmation of the above assignments is evidenced from the electric-field dependence of the measured piezoresponse (Fig. 2). It was previously pointed out that it is essential to check local electromechanical measurements for possible artefacts, such as the contribution of extrinsic electrostatics24. As seen in Fig. 2, the dominant effect of applied bias is to impose an offset on the measured signal in both Cu0.4In1.2P2S6 and CuInP2Se6, while keeping the contrast between entities largely unchanged.
This conclusion is further confirmed by analysis of select 1D profiles from the data in Fig. 2, as shown in Fig. 3. Indeed, relative enhancement of piezoresponse is maintained irrespective of applied field (Fig. 3a, c), while domain walls in Cu0.4In1.2P2S6 reveal approximately average signal between up and down-oriented domains (Fig. 3b). At the same time, at both −3V (Fig. 2f) and +2 V (Fig. 2j), the domain structure of CuInP2Se6 begins to evolve in applied field, respectively shrinking and growing the regions of finite piezoresponse.
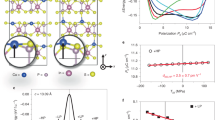
Piezoresponse line scans presented in Fig. 2(a–j) for a CuInP2S6 and b CuInP2Se6 at DC biases ranging from −3V to +2 V. c CuInP2Se6 piezoresponse as a function of applied voltage for domain wall, AFE domain, and FE domain derived from Supplementary Fig. 2(d) Schematic of a canonical double-hysteresis loop for antiferroelectrics. Insets illustrate a schematic top view of the surface, with spatially separated AFE (light gray) and FE (dark gray) domains.
Given all of the above measurements, we propose that CuInP2Se6 exhibits coexistence of antipolar and polar regions, identified, respectively, by zero and finite piezoresponse signals. The domain walls are then the boundaries separating these regions. Given the propensity of CuInP2Se6 toward antiferroelectric ordering (12 and see below), the polar and antipolar regions would correspond to ferrielectric and antiferroelectric phases, respectively.
This scenario of phase separation can be rationalized by considering the real-space structures underpinning the hallmark property of antiferroelectrics—a double-hysteresis switching loop (Fig. 3d)26,27,28. Double hysteresis corresponds to the switching of antiferroelectric configuration with net zero polarization to ferroelectric structure with nonzero polarization. Uniform antiferroelectric structure is, therefore, expected only in a very small range of applied fields27. At finite field, the system exhibits a state of finite polarization. In the real space, the structure with finite polarization can manifest as two distinct states: either the system is uniformly polarized in an applied field, or it exhibits non-uniform distribution of polarization (schematically shown in the inset of Fig. 3d), such that local regions of ferrielectric and antiferroelectric phases emerge. We believe the second case is the appropriate representation of CuInP2Se6 in our measurements.
Our argument for the coexistence of ferrielectric and antiferroelectric phases in CuInP2Se6 is supported by Raman spectroscopy and DFT calculations. Both Raman and SHG spectroscopy, carried out on freshly cleaved crystalline flakes of CuInP2Se6, clearly detect the transition below ~250 K (Fig. 4a, d). The peaks at 203 and 219 cm−1 in Raman spectrum appear first at around 250 K (Fig. 4a, b) and their integrated intensity continues to grow, eventually saturating below ~180 K (Supplementary Fig. 3). Simultaneously measured SHG intensity (Fig. 4d) shows a rapid increase below 220 K. Notably, SHG detects breaking of the inversion symmetry, therefore implying the development of either ferri- or ferroelectric ordering in the probed volume of the technique.
a Temperature dependent Raman spectroscopy of a CuInP2Se6 crystal, represented as a heat map. The phase transition below ~250 K is clearly visible (yellow arrow). b Individual Raman spectra at several measured temperatures. c Comparison of the Raman spectrum at 7 K to the DFT calculations for the ferroelectric (FE) and antiferroelectric (AFE) configurations. d The intensity of second harmonic generation (SHG) across the phase transition at 200 K.
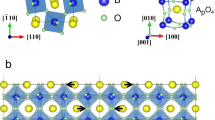
Further, we compared the experimental Raman spectra to those calculated by DFT in the ferrielectric and antiferroelectric ground states, as shown in Fig. 4c. The AFE state in these calculations corresponds to an alternating displacement of Cu atoms along the b (or a) crystallographic direction, between opposite sides of each layer (Supplementary Fig. 4b), consistent with the prior work12. The In3+ in this case is located near the equatorial plane of each layer. In contrast, in the ferrielectric state, the Cu1+ and In3+ are offset in opposite directions relative to the midplane of the layers, but the offsets of each are identical within each cation sublattice.
The characteristic calculated signature of the AFE state appears to be a peak around 300 cm−1. It is negligible for the calculated spectra for the FE configurations, while prominent in the experiment (Fig. 4c). Meanwhile, the three-peak structure between 400 cm−1 and 500 cm−1 is best captured by a combination of the FE and AFE states. The probing volume of piezoresponse force microscopy measurements are comparable to the radius of the tip, ~20–50 nm, while that of optical spectroscopies ~ 1μm; thus, both are still probing near-surface regions. Note, the X-ray diffraction study of CuInP2Se6 across the phase transition, on the other hand, shows that the structure of
CuInP2Se6 belongs to the non-centrosymmetric space group P31c (No. 159) at 100 K and 180 K (Supplementary Table 1a), Supplementary Fig. 5). At 250 K, the best fit is to the centrosymmetric space group P\(\bar 3\) 1c (No. 163) (Supplementary Table 1c)). These results largely agree with previous work8, indicating order-disorder type ferrielectric ordering in CuInP2Se6. Bulk-averaging measurements are therefore most consistent with ferrielectric ordering (Supplementary Fig. 5, Supplementary Fig. 6). However, in light of the similar energies between ferroelectric and antiferroelectric states (Supplementary Fig. 4), it is likely that uniform states of either kind can be preferred depending on specific experimental conditions.
Further insight into the structure and energetics of the AFE and FE phases and the AFE/FE domain walls has been gained using DFT calculations of large supercells, which accommodate such boundaries. The energetics and structures of several possible AFE configurations are shown in Supplementary Fig. 4. Consistent with prior work12, under zero strain, all bulk AFE structures have a higher energy than the bulk FE structure. Meanwhile, calculated energies of all three types of AFE/FE boundaries are small, within 2 meV/nm2 of each other, while the energy of a FE/FE domain wall is much higher, 21 meV/nm2 (Fig. 5). This result indicates that the formation of the observed mixed AFE/FE state is largerly governed by the energetics of the respective domains and that there is a high likelihood of formation of AFE/FE boundaries.
Discussion
The complete analysis of phase coexistence CuInP2Se6 falls outside the scope of this manuscript. However, we have carried out analytical modeling of the mixed free energy functional within the Landau–Ginzburg–Devonshire framework (Supplementary Discussion). The functional incorporates the contributions to the free energy from ferroelectric, antiferroelectric, antiferrodistortive order parameters, as well as coupling and striction terms. Importantly, although the coexistence of antiferroelectric and ferroelectric order parameters is intuitively simple, its detailed functional is very complicated. The variation of the order parameter across the domain wall is opposite for the ferroelectric and antiferroelectric end-states: in ferroelectrics, polarization drops to zero at the domain wall (x = x0 in Supplementary Eq. (18)), while the antiferroelectric order parameter A increases at the domain wall (x = y0 in Supplementary Eq. (19)). Our experimental observable is strain, and specifically piezoresponse measured as a voltage derivative of strain. In the case of the FE/AFE boundary we do indeed predict a maximum strain at the wall within the approximations of the model (Supplementary Fig. 7). This behavior can be rationalized by analogy with double-hysteresis strain loops in macroscopic antiferroelectric switching (schematic in Fig. 3d). Upon onset of polarization (transition from AFE to FE phase), the lattice experiences maximum deformation (expansion in perovskite oxides29,30) that exceeds subsequent deformation in the ferroelectric state (due to piezoresponse). In our interpretation, the AFE–FE domain boundary in CuInP2Se6 is precisely the region of phase separation. The result of the LGD modeling, showing maximum strain at the boundary, supports the analogy between AFE/FE transition due to electric field (in macroscopic double-hysteresis loops) and due to phase separation in real-space (in our measurements). Although we cannot yet model the piezoresponse (dynamic strain), it is also maximized in the macroscopic hysteresis loops at the AFE/FE switching, and could therefore be maximum in our measurements in Fig. 1 and 2. Based on these results, piezoelectric domain walls should also be generally found in partially polarized antiferroelectrics.
Using quantitative piezoelectric microscopy, combined with DFT calculations and optical spectroscopy, we have revealed unusual domain-wall properties in polar CuInP2Se6, where domain walls exhibit maximum piezoresponse at the domain walls in contrast to the expectations for ferroelectrics. Whereas polar walls were previously detected in in antiferroelectric PbZrO331 and in ferroelastic CaTiO332,33, we have inferred that in CuInP2Se6 the domain walls separate regions of antiferroelectric and ferrielectic ordering. These domain walls should be general for antiferroelectrics while being distinct from domain walls in either ferroelectric or antiferroelectric phases, thus emerging as a new entity in the context of domain-wall electronics19. Meanwhile, the observation of antiferroelectric state confirms theoretical modeling of very small energy differences between ferrielectric and antiferroelectic states in CuInP2Se6. The ability to define and control locally polarized, mesoscale regions in an otherwise non-polar matrix may provide a path to integrate ferroic and electronic functionality via van der Waals interfaces, which is complementary to ferroelectric materials and that may persist down to single layer12.
Methods
Crystal growth
The single crystal CuInP2Se6 was grown from gas phase by chemical transport reactions. Iodine has been used as transport agent with concentration of 4–5 mg/cm3. The temperature of evaporation zone was 870 K, and for the crystallization zone temperature equals 850 K. The duration of the growth process was 350 h. The resulting product was thin single crystal plates with dimensions near 10 × 5 × 0.1 mm3. Cu0.4In1.2P2S6 single crystals were synthesized through the vapor transport method. Starting materials, sealed in fused silica ampules, were heated to 750–775 °C at a rate of 30 °C/h and held at that temperature for 4 days and then cooled at a rate of 20 °C/h.
PFM imaging
Ultrahigh vacuum contact PFM imaging and polarization switching were performed on an Omicron AFM/STM, interfaced with a Nanonis controller package. The chamber pressure was 1 × 10−10 mbar or better. The samples were mounted on a standard Omicron sample plate and affixed with a silver conductive epoxy (Epo-Tek EJ2189-LV). A clean surface was prepared by Scotch tape method in UHV. Images of CuInP2S6 shown in this paper were acquired in an Ar-filled glove-box using Bruker-Icon AFM. The freshly cleaved surface was likewise prepared shortly before the measurement.
Single crystal XRD
The structure of single crystals was characterized by using a Rigaku XtalLAB PRO diffractometer with graphite monochromatized Mok-alpha radiation (lambda = 0.71073 Angstrom) equipped with a Dectris Pilatus 200 K and an Oxford Cryosystems N-HeliX cryocooler for temperature ranging from 100 to 293 K.
Raman spectroscopy
The Raman spectra were measured in a custom-built micro-Raman setup. The samples were excited with a continuous wave (cw) diode-pumped solid-state laser (Excelsior, Spectra Physics, 532 nm, 100 mW) through an upright microscope using a ×50 long-working distance objective with NA (numeric aperture) = 0.5. The typical incident laser power on a sample was maintained at ~ 100 μW to reduce possible laser heating and damaging of the samples during Raman spectra acquisition. The scattered Raman light was analyzed by a spectrometer (Spectra Pro 2300i, Acton, f = 0.3 m) that was coupled to the microscope and equipped with a 1800 groves/mm grating and a CCD camera (Pixis 256BR, Princeton Instruments). The low-temperature Raman spectra were measured using a liquid He-cryostat (MicrostatHiResII, Oxford Instruments) with a temperature controller (MercuryiT, Oxford Instruments) that allowed precise control from 3.6 to 300 K. Raman spectra were sampled with 10 K step from 100 to 250 K, and also at 4, 7, and 20 K. The cryostat was mounted on a motorized XY microscope stage (Marzhauser) under the microscope of the micro-Raman setup. The cryostat was evacuated to the base pressure of 7 × 10−7 mbar prior to cool down.
Second harmonic measurements
Second harmonic generation (SHG) measurements were conducted using a 50 fs Ti:sapphire laser (Micra, Coherent) at 800 nm and 80 MHz repetition rate. The laser beam was passed through a half-wave plate mounted in a rotation stage and was directed into an upright microscope (Olympus) and focused onto a sample surface using a ×50 microscope objective (Numerical Aperture: NA = 0.5) to a few micron spot. The laser energy at the sample surface was ~0.1 W. The SHG light was collected in backscattering configuration using the same objective and was directed to a monochromator (Spectra Pro 2300i, Acton, f = 0.3 m) that was coupled to the microscope and equipped with a 150 grooves/mm grating and a CCD camera (Pixis 256BR, Princeton Instruments). Before entering the monochromator, the SHG light was passed through a short-pass cutoff filter (650 nm) and a polarizer to filter out the fundamental excitation light at 800 nm and select the SHG polarization parallel to that of the excitation light. The low-temperature SHG measurements were conducted using the same liquid He-cryostat, which was used for Raman measurements.
DFT calculations
The DFT calculations (relaxations and Γ-point phonon frequencies) in this study use the VASP 5.3.5 computational package34 and are carried out under the Perdew–Burke–Ehrenhof generalized gradient approximation (GGA) and the the DFT-D2 method as developed by Grimme35. The recommended VASP PAW pseudopotentials were used. All calculations used a 600 eV energy cutoff. Raman frequencies and intensities are calculated using the package developed by Fonari and Stauffer36. The calculations were performed on two phases of CuInP2Se6: a 20-atom ferroelectric (FE) phase, and a 40-atom 1 × 2 × 1 antiferrolectric (AFE) phase. The setup for the Cu atoms in the AFE unit cell is the same as that found by Song et al.12 For phonon calculations, both structures were relaxed so that the forces are less than 5e−8 eV/Å to eliminate residual spurious forces. The FE/FE and FE/AFE domain-wall calculations are performed using 8 × 2 × 1 supercells containing 160 atoms. These calculations use a Γ-centered Monkhorst-Pack (MP) k-point grid of 1 × 4 × 2. All atoms were relaxed until all forces were smaller than 0.02 eV/Å. The domain boundary energy per unit area is calculated as
where Etotal is the supercell energy, Ephase1 and Ephase2 are the energies for the requisite number of atoms in those phases, and S is the cross-sectional area of the boundary.
Data availability
Source data for the scanning probe images, results of optical spectroscopy and first principles calculations presented in this manuscript will be shared upon reasonable request.
Code availability
The data analysis was carried out with widely accepted commercial and open source software without any significant code customization.
References
Susner, M. A., Chyasnavichyus, M., McGuire, M. A., Ganesh, P. & Maksymovych, P. Metal thio‐ and selenophosphates as multifunctional van der Waals layered materials. Adv. Mater. 29, 1602852 (2017).
Chang, K. et al. 2D ferroelectrics: enhanced spontaneous polarization in ultrathin SnTe films with layered antipolar structure. Adv. Mater. 31, 1970016 (2019).
Wu, M. & Jena, P. The rise of two-dimensional van der Waals ferroelectrics. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 8, e1365 (2018).
Chang, K. et al. Discovery of robust in-plane ferroelectricity in atomic-thick SnTe. Science 353, 274–278 (2016).
Liu, F. et al. Room-temperature ferroelectricity in CuInP2S6 ultrathin flakes. Nat. Commun. 7, 12357 (2016).
Maisonneuve, V., Cajipe, V. B., Simon, A., Von Der Muhll, R. & Ravez, J. Ferrielectric ordering in lamellar CuInP2S6. Phys. Rev. B 56, 10860–10868 (1997).
Simon, A., Ravez, J., Maisonneuve, V., Payen, C. & Cajipe, V. B. Paraelectric–ferroelectric transition in the lamellar thiophosphate CuInP2S6. Chem. Mater. 6, 1575–1580 (1994).
Bourdon, X., Maisonneuve, V., Cajipe, V. B., Payen, C. & Fischer, J. E. Copper sublattice ordering in layered CuMP2Se6 (M = In, Cr). J. Alloy. Compd. 283, 122–127 (1999).
Vysochanskii, Yu. M., Molnar, A. A., Gurzan, M. I., Cajipe, V. B. & Bourdon, X. Dielectric measurement study of lamellar CuInP2Se6: successive transitions towards a ferroelectric state via an incommensurate phase? Solid State Commun. 115, 13–17 (2000).
Liubachko, V. et al. Anisotropic thermal properties and ferroelectric phase transitions in layered CuInP2S6 and CuInP2Se6 crystals. J. Phys. Chem. Solids 111, 324–327 (2017).
Brehm, J. A. et al. Tunable quadruple-well ferroelectric van der Waals crystals. Nat. Mater. 19, 43–48 (2020).
Song, W., Fei, R. & Yang, L. Off-plane polarization ordering in metal chalcogen diphosphates from bulk to monolayer. Phys. Rev. B 96, 235420 (2017).
Vysochanskii, Y. M., Molnar, A. A., Gurzan, M. I. & Cajipe, V. B. Phase transitions in CuInP2(SexS1−x)6 layered crystals. Ferroelectrics 257, 147–154 (2001).
Junquera, J. & Ghosez, P. Critical thickness for ferroelectricity in perovskite ultrathin films. Nature 422, 506–509 (2003).
Belianinov, A. et al. CuInP2S6 room temperature layered ferroelectric. Nano Lett. 15, 3808–3814 (2015).
Chyasnavichyus, M. et al. Size-effect in layered ferrielectric CuInP2S6. Appl. Phys. Lett. 109, 172901 (2016).
Neumayer, S. M. et al. Giant negative electrostriction and dielectric tunability in a van der Waals layered ferroelectric. Phys. Rev. Mater. 3, 24401 (2019).
Meier, D. Functional domain walls in multiferroics. J. Phys. Condens. Matter 27, 463003 (2015).
Catalan, G., Seidel, J., Ramesh, R. & Scott, J. F. Domain wall nanoelectronics. Rev. Mod. Phys. 84, 119–156 (2012).
Rodriguez, B. J. et al. Domain growth kinetics in lithium niobate single crystals studied by piezoresponse force microscopy. Appl. Phys. Lett. 86, 012906 (2005).
Kalinin, S. V., Rar, A. & Jesse, S. A decade of piezoresponse force microscopy: progress, challenges, and opportunities. IEEE Trans. Ultrason. Ferroelectr. 53, 2226–2252 (2006).
Jesse, S. & Kalinin, S. V. Band excitation in scanning probe microscopy: sines of change. J. Phys. D. Appl. Phys. 44, 464006 (2011).
Jesse, S. et al. Resolution theory, and static and frequency-dependent cross-talk in piezoresponse force microscopy. Nanotechnology 21, 405703 (2010).
Balke, N. et al. Exploring local electrostatic effects with scanning probe microscopy: implications for piezoresponse force microscopy and triboelectricity. ACS Nano 8, 10229–10236 (2014).
Jesse, S., Mirman, B. & Kalinin, S. V. Resonance enhancement in piezoresponse force microscopy: Mapping electromechanical activity, contact stiffness, and Q factor. Appl. Phys. Lett. 89, 022906 (2006).
Hatt, R. A. & Cao, W. Landau-Ginzburg model for antiferroelectric phase transitions based on microscopic symmetry. Phys. Rev. B 62, 818–823 (2000).
Tolédano, P. & Guennou, M. Theory of antiferroelectric phase transitions. Phys. Rev. B 94, 014107 (2016).
Misirlioglu, I. B., Pintilie, L., Boldyreva, K., Alexe, M. & Hesse, D. Antiferroelectric hysteresis loops with two exchange constants using the two dimensional Ising model. Appl. Phys. Lett. 91, 202905 (2007).
Pan, W., Zhang, Q., Bhalla, A. & Cross, L. E. Field-forced antiferroelectric-to-ferroelectric switching in modified lead zirconate titanate stannate ceramics. J. Am. Ceram. Soc. 72, 571–578 (1989).
Zhou, L., Zimmermann, A., Zeng, Y.-P. & Aldinger, F. Fatigue of field-induced strain in antiferroelectric Pb0.97La0.02(Zr0.77Sn0.14Ti0.09)O3 Ceramics. J. Am. Ceram. Soc. 87, 1591–1593 (2004).
Wei, X.-K. et al. Ferroelectric translational antiphase boundaries in nonpolar materials. Nat. Commun. 5, 3031 (2014).
Barone, P., Di Sante, D. & Picozzi, S. Improper origin of polar displacements at CaTiO3 and CaMnO3 twin walls. Phys. Rev. B 89, 144104 (2014).
Aert, S. V. et al. Direct observation of ferrielectricity at ferroelastic domain boundaries in CaTiO3 by electron microscopy. Adv. Mater. 24, 523–527 (2012).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab-initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Grimme, S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J. Comput. Chem. 27, 1787–1799 (2006).
Fonari, A. & Stauffer, S. vasp_raman.py. https://github.com/raman-sc/VASP/ (2013).
Acknowledgements
A portion of the work at ORNL, including ambient scanning probe microscopy and data interpretation, were supported by the US Department of Energy, Office of Science, Basic Energy Sciences, Materials Science and Engineering Division. A.D. wish to acknowledgement the support of the CIEE/Baltic-American Freedom Foundation in funding parts of this work. Raman, SHG, and SPM measurements were conducted at the Center for Nanophase Materials Sciences, which is a DOE Office of Science User Facility. A.N.M. acknowledges National Academy of Sciences of Ukraine and has received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Skłodowska-Curie grant agreement No 778070. The work at Vanderbilt University was supported in part by the U.S. Department of Energy, Office of Science, Basic Energy Sciences, Materials Science and Engineering Division grant DE-FG02-09ER46554 and by the McMinn Endowment at Vanderbilt University. Calculations were performed at the National Energy Research Scientific Computing Center, a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231 and using systems provided by the U.S. Department of Defense’s High Performance Computing Modernization Program (HPCMP). The authors are grateful for funding support from AFOSR (LRIR#16RXCOR322).
Author information
Authors and Affiliations
Contributions
A.D., K.K., S.N., M.C. carried out imaging experiments in ambient and vacuum environments. A.P. carried out Raman and SHG spectroscopies. F.Y., B.C. carried out X-ray diffraction. J.A.B., L.T., A.O. carried out first principles modeling of structure and domain walls. S.T.P. supervised the DFT calculations and participated in theoretical analysis and paper writing. T.F. and J.A.B. calculated Raman spectra. M.A.S., M.A.M. provided the thiophosphate crystal, helped with data interpretation and manuscript writing. E.A.E. and A.N.M. carried out analytical modeling. A.D.,. J.B., Y.V. provided the selenide crystal. A.D., J.B., Y.V., N.B., S.V.K. helped with data interpretation and manuscript writing. P.G. helped with theoretical interpretation and manuscript writing. P.M. led the research effort and manuscript writing. P.M., K.K., and A.N.M. developed the ferroelectric/antiferroelectric phase coexistence picture.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Chun-Gang Duan, Dmitri Tenne and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Dziaugys, A., Kelley, K., Brehm, J.A. et al. Piezoelectric domain walls in van der Waals antiferroelectric CuInP2Se6. Nat Commun 11, 3623 (2020). https://doi.org/10.1038/s41467-020-17137-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-17137-0
This article is cited by
-
High-performance van der Waals antiferroelectric CuCrP2S6-based memristors
Nature Communications (2023)
-
Local probing of the non-uniform distribution of ferrielectric and antiferroelectric phases
Nano Research (2023)
-
Photo-magnetization in two-dimensional sliding ferroelectrics
npj 2D Materials and Applications (2022)
-
Continuously tunable ferroelectric domain width down to the single-atomic limit in bismuth tellurite
Nature Communications (2022)
-
Ferroelectric order in van der Waals layered materials
Nature Reviews Materials (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.