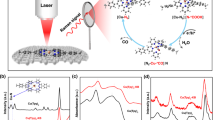
Abstract
For most metal-containing CO2 reduction reaction (CO2RR) electrocatalysts, the unavoidable self-reduction to zero-valence metal will promote hydrogen evolution, hence lowering the CO2RR selectivity. Thus it is challenging to design a stable phase with resistance to electrochemical self-reduction as well as high CO2RR activity. Herein, we report a scenario to develop hydrocerussite as a stable and active electrocatalyst via in situ conversion of a complex precursor, tannin-lead(II) (TA-Pb) complex. A comprehensive characterization reveals the in situ transformation of TA-Pb to cerussite (PbCO3), and sequentially to hydrocerussite (Pb3(CO3)2(OH)2), which finally serves as a stable and active phase under CO2RR condition. Both experiments and theoretical calculations confirm the high activity and selectivity over hydrocerussite. This work not only offers a new approach of enhancing the selectivity in CO2RR by suppressing the self-reduction of electrode materials, but also provides a strategy for studying the reaction mechanism and active phases of electrocatalysts.
Similar content being viewed by others
Introduction
Electrocatalysis has emerged as a promising technology for renewable energy conversion and storage1,2,3,4, where a key factor is the development of electrocatalysts with higher activity, better selectivity, longer stability, and lower cost5,6. While the activity and stability are the two ends of a seesaw, the high activity of electrocatalysts often cannot be sustained for a long time, mainly because of the undesirable reconstruction of electrode surfaces. With the development of in situ characterization techniques, researchers have observed the structural transformation of electrocatalysts during the electrolysis7. Many efforts have been devoted to exploring the real active species derived from the pre-catalysts. For instance, metal oxyhydroxides, derived from the oxidative transformation of metal chalcogenides and pnictides, are found to be the active species for the oxygen evolution reaction (OER), promoting the rapid developments of highly efficient electrocatalytic materials for OER8,9,10. Thus the exploration of the real active species is of great importance for the rational design and synthesis of advanced electrocatalysts with high intrinsic activity.
Electrochemical CO2 reduction reaction (CO2RR) can convert the greenhouse gas (CO2) to various value-added chemicals11,12,13,14,15,16, while the competing hydrogen evolution reaction (HER) is usually more favorable on many metallic electrodes. Although many high-valence metal electrocatalysts are proved to be reduced to zero-valence metal at CO2RR condition, such as BiOI17, PbO218, SnO219, CuO20, In2O321, it was found the residual metastable metal oxides are tightly correlated with the high selectivity towards CO2RR22,23,24. However, with the self-reduction occurring, HER becomes more and more dominant, leading to a diminished CO2RR efficiency. Besides, many complex electrocatalysts also undergo unavoidable dissociation and self-reduction under cathodic working conditions. For example, a Ni(II) benzenedithiol complex was revealed to be completely transformed to Ni nanosheets under cathodic conditions25. A Cu(II) phthalocyanine complex undergoes reversible conversion to metallic Cu clusters, which acts as the active species in CO2RR26. The self-reduction of electrocatalysts and the desirable CO2RR are actually competitive processes. To achieve high selectivity, developing electrocatalysts with predominant CO2RR over self-reduction is highly desirable.
Herein, we report a scenario to make effective use of the electrochemical structure evolution of a complex pre-catalyst, tannin–lead(II) (denoted as TA–Pb), toward high formate selectivity in CO2RR. The TA–Pb pre-catalyst performs a formate Faradaic efficiency (FE) of up to 96.4 ± 0.9%. Through a set of comprehensive characterizations, it is identified that TA–Pb is transformed to cerussite (PbCO3, denoted as PCO) at first, then sequentially to hydrocerussite (Pb3(CO3)2(OH)2, denoted as PCOH) at steady state, which essentially serves as the active phase for highly selective formate production. In addition, we also synthesize pure cerussite nanoparticles and hydrocerussite nanoplates to confirm the transformation mechanism and the key role of hydrocerussite in CO2RR, respectively. Moreover, the density functional theory (DFT) calculations also reveal the high formate selectivity, which can be attributed to the appropriate binding strength with HCOO* on hydrocerussite. All the results unveil hydrocerussite as a highly selective and stable phase for formate production in CO2RR.
Results
Electrochemical performances and transformation of TA-Pb
The tannin–lead(II) (TA–Pb) complex film is prepared by simply mixing Pb(II) and tannin aqueous solution in the presence of carbon fiber paper (CP) as the substrate (Fig. 1a). By examining with a high-resolution transmission electron microscope (HRTEM), the coordination of TA and Pb(II) forms a layer of amorphous film contacting closely to the substrate with the thickness of ~20 nm for single-layer TA–Pb with CP as the substrate (inset in Fig. 1a, Supplementary Fig. 1 and Supplementary Note 1). The extended X-ray absorption fine structure (EXAFS) exhibits clear coordination of Pb–O and Pb–C for a five-membered ring in a chelate ligand (Fig. 1b)27, suggesting the 6-coordinated Pb(II) ions as reported before28.
a A scheme illustrated for the TA–Pb preparation. The inset is the HRTEM image of single-layer TA–Pb. Scale bar, 10 nm. b Pb L3-edge EXAFS spectrum of TA–Pb. The inset is the proposed structure of TA–Pb. c FEs of 3-layer TA–Pb at steady state under different potentials. d j-t curve and corresponding formate FE of 3-layer TA–Pb at steady state (stage III in the inset) under −0.92 V. The inset is the j-t curve of the as-prepared TA–Pb, which can be divided into three stages labeled as I, II, and III. e 1H-NMR spectra of formate by using 12CO2 and 13CO2 as feedstocks by using 0.5 M Na2SO4 as the electrolyte to eliminate the interference of NaHCO3. Error bars correspond to the standard error of the mean.
The electrochemical activity was tested in a standard three-electrode system with 0.5 M NaHCO3 as the electrolyte (Supplementary Fig. 2). Before CO2RR tests, all the samples were pre-treated under −0.92 V for 30 min to reach the steady state. Liquid products were detected by nuclear magnetic resonance (NMR), while the gaseous ones were detected by gas chromatography (GC). The products in CO2RR with single-layer TA–Pb as pre-catalyst are formate, CO, and H2, which is in accordance with other reported Pb-based electrocatalysts29,30,31. And −0.92 V vs. reversible hydrogen electrode (RHE) is the optimum potential to achieve the highest formate FE (Supplementary Fig. 3 and Supplementary Note 2). The formate FE can be further improved by increasing the layers of the TA–Pb, and the 3-layer TA–Pb complex shows the highest formate FE of 96.4 ± 0.9% at the optimum potential of −0.92 V with a small amount of H2 and negligible CO. This is almost the highest value among Pb-based electrocatalysts (Supplementary Table 1). The formate FE remains above 90% at a wide potential range from −0.82 to −1.12 V (Fig. 1c). The result of inductively coupled plasma-mass spectrometry (ICP-MS) exhibits an extremely low Pb loading of ~25 μg cm−2 for 3-layer TA–Pb, thus leading to a high formate turnover frequency (TOF) of 0.055 s−1 at the optimum potential of −0.92 V. Compared with the TA–Pb pre-catalyst, Pb foil displays much lower formate FEs of <40% (Supplementary Fig. 4). It is also noticed that the j-t curves of the as-prepared 3-layer TA-Pb can be divided into three stages, i.e., stage I (0–3 min) with current density sharply declining, stage II (3–30 min) with current density increasing mildly, and stage III (>30 min) with almost constant current density (inset in Fig. 1d). These stages indicate the structural evolution of TA–Pb, whose details will be discussed later. At a steady state, the derived active species performs excellent stability of both formate FE and current density for 10 h (Fig. 1d). Labeled 13CO2 was used to verify the carbon source of produced formate in control experiments under the optimum potential. As shown in the 1H-NMR spectrum in Fig. 1e, the H12COO− shows the chemical shift only at 8.35 ppm. The appearance of two new peaks at 8.61 and 8.13 ppm indicates the formation of H13COO−, reflecting that carbon in formate is from CO2 rather than the decomposition of the complex.
Based on the three stages in Fig. 1d inset, we have captured another two different states derived from TA–Pb in the electrolysis (Fig. 2a). The X-ray diffraction (XRD) patterns show that the two intermediate phases are cerussite (PbCO3) and hydrocerussite (Pb3(CO3)2(OH)2), respectively (Fig. 2b). And the phase of hydrocerussite maintains after a long-term test (Supplementary Fig. 5). The TA–Pb derived PbCO3 and Pb3(OH)2(CO3)2 are denoted as t-PCO and t-PCOH hereafter. Their corresponding HRTEM images show the decreasing thickness and increasing crystallinity along with the cathodic electrolysis (Supplementary Fig. 6). The structures of these intermediates were further identified by quasi-in-situ X-ray fine structure (XAFS). The EXAFS spectra of t-PCO and t-PCOH match well with the references cerussite and hydrocerussite, respectively (Fig. 2c). The similar Pb L3-edge in the X-ray absorption near edge structures (XANES) of different stages indicates that the valence state of Pb remains unchanged during the electrochemical CO2RR measurements (Fig. 2d).
a Illustration of the transformation from TA-Pb to t-PCO and t-PCOH. b XRD patterns, c Quasi-in-situ Pb L3-edge EXAFS, d XANES spectra, e O 1s, and f Pb 4f 7/2 XPS spectra of TA–Pb, t-PCO and t-PCOH. The XRD peaks from the substrate are labelled by black stars. g Time-dependent in situ Raman spectra of TA–Pb under CO2 bubbling. h Potential-dependent in situ ATR-FTIR spectra of hydrocerussite with CO2 bubbling. The bands around 1640 and 1220 cm−1 are attributed to the adsorbed interfacial water and the vibration of Si–O from silicon as the reflection window, respectively51.
The X-ray photoelectron spectra (XPS) of TA-Pb clearly show the organic functional groups of tannin molecules in the C 1s and O 1s spectra (Fig. 2e and Supplementary Fig. 7). However, these peaks of organic functional groups completely disappear in the t-PCO, suggesting the decomposition of the TA-Pb complex in stage I. The symmetric O 1s peak of t-PCO at 532.7 eV suggests the O element only exists in the form of CO32− 32. However, in t-PCOH, the appearance of a new peak represented OH− confirms the formation of hydrocerussite32. Similarly, the symmetric peak at 138.8 eV is attributed to PbCO3 in the Pb 4f 7/2 spectra of t-PCO (Fig. 2f), while the peak at 138.3 eV in t-PCOH represents the formation of Pb-OH33. It should be pointed out that no Pb(0) is found throughout the whole process. And the cyclic voltammetry (CV) curve of t-PCOH shows no redox peak in the tested range, firmly verifying the stability of hydrocerussite in CO2RR (Supplementary Fig. 8).
The transformation of the TA-Pb complex was further investigated by Raman spectroscopy and Fourier transform infrared (FTIR) spectroscopy. The time-dependent in situ Raman spectra are shown in Fig. 2g. It is clearly shown that the fluorescent intensity from the ligand tannin ascends at first and then descends with the time prolonging (Supplementary Fig. 9,10), indicating the TA-Pb complex undergoes a part-to-whole dissociation34. A small peak at 1065 cm−1 appears after electrolysis for 210s, which is attributed to C–O symmetric stretching vibration of CO32− 35, indicating the formation of t-PCO. Because of the similar Raman spectroscopy shape of cerussite and hydrocerussite in this region36, the formation of t-PCOH cannot be distinguished from Fig. 2g. It should be also noted that the peak of CO32− appears as early as the ascending process of fluorescence, which means that the dissociation of TA-Pb and the formation of t-PCO are accompanying rather than separate and sequential. Moreover, in ex situ FTIR spectra, the disappearance of the complex peaks again confirms the dissociation of the complex (Supplementary Fig. 11). In situ attenuated total reflectance-Fourier transform infrared (ATR-FTIR) spectroscopy was employed to investigate the reaction path of hydrocerussite. As shown in Fig. 2h, with the applied potential decreasing, the intensity of bands at ~1360 cm−1 gradually increases (Supplementary Fig. 12 and Supplementary Note 3), which can be associated with the vibration of O–C–O in the two-oxygen bridge-bonded formate species (*HCOO)37, confirming the *HCOO pathway of hydrocerussite (Supplementary Fig. 13). No obvious band associating with CO* can be found in the region of 1900–2100 cm−1, indicating that the formation of CO on hydrocerussite is almost inhibited38, which is consistent with the above experimental FE results. All the above results confirm that the TA–Pb complex electrochemically dissociates and transforms into cerussite and hydrocerussite sequentially, in which the valence state of Pb remains +2 during the whole electrolysis, suggesting hydrocerussite to be the active species for electrochemical CO2RR via the pathway of *HCOO as the intermediate.
Performances of as-prepared cerussite and hydrocerussite
To further investigate the transformation of cerussite to hydrocerussite, we prepared cerussite nanoparticles (denoted as c-PCO) and studied their behavior under the same conditions of CO2RR. The TEM image of the as-prepared c-PCO shows the irregular nanoparticles (Fig. 3a and Supplementary Fig. 14a). After tested at −0.92 V in the presence of CO2 for 30 min, it is found that the c-PCO nanoparticles completely transform to monocrystalline hexagonal nanosheets (Fig. 3b and Supplementary Fig. 14b). The corresponding selected area electron diffraction (SAED) pattern shows the dominant exposed facet of (0001) (inset in Fig. 3b). XRD pattern of the hexagonal nanosheets matches well with hexagonal hydrocerussite without any impurity (Fig. 3c), and the nanosheets is named as c-PCOH. XPS and ex situ Raman spectra also confirm the phase change from cerussite to hydrocerussite (Supplementary Figs. 15, 16). By studying the transformation process, it is found that the c-PCO nanoparticles first convert to cerussite nanoprisms via an Ostwald ripening process39,40, then to hexagonal hydrocerussite nanosheets through the selective etching of CO2 and the insertion of OH− (see more details in Supplementary Figs. 17–20 and Supplementary Notes 4–7).
a TEM image of c-PCO. Scale bar, 500 nm. b TEM image of c-PCOH transformed from c-PCO. Scale bar, 500 nm. The inset is the corresponding SAED pattern. Scale bar, 2 1/nm. c XRD patterns of c-PCO and c-PCOH. The peaks from the substrate are labelled by black stars. d SEM image of the as-prepared h-PCOH. Scale bar, 10 μm. e XRD patterns of h-PCOH before and after the CO2RR test for 5 h. The peaks from the substrate are labelled by black stars. f Comparison of formate FEs of t-PCOH, h-PCOH, and Pb foil at different potentials. Error bars correspond to the standard error of the mean.
The hydrocerussite nanoplates (shorted as h-PCOH) were also fabricated to estimate their CO2RR performance. The SEM image of the as-prepared hydrocerussite nanoplates performs quasi-hexagonal nanoplates with the diameter of several microns (Fig. 3d). After the CO2RR measurements, all the results of SEM images (Supplementary Fig. 21), XRD patterns (Fig. 3e), XPS spectra (Supplementary Fig. 22) and ex situ Raman spectra (Supplementary Fig. 23) indicate that the morphology, structure, and composition of the h-PCOH remain unchanged, confirming that hydrocerussite is stable and the active species for CO2RR. When compared the CO2RR performances of h-PCOH with t-PCOH, it is found that h-PCOH generates the similar products of dominant formate, a small amount of H2, and trace CO (Supplementary Fig. 24a). Specifically, h-PCOH performs the formate FE of 90.1 ± 0.8% at −0.92 V with the stability of over 10 h (Fig. 3f and S24b). The slightly lower FE of h-PCOH may originate from the poor coverage of the relatively large h-PCOH nanoplates (Supplementary Fig. 21), leaving part of the carbonaceous substrate exposed to give off much H2. The result, in turn, confirms the high coverage of in situ formed t-PCOH. Moreover, limited by the high mass loading of h-PCOH (4.01 mg cm−2 for Pb), its TOF is calculated to be only 6.8 × 10−4 s−1, which is 80 times lower than that of t-PCOH, further indicating a high catalytic efficiency of the complex-derived hydrocerussite.
DFT calculations
To understand the chemical origin of high formate selectivity in CO2RR over hydrocerussite, DFT calculations were performed. The hydrocerussite models are structured, and the optimized lattice parameters of 5.28 × 5.30 × 23.68 Å are in good agreement with the experiments (Supplementary Fig. 25a)41. As observed above, hydrocerussite prefers to expose the (0001) surface. In this way, there are three possible terminations of hydrocerussite (0001), denoted with Layer A, B, and C, as shown in Supplementary Fig. 25b. The B-termination is thermodynamically most stable with the surface energies (Es) of −0.24 eV nm−2 relative to A (Es = −0.04 eV nm−2) and C (Es = 2.64 eV nm−2). Besides, since hydrocerussite is in situ produced from the complex pre-catalyst, two kinds of vacancies (CO32− or OH− removal) are considered herein. As a consequence, six possible active sites on hydrocerussite are examined to compared with the reference metallic Pb(111), including perfect A, B, and C terminations, denoted as A-p, B-p, and C-p, and defected A, B, and C ones, denoted as A-d, B-d, and C-d (Supplementary Fig. 25b). Then we calculated the adsorption energies of all the possible intermediates in CO2RR to producing H2, CO, and formate, respectively. According to the result of in situ ATR-FTIR spectra, *HCOO adsorption energy is chosen as the descriptor to establish the correlation between different active sites and adsorbates, as shown in Supplementary Fig. 26.
The reaction free energies (ΔG) of all possible elementary steps are calculated and plotted versus the adsorption free energy of *HCOO [Gad(HCOO)] (Fig. 4a), where the solid lines represent the ΔG-determining steps of HCOOH, CO, and H2 production. The HCOOH production can follow two paths via either *COOH or *HCOO, crossed at about −1.3 eV. On A-p, B-p, and C-p, the ΔG for HCOOH production is unfavored (about 2.0 eV), which means at least −2.0 V is needed to produce HCOOH on the perfect surfaces. On the contrary, the ΔG-determining step on defected surfaces is smaller than 0.5 eV. On A-d and C-d, HER is more favorable than HCOOH and CO. However, HCOOH is most preferred over B-d via the *HCOO pathway, and the product selectivity preference obeys the order of HCOOH > H2 > CO, which is exactly consistent with our experiments. Besides, B-d is the most stable termination and should be the dominant site of hydrocerussite. In comparison, the HCOOH activity and selectivity on Pb(111) are lower than the B-d of hydrocerussite, in agreement with the low HCOOH FE of Pb foil about 40% (Supplementary Fig. 4b). The explicit reaction free energy diagrams under 0 V vs. RHE on B-d of hydrocerussite and Pb(111) are displayed in Supplementary Fig. 27. On B-d, HCOOH is more favorable than H2 and CO in thermodynamics due to the stronger adsorption of *HCOO than *H and *COOH by 0.61 and 1.24 eV, respectively. On Pb(111), although *HCOO is also more preferred than *H, their small energy difference of only 0.17 eV together with the higher concentration of proton than CO2 in an electrolyte, can actually reverse the preference of HCOOH and H2. Figure 4b is the two-dimensional map of activity and selectivity of the sites of hydrocerussite, where Gad(*COOH) is introduced as another dimension and varying independently with Gad(*HCOO). The map contains four regions, which represent different products. Only B-d shows an obvious HCOOH preference and activity, further confirming B-d as the active site.
a Reaction free energies of involved elementary reactions plot versus Gad(*HCOO). b Two-dimensional map of activity and selectivity for CO2RR. Different regions represent different products, and colors represent the negative ΔG of GDS measured as the label on the right side. c Free energy diagrams of CO2RR into HCOOH under different experimental potentials; insets are structures of initial (IS), transition (TS) and final (FS) state of CO2 protonation (1) and HCOOH formation (2); purple, red, gray, and white atoms are Pb, O, C, and H, respectively; green atoms represent H that participate in the reaction. d Experimental partial current density of formate (jexp) versus theoretical charge transfer rate k (10−17 C ∙ s−1 ∙ site−1). Error bars correspond to the standard error of the mean.
To analyze the effect of applied potential on CO2RR into HCOOH, the potential-dependent barriers and reaction energies under different experimental potentials are calculated (Fig. 4c). At −0.82 V vs. RHE, the elementary reactions CO2(g) + (H+ + e−) → *HCOO and *HCOO + (H+ + e−) → HCOOH are both exothermic, with a barrier of 0.82 and 0.57 eV, respectively. In kinetics, CO2 protonation is still more difficult than the formation of HCOOH and can be considered as the rate-determining step (RDS). As the potential decreases, the activation energy of CO2 protonation becomes lower gradually, which will increase the reaction rate and HCOOH partial current density in the experiment according to the transition state theory. Therefore, we further perform a microkinetic simulation to calculate the charge transfer rate of a single active site (k) at different applied potentials. Figure 4d shows the experimental HCOOH partial current density (jexp) plotted versus our theoretical charge transfer rate. A nice linear correlation has been established, confirming our calculations and analysis above regarding the active site and reaction mechanism.
Stablity of hydrocerussite
In the whole electrolysis, we attribute the high formate FE and electrochemical stability of hydrocerussite to its dominant CO2RR. In this sense, both the electrochemical reduction from hydrocerussite to metal Pb and the competing HER are suppressed. It can be evidenced by the comparison of linear scan voltammetry (LSV) curves in Ar and CO2 (Supplementary Fig. 28). All the redox peaks under Ar completely disappear in CO2, suggesting the inhibition of Pb reduction under CO2 bubbling. Another controlled experiment is to test the stability of h-PCOH at −0.92 V under Ar for 5 h. Different from the results under CO2, the FE of hydrogen dramatically rises to over 80%, and the formate FE decreases to around 5% (Fig. 5a and Supplementary Fig. 29). Besides, with the electrolysis time prolonging, the hydrogen FE becomes larger and larger, while the formate FE goes smaller. And no CO can be detected under this condition. It should be noted that the total FE of all the products is obviously smaller than 100%, suggesting that parts of the provided electrons are used to reduce the hydrocerussite. This conjecture can be further confirmed by the XRD pattern of this sample after electrolysis for 5 h. As shown in Fig. 5b, the appearance of XRD peaks from PbO and metal Pb clearly demonstrates the decomposition and reduction of hydrocerussite under this condition, which is in accordance with the Pourbaix diagram of lead in the presence of CO32− 42. In addition, when the reduced hydrocerussite is tested in CO2 again, obvious decay of formate FE (~60%) can be found just as our expectation (Fig. 5c). From the above results, it is sure that the presence of CO2 is of great importance to maintain the stability of hydrocerussite under cathodic conditions. Without CO2, hydrocerussite is gradually decomposed and finally reduced to metal Pb, accompanying with enhanced hydrogen evolution and weakened selectivity of formate production (Fig. 5d). In other words, the preference of CO2RR on hydrocerussite can effectively suppress the self-reduction of the electrocatalyst and the accompanying enhanced HER.
a FEs of h-PCOH at −0.92 V for 5 h in Ar. b Comparison of XRD patterns of h-PCOH after electrolysis under −0.92 V for 5 h in CO2 and in Ar. The peaks from the substrate of CP are labelled by black stars. c FEs of tested h-PCOH at different potentials in CO2. d Behaviors of hydrocerussite as the cathodic electrocatalyst. Error bars correspond to the standard error of the mean.
Discussion
In summary, we have revealed the dynamic change of TA–Pb complex film as a model pre-catalyst under the conditions of CO2RR, and finally unveiled hydrocerussite as the new active species for formate generation. The rapid transformation of TA–Pb to cerussite (t-PCO) and subsequent conversion to hydrocerussite (t-PCOH) are revealed during the electrochemical CO2RR conditions. t-PCOH is found to be the active species to produce formate with an optimum FE of 96.4 ± 0.9%. In addition, cerussite nanoparticles are prepared to verify the phase transformation to hydrocerussite. The hydrocerussite nanoplates are also directly fabricated, and perform similar high formate FE and long stability with t-PCOH, further confirming the key role of hydrocerussite. DFT calculations indicate that the hydrocerussite is highly active and selective for formate production. The excellent stability of hydrocerussite originates from its dominance of CO2RR, thus the reduction of the electrocatalyst itself and consequent HER is blocked. This work not only opens a facile avenue to improve the CO2RR selectivity by suppressing the reduction of the electrocatalysts, but also establishes a guideline for fundamentally understanding the transformation process and active species of metal-complex catalytic materials for cathodic reactions.
Methods
Depositing TA–Pb complex on substrates
For a typical synthesis of a single-layer TA–Pb complex, a piece of the substrate was put in a clean and empty 20 mL vessel with the addition of 10 mL 10 mM Pb(NO3)2. After sufficient adsorption for 15 min, 10 mL 9 mg mL−1 tannic acid (TA) solution was quickly added. 2 M NaOH was then added to adjust pH to ~7. Then the vessel was gently shaken and stood at room temperature without disturbance for 6 h. At last, the product was washed with water and dried naturally. To prepare multiple-layer TA-Pb, this procedure was repeated for suitable times. For instance, if this procedure was repeated for three times, the as-prepared products are named as the 3-layer TA–Pb. For environmental concerns, the Pb-containing residual reaction solution was collected and stored in a dedicated container. CP was used as the substrate in electrochemical measurements. Before deposition, CP was cut into rectangular pieces with a size of 1 × 3 cm2 and immersed in acetone and water for 15 min in sequence. Rutile TiO2 nanorod arrays supporting on F-doped tin oxide (FTO) glass were used as the substrate for TEM observation and ex situ FTIR spectroscopy. FTO glass was cut into a rectangular shape with a size of 1 × 2.5 cm2, and sonicated in diluted HCl, acetone, and water for 15 min in sequence. To prepare rutile TiO2 nanorod arrays, 15 mL water, 15 mL concentrated HCl, and 0.5 mL tetrabutyl titanate were added to a Teflon-lined stainless-steel autoclave and stirred for 15 min. A piece of clean FTO glass was put into the autoclave with the conductive side facing down. Then the autoclave was sealed and treated at 180 °C for 1 h. After the reactor cooled down naturally, the FTO with the white product was washed with water and alcohol, respectively, and dried naturally. Then the product was calcined in air at 500 °C for 2 h with the heating rate of 5 °C min−1 to finally obtain the rutile TiO2 nanorod arrays.
Synthesis of c-PCO nanoparticles
c-PCO nanoparticles were prepared by a simple precipitation method. Briefly, 5 mL 1.2 M Na2CO3 and 5 mL 1.2 M Pb(OAc)2·3H2O were mixed and stirred for 5 min. Then 10 mL water was added and stirred for another 1 h at room temperature. The white product was collected by centrifugation and washed with water and ethanol several times, then dried in a vacuum oven for 6 h.
Synthesis of h-PCOH nanoplates
2.50 g Pb(NO3)2, 2.25 g urea, 0.075 g polyethylene glycol with the molecular weight of 2000 (PEG-2000), and 200 mL water were added in a flask. The flask was vigorously stirred and refluxed at 105 °C for 5 h. The product was collected by centrifugation and washed with water and ethanol several times, then dried in a vacuum oven for 6 h.
Characterization
The transmission electron microscopy (TEM) images and high-resolution TEM (HRTEM) images were carried out with a JEOL JEM-2100F microscope. The scanning electron microscopy (SEM) images were taken with a Hitachi S-4800 microscope. The X-ray absorption fine structure (XAFS) were performed at the 1W1B beamline of Beijing Synchrotron Radiation Facility (BSRF). And the XAFS spectra were analyzed with the ATHENA software package43. The k-weighting was set to 1 for the Fourier transforms. Fourier transforms of χ(k) were performed in the k-range of 2–8 Å−1 with the Hanning window function. All the EXAFS spectra were without phase correction. The gaseous products of electrochemical CO2RR were detected by a GC (Shimadzu GC-2010). And the formate was measured by a 400 MHz NMR spectrometer (Bruker AVANCE III HD). The determination of formate was based on the internal standard method by using 100 ppm dimethylsulfoxide (DMSO) as the internal standard substance. The XRD patterns were recorded on a Bruker D8-Focus diffraction system with a Cu Kα source (λ = 1.54056 Å). The ICP-MS was collected on an Agilent 7700X instrument. The XPS were carried out with a Thermo ESCALAB 250XI spectrometer. All the peaks were calibrated with C 1s spectrum at the binding energy of 284.8 eV. The Raman spectra were recorded on a Renishaw inVia reflex Raman microscope under an excitation of 532 nm laser with the power of 20 mW. The ex situ FTIR were taken with a Bruker ALPHA-T FTIR spectrometer.
Electrochemical measurements
All the electrochemical measurements were taken with a CHI 650e electrochemical workstation (CH Instruments, Austin, TX). A typical three-electrode system was employed in a home-made H-type electrolytic cell. Generally, 0.5 M NaHCO3 was used as the electrolyte. Only with 13CO2 as the feedstock, 0.5 M Na2SO4 was used as the electrolyte to eliminate the effect of carbonate species from NaHCO3. Before the measurements, Ar or CO2 was bubbled to the system for over 30 min to remove the dissolved oxygen and continuously bubbled throughout the measurements. TA–Pb supported on CP and Pb foil were used as a working electrode directly. For the powder samples like c-PCO and h-PCOH, 5 mg sample was first dispersed in 1 mL ethanol with the addition of 20 μL 5% Nafion 117 solution. After sufficient sonification, all the 1 mL homogeneous ink solution was carefully dropped on a piece of CP with the exposed area of 1 cm2 by epoxy coating, making the mass loading to be 5 mg cm−2. Saturated calomel electrode (SCE) and Pt sheet were used as the reference electrode and counter electrode, respectively. All the potentials mentioned in this work were against the RHE without additional description. The scan rate for all the voltammetry was 10 mV s−1. Before all CO2RR measurements, each sample was tested at −0.92 V for 30 min to achieve the steady state. For potential-dependent FE measurements, the sample was maintained at the specific potential for another 30 min to accumulate enough products. For environmental concerns, we analyzed the Pb content in the electrolyte after tests by ICP-MS. The result showed that only 4.418 μg L−1 Pb was detected, which was obviously lower than the Chinese Standards for Drinking Water Quality (GB 5749-2006) of 0.01 mg L−1 for Pb, indicating that the use of hydrocerussite as electrocatalyst for CO2RR was eco-friendly.
Calculation of TOF
The calculation of TOF is based on Eq. (1) as follows.
where \({\it{n}}_{\mathrm{f}}\) is the amount of the generated formate, \({\it{n}}_{\it{c}}\) is the amount of the active catalyst site, and t is the duration time. In this work, we assume all the Pb sites are active for the reaction. The generated formate is calculated according to Eq. (2).
where \({\it{Q}}\) is the integrated coulombs from the I-t curve of TA-Pb, FEf is the FE of formate, and F is the Faradaic constant.
Electrochemical in situ spectroscopy
In situ ATR-FTIR spectra were obtained on a Nicolet 6700 FTIR spectrometer with silicon as the prismatic window. A thin layer of gold film was chemically deposited on the surface of the silicon prismatic prior to each experiment. Then 20 μL sample ink was carefully dropped on the surface of the gold film, together served as the working electrode. Pt sheet and Ag/AgCl were used as the counter electrode and the reference electrode, respectively. 0.5 M NaHCO3 was employed as the electrolyte. CO2 or argon was bubbling to the electrolyte in advance and continuously bubbled throughout the experiment. The in situ Raman spectroscopy of the decomposition of TA–Pb was carried out on the same Raman microscope mentioned before at −1.22 V vs. RHE in 0.5 M NaHCO3 with CO2 bubbling. The electrolytic cell was homemade by Teflon with a piece of round quartz glass as the cover to protect the objective of the microscope. A piece of TA–Pb supported on CP was inserted through the wall of the cell to keep the plane of the working electrode perpendicular to the incident laser. Pt wire as the counter electrode was rolled to a circle around the working electrode. SCE was used as a reference electrode. Quasi-in-situ XAFS spectra were acquired by measuring the electrochemical performances of the sample just near the synchrotron radiation facility, then the tested sample was immediately delivered to the facility for XAFS measurements.
Computational details
DFT calculations were performed with the Vienna Ab initio Simulation Package44,45. The revised Perdew-Burke-Ernzerhof (rPBE)46 exchange-correlation functional was adopted as the level of generalized gradient approximation (GGA). The atomic valence orbitals were described by plane-wave basis sets with the kinetic cutoff energies of 400 eV. A Gaussian smearing with a width of 0.2 eV was used. All the total energy calculations were converged at 0.05 eV/Å. The hydrocerussite (0001) surface with a vacuum of 20 Å was used to model experimental hydrocerussite samples. Six layers were contained in the slab, with the top three relaxed and the rest fixed. A (4 × 4) Pb(111) slab with 4 layers was used to model Pb foil, where the top two were allowed to be relaxed. To calculate the protonation barriers, a layer of H2O with a density of ~1 g cm−2 was introduced upon the surface of catalysts.
Reaction phase diagram
All the adsorption free energies of intermediates were first calculated, referenced to CO(g), H2(g), and H2O(g). All the adsorption free energies could be correlated with that of *HCOO, in the format of Gad(*X) = a × Gad(*HCOO) + b, where Gad(*X) was the adsorption free energy of intermediate X and Gad(*HCOO) was that of *HCOO, used as descriptor herein. Then, the reaction free energy (ΔG) of all involved elementary steps, such as *COOH + (H+ + e−) → HCOOH, can be calculated by ΔG = G(HCOOH) − G(H+ + e−) − Gad(*COOH), where G(HCOOH) was the chemical potential of formic acid and G(H+ + e−) was referred to 1/2 H2 under U = 0 V vs. RHE47, respectively, referenced to the same criterion with adsorption energies. Obviously, G(HCOOH) and G(H+ + e−) were constants, and Gad(COOH*) was linearly correlated with Gad(*HCOO). Therefore, the reaction free energy as a linear function of Gad(*HCOO) could be obtained (Fig. 4a), which was defined as the reaction phase diagram in our previous report48. Besides, a two-dimensional map of activity and selectivity (Fig. 4b) could be obtained by making Gad(*COOH) vary independently with Gad(*HCOO) and analytically calculating the corresponding reaction free energy at every pair of Gad(*COOH) and Gad(*HCOO), which can give a more accurate description on the activity and selectivity.
Potential-dependent barrier and reaction energy
The potential effect on thermodynamic reaction free energy was considered by changing the chemical potential of (H+ + e−) by –eU, as suggested in the computational hydrogen electrode47 approximation. The potential-dependent kinetic barriers of electrochemical reaction (*A + H+ + e− → *AH) were calculated by using an equivalent analogous non-electrochemical reaction (*A + *H → *AH) combined with Marcus theory, an effective method developed by Janik et al.49,50.
Microkinetics simulations
The rate of CO2 protonation is considered as the total reaction rate since it is the RDS. The rate constant (a) was determined by:
where Ga is the activation free energy; kb is the Boltzmann constant and T is temperature. A is the prefactor and calculated by:
where h is the Planck constant; Qts and Q refer the partition functions of the transition and initial states, respectively. A was approximated to be 1013 s−1 for surface reactions in this work. The forward rate of CO2 protonation [CO2(g) + (H+ + e−) + * → *HCOO] was calculated by:
where c(CO2), c(H+) and θ* are the concentration of CO2 and proton in electrolyte and coverage of the free active site, respectively. The charge transfer rate on a single active site (k) is:
where z is the total number of electrons transferred in the overall reaction, F = 1.6 × 10−19.
In principle, c(CO2), c(H+) and θ* are constant at different potentials, hence the term [c(CO2)c(H+)θ*] is assumed to be 1 in this study. By this approximation, the charge transfer rate k under different potentials can be estimated.
References
Seh, Z. W. et al. Combining theory and experiment in electrocatalysis: Insights into materials design. Science 355, eaad4998 (2017).
Wakerley, D. et al. Bio-inspired hydrophobicity promotes CO2 reduction on a Cu surface. Nat. Mater. 18, 1222–1227 (2019).
Long, C. et al. Electrochemical reduction of CO2 over heterogeneous catalysts in aqueous solution: Recent progress and perspectives. Small Methods 3, 1800369 (2018).
Lewis, N. S. & Nocera, D. G. Powering the planet: Chemical challenges in solar energy utilization. Proc. Natl Acad. Sci. USA 103, 15729–15735 (2006).
Gao, S. et al. Partially oxidized atomic cobalt layers for carbon dioxide electroreduction to liquid fuel. Nature 529, 68 (2016).
Ross, M. B. et al. Designing materials for electrochemical carbon dioxide recycling. Nat. Catal. 2, 648–658 (2019).
Handoko, A. D., Wei, F., Jenndy, Yeo, B. S. & Seh, Z. W. Understanding heterogeneous electrocatalytic carbon dioxide reduction through operando techniques. Nat. Catal. 1, 922–934 (2018).
Jin, S. Are metal chalcogenides, nitrides, and phosphides oxygen evolution catalysts or bifunctional catalysts? ACS Energy Lett. 2, 1937–1938 (2017).
He, Q. et al. Highly defective Fe-based oxyhydroxides from electrochemical reconstruction for efficient oxygen evolution catalysis. ACS Energy Lett. 3, 861–868 (2018).
Fan, K. et al. Direct observation of structural evolution of metal chalcogenide in electrocatalytic water oxidation. ACS Nano 12, 12369–12379 (2018).
Voiry, D., Shin, H. S., Loh, K. P. & Chhowalla, M. Low-dimensional catalysts for hydrogen evolution and CO2 reduction. Nat. Rev. Chem. 2, 0105 (2018).
Gu, J., Hsu, C.-S., Bai, L., Chen, H. M. & Hu, X. Atomically dispersed Fe3+ sites catalyze efficient CO2 electroreduction to CO. Science 364, 1091–1094 (2019).
Wu, J., Sharifi, T., Gao, Y., Zhang, T. & Ajayan, P. M. Emerging carbon-based heterogeneous catalysts for electrochemical reduction of carbon dioxide into value-added chemicals. Adv. Mater. 31, e1804257 (2019).
Liu, Y. & McCrory, C. C. L. Modulating the mechanism of electrocatalytic CO2 reduction by cobalt phthalocyanine through polymer coordination and encapsulation. Nat. Commun. 10, 1683 (2019).
Jiang, K. et al. Metal ion cycling of Cu foil for selective C–C coupling in electrochemical CO2 reduction. Nat. Catal. 1, 111–119 (2018).
Luc, W. et al. Two-dimensional copper nanosheets for electrochemical reduction of carbon monoxide to acetate. Nat. Catal. 2, 423–430 (2019).
Han, N. et al. Ultrathin bismuth nanosheets from in situ topotactic transformation for selective electrocatalytic CO2 reduction to formate. Nat. Commun. 9, 1320 (2018).
Lee, C. H. & Kanan, M. W. Controlling H+ vs CO2 reduction selectivity on Pb electrodes. ACS Catal. 5, 465–469 (2014).
Dutta, A. et al. Probing the chemical state of tin oxide NP catalysts during CO2 electroreduction: a complementary operando approach. Nano Energy 53, 828–840 (2018).
Raciti, D., Livi, K. J. & Wang, C. Highly dense Cu nanowires for low-overpotential CO2 reduction. Nano Lett. 15, 6829–6835 (2015).
Liang, Y., Zhou, W., Shi, Y., Liu, C. & Zhang, B. Unveiling in situ evolved In/In2O3−x heterostructure as the active phase of In2O3 toward efficient electroreduction of CO2 to formate. Sci. Bull. https://doi.org/10.1016/j.scib.2020.1004.1022 (2020).
Chen, Y., Li, C. W. & Kanan, M. W. Aqueous CO2 reduction at very low overpotential on oxide-derived Au nanoparticles. J. Am. Chem. Soc. 134, 19969–19972 (2012).
Kumar, B. et al. Reduced SnO2 porous nanowires with a high density of grain boundaries as catalysts for efficient electrochemical CO2-into HCOOH conversion. Angew. Chem. Int. Ed. 56, 3645–3649 (2017).
Deng, W. et al. Crucial role of surface hydroxyls on the activity and stability in electrochemical CO2 reduction. J. Am. Chem. Soc. 141, 2911–2915 (2019).
Hu, C. et al. In situ electrochemical production of ultrathin nickel nanosheets for hydrogen evolution electrocatalysis. Chem 3, 122–133 (2017).
Weng, Z. et al. Active sites of copper-complex catalytic materials for electrochemical carbon dioxide reduction. Nat. Commun. 9, 415 (2018).
Hartley, J. M. et al. EXAFS study into the speciation of metal salts dissolved in ionic liquids and deep eutectic solvents. Inorg. Chem. 53, 6280–6288 (2014).
Ejima, H. et al. One-step assembly of coordination complexes for versatile film and particle engineering. Science 341, 154–157 (2013).
Innocent, B. et al. Electro-reduction of carbon dioxide to formate on lead electrode in aqueous medium. J. Appl. Electrochem. 39, 227–232 (2008).
He, Z. et al. Electrochemically created roughened lead plate for electrochemical reduction of aqueous CO2. Catal. Commun. 72, 38–42 (2015).
García, J., Jiménez, C., Martínez, F., Camarillo, R. & Rincón, J. Electrochemical reduction of CO2 using Pb catalysts synthesized in supercritical medium. J. Catal. 367, 72–80 (2018).
Jana, A., Ba, Q. & Kim, K. S. Compositional and dimensional control of 2D and quasi‐2D lead halide perovskites in water. Adv. Funct. Mater. 29, 1900966 (2019).
Yu, X., Diao, Q., Zhang, X., Lee, Y.-I. & Liu, H.-G. In situ generated Pb nanoclusters on basic lead carbonate ultrathin nanoplates as an effective heterogeneous catalyst. CrystEngComm 19, 2860–2869 (2017).
Shi, Y., Yu, Y., Liang, Y., Du, Y. & Zhang, B. In situ electrochemical conversion of an ultrathin tannin nickel iron complex film as an efficient oxygen evolution reaction electrocatalyst. Angew. Chem. Int. Ed. 58, 3769–3773 (2019).
Frantz, J. D. Raman spectra of potassium carbonate and bicarbonate aqueous fluids at elevated temperatures and pressures: Comparison with theoretical simulations. Chem. Geol. 152, 211–225 (1998).
Brooker, M. H., Sunder, S., Taylor, P. & Lopata, V. J. Infrared and Raman spectra and X-ray diffraction studies of solid lead(II) carbonates. Can. J. Chem. 61, 494–502 (1983).
Jiang, K., Wang, J.-Y., Zhao, T.-T. & Cai, W.-B. Formic acid oxidation at palladium electrode in acidic media containing chloride anions: an in situ ATR-SEIRAS investigation. J. Electroanal. Chem. 800, 77–81 (2017).
Cuesta, A., Cabello, G., Osawa, M. & Gutiérrez, C. Mechanism of the electrocatalytic oxidation of formic acid on metals. ACS Catal. 2, 728–738 (2012).
Gao, D., Zhang, X. & Gao, W. Formation of bundle-shaped beta-NaYF4 upconversion microtubes via Ostwald ripening. ACS Appl. Mater. Inter. 5, 9732–9739 (2013).
Li, R., Luo, Z. & Papadimitrakopoulos, F. Redox-assisted asymmetric Ostwald ripening of CdSe dots to rods. J. Am. Chem. Soc. 128, 6280–6281 (2006).
Martinetto, P., Anne, M., Dooryhée, E., Walter, P. & Tsoucaris, G. Synthetic hydrocerussite, 2PbCO3·Pb(OH)2, by X-ray powder diffraction. Acta Crystallogr. C 58, i82 (2002).
Vasquez, F. A., Heaviside, R., Tang, Z. & Taylor, J. S. Effect of free chlorine and chloramines on lead release in a distribution system. J. Am. Water Works Ass. 98, 144–154 (2006).
Ravel, B. & Newville, M. ATHENA, ARTEMIS, HEPHAESTUS: data analysis for X-ray absorption spectroscopy using IFEFFIT. J. Synchrotron Radiat. 12, 537–541 (2005).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comp. Mater. Sci. 6, 15–50 (1996).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Zhang, Y. & Yang, W. Comment on “Generalized gradient approximation made simple”. Phys. Rev. Lett. 80, 890 (1997).
Nørskov, J. K. et al. Origin of the overpotential for oxygen reduction at a fuel-cell cathode. J. Phys. Chem. B 108, 17886–17892 (2004).
Han, M. et al. Toward computational design of catalysts for CO2 selective reduction via reaction phase diagram analysis. Adv. Theory Simul. 1800200 (2019).
Nie, X., Esopi, M. R., Janik, M. J. & Asthagiri, A. Selectivity of CO2 reduction on copper electrodes: the role of the kinetics of elementary steps. Angew. Chem. Int. Ed. 52, 2459–2462 (2013).
Akhade, S. A., Bernstein, N. J., Esopi, M. R., Regula, M. J. & Janik, M. J. A simple method to approximate electrode potential-dependent activation energies using density functional theory. Catal. Today 288, 63–73 (2017).
Katayama, Y. et al. An in situ surface-enhanced infrared absorption spectroscopy study of electrochemical CO2 reduction: selectivity dependence on surface C-bound and O-bound reaction intermediates. J. Phys. Chem. C 123, 5951–5963 (2018).
Acknowledgements
We acknowledge the National Natural Science Foundation of China (Nos. 21871206, 21901180, 21422104, 91845103, and 21802124), the Natural Science Foundation of Tianjin City (No. 17JCJQJC44700), China Postdoctoral Science Foundation (No. 2019TQ0226), the Strategic Priority Research Program of Chinese Academy of Sciences (No. XDB36030200), and Liaoning Revitalization Talents Program (XLYC1907099) for financial support. We acknowledge Dr. Lirong Zheng and the 1W1B beamline of the Beijing Synchrotron Radiation Facility for supporting this project.
Author information
Authors and Affiliations
Contributions
B.Z. conceived and directed the project. B.Z. and Y.S. designed the experiments. Y.S and Y.J. carried out the experiments. J.L. and J.X. performed and analyzed the DFT calculations. Y.L. carried out the in situ Raman spectroscopy. Y.S. and Y.L. conducted the in situ ATR-FTIR spectroscopy. Y.S. and J.L. wrote the paper. Y.Y., J.X., and B.Z. revised the paper. All authors discussed the results and commented on the paper.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Su-Il In, Fabiola Martínez, and other, anonymous, reviewer(s) for their contributions to the peer review of this work. Peer review reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Shi, Y., Ji, Y., Long, J. et al. Unveiling hydrocerussite as an electrochemically stable active phase for efficient carbon dioxide electroreduction to formate. Nat Commun 11, 3415 (2020). https://doi.org/10.1038/s41467-020-17120-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-17120-9
This article is cited by
-
Durable CO2 conversion in the proton-exchange membrane system
Nature (2024)
-
Strongly Coupled Ag/Sn–SnO2 Nanosheets Toward CO2 Electroreduction to Pure HCOOH Solutions at Ampere-Level Current
Nano-Micro Letters (2024)
-
Regulating p-orbital of metallic bismuth nanosheets via transition-metal oxides enables advanced CO2 electroreduction
Science China Materials (2024)
-
Promoting water dissociation for efficient solar driven CO2 electroreduction via improving hydroxyl adsorption
Nature Communications (2023)
-
Electrosynthesis of formamide from methanol and ammonia under ambient conditions
Nature Communications (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.