Abstract
Meteoroid bombardment of the Earth-Moon system must have caused catastrophic damage to the terrestrial ecosphere. However, ancient meteoroid impacts and their relations to environmental changes are not well understood because of erosion and/or resurfacing processes on Earth. Here, we investigate the formation ages of 59 lunar craters with fresh morphologies and diameters greater than approximately 20 km and first find that 8 of 59 craters were formed simultaneously. Considering the radiometric ages of ejecta from Copernicus crater and impact glass spherules from various Apollo landing sites, we conclude that sporadic meteoroid bombardment occurred across the whole Moon at approximately 800 Ma. Based on crater scaling laws and collision probabilities with the Earth and Moon, we suggest that at least (4–5) × 1016 kg of meteoroids, approximately 30–60 times more than the Chicxulub impact, must have plunged into the Earth-Moon system immediately before the Cryogenian, which was an era of great environmental changes.
Similar content being viewed by others
Introduction
Understanding meteoroid bombardment of the Earth system is an issue of both great scientific interest and practical importance because impacts are potentially hazardous to the Earth. Since the 541 Ma Cambrian biodiversity explosion, mass extinction events have occurred at least five times (the so-called Big five events)1, and extra-terrestrial impacts are considered a potential cause of some of them (e.g., Late Triassic2 and Cretaceous-Palaeogene extinctions3), competing with the flood basalt eruption-related hypotheses4.
After the first discovery of fossil L-chondrites in Ordovician limestones in Sweden5, abundant L-chondrites, meteorite-tracing chromite grains and iridium enrichment have been found in Sweden, England, Scotland, China, and Russia in rocks whose stratigraphic ages are 470 ~ 480 million years (Ma)6,7. Moreover, several large terrestrial craters in the Northern Hemisphere have been found to have radiometric ages of approximately 430 ~ 470 Ma8. Further, approximately two-thirds of ordinary L-chondrites are known to be heavily shocked and degassed, with 39Ar–40Ar ages near 470 Ma9. Therefore, it is generally considered that the L-chondrite parent body suffered a major impact approximately 470 million years ago and was catastrophically disrupted, causing a very large meteoroid shower on Earth for several million years10. Recently, Schmitz et al.11 suggested that the extraordinary amounts of dust during >2 Myr cooled the Earth and triggered Ordovician icehouse conditions, sea-level fall, and major faunal turnovers related to the Great Ordovician Biodiversification Event. However, to date, other ancient meteoroid impacts and their relations to environmental changes have not been well understood because of erosion and/or resurfacing processes on Earth.
Another way to reveal ancient meteoroid impacts on Earth is to investigate the lunar crater record because there is less weathering and erosion on the Moon. The lunar orbiter, Kaguya provides us a new insight that disruption of asteroid had occurred and formed the several craters larger than 20 km simultaneously on the Moon approximately 800 Ma. Based on crater scaling laws and collision probabilities with the Earth and Moon, at least (4–5) × 1016 kg of meteoroids, approximately 30–60 times more than the Chicxulub impact, must have struck the Earth, immediately before the Cryogenian, which was an era of great environmental and biological changes.
Results and discussion
Observation of crater size-frequency distribution on the Moon
Crater size-frequency distribution measurement is a well-established technique to derive relative and absolute ages of planetary surfaces12; thus, the density of 0.1–1 km-diameter craters in the ejecta of a large crater (>20 km) potentially gives the formation age of the large crater itself. In this study, we investigate the formation age distribution of 59 lunar craters with fresh morphology and diameters larger than approximately 20 km (Fig. 1) using the software tool craterstats13. Typical craters and small craters counted for their crater size-frequency distribution measurement are shown in Fig. 2. Here, we select and investigate the regions where there is no pond (impact melt region) to avoid the target property effects that may cause craters formed in impact melts to be smaller than those in ejecta, as discussed by13.
a Mosaics of the Terrain Camera images of individual craters shown in simple cylindrical map projection and b the cumulative size-frequency distributions, from which ages are identical to that of Copernicus crater. The small craters around the central main crater are counted for the determination of the central crater itself. b Shows their cumulative size-frequency distributions. Error bars are estimated by the formula (n ± n1/2)/A, where n is the cumulative number of craters and A is the counted area.
First, we estimate the formation ages of individual craters using the conventional constant flux model over 3 billion years (another model is discussed later). Table 1 summarizes the estimated formation ages of 59 lunar craters with fresh morphology. The remarkable new finding is that eight of 59 craters, including Copernicus, are concentrated at approximately 660 Ma, and the weighted mean is 658 ± 16 Ma (Fig. 3b). The spatial distribution of these craters seems to be slightly concentrated in the equatorial plane, but there is no significant difference between the far and near sides (Fig. 1).
To evaluate the probability of the observed concentration of crater ages, we perform a simple test using Monte Carlo simulation. We assume that craters are created with uniform probability within an age range from 3.0 Ga to 0 Ga and compute the ages of the 59 craters using a uniformly distributed pseudo-random number. The procedure is iterated 100,000 times. The results show that the possibility that seven of the 59 craters formed at the same time (for 50 Ma from 630 Ma to 680 Ma) by chance is 0.69%, where the 54S161E crater (747 ± 92 Ma) is masked because it is an obvious outlier with large uncertainties (if the 4S161E crater is included, the possibility that eight of the 59 craters formed during a 100 Ma interval by chance is 7%). From these considerations, we conclude that sporadic meteorite bombardment occurred across the whole Moon, possibly due to the disruption of asteroids, analogous to the Ordovician meteorite shower.
According to Shibaike et al.14, the mass of an impactor can be estimated from the density of the impactor, the density of the crust, the velocity of the impactor and the diameter of the crater (see “Methods” for details). Assuming a density of near-Earth asteroids (1.29 g cm−3 for C-type asteroid Ryugu15, 1.9 g cm−3 for S-type asteroid Itokawa16 and 2.7 g cm−3 for S-type asteroid Eros17) and a relative velocity of 20 km sec−1 of Earth-crossing asteroids to the Moon18,19, the masses and sizes of the impactors for eight lunar craters formed at 660 Ma are calibrated (see Table 2). As a result, the total mass of the asteroid shower on the Moon is estimated to be (1.3–1.6) × 1015 kg, corresponding to an impactor 10–13 km in diameter.
Consideration of absolute age of clustered craters
To date, the lunar impact history has been well investigated based on lunar impact glasses collected by the Apollo/Luna missions and/or lunar meteorites. The age of Copernicus crater is generally taken as ~800 Ma based on both crater chronology20 and the radiometric dating of 12033 brecciated soil, which is considered to consist of ejecta from Copernicus crater21,22. The discrepancy in crater age between 800 Ma20 and 660 Ma in this study is due to the difference in the selected area to be counted as follows. In fact, we investigated the same area as Hiesinger et al.20, giving an age of 797 ± 52 Ma, whereas Hiesinger et al.20 also reported ages of 678 ± 81 Ma for the area observed by KAGUYA CE1 and 678 ± 270 Ma for the Copernicus ray. In addition, we investigate other areas around Copernicus crater (floor, ejecta area and melt region near central peak), giving ca. 660 Ma (Fig. 4). All of these results mean that there is no discrepancy in counting and calibration between previous work20 and this study. We also realize that the selected area with an age of 800 Ma is close to the centre of Copernicus crater and tends to be affected by secondary craters, so a counting method yielding a younger age of 660 Ma is correct for Copernicus crater. Note that the most important of the new findings is that eight craters, including Copernicus, show identical relative ages based on a constant flux model.
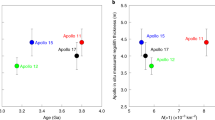
On the other hand, the absolute age of Copernicus crater is considered to be 800 Ma based on the radiometric ages of 12033 brecciated soil collected from the ejecta of Copernicus crater21,22. In addition, Zellner et al. (2015)23 recently reported that 40Ar/39Ar data for impact spherules from Apollo 12, 14, 16, and 17 samples show an 800 Ma spike, similar to that of the 12033 breccia, and concluded that there must have been a transient increase in the global lunar impact flux at 800 Ma other than Copernicus crater, in the context of diverse compositional ranges and sample locations of impact glass spherules. Such geochemical observations of simultaneous global lunar impacts recorded in Apollo samples well match the coincidence of (at least) eight crater formations derived from our observations, of which the probability is 0.69%. From these considerations, we infer that these two observations must be related to each other and newly propose a constant with a spike model of ~800 Ma instead of a conventional constant model (details of a new model are discussed in the next section).
This scenario in which sporadic asteroid showers did not occur at 660 Ma but at 800 Ma is also supported by recent LRO observations and/or numerical simulations of the asteroid families as follows24,25,26,27. Based on the temperature of large impact ejecta with crater sizes larger than 10 km in diameter, Mazrouei et al.24 reported that there is no evidence of a sporadic peak at approximately 660 Ma, although they found that the production rate of D ≥ 10 km lunar craters was 2–3 times higher over the last ~290 Myr. However, the age of 800 Ma is very close to the limit of resolution shown in Fig. 3 in Mazrouei et al.24, so there is no contradiction with the 800 Ma spike model. Furthermore, numerical simulation of the orbits of asteroid families also provides crucial chronological information about the impact flux to the inner solar system. A recent investigation of the dynamics of the asteroid family and the best available Yarkovsky measurement suggest25 that the breakup of 847 Agnia (669–1003 Ma) and/or 480 Hansa (763–950 Ma) was related to the sporadic asteroid shower at 660 Ma. However, it is known that these families are not sizable enough and/or not well enough positioned to produce the sporadic asteroid shower, including Copernicus crater with a diameter of 93 km, for which impactor is expected to be 10 km in diameter (Table 2). Moreover, the Agnia family is located near the 5:2 resonance, where the probability of a projectile hitting the Moon is very low (~10−5)26. The Hansa family also has difficulty producing an impactor of 10 km for Copernicus because it is located at high inclinations near the 3:1 and 8:3 resonances. However, the Eulalia family, whose age is 830 [+370, −100] Ma, could potentially have produced an impact spike at ~800 Ma. According to Bottke et al.27, when the parent body of Eulalia was disrupted, a large share of the sizable family was directly injected into the 3:1 resonance at low inclinations. This disruption certainly could have produced an impact spike on terrestrial planets and/or their satellites inside the asteroid belt. Interestingly, the Eulalia family is a carbonaceous chondrite family and is considered to be the parent body of near-Earth C-type asteroids, such as Bennu and Ryugu27. Such an asteroid shower must have contaminated the lunar surface with volatile elements. This scenario is harmonized with (i) the observation of H2O in Copernicus crater that may reflect retention of volatiles from hydrous impactors28; (ii) the scenario that may have been formed by a cometary nucleus, 4 km in diameter based on geochemistry of the 12033 breccia29; and (iii) recent KAGUYA remote-sensing observation of persistent C+ emitted from the whole Moon, which is significantly larger than influxes due to solar wind and/or current micrometeoroid accretion30 and suggests that the lunar surface might have been contaminated by volatile-rich impactors in the past.
Crater age distribution by the 800 Ma spike model
It is obvious that the break-up of large asteroids increases not only the large (>20 km) crater production rate but also the small (0.1–1 km) crater production rate. From these considerations, we propose the new simplest model: a constant flux with a spike between 830 and 800 Ma for small craters (0.1–1 km), as shown in Fig. 4 (hereafter, we call this concept the 800 Ma spike model). The basic idea is that the crater counting age of Copernicus crater must be identical to the radiometric age of 800 Ma and that the fluxes before and after the sporadic spike at ~800 Ma were constant. Although the duration time of the spike is slightly uncertain, we assume that this duration was 30 Ma (from 830 Ma to 800 Ma), based on the break-up age of Eulalia26 and the radiometric age of Copernicus crater21,22 and/or the deviation of eight clustered ages (658 ± 16 Ma) for a constant model. Figure 5 illustrates the difference between the conventional constant flux model and the 800 Ma spike model. The constant flux of the new spike model is 75% (=663 Ma/800 Ma) of the conventional constant flux model, and the flux between 800 Ma and 830 Ma is 23 times higher than that in other eras (Fig. 5a) to ensure that the total crater production over 3 billion years is identical for both models, as shown in Fig. 5b).
As a result, the modified age distribution shows that 16 of the 59 craters coincide with that of Copernicus crater within the analytical certainties (Fig. 3b, Table 2), although the large (>20 km) crater production rate and the small (0.1–1 km) crater production rate might be coupled in this model. However, the estimated total masses are not significantly changed ((1.3–1.6) × 1015 kg for the constant flux model and (1.8–2.3) × 1015 kg for the 800 Ma spike model) because Copernicus crater is dominant among the eight coincident craters (by the constant model) and the 17 coincident craters (by the spike model). Therefore, the latter discussion on the total mass estimation of the impactor is not affected by the choice of a flux model with/without the spike. Moreover, it should also be noted that the slopes of the lines <300 Ma in both models in Fig. 6 are gentler than those of other eras, which is quite consistent with the previous study that the production rate of lunar craters (>10 km) has been 2–3 times higher over the last ~290 Myr, which is derived from an independent approach based on the temperature of large impact ejecta24.
The estimated ages of 59 craters based on the constant flux model and the 800 Ma spike model are shown in descending order. In both models, it is obvious that the slopes of the lines less than a few million years and ~800 Ma are gentler than those of other eras (e.g., 300–660 Ma and/or >800 Ma), suggesting the recent increase in impact flux forming the large craters (D > 20 km).
Recent observations by Chandrayaan-131 and LADEE32 suggest that an active water cycle exists on the Moon and that hydrated soil is present under the desiccated soil layer of several centimetres over the Moon surface. In particular, Li and Milliken31 discuss that the Copernicus crater exhibits high water content that may reflect the retention of volatiles from hydrous impactors according to the Moon Mineralogy Mapper. In addition, we recently found that C+ is persistently emitted from the whole of the Moon as detected by the lunar orbiter KAGUYA and that this flux is significantly larger than the influx estimated from solar wind and/or current micrometeoroid accretion30. These observations suggest that volatile elements are ubiquitous over the lunar surface and that the Moon is currently in the process of losing volatiles (water, carbon, etc.), although when and how the surface of the Moon attained and/or retained such volatiles has been enigmatic. Assuming the CI-like chemical composition (a few wt.% of carbon and H2O), our scenario predicts that a C-type asteroid shower at 800 Ma must have supplied ~1014 kg of carbon and H2O to the lunar surface. This new paradigm undoubtedly should place new constraints on the history of lunar volatiles.
Estimated flux on the Earth
Since the Earth–Moon system has been co-evolving over 4.5 billion years, this new finding provides us with crucial insight into the Earth–Moon system because asteroid showers must have occurred not only on the Moon but also on the Earth. Based on the probability ratio of collisions with the Earth and the Moon of 23:133, we conclude that a mass of (4–5) × 1016 kg (corresponding to a diameter of ~30–40 km and ~30–60 times greater in mass than the Chicxulub asteroid impactor34) must have collided successively on the Earth at ~800 Ma, i.e., immediately before the Cryogenian (720–635 Ma), which was an era of great environmental and biological changes35,36. To date, however, no direct geological evidence of a large-scale impact in the Neoproterozoic has been found37. Moreover, remarkable Ir concentrations as well as other platinum-group elements (PGE) anomalies, such as those at the K–T boundary34, have not been found, although only the Marinoan glaciation (650–635 Ma) is characterized by increased concentrations of Ir38,39. The straightforward interpretation is that the following large-scale Neoproterozoic glaciations, the so-called Snowball Earth (that is, the Kaigas-Sturtian glaciation from 730 to 700 Ma and the Marinoan glaciation) and/or their deglaciation processes, might have erased a significant part of the earlier geological and/or geochemical history, as discussed by40.
To date, the impact history and subsequent effects on the environment in the Neoproterozoic and Cryogenic have not been understood because terrestrial craters are not well preserved due to erosion. Koeberl and Ivanov41 recently discussed the mechanical effects of one impact of an asteroid 5–10 km in diameter on the Snowball Earth environment, suggesting that the products of impact (mainly water vapour) could be quickly distributed over a substantial part of the globe, influencing the global circulation (e.g., facilitating cloud formation), because one impact cratering event (shock waves and impact crater formation) might produce much dust that entered the atmosphere and might have caused albedo changes. Recently, Schmitz et al.11 noted that the Ordovician meteorite shower should have triggered the mid-Ordovician ice age based on the sizes of the remaining terrestrial craters. Thus, large asteroid showers should influence the global ecosphere in some ways, although mechanisms are not well realized because of the unknown characteristics of the dust, e.g., size, albedo, mineralogy, and chemical composition.
Interestingly, Reinhard et al.42 found that the average P content of late Tonian samples is more than four times greater than that of pre-Cryogenian samples and noted that a fundamental shift in the phosphorus cycle may have occurred during the late Proterozoic Eon after 800 Ma (until 635 Ma). Our new finding suggests that ~1014 kg of extra-terrestrial P should have accreted across the Earth assuming CI chondrite composition (P = 0.1 wt.%) at 800 Ma, which is one order of magnitude higher than the total P amount of the modern sea (assuming that the volume of modern seas is 13.5 × 108 km3 and the concentration of P is ~3 μg/litre). In general, large-scale changes in marine biogeochemical cycles are undoubtedly forced by tectonic and magmatic processes and chemical weathering of the continental crust, but our new finding suggests that the flux of extra-terrestrial bioavailable elements might also have influenced marine biogeochemical cycles42, marine redox states43, severe perturbations to Earth’s climate system44, and the emergence of animals45,46. Thus, lunar crater chronology provides new insight into external forcing from asteroids that might have driven ecosystems towards larger and increasingly complex organisms after 800 Ma, although further quantitative discussion will be required.
Methods
The method of crater size-frequency measurement
The model ages of the lunar craters were determined by crater size-frequency measurements on ejecta blankets of the craters using image data obtained by the Terrain Camera (TC) onboard SELENE. The lunar explorer SELENE (KAGUYA) was launched on 14 September 2007 and had a nominal observation of 1 year at an altitude of 100 km47. The TC is a panchromatic push-broom imager with two optical heads (TC1 and TC2) to acquire stereo data for the entire surface of the Moon with an average resolution of 10 m/pixel. The details of the instruments have been published elsewhere48,49.
The technique of crater size-frequency measurement has been described in detail in several papers50,51,52. Therefore, we briefly present the procedure. Based on the simple idea that older surfaces accumulate more craters, the relative age is determined by measuring the cumulative crater frequency at a reference diameter (usually > 1 km), where the measurement of the crater size-frequency distribution (CSFD) is carried out with remote sensing image data. The cratering chronology formulated by relating crater frequencies to the radiometric ages of Apollo and Luna samples enables us to convert the crater frequency into an absolute model age.
We used images that are map-projected in a transverse Mercator projection with a resolution of 10 m/pixel at the central meridian of the projection because this projection introduces little distortion in a narrow area. Crater counting was performed within the continuous ejecta out to one crater radius from the crater rim. In this study, we eliminated obvious secondary craters based on their morphological characteristics, such as chain craters, elliptical craters, and clusters.
In general, self-secondary cratering would cause the estimated ages to be older than the actual ages53,54. Although self-secondary craters54,55 may be included in our counting, the effect of self-secondary craters on the age determination is sufficiently small to ignore. The crater frequency (the density of craters larger than 1 km in diameter) of Giordano Bruno, which is the youngest crater among those investigated in this study, is 4.9 × 10−6 km−2, which is considered the maximum flux value of self-secondary craters if the age is zero (in actuality, this value is the summation of both self-secondary craters and cumulative craters after Giordano Bruno formation). Thus, the maximum contribution of self-secondary craters is ~100 times smaller than that corresponding to 660 Ma (5.5 × 10−4 km−2), suggesting that self-secondary crates should be <1/100 of the small craters counted on the continuous ejecta for craters with a model age of 660 Ma. Therefore, self-secondary craters do not affect the discussion of this paper.
We used the lunar standard CSFD and the cratering chronology model proposed by Neukum and co-workers55,56,57 to obtain the absolute model age from the CSFD measurement. More recently, the standard CSFD and the chronology model have been updated52,57. However, in the diameter range (a few hundred metres to a few tens of metres) and the age range (0.1 Ga) used in this study, the differences between the models are insignificant42 and produce only slight differences in the estimated ages58. Therefore, we adopted the Neukum model55 in this study. The model ages from crater counts are principally limited by the statistical error. The statistical error of individual data points in our crater frequency measurements is mostly <30% (1 sigma).
Estimation of the size and mass of the impactor
According to Shibaike et al.14 (originally from Abramov et al.59), the mass of the impactor can be estimated from the density of the impactor, the density of the crust, the velocity of the impactor and the diameter of craters as follows:
where ρi and ρt are the densities of the impactor and the crust and v, m, and g are the impact speed, impactor mass, and gravity, respectively. Assuming a density of near-Earth asteroids (1.29 g cm−3 for C-type asteroid Ryugu15, 1.9 g cm−3 for S-type asteroid Itokawa16 and 2.7 g cm−3 for S-type asteroid Eros17) and a relative velocity of 20 km s−1 for Earth-crossing asteroids to the Moon18,19, the mass and size of the impactors for 17 lunar craters that coincide with the formation of Copernicus crater are shown in Table 2. It should be noted that these parameters do not affect the conclusion much, even if the density changes from 2.5 to 3.5 g cm−3 and the velocity changes from 10 to 20 km s−1. Although numbers of smaller craters <20 km in diameter would increase, the observed craters with sizes of 35–93 km are the main contributor to the total mass of bombardment (e.g., masses of the impactors for a D = 10 km crater and a D = 3 km crater are 1/100 and 1/106 of those for a D = 35 km crater, respectively).
Data availability
All crater-counting data analyzed during this study are provided in Table 1 and in Supplementary Information.
Code availability
We used the software tool craterstats14 to fit the observed crater size distributions to the crater production function and to calculate its errors (http://hrscview.fu-berlin.de/software.html).
References
Raup, D. M. & Sepkoski, J. J. Mass extinctions in the marine fossil record. Science 215, 1501–1503 (1982).
Onoue, T. et al. Bolide impact triggered the Late Triassic extinction event in equatorial Panthalassa. Sci. Rep. 6, 29609 (2016).
Schulte, P. et al. The Chicxulub asteroid impact and mass extinction at the Cretaceous-Paleogene boundary. Science 327, 1214–1218 (2010).
Richards, M. A. et al. Triggering of the largest Deccan eruptions by the Chicxulub impact. GSA Bull. 127, 1507–1520 (2015).
Thorslund, P. & Wickman, F. E. Middle Ordovician chondrite in fossiliferous limestone from Brunflo, central Sweden. Nature 289, 285–286 (1981).
Wilde, P. et al. Iridium abundances across the Ordovician-Silurian stratotype. Science 233, 339–341 (1986).
Schmitz, B., Häggström, T. & Tassinari, M. Sediment-dispersed extraterrestrial chromite traces a major asteroid disruption event. Science 300, 961–964 (2003).
Schmitz, B., Tassinari, M. & Peucker-Ehrenbrink, B. A rain of ordinary chondritic meteorites in the early Ordovician. Earth Planet. Sci. Lett. 194, 1–15 (2001).
Bogard, D. Impact ages of meteorites: a synthesis. Meteoritics 30, 244–268 (1995).
Heck, P. R. et al. Fast delivery of meteorites to Earth after a major asteroid collision. Nature 430, 323–325 (2004).
Schmitz, B. et al. An extraterrestrial trigger for the mid-Ordovician ice age: Dust from the breakup of the L-chondrite parent body. Sci. Adv. 5, eaax4184 (2019).
Michael, G. G. & Neukum, G. Planetary surface dating from crater size-frequency distribution measurements: partial resurfacing events and statistical age uncertainty. Earth Planet. Sci. Lett. 294, 223–229 (2010).
van der Bogert, C. H. et al. Origin of discrepancies between crater size-frequency distributions of coeval lunar geologic units via target property contrasts. Icarus 298, 49–63 (2017).
Shibaike, Y., Sasaki, T. & Ida, S. Excavation and melting of the Hadean continental crust by Late Heavy Bombardment. Icarus 266, 189–203 (2016).
Watanabe, S. et al. Hayabusa2 arrives at the carbonaceous asteroid 162173 Ryugu—a spinning top–shaped rubble pile. Science 364, 268–272 (2019).
Fujiwara, A. et al. The Rubble-Pile Asteroid Itokawa as observed by Hayabusa. Science 312, 1330–1334 (2006).
Yeomans, D. K. et al. Radio science results during the NEAR-shoemaker spacecraft rendezvous with eros. Science 289, 2085–2088 (2000).
Feuvre, M. L. & Wieczorek, M. A. Nonuniform cratering of the terrestrial planets. Icarus 197, 291–306 (2008).
Ito, T. & Malhotra, R. Asymmetric impacts of near-Earth asteroids on the Moon. AA 519, A63 (2010).
Hiesinger, H. et al. How old are young lunar craters? J. Geophys. Res. 117, E00H10 (2012).
Bogard, D. D. et al. 39Ar-40Ar dating of two lunar granites: the age of Copernicus. Geochimica et. Cosmochimica Acta 58, 3093–3100 (1994).
Eberhardt, P. et al. How old is the crater copernicus? Moon 8, 104–114 (1973).
Zellner, N. E. B. & Delano, J. W. 40Ar/39Ar ages of lunar impact glasses: Relationships among Ar diffusivity, chemical composition, shape, and size. Geochimica Et. Cosmochimica Acta 161, 203–218 (2015).
Mazrouei, S. et al. Earth and Moon impact flux increased at the end of the Paleozoic. Science 363, 253–257 (2019).
Spoto, F., Andrea Milani, A. & Knezevic, Z. Asteroid family ages. Icarus 257, 275–289 (2015).
Bottke, W. F. et al. Iron meteorites as remnants of planetesimals formed in the terrestrial planet region. Nature 439, 821–824 (2006).
Bottke, W. F. et al. In search of the source of asteroid (101955) Bennu: Applications of the stochastic YORP model. Icarus 247, 191–217 (2015).
Milliken, R. E. & Li, S. Remote detection of widespread indigenous water in lunar pyroclastic deposits. Nat. Geosci. 10, 561–565 (2017).
Morgan, J. W., Ganapathy, R., Laul, J. C. & Anders, E. Lunar crater Copernicus: search for debris of impacting body at Apollo 12 site. Geochimica et. Cosmochimica Acta 37, 141–154 (1973).
Yokota, S. et al. KAGUYA observation of global emissions of indigenous carbon ions from the Moon. Sci. Adv. 6, eaba1050 (2020).
Li, S. & Milliken, R. E. Water on the surface of the moon as seen by the moon mineralogy mapper: distribution, abundance, and origins. Sci. Adv. 3, e1701471 (2017).
Benna, M. et al. Lunar soil hydration constrained by exospheric water liberated by meteoroid impacts. Nat. Geosci. 12, 333–338 (2019).
Ito, T. & Malhotra, R. Dynamical transport of asteroid fragments from the m 6 resonance. Adv. Space Res. 38, 817–825 (2006).
Alvarez, L. W. et al. Extraterrestrial cause for the Cretaceous-tertiary extinction. Science 208, 1095–1108 (1980).
Macdonald, F. A. et al. Calibrating the Cryogenian. Science 327, 1241–1243 (2010).
Shields-Zhou, G. & Och, L. The case for a Neoproterozoic oxygenation event: geochemical evidence and biological consequences. GSA Today 21, 4–11 (2011).
Database of earth Craters (the Planetary and Space Science Centre University of New Brunswick); http://www.passc.net/EarthImpactDatabase/Agesort.html (2019).
Bodiselitsch, B., Koeberl, C., Master, S. & Reimold, W. U. Estimating duration and intensity of Neoproterozoic snowball glaciations from Ir anomalies. Science 308, 239–242 (2005).
Ivanov, A. V., Mazukabzov, A. M., Stanevich, A. M., Palesskiy, S. V. & Kozmenko, O. A. Testing the snowball Earth hypothesis for the Ediacaran. Geology 41, 787–790 (2013).
Keller, C. B. et al. Neoproterozoic glacial origin of the great unconformity. Proc. Natl Acad. Sci. USA 116, 1136–1145 (2019).
Koeberl, C. & Ivanov, B. A. Asteroid impact effects on Snowball Earth. Meteorit. Planet. Sci. 54, 2273–2285 (2019).
Reinhard, C. T. et al. Evolution of the global phosphorus cycle. Nature 541, 386–389 (2017).
Hoffman, P. F. & Schrag, D. P. The Snowball Earth hypothesis: testing the limits of global change. Terra Nova 14, 129–155 (2002).
Erwin, D. H. et al. The Cambrian conundrum: early divergence and later ecological success in the early history of animals. Science 334, 1091–1097 (2011).
Love, G. D. et al. Fossil steroids record the appearance of Demospongiae during the Cryogenian period. Nature 457, 718–721 (2009).
Brocks, J. J. et al. The rise of algae in Cryogenian oceans and the emergence of animals. Nature 548, 578–581 (2017).
Kato, M., Sasaki, S., Tanaka, K., Iijima, Y. & Takizawa, Y. The Japanese lunar mission SELENE: science goals and present status. Adv. Space Res. 42, 294–300 (2008).
Haruyama, J. et al. Global lunar-surface mapping experiment using the Lunar Imager/Spectrometer on SELENE. Earth Planets Space 60, 243–255 (2008).
Haruyama, J. et al. Long-lived volcanism on the lunar farside revealed by SELENE Terrain camera. Science 323, 905–908 (2009).
Stöffler, D. & Ryder, G. Stratigraphy and isotope ages of lunar geologic units: chronological standard for the inner solar system. Space Sci. Rev. 96, 9–54 (2001).
Hartmann, W. K. & Neukum, G. Cratering chronology and the evolution of Mars. Space Sci. Rev. 96, 165–194 (2001).
Shoemaker, E. M. et al. Television observations from Surveyor. in Surveyor Program Results. U.S. National Aeronautics and Space Administration Special Publication SP-184, 19–128 (NASA 1969).
Xiao, Z. & Strom, R. G. Problems determining relative and absolute ages using the small crater population. Icarus 220, 254–267 (2012).
Zanetti, M. et al. Evidence for self-secondary cratering of Copernican-age continuous ejecta deposits on the Moon. Icarus 298, 64–77 (2017).
Neukum, G. Meteoriten bombardment und Datierung planetarer Oberflachen, 186. Habilitation Dissertation for Faculty Membership, University of Munich (1983).
Neukum, G. & Ivanov, B. A. Cratering size distributions and impact probabilities on Earth from lunar, terrestrial planet, and asteroid cratering data in Hazards due to comets and asteroids (ed. Gehrels T.) 359–416. (The University of Arizona Press, Tucson, 1994).
Neukum, G., Ivanov, B. A. & Hartmann, W. K. Cratering records in the inner solar system in relation to the lunar reference system. Space Sci. Rev. 96, 55–86 (2001).
Morota, T. et al. Timing and characteristics of the latest mare eruption on the Moon. Earth Planet. Sci. Lett. 302, 255–266 (2011).
Abramov, O., Wong, S. M. & Kring, D. A. Differential melt scaling for oblique impacts on terrestrial planets. Icarus 218, 906–916 (2012).
Acknowledgements
We wish to express their sincere thanks to all the members of the SELENE project. We thank Prof. Tajika from the University of Tokyo for useful discussion. This work was partly supported by Japan Society for the Promotion of Science (JSPS) KAKENHI Grants (No. 18H01269).
Author information
Authors and Affiliations
Contributions
K.T. conducted the entire research theme and wrote the paper. T.M. and M.K. contributed all of the analysed data and wrote the method.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Alexei Ivanov, Christian Koeberl and William Bottke for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Terada, K., Morota, T. & Kato, M. Asteroid shower on the Earth-Moon system immediately before the Cryogenian period revealed by KAGUYA. Nat Commun 11, 3453 (2020). https://doi.org/10.1038/s41467-020-17115-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-17115-6
This article is cited by
-
Phosphate environment and phosphate uptake studies: past and future
Journal of Plant Research (2024)
-
Fine-grained interplanetary dust input during the Turonian (Late Cretaceous): evidence from osmium isotope and platinum group elements
Scientific Reports (2023)
-
Shapes, structures, and evolution of small bodies
Astrodynamics (2021)
-
Lunar impact crater identification and age estimation with Chang’E data by deep and transfer learning
Nature Communications (2020)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.