Abstract
Quantum systems combining indistinguishable photon generation and spin-based quantum information processing are essential for remote quantum applications and networking. However, identification of suitable systems in scalable platforms remains a challenge. Here, we investigate the silicon vacancy centre in silicon carbide and demonstrate controlled emission of indistinguishable and distinguishable photons via coherent spin manipulation. Using strong off-resonant excitation and collecting zero-phonon line photons, we show a two-photon interference contrast close to 90% in Hong-Ou-Mandel type experiments. Further, we exploit the system’s intimate spin-photon relation to spin-control the colour and indistinguishability of consecutively emitted photons. Our results provide a deep insight into the system’s spin-phonon-photon physics and underline the potential of the industrially compatible silicon carbide platform for measurement-based entanglement distribution and photonic cluster state generation. Additional coupling to quantum registers based on individual nuclear spins would further allow for high-level network-relevant quantum information processing, such as error correction and entanglement purification.
Similar content being viewed by others
Introduction
The rise of quantum networks depends crucially on scalable quantum systems that combine quantum memories with long coherence times1,2 and stable optical emission to mediate entanglement via interference of indistinguishable photons3,4,5,6,7,8. In this regard, solid-state quantum systems are very appealing thanks to well-established fabrication techniques that promise chip-based integration and mass production9. A caveat coming along with many solid-state systems is strong coupling to charge fluctuations, which leads to large spectral diffusion and ionisation, especially under off-resonant laser excitation and in surface proximity10,11. Recently, spectral stability has been greatly improved for divacancy centres in charge-depleted semiconductor diode structures, albeit ionisation remains an issue12. Alternatively, one can resort to systems with inversion symmetry, e.g. with germanium-vacancy13,14, tin-vacancy centres15, and silicon-vacancy16 centres in diamond. For the latter, practical multi-millisecond spin coherence times have been demonstrated at ultracold temperatures in the millikelvin range17.
Here, we use semiconductor colour centres that provide a naturally stable spin–photonic interface at temperatures up to 6.9 K and demonstrate spin-controlled quantum optical interference of indistinguishable and distinguishable photons. This milestone experiment demonstrates that the system possesses the necessary prerequisites for remote entanglement generation as targeted in scalable quantum networks.
Our technological platform is silicon carbide (SiC), which has recently acquired great interest in the quantum community as it is industrially compatible and hosts several appealing optically addressable spin-active quantum defects18,19,20,21. We investigate here the negatively charged silicon vacancy centre at hexagonal lattice site (h-VSi) in the common 4H polytype of SiC22. Despite the lack of inversion symmetry, it was recently shown that the optical transition of h-VSi is decoupled from charge fluctuations through identical wavefunction symmetries in the ground and V1 excited states (ESs)23. Thanks to weak phonon coupling in the ground state (GS), millisecond spin coherence times are achieved20,24.
Results
Spin-optical system of silicon vacancies in silicon carbide
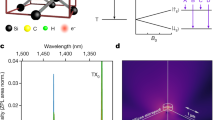
Our 4H-SiC host crystal is an isotopically purified (0001) epitaxial layer (28Si ~99.85%, 12C ∼99.98%), which is irradiated with 2 MeV electrons to generate isolated single h-VSi centres as shown in Fig. 1a. The crystal is slightly n-type to ensure that h-VSi centres are in the desired negatively charged state (see “Methods”). As shown in Fig. 1b, the h-VSi centre presents a spin quartet system \((S = {\textstyle{3 \over 2}})\). At zero external magnetic field, spin sublevels \(m_{{{\mathrm{S}}}} = \pm {\textstyle{1 \over 2}}\) and \(m_{{{\mathrm{S}}}} = \pm {\textstyle{3 \over 2}}\) are pairwise degenerate in the GS and the V1 ES. As the GS zero field splitting is relatively small at 4.5 MHz22, we apply a magnetic field (B ≈ 9 G) along the system’s symmetry axis (c-axis). This lifts the degeneracy and suppresses parasitic spin mixing due to external stray fields. Optical transitions are linearly polarised and associated with two zero phonon line (ZPL) transitions at 861.7 nm. They are assigned to \(\left| { \pm 1/2} \right\rangle _{{{{\mathrm{GS}}}}} \leftrightarrow \left| { \pm 1/2} \right\rangle _{{{{\mathrm{ES}}}}}\) and \(\left| { \pm 3/2} \right\rangle _{{{{\mathrm{GS}}}}} \leftrightarrow \left| { \pm 3/2} \right\rangle _{{{{\mathrm{ES}}}}}\) transitions and labelled A1 and A2, respectively. The energy separation between the two transitions is about 1 GHz, which is mainly determined by the ES zero field splitting22. It was recently shown that all optical transitions are fully spin conserving, which provides several pathways for spin–photon entanglement generation9,25. However, spin-flip processes can still be mediated by non-radiative intersystem crossing involving metastable states, which allows e.g. for deterministic spin state initialisation22,26. Note that we do not consider the system’s second ES, V1’, whose fluorescence at 858 nm is strongly reduced at cryogenic temperatures due to ultrafast relaxation to the V1 state20. Thus, and as shown in Fig. 1c, off-resonant excitation results in photoluminescence in the V1 ZPL (with 8% Debye–Waller factor27) or the associated phonon side band (PSB) with 6 ns lifetime20.
a Crystallographic structure of 4H-SiC and position of h-VSi centre (highlighted by a pink sphere symbolising a missing Si atom). b Level structure of the h-VSi centre at zero magnetic field. Ground state (GS) and V1 excited state show degenerate sublevels \(m_{{{\rm{S}}}} = \pm {\textstyle{1 \over 2}}\) and \(m_{{{\rm{S}}}} = \pm {\textstyle{3 \over 2}}\). Optical transitions between V1 and GS are spin conserving and associated with the transitions A1 and A2. Emission from the second excited state, V1’, is not observed owing to ultrafast relaxation (dashed arrows). c Single h-VSi centre emission spectrum under off-resonant excitation. d ZPL emission fine structure recorded over 20 min. The red dots are raw data. The two emission lines associated with A1 and A2 transitions are clearly resolved. The blue dashed line is a Lorentzian fit to the raw data, giving linewidths (FWHM) of 86 ± 6 and 77 ± 6 MHz for the A1 and A2 lines, respectively. The black line is data after deconvolution correction for the finite linewidth of the scanning Fabry–Pérot cavity (Lorentzian FWHM of 29 ± 2 MHz), the resulting real emission linewidths are 57 ± 6 and 48 ± 6 MHz, respectively, which is very close to the Fourier transform limit. e Second-order autocorrelation function recorded for a single h-VSi centre under pulsed off-resonant excitation (pulse energy: 5.7 pJ). We observe g2 (τ = 0) = 0.12 ± 0.01, clearly indicating single-photon emission. f g2 (τ = 0) as a function of laser pulse energy. The line is a guide to the eye. Error bars correspond to one standard error.
High-resolution ZPL emission spectrum
Single h-VSi centres are addressed via confocal microscopy (see “Methods”). Figure 1d shows the fine structure of the V1 ZPL emission, recorded at a temperature of T = 5.0 K. To this end, we use continuous-wave off-resonant excitation at 730 nm with an optical power of about 0.15 mW, which is almost 3 times higher than the saturation power20. As a high-resolution spectrometer, we use a home-built tunable Fabry–Pérot filter cavity with a linewidth of 29 ± 2 MHz. By integrating the emission spectrum over 20 min, we clearly resolve the two optical lines corresponding to the spin-conserving A1 and A2 transitions. Surprisingly, even under strong off-resonant excitation, the linewidths remain very close to the lifetime limit (~27 MHz). Taking into account the finite spectral resolution of the filter cavity (29 ± 2 MHz) via deconvolution of two Lorentzians, we infer emission linewidths of 57 ± 6 and 48 ± 6 MHz for the A1 and A2 transitions, respectively.
Single-photon emission purity
Aside from superior spectral purity and robustness, perfect two-photon interference crucially requires the interfering photons to be in pure single-photon states, i.e. not degraded by spurious multi-photon contributions28. To evaluate the quality of our quantum light source, we use pulsed off-resonant excitation at 780 nm (PicoQuant LDH-P-C-780, pulse length: 56 ps, repetition rate: 20.5 MHz) and record the second-order autocorrelation function g2 (τ) of ZPL photons in a standard Hanbury Brown and Twiss arrangement29. As shown in Fig. 1e, we observe a strong antibunching at zero time delay, clearly evidencing that the defect is a single-photon source (g2 (τ = 0) < 0.5). Figure 1f shows the recorded value of g2 (τ = 0) as a function of the laser pulse energy above saturation (4 pJ, see Supplementary Note 1). The increase of g2 (τ = 0) is mainly due to noise from background fluorescence below 6 pJ (see Supplementary Note 3). Above 6 pJ, the increased probability to induce two optical excitations during one laser pulse degrades g2 (τ = 0). However, under all conditions, we observe g2 (τ = 0) < 0.25 without any background subtraction, which underlines the h-VSi centre’s single-photon emission quality.
Indistinguishable photon generation
To prove that the h-VSi centre generates streams of indistinguishable photons in the A1 and A2 transitions, we perform a Hong–Ou–Mandel (HOM) interference30 experiment on two consecutively emitted photons31. Figure 2a shows the related set-up schematically. We use the off-resonant picosecond laser to excite the single defect twice with an interval of δt = 48.7 ns, and we repeat this sequence every 10⋅δt = 487 ns. The laser pulse energy is set to 5.5 pJ, corresponding to about 74% excitation probability per pulse and the detected ZPL photon count is about 10−4 per pulse (see Supplementary Note 1). The ZPL emission is coupled into a single-mode fibre-based unbalanced Mach–Zehnder interferometer with a path travel time difference of δt = 48.7 ns. The interferometer’s outputs are connected to superconducting nanowire single-photon detectors (SNSPDs; Photon Spot Inc.) with sub-ns time resolution. We record the time differences between both SNSPD detection events using a time tagger (Swabian Instruments). The timing jitter of our detection system is about 0.4 ns.
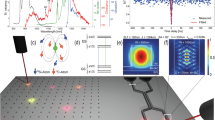
a Schematic set-up for HOM interference with two photons from a single h-VSi centre in SiC. Two laser pulses excite the h-VSi centre with a time delay δt = 48.7 ns. Consecutively emitted ZPL photons are sent to an unbalanced Mach–Zehnder interferometer. SNSPD and coincidence electronics are used to record the two-photon statistics at the output. b Two-photon coincidence counts as a function of the detection time delay between both SNSPDs. The strongly suppressed peak at zero time delay witnesses Hong–Ou–Mandel interference. The grey area between dashed lines symbolises the integration time window that is used for evaluating the interference contrast V0 = 0.69 ± 0.02. A two-photon coincidence occurs approximately every 84 s. The results shown are raw data without any correction.
Let us assume now that two consecutive ZPL photons enter the interferometer during one experimental sequence (i.e. no non-radiative intersystem crossing occurred). The most interesting case occurs when the early and the late photons take the long and short interferometer paths, respectively, and thus arrive simultaneously at the output beam-splitter (BS2) through different inputs. Provided that both photons are indistinguishable, HOM interference occurs and they must leave BS2 as a pair through the same output port30. Experimentally, this is measured through the reduction of coincidence events at zero time delay between both SNSPDs. Note that the normalised coincidence rate reduction is a direct measure of the photon indistinguishability. The normalisation process is actually implemented automatically in our set-up. Namely, 25% of the successfully created photon pairs take wrong opposite paths, i.e. the early and the late photons take the short and long interferometer paths, respectively. In this case, they arrive at BS2 with a time difference of ±2⋅δt. As this delay exceeds the ES lifetime (6 ns), no interference is observed. Similarly, the remaining 50% of the paired photons choose identical interferometer paths and arrive at BS2 without interference with a time difference of ±δt. Thus we expect that the five detection rates associated with the different coincidence time differences A−2⋅δt, A−δt, A0, A+δt and A+2⋅δt show the well-known ratio of 1:2:0:2:131.
Figure 2b shows typical raw data for the HOM experiment. The central peak at τ = 0 ns is strongly suppressed compared to the side peaks at τ = ±δt and τ = ± 2⋅δt. Each peak exhibits an exponential decay of 6 ns corresponding to the V1 ES lifetime. Following the analysis by Santori et al.31, we determine the raw HOM interference visibility \(V_0 = 1 - 2 \cdot \frac{{A_0}}{{A_{ - {\updelta}t} + A_{ + {\updelta}t}}} = 0.69 \pm 0.02\). Since this value greatly exceeds 2⋅g(2) (τ = 0), generation of two-photon entanglement can be straightforwardly implemented32,33,34. The HOM interference visibility is comparable to those reported for two consecutive photons from quantum dots with off-resonant excitation (0.53–0.86)35,36,37.
Spin-controlled distinguishable photon generation
As mentioned earlier (see Fig. 1b, d), optical transitions are spin conserving and intimately linked to spin sublevels, i.e. \(\left| { \pm 1/2} \right\rangle _{{{{\mathrm{GS}}}}} \leftrightarrow \left| { \pm 1/2} \right\rangle _{{{{\mathrm{ES}}}}}\) levels are connected via the A1 optical transition and \(\left| { \pm 3/2} \right\rangle _{{{{\mathrm{GS}}}}} \leftrightarrow \left| { \pm 3/2} \right\rangle _{{{{\mathrm{ES}}}}}\) via A2. Consequently, without intersystem crossing, repeated off-resonant excitation leads to streams of consecutively emitted indistinguishable photons in the A1 or photons in the A2 transition, respectively. As one of the system’s key assets, we highlight that the h-VSi centre in SiC possesses a GS spin quartet with a coherence time that exceeds the ES lifetime by at least five orders of magnitude20,22. This provides a direct control mechanism of the colour of consecutively emitted photons, e.g. by flipping the GS spin from the subspace \(\left| { \pm 1/2} \right\rangle _{{{{\mathrm{GS}}}}}\) to \(\left| { \pm 3/2} \right\rangle _{{{{\mathrm{GS}}}}}\), the first and second photon will be in A1 and A2, respectively. Figure 3a shows the experimental sequence. The four GS spin levels are non-degenerate due to the external magnetic field. After the first excitation, we apply a short radiofrequency (RF) wave pulse at a frequency of 30.3 MHz. Note that, owing to the high RF pulse power and the short pulse duration, all GS spin transitions are driven simultaneously. However, our independent resonant excitation measurements and theoretical modelling show that spin driving between the \(\left| { \pm 1/2} \right\rangle _{{{{\mathrm{GS}}}}}\) and \(\left| { \pm 3/2} \right\rangle _{{{{\mathrm{GS}}}}}\) subspaces still reaches fidelities of about 70% (for more details, see Supplementary Note 4). Figure 3b shows the resulting HOM interference pattern at RF power of 30 dBm and a pulse length of 19 ns, which corresponds to a π/2-pulse (see Supplementary Note 4). The coincidence peak at zero time delay reappears clearly, due to the emission of distinguishable photons. In addition, as shown in Fig. 3c, the interference pattern around zero time delay shows the expected modulation with a frequency of ≈1 GHz, matching the frequency difference between A1 and A2 optical transitions38. We note that the high RF pulse power causes significant optical linewidth broadening due to thermal heating, limiting the maximum HOM visibility to 0.56 ± 0.04 and Vmax = 0.73 ± 0.05 after correcting for experimental imperfections (as discussed later and in Supplementary Note 4). By normalising the recorded and corrected visibility Vmeasured to Vmax, we obtain a corrected HOM visibility of \(V_{{{{\mathrm{norm}}}},\pi /2} = \frac{{V_{{{{\mathrm{measured}}}}}}}{{V_{{{{\mathrm{max}}}}}}} = 0.65 \pm 0.07\), which matches the expectation for a π/2-pulse (for details, see Supplementary Note 4). To prove that our spin-to-photon interface is indeed based on coherent spin manipulation, we repeat the experiment with two additional RF pulse lengths of 10 and 29 ns (corresponding to a π/4-pulse and 3π/4-pulse, respectively). The observed visibilities are \(V_{{{{\mathrm{norm}}}},\pi /4} = 0.90 \pm 0.09\) and \(V_{{{{\mathrm{norm}}}},3\pi /4} = 0.47 \pm 0.17\), respectively. Data for the three measurements above is shown in Fig. 3d. The data match the theoretical model very precisely, which is based on independently measured Rabi oscillations (see Supplementary Note 4). Consequently, the results corroborate that the photonic emission of the h-VSi centre can be controlled by coherent spin manipulation, which is crucial for remote entanglement generation5,6,7,8,39,40.
a Schematics for spin-controlled generation of distinguishable photons from a single h-VSi centre. The sketch shows the realisation when the system is initially in the \(m_{{{\mathrm{S}}}} = \pm {\textstyle{1 \over 2}}\) subspace. The first laser excitation results in a red photon (A1 line). A subsequent RF pulse with variable duration transfers population (partially) from \(m_{{{\mathrm{S}}}} = \pm {\textstyle{1 \over 2}}\) to \(m_{{{\mathrm{S}}}} = \pm {\textstyle{3 \over 2}}\). The second excitation results in a blue photon (A2 line), which makes the two interfering photons maximally distinguishable, and projects the system into the \(m_{{{\mathrm{S}}}} = \pm {\textstyle{3 \over 2}}\) subspace. b Two-photon coincidence counts as a function of the delay time for a RF pulse duration of 19 ns (corresponding to a π/2-pulse). The coincidence peak at zero time delay reappears. Data are recorded at 0.1 ns timing resolution and averaged over three points to improve signal to noise. c Zoom-in of the HOM interference pattern revealing the fringe pattern with the expected modulation at 0.965 ± 0.006 GHz. Red dots are uncorrected data, and the blue line is the fit to the data (for details on the fit model, see Supplementary Note 7). d HOM contrast as a function of the RF pulse duration. Rabi-like oscillations are observed, demonstrating that coherent spin manipulation controls the degree of photon indistinguishability. Red dots are data and the blue line is the theoretical model considering independently measured Rabi oscillations (see Supplementary Note 4). Error bars represent one standard error.
Temperature stability of spin–photonic properties
In the last step, we provide a deeper insight into the system’s temperature-dependent spin–phonon–photon physics. For this, we consider the visibility reduction in the raw data of the HOM experiment without RF pulses. To explain deviations from non-unity visibility, we consider six detrimental factors: (i) pure dephasing in the ES due to phonon scattering41, (ii) spectral diffusion due to local charge redistribution42, (iii) two-photon emission during one laser pulse31,43, (iv) background counts, e.g. laser breakthrough, bulk and surface fluorescence, and Raman scattering, (v) interferometer imperfections, e.g. non-unity fringe contrast and unbalanced beam splitter transmissivity and reflectivity31, and (vi) the photon arrival timing jitter at BS2, e.g. due to finite laser pulse duration44 as well as timing jitter of the laser. We infer that factors (v) and (vi) amount to 1% and 0.8% contrast reduction, respectively (see Supplementary Notes 2 and 3). Experimentally, we minimise the fast components of factors (iii) and (iv) by time-gating the coincidence detection, i.e. detector clicks are only considered posterior to a delay time tStart (see “Methods”). Generally, we find that the visibility saturates for tStart > 1.5 ns, indicating that laser-induced noise is efficiently filtered out at this point. To infer the contribution of pure dephasing and spectral diffusion, we extend the analysis by Thoma et al.41 and include coincidence window gating with start and stop delays tStart and tStop, respectively (for more details, see Supplementary Note 5). This provides us with an additional tuning knob, as we can now actively control the time window Δt = tStop − tStart in which we give pure dephasing (single-phonon scattering in the ES) a chance to degrade the fringe visibility in the HOM experiments (see Fig. 4a). As an example, Fig. 4b shows the HOM pattern at T = 5.0 K for tStart = 3.5 ns and a short time window Δt = 4 ns. For those settings, we obtain an uncorrected raw visibility of V0,gated = 0.85 ± 0.04. For arbitrary time gating settings, we find an analytic expression for the expected HOM visibility:
a Visualisation of the time-resolved HOM experiment (not to scale for better visualisation). The black solid line symbolises the single-photon wavefunction, while the black dashed line represents its envelope. For short times close to 0 ns, laser noise photons are observed (red pulse). This contribution is conveniently filtered out by only accepting detection events posterior to the start gate delay tStart. In our visualisation, the photon wave function experiences a phase kick at a time delay of about 10 ns, due to phonon scattering in the V1 excited state. By having a variable stop gate time tStop, we effectively control the integration window Δt = tStop − tStart. This allows us to infer the time scale of pure dephasing. b Uncorrected HOM pattern at T = 5.0 K for tStart = 3.5 ns and Δt = 4 ns. Owing to the short time gating, the raw visibility increases to V0 = 0.85 ± 0.04, which matches the theoretical expectation (0.80 ± 0.01) considering only experimental imperfections (see Supplementary Note 3). Dots are data and lines are visual guides. c Corrected HOM visibility at tStart = 3.5 ns and varying Δt and at three different temperatures. For Δt → 0 ns, visibilities approach unity, as pure dephasing is completely suppressed. Dots are data (red circles: 5.0 K, blue cross marks: 5.9 K, and green triangles: 6.8 K), and lines with associated colours are fits for data at each temperature according to Eq. (1). d Temperature-dependent pure dephasing rate \(\gamma _{{{{\mathrm{max}}}}}^\prime\) (red circles) and associated spectral diffusion amplitude \({{\Gamma }}_0^\prime\) (black squares). The red line is the fit considering the model described with Eq. (2). The black line is a guide to the eye. Error bars in c and d correspond to one standard error.
Here \({{\Gamma }} = {\textstyle{1 \over {6\,{{{\mathrm{ns}}}}}}}\) is the inverse ES lifetime, and \(\gamma = {{\Gamma }}_0^\prime [{1 - {{{\mathrm{e}}}}^{ - \left( {\delta t/\tau _{{{\mathrm{c}}}}} \right)^2}}] + 2\gamma^\prime\), with \({{\Gamma }}_0^\prime\) being the amplitude of spectral diffusion, τc the associated time constant and γ' the pure dephasing rate of the single emitter. To infer γ, the experimental data has to be corrected for experimental imperfections (interferometer, finite signal-to-noise ratio and photon arrival timing jitter). Figure 4c shows the corrected HOM visibility as a function of Δt for fixed tStart = 3.5 ns. To gain more insights of the system, the measurements are performed by adjusting the cryostat to three different temperatures T = 5.0, 5.9, and 6.8 K. By fitting each data set with the model in Eq. (1), we extract γ. We note that one contribution to spectral diffusion is thermal ionisation of nearby charge traps, usually occurring at several tens of Kelvin45,46,47. Thus, in our experiments, spectral diffusion is attributed to laser ionisation, which depends very weakly on temperature and occurs usually at a microsecond time scales47. Consequently, we have τc ≫ δt, such that HOM visibility reduction is essentially only limited by pure dephasing (γ'). This permits us to provide an upper limit for the pure dephasing rate \(\gamma _{{{{\mathrm{max}}}}}^\prime\) (obtained from the HOM experiments), as well as the associated amplitude of spectral diffusion \({{\Gamma }}_0^\prime\) (obtained from slow absorption linewidth measurements). The results of the temperature-dependent measurements are summarised in Fig. 4d. As expected, we find that \({{\Gamma }}_0^\prime\) remains nearly constant over the measured temperature range. The increase of \(\gamma _{{{{\mathrm{max}}}}}^\prime\) is described by vibronic interaction of the V1 and V1’ ESs27, which are separated by a relatively small energy gap of ΔE = 4.4 meV. As we detail in Supplementary Note 6, at the experimental temperatures, single acoustic phonon scattering processes cause pure dephasing with a rate given by
Here kB is Boltzmann’s constant and the prefactor A describes the phonon interaction strength. By fitting the data, we obtain A = 2π⋅(237 ± 12) MHz (meV)−3. Interestingly, we find that pure dephasing for the h-VSi centre is comparatively low at cryogenic temperatures, e.g. considering photonic interference experiments without any time-gating, pure dephasing reduces the optical coherence time to half of the transform limit (2Γ−1 = 12 ns) only at Tcrit > 6.9 K. This temperature is comparable to quantum dot single-photon sources48 and conveniently surpassed with standard cryostat equipment. Below Tcrit, the remaining small emission linewidth broadening is mainly due to slow spectral diffusion. Although this does not present a significant influence for HOM experiments, it may be even further suppressed with improved crystal growth and associated annealing procedures to reduce charge traps. Alternatively, electronic device structures might be promising to control the charge environment12,49,50,51.
Discussion
In summary, we have demonstrated spin-controlled generation of indistinguishable and distinguishable photons from a single h-VSi centre in SiC. Despite performing our experiments under strong off-resonant excitation, pure dephasing, and spectral diffusion are exceptionally low, such that the quality of our raw data is sufficient for photonic entanglement generation32,33,34. Our semiconductor platform has thus demonstrated a level of spectral stability, which is on par with inversion-symmetry defects in diamond13,14,15,16, quantum dots36,41, and single molecules34. Furthermore, we showed that the system possesses an intimate spin–photon interface through which we deterministically tuned the degree of photon indistinguishability via coherent spin manipulation. Note that the system’s millisecond spin coherence times22 are sufficient for high-level spin–photon manipulation, such as remote entanglement generation5,6,7 in a scalable quantum repeater network8. Implementing the related protocols necessitates optimised RF driving to reduce heating issues, which will suppress pure dephasing to negligible levels. To provide the necessary optical phase reference, resonant excitation is required, which requires several orders of magnitude lower optical powers, such that spectral diffusion will also be greatly suppressed52. In the perspective of quantum repeaters, long storage time quantum memories can be conveniently realised with recently demonstrated coupling to individual nuclear spins22. Implementation of state-of-the-art SiC photonic nanostructures would further increase light collection efficiency and ultra-compact chip-based integration53, such that it will become realistic to use our system for generation of high-photon-number cluster states54.
Methods
Sample preparation
The 100-µm-thick 4H-28Si12C silicon carbide layer is grown by chemical vapour deposition on an n-type (0001) 4H-SiC substrate. The isotope purity is measured by secondary ion mass spectroscopy and inferred to be ∼99.85% for 28Si and ∼99.98% for 12C. Current–voltage measurements at room temperature shows that the layer is n-type with a free carrier concentration of ∼6 × 1013 cm−3, which is close to the concentration of shallow nitrogen donors of ∼3.5 × 1013 cm−3. Deep-level transient spectroscopic measurements show that the dominant electron trap in the layer is related to the carbon vacancy with a concentration in the mid 1012 cm−3 range. Minority carrier lifetime mapping of the carrier shows a homogeneous carrier lifetime of ∼0.6 µs. We expect the real value to be twice as high, as an optical method with high injection was used55. Thus the density of all electron traps should be limited to the mid 1013 cm−3 range56. Individually addressable silicon vacancy centres were created through room temperature electron beam irradiation at 2 MeV with a fluence of 1012 cm−2. Parasitic defects, such as carbon vacancies, interstitials, anti-sites, and their associated defects, are expected to be below mid 1012 cm−3. Some interstitial-related defects were removed by subsequent annealing at 300 °C for 30 min.
To improve light extraction efficiency out of the high refractive index material (n ≈ 2.6), we fabricate a solid immersion lens using a focussed ion beam milling machine (Helios NanoLab 650). The related surface contaminations and modifications are subsequently removed by wet and dry etching treatments19.
Experimental set-up
All the experiments were performed at cryogenic temperatures in a Montana Instruments Cryostation. A home-built confocal microscope20 was used for optical excitation and subsequent fluorescence detection of single silicon vacancies.
Continuous-wave off-resonant optical excitation of single silicon vacancy centres was performed with a 730 nm laser diode. Pulsed off-resonant excitation at 780 nm was performed using a picosecond laser diode (PicoQuant LDH-P-C-780). For resonant optical excitation at 861.7 nm, we used an external cavity tunable diode laser (Toptica DLC DL PRO 850). All lasers are spatial-mode cleaned by coupling to a single-mode fibre. For the picosecond laser, we employ a 780-nm bandpass filter after the fibre output to suppress Raman noise. Light is focussed onto the sample with a vacuum-compatible microscope objective (Zeiss EC Epiplan-Neofluar ×100, NA = 0.9).
Note that the used 4H-SiC sample was flipped to the side, i.e. by 90° compared to the c-axis, such that the polarisation of the excitation lasers is parallel to the c-axis (E||c), which allows to excite the V1 ES with maximum efficiency20,57.
The fluorescence emission is collected by the same microscope objective and split by a dichroic mirror (Semrock Versa Chrome Edge) into two parts, i.e. ZPL (at 861.7 nm) and PSB (at 875–950 nm). PSB fluorescence is detected using a silicon avalanche photodiode (Excelitas SPCM-AQRH-W4).
ZPL emission is directed to a fully fibred Mach–Zehnder-type interferometer with a path length difference of ≈10 m. A fibre polarisation controller in the long interferometer arm allows to match the photon polarisation rotation experienced in both arms. Both interferometer outputs are directed to SNSPDs (PhotonSpot Inc.) with 80–85% detection efficiency and sub-Hz dark count rates.
In order to coherently manipulate GS spin populations, microwaves are applied through a 50-µm-thick copper wire spanned over the 4H-SiC sample in close proximity to the investigated h-VSi defect centre.
Filter cavity for ZPL fine structure investigation
To investigate the fine structure of the ZPL, we use a home-built fibre-coupled plano-concave Fabry–Pérot cavity. The cavity has the following specifications: free spectral range: 5.145 GHz; finesse: 177 ± 10; linewidth: 29 ± 2 MHz; input-fibre-to-output-fibre transmission: 80%. The cavity length is tunable via a piezoelectric actuator on which one of the two mirrors is glued. The cavity housing is made from Invar to ensure good thermal stability. The typical drift of the cavity was measured to be on the order of 5 kHz s−1.
Further details on how the cavity was used for resolving the fine structure of the ZPL emission are given in Supplementary Note 8.
Time-gating scheme
To filter out noise components induced by the off-resonant high-power pulsed laser excitation and to perform time-resolved HOM experiments for investigation of pure dephasing, a time-gated photon detection scheme is implemented by software. All photon click signals from the SNSPDs are time tagged by coincidence electronics (Swabian Instruments Time Tagger 20) and referenced to the laser pulse timing. Via software postprocessing, we then implement time-gating by validating only photon clicks between tStart ≤ t ≤ tStop (here t = 0 represents the earliest possible photon arrival time). Owing to the software implementation on the Time Tagger 20, the experimental data points with different settings of (tStart, tStop) are obtained within a single measurement.
Data availability
All data are available upon reasonable request from the corresponding authors.
Change history
07 October 2021
A Correction to this paper has been published: https://doi.org/10.1038/s41467-021-25869-w
References
Yang, S. et al. High-fidelity transfer and storage of photon states in a single nuclear spin. Nat. Photon. 10, 507–511 (2016).
Abobeih, M. H. et al. One-second coherence for a single electron spin coupled to a multi-qubit nuclear-spin environment. Nat. Commun. 9, 2552 (2018).
Duan, L. M., Lukin, M. D., Cirac, J. I. & Zoller, P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413–418 (2001).
Kimble, H. J. The quantum internet. Nature 453, 1023–1030 (2008).
Bernien, H. et al. Heralded entanglement between solid-state qubits separated by three metres. Nature 497, 86–90 (2013).
Hensen, B. et al. Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres. Nature 526, 682–686 (2015).
Humphreys, P. C. et al. Deterministic delivery of remote entanglement on a quantum network. Nature 558, 268–273 (2018).
Rozpȩdek, F. et al. Near-term quantum-repeater experiments with nitrogen-vacancy centers: overcoming the limitations of direct transmission. Phys. Rev. A 99, 052330 (2019).
Awschalom, D. D., Hanson, R., Wrachtrup, J. & Zhou, B. B. Quantum technologies with optically interfaced solid-state spins. Nat. Photon. 12, 516–527 (2018).
Chu, Y. et al. Coherent optical transitions in implanted nitrogen vacancy centers. Nano Lett. 14, 1982–1986 (2014).
Riedel, D. et al. Deterministic enhancement of coherent photon generation from a nitrogen-vacancy center in ultrapure diamond. Phys. Rev. X 7, 031040 (2017).
Anderson, C. P. et al. Electrical and optical control of single spins integrated in scalable semiconductor devices. Science 366, 1225–1230 (2019).
Bhaskar, M. K. et al. Quantum nonlinear optics with a germanium-vacancy color center in a nanoscale diamond waveguide. Phys. Rev. Lett. 118, 223603 (2017).
Siyushev, P. et al. Optical and microwave control of germanium-vacancy center spins in diamond. Phys. Rev. B 96, 081201(R) (2017).
Trusheim, M. E. et al. Transform-limited photons from a coherent tin-vacancy spin in diamond. Phys. Rev. Lett. 124, 023602 (2020).
Rogers, L. J. et al. Multiple intrinsically identical single-photon emitters in the solid state. Nat. Commun. 5, 4739 (2014).
Sukachev, D. D. et al. Silicon-vacancy spin qubit in diamond: a quantum memory exceeding 10 ms with single-shot state readout. Phys. Rev. Lett. 119, 223602 (2017).
Christle, D. J. et al. Isolated electron spins in silicon carbide with millisecond coherence times. Nat. Mater. 14, 160–163 (2015).
Widmann, M. et al. Coherent control of single spins in silicon carbide at room temperature. Nat. Mater. 14, 164–168 (2015).
Nagy, R. et al. Quantum properties of dichroic silicon vacancies in silicon carbide. Phys. Rev. Appl. 9, 034022 (2018).
Kraus, H. et al. Magnetic field and temperature sensing with atomic-scale spin defects in silicon carbide. Sci. Rep. 4, 5303 (2014).
Nagy, R. et al. High-fidelity spin and optical control of single silicon-vacancy centres in silicon carbide. Nat. Commun. 10, 1954 (2019).
Udvarhelyi, P. et al. Spectrally stable defect qubits with no inversion symmetry for robust spin-to-photon interface. Phys. Rev. Appl. 11, 044022 (2019).
Simin, D. et al. Locking of electron spin coherence above 20 ms in natural silicon carbide. Phys. Rev. B 95, 161201 (2017).
Economou, S. E. & Dev, P. Spin-photon entanglement interfaces in silicon carbide defect centers. Nanotechnology 27, 504001 (2016).
Dong, W., Doherty, M. W. & Economou, S. E. Spin polarization through intersystem crossing in the silicon vacancy of silicon carbide. Phys. Rev. B 99, 184102 (2019).
Udvarhelyi, P. et al. Vibronic states and their effect on the temperature and strain dependence of silicon-vacancy qubits in 4H silicon carbide. Phys. Rev. Appl. in press (2020).
Martin, A., Alibart, O., De Micheli, M. P., Ostrowsky, D. B. & Tanzilli, S. A quantum relay chip based on telecommunication integrated optics technology. New J. Phys. 14, 025002 (2012).
Brown, B. R. H. & Twiss, R. Q. A test of a new type of stellar interferometer on Sirius. Nature 17, 1046–1048 (1956).
Hong, C. K., Ou, Z. Y. & Mandel, L. Measurement of subpicosecond time intervals between two photons by interference. Phys. Rev. Lett. 59, 2044–2046 (1987).
Santori, C., Fattal, D., Vuckovic, J., Solomon, G. S. & Yamamoto, Y. Indistinguishable photons from a single-photon device. Nature 419, 594–597 (2002).
Fattal, D. et al. Entanglement formation and violation of Bell’s inequality with a semiconductor single photon source. Phys. Rev. Lett. 92, 037903 (2004).
Patel, R. B. et al. Quantum interference of electrically generated single photons from a quantum dot. Nanotechnology 21, 274011 (2010).
Rezai, M., Wrachtrup, J. & Gerhardt, I. Polarization-entangled photon pairs from a single molecule. Optica 6, 34–40 (2019).
Gazzano, O. et al. Bright solid-state sources of indistinguishable single photons. Nat. Commun. 4, 1425 (2013).
Gschrey, M. et al. Highly indistinguishable photons from deterministic quantum-dot microlenses utilizing three-dimensional in situ electron-beam lithography. Nat. Commun. 6, 7662 (2015).
Somaschi, N. et al. Near-optimal single-photon sources in the solid state. Nat. Photon. 10, 340–345 (2016).
Legero, T., Wilk, T., Hennrich, M., Rempe, G. & Kuhn, A. Quantum beat of two single photons. Phys. Rev. Lett. 93, 070503 (2004).
Matsukevich, D. N., Maunz, P., Moehring, D. L., Olmschenk, S. & Monroe, C. Bell inequality violation with two remote atomic qubits. Phys. Rev. Lett. 100, 150404 (2008).
Rosenfeld, W. et al. Event-ready Bell test using entangled atoms simultaneously closing detection and locality loopholes. Phys. Rev. Lett. 119, 010402 (2017).
Thoma, A. et al. Exploring dephasing of a solid-state quantum emitter via time- and temperature-dependent Hong-Ou-Mandel experiments. Phys. Rev. Lett. 116, 033601 (2016).
Bernien, H. et al. Two-photon quantum interference from separate nitrogen vacancy centers in diamond. Phys. Rev. Lett. 108, 043604 (2012).
Flagg, E. B., Polyakov, S. V., Thomay, T. & Solomon, G. S. Dynamics of nonclassical light from a single solid-state quantum emitter. Phys. Rev. Lett. 109, 163601 (2012).
Huber, T., Predojević, A., Föger, D., Solomon, G. & Weihs, G. Optimal excitation conditions for indistinguishable photons from quantum dots. New J. Phys. 17, 123025 (2015).
Giesz, V. et al. Cavity-enhanced two-photon interference using remote quantum dot sources. Phys. Rev. B 92, 161302(R) (2015).
Kambs, B. & Becher, C. Limitations on the indistinguishability of photons from remote solid state sources. New J. Phys. 20, 115003 (2018).
Wolters, J., Sadzak, N., Schell, A. W., Schröder, T. & Benson, O. Measurement of the ultrafast spectral diffusion of the optical transition of nitrogen vacancy centers in nano-size diamond using correlation interferometry. Phys. Rev. Lett. 110, 027401 (2013).
Reimer, M. E. et al. Overcoming power broadening of the quantum dot emission in a pure wurtzite nanowire. Phys. Rev. B 93, 195316 (2016).
Bathen, M. E. et al. Electrical charge state identification and control for the silicon vacancy in 4H-SiC. npj Quantum Inf. 5, 111 (2019).
Widmann, M. et al. Electrical charge state manipulation of single silicon vacancies in a silicon carbide quantum optoelectronic device. Nano Lett. 19, 7173–7180 (2019).
Rühl, M., Bergmann, L., Krieger, M. & Weber, H. B. Stark tuning of the silicon vacancy in silicon carbide. Nano Lett. 20, 658–663 (2020).
Senellart, P., Solomon, G. & White, A. High-performance semiconductor quantum-dot single-photon sources. Nat. Nanotechnol. 12, 1026–1039 (2017).
Lukin, D. M. et al. 4H-silicon-carbide-on-insulator for integrated quantum and nonlinear photonics. Nat. Photon. https://doi.org/10.1038/s41566-019-0556-6 (2019).
Rao, D. D. B., Yang, S. & Wrachtrup, J. Generation of entangled photon strings using NV centers in diamond. Phys. Rev. B 92, 081301(R) (2015).
Kimoto, T. & Cooper, J. A. Fundamentals of Silicon Carbide Technology: Growth, Characterization, Devices and Applications (John Wiley & Sons, 2014).
Danno, K., Nakamura, D. & Kimoto, T. Investigation of carrier lifetime in 4H-SiC epilayers and lifetime control by electron irradiation. Appl. Phys. Lett. 90, 202109 (2007).
Janzén, E. et al. The silicon vacancy in SiC. Phys. B Condens. Matter 404, 4354–4358 (2009).
Acknowledgements
We warmly thank Christoph Becher, Jürgen Eschner, and Mete Atatüre for fruitful discussions regarding data analysis. We thank Andy Steinmann, Mario Hentschel, Jonas Meinel, Stephan Hirschmann, Ilja Gerhardt, Timo Görlitz, Matthias Widmann, Torsten Rendler, Yu-Chen Chen, Thomas Kornher, Kai-Mei Fu, Karsten Frenner, Photon Spot Inc., PicoQuant GmbH, and Swabian Instruments GmbH for technical help. N.M., C.B., R.N., I.G., E.H., D.L., M.J., M.N., D.D., V.V., R.K., R.S., J.W. and F.K. acknowledge support by the European Research Council (ERC) grant SMel, the European Commission Marie Curie ETN “QuSCo” (GA No 765267), the Max Planck Society, the Humboldt Foundation, and the German Research Foundation (SPP 1601). R.N. acknowledges support by the Carl-Zeiss-Stiftung. N.T.S. acknowledges the Swedish Research Council (grant No. VR 2016-04068). J.U.-H. thanks the Swedish Energy Agency (43611-1). N.T.S. and J.U.-H. thank the Knut and Alice Wallenberg Foundation (Grant No. KAW 2018.0071). A.G., N.T.S., and J.U.-H. thank the EU H2020 project QuanTELCO (Grant No. 862721). T.O. thanks the Japan Society for the Promotion of Science (Grant No. JSPS KAKENHI 17H01056 and 18H03770). A.G. acknowledges the National Excellence Program of Quantum-Coherent Materials Project (Hungarian NKFIH Grant No. KKP129866), the EU QuantERA Q-Magine Project (Grant No. 127889), the QuantERA Nanospin Project (Grant No. 127902) and the National Quantum Technology Program (Grant No. 2017-1.2.1-NKP-2017- 00001). A.G. and J.W. acknowledge the EU-FET Flagship on Quantum Technologies through the project ASTERIQS. J.W. and F.K. acknowledge the EU-FET Flagship on Quantum Technologies through the project QIA.
Author information
Authors and Affiliations
Contributions
N.M., R.N., J.W., and F.K. conceived and designed the experiment; N.M., I.G., E.H., D.L., and F.K. performed the experiment; C.B., M.J., V.V., R.K., and R.S. provided experimental assistance; N.M., P.U., G.T., A.G., J.W., and F.K. analysed the data; J.U.-H. and N.T.S. prepared and characterised SiC materials; T.O. performed electron beam irradiation; R.N. fabricated solid immersion lenses; N.M., I.G., and M.N. developed software for data acquisition and experimental control; N.M., C.B., D.L., D.D., V.V., P.U., G.T., A.G., J.W., and F.K. provided theoretical support. N.M., J.W., and F.K. wrote the manuscript. All authors provided helpful comments during the writing process.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Morioka, N., Babin, C., Nagy, R. et al. Spin-controlled generation of indistinguishable and distinguishable photons from silicon vacancy centres in silicon carbide. Nat Commun 11, 2516 (2020). https://doi.org/10.1038/s41467-020-16330-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-16330-5
This article is cited by
-
Analysis, recent challenges and capabilities of spin-photon interfaces in Silicon carbide-on-insulator
npj Nanophotonics (2024)
-
Spectral stability of V2 centres in sub-micron 4H-SiC membranes
npj Quantum Materials (2024)
-
The silicon vacancy centers in SiC: determination of intrinsic spin dynamics for integrated quantum photonics
npj Quantum Information (2024)
-
Inverted fine structure of a 6H-SiC qubit enabling robust spin-photon interface
npj Quantum Information (2022)
-
Silicon carbide incorporates quantum gates
Nature Materials (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.