Abstract
The classification of topological insulators predicts the existence of high-dimensional topological phases that cannot occur in real materials, as these are limited to three or fewer spatial dimensions. We use electric circuits to experimentally implement a four-dimensional (4D) topological lattice. The lattice dimensionality is established by circuit connections, and not by mapping to a lower-dimensional system. On the lattice’s three-dimensional surface, we observe topological surface states that are associated with a nonzero second Chern number but vanishing first Chern numbers. The 4D lattice belongs to symmetry class AI, which refers to time-reversal-invariant and spinless systems with no special spatial symmetry. Class AI is topologically trivial in one to three spatial dimensions, so 4D is the lowest possible dimension for achieving a topological insulator in this class. This work paves the way to the use of electric circuits for exploring high-dimensional topological models.
Similar content being viewed by others
Introduction
Topological insulators are materials that are insulating in the bulk but host surface states protected by nontrivial topological features of their bulk bandstructures1,2. They are classified according to symmetry and dimensionality3,4,5,6,7, with each class having distinct and interesting properties. The celebrated two-dimensional Quantum Hall (2DQH) phase8, for instance, has topological edge states that travel unidirectionally on the one-dimensional (1D) edge, whereas three-dimensional (3D) topological insulators based on spin-orbit coupling have surface states that act like massless 2D Dirac particles. The classification of topological insulators contains hypothetical high-dimensional phases3 that cannot be realised with real materials, since electrons only move in one, two, or three spatial dimensions. These include several types of four-dimensional Quantum Hall (4DQH) phases, which are characterised by a 4D topological invariant called the second Chern number and exhibit a much richer phenomenology than the 2DQH phase9,10,11,12. In recent years, topological phases have been implemented in a range of engineered systems including cold atom lattices13, photonic structures14, acoustic and mechanical resonators15,16, and electric circuits17,18,19,20,21,22,23,24,25,26,27,28. Some of these platforms can realise lattices that are hard to achieve in real materials, raising the intriguing prospect of using them to create high-dimensional topological insulators. Although there have been demonstrations of topological pumps that map 4D topological lattice states onto lower-dimensional systems29,30,31,32, there has been no experimental realisation of a 4D topological insulator with protected surface states on a 3D surface.
Here, we describe the implementation of a 4DQH phase using electric circuits to access higher dimensions. Since electric circuits are defined in terms of lumped (discrete) elements and their interconnections, lattices with genuine high-dimensional structure can be explicitly constructed by applying the appropriate connections33,34,35. In this way, we experimentally implement a 4D lattice hosting the first realisation of a Class AI topological insulator5,6, which has no counterpart in three or fewer spatial dimensions.
In the symmetry-based classification of topological phases3,4,5,6,7, Class AI includes time-reversal (T) symmetric, spinless systems that are not protected by any special spatial symmetries. Whereas the 2DQH phase is tied to nontrivial values of the first Chern number, which requires T-breaking36, 4DQH phases rely on the second Chern number, which does not9,10,11,12. Even though the Class AI conditions are ubiquitous13,14, the class is topologically trivial in one to three dimensions3,4,5,6,7. Hence, realising a Class AI topological insulator requires going to at least 4D. We focus on a theoretical 4D lattice model recently developed by one of the authors37, which exhibits a nonzero second Chern number with vanishing first Chern numbers. Hence, we obtain the first observations of topological surface states that are intrinsically tied to 4D band topology, with no connection to lower-dimensional topological invariants.
The present approach, based on circuit connections, is distinct from other recently-investigated methods for accessing higher-dimensional models. One of the alternatives involves manipulating internal degrees of freedom, such as oscillator modes, to act as synthetic dimensions38,39,40,41,42,43,44,45,46,47,48,49,50,51,52. Although there have been theoretical proposals for using synthetic dimensions to build 4D topological lattices40,43, all experiments so far have been limited to 1D and 2D51. Another approach involves adiabatic topological pumping schemes, which map high-dimensional models onto lower-dimensional setups by replacing spatial degrees of freedom with tunable parameters29,30,31,32. As mentioned above, 2D topological pumps based on cold atoms and photonics have recently been used to explore Class A (T-broken) 4DQH systems30,53,54. However, topological pumps have the drawback of being inherently limited to probing specific quasi-static solutions of a high-dimensional system, without realising a genuinely high-dimensional lattice. Moreover, in those experiments the second Chern number in 4D is not truly independent of the first Chern numbers in 2D, which are nonzero.
Our 4D lattice is implemented using electric circuits with carefully chosen capacitive and inductive connections. The lattice model has two topologically distinct phases: a 4DQH phase and a conventional (i.e. topologically trivial) 4D band insulator, with the choice of phase governed by a parameter m that maps to certain combinations of capacitances and inductances. Using impedance measurements that are equivalent to finding the local density of states (LDOS), we show that the 4DQH phase hosts surface states on the 3D surface, while the conventional insulator phase has only bulk states. By varying the driving frequency, we show that the topological surface states span a frequency range corresponding to a bulk bandgap, as predicted by theory. Our experimental results also agree well with circuit simulations. This work demonstrates that electric circuits are a flexible and practical way to realise higher-dimensional lattices, paving the way for the exploration of other previously-inaccessible topological phases.
Results
4DQH model and circuit realisation
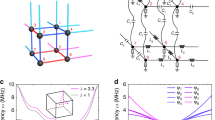
The 4D lattice model is shown schematically in Fig. 1a. The spatial coordinates are denoted x, y, z, and w. The lattice contains four sublattices labelled A, B, C and D, with sites connected by real nearest neighbour hoppings ±J. The four bands host two pairs of Dirac points in the Brillouin zone; each pair is the time-reversed counterpart of the other. To control the pairs separately, long-range hoppings with amplitudes \(\pm J^{\prime}\) and ±J″ are added within the x–z plane (these hoppings are omitted from Fig. 1a for clarity, but are shown in Fig. 1c). Upon adding mass +m to the A and B sites, and −m to the C and D sites, the Dirac masses for the different Dirac point pairs close at \(m=J^{\prime} -2J^{\prime\prime}\) and \(m=J^{\prime\prime} -2J^{\prime}\). These gap closings are topological transitions, such that, for \(J^{\prime\prime} \,=\,-J^{\prime}\), the second Chern number of the lower bands is −2 (nontrivial) if \(| m| \,<\,3| J^{\prime} |\). Since T is unbroken, the first Chern number is always zero, so the model exhibits QH behaviour stemming purely from the second Chern number37. For further details about the model, see Supplementary Note 1.
a Schematic of the 4D tight-binding model. Each unit cell consists of four sites labelled A–D. Hollow and filled circles respectively denote positive (m) and negative (−m) on-site masses, while yellow solid lines and blue dashes respectively denote positive (J) and negative (−J) hoppings. b Photographs of the circuit. c Schematic of the circuit; positive (negative) masses are realised by capacitors (inductors) connecting the sites to ground, and hoppings are realised using capacitors or inductors connecting different sites. The components shown here are C0 = 1 nF (yellow lines), L0 = 2 mH (blue dashes), \(C^{\prime} =2\ {\rm{nF}}\) (purple curves), \(L^{\prime} =1\ {\rm{mH}}\) (green curves), and Cm = 2mC0 (grey dashes). Each site is grounded by a set of additional circuit components (see Supplementary Note 2); for clarity, only the grounding components for two sites (in the dashed red box) are depicted.
We take J = 1 and \(J^{\prime} =-J^{\prime\prime} =2\), so that the topological transition of the bulk lattice occurs at m = ±6. We target a finite 4D lattice with six sites along the x and z directions, and two sites along y and w. To mitigate finite-size effects, periodic boundary conditions are applied in y and w using nearest neighbour type connections between opposite ends of the lattice. This corresponds to sampling at ky = kw = 0 in momentum space, where the gap closing occurs during the topological transition (see Supplementary Note 1). Regardless of these periodic boundary conditions, the spatial dimensionality established by the connectivity of the lattice sites is 4D33. The lattice has a total of 144 sites, of which we consider 16 to be bulk sites (defined as being more than two sites away from a surface) and 128 to be surface sites.
The finite 4D lattice is implemented with a set of connected printed circuit boards, shown in Fig. 1b. Each site i of the tight-binding model maps to a node on the circuit, and the mass term maps to a circuit component of conductance −Dii connecting the node to ground. Each hopping Jij between sites i and j maps to a circuit element of conductance Dij connecting the nodes. We add extra grounding components with conductance \({D}_{ii}^{\prime}\) in parallel with −Dii. If an external AC current Ii flows into each node i at frequency f, and Vi is the complex AC voltage on that node, Kirchhoff’s law states that
We define Dij( f ) = iαHij( f ), where α is a positive real constant. Then capacitances (inductances) correspond to positive (negative) real values of Hij. We require that at a reference working frequency f = f0, the values of Hij(f0) match the desired tight-binding lattice Hamiltonian (see “Methods”). We then tune \(D^{\prime}\) so that for f = f0,
for some target energy E; the required value of \(D^{\prime}\) depends on the m parameter. Equation (1) now becomes
where Lij are the components of the circuit Laplacian L. The impedance between node r and ground is
It can be shown that \({\rm{Re}}[{Z}_{r}({f}_{0})]\) is, up to a scale factor, the LDOS of the target lattice at energy E (see “Methods”). For further details about the circuit analysis, see Supplementary Note 2.
Experimental results
Figure 2a shows the band diagram of the infinite bulk tight-binding model as a function of the mass detuning parameter m. For ∣m∣ < 6, the system is in a 4DQH phase, with a topologically nontrivial bandgap centred at E = 0, which hosts topological surface states.
a Calculated band diagram for the infinite 4D lattice. The bulk bands are shown in grey. For ∣m∣ < 6, there is a bandgap associated with nontrivial second Chern number, accompanied by topological surface states (shaded green). For ∣m∣ > 6, the bandgap is trivial. b Calculated band diagram for 144-site lattice with periodic boundary conditions along y and w. Colours indicate the degree of surface concentration of the energy states, as defined Eq. (5). Due to finite-size effects, surface states occur at ∣m∣ ≲ 2 and the gap closing is shifted to ∣m∣ ≈ 4. The parameters corresponding to subplots c–f are indicated with pink dots. c–f Experimentally-obtained LDOS maps for different m and E, measured at working frequency f = f0. Surface states are observed in c, d consistent with theoretical predictions.
The band diagram for the 144-site tight-binding model is shown in Fig. 2b. The colours of the curves indicate the degree to which each eigenstate is concentrated on the surface, as defined by
where ψ(r) denotes the energy eigenfunction, whose magnitudes are averaged over either surface or bulk sites. Due to the finite lattice size, both the bulk and surface spectrum are split into sub-bands. The closing of the bulk gap is shifted to ∣m∣ ≈ 4, and the surface states occur most prominently at small values of E and ∣m∣.
We now fabricate a set of circuits with parameters m ∈ {0, 1, …, 8} and E ∈ {0, 1}. Figure 2c–f shows the measured LDOS (at f = f0) for four representative samples. From the experimental data, we see that the surface LDOS is high and the bulk LDOS is low when in the topologically nontrivial bandgap (Fig. 2c, d). For E = 0, m = 4, which corresponds roughly to the gap-closing point, there is no significant difference between the surface and bulk LDOS. For E = 0, m = 8, the LDOS on all sites is low, consistent with being in a topologically trivial bandgap. These results also agree well with circuit simulations (see Supplementary Note 3). The robustness of the surface states, a feature imparted by topological protection, can be inferred from the fact that each individual circuit component has up to 10% deviation in its capacitance or inductance (see “Methods”). We emphasise that the surface states cannot be explained by the first Chern numbers, which are necessary zero since the circuit design is T symmetric.
To confirm that the discrepancy between Fig. 2a and b is just a finite-size effect, Fig. 3 shows calculated band edges (i.e. the pair of eigenvalues closest to E = 0) for a series of lattices with 6, 8, 10, 14, 20, and 50 sites along both x and z (the lattices are kept two sites wide along y and w, with periodic boundary conditions). The colours indicate whether the eigenstate is concentrated on the surface (red) or in the bulk (blue). As the size of the lattice increases in x and z, the eigenvalues at large m (in the conventional insulator regime) approach the predicted bulk band edges, while the eigenvalues in the topological insulator regime spread over a larger range of m corresponding to the topologically nontrivial gap.
To quantify the difference between the 4DQH and conventional insulator phases, we examine the ratio of the mean LDOS on surface sites to the mean LDOS on bulk sites, for different values of the mass detuning parameter m (Fig. 4a). The ratio is derived from experimental measurements performed at f = f0, corresponding to E = 0; with increasing m, it decreases sharply from around 4.5 in the 4DQH regime to around 1 in the conventional insulator regime. Circuit simulations produce results in agreement with the experimental data (Fig. 4f).
a Ratio of surface to bulk LDOS, measured at f = f0, versus m. b–e Mean values of the LDOS measure \({\rm{Re}}[{Z}_{r}]\) on surface and bulk sites, versus working frequency f. For these subplots, measurements were only taken over sites in the 2D plane (y, w) = (1, 0). The reference working frequency f0 (corresponding to E = 0) is indicated by the vertical dotted line. For small m, we observe an elevated surface LDOS measure over a range of frequencies coincident with a bulk gap. Upon increasing m, the gap closes. f–j The corresponding circuit simulation results, obtained using the same circuit parameters and with manufacturer-supplied estimates for the capacitor and inductor resistances. The results in f, and the solid curves and dashes in g–j, assume no disorder in the circuit components. The red and blue areas in g–j indicate the range of impedances assuming 10% variation in individual capacitances and inductances, over 50 independent disorder realisations.
The frequency dependence of the circuit impedance is also consistent with the spectral features of a topological insulator at small values of m. Figure 4b–e plots the experimentally-obtained frequency dependence of the LDOS measure \({\rm{Re}}[{Z}_{r}]\), averaged over surface or bulk sites. To interpret these results, recall that the impedance measurements probe the response at fixed energy (in this case, E = 0) of an effective Hamiltonian H(f) that depends parametrically on the frequency f [Eq. (6)], and matches the target tight-binding model at f = f0. For m = 0 (Fig. 4b), the circuit exhibits a strong edge response and suppressed bulk response at f = f0, consistent with the fact that H(f0) has a topologically nontrivial gap at E = 0. For f ≠ f0, the effective Hamiltonian H(f) deviates from the target model (e.g. the positive and negative hoppings become unequal in magnitude, lifting the band degeneracy), but remains in Class AI. So long as the gap remains open, H(f) must possess a topologically nontrivial gap at E = 0 associated with the same second Chern number. The signatures of the topological bandgap persist as m is slightly increased (Fig. 4c); upon further increasing m, the bulk gap closes and thereafter the surface and bulk LDOS measures exhibit no notable frequency dependent features (Fig. 4d, e). These experimental results are in good agreement with simulations (Fig. 4g–j).
Discussion
We have used electric circuits to implement a 4D lattice hosting a 4D Quantum Hall phase. This is the first experimental demonstration of a topological lattice with a 4D structure, and of a Class AI topological insulator. This is also the first experimental exploration of a 4DQH model with nontrivial second Chern number but trivial first Chern numbers. Using impedance measurements, we have demonstrated that the LDOS on the 3D surface is enhanced in the 4DQH phase, due to the presence of topological surface states, and that the enhanced surface response spans the frequency range of the bulk bandgap. The gap-closing associated with a topological phase transition is clearly observed, despite being shifted by finite-size effects. In future work, it is desirable to find ways to probe the detailed features of the 3D surface states, which are predicted to be two robust isolated Weyl points of the same chirality, a situation that does not occur in lower-dimensional topological models37. The successful implementation of 4D lattices of very substantial size (144 sites) shows that electric circuits are an excellent platform for exploring exotic band topological effects, and a promising alternative to the synthetic dimensions approach to realising higher-dimensional lattices51.
While this work was being done, we became aware of related theoretical proposals to use circuits to realise high-dimensional TIs55,56.
Methods
Circuit implementation and experimental procedure
The implementation of the LC circuit, so as to map its impedance response to a target Hamiltonian, follows a design strategy similar to recent works, which targeted different topological models20,21,22,23,26,27,28. As explained in the main text, positive and negative hoppings in the tight-binding Hamiltonian are represented by capacitors and inductors respectively. Defining the complex conductance between sites i and j as Dij = iαHij, we take α = 2πf0C0 to map the positive nearest neighbour hopping J = 1 to capacitance C0 = 1 nF, and the long-range hopping \(J^{\prime}\) to capacitance \(C^{\prime} \,=\,2\ {\rm{nF}}\), at f = f0. Next, setting \({f}_{0}\,=\,1/(2\pi \sqrt{{L}_{0}{C}_{0}}\ ) \approx 113\ {\rm{kHz}}\) maps the negative nearest neighbour hopping to inductance L0 = 2 mH, and the negative long-range hopping J″ = −2 to \(L^{\prime} =1\ {\rm{mH}}\). Each site is connected to ground by additional components to satisfy Eq. (2); see Supplementary Note 2. The required capacitances are obtained by connecting 1 nH capacitors (Murata GCM155R71H102KA37D) in series or parallel, and the inductances are achieved by connecting 1 mH inductors (Taiyo Yuden LB2518T102K).
The circuit is divided into several printed circuit boards (PCBs), stacked on top of each other. Each PCB is divided into 6 × 6 = 36 nodes, corresponding to the dimensions of the 4D lattice in the x–z plane (see Fig. 1c of the main text). Each x–z lattice plane actually consists of several PCBs stacked with vertical electrical interconnects, in order to fit all the necessary circuit components.
We measure the impedance between any given node r and the common ground by applying a 1 V sine wave of frequency f0 on that node, and measuring the voltage Vr and the current Ir. As stated in Eq. 4, the impedance between node r and the ground is the rth diagonal term of the inverse of the circuit Laplacian L. Using Eq. (3), one obtains20,27
where ψn(r) is the n-th energy eigenstate’s amplitude on site r, and En is the corresponding eigenenergy. Thus, if the impedance measurement is performed at f = f0, then \({\rm{Re}}[{Z}_{r}]\,=\,(1/\pi \alpha ){\sum }_{n}\delta (E\,-\,{E}_{n})\ | {\psi }_{n}(r){| }^{2}\) is equivalent to the lattice’s LDOS at energy E. With resistances present, the eigenenergies in Eq. (6) acquire an imaginary part, which has the effect of smoothing out the impedance curves (see Supplementary Note 3).
Circuit simulations
All circuit simulations are performed with ngspice, a free software circuit simulator. We assign to each 1 nF capacitor a 10 Ω resistance, consistent with the resistance in the manufacturer-supplied SPICE model at our operating frequency. For each 1 mH inductor, we assign a 24 Ω resistance consistent with the manufacturer-provided data sheet. Each resistance is applied in series with the corresponding capacitive or inductive element. Other sources of resistance, such as the PCB interconnects, are much harder to characterise and were thus not accounted for in the circuit simulations. To model the disorder in the capacitors and inductors, we apply 10% uniformly-distributed disorder to each capacitance and inductance, consistent with the stated tolerances in their data sheets. The simulations are performed like the experiments: i.e. sine wave voltage source is applied to each node, and the steady-state voltage and current are used to determine the complex impedance.
Data availability
The circuit measurement data that support the findings of this study are available in DR-NTU(data) with the identifier “https://doi.org/10.21979/N9/KXL3TD”57.
Code availability
Ngspice and Python code used for circuit simulation and generating all plots can be found in DR-NTU(data) with the identifier “https://doi.org/10.21979/N9/KXL3TD”57.
References
Hasan, M. Z. & Kane, C. L. Colloquium: topological insulators. Rev. Mod. Phys. 82, 3045–3067 (2010).
Qi, X.-L. & Zhang, S.-C. Topological insulators and superconductors. Rev. Mod. Phys. 83, 1057–1110 (2011).
Altland, A. & Zirnbauer, M. R. Nonstandard symmetry classes in mesoscopic normal-superconducting hybrid structures. Phys. Rev. B 55, 1142–1161 (1997).
Kitaev, A. Periodic table for topological insulators and superconductors. AIP Conference Proceedings 1134, 22 (2009).
Schnyder, A. P., Ryu, S., Furusaki, A. & Ludwig, A. W. W. Classification of topological insulators and superconductors in three spatial dimensions. Phys. Rev. B 78, 195125 (2008).
Ryu, S., Schnyder, A. P., Furusaki, A. & Ludwig, A. W. W. Topological insulators and superconductors: tenfold way and dimensional hierarchy. N. J. Phys. 12, 065010 (2010).
Chiu, C.-K., Teo, J. C. Y., Schnyder, A. P. & Ryu, S. Classification of topological quantum matter with symmetries. Rev. Mod. Phys. 88, 035005 (2016).
Klitzing, Kv, Dorda, G. & Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized hall resistance. Phys. Rev. Lett. 45, 494–497 (1980).
Avron, J., Sadun, L., Segert, J. & Simon, B. Topological invariants in fermi systems with time-reversal invariance. Phys. Rev. Lett. 61, 1329 (1988).
Fröhlich, J. & Pedrini, B. New applications of the chiral anomaly. In Mathematical Physics 2000 (eds Fokas, A., Grigoryan, A., Kibble, T. & Zegarlinski, B.), 9–47 (Word Scientific, 2000).
Zhang, S.-C. A four-dimensional generalization of the quantum hall effect. Science 294, 823–828 (2001).
Sugawa, S., Salces-Carcoba, F., Perry, A. R., Yue, Y. & Spielman, I. Second chern number of a quantum-simulated non-abelian yang monopole. Science 360, 1429–1434 (2018).
Cooper, N. R., Dalibard, J. & Spielman, I. B. Topological bands for ultracold atoms. Rev. Mod. Phys. 91, 015005 (2019).
Ozawa, T. et al. Topological photonics. Rev. Mod. Phys. 91, 015006 (2019).
Yang, Z. et al. Topological acoustics. Phys. Rev. Lett. 114, 114301 (2015).
Huber, S. D. Topological mechanics. Nat. Phys. 12, 621–623 (2016).
Ningyuan, J., Owens, C., Sommer, A., Schuster, D. & Simon, J. Time- and site-resolved dynamics in a topological circuit. Phys. Rev. X 5, 021031 (2015).
Albert, V. V., Glazman, L. I. & Jiang, L. Topological properties of linear circuit lattices. Phys. Rev. Lett. 114, 173902 (2015).
Hadad, Y., Soric, J. C., Khanikaev, A. B. & Alù, A. Self-induced topological protection in nonlinear circuit arrays. Nat. Electron. 1, 178–182 (2018).
Lee, C. H. et al. Topolectrical circuits. Commun. Phys. 1, 39 (2018).
Imhof, S. et al. Topolectrical-circuit realization of topological corner modes. Nat. Phys. 14, 925–929 (2018).
Luo, K., Yu, R. & Weng, H. Topological nodal states in circuit lattice. Research 2018, 6793752 (2018).
Ezawa, M. Higher-order topological electric circuits and topological corner resonance on the breathing kagome and pyrochlore lattices. Phys. Rev. B 98, 201402 (2018).
Wang, Y., Lang, L.-J., Lee, C. H., Zhang, B. & Chong, Y. D. Topologically enhanced harmonic generation in a nonlinear transmission line metamaterial. Nat. Commun. 10, 1102 (2019).
Lu, Y. et al. Probing the berry curvature and fermi arcs of a weyl circuit. Phys. Rev. B 99, 020302 (2019).
Serra-Garcia, M., Süsstrunk, R. & Huber, S. D. Observation of quadrupole transitions and edge mode topology in an lc circuit network. Phys. Rev. B 99, 020304 (2019).
Helbig, T. et al. Band structure engineering and reconstruction in electric circuit networks. Phys. Rev. B 99, 161114 (2019).
Hofmann, T., Helbig, T., Lee, C. H., Greiter, M. & Thomale, R. Chiral voltage propagation and calibration in a topolectrical chern circuit. Phys. Rev. Lett. 122, 247702 (2019).
Thouless, D. Quantization of particle transport. Phys. Rev. B 27, 6083 (1983).
Kraus, Y. E., Ringel, Z. & Zilberberg, O. Four-dimensional quantum hall effect in a two-dimensional quasicrystal. Phys. Rev. Lett. 111, 226401 (2013).
Petrides, I., Price, H. M. & Zilberberg, O. Six-dimensional quantum hall effect and three-dimensional topological pumps. Phys. Rev. B 98, 125431 (2018).
Lee, C. H., Wang, Y., Chen, Y. & Zhang, X. Electromagnetic response of quantum hall systems in dimensions five and six and beyond. Phys. Rev. B 98, 094434 (2018).
Jukić, D. & Buljan, H. Four-dimensional photonic lattices and discrete tesseract solitons. Phys. Rev. A 87, 013814 (2013).
Ezawa, M. Electric circuits for non-hermitian chern insulators. Phys. Rev. B 100, 081401 (2019).
Li, L., Lee, C. H. & Gong, J. Emergence and full 3d-imaging of nodal boundary seifert surfaces in 4d topological matter. Commun. Phys. 2, 135 (2019).
Thouless, D. J., Kohmoto, M., Nightingale, M. P. & denNijs, M. Quantized hall conductance in a two-dimensional periodic potential. Phys. Rev. Lett. 49, 405–408 (1982).
Price, H. M. Four-dimensional topological lattices without gauge fields. Preprint at https://arxiv.org/abs/1806.05263 (2020).
Boada, O., Celi, A., Latorre, J. I. & Lewenstein, M. Quantum simulation of an extra dimension. Phys. Rev. Lett. 108, 133001 (2012).
Celi, A. et al. Synthetic gauge fields in synthetic dimensions. Phys. Rev. Lett. 112, 043001 (2014).
Price, H. M., Zilberberg, O., Ozawa, T., Carusotto, I. & Goldman, N. Four-dimensional quantum hall effect with ultracold atoms. Phys. Rev. Lett. 115, 195303 (2015).
Mancini, M. et al. Observation of chiral edge states with neutral fermions in synthetic hall ribbons. Science 349, 1510–1513 (2015).
Stuhl, B. K., Lu, H.-I., Aycock, L. M., Genkina, D. & Spielman, I. B. Visualizing edge states with an atomic bose gas in the quantum hall regime. Science 349, 1514–1518 (2015).
Ozawa, T., Price, H. M., Goldman, N., Zilberberg, O. & Carusotto, I. Synthetic dimensions in integrated photonics: from optical isolation to four-dimensional quantum hall physics. Phys. Rev. A 93, 043827 (2016).
Price, H. M., Zilberberg, O., Ozawa, T., Carusotto, I. & Goldman, N. Measurement of chern numbers through center-of-mass responses. Phys. Rev. B 93, 245113 (2016).
Yuan, L., Shi, Y. & Fan, S. Photonic gauge potential in a system with a synthetic frequency dimension. Opt. Lett. 41, 741–744 (2016).
Ozawa, T. & Carusotto, I. Synthetic dimensions with magnetic fields and local interactions in photonic lattices. Phys. Rev. Lett. 118, 013601 (2017).
Price, H. M., Ozawa, T. & Goldman, N. Synthetic dimensions for cold atoms from shaking a harmonic trap. Phys. Rev. A 95, 023607 (2017).
Yuan, L., Lin, Q., Xiao, M. & Fan, S. Synthetic dimension in photonics. Optica 5, 1396–1405 (2018).
Price, H. M., Ozawa, T. & Schomerus, H. Synthetic dimensions and topological chiral currents in mesoscopic rings. Preprint at https://arxiv.org/abs/1907.04231 (2020).
Lustig, E. et al. Photonic topological insulator in synthetic dimensions. Nature 567, 356–360 (2019).
Ozawa, T. & Price, H. M. Topological quantum matter in synthetic dimensions. Nat. Rev. Phys. 1, 349–357 (2019).
Dutt, A. et al. A single photonic cavity with two independent physical synthetic dimensions. Science 367, 59–64 (2020).
Lohse, M., Schweizer, C., Price, H. M., Zilberberg, O. & Bloch, I. Exploring 4d quantum hall physics with a 2d topological charge pump. Nature 553, 55–58 (2018).
Zilberberg, O. et al. Photonic topological boundary pumping as a probe of 4d quantum hall physics. Nature 553, 59–62 (2018).
Ezawa, M. Electric circuit simulations of nth -chern-number insulators in 2n -dimensional space and their non-hermitian generalizations for arbitrary n. Phys. Rev. B 100, 075423 (2019).
Yu, R., Zhao, Y. X. & Schnyder, A. P. A genuine realization of the spinless 4d topological insulator by electric circuits. Preprint at https://arxiv.org/abs/1906.00883 https://academic.oup.com/nsr/advance-article/doi/10.1093/nsr/nwaa065/5820240 (2020).
Wang, Y. Replication data for: circuit implementation of a four-dimensional topological insulator. https://doi.org/10.21979/N9/KXL3TD (2020).
Acknowledgements
We are grateful to C.H. Lee and T. Ozawa for helpful discussions. This work was supported by the Singapore MOE Academic Research Fund Tier 3 Grant MOE2016-T3-1-006, Tier 1 Grants RG187/18 and RG174/16(S), and Tier 2 Grant MOE2018-T2-1-022(S). H.M.P. is supported by the Royal Society via grants UF160112, RGF/EA/180121 and RGF/R1/180071.
Author information
Authors and Affiliations
Contributions
Y.W. designed and fabricated the samples, and performed the experiments and simulations. B.Z. and Y.C. supervised the project. Y.W., H.M.P., B.Z. and Y.C. contributed to the theoretical analysis and the writing of the paper.
Corresponding authors
Ethics declarations
Competing interest
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Andrea Alu and Ronny Thomale for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Wang, Y., Price, H.M., Zhang, B. et al. Circuit implementation of a four-dimensional topological insulator. Nat Commun 11, 2356 (2020). https://doi.org/10.1038/s41467-020-15940-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-15940-3
This article is cited by
-
Bulk-local-density-of-state correspondence in topological insulators
Nature Communications (2023)
-
Higher-order topological corner state in a reconfigurable breathing kagome lattice consisting of magnetically coupled LC resonators
Scientific Reports (2023)
-
Three-dimensional non-Abelian Bloch oscillations and higher-order topological states
Communications Physics (2023)
-
Hyperbolic band topology with non-trivial second Chern numbers
Nature Communications (2023)
-
Anyonic bound states in the continuum
Communications Physics (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.