Abstract
The quantum limit is quite easy to achieve once the band crossing exists exactly at the Fermi level (EF) in topological semimetals. In multilayered Dirac fermion systems, the density of Dirac fermions on the zeroth Landau levels (LLs) increases in proportion to the magnetic field, resulting in intriguing angle- and field-dependent interlayer tunneling conductivity near the quantum limit. BaGa2 is an example of a multilayered Dirac semimetal with its quasi-2D Dirac cone located at EF, providing a good platform to study its interlayer transport properties. In this paper, we report the negative interlayer magnetoresistance induced by the tunneling of Dirac fermions between the zeroth LLs of neighboring Ga layers in BaGa2. When the field deviates from the c-axis, the interlayer resistivity ρzz(θ) increases and finally results in a peak with the applied field perpendicular to the c-axis. These unusual interlayer transport properties are observed together in the Dirac semimetal under ambient pressure and are well explained by the model of tunneling between Dirac fermions in the quantum limit.
Similar content being viewed by others
Introduction
Topological semimetals have attracted tremendous attention due to their novel properties, such as high carrier mobility, large transverse magnetoresistance (MR), non-trivial Berry phase, and chiral anomaly1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32. Quantum oscillations, from which the Berry phase, quantum mobility, and effective mass can be extracted, is a routine method in the transport measurement to study topological materials. Obvious Shubnikov–de Haas (SdH) oscillation has been observed in graphene and 3D topological semimetals, e.g. Cd3As27,8,9,10,11,12, Na3Bi3,4,5,6, TaAs family13,14,15,16,17,18,19,20,21,22,23,30,31,32, and MoTe224,25,26,27,28,29. A particular interesting case is that only the zeroth LL is occupied and no more quantum oscillations should be observed once the quantum limit is achieved. In 2D Dirac/Weyl system, the LL energy of the 2D Dirac/Weyl band can be described as \(\varepsilon =\pm \!{v}_{{\rm{F}}}\sqrt{2e\hslash B| n| }\) (n = 0, ±1, ±2...)33. Once the Dirac/Weyl point locates at EF, the quantum limit is easily reached when a small field is applied and the zeroth LL is always locked at EF. Thus, the zeroth LL’s degeneracy increases dramatically with the field and the Dirac/Weyl fermions on the zeroth LLs participate in the interlayer magnetotransport directly through tunneling mechanism34, inducing the exotic phenomena of negative interlayer magnetoresistance (NIMR) and interlayer resistivity peak as shown in α-(BEDT-TTF)2I3 and YbMnBi234,35,36. However, the 2D Dirac cone in α-(BEDT-TTF)2I3 only exists under pressure and the NIMR is absent in YbMnBi234,35,36.
BaGa2 is recently predicted to be a candidate of Dirac semimetals. The crystal structure of BaGa2 consists of Ga honeycomb-net layers and Ba layers. Its quasi-2D Dirac cone originates from Ga pz orbitals with the Dirac point located at EF37, while Ba layer between two Ga honeycomb-net layers act as the interlayer transport barrier. Thus, BaGa2 is believed as an ideal candidate of quasi-2D Dirac material and it provides a good platform to investigate the unusual interlayer transport properties induced by the tunneling of Dirac fermions on the zeroth LLs. Figure 1a presents the schematic illustration of the Dirac fermion interlayer tunneling on the zeroth LLs in BaGa2.
a Crystal structure and schematic of the interlayer tunneling of zeroth LLs’s Dirac fermions of BaGa2. The red and blue balls represent Ga and Ba atoms, respectively. b Single crystal X-ray diffraction pattern. Inset: the picture of BaGa2 crystal. c Powder X-ray diffraction pattern with refined lattice parameters a = 4.43 Å and c = 5.08 Å (SG: P6/mmm). d Temperature dependence of in-plane ρxx(T) and interlayer ρzz(T). Inset: field dependence of Hall resistivity ρxy at 2 K. e In-plane MR at different temperatures.
In this work, the quasi-2D Dirac cone at K with the Dirac point located at EF is confirmed by the first-principles calculations, angle-dependent dHvA oscillations and angle-resolved photoemission spectroscopy (ARPES) measurements. The above-mentioned NIMR and peak in angle-dependent interlayer resistivity are both observed clearly in BaGa2 for the first time and well explained by the model of Dirac fermion tunneling between the zeroth LLs34.
Results
Materials characteristic and in-plane transport properties
BaGa2 single crystals are grown by self-flux method (see the “Methods” section). The crystal structure consists of Ba planes and the Ga honeycomb-net planes which shows 2D characteristic. The (00l) lattice plane and lattice parameters are determined by the X-ray diffraction (XRD) measurements on BaGa2 single crystal and powder as shown in Fig. 1b and c. Both the in-plane resistivity (ρxx) and the interlayer resistivity (ρzz) show metallic behavior (Fig. 1d). The ratio of ρzz/ρxx is about 26 at 2.5 K, indicating a moderate electronic structure anisotropy. The measurements of Hall resistivity ρxy reveal that the in-plane dominant carrier is hole-like with the carrier concentration and mobility estimated to be nh = 4.28 × 1021 cm−3 and μh = 3277 cm2 V−1 s−1 at 2 K. The MR of BaGa2 reaches 400% and shows no sign of SdH oscillation (Fig. 1e).
dHvA quantum oscillations
dHvA oscillations at various temperatures with the magnetic field along [00l] direction is shown in Fig. 2a. Four fundamental frequencies Fα = 36.9 T, Fβ = 56.6 T, Fγ = 356.0 T, Fη = 1862.0 T are confirmed to exist after fast Fourier transform (FFT) analysis of the oscillatory component ΔM as shown in Fig. 2b and c.
The dHvA oscillations can be described by the Lifshitz–Kosevich (LK) formula38
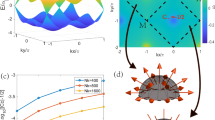
where RT = (λTμ/B)/sinh(λTμ/B), RD = exp(−λTDμ/B) and λ = (2π2kBm0)/(ℏe). μ is the ratio of effective mass m* to free electron mass m0, and TD is the Dingle temperature. γ = 0, δ = 0 for a 2D system, and γ = 1/2, δ = ±/8 for a 3D system. β = ϕB/2π and ϕB is the Berry phase. The inset of Fig. 2c displays the temperature-dependent FFT amplitudes and fittings using the thermal factor RT in LK formula. The obtained effective cyclotron masses are quite small, comparable with those in topological semimetals, due to the almost linear dispersion though they all originate from trivial bands lately determined by the magnetotransport analysis and first-principles calculations. In order to extract the Berry phase conveniently, we applied four-band LK formula fitting directly. The fitting result is displayed in Fig. 2d with the violet dots being experimental results and the red line being the fitting curve. All of the Berry phase of these four pockets greatly deviate from the non-trivial value π implying that these bands may be trivial. Detailed data is exhibited in Table 1. The angle-dependent dHvA oscillation measurements are applied to further reveal the Fermi surface of BaGa2 as exhibited in Fig. 3a. Figure 3b and c shows the FFT spectra of the corresponding dHvA oscillations with the B rotating from B//c to B//ab. The fundamental frequencies increase with the angle θ and vanish at θ = 90°, indicating the moderate electronic structure anisotropy of these trivial bands. If these trivial bands are highly 2D-like, these frequencies should vanish once the magnetic field rotates by a small angle, which is inconsistent with the experimental measurements that Fα, Fβ, and Fγ are still observable at θ = 56°. Besides, the twofold symmetry of polar plot MR (Fig. 3d) with B always vertical to I at 2.5 K and the ratio of ρxx(14 T, 0°)/ρxx(14 T, 90°) ≈ 5 also indicate a moderate electronic structure anisotropy in BaGa2.
a Angle-dependent dHvA oscillations at 1.8 K. b Corresponding FFT spectra with θ varying from 0° to 90°. c FFT frequencies as a function of angle. Solid red line is the fitting curve with equation F = F0/cos θ. Error bars are estimated from sample holders and defined as s.d. d Polar plot of MR at 9 T (violet dots) and 14 T (red dots) with B always vertical to I at 2.5 K.
First-principles calculations
The band structure and Fermi surfaces of BaGa2 calculated with spin–orbit coupling (SOC) effect included are shown in Fig. 4. As exhibited in Fig. 4a, the Dirac cone locates exactly at K point (EF) in the Brillouin zone (BZ), which is consistent with previous work37. In addition, there exist three trivial bands crossing the Fermi level with the corresponding FSs demonstrated in Fig. 4b–d. The hole-type FSs (Fig. 4b and c) are open-orbit FSs along the kz direction exhibiting quasi-2D characteristic. Notably, different from the ideal cylindrical Fermi surface the lotus-root shape hole-type FS in Fig. 4b has two evident cross sections indicating the existence of kz dispersion, which is consistent with the angle-dependent dHvA oscillations (Fig. 3). According to the Onsager relation F = (ϕ0/2π2) = (ℏ/2πe)A, the frequency F is proportional to the extreme cross section A of FS normal to the magnetic field. The calculated dHvA frequencies from the hole-type Fermi surface Fig. 4b are 61.4 and 430.1 T corresponding to the observed frequencies Fβ and Fγ. The calculated frequency from the other hole-type Fermi surface Fig. 4c is 2273.4 T corresponding to the observed frequency Fη. The calculated largest frequency from the electron-type Fermi surface (Fig. 4d) is 4608.3 T which is too high to be observed at 2.5 K and 14 T. The observed frequency Fα may originate from the electron-type Fermi surface (Fig. 4d) as there is a branch along K–H according to the calculations. Thus, the trivial Berry phases obtained from the fitting are acceptable since they are all from the trivial bands. As for the Dirac band, no frequencies corresponding to the oscillation should be observed since it is located exactly at EF. In addition to the Dirac cone, our first-principles calculations reveal that there is an electron-type pocket along L–H and two hole-type pockets at Γ point in the BZ, which is slightly different from previous results in which there seems to be an extra analogous hole-type pocket at H point and only one hole-type pocket at Γ point37. The difference is acceptable considering that different calculation methods are employed. Besides, in real materials the Fermi surface is affected by many factors, such as temperature, magnetic field, defects, etc. According to the calculations, the Dirac point locates at the high-symmetry point K and EF. Although the Dirac point is not protected by the crystal symmetry and opens a small gap of ~10 meV by considering the SOC effect, the low-energy excitation can still be described by the Dirac equation and possesses the characteristic of Dirac fermions.
ARPES measurement
The electronic structure of BaGa2 is measured by ARPES and the quasi-2D Dirac cone at the K point is revealed. Figure 5a shows a schematic drawing of the 3D BZ and its projected surface BZ onto the (00l) surface measured. The FS is shown in Fig. 5b. The most obvious feature is a nearly circular pocket around the \(\overline{{\rm{K}}}\) point. Besides this pocket, there are several much weaker features around the \(\overline{\Gamma }\) and \(\overline{{\rm{K}}}\) points where several bands cross the Fermi energy. This can be seen more clearly in the ARPES spectra along the high-symmetry directions as shown in Fig. 5c. The experimental spectra show an overall agreement with the calculated dispersions at different kz values. There also exist a few extra band dispersions near the Fermi energy (indicated by red circles in Fig. 5c) originating from surface states which is consistent with the first-principles calculations, as shown in Fig. 5d. Besides, the experimental dispersions which are away from Fermi energy show a mixture of calculated dispersions ranging from kz = 0 and kz = 0.5c* (the dispersions at the kz boundaries are colored black in Fig. 5d), suggesting a very strong kz-broadening39.
a Schematic drawing of the 3D Brillouin zone with high symmetry points marked by red points and its projected surface Brillouin zone to (001) surface. b Measured Fermi surface with corresponding Brillouin zone. c Measured electronic dispersion along \(\overline{{{\Gamma }}}-\overline{{\rm{K}}}-\overline{{\rm{M}}}-\overline{{\rm{\Gamma }}}\) direction. d Calculated bulk and surface electronic dispersion of the Ba&Ga-terminated BaGa2 (001) surface with different kz along \(\overline{{\rm{\Gamma }}}-\overline{{\rm{K}}}-\overline{{\rm{M}}}-\overline{{\rm{\Gamma }}}\) direction. e Schematic drawing shows the slices (purple plane) which cut through the Dirac cones at different ky. f Electronic dispersions cut through the Dirac cones at corresponding ky and corresponding electronic dispersions in the upper panel after normalization by integrating energy distribution curve (EDC). g kz dependence of electronic dispersions cut through the Dirac point and corresponding electronic dispersions in the upper panel after normalization by integrating EDC. The unit of kz is 2π/c.
We zoom in the dispersion near EF to further reveal the Dirac cone at the K point. The dispersion at ky = 0 is shown in Fig. 5f. Due to the matrix element effect40, the left branch is much weaker than the right branch. To enhance the visualization of the dispersion on both sides, we show in Fig. 5g the normalized spectra by integrating each energy distribution curve (EDC). In addition to the Dirac cone at the K point, there is an extra dispersion originating from the surface state, which is consistent with the calculations. The evolution of Dirac cone along the ky direction is shown in Fig. 5f. Moving away from the K point, the dispersion shifts down in energy and becomes more parabolic, in agreement with a Dirac cone at the K point as shown in Fig. 5a. The kz-dependence of the Dirac cone is shown in Fig. 5g. Similar behavior is also observed, with the dispersion shifting down in energy when moving away from K point (kz = 2c*). However, the kz dispersion of the Dirac cone is much weaker than ky dispersion and the Fermi velocity along kz is almost one order of magnitude less than ky, suggesting that the Dirac cone is quasi-2D like centered at K point.
Interlayer transport properties
BaGa2 provides an ideal platform to study the unusual interlayer transport properties caused by the tunneling of Dirac fermions between the zeroth LLs since the Ga honeycomb-net layer contributes the quasi-2D Dirac cone and the Ba layer between adjacent two Ga honeycomb-net layers provides the barriers.
a The schematic illustration of interlayer transport experiment setup. I flows along c, and θ is the angle between B and I. b Angle dependence of interlayer resistivity ρzz at 2.5 K under different magnetic fields. c Angle dependence of ρzz at 2.5 K and 14 T (red dots) with the fitting by Eq. (3) (black line). d and e Field dependence of ρzz at various temperatures and angles, respectively.
Figure 6b presents the angle-dependent interlayer resistivity ρzz(B, θ) at 2.5 K under different fields. It shows the interlayer resistivity peak at θ = 90°. θ is the angle between B and I as defined in Fig. 6a. Besides, the interlayer resistivity decreases with the increasing field, resulting in the NIMR at θ = 0°, as shown in Fig. 6b, d and e. The NIMR decreases quickly when temperature changes from 2.5 to 70 K. Both of these anomalous interlayer transport properties can be understood based on the tunneling of Dirac fermions between the zeroth LLs. According to previous works34,36, the interlayer Dirac fermion tunneling conductivity \({\sigma }_{{\rm{t}}}^{{\rm{LL}}0}({\bf{B}},\theta )\) can be described as
where A is a field-independent parameter, θ is the angle between B and I, and c is the distance of the adjacent two Ga layers. When the field is applied parallel to I along c-axis (θ = 0°), the tunneling conductivity is simplified as \({\sigma }_{{\rm{t}}}^{{\rm{LL0}}}({\bf{B}},{0}^{\circ })\) = A\(\left|{\bf{B}}\right|\). In this case, the tunneling conductivity increases proportional to the magnetic field, leading to the NIMR as exhibited in Fig. 6d. When θ increases from 0° to 90°, the interlayer tunneling conductivity decreases gradually because of the suppression of 2D LL quantization, resulting in the interlayer resistivity peak as shown in Fig. 6b.
In an ideal 2D Dirac system, the interlayer transport is only contributed by the tunneling of Dirac fermions between the zeroth LLs (tunneling channel) and the resistivity exhibits the equivalent peak values at θ = 90° under different fields34,35. However, as shown in Fig. 6b, the interlayer resistivity peak increases with the increasing field. The inconsistency is reasonable since there also exist trivial bands contributing the positive interlayer MR except for the Dirac band. As discussed in the angle-dependent dHvA oscillations, the results from first-principles calculations, the ratio of ρxx(14 T, 0°)/ρxx(14 T, 90°) ≈ 5, and ρzz/ρxx ≈ 26, the electronic anisotropy of these trivial bands are analyzed as moderate. Based on these discussion, we assume the trivial bands contribute to the interlayer transport through a momentum relaxation mechanism (i.e. coherent band transport) and describe it with Drude model. Considering both the tunneling mechanism and momentum relaxation mechanism, the total interlayer resistivity is described as
where σc(B, θ) is the conductivity from the coherent trivial bands. As shown in the Supplementary Table 1, all of the trivial bands do not reach the quantum limit, so the conductivity σc(B, θ) is taken as \({\sigma }_{0}/(1+k\cdot {B}_{xy}^{2})\) for low field approximation (σ0 is the Drude conductivity, k is a constant, Bxy = ∣B∣sin θ). B0 is a fitting parameter34. At θ = 90°, the tunneling channel is suppressed [\({\sigma }_{{\rm{t}}}^{{\rm{LL0}}}({\bf{B}},9{0}^{\circ })\) = 0] and the interlayer resistivity mainly originates from the trivial bands. In such case, the interlayer resistivity is described as ρzz(B, 90°) = 1/σzz(B, 90°) = 1/(σc(B, 90°) + B0). As shown in Fig. 6e the fitting curve matches well with the experimental data. Therefore, to a certain extent, the contribution from trivial bands to interlayer transport can be described by Drude model.
The total interlayer transport properties can be considered as the result of the competition between the tunneling mechanism and momentum relaxation mechanism. When θ is close to 0°, the trivial band-induced positive MR is relatively small because the field-induced scattering is very weak (absence of Lorentz force). However, the density of states (DOS) at Dirac point increases dramatically with the increasing field since the Dirac cone is located exactly at EF. In this case, the tunneling mechanism dominants the interlayer transport, resulting in the NIMR as shown in Fig. 6b, d and e. The angle-dependent and field-dependent unusual interlayer resistivity can be well fitted by Eq. (3), as shown in Fig. 6c and e. When θ increases from 0° to 90°, the tunneling of Dirac fermions between the zeroth LLs is suppressed while the trivial band induced positive MR increases due to the enhancement of the Lorentz force-induced scattering. It is consistent with the observed interlayer MR, where the NIMR vanishes gradually and positive MR increases with θ varying from 0∘ to 90∘. These resistivity curves are well fitted by Eq. (3) as shown in Fig. 6c and e. These anomalous interlayer transport properties induced by the tunneling of Dirac fermions between the zeroth LLs have also been observed in (BEDT-TTF)2I3, where the Dirac cone only exists under pressure34,35. YbMnBi2 is another quasi-2D topological material that exhibits the same anomalous interlayer transport properties36, in which the NIMR was not observed possibly due to the large positive MR induced by other bands overwhelming the signature of NIMR. To our knowledge, BaGa2 is the only material that exhibits both NIMR and interlayer resistivity peak at ambient pressure.
Discussions
To further understand the observed NIMR in BaGa2, we discuss on the possibly different origins of the negative magnetoresistance (NMR) below. BaGa2 is a non-magnetic material, spin flip may not be a suitable reason for the NIMR in BaGa241. Secondly, the NMR has also been observed in topologically trivial materials at high field such as graphite, where the NMR is induced by the ellipsoidal Fermi surfaces approaching the quantum limit42. As displayed in the Supplementary Table 1, all of the trivial bands in BaGa2 are not under the quantum limit with the field of 14 T. In addition, the NIMR in BaGa2 appears once a quite small field is applied. Thus, the scenario of trivial bands under quantum limit does not apply in BaGa2. Thirdly, the NMR induced by chiral anomaly has been widely observed in 3D Dirac and Weyl semimetals5,9,12,21,22, which usually has the form of Δσxx ∝ B2 or B depending on the Fermi energy43. However, the Dirac cone in BaGa2 opens a small energy gap (~10 meV) when SOC is considered and it will not evolve into Weyl cones when time reversal symmetry is broken (applying the magnetic field). So the chiral anomaly is absent in BaGa2 when I//B. Besides, the in-plane NMR is not observed when the field is parallel to the current in BaGa2 (Supplementary Fig. 1). Thus the scenario of chiral anomaly induced NMR does not apply either. Fourthly, current jetting can often cause the NMR44, which has been explained in detail in ref. 45. Specifically, it is caused by the inhomogeneous spatial distribution of the current in the sample22,45. In order to eliminate the current jetting effect, the four-probe AC transport method is applied in the interlayer transport measurement and the current probe with silver paste almost contact fully on the samples’ upper and lower surfaces (Supplementary Fig. 2) to make the current flow cross the sample homogeneously. Besides, the NIMR in BaGa2 decreases quickly with the increasing temperature, inconsistent with the current jetting effect44. Finally, the NIMR can arise in high-purity layered metal PdCoO2 with the residual resistivity ρxx ranging from about 10 to 40 nΩ cm in most single crystals46. As for BaGa2, the residual resistivity ρxx and ρzz are about 440 nΩ cm and 11.44 µΩ cmwhich are larger than that of PdCoO2 at least one order of magnitude. So the condition 4tc > ℏωc (εn = (n + 1/2)ℏωc + 2tccos(kzc), tc is interlayer transfer integral) describing the Landau levels for quasi-2D Fermi surface under the magnetic field in the quasi-2D metal material PdCoO2 may not be fulfilled here. Besides, the interlayer MR in PdCoO2 increases quickly at low field and decreases at high field when field deviates from c-axis which is quite different from that of BaGa2. From the above, we conclude that the interlayer NMR and the interlayer resistivity peak result from the tunneling of Dirac fermions between the zeroth LLs.
In summary, BaGa2 is a multilayered Dirac semimetal with quasi-2D Dirac cone located at EF, which is confirmed by the first-principles calculations, angle-dependent dHvA oscillations and ARPES measurements. The unusual interlayer transport properties (NIMR and peak in angle-dependent interlayer resistivity) originating from the tunneling of Dirac fermions on the zeroth LLs are both observed in BaGa2 under ambient pressure for the first time. Our findings highlight the unusual role of the zeroth LLs in interlayer magnetotransport and enrich the novel transport properties of topological materials at quantum limit.
Methods
Crystal growth and magnetotransport measurements
The single crystal BaGa2 was grown by self-flux method. The ingredient ratio with Ba:Ga = 41.7:58.3 were put into the alumina crucible and sealed into a quartz ampoule. Then the ampoule was heated to 950 °C and kept for 50 h to make sure the materials have melted and mixed thoroughly. The process of crystal growth was carried up in cooling at 3 °C/h to 700 °C. The BaGa2 single crystal was obtained after centrifuging the excess flux at that temperature. The atomic composition of BaGa2 was checked by energy-dispersive x-ray spectroscopy (EDS, Oxford X-Max 50). The crystal structure was determined by XRD in Bruker D8 Advance x-ray diffractometer. TOPAS-4.2 was employed for refinement. The electric transport and magnetic properties were collected in Quantum Design PPMS-14 T and MPMS-3 SQUID VSM system.
Angle-resolved photoemission spectroscopy
ARPES measurements were taken at BL13U of Hefei National Synchrotron Radiation Laboratory and our home laboratory. The crystals were cleaved in situ and measured at a temperature of T ≈ 15 K in vacuum with a base pressure better than 1 × 10−10 torr.
Band structure calculations
The electronic structures of BaGa2 were studied by using first-principles calculations. The projector augmented wave (PAW) method47,48 as implemented in the VASP package49,50,51 was used to describe the core electrons. The SCAN type exchange-correlation potential was adopted52. The kinetic energy cutoff of the plane-wave basis was set to be 400 eV. A 20 × 20 × 18 k-point mesh was utilized for the BZ sampling and the Fermi surface was broadened by the Gaussian smearing method with a width of 0.05 eV. Both cell parameters and internal atomic positions were fully relaxed until the forces on all atoms were smaller than 0.01 eV/A. Once the equilibrium structures were obtained, the electronic structures were calculated with the SOC effect. The Fermi surfaces were studied by using the maximally localized Wannier functions (MLWF) method53,54. To study the surface states, a 1 × 1 two-dimensional supercell with an BaGa2 slab containing 59 atoms and a 20 Å vacuum was employed to simulate the BaGa2 (001) surface.
Data availability
The authors declare that the data supporting the findings of this study are available within the article and its Supplementary Information. Extra data are available from the corresponding authors upon reasonable request.
References
Novoselov, K. S. et al. Two-dimensional gas of massless Dirac fermions in graphene. Nature 438, 197–200 (2005).
Zhang, Y., Tan, Y.-W., Stormer, H. L. & Kim, P. Experimental observation of the quantum Hall effect and Berry’s phase in graphene. Nature 438, 201–204 (2005).
Wang, Z. et al. Dirac semimetal and topological phase transitions in A3Bi (A = Na, K, Rb). Phys. Rev. B 85, 195320 (2012).
Liu, Z. et al. Discovery of a three-dimensional topological Dirac semimetal, Na3Bi. Science 343, 864–867 (2014).
Xiong, J. et al. Evidence for the chiral anomaly in the Dirac semimetal Na3Bi. Science 350, 413–416 (2015).
Xiong, J. et al. Anomalous conductivity tensor in the Dirac semimetal Na3Bi. EPL 114, 27002 (2016).
Liu, Z. et al. A stable three-dimensional topological Dirac semimetal Cd3As2. Nat. Mater. 13, 677–681 (2014).
Borisenko, S. et al. Experimental realization of a three dimensional Dirac semimetal. Phys. Rev. Lett. 113, 027603 (2014).
Liang, T. et al. Ultrahigh mobility and giant magnetoresistance in the Dirac semimetal Cd3As2. Nat. Mater. 14, 280–284 (2015).
He, L. et al. Quantum transport evidence for the three dimensional Dirac semimetal phase in Cd3As2. Phys. Rev. Lett. 113, 246402 (2014).
Li, C.-Z. et al. Giant negative magnetoresistance induced by the chiral anomaly in individual Cd3As2 nanowires. Nat. Commun. 6, 10137 (2015).
Li, H. et al. Negative magnetoresistance in dirac semimetal Cd3As2. Nat. Commun. 7, 10301 (2016).
Weng, H., Fang, C., Fang, Z., Bernevig, B. A. & Dai, X. Weyl semimetal phase in noncentrosymmetric transition-metal monophosphides. Phys. Rev. X 5, 011029 (2015).
Xu, S.-Y. et al. Discovery of a Weyl fermion semimetal and topological Fermi arcs. Science 349, 613–617 (2015).
Huang, S.-M. et al. A Weyl Fermion semimetal with surface fermi arcs in the transition metal monopnictide TaAs class. Nat. Commun. 6, 7373 (2015).
Lv, B. Q. et al. Experimental discovery of Weyl semimetal TaAs. Phys. Rev. X 5, 031013 (2015).
Lv, B. et al. Observation of Weyl nodes in TaAs. Nat. Phys. 11, 724–727 (2015).
Xu, S.-Y. et al. Experimental discovery of a topological Weyl semimetal state in TaP. Sci. Adv. 1, e1501092 (2015).
Xu, N. et al. Observation of Weyl nodes and Fermi arcs in tantalum phosphide. Nat. Commun. 7, 11006 (2016).
Liu, Z. et al. Evolution of the Fermi surface of Weyl semimetals in the transition metal pnictide family. Nat. Mater. 15, 27–31 (2016).
Huang, X. et al. Observation of the chiral-anomaly-induced negative magnetoresistance in 3D Weyl semimetal TaAs. Phys. Rev. X 5, 031023 (2015).
Zhang, C.-L. et al. Signatures of the Adler–Bell–Jackiw chiral anomaly in a Weyl fermion semimetal. Nat. Commun. 7, 10735 (2016).
Arnold, F. et al. Negative magnetoresistance without well defined chirality in the Weyl semimetal TaP. Nat. Commun. 7, 11615 (2016).
Sun, Y., Wu, S.-C., Ali, M. N., Felser, C. & Yan, B. Prediction of Weyl semimetal in orthorhombic MoTe2. Phys. Rev. B 92, 161107 (2015).
Wang, Z. et al. MoTe2: a type-II Weyl topological metal. Phys. Rev. Lett. 117, 056805 (2016).
Tamai, A. et al. Fermi arcs and their topological character in the candidate type-II Weyl semimetal MoTe2. Phys. Rev. X 6, 031021 (2016).
Deng, K. et al. Experimental observation of topological Fermi arcs in type-II Weyl semimetal MoTe2. Nat. Phys. 12, 1105–1110 (2016).
Jiang, J. et al. Signature of type-II Weyl semimetal phase in MoTe2. Nat. Commun. 8, 13973 (2017).
Huang, L. et al. Spectroscopic evidence for a type II Weyl semimetallic state in MoTe2. Nat. Mater. 15, 1155–1160 (2016).
Yang, L. et al. Weyl semimetal phase in the noncentrosymmetric compound TaAs. Nat. Phys. 11, 728–732 (2015).
Hu, J. et al. π Berry phase and Zeeman splitting of Weyl semimetal TaP. Sci. Rep. 6, 18674 (2015).
Shekhar, C. et al. Extremely large magnetoresistance and ultrahigh mobility in the topological Weyl semimetal candidate NbP. Nat. Phys. 11, 645–649 (2015).
Ando, T. Physics of graphene: zero-mode anomalies and roles of symmetry. Prog. Theo. Phys. Suppl. 176, 203–226 (2008).
Osada, T. Negative interlayermagnetoresistance and zero-mode Landau level in multilayer Dirac electron systems. J. Phys. Soc. Jpn. 77, 084711 (2008).
Tajima, N., Sugawara, S., Kato, R., Nishio, Y. & Kajita, K. Effect of the zero-mode Landau level on interlayer magnetoresistance in multilayer massless Dirac fermion systems. Phys. Rev. Lett. 102, 176403 (2009).
Liu, J. et al. Unusual interlayer quantum transport behavior caused by the zeroth Landau level in YbMnBi2. Nat. Commun. 8, 646 (2017).
Gibson, Q. et al. Three-dimensional Dirac semimetals: design principles and predictions of new materials. Phys. Rev. B 91, 205128 (2015).
Shoenberg, D. Magnetic Oscillations in Metals (Cambridge University Press, 2009).
Wadati, H. et al. Strong localization of doped holes in La1−xSrxFeO3 from angle-resolved photoemission spectra. Phys. Rev. B 74, 115114 (2006).
Damascelli, A., Hussain, Z. & Shen, Z.-X. Angle-resolved photoemission studies of the cuprate superconductors. Rev. Mod. Phys. 75, 473–541 (2003).
Ritchie, L. et al. Magnetic, structural, and transport properties of the Heusler alloys Co2MnSi and NiMnSb. Phys. Rev. B 68, 104430 (2003).
Fauqué, B. et al. Two phase transitions induced by a magnetic field in graphite. Phys. Rev. Lett. 110, 266601 (2013).
Dai, X., Lu, H.-Z., Shen, S.-Q. & Yao, H. Detecting monopole charge in Weyl semimetals via quantum interference transport. Phys. Rev. B 93, 161110 (2016).
Hu, J., Rosenbaum, T. & Betts, J. Current jets, disorder, and linear magnetoresistance in the silver chalcogenides. Phys. Rev. Lett. 95, 186603 (2005).
Pippard, A. B. Magnetoresistance in Metals, vol. 2 (Cambridge University Press, 1989).
Kikugawa, N. et al. Interplanar coupling-dependent magnetoresistivity in high-purity layered metals. Nat. Commun. 7, 10903 (2016).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comp. Mater. Sci. 6, 15–50 (1996).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Sun, J., Ruzsinszky, A. & Perdew, J. P. Strongly constrained and appropriately normed semilocal density functional. Phys. Rev. Lett. 115, 036402 (2015).
Marzari, N. & Vanderbilt, D. Maximally localized generalized Wannier functions for composite energy bands. Phys. Rev. B 56, 12847–12865 (1997).
Souza, I., Marzari, N. & Vanderbilt, D. Maximally localized Wannier functions for entangled energy bands. Phys. Rev. B 65, 035109 (2001).
Kokalj, A. Computer graphics and graphical user interfaces as tools in simulations of matter at the atomic scale. Comp. Mater. Sci. 28, 155–168 (2003).
Acknowledgements
We thank T. Qian, G.F. Chen, and H.C. Lei for helpful discussions. This work is supported by the National Natural Science Foundation of China (Nos.11874422, 11574391, 11725418, 11774422, 11774424), the Ministry of Science and Technology of China (Nos. 2019YFA0308602, 2019YFA0308603, 2017YFA0302903) and the Fundamental Research Funds for the Central Universities, and the Research Funds of Renmin University of China (Nos. 18XNLG14, 19XNLG18, 19XNLG13). Computational resources were provided by the Physical Laboratory of High Performance Computing at Renmin University of China. The Fermi surfaces were prepared with the XCRYSDEN program55.
Author information
Authors and Affiliations
Contributions
T.-L.X. coordinated the project and designed the experiments. S.X. and Y.-Y.W. synthesized the single crystals of BaGa2 with the assistance of Q.-H.Y., L.-L.S. and Y.S. C.B. and S.Z. performed the ARPES measurements. P.-J.G., K.L. and Z.-Y.L. performed ab initio calculations. S.X. performed the magneto-transport measurements with the assistance of Y.-Y.W. S.X., C.B. and P.-J.G. plotted the figures and analyzed the experimental data. S.X., Y.-Y.W., and T.-L.X. wrote the paper. All authors discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Su-Yang Xu and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Xu, S., Bao, C., Guo, PJ. et al. Interlayer quantum transport in Dirac semimetal BaGa2. Nat Commun 11, 2370 (2020). https://doi.org/10.1038/s41467-020-15854-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-15854-0
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.