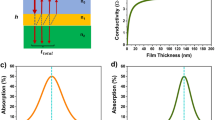
Abstract
Thermal detectors are a cornerstone of infrared and terahertz technology due to their broad spectral range. These detectors call for efficient absorbers with a broad spectral response and minimal thermal mass. A common approach is based on impedance-matching the sheet resistance of a thin metallic film to half the free-space impedance. Thereby, one can achieve a wavelength-independent absorptivity of up to 50%. However, existing absorber films typically require a thickness of the order of tens of nanometers, which can significantly deteriorate the response of a thermal transducer. Here, we present the application of ultrathin gold (2 nm) on top of a surfactant layer of oxidized copper as an effective infrared absorber. An almost wavelength-independent and long-time stable absorptivity of 47(3)%, ranging from 2 μm to 20 μm, can be obtained. The presented absorber allows for a significant improvement of infrared/terahertz technologies in general and thermal detectors in particular.
Similar content being viewed by others
Introduction
Efficient absorbers of electromagnetic radiation are a fundamental element of infrared (IR)/terahertz (THz) technology, and of specific importance for the development of sensitive detectors. In particular, thermal IR/THz detectors have remained the only technology covering the entire spectral range from the visible to the far-IR (THz) regime, facilitating applications ranging from spectrochemical analysis to security and astronomy1,2,3,4,5,6. Thereby, they exploit the conversion of the absorbed photothermal power to either a change in electrical resistance or electric potential, as in bolometers or pyroelectrics and thermocouples, respectively1. More recently, microelectromechanical and nanoelectromechanical systems (MEMS/NEMS) have demonstrated exceptional potential as IR and THz detectors due to strong photothermally-induced detuning of their mechanical resonance frequency7,8,9,10,11,12,13,14.
Despite such variations in detection paradigms, the development of efficient absorbers remains a crucial task in the development of high-performance IR/THz detectors. A suited absorber, in this case, should provide long-term stability, a broad and flat spectral response, while having an negligible thermal mass. This has been the focus for advancement in IR/THz detection for decades and has led to a reduction in effective thickness of the absorber to the order of 10 nm in the present day1.
At this scale, contemporary solutions are numerous: from antenna structures11,15,16,17 to metamaterials18,19,20, which promise absorptivities up to 100% but are always limited by their resonance bandwidth. A progressive solution to improve the spectral range of detection has been to use a stack of plasmonic structures with differing lateral size; nonetheless, the bandwidth of these sensors remains limited e.g., from 0.8 to 1.3 THz21. A most recent thrust toward the ultimate limit of uncooled detection has been to employ the exceptional properties of 2D materials as graphene22, even making the detector itself the primary absorber, for example, as uncooled NEMS resonator8. However, due to graphene’s low absorptivity in the near-IR to mid-IR of only 2.3%23,24, modifications using plasmonic metastructures are still required25, limiting the absorber again to a certain bandwidth.
In the modern age of nano-scale and atomic-scale detectors, we may need to return to a classic, old-fashioned approach: to engineer the sheet resistance of a thin metal such that it matches half the free space impedance \(\sqrt {\mu _0/4\varepsilon _0} \approx 188\, \Omega\)26,27,28. Based on the theory introduced by Woltersdorff28 and further extended by Hadley et al.29 and Hilsum30, a wavelength-independent absorptivity of up to 50% can be achieved, assuming the optical constants n, k are approximately equal — which, for metals such as gold, is only valid in the far-IR.
Many approaches using thin layers of e.g., bismuth, silver (Ag), or platinum31,32,33,34,35,36, unseeded metastructures37, and alloys, such as titanium nitride (TiN), nickel chromium (NiCr)9,10, and indium tin oxide (ITO)38, have been successfully tested for this purpose. However, some alloys/metals are prone to oxidization, which can affect the absorptivity over time. Regarding the thickness needed to match the desired impedance, alloys such as TiN, with an optimum of 14 nm, are often in the same dimension as the detecting element itself7,9,10. Other metals, such as gold, need a comparably large thickness to reach the percolation threshold, setting a lower limit for thin-film thickness at the insulator-to-metal transition, which normally makes them too conductive to match the necessary sheet resistance39. Alternatively, an impedance-matched absorber based on chemically doped graphene has been demonstrated in the THz regime40. However, the response towards shorter wavelengths has not been investigated. While graphene is ultimately the thinnest material, the fabrication and integration of such an absorber is relatively complex.
Recently, it has been shown that it is possible to fabricate ultrathin metal films (UTMF) of Ag41 and Au42 far below the typical percolation limit, using a surfactant layer of oxidized copper.
Here, we demonstrate the application of this technique to fabricate an ultrathin Au layer as an efficient, broad spectral impedance-matched IR absorber. Figure 1 shows a schematic illustration of the fabricated samples used for this study. Due to the differing optical and electrical properties of ultrathin gold compared to bulk values, it is possible to gain an almost wavelength-independent absorptivity of 47(3)% down to below 2 μm with films only 2 nm thick. With its low thermal mass, good stability, and easy producibility, the presented absorber allows for a significant improvement of IR/THz technologies in general and thermal detectors in particular.
Results
Theoretical model of impedance-matched absorption
The model of impedance-matched absorption28,29,30 is based on the assumption that the refractive index n and extinction coefficient κ of the metal are to be equal. From our knowledge the validity of this criteria has yet not been discussed, especially in regard to the limiting wavelength where it can be applied. To get a better understanding of when this assumption is valid, the Drude model is used and rewritten in terms of plasma frequency ωp and electrical resistivity ρ:
where ω is the angular frequency of the optical field. The refractive index and extinction coefficient is then given by \(n = \sqrt {\left| {\hat \varepsilon } \right| + \varepsilon _1}\) and \(\kappa = \sqrt {\left| {\hat \varepsilon } \right| - \varepsilon _1}\), respectively. It can clearly be seen, in order for the assumption (n = κ) to be valid, the imaginary part of the relative permittivity ε2 must dominate. This is true when
In this regime, the Drude model can then be simplified to
where it can be seen that the real part is limited to some finite value; whereas, the imaginary part is increasing for longer wavelengths. For gold, assuming bulk values ρ = 2.2 × 10−8 Ω·m and ωp = 2π·2.1 PHz, this limit is approximately at a wavelength of 56 μm. Below this limit it should not be possible to achieve high absorptivity, unless the material parameters change, which is indeed the case for UTMFs39. Especially, regarding electrical properties, the resistivity can be many factors of magnitude higher than compared to bulk43,44,45. To a certain extent, this can be described by the so-called scattering hypothesis; whereby, the materials’ resistivity is defined as a sum of scattering contributions46
where ρ0 is the bulk resistivity, ρGB ∝ D−1 is the grain-boundary contribution, ρSS ∝ d−1 is the surface scattering contribution, and ρSR ∝ d−3 is the roughness contribution. Here, d is the metal thickness and D the mean grain width of the metal film. For thin films, one can approximate D to be equal to d45. However, with increasing thickness, a limiting grain size of D∞ is reached. The grain-boundary contribution can therefore be extended to ρGB ∝ 1/D∞ + 1/(Cd), where D∞ is often found to be limited up to ~20 nm, respectively the range of the materials’ electron mean free path. The dimensionless factor C typically ranges from 0.5 to 145. Below percolation, ohmic bridges and tunneling effects govern the resistivity, which can be described by e.g., Monte-Carlo simulations or the filamentary vibron quantum percolation model47,48, but however, are beyond the scope of this study. Collectively, all these resistivity contributions lead to broaden the absorptivity bandwidth of thin films down to shorter wavelengths, as described by Eq. (2).
Resistivity and sheet resistance of UTMF
Figure 2 shows the measured resistivity and corresponding sheet resistance of seeded vs. unseeded gold as a function of the deposited layer thickness. Consistent with previous studies on ultrathin copper and gold films41,43,49, the resistivity can be partly fitted by the scattering hypothesis Eq. (4) including a variable offset to compensate the percolation threshold and potential uncertainty of the effective film thickness. The data can be well described by the model down to 2 nm, including a positive offset of 1.84 nm and is governed by the grain-boundary and surface scattering term ∝ d−1. The offset can be related to the percolation threshold. It is exactly between 1.5 and 2 nm where the resistivity drops below the insulator-to-metal transition value of around 6 μΩ·m, defined by Ioffe-Regel50. Thus, percolation must occur in between those samples. As can be seen, Au layers below 1.5 nm show an unexpected reverse trend of the resistivity with increasing thickness. This effect has previously been observed for UTMFs below percolation and can be related to the growth of islands and isolated atoms, which act as additional scattering centers51,52 (For more details see Supplementary Note 3).
a Measured resistivity of seeded and unseeded Au layers as a function of deposited thickness. Due to the oxidized copper seed layer a metallic behavior of Au can be obtained down to 2 nm. The resistivity can be well described by the scattering hypothesis Eq. (4) and is strongly governed by grain-boundary and surface scattering ∝ d−1. In order to fit the data, a 1.84 nm offset is included to compensate the percolation threshold and uncertainty of effective thickness. b Resulting sheet resistance of the same samples. Thus, the optimal thickness for impedance-match to 188 Ω is expected around 2.5 nm. Bulk gold data taken from60. Error bars represent the standard deviation obtained from ten measurements on each sample. Source data are provided as a Source Data file.
Compared to the bulk resistivity of Au with 2.2 × 10−8 Ω·m, the 13 nm thick layer converges to a three times higher value. As mentioned, the grain-boundary scattering term includes a limiting grain size factor of 1/D∞, which significantly lifts the resistivity up to a thickness in the range of the electron mean free path ~20 nm. Thus, with respect to previous studies45, such an increased value can be expected. Regarding the measured sheet resistance, the optimal thickness for matching with half the free space impedance to 188 Ω is expected around 2.5 nm Au.
To investigate whether there is a potential contribution of the oxidized copper used as seed layer, additional experiments with varying Cu thicknesses revealed that bare Cu could be also used as an impedance-matched absorber but only if measured directly after deposition. However, due to oxidization over time41,53, all reference samples with oxidized copper showed a significant increase of resistivity back to the insulating state, and consequential loss of absorptivity. Regarding the presented data, all samples used were taken from a single processed wafer with an initial deposited Cu thickness of 1.2(2) nm. A comparison between seeded and unseeded membranes of this batch showed no significant dependence of the electrical or optical properties on the oxidized seed layer thickness.
Plasma frequency and wavelength-independent absorptivity
In order to obtain a proper fit for the transmittance and reflectivity of ultrathin Au, optical data for the LPCVD SixNy was needed. This was extracted from multiple Fourier transformed IR (FTIR) spectroscopy measurements on bare LPCVD SixNy membranes shown in Fig. 3a. Here, the drop of transmittance and slight increase of reflectivity between 9 to 12 μm is an intrinsic material behavior of SixNy54. Using an optical model55 adapted to a single SixNy layer, to predict the transmittance and reflectivity, a nonlinear fit was done at each wavelength separately, in order to estimate the optical constants (see Supplementary Methods for more details). To reduce the uncertainty of the fit, the measured data were grouped into spectral blocks with 50% overlap. This increases the amount of data per spectral point at the cost of spectral resolution. The result is shown in Fig. 3b with 618 spectral points. Note that the fit is not Kramers-Kronig constrained56, which was not possible due to the limited spectral range of the measurements. However, for the purpose of this paper the data is deemed acceptable.
a Average of ten individual FTIR measurements on 50 nm silicon nitride membranes. b Fitted optical constants using a general matrix model55 by grouping measured data into fixed wavelength points, from which the optical constants were estimated individually (see Supplementary Methods). The shaded region indicates the uncertainty estimated as a 50% increase in sum of squared residuals. Source data are provided as a Source Data file.
Figure 4a shows the measured transmittance and reflectivity of all seeded gold layers. The data is fitted by using the above-mentioned optical model, in combination with the Drude model from Eq. (1), and including the previous extracted optical properties for SixNy. As can be seen from the R2 coefficient of determination, the thicker layers show a metallic behavior and can be well fitted down to 2 nm, consistent with the percolation threshold obtained before. For those thicknesses, the extracted plasma frequency with ωp ≈ 2π·3.0(7) PHz is slightly increased compared to bulk but remains constant within its uncertainty. Due to the loss of metallic behavior, the model can not be effectively applied below percolation (2 nm), which can be clearly seen by the dropping R2 coefficient. In this region, an increase of the transmittance from the 0.35 nm to the 0.7 and 1 nm sample can be observed. Previous studies on thin Au layers around the percolation threshold have confirmed this antireflection phenomena57, whose origin lies in the divergence of the dielectric constant ε1 in that region39. One could, therefore, suggest the use of ultrathin Au below percolation as potential anti-reflection coating.
a Measured transmittance and reflectivity of (seeded) Au layers, obtained by FTIR spectroscopy. All spectra are fitted by the given Drude Model Eq. (1), including the measured resistivity. R2 is the coefficient of determination for each fit. As for thicker layers, all spectra are in good agreement with the optical properties of a metallic film, the layers below 2 nm show a divergence, due to the insulator-to-metal transition. For the metallic-like layers, the obtained plasma frequency remains constant with ωp ~ 2π·3.0(7) PHz. b Absorptivity as a function of deposited gold thickness and wavelength obtained experimentally from FTIR measurements. The data has been linearly interpolated for the plot. Each horizontal grid line corresponds to a sample. All measured layers were evaporated on 50 nm SixNy membranes comprising an oxidized copper seed layer. c Calculated absorptivity using the fitted Drude parameters and measured resistivity via Eq. (1) and extracted optical properties of SixNy. Source data are provided as a Source Data file.
Figure 4b shows the measured, linearly interpolated absorptivity (1—reflectivity—transmittance), plotted over the wavelength and deposited Au thickness. One can clearly determine a maximum absorptivity of 40–50% between the 2 nm and 4 nm Au layer, with a slight decrease towards smaller wavelengths. The absorption peak with a maximum at 12 μm below a gold thickness of 2 nm is a contribution from the supporting SixNy substrate, as can be seen in Fig. 3. The slight increase in absorptivity for the thinnest Au layer of 0.35 nm could be related to the observed reverse trend of the resistivity as can be seen in Fig. 2. A comparison of the average transmittance and reflectivity, as function of the sheet resistance, to the general impedance-match theory28,29,30 can be found in the Supplementary Note 1. Regarding long-term stability, subsequent measurements verified, that the 2 nm samples showed no significant change in absorptivity over a period of five month being stored under ambient conditions. Investigations of similar Au thin films on oxidized Cu also showed a high stability58.
Figure 4c presents the corresponding calculated absorptivity based on the previously obtained optical properties of bare SixNy and the relative permittivity (see Eq. (1)), comprising the measured resistivity and extracted plasma frequency. A comparison to the data shows a good agreement with a minimal offset of ~ 0.35 nm towards the optimal thickness, which lies in the uncertainty of the quartz sensor. With respect to the derived criteria Eq. (2), the increased resistivity and plasma frequency lead to an almost wavelength-independent high absorptivity, ranging from 2 μm up to the detection limit of 20 μm. It is expected that the given absorptivity remains constant also in the far-IR (THz) regime.
Dominance of the imaginary part of relative permittivity
In a final step, the dielectric functions of each metallic layer is extracted via Eq. (1) and plotted in Fig. 5. As can be clearly seen by the ratio |ε2/ε1| (black line), for the 2 nm Au film the magnitude of the imaginary part ε2 is larger than that of the the real part ε1 over the entire spectral range, in good agreement with the derived criteria Eq. (2). Consequentially, this determines the lower spectral limit of the fabricated impedance-matched absorber to 2 μm. For thicker gold films, the |ε2/ε1| > 1 is reached with increasing wavelengths. Regarding the criteria itself, it should be possible to further broaden the wavelength-independent absorptivity by using a material with a larger plasma frequency and higher resistivity such as e.g., aluminum, or by other engineered materials such as doped semiconductors, which needs to be further investigated.
Extracted relative permittivity for increasing gold layer thickness, based on the fitted Drude model Eq. (1). The solid black line represents the ratio of the imaginary vs real part of the permittivity. For thinner layers, where impedance-matched absorption occurs, the imaginary part strongly dominates with increasing wavelength, in good agreement with the derived criteria Eq. (2). The bulk data is for evaporated gold taken from the ref. 61. Source code available on request.
Discussion
We have demonstrated the application of ultrathin 2 nm Au as a highly efficient, broad spectral, impedance-matched absorber. In good agreement with theoretical assumptions, it was possible to gain 47(3)% absorptivity over the entire near- and mid-IR range from 2 to 20 μm. According to the theory, this wavelength-independent absorptivity is expected to be also valid in the far-IR (THz) domain, as demonstrated by previous studies40. Electrical and optical analysis of the deposited Au layers demonstrated the significantly increased resistivity and impact on the optical properties of such ultrathin metal films, which broaden the lower limit of impedance-matched absorption to 2 μm. In this context, it was possible to approximately match the optimal sheet resistance of 188 Ω. The extracted dielectric functions verified, that for those samples the imaginary part of the relative permittivity is strongly enhanced compared to the real part, which in this region can be almost neglected. In the course of this study the optical constants of LPCVD SixNy in the range of 2 to 20 μm were obtained experimentally and further used to estimate the absorptivity. Comprising a small offset of the layer thickness, the calculated absorptivity is in well agreement with the experimental results. Furthermore, the obtained transmittance and reflectance below percolation < 1.84 nm indicate the potential use of ultrathin Au to be used as anti-reflection coating. Overall, considering its negligible small thermal mass, and constant broad spectral absorptivity, we suggest that the fabricated absorber is well-suited to be used in thermal IR and THz detector applications.
Methods
Fabrication of ultrathin gold
Figure 1 shows a schematic illustration of the fabricated samples used for this study. All experiments were conducted on 50 nm thin silicon nitride (SixNy) deposited by low-pressure chemical vapor deposition (LPCVD), acting as a support layer with minimal absorptivity. The 2.5 mm × 2.5 mm squared membranes were structured by standard UV lithography and backside released in potassium hydroxide (KOH). For the ultrathin gold fabrication, a Cu layer was deposited by sputter deposition using a Von Ardenne LS 730S. The deposition rate was set to 1.5 Å s−1, extrapolated from several test depositions. For all samples used in this work, an initial Cu thickness of 1.2(2) nm was deposited. To ensure a smooth and clean surface, the SixNy membranes were plasma cleaned using Argon-based reactive ion etching in the same vacuum chamber, immediately before Cu deposition. Following Maniyara et al.42, the samples were then stored in air for one day to undergo oxidation. During this process, oxidization of Cu can lead to an increase of volume up to 68% (assuming formation of Cu2O42). Thus, the resulting seed layer thickness is expected to be slightly larger than the initial deposited film. In a final step, gold was evaporated from a tungsten boat with a comparably low rate of 0.3 Å s−1 at 3 × 10−8 mbar. The deposition rate and extracted nominal thickness was monitored by a quartz resonating sensor. The thin-film morphology was analysed by means of atomic force microscope images of the 2 nm absorber and bare SixNy, showing a smooth and uniform surface without confined grains (see Supplementary Note 2). Thus, the fabricated UTMFs above the extracted percolation threshold of 1.84 nm can be treated as a continuous metal film.
Optical characterization
All optical spectra were recorded via FTIR spectroscopy conducted with a Bruker Tensor 27. In order to minimize systematic deviations, transmittance and reflectivity measurements were performed within one measurement using a specified A 510/Q-T set-up and an aperture of 2 mm. In order to model the optical behavior, a general matrix method to predict the transmittance and reflectivity has been implemented55 (see Supplementary Methods).
Electrical characterization
The resistivity and sheet resistance were obtained by a homemade four-point-probe setup made of a cylindrical probe-head provided by Jandel, a Keithley 6221 current source, and a Keithley 2182 A nanovoltmeter. The probe-head was attached to a load bending beam Burster 8511–5050 to monitor the contact force applied on the surface during measurements. All samples were measured in a current range of 10−7–10−3 A and maximum contact force of 2.2 N.
References
Rogalski, A. Infrared and Terahertz Detectors. 3rd edn (CRC Press, 2019).
Minoglou, K. et al. Infrared image sensor developments supported by the european space agency. Infrared Phys. Technol. 96, 351 (2019).
Liu, J., Xiao, L., Liu, Y., Cao, L. & Shen, Z. Development of long-wavelength infrared detector and its space-based application requirements. Chin. Phys. B 28, 028504 (2019).
Gerlach, G. In Carbon Dioxide Sensing (eds. Gerlach, G. et al.) 157–190 (CRC Press, 2019).
Talghader, J. J. In Image Sensing Technologies: Materials, Devices, Systems, and Applications V (eds. Dhar, N. K. & Dutta, A. K.) 1065609 (SPIE, 2018).
Généreux, F. et al. Infrared Technology and Applications XLIV, 106241D. (SPIE, 2018).
Piller, M., Luhmann, N., Chien, M. H. & Schmid, S. Optical Sensing, Imaging, and Photon Counting: From X-Rays to THz 2019, Vol. 11088 (SPIE, 2019).
Blaikie, A., Miller, D. & Alemán, B. J. A fast and sensitive room-temperature graphene nanomechanical bolometer. Nat. Commun. 10, 4726 (2019).
Laurent, L., Yon, J. J., Moulet, J. S., Roukes, M. & Duraffourg, L. 12-μm—Pitch electromechanical resonator for thermal sensing. Phys. Rev. Appl. 9, 024016 (2018).
Zhang, X. C., Myers, E. B., Sader, J. E. & Roukes, M. L. Nanomechanical torsional resonators for frequency-shift infrared thermal sensing. Nano Lett. 13, 1528–1534 (2013).
Hui, Y., Gomez-Diaz, J. S., Qian, Z., Alù, A. & Rinaldi, M. Plasmonic piezoelectric nanomechanical resonator for spectrally selective infrared sensing. Nat. Commun. 7, 11249 (2016).
Zhang, Y., Watanabe, Y., Hosono, S., Nagai, N. & Hirakawa, K. Room temperature, very sensitive thermometer using a doubly clamped microelectromechanical beam resonator for bolometer applications. Appl. Phys. Lett. 108, 163503 (2016).
Zhang, Y., Hosono, S., Nagai, N., Song, S.-H. & Hirakawa, K. Fast and sensitive bolometric terahertz detection at room temperature through thermomechanical transduction. J. Appl. Phys. 125, 151602 (2019).
Gokhale, V. J. & Rais-Zadeh, M. Uncooled infrared detectors using gallium nitride on silicon micromechanical resonators. J. Microelectromech. Syst. 23, 803–810 (2014).
Ma, W., Wen, Y. & Yu, X. Broadband metamaterial absorber at mid-infrared using multiplexed cross resonators. Opt. Express 21, 30724–30730 (2013).
Yu, P., Wu, J., Ashalley, E., Govorov, A. & Wang, Z. Dual-band absorber for multispectral plasmon-enhanced infrared photodetection. J. Phys. D 49, 365101 (2016).
Gou, J., Niu, Q., Liang, K., Wang, J. & Jiang, Y. Frequency modulation and absorption improvement of THz micro-bolometer with micro-bridge structure by spiral-type antennas. Nanoscale Res. Lett. 13, 74 (2018).
Yin, S. et al. High-performance terahertz wave absorbers made of silicon-based metamaterials. Appl. Phys. Lett. 107, 073903 (2015).
Takagawa, Y., Ogawa, S. & Kimata, M. Detection wavelength control of uncooled infrared sensors using two-dimensional lattice plasmonic absorbers. Sensors 15, 13660–13669 (2015).
Jin, Y. et al. Ultrabroadband light absorption by a sawtooth anisotropic metamaterial slab. Nano Lett. 12, 1443–1447 (2012).
Liu, S., Chen, H. & Cui, T. J. A broadband terahertz absorber using multi-layer stacked bars. Appl. Phys. Lett. 106, 151601 (2015).
Rogalski, A. Graphene-based materials in the infrared and terahertz detector families: a tutorial. Adv. Opt. Photonics 11, 314–379 (2019b).
Yan, H. et al. Infrared spectroscopy of Wafer-scale graphene. ACS Nano 5, 9854–9860 (2011).
Zanotto, S. et al. Coherent absorption of light by graphene and other optically conducting surfaces in realistic on-substrate configurations. APL Photonics 2, 016101 (2017).
Shimatani, M. et al. Infrared Technology and Applications XLV. (SPIE, 2019).
Hagen, E. & Rubens, H. Die absorption ultravioletter, sichtbarer und ultraroter strahlen in dünnen metallschichten. Ann. der Phys. 313, 432–454 (1902).
Hagen, E. & Rubens, H. Ãœber beziehungen des reflexions- und emissionsvermögens der metalle zu ihrem elektrischen leitvermögen. Ann. der Phys. 316, 873–901 (1903).
Woltersdorff, W. Über die optischen konstanten dünner metallschichten im langwelligen ultrarot. Z. f.ür. Phys. 91, 230–252 (1934).
Hadley, L. N. & Dennison, D. M. Reflection and transmission interference filters. J. Opt. Soc. Am. 37, 451–465 (1947).
Hilsum, C. Infrared absorption of thin metal films at non-normal incidence. J. Opt. Soc. Am. 45, 135–136 (1955).
Kruse, P. W. Uncooled Thermal Imaging Arrays, Systems, and Applications (SPIE, 2001).
Ajakaiye, O., Grade, J., Shin, C. & Kenny, T. Wafer-scale fabrication of infrared detectors based on tunneling displacement transducers. Sens. Actuators A 134, 575–581 (2007).
Bauer, S. et al. Thin metal films as absorbers for infrared sensors. Sens. Actuators A 37-38, 497–501 (1993).
Lang, W., Kühl, K. & Sandmaier, H. Absorbing layers for thermal infrared detectors. Sens. Actuators A 34, 243–248 (1992).
Mahan, G. D. & Marple, D. T. F. Infrared absorption of thin metal films: Pt on Si. Appl. Phys. Lett. 42, 219 (1983).
Sreekanth, K. V. et al. Progress in Optical Science and Photonics. 3–27 (Springer, Singapore, 2019).
Kim, S. J. et al. Superabsorbing, artificial metal films constructed from semiconductor nanoantennas. Nano Lett. 16, 3801–3808 (2016).
Brown, E. R., Zhang, W. D., Chen, H. & Mearini, G. T. THz behavior of indium-tin-oxide films on p-Si substrates. Appl. Phys. Lett. 107, 091102 (2015).
Hövel, M., Gompf, B. & Dressel, M. Dielectric properties of ultrathin metal films around the percolation threshold. Phys. Rev. B 81, 035402 (2010).
Pham, P. H. et al. Broadband impedance match to two-dimensional materials in the terahertz domain. Nat. Commun. 8, 2233 (2017).
Formica, N. et al. Ultrastable and atomically smooth ultrathin silver films grown on a copper seed layer. ACS Appl. Mater. Interfaces 5, 3048–3053 (2013).
Maniyara, R. A. et al. Tunable plasmons in ultrathin metal films. Nat. Photonics 13, 328–333 (2019).
Schmiedl, E., Wissmann, P. & Finzel, H. U. The electrical resistivity of ultra-thin copper films. Z. fur Naturforsch. 63a, 739–744 (2008).
Wu, W., Brongersma, S. H., Van Hove, M. & Maex, K. Influence of surface and grain-boundary scattering on the resistivity of copper in reduced dimensions. Appl. Phys. Lett. 84, 2838 (2004).
Sambles, J. R., Elsom, K. C. & Jarvis, D. J. The electrical resistivity of gold films. Philos. Trans. R. Soc. A 304, 365–396 (1982).
P. Wißmann, P. & Finzel, H.-U. Electrical Resistivity of Thin Metal Films, 223rd edn (ed. Höhler, G.) (Springer, Verlag, 2007).
Finzel, H.-U. & Wißmann, P. Monte-Carlo calculations of the electrical resistance of ultra-thin metal films. Z. f.ür. Naturforsch. A 40a, 161–163 (1985).
Phillips, J. C. Anomalous hopping exponents of ultrathin metal films. Phys. Rev. B 64, 035411 (2001).
Henriquez, R. et al. Effect of a metallic surfactant on the electrical percolation of gold films. Appl. Surf. Sci. 489, 403–408 (2019).
Ioffe, A. F. & Regel, A. R. Non-crystalline, amorphous and liquid electronic semiconductors. Prog. Semicond. 4, 237f (1960).
Gruznev, D. V. et al. Growth of Au thin film on Cu-modified Si(1 1 1) surface. Surf. Sci. 603, 3400–3403 (2009).
Korczak, Z. & Kwapiński, T. Electrical conductance at initial stage in epitaxial growth of Pb, Ag, Au and In on modified Si (1-1-1) surface. Surf. Sci. 601, 3324–3334 (2007).
Drobny, V. & Pulfrey, L. Properties of reactively-sputtered copper oxide thin films. Thin Solid Films 61, 89–98 (1979).
Yamada, S., Schmid, S., Larsen, T., Hansen, O. & Boisen, A. Photothermal infrared spectroscopy of airborne samples with mechanical string resonators. Anal. Chem. 85, 10531–10535 (2013).
Centurioni, E. Generalized matrix method for calculation of internal light energy flux in mixed coherent and incoherent multilayers. Appl. Opt. 44, 7532–7539 (2005).
de, R. & Kronig, L. On the theory of dispersion of X-rays. J. Opt. Soc. Am. 12, 547–557 (1926).
Gompf, B., Beister, J., Brandt, T., Pflaum, J. & Dressel, M. Nanometer-thick Au-films as antireflection coating for infrared light. Opt. Lett. 32, 1578–1580 (2007).
Tsukanov, D. A., Bondarenko, L. V. & Borisenko, E. A. Stability of electric characteristics of au films on Si(111) 5.55 x 5.55-Cu surface exposed to oxygen. Tech. Phys. Lett. 36, 875–877 (2010).
Luhmann, N. et al. Source data—ultrathin 2nm gold as ideal impedance-matched absorber for infrared light. Zenodo https://doi.org/10.5281/zenodo.3667418 (2020).
W. M. Haynes, W. M. CRC Handbook of Chemistry and Physics, 91st edn (CRC Press, 2010).
Olmon, R. L. et al. Optical dielectric function of gold. Phys. Rev. B 86, 235147 (2012).
Acknowledgements
We wish to acknowledge the support of Philipp Altpeter and Philipp Paulitschke for giving access to the clean room facilities of LMU Munich. Furtherstill, we want to thank our technicians Sophia Ewert, Michael Buchholz, and Patrik Meyer for their ongoing support. Special thanks to Christoph Eisenmenger-Sittner from the physical department for condensed matter at TU Wien for providing access to their homemade four-point-probe station. And we would like to thank Michael Feiginov and Pedram Sadeghi for the discussions. In addition we would like to thank Jonas Hafner for his support on the AFM. D.H. and U.L.A. acknowledge support from the Villum foundation and the Danish National Research Foundation. This work has received funding from the European Research Council under the European Union’s Horizon 2020 research and innovation program (Grant Agreement-716087-PLASMECS).
Author information
Authors and Affiliations
Contributions
Fabrication and measurements were performed by N.L., while modeling and data analysis was done by D.H. and N.L; results and data interpretation were discussed by N.L., D.H., M.P., H.K., M.-H.C., R.G.W., and S.S. Further, N.L., D.H., M.P., H.K., M.-H.C., R.G.W., S.S., and U.L.A. have contributed to writing of the manuscript. U.L.A. and S.S. supervised the research.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source Data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Luhmann, N., Høj, D., Piller, M. et al. Ultrathin 2 nm gold as impedance-matched absorber for infrared light. Nat Commun 11, 2161 (2020). https://doi.org/10.1038/s41467-020-15762-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-15762-3
This article is cited by
-
Large area single crystal gold of single nanometer thickness for nanophotonics
Nature Communications (2024)
-
Voltage-controlled nonlinear optical properties in gold nanofilms via electrothermal effect
Nature Communications (2024)
-
Frequency Selective Surface-Based Electromagnetic Absorbers: Trends and Perspectives
Wireless Personal Communications (2023)
-
Simultaneous measurement of temperature and refractive index based on an SPR Silicon core fiber sensor with a fused silica grating design
Optical and Quantum Electronics (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.