Abstract
Various promising qubit concepts have been put forward recently based on engineered superconductor subgap states like Andreev bound states, Majorana zero modes or the Yu-Shiba-Rusinov (Shiba) states. The coupling of these subgap states via a superconductor strongly depends on their spatial extension and is an essential next step for future quantum technologies. Here we investigate the spatial extension of a Shiba state in a semiconductor quantum dot coupled to a superconductor. With detailed transport measurements and numerical renormalization group calculations we find a remarkable more than 50 nm extension of the zero energy Shiba state, much larger than the one observed in very recent scanning tunneling microscopy measurements. Moreover, we demonstrate that its spatial extension increases substantially in a magnetic field.
Similar content being viewed by others
Introduction
Superconductor nanostructures are the most advanced platforms for quantum computational architectures thanks to the macroscopic coherent wavefunction and the robust protection by the superconducting gap. Recently, various qubit concepts like the Andreev (spin) qubits1,2,3,4,5, Majorana box qubits6,7,8, braiding with Majorana zero modes in a Majorana or a Shiba-chain9,10,11,12,13,14,15,16,17,18 have been put forward or even implemented. All these qubits are based on their associated subgap states such as Andreev bound states19, Majorana zero modes18,20,21,22,23,24,25,26 or Shiba states27,28,29,30. The Shiba state is formed when a magnetic adatom or its artificial version (quantum dot) is coupled to a superconductor and the localized magnetic moment creates a subgap state by binding an anti-aligned quasiparticle from the superconductor. Depending on the coupling strength between the superconductor and the magnetic moment, the ground state can be either the screened local moment with singlet character, \(\left|S\right\rangle\) or the unscreened doublet states, \(\left|D\right\rangle\).
The coupling of these subgap states via a superconductor is an essential next step towards 2-qubit operations or state engineering, e.g. an Andreev molecule31,32,33 or a Majorana-chain, which consists of series of adatoms or quantum dots interlinked by the superconductor9,10,11,12,13,14,15,16,17,18,34,35,36. Obviously, the coupling between such subgap states strongly depends on their spatial extension into the superconductor, so it is required for these localized states to extend as much as possible.
So far, the spatial extent and structure of the Shiba states were investigated by STM measurements on magnetic adatoms deposited on the surface of a superconductor37,38,39,40 and, interestingly, it revealed that the dimensionality plays a crucial role39. In a three dimensional isotropic s-wave superconductor, it was found that the Shiba states decay over a very short distance of the order of \({\sim} 1\) nm37,38, but extends one order of magnitude further, as far as \({\sim} 10\) nm, if the impurity is placed on the surface of a two-dimensional superconductor39,41.
Shiba states were widely studied in two different types of systems: (a) in STM measurements, when magnetic particles are deposited on the surface of a superconductor37,38,39,40,41,42,43,44,45,46,47,48, and (b) in nanocircuits, when a quantum dot is attached to the superconductor49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69. The STM geometry allows for the spatial mapping of the Shiba state37,38,39,40, but the strength of the coupling between the magnetic adatom and the substrate is mostly determined by the microscopic details and its tuning remains quite challenging43,45. In contrast, the quantum dot realization enables the tuning of the energy of the Shiba state via the level position or the tunnel couplings by using external gate voltages61,62. Another advantage of the latter setup is the potential to apply an external magnetic field without stability issues.
In this work, we investigate the spatial extension of the Shiba state formed when an artificial atom is strongly coupled to a superconductor. The Shiba state is observed at a remarkably large distance of more than 50 nm. Furthermore, we explore the effect of an external magnetic field on the extension of the Shiba state, as it is relevant to access topological superconducting states. Remarkably, with increasing magnetic field, the spatial extension increases significantly further.
Results
Implementation of the Shiba device
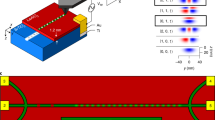
In this paper, we implement a combined approach of systems (a) and (b), where a tunnel probe is attached to a superconductor–quantum dot hybrid. The schematics of the used device are shown on Fig. 1a. A quantum dot (QD in gray) is strongly coupled to a superconductor (SC in red), leading to the formation of a Shiba state. An additional tunnel electrode (N in yellow) is coupled weakly to the superconductor at a fixed distance from the dot. Applying a small bias between SC and N, the tunnel current, \({I}_{{\rm{T}}}\) and the corresponding differential conductance, \({G}_{{\rm{T}}}\) are measured, while the energy of the Shiba state is tuned by the plunger gate \({g}_{{\rm{P}}}\).
a The normal metal-superconductor-quantum dot (N–SC–QD) setup used in our measurements. The QD is strongly coupled to the s-wave superconductor, giving rise to the Shiba state. The normal lead N is coupled to the superconductor at a finite distance \({x}_{{\rm{T}}}\) from the dot, and acts as a tunnel probe and measures the current as the energy of the Shiba state is tuned. The external magnetic field B is applied in-plane of the wafer. b False color SEM image of the device, and c cross section of the device. The QD is formed in an InAs nanowire (gray) by applying voltages on the bottom gate electrodes (yellow). The plunger gate \({g}_{{\rm{P}}}\) controls the level position of the dot, the barrier gate \({g}_{{\rm{B}}}\) isolates the QD. Tunneling to N is controlled by a series of gates. The width of the superconductor is 250 nm and below the superconductor a segment with length of 50–60 nm is cut from the nanowire.
The device is implemented in an InAs semiconducting nanowire (gray), contacted by a 250 nm wide Pb superconducting electrode in the middle (SC in red), and one normal contact (N in yellow) on the left side (see the scanning electron microscope (SEM) image in panel b and the cross section in panel c of Fig. 1). The electron density in the nanowire is tuned by an array of gates fabricated below the nanowire. The nanowire was cut by focused ion beam (FIB) prior to the deposition of the superconducting contact to suppress the direct tunnel coupling between the two arms70,71. The width of the FIB cut is about ~50–60 nm. The quantum dot is formed in the right arm of the wire and its level position is tuned by the voltage \({V}_{{\rm{P}}}\) on the plunger gate \({g}_{{\rm{P}}}\). The tunnel coupling to the right side can be turned on and off by the barrier gate \({g}_{{\rm{B}}}\). Although not displayed in Fig. 1, there is a normal electrode to the right of \({g}_{{\rm{B}}}\), which allows us to measure direct transport through the quantum dot (see Methods). The bulk coherence length for Pb is about \({\xi }_{0}\simeq 80\) nm, however, in e-beam evaporated, disordered layers, where the elastic mean free path is considerably reduced72, the coherence length is limited to \({\xi }_{0}\) = 20–40 nm. An in-plane magnetic field \(B\) is applied perpendicular to the nanowire axis. Further details on the fabrication and the experimental techniques are presented in the Methods.
Observation of the Shiba state in the tunnel current
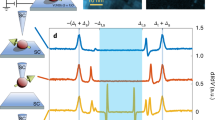
First we present the results of transport measurements for the strongly coupled superconductor–quantum dot setup isolated from the rest of the device on the right by \({g}_{{\rm{B}}}\). The differential conductance of the tunnel probe, \({G}_{{\rm{T}}}\) is shown in Fig. 2 as a function of \({V}_{{\rm{B}}}\) and \({V}_{{\rm{P}}}\) for different values of the magnetic field. In the absence of magnetic field (see panel a), two pairs of resonances with enhanced conductance are present on top of a smooth conductance background of about \(0.1{G}_{0}\) (with \({G}_{0}=2{e}^{2}/h\) the conductance quantum). The conductance increment along the lines is about \(0.005{G}_{0}\). We use the plunger gate voltage \({V}_{{\rm{P}}}\) to tune the level position and subsequently the charge on the quantum dot, while the barrier gate voltage \({V}_{{\rm{B}}}\) is used to isolate the dot from the rest of the nanowire on its right side. The barrier gate \({g}_{{\rm{B}}}\) has a cross capacitance to the dot, resulting a tilt of the otherwise horizontal resonances. As we explained below, the enhanced conductance lines are the signatures of the zero-energy Shiba state. The presence of the current enhancement is striking, since in usual STM setups the Shiba wavefunction is observed only up to a distance of 10 nm. In contrast, we observe the Shiba state more than 50 nm away from the quantum dot.
a–c Differential conductance \({G}_{{\rm{T}}}\) for the tunnel probe as the function of the barrier gate voltage \({V}_{{\rm{B}}}\) and plunger gate voltage \({V}_{{\rm{P}}}\) for various magnetic fields, as indicated in the panels. The two pair of parallel resonances in the differential conductance map are signatures of the even-odd and odd-even transition of the Shiba state (the upper ones are marked by white circle and triangle) d line-cuts at \({V}_{{\rm{B}}}=-1.497\) V for each value of the magnetic field is represented (indicated by the arrows below panels a–c). The blue line corresponds to \(B=0\), the red line to \(B=150\) mT and the green line to \(B=250\) mT. Since the critical magnetic field is \({B}_{{\rm{c}}}=230\) mT, the differential conductance enhancement vanishes for \(B \, > \, {B}_{{\rm{c}}}\).
Remarkably, applying a magnetic field smaller than the critical field, the conductance enhancement significantly increases (see Fig. 2b, being measured in 150 mT). The largest conductance peak we observe is of size \(\Delta {G}_{{\rm{T}}}(B=150\ {\rm{mT}})\simeq 0.1{G}_{0}\), approximately 20 times larger than the zero magnetic field value.
In a 250 mT magnetic field, above the critical field of the superconductor, \({B}_{{\rm{c}}}=230\) mT, the resonances vanish (see Fig. 2c), indicating that the origin of the signal is related to superconductivity. To further illustrate the strong dependence of the signal on the magnetic field, we present in panel c line-cuts at a fixed \({V}_{{\rm{B}}}\)\(\simeq -1.5\) V for the same magnetic fields as in the other panels.
In the following, let us understand what condition of the quantum dot is linked to the tunnel current enhancement. As discussed in the Methods, our device is equipped with an extra normal electrode N\({}_{{\rm{QD}}}\) on the right of the quantum dot, which was previously isolated from the rest of the device by the large negative \({V}_{{\rm{B}}}\) voltage. Increasing \({V}_{{\rm{B}}}\) to more positive values opens up the barrier to N\({}_{{\rm{QD}}}\), which allows for a direct transport characterization of the quantum dot. In this way, we were able to measure in parallel both the differential conductance through the quantum dot itself, \({G}_{{\rm{QD}}}\), and the conductance through the tunnel probe, \({G}_{{\rm{T}}}\). Figure 3a and b show the conductance of the tunnel probe and the quantum dot, respectively, in a larger gate voltage window in the absence of an external magnetic field. The region marked by a white dotted rectangle is the particular voltage window in Fig. 2a. Let us follow the resonances (marked by circle and triangle) in the plot of the tunnel current as \({V}_{{\rm{B}}}\) increases.
Differential conductance of the tunnel probe (panel a) and the quantum dot (panel b) in a larger gate voltage range without magnetic field. The white dashed rectangle marks the region already presented in Fig. 2a. For more positive \({V}_{{\rm{B}}}\), the quantum dot also couples to the right normal lead, N\({}_{{\rm{QD}}}\), while the conductance enhancement persists in \({G}_{{\rm{T}}}\). The coincidence of the conductance lines on panels a and b indicates that the tunnel probe measures the level structure of the quantum dot non-locally. c Finite bias characterization of the quantum dot with open barrier at \({V}_{{\rm{B}}}=-0.83\) V, along the white dotted line in panel b. The eye-shaped crossing is the signature of the Shiba state, \(S\) and \(D\) denotes the ground state character.
For \({V}_{{\rm{B}}}\ {\gtrsim} -\! 1.1\) V the tunnel barrier becomes sufficiently small, and transport through the quantum dot also sets in (see panel b of Fig. 3). The similarities between the resonances in \({G}_{{\rm{T}}}\) and those in \({G}_{{\rm{QD}}}\) indicate that the two conductances are related; the tunnel conductance enhancement is linked to the level position of the quantum dot, i.e. the enhancement is observed when the dot is on resonance with the Fermi level of the superconductor. (See Supplementary Note 1 for transport characterization of the quantum dot in an even larger gate voltage window.)
To gain further insight to the level structure of the quantum dot, a finite bias measurement was performed along the white dashed line on Fig. 3b, at \({V}_{{\rm{B}}}=-0.83\) V. The results are shown in Fig. 3c. The eye-shaped crossing of the subgap conductance lines are the usual fingerprints of the Shiba state (see e.g. ref. 50). The results presented in Fig. 3 show that there is strong coupling between superconductor and quantum dot. In the previously shown measurements of Figs. 2, 3a and 3b, the enhanced conductance lines correspond to the Shiba state when its energy is tuned to zero by \({V}_{{\rm{P}}}\). These resonances (marked by white triangle and circle) correspond to the singlet-doublet and doublet-singlet transitions of the Shiba state. Since the position of the \({G}_{{\rm{T}}}\) enhancement lines coincides with these transitions, we conclude that—even in the case of large tunnel barriers when the quantum dot is coupled only to the superconductor (i.e. for \({V}_{{\rm{B}}} \, {<}{-}1.1\) V)—the conductance enhancement takes place when the energy of the Shiba state is tuned to zero. These results provide direct evidence that the tunneling electrode N indeed probes the Shiba state, and implies that the Shiba state extends in real space over the distance between the dot and the tunnel probe, separated by an impressive distance of 50–250 nm. Here the width of the FIB cut gives the lower and the entire width of the superconducting lead the upper bound (see Fig. 1c).
Further increased extension in magnetic field
A detailed analysis of the finite magnetic field behavior is presented on Fig. 4. Panel a shows the reduction of the superconducting gap, \(\Delta\) with the magnetic field measured on the quantum dot. The gap smoothly decreases in magnetic field and continuously vanishes at \({B}_{{\rm{c}}}=230\) mT, the critical field. The white dashed line is a fit, discussed below.
a Reduction of the superconducting gap with increasing magnetic field measured at \({V}_{{\rm{P}}}=-0.7\) V, \({V}_{{\rm{B}}}=-0.6\) V. The dashed line shows the fit with Eq. (3). b Evolution of the conductance enhancement with magnetic field measured along the dashed line on Fig. 3a. The gray dotted lines are guides to the eye. c The excess current (spectral weight) associated with the zero-energy Shiba state on panel b. The curves show the integrated excess tunnel conductance, \(\Delta {G}_{{\rm{T}}}({V}_{{\rm{P}}})\), after subtracting the \({V}_{{\rm{P}}}\) independent background conductance. For the red/blue curve the integration along \({V}_{{\rm{P}}}\) was carried out for resonance marked by triangle/circle on panel b. The integration window was converted to energy by the level arm of the dot. d NRG simulation of the excess current in the tunnel probe for different ratios of the distance between the dot and the tunnel probe, \({x}_{{\rm{T}}}\) and the zero field coherence length of Pb, \({\xi }_{0}\) using \({\varepsilon }_{{\rm{d}}}=-U/10\).
The detailed evolution of the tunnel current enhancement with the magnetic field—measured along the dashed line in Fig. 3a at \({V}_{{\rm{B}}}=-1.25\) V—is shown on Fig. 4b. While close to \(B=0\), the peaks are barely visible, they are strongly enhanced with increasing magnetic field, particularly between 100 and 200 mT. For higher field values the peaks decrease and they disappear above \({B}_{{\rm{c}}}\). Note that the increasing separation of the conductance peaks with magnetic field is consistent with the Zeeman splitting of the Shiba state61.
Discussion
To explain the magnetic field dependence of the conductance enhancement and to probe the spatial extension of the Shiba state, we have set up a theoretical framework that allows us to compute the tunneling current though the normal lead N in a N–SC–QD geometry in a non-perturbative fashion. We assume that the quantum dot is coupled to the superconductor at \({\bf{x}}=0\), while the normal lead is contacted to the superconductor further away at a coordinate \({{\bf{x}}}_{{\rm{T}}}\). Moreover, we consider that the tunnel probe acts as an STM tip and measures the local density of states by injecting electrons at \({{\bf{x}}}_{{\rm{T}}}\). Electrons entering the superconductor propagate to the quantum dot, scatter on it, and propagate back to be extracted at a later time but at the same position (The model is detailed in the Methods).
For a practical calculation, we need to determine the \(T\)-matrix that describes the scattering of the conduction electrons on the artificial atom. In our model, this is related to Green’s function of the creation operators on the quantum dot, as first discussed by Langreth73. Close to the parity changing transition and close to zero bias, the quasiparticles’ contribution is irrelevant, and only the subgap states contribute. Using field theoretical methods, we computed the total current flowing from the normal lead through the Shiba state by performing a numerical renormalization group (NRG) calculation.
Figure 4c and d compare the experimental and NRG results as a function of magnetic field. In panel c the spectral weight for the experimental data is evaluated along the two dashed lines in panel b. The \({V}_{{\rm{P}}}\) independent conductance background was subtracted from \({G}_{{\rm{T}}}({V}_{{\rm{P}}})\), and the excess tunnel conductance \(\Delta {G}_{{\rm{T}}}({V}_{{\rm{P}}})\) was integrated for the enhancement peaks (marked by circle and triangle) to get the total excess current/spectral weight induced by the Shiba state. The NRG-computed excess currents (see Eq. (14) of Methods) are displayed for different ratios of \({x}_{{\rm{T}}}\) and \({\xi }_{0}\) in panel d, and show a close resemblance to the experimentally observed field dependence. For both panels and for low magnetic fields, the excess current strongly increases with the magnetic field, has a maximum, and linearly decreases at higher fields to vanish at the critical field, \({B}_{{\rm{c}}}=230\) mT.
In order to understand this field dependence, it is instructive to display the results obtained for a classical spin on the dot (see Methods). This minimal model captures most of the experimentally observed features and it is in good agreement with the NRG results (see Methods). In the classical case, the current carried by the Shiba state at the transition reads
Here \({g}_{{\rm{NS}}}\) stands for the dimensionless conductance of the N–SC contact in the normal state (in units of \(2{e}^{2}/h\)), \({u}_{{\rm{S}}}({{\bf{x}}}_{{\rm{T}}})\) and \({v}_{{\rm{S}}}({{\bf{x}}}_{{\rm{T}}})\) denote the electron and hole parts of the bound Shiba state’s wavefunction, and \({\varrho }_{{\rm{S}}}\) is the density of states in the superconductor. The amplitude \(| {u}_{{\rm{S}}}({{\bf{x}}}_{{\rm{T}}}){|}^{2}+| {v}_{{\rm{S}}}({{\bf{x}}}_{{\rm{T}}}){|}^{2}\) can be easily computed for a spherical Fermi surface, yielding
with \(A({{\bf{x}}}_{{\rm{T}}})\) a geometry, position, and spatial dimension dependent dimensionless amplitude, and \(\xi =\hslash {v}_{{\rm{F}}}/\pi \Delta\) the superconducting coherence length of the Pb with \({v}_{{\rm{F}}}\) the Fermi velocity.
Apparently, the magnetic field dependence of the gap and thus that of the correlation length, \({\xi }_{0}\to \xi (B)\), is mostly responsible for the unusual magnetic field dependence observed in our experiment. In the framework of Ginzburg–Landau theory, the order parameter in an external magnetic field is given by \(\Delta (B)={\Delta }_{0}{(1-{B}^{2}/{B}_{{\rm{c}}}^{2})}^{1/2}\), where \({\Delta }_{0}\approx 0.25\ {\rm{meV}}\) is the zero-field gap, \(B\) the magnetic field, and \({B}_{{\rm{c}}}\) stands for the critical magnetic field at which superconductivity vanishes. Experimentally, however, we find a slightly different functional form for the suppression, qualitatively similar to that observed in thin films72,74 (dashed line on Fig. 4a), as
with \({\Delta }_{0}=250\ \mu\)eV and \({B}_{{\rm{c}}}=230\) mT. Note that this value of the induced gap is smaller than the bulk, 1.1 meV gap of Pb75, but comparable to the ones measured in similar films64,76. For \({x}_{{\rm{T}}} \, > \, {\xi }_{0}\), Eq. (3) together with Eq. (2) implies an exponential increase in the current with increasing magnetic field and then a suppression close to \({B}_{{\rm{c}}}\) due to the prefactor \({\xi }^{-1}\). This is consistent with the upturn of measured current enhancement at low fields, below \(120\) mT (see Fig. 4c), and its suppression close to the critical field. According to Eq. (2), the current should be maximal for \({x}_{{\rm{T}}}\approx \pi \xi (B)/2\). Using \(B\approx 180\) mT – where the total excess current is maximal (see Fig. 4c)—this condition yields to \({x}_{{\rm{T}}}\approx 3{\xi }_{0}\). Note, however, that the theory slightly overestimates the magnetic field value where the excess current is maximal – and so underestimates the ratio of \({x}_{{\rm{T}}}/{\xi }_{0}\). This deviation may originate from the fact that our model idealizes the setup, i.e. neglects the presence of quasiparticles and a possibly finite subgap density of states. Keeping this deviation in mind, the obtained ratio is still roughly consistent with our geometrical parameters, the separation of the quantum dot and the normal electrodes \({x}_{{\rm{T}}}\approx\) 50–250 nm, and a reduced coherence length, \({\xi }_{0}\approx\) 20–40 nm, compatible with a diffusive superconductor.
Let us turn to differences compared to typical STM measurements of Shiba states: In STM characterization of the Shiba wavefunction, \({I}_{{\rm{Shiba}}}\) is significantly weaker. Moreover, it oscillates upon varying the tip-adatom distance, \({{\bf{x}}}_{{\rm{T}}}\), and becomes unobservable at distances larger than 10 nm for 3D superconductors. These characteristic differences originate in the quite different geometries used in our setup and in STM experiments.
In STM measurements, the amplitude \(| A({{\bf{x}}}_{{\rm{T}}}){|}^{2}\) is responsible for the spatial oscillations. It has a modulation of \(| \sin ({k}_{{\rm{F}}}{x}_{{\rm{T}}}){|}^{2}\), which originates in the point-like nature of the tunnel probe30,39, and the fact that one usually tunnels either to the electron- or hole-like states with amplitudes \(| {u}_{{\rm{S}}}({{\bf{x}}}_{{\rm{T}}}){|}^{2}\) and \(| {v}_{{\rm{S}}}({{\bf{x}}}_{{\rm{T}}}){|}^{2}\), respectively. In contrast, in our setup, two effects seem to eliminate these oscillations. First, the N–SC interface has a large tunnel surface (\({\approx} {d}^{2}\) where \(d\) is the nanowire diameter, \(d\approx 80\) nm), and the nanowire contains many conductance channels. Therefore, averaging for different distances and tunneling paths is expected to reduce oscillations both in distance (not accessible in our setup) as well as in the \(B\) field dependence77. We remark that to observe magnetic field-induced quantum fluctuations, one would need to pierce more than a flux quantum through the tunneling area, which would require a field comparable or larger than the critical field, \({B}_{{\rm{c}}}\). Second, possibly more importantly, at the transition point the electron and hole-like contributions add up and, surprisingly, the combination \(| {u}_{{\rm{S}}}({{\bf{x}}}_{{\rm{T}}}){|}^{2}+| {v}_{{\rm{S}}}({{\bf{x}}}_{{\rm{T}}}){|}^{2}\)does not contain any oscillating term in any dimension. This indicates that the interference effects probably play little role right at the transition, where our measurements were carried out. Note, that away from the transition point, where the Shiba state is at finite energy, the Shiba-related conductance enhancement of the tunnel probe was also observed, but it was weaker in accordance with the argument above (for details see Supplementary Note 2).
In an STM geometry \({I}_{{\rm{Shiba}}}\) is a small signal (\(\sim\)pA)39, while in our measurement, it can reach values as large as \({I}_{{\rm{Shiba}},\max }\approx 0.7\ {\rm{nA}}\) (at the excitation of \({V}_{{\rm{AC}}}=10 \, {\mu}\)V), even though the normal electrode is at a separation \({x}_{{\rm{T}}}\approx\) 50–250 nm away from the quantum dot. According to Eq. (2), \({I}_{{\rm{Shiba}}}\) is directly proportional to \({g}_{{\rm{NS}}}\ | A{|}^{2}\). The small \({I}_{{\rm{Shiba}}}\) for typical STM experiments is a result of two factors: the weak tunnel coupling \({g}_{{\rm{NS}}}\ll 1\) and also the fast, \(1/{({k}_{{\rm{F}}}{x}_{{\rm{T}}})}^{2}\) decay of \(| A({{\bf{x}}}_{\text{T}}){|}^{2}\) in a 3D superconductor. In our case, \({g}_{{\rm{NS}}}\) is relatively large, in the range of 0.1–1. Additionally, the N–SC tunneling area is very large, \({\sim} {d}^{2} \sim {x}_{{\rm{T}}}^{2}\), compensating the decay of \(| A({{\bf{x}}}_{{\rm{T}}}){|}^{2}\), in close resemblance to lower dimensional superconductors. A combination of these effects can explain how the Shiba state can be observed even from a remote position, significantly larger than the one in STM measurements37,38,39,40. In our quantum dot based setup, the observation distance is determined essentially only by the coherence length of the superconductor, and the coupling between Shiba states hosted around quantum dots can be achieved at significantly larger distances than in case of adatoms.
Finally, let us contrast our findings with the results of Cooper pair splitter measurements, where two quantum dots are attached to both sides of the superconductor, and contrary to our setup, current flows from the superconductor through both quantum dots towards the normal leads. Current correlations between the two arms are induced by splitting up Cooper pairs78,79,80,81,82. There, electronic correlations extend over distances of about 50–200 nm, comparable with the separation \({x}_{{\rm{T}}}\approx\) 50–250 nm in our experiment. However, while the Shiba current, \({I}_{{\rm{Shiba}}}\) increases in a magnetic field, the Cooper pair splitting signal gets strongly suppressed83.
In conclusion we have studied the Shiba state in a SC–QD hybrid device by measuring the differential conductance in a tunnel probe attached to the superconductor at distance of 50–250 nm away from the quantum dot. A large current enhancement has been observed when the Shiba resonance is tuned to zero energy. In an external magnetic field, the signal is further enhanced, implying an exponential growth for the extension of the Shiba state. The observed behavior is consistent with our microscopic theoretical model and field theoretical calculations. In our device, we can access the Shiba state from a remarkably large distance compared to previous experiments on magnetic impurities on superconducting substrates. These results establish an important milestone towards the realization of Shiba chains implemented by a series of quantum dots attached to superconductors.
Methods
Sample fabrication and measurement details
An SEM micrograph of the measured device is shown in Fig. 1b. First, 9 bottom gate electrodes were defined by electron beam lithography and evaporation of 4 nm Ti and 18 nm Pt. Two \(1.3\ \mu\)m wide gates were used below the normal contacts and one, 250 nm wide below the superconductor. The remaining 3 + 3 bottom gates are 30 nm wide with 100 nm period. The gates were covered by 25 nm SiN\({}_{{\rm{x}}}\), using plasma enhanced chemical vapor deposition, to serve as an insulating layer70. The SiN\({}_{{\rm{x}}}\) was removed at the end of bottom gate electrodes by reactive ion etching with CHF\({}_{3}\)/O\({}_{2}\)84, to contact the gate electrodes. The InAs nanowire was deposited by micro-manipulator onto the SiN\({}_{{\rm{x}}}\) layer, approximately perpendicular to the bottom gates. The NWs were grown by gold catalyst assisted MBE growth85,86, using a two-step growth method to suppress the stacking faults87. The normal (N and N\({}_{{\rm{QD}}}\)), Ti/Au (4.5/100 nm) and superconducting (SC), Pd/Pb/In (4.5/110/20 nm) contact were defined in further e-beam lithography and evaporation steps76. The later has a width of 250 nm. Prior to the evaporation, the nanowire was passivated in ammonium sulfide solution to remove the native oxide from the surface88.
Prior to the deposition of the superconducting contact the nanowire was cut by FIB to prevent direct tunneling between the NW segments, which can lead to spurious effects70,71. The width of the FIB cut was about 50 nm, giving a lower bound for the distance of the quantum dot and the tunnel probe.
The measurements were done in a Leiden Cryogenics CF-400 top loading cryo-free dilution refrigerator equipped with a 9+3 T 2D vector-magnet. The measurements were done at a bath temperature of 35 mK. Prior to the cool down, the sample was pumped overnight to remove the adsorbed water contamination from the surface of the nanowire. The currents were measured by standard lock-in technique at 237 Hz. The AC signal of \({V}_{{\rm{AC}}}=10\ \mu\)V was applied to the superconducting electrode. The currents in the left and right arm were measured simultaneously via the two normal leads by home-built I/V converters. The DC bias was applied symmetrically to the normal leads. An in-plane magnetic field was applied parallel to the superconducting electrode, perpendicular to the nanowire. The circuit diagram is shown in Fig. 5. In most of the measurements presented in the main text, N\({}_{{\rm{QD}}}\) was electrically isolated from the rest of the device by applying a large negative voltage on gate \({g}_{{\rm{B}}}\).
Shiba bound state and the parity crossing transition
We model the superconductor using the s-wave BCS theory89
where \({c}_{{\bf{k}}\sigma }^{\dagger }\) is the creation operator of a spin \(\sigma\) and momentum \({\bf{k}}\) and \(\Delta\) is the superconducting order parameter, which can be considered real.
The QD can be described by means of the Anderson model,
with \({\varepsilon }_{d}\) is the single particle energy and \(U\) is the on-site Coulomb energy. The operator \({d}_{\sigma }^{\dagger }\) here creates an electron with spin \(\sigma\) on the dot, and \({n}_{\sigma }={d}_{\sigma }^{\dagger }{d}_{\sigma }\). In our geometry the dot is located at the position \({\bf{x}}=0\) and is tunnel-coupled to the superconductor (See Fig. 6a), as described by the Hamiltonian
The factor \({\alpha }_{{\bf{k}}}\), normalized to one at the Fermi surface, \({\langle |{\alpha }_{{\bf{k}}}{|}^{2}\rangle }_{{\rm{F.S.}}}=1\), accounts for the directional dependence of the tunneling, and prefers tunneling directions perpendicular to the SC–QD interface in our geometry.
In the local moment regime, we can neglect charge fluctuations of the dot, and describe it in terms of a simple Kondo model,
with \({J}_{{\bf{k}}{\bf{k}}^{\prime} }={\alpha }_{{\bf{k}}}{\alpha }_{{\bf{k}}^{\prime} }{J}_{0}\), and \({J}_{0}\propto {t}_{{\rm{S}}}^{2}/U\) the exchange coupling to the spin of the quantum dot, \({\bf{S}}\).
This latter Hamiltonian can be solved exactly in the classical limit28, where one finds a subgap resonance at an energy:
where \(\tilde{j}=\pi j/2\), and \(j={J}_{0}{\varrho }_{{\rm{S}}}\) stands for the standard dimensionless Kondo coupling. With increasing coupling strength the bound state energy \({E}_{0}\) eventually crosses zero, and the impurity binds to itself a quasiparticle of opposite spin direction.
Although this classical calculation captures the parity changing transition, determines its location incorrectly. In reality, the phase transition originates from the competition between the superconducting correlations and the Kondo screening of the spin, and the transition takes place when \(\Delta \simeq {T}^{* }\), with \({T}^{* }\) a characteristic Fermi liquid temperature scale. Deep in the local moment regime, \({T}^{* }\) can be identified as the Kondo temperature, \({T}^{* }\simeq {T}_{{\rm{K}}}\), but it becomes of the order of the tunneling rate \({\Gamma }_{{\rm{S}}}\) between the dot and the superconductor close to the mixed valence regime. For \({T}^{* }< \, \Delta\), the spin of the dot remains unscreened down to zero temperature, resulting in a doublet ground state \(\left|D\right\rangle\) = {\(\left|\Uparrow \right\rangle ,\left|\Downarrow \right\rangle\)} and a first excited singlet state, \(\left|S\right\rangle\), the so-called Shiba state inside the gap. By increasing the tunneling rate \({\Gamma }_{{\rm{S}}}\), the spin in the QD binds a quasiparticle from the superconductor, and \(\left|S\right\rangle\) becomes the ground state. The corresponding qualitative phase diagram is displayed in Fig. 6b.
In the experiments, changing the voltage \({V}_{{\rm{P}}}\) corresponds to moving along the red horizontal line in the phase diagram. At the intersections with the “dome” (denoted by the circle and the triangle), the Shiba state is at zero energy, and is in resonance with the Fermi energy, \({E}_{{\rm{F}}}\) of the tunneling electrode N, leading to the observed sudden increase in the zero voltage differential conductance.
Tunnel conductance and current
In our setup, the normal lead acts as an STM tip measuring the differential conductance across the device at a point \({{\bf{x}}}_{{\rm{T}}}\) away from the dot. In the small SC–N tunneling limit Andreev processes can be neglected, and tunneling from the normal electrode to the superconductor yields at \(T=0\) temperature a current
at a finite voltage bias \({V}_{{\rm{bias}}}=V\). Here \({\varrho }_{{\rm{N}}}\) denotes the density of states in the normal lead, \({t}_{{\rm{N}}}\) is the tunneling amplitude between the superconductor and the normal contact, and \(\varrho ({\bf{x}},\omega )=-{\rm{Im}}\ {G}_{\sigma }({\bf{x}},\omega )/\pi\) is the energy dependent density of states in the superconductor at position \({{\bf{x}}}_{{\rm{T}}}\). This latter can be expressed in terms of the Fourier transform of the retarded Green’s function, \({G}_{\sigma }({{\bf{x}}}_{{\rm{T}}},\omega )=-{\rm{i}}\langle \{{\psi }_{\sigma }({{\bf{x}}}_{{\rm{T}}},t),{\psi }_{\sigma }^{\dagger }({{\bf{x}}}_{{\rm{T}}},0)\}\rangle \ \Theta (t)\).
Green’s function \({G}_{\sigma }({{\bf{x}}}_{{\rm{T}}},\omega )\) can be obtained by means of standard many-body theory, invoking Nambu spinors, \(\{{\phi }_{\sigma \tau }\}\equiv ({\psi }_{\uparrow },{\psi }_{\downarrow },{\psi }_{\downarrow }^{\dagger },-{\psi }_{\uparrow }^{\dagger })\), and corresponding propagators, \(G\to \hat{G}\). In this language, the quantum dot induced part of the propagator \(\hat{G}\) can be expressed as
Here \(\hat{g}({{\bf{x}}}_{{\rm{T}}},0,\omega )\) describes the propagation of an electron (or hole) in the superconductor from the dot to the probe at an energy \(\omega\),
with the Pauli matrices \({\tau }_{x}\) and \({\tau }_{z}\) acting in the Nambu space, while the \(T\)-matrix \(\hat{{\mathcal{T}}}(\omega )\) describes scattering off the quantum dot.
We focus on transport through midgap states, i.e. \(| \omega | \, < \, \Delta\). There the propagators \(\hat{g}({{\bf{x}}}_{{\rm{T}}},0,\omega )\) are real, and the tunneling density of states \(\varrho ({\bf{x}},\omega )\) is related to \({\rm{Im}}\hat{{\mathcal{T}}}(\omega )\).
In the classical limit, we can determine \(\hat{{\mathcal{T}}}\) analytically,
and extract the strength of its poles within the gap. At the transition points, \(j=2/\pi\), and expressing furthermore propagator \(\hat{g}({{\bf{x}}}_{{\rm{T}}},0,\omega =0)\) we arrive at Eq. (2) displayed in the main text.
In the framework of the Anderson model, we first introduce the spinors \(\{{D}_{\sigma \tau }\}\equiv ({d}_{\uparrow },{d}_{\downarrow },-{d}_{\downarrow }^{\dagger },{d}_{\uparrow }^{\dagger })\). Similar to ref. 90, it is easy to show that the \(T\)-matrix is directly related to the \(d\)-levels’ Nambu propagator,
The subgap structure of \({\hat{{\mathcal{G}}}}_{DD}\) is completely determined by the transition matrix elements \(\alpha \equiv \langle \Uparrow | {d}_{\uparrow }^{\dagger }| S\rangle\) and \(\beta \equiv \langle \Uparrow | {d}_{\downarrow }| S\rangle\), and the energy difference \({E}_{S}\) of the singlet ground state \(\left|S\right\rangle\) and the many-body Shiba excitations, \(\left|\Uparrow \right\rangle\) and \(\left|\Downarrow \right\rangle\), related by time reversal symmetry. At the transition point, the electron and hole contributions add up, and the expression of the tunnel current simplifies to
with \({\Gamma }_{{\rm{S}}}=2\pi {t}_{{\rm{S}}}^{2}{\varrho }_{{\rm{S}}}\), and \({\Gamma }_{{\rm{S}}}/\hslash\) the tunneling rate from the quantum dot to the superconductor. The results shown on Fig. 4d of the main text are generated by Eq. (14). Note that the many-body expression differs from the classical one solely by the factor \({\Gamma }_{{\rm{S}}}(| \alpha {|}^{2}+| \beta {|}^{2})\), which replaces the gap \(\Delta =\hslash {v}_{{\rm{F}}}/(\xi \pi )\) in the prefactor of the classical expression.
The matrix elements \(\alpha\) and \(\beta\) can be directly extracted from NRG computations. A comparison between the two approaches is presented in Fig. 7. They both give similar results. Small quantitative differences are presumably due to the fact that the classical picture is not able to capture neither the mixed valence regime nor the proper Kondo scale, in contrast to the more elaborate NRG approach.
Data availability
The data that support the plots within this paper and other findings of this study are available at https://doi.org/10.5281/zenodo.3604194.
References
Padurariu, C. & Nazarov, Y. V. Spin blockade qubit in a superconducting junction. EPL (Europhys. Lett.) 100, 57006 (2012).
Janvier, C. et al. Coherent manipulation of andreev states in superconducting atomic contacts. Science 349, 1199–1202 (2015).
Park, S. & Yeyati, A. L. Andreev spin qubits in multichannel rashba nanowires. Phys. Rev. B 96, 125416 (2017).
Hays, M. et al. Direct microwave measurement of andreev-bound-state dynamics in a semiconductor-nanowire josephson junction. Phys. Rev. Lett. 121, 047001 (2018).
Tosi, L. et al. Spin-orbit splitting of andreev states revealed by microwave spectroscopy. Phys. Rev. X 9, 011010 (2019).
Leijnse, M. & Flensberg, K. Introduction to topological superconductivity and majorana fermions. Semicond. Sci. Technol. 27, 124003 (2012).
Aasen, D. et al. Milestones toward majorana-based quantum computing. Phys. Rev. X 6, 031016 (2016).
Aguado, R. Majorana quasiparticles in condensed matter. Rivista Nuovo Cimento 40, 523 (2017).
Sau, J. D. & Sarma, S. D. Realizing a robust practical majorana chain in a quantum-dot-superconductor linear array. Nat. Commun. 3, 964 (2012).
Choy, T.-P., Edge, J. M., Akhmerov, A. R. & Beenakker, C. W. J. Majorana fermions emerging from magnetic nanoparticles on a superconductor without spin-orbit coupling. Phys. Rev. B 84, 195442 (2011).
Nadj-Perge, S., Drozdov, I. K., Bernevig, B. A. & Yazdani, A. and Ali Yazdani, "Proposal for realizing majorana fermions in chains of magnetic atoms on a superconductor. Phys. Rev. B 88, 020407 (2013).
Braunecker, B. & Simon, P. Interplay between classical magnetic moments and superconductivity in quantum one-dimensional conductors: toward a self-sustained topological majorana phase. Phys. Rev. Lett. 111, 147202 (2013).
Pientka, F., Glazman, L. I. & von Oppen, F. Topological superconducting phase in helical shiba chains. Phys. Rev. B 88, 155420 (2013).
Klinovaja, J., Stano, P., Yazdani, A. & Loss, D. Topological superconductivity and majorana fermions in rkky systems. Phys. Rev. Lett. 111, 186805 (2013).
Nakosai, S., Tanaka, Y. & Nagaosa, N. Two-dimensional \(p\)-wave superconducting states with magnetic moments on a conventional \(p\)-wave superconductor. Phys. Rev. B 88, 180503 (2013).
Vazifeh, M. M. & Franz, M. Self-organized topological state with majorana fermions. Phys. Rev. Lett. 111, 206802 (2013).
Kim, Y., Cheng, M., Bauer, B., Lutchyn, R. M. & Sarma, S. D. Helical order in one-dimensional magnetic atom chains and possible emergence of majorana bound states. Phys. Rev. B 90, 060401 (2014).
Nadj-Perge, S. et al. Observation of majorana fermions in ferromagnetic atomic chains on a superconductor. Science 346, 602–607 (2014).
Beenakker, C. W. J. & van Houten, H. Josephson current through a superconducting quantum point contact shorter than the coherence length. Phys. Rev. Lett. 66, 3056–3059 (1991).
Sau, J. D., Lutchyn, R. M., Tewari, S. & Sarma, S. D. Generic new platform for topological quantum computation using semiconductor heterostructures. Phys. Rev. Lett. 104, 040502 (2010).
Alicea, J. Majorana fermions in a tunable semiconductor device. Phys. Rev. B 81, 125318 (2010).
Lutchyn, R. M., Sau, J. D. & Sarma, S. D. Majorana fermions and a topological phase transition in semiconductor-superconductor heterostructures. Phys. Rev. Lett. 105, 077001 (2010).
Oreg, Y., Refael, G. & von Oppen, F. Helical liquids and majorana bound states in quantum wires. Phys. Rev. Lett. 105, 177002 (2010).
Leijnse, M. & Flensberg, K. Parity qubits and poor man’s majorana bound states in double quantum dots. Phys. Rev. B 86, 134528 (2012).
Mourik, V., Zuo, K., Frolov, S. M., Plissard, S. R., Bakkers, E. P. A. M. & Kouwenhoven, L. P. Signatures of majorana fermions in hybrid superconductor-semiconductor nanowire devices,. Science 336, 1003–1007 (2012).
Deng, M. T. et al. Majorana bound state in a coupled quantum-dot hybrid-nanowire system. Science 354, 1557–1562 (2016).
Luh, Y. Bound state in superconductors with paramagnetic impurities. Acta Phys. Sin. 21, 75 (1965).
Shiba, H. Classical spins in superconductors. Prog. Theor. Phys. 40, 435–451 (1968).
Rusinov, A. I. On the theory of gapless superconductivity in alloys containing paramagnetic impurities. Sov. J. Exp. Theor. Phys. 29, 1101 (1969).
Balatsky, A. V., Vekhter, I. & Zhu, J.-X. Impurity-induced states in conventional and unconventional superconductors. Rev. Mod. Phys. 78, 373–433 (2006).
Scherübl, Z., Pályi, A. & Csonka, S. Transport signatures of an andreev molecule in a quantum dot-superconductor-quantum dot setup. Beilstein J. Nanotechnol. 10, 363–378 (2019).
Pillet, J.-D., Benzoni, V., Griesmar, J., Smirr, J.-L. & Girit, Ç Ö. Nonlocal josephson effect in andreev molecules. Nano Lett. 19, 7138–7143 (2019).
Kornich, V., Barakov, H. S. & Nazarov, Y. V. Fine energy splitting of overlapping andreev bound states in multiterminal superconducting nanostructures. Phys. Rev. Res. 1, 033004 (2019).
Kim, H. et al. Toward tailoring majorana bound states in artificially constructed magnetic atom chains on elemental superconductors. Sci. Adv. 4, eaar5251 (2018).
Steinbrecher, M. et al. Non-collinear spin states in bottom-up fabricated atomic chains. Nature Commun. 9, 2853 (2018).
Kamlapure, A., Cornils, L., Wiebe, J. & Wiesendanger, R. Engineering the spin couplings in atomically crafted spin chains on an elemental superconductor. Nat. Commun. 9, 3253 (2018).
Ji, S.-H. et al. High-resolution scanning tunneling spectroscopy of magnetic impurity induced bound states in the superconducting gap of pb thin films. Phys. Rev. Lett. 100, 226801 (2008).
Choi, D.-J. et al. Mapping the orbital structure of impurity bound states in a superconductor. Nat. Commun. 8, 15175 EP (2017).
Ménard, G. C. et al. Coherent long-range magnetic bound states in a superconductor. Nat. Phys. 11, 1013 (2015).
Ruby, M., Peng, Y., von Oppen, F., Heinrich, B. W. & Franke, K. J. Orbital picture of Yu–Shiba–Rusinov multiplets. Phys. Rev. Lett. 117, 186801 (2016).
Ménard, G. C. et al. Two-dimensional topological superconductivity in pb/co/si(111). Nat. Commun. 8, 2040 (2017).
Yazdani, A., Jones, B. A., Lutz, C. P., Crommie, M. F. & Eigler, D. M. Probing the local effects of magnetic impurities on superconductivity. Science 275, 1767–1770 (1997).
Hatter, N., Heinrich, B. W., Ruby, M., Pascual, J. I. & Franke, K. J. Magnetic anisotropy in shiba bound states across a quantum phase transition. Nat. Commun. 6, 8988 (2015).
Cornils, L. et al. Spin-resolved spectroscopy of the Yu–Shiba–Rusinov states of individual atoms. Phys. Rev. Lett. 119, 197002 (2017).
Farinacci, L. et al. Tuning the coupling of an individual magnetic impurity to a superconductor: Quantum phase transition and transport. Phys. Rev. Lett. 121, 196803 (2018).
Heinrich, B. W., Pascual, J. I. & Franke, K. J. Single magnetic adsorbates on s-wave superconductors. Prog. Surf. Sci. 93, 1–19 (2018).
Kezilebieke, S., Dvorak, M., Ojanen, T. & Liljeroth, P. Coupled Yu–Shiba–Rusinov states in molecular dimers on nbse2. Nano Lett. 18, 2311–2315 (2018).
Schneider, L. et al. Magnetism and in-gap states of 3d transition metal atoms on superconducting Re. Preprint at http://arxiv.org/abs/1903.10278 (2019).
Buitelaar, M. R., Nussbaumer, T. & Schönenberger, C. Quantum dot in the kondo regime coupled to superconductors. Phys. Rev. Lett. 89, 256801 (2002).
Eichler, A. et al. Even-odd effect in andreev transport through a carbon nanotube quantum dot. Phys. Rev. Lett. 99, 126602 (2007).
Sand-Jespersen, T. et al. Kondo-enhanced andreev tunneling in inas nanowire quantum dots. Phys. Rev. Lett. 99, 126603 (2007).
Deacon, R. S. et al. Tunneling spectroscopy of Andreev energy levels in a quantum dot coupled to a superconductor. Phys. Rev. Lett. 104, 076805 (2010).
Deacon, R. S. et al. Kondo-enhanced andreev transport in single self-assembled inas quantum dots contacted with normal and superconducting leads. Phys. Rev. B 81, 121308 (2010).
Dirks, T. et al. Transport through andreev bound states in a graphene quantum dot. Nat. Phys. 7, 386 (2011).
Kim, B.-K. et al. Transport measurement of andreev bound states in a kondo-correlated quantum dot. Phys. Rev. Lett. 110, 076803 (2013).
Pillet, J.-D. et al. Andreev bound states in supercurrent-carrying carbon nanotubes revealed. Nat. Phys. 6, 965 (2010).
Chang, W., Manucharyan, V. E., Jespersen, T. S., NygÅrd, J. & Marcus, C. M. Tunneling spectroscopy of quasiparticle bound states in a spinful josephson junction. Phys. Rev. Lett. 110, 217005 (2013).
Pillet, J.-D., Joyez, P., Žitko, R. & Goffman, M. F. Tunneling spectroscopy of a single quantum dot coupled to a superconductor: from kondo ridge to andreev bound states. Phys. Rev. B 88, 045101 (2013).
Kumar, A. et al. Temperature dependence of andreev spectra in a superconducting carbon nanotube quantum dot. Phys. Rev. B 89, 075428 (2014).
Schindele, J., Baumgartner, A., Maurand, R., Weiss, M. & Schönenberger, C. Nonlocal spectroscopy of andreev bound states. Phys. Rev. B 89, 045422 (2014).
Lee, E. J. H. et al. Spin-resolved andreev levels and parity crossings in hybrid superconductor-semiconductor nanostructures. Nat. Nanotechnol. 9, 79 (2014).
Jellinggaard, A., Grove-Rasmussen, K., Madsen, M. H. & Nygård, J. Tuning Yu–Shiba–Rusinov states in a quantum dot. Phys. Rev. B 94, 064520 (2016).
Lee, E. J. H. et al. Scaling of subgap excitations in a superconductor-semiconductor nanowire quantum dot. Phys. Rev. B 95, 180502 (2017).
Gramich, J., Baumgartner, A. & Schönenberger, C. Andreev bound states probed in three-terminal quantum dots. Phys. Rev. B 96, 195418 (2017).
Li, S., Kang, N., Caroff, P. & Xu, H. Q. 0–\(\pi\). Phys. Rev. B 95, 014515 (2017).
Bretheau, L. et al. Tunnelling spectroscopy of andreev states in graphene. Nat. Phys. 13, 756 (2017).
Su, Z. et al. Andreev molecules in semiconductor nanowire double quantum dots. Nat. Commun. 8, 585 (2017).
Su, Z. et al. Mirage andreev spectra generated by mesoscopic leads in nanowire quantum dots. Phys. Rev. Lett. 121, 127705 (2018).
Su, Z. et al. Erasing odd-parity states in semiconductor quantum dots coupled to superconductors. arXiv:1904.05354 (2019).
Fülöp, G. et al. Local electrical tuning of the nonlocal signals in a cooper pair splitter. Phys. Rev. B 90, 235412 (2014).
Fülöp, G. et al. Magnetic field tuning and quantum interference in a cooper pair splitter. Phys. Rev. Lett. 115, 227003 (2015).
Morris, D. E. & Tinkham, M. Effect of magnetic field on thermal conductivity and energy gap of superconducting films. Phys. Rev. Lett. 6, 600–602 (1961).
Langreth, D. C. Friedel sum rule for anderson’s model of localized impurity states. Phys. Rev. 150, 516–518 (1966).
Anthore, A., Pothier, H. & Esteve, D. Density of states in a superconductor carrying a supercurrent. Phys. Rev. Lett. 90, 127001 (2003).
Franke, K. J., Schulze, G. & Pascual, J. I. Competition of superconducting phenomena and kondo screening at the nanoscale. Science 332, 940–944 (2011).
Gramich, J., Baumgartner, A. & Schönenberger, C. Subgap resonant quasiparticle transport in normal-superconductor quantum dot devices. Appl. Phys. Lett. 108, 172604 (2016).
H. Bouchiat, H. Nanophysics: Coherence and Transport : École d’Été de Physique des Houches : Session LXXXI : 28 June–30 July, 2004, Euro Summer School, Nato Advanced Study Institute, Ecole Thematique du CNRS (Elsevier, Amsterdam San Diego, CA, 2005).
Hofstetter, L., Csonka, S., Nygard, J. & Schönenberger, C. Cooper pair splitter realized in a two-quantum-dot y-junction. Nature 461, 960 (2009).
Herrmann, L. G. et al. Carbon nanotubes as cooper-pair beam splitters. Phys. Rev. Lett. 104, 026801 (2010).
Hofstetter, L. et al. Finite-bias cooper pair splitting. Phys. Rev. Lett. 107, 136801 (2011).
Das, A. et al. High-efficiency cooper pair splitting demonstrated by two-particle conductance resonance and positive noise cross-correlation. Nat. Commun. 3, 1165 (2012).
Schindele, J., Baumgartner, A. & Schönenberger, C. Near-unity cooper pair splitting efficiency. Phys. Rev. Lett. 109, 157002 (2012).
Hofstetter, L. Hybrid Quantum Dots in InAs. PhD thesis, Universität Basel, https://nanoelectronics.unibas.ch/publications/phd-theses/ (2011).
Wong, T. K. S. & Ingram, S. G. Fabrication of sub 20 nm trenches in silicon nitride using chf3/o2 reactive ion etching and oblique metallization. J. Vac. Sci. Technol. B: Microelectron. Nanometer Struct. Process. Meas. Phenom. 10, 2393–2397 (1992).
Aagesen, M. et al. Molecular beam epitaxy growth of free-standing plane-parallel inas nanoplates. Nat. Nanotechnol. 2, 761–764 (2007).
Madsen, M. H. et al. Experimental determination of adatom diffusion lengths for growth of inas nanowires. J. Cryst. Growth 364, 16–22 (2013).
Shtrikman, H. et al. Method for suppression of stacking faults in wurtzite III–V nanowires. Nano Lett. 9, 1506–1510 (2009).
Suyatin, D. B., Thelander, C., Björk, M. T., Maximov, I. & Samuelson, L. Sulfur passivation for ohmic contact formation to inas nanowires. Nanotechnology 18, 105307 (2007).
Schrieffer, J. R. Theory of Superconductivity. (Benjamin/Cummings, New York, 1964).
Costi, T. A. Kondo effect in a magnetic field and the magnetoresistivity of kondo alloys. Phys. Rev. Lett. 85, 1504–1507 (2000).
Acknowledgements
The authors acknowledge Morten H. Madsen for MBE growth, Titusz Fehér, Jens Paaske, András Pályi, Dimitri Roditchev, Pascal Simon, and Attila Virosztek for useful discussions. We also acknowledge SNI NanoImaging Lab for FIB cutting, and M.G. Beckerné, F. Fülöp, and M. Hajdú for their technical support. This work was supported by the National Research Development and Innovation Office of Hungary within the Quantum Technology National Excellence Program 2017-1.2.1-NKP-2017-00001, by the New National Excellence Program of the Ministry of Human Capacities, by QuantERA SuperTop project 127900, by AndQC FetOpen project, by Nanocohybri COST Action CA16218, by the BME-Nanotechnology FIKP grant (BME FIKP-NAT), and by the Danish National Research Foundation. CPM was supported by the Romanian National Authority for Scientific Research and Innovation, UEFISCDI, under project no. PN-III-P4-ID-PCE-2016-0032. CS acknowledges support from the Swiss National Science Foundation through grant Nr. 20020\(\_\)L7263a and through the National Center of Competence in Research on Quantum Science and Technology (QSIT).
Author information
Authors and Affiliations
Contributions
Experiments were designed by C.S. and S.C., wires were developed by J.N., devices were developed and fabricated by G.F. and J.G., measurements were carried out and analyzed by Z.S., G.F., A.B., P.M., T.E., and S.C. Theoretical analysis was given by C.P.M. and G.Z. And Z.S., C.P.M., G.Z., and S.C. prepared the manuscript. Correspondence should be addressed to S.C.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Scherübl, Z., Fülöp, G., Moca, C.P. et al. Large spatial extension of the zero-energy Yu–Shiba–Rusinov state in a magnetic field. Nat Commun 11, 1834 (2020). https://doi.org/10.1038/s41467-020-15322-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-15322-9
This article is cited by
-
Robust poor man’s Majorana zero modes using Yu-Shiba-Rusinov states
Nature Communications (2024)
-
Enhancing the excitation gap of a quantum-dot-based Kitaev chain
Communications Physics (2024)
-
Intermediate states in Andreev bound state fusion
Communications Physics (2023)
-
Parallel InAs nanowires for Cooper pair splitters with Coulomb repulsion
npj Quantum Materials (2022)
-
Experimental review on Majorana zero-modes in hybrid nanowires
Science China Physics, Mechanics & Astronomy (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.