Abstract
Until now, a specifically designed functional molecular species has been recognized as an absolute necessity for realizing the diode’s behavior in molecular electronic junctions. Here, we suggest a facile approach for the implementation of a tailored diode in a molecular junction based on non-functionalized alkyl and conjugated molecular monolayers. A two-dimensional semiconductor (MoS2 and WSe2) is used as a rectifying designer at the alkyl or conjugated molecule/Au interface. From the adjustment of band alignment at molecules/two-dimensional semiconductor interface that can activate different transport pathways depending on the voltage polarity, the rectifying characteristics can be implemented and controlled. The rectification ratio could be widely tuned from 1.24 to 1.83 × 104 by changing the molecular species and type and the number of layers of the two-dimensional semiconductors in the heterostructure molecular junction. Our work sets a design rule for implementing tailored-diode function in a molecular heterojunction structure with non-functionalized molecular systems.
Similar content being viewed by others
Introduction
The ultimate objectives in the field of molecular electronics are to realize electronic functionalities, such as rectifying, optical switching, and thermoelectric effects, at the device miniaturization limit and to systemize all the aspects of the charge transport mechanisms for rational device design1,2,3,4,5,6,7,8,9,10,11,12. Specially designed molecular species have been utilized for the realization of specific (or desired) device functions. For example, the D-σ-A type molecules have been widely used for a diode component, where the highest-occupied molecular orbital (HOMO) of the donor and the lowest-unoccupied molecular orbital (LUMO) of the acceptor are closely aligned to the Fermi level of electrodes, i.e., the frontier orbital level of each molecular unit is asymmetrically positioned with respect to the electrodes9,10. This asymmetric energy alignment in the junction can cause the different sequential tunneling through the acceptor and donor depending on the polarity of the applied voltage, which could yield the rectification property of the molecular junction. In the case of the ferrocenyl molecules that composed of long alkyl chain and ferrocenyl termini unit, they can also exhibit the rectification characteristic because the charge transport pathways are mainly determined by the relative HOMO level of the ferrocenyl unit according to voltage polarities11,12. In this sense, specially designed molecular species that can differently engineer the band alignment of the molecular units according to the voltage polarity is dispensable for implementing a desirable diode’s behavior in molecular electronic junction.
In this point of view, non-functionalized molecules such as alkanethiol or conjugated molecules that only exhibit symmetric tunneling transport have been excluded from the realization of electronic diode functions13,14. However, even these widely studied molecules can present the desired electronic functionality as the interfacial band alignment is properly adjusted in molecular heterojunctions. Here, we present a novel strategy and design rule for realizing molecular-scale diode features based on the energy band engineering between simple alkanethiol or conjugated molecules and 2D semiconductors. We systematically engineer the band alignment by inserting 2D semiconductors between molecules and metal (Au), resulting in different charge transport pathways according to voltage polarities without introducing specially designed molecules. In addition, the rectifying characteristics are tunable by controlling the essential constituents such as the molecular species, molecular length, 2D semiconductors, and the number of layers. Our work sets a generalized design rule for implementing rectifying characteristics in a molecular heterojunction structure with non-functionalized molecules and 2D semiconductors.
Results
Molecular heterojunction structure
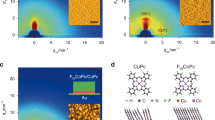
Figure 1a shows a schematic diagram of the molecular heterojunction structure composed of a molecular self-assembled monolayer (SAM) and MoS2 stacked on an Au/SiO2/Si substrate, of which the electrical properties are investigated by conductive atomic force microscopy (CAFM). Five non-functionalized molecular species that differ in terms of the molecular length and the HOMO-LUMO gap (i.e., benzene-1-monothiol (denoted as OPT1), biphenyl-4-monothiol (OPT2), 1-octanemonothiol (C8), 1-decanemonothiol (C10), and 1-dodecanemonothiol (C12)) are used herein. As a representative 2D semiconductor, an n-type NL-MoS2 with different numbers of layers (NL = 1L, 2L, and 3L) and p-type 1L-WSe2 are used to form a heterojunction with the SAMs (right of Fig. 1a). Introducing 2D semiconductors (sub-1 nm thick) at the molecule/Au interface allows us to modify the interfacial band profile across the junction while maintaining the molecular-scale junction size. In addition, judicious choice of the 2D semiconductor type (n- or p-type) and the number of semiconductor layers enables adjustment of the interfacial barrier between the SAMs and 2D semiconductors, as well as the majority carriers, in a highly designed manner. Figure 1b shows the optical images and topological line profiles of MoS2 and WSe2 exfoliated on the SiO2/Si substrate. The measured height of ~0.7 nm indicates that both MoS2 and WSe2 are monolayer thick. In the Raman spectra shown in Fig. 1c, the E12g and A1g vibrational modes are observed at 383 and 402 cm−1 with of spacing of Δ = 18.5 cm−1 for monolayer (1L)-MoS2 (red line) and 247 cm−1 with spectral overlapping for 1L-WSe2 (blue line), confirming the monolayer structure15,16. AFM investigation, Raman, and photoluminescence (PL) spectroscopy are used to characterize the various transition metal dichalcogenides (TMDs) used in this work (Supplementary Fig. 1)15,16. For the electrical measurements, the Au tip coated with the non-functionalized SAMs is carefully placed on the 2D semiconductors with the loading force (FL) = 1 nN17. The details of the experimental methods and sample preparation are described in the Methods section.
a Schematic of molecular heterojunction composed of OPT2 and 1L-MoS2 stacked on an Au/SiO2/Si substrate using the CAFM technique (left). Note that the tip-loading force (FL) was fixed at 1 nN to prevent variation in the interfacial coupling between the molecules and TMDs. Five different molecular species (OPT (n = 1, 2) and C (n = 8, 10, 12)) and two different 2D semiconductor types (NL (1L, 2L, or 3L)-MoS2, and 1L-WSe2) are shown (Right). b Topological line-profiles of 1L-MoS2 (red line) and 1L-WSe2 (blue line) on SiO2/Si substrate from AFM in non-contact scanning mode. Arrow in optical image of each TMD indicates the investigation range of the line-profiles. c Raman spectra of 1L-MoS2 (red line) and 1L-WSe2 (blue line).
Electrical characteristics
Figure 2a shows the representative current-voltage (I-V) characteristics for five different molecular junctions, i.e., Au/OPT2/1L-MoS2/Au (red solid circle), Au/OPT2/1L-WSe2/Au (cyan solid circle), Au/OPT2/Au, Au/1L-WSe2/Au, and Au/1L-MoS2/Au. Note that the Au tip is grounded, and a voltage is applied to the bottom Au electrode. For the junctions composed of only TMDs or OPT2 (represented by black dashed lines), all I-V characteristics exhibit symmetric behavior (rectification ratio (RR) = ~1, defined as |I (V = 1 V)|/|I (V = −1 V)|) due to the single transport barrier located in-between the Fermi level (EF) of the Au electrodes. However, when the molecular heterojunctions is formed with 1L-MoS2 and 1L-WSe2, the I-V curves change asymmetrically. In particular, the RR of these devices is strongly dependent on the 2D semiconductor type. For the OPT2/1L-MoS2 junction, RR = 1.79 × 103, which is much larger than that of the OPT2/1L-WSe2 junction (RR = 2.31) (Fig. 2a). In fact, this value exceeds the theoretical rectification limit (RR = 20) of a molecular junction containing only σ- or π-bonded molecular SAMs18. More specifically, the OPT2/1L-MoS2 junction shows distinct asymmetry compared with the OPT2/1L-WSe2 junction, with a lower I at V < 0 and higher I at V > 0. Such rectifying behavior is reproducibly obtained for both molecular heterojunctions through statistical investigation of the I-V characteristics on several positions (more than five positions) at different samples (more than four samples) (200–1100 times), as shown in the contour plots in Fig. 2b and Supplementary Figs. 2–4. The statistical histogram of RR for the OPT2/1L-MoS2 junction shows a higher value (RR = (1.38 ± 0.73) × 103) than that for the OPT2/1L-WSe2 junction (RR = 2.46 ± 1.42) (Fig. 2c). Note that the maximum RR for the OPT2/1L-MoS2 junction is found to be ~1.83 × 104 (Supplementary Fig. 4).
a Representative I-V characteristics of the junctions without OPT2 or TMDs (black dotted line), OPT2/1L-WSe2 (cyan solid circle), and OPT2/1L-MoS2 (red solid circle) junctions. b Contour maps of transport I for OPT2/1L-WSe2 (left) and OPT2/1L-MoS2 (right) junctions according to V and number of junctions. c Statistical histograms of RR for OPT2/1L-MoS2 and OPT2/1L-WSe2 junctions. The line curves are fitting results from Gaussian function. Note the total numbers of OPT2/1L-WSe2 and OPT2/1L-MoS2 junctions are 200 and 1100, respectively. d Interfacial energy band alignments for Au/OPT2/1L-MoS2/Au junction at V = 0 V, V = 1.0 V, and V = −1.0 V. Note that the Eg of 1L-MoS2 is set to ~1.8 eV.
Interfacial energy band alignment for molecular heterojunction
To understand the rectifying mechanism and the difference in the RR for the OPT2/1L-MoS2 and OPT2/1L-WSe2 junctions, we establish different interfacial energy band alignments for both heterojunctions, corresponding to the different applied voltages (V = 0, 1.0, and −1.0 V) (Fig. 2d and Supplementary Fig. 5). For example, at V = 0 V, the equilibrium energy band diagrams of the molecular heterojunctions can be schematically represented by considering the EF position of Au and the energy bands of the interfacial constituents (OPT2 and TMDs). Three interfaces are consistently present in the molecular heterojunctions: top Au-tip/OPT2, OPT2/TMDs, and TMDs/bottom Au electrode. Because the interface of top Au-tip/OPT2 is chemically bonded by Au-S covalent contact, the OPT2 orbital levels having a HOMO-LUMO gap (Eg) = ~4 eV could shift in response to the change in the EF of the top Au-tip upon application of a voltage14,17. At the interface of OPT2/TMDs, however, the TMD layers cannot undergo chemical-linking with the anchoring group (–CH) of OPT2 on one side. When a voltage is applied, the interfacial barrier between OPT2 and the TMDs changes. Lastly, at the interface of TMDs/bottom Au, the EF of the bottom Au electrode is strongly pinned to the bandgap of the TMDs due to the dichalcogenide vacancy energy states19,20,21,22, forming a constant interfacial TMD/Au barrier even when a voltage is applied. Under this circumstance, the energy band alignments at the Au-tip/OPT2 and TMD/Au interfaces can shift independently according to the applied voltage. Consequently, the effective transport width could be varied depending on the voltage polarity and the TMD type (Fig. 2d and Supplementary Fig. 5). For example, in the case of OPT2/1L-MoS2, the conduction band edge of 1L-MoS2 is located between the applied bias window when V = 1.0 V, which eventually shortens the effective transport width (dtot = dm) (the left of Fig. 2d). This interfacial energy band alignment significantly enhances the transport because the majority carriers (i.e., electrons in this case) are transported only across the OPT2 barrier (dtot = dm), and not across the other interfacial barriers. In contrast, at V = −1.0 V, the transport can be largely suppressed by the longer transport width \(({d}_{\mathrm{tot}} \, = \, {d}_{\mathrm{m}} + {d}_{{\mathrm{MoS}}_{2}})\) because of the additional 1L-MoS2 barrier (the right of Fig. 2d). As a result, this heterojunction type can lead to a larger RR. In the case of OPT2/1L-WSe2, however, the majority carriers (i.e., holes in this case) must move across all the interfacial barriers (both the OPT2 and the 1L-WSe2 barriers) regardless of the voltage polarities (Supplementary Fig. 5). This is because the valance band edge of 1L-WSe2 could not be located between the applied bias window due to the midgap pinning21,22, leading to a smaller RR. In order to further investigate the Fermi-level pinning behavior at the metal/WSe2 interface, we additionally conduct the I-V measurements for the OPT2/1L-WSe2 junction using another bottom electrode (Pt) in addition to Au. The electrical characteristic and the extracted RR value are rarely changed as compared with those of the OPT2/1L-WSe2 junction using the Au electrode (Supplementary Figs. 6 and 7). This is presumably because the Fermi-level of the metal is similarly pinned at the mid-gap states of 1L-WSe2 regardless of the metal work functions (Au (~5.1 eV) and Pt (5.7 eV)) although the Fermi levels of both metals can align relatively well with the valance band edge of WSe2 only if considering their work functions23. According to previous literature, it has been well known that the mid-gap states can be formed by both defect states originated from naturally existing vacancies of WSe2 and virtual gap states induced by metal wave function penetration, which results in the strong Fermi-level pinning22. Therefore, our control experimental results support our energy-band diagram model for the Au/OPT2/1L-WSe2/Au junction that is based on the mid-gap pining for the WSe2 case. It is noted that an additional experiment such as the analysis of gate-dependent electrical characteristics is desired for the direct evidence for where the Fermi-level of the electrode is aligned into the 1L-WSe2. Considering these facts, the interfacial band alignments and the change in the transport widths depending on the voltage polarity are recognized as important factors influencing the rectifying properties in these molecular heterojunctions.
Tunable rectification in molecular heterojunction
Engineering of the molecular rectifying features by controlling the essential constituents of the molecular heterojunction, such as the molecular species, molecular length, and the number of MoS2 layers, is investigated. Note that the statistical data for molecular SAMs/1L-MoS2 junctions in Fig. 3 are obtained from 1L-MoS2 (Sample #1). Figure 3a shows the representative I-V characteristics for the Au/OPT2 (or C12)/NL-MoS2 (number of layer (NL) = 1L, bilayer (2L), or trilayer (3L))/Au junction. Three interesting transport phenomena are observed. First, I is approximately three orders of magnitude higher for the OPT2/NL-MoS2 junction than for the C12/NL-MoS2 junction. The degree of decay in the quantum wave function through the OPT2 tunnel barrier is smaller than that through the C12 barrier due to the smaller HOMO-LUMO gap and the shorter molecular length, leading to greater conductance in OPT2/NL-MoS2 junction. Second, in the forward-bias region, I remains almost constant, independent of the number of MoS2 layers. In fact, because the conduction band edges of NL-MoS2 are located between the EF of both Au electrodes at V > 0, the transport I is mainly determined by the molecular barrier height, not by the number of the MoS2 layers. Lastly, in the reverse bias region, I increases as the number of MoS2 layers increases. In general, increasing the number of MoS2 layers can lead to a reduction of the interfacial barrier height at the NL-MoS2/Au junction due to bandgap reduction derived from the strong interlayer electronic coupling between the sulfur atoms and the quantum confinement effect24,25. Furthermore, because charge transport at the Au/NL-MoS2/Au junction can be explained by the Schottky emission mechanism (Supplementary Fig. 8), the increase in the reverse bias current mainly originates from reduction of the MoS2 barrier. Consequently, RR decreases with increasing number of MoS2 layers. Figure 3b presents the statistical values (left) and histograms (right) of the RR for the OPT2/NL-MoS2 and C12/NL-MoS2 junctions according to the number of MoS2 layers. Generally, the RR decreases as the number of MoS2 layers increases, regardless of the molecular species. Note that the same tendency is also observed for the other molecular heterojunctions (OPT1, C8, and C10-based) (Supplementary Figs. 9 and 10). This result implies that the use of 1L-MoS2 maximizes the rectifying ability of the molecular heterojunction, regardless of the molecular species.
a Representative I-V characteristics for the Au/OPT2 (or C12)/NL-MoS2 (NL = 1L, 2L, or 3L)/Au junction. b RR plots of OPT2/NL-MoS2 and C12/NL-MoS2 junctions as a function of the number of MoS2 layers. As the NL was increased from 1 to 3, the RR decreased from (1.68 ± 0.63) × 103 to (1.75 ± 0.35) × 102 for the OPT2/NL-MoS2 junction, and from (7.41 ± 1.00) × 102 to (2.07 ± 0.17) × 102 for the C12/NL-MoS2 junction. The statistical histograms of RR for OPT2/NL-MoS2 and C12/NL-MoS2 as a function of the number of MoS2 layers are shown in the right figure. c Representative I-V characteristics for OPT(n) (n = 1 or 2)/1L-MoS2 and C(n) (n = 8, 10, or 12)/1L-MoS2 junctions. As n increased, the RR increased from (3.87 ± 1.95) × 102 to (1.68 ± 0.63) × 103 for OPT(n)/1L-MoS2, and (2.08 ± 1.26) × 102 to (7.41 ± 1.00) × 102 for the C(n)/1L-MoS2 junction. d RR plots of OPT(n)/1L-MoS2 and C(n)/1L-MoS2 junctions as a function of the molecular length. The statistical histograms of RR for OPT(n)/1L-MoS2 (n = 1 and 2) and C(n)/1L-MoS2 (n = 8, 10, and 12) junctions are shown in the right figure. The error bars in (b) and (d) indicate the standard deviations of RR obtained from at least 100 different positions of each junction. Note that the molecular length for each molecule is 0.7 (OPT1), 1.1 (OPT2), 1.26 (C8), 1.51 (C10), and 1.76 nm (C12), respectively.
Figure 3c shows the representative I-V characteristics for the Au/OPT(n) (n = 1 or 2)/1L-MoS2/Au and Au/C(n) (n = 8, 10, or 12)/1L-MoS2/Au junctions. Generally, longer molecules lead to decreased conductance due to the increase of the tunneling length in the molecular heterojunction13,14. However, the transport I at V < 0 decreases more significantly than that at V > 0 when a longer molecule is used, leading to a larger RR. Inserting the thicker insulating layer between the metal and the semiconductor can further alleviate the EF pinning effects by reduction of the metal-induced gap state (MIGS) originating from further attenuation of the charge wave function across the insulating layer26,27. In this regard, inserting the longer molecules acting as an insulating layer between the Au-tip and 1L-MoS2 might lead to further unpinning of the EF by reduction of MIGS density in 1L-MoS2. As a result, the upward shift of the 1L-MoS2 barrier due to the unpinning effect can further decrease I at V < 0. Figure 3d presents the statistical average values (left) and histograms (right) of RR for the OPT(n) (or C(n))/1L-MoS2 junction according to the molecular length. As shown in Fig. 3d, RR increases when longer molecules are used, regardless of the number of MoS2 layers. In particular, the RR of OPT2 is much larger than that of C8 despite the similar molecular length, which is due to the higher forward-bias current, attributed to the smaller HOMO-LUMO gap of the former13,18. This result allows us to define another design rule stating that molecules with longer backbone structures and smaller HOMO-LUMO gaps can improve the rectifying ability of the molecular heterojunction.
Pathway-dependent charge transport mechanism and rectifier design rule
In order to generalize the rectifying characteristics in the developed molecular heterojunctions, the electrical characteristics are theoretically modeled based on the pathway-dependent charge transport mechanism by considering the voltage polarity. As shown in Fig. 2d, tunneling across the molecular barrier is the dominant transport mechanism at V > 0, while the tunneling and Schottky emission across the molecular and NL-MoS2 barriers are the dominant transport mechanisms at V < 0, which largely suppresses the transport I. The details of the charge transport equations are further discussed in the Methods Section and Supplementary Information (Supplementary Fig. 11). Considering the effect of the applied voltage polarity on the pathway-dependent charge transport mechanisms, the current density (J)-V characteristics and RR of the Au/OPT(n) (n = 1 or 2) or C(n) (n = 8, 10, or 12)/NL-MoS2/Au junctions (Fig. 4a, b) are estimated. The estimated RR values are in good agreement with the experimental RR value, and the trend of RR depending on the junction constituents is also well described. Further, to establish a design rule for the diode characteristics, we predict the RR as a function of the molecular length and barrier height in non-functionalized molecular junction systems with interfacial NL-MoS2, as shown in the contour plots in Fig. 4c for molecular lengths from 0.5 to 2.5 nm and barrier heights from 1.5 to 6.0 eV. Note that the selected range of molecular variables can cover the major σ- and π-bonded molecular SAMs that are widely used in molecular junctions13,18. In Fig. 4c, the RR increases with increasing molecular length and lower molecular barrier height, but decreases as the number of MoS2 layers increases, consistent with the experimental results. From these RR contour maps, the rectifying characteristics of molecular heterojunctions consisting of non-functionalized SAMs and NL-MoS2 could be generalized and the molecular junction structure having the maximum RR could be designed.
a J-V plots for Au/OPT(n) (n = 1 or 2) and C(n) (n = 8, 10, or 12)/1L-MoS2/Au junctions calculated from the pathway-dependent charge transport mechanism (Eqs. (1)–(3) and Supplementary Fig. 11). b RR plots as a function of the molecular species. The solid lines were calculated from the pathway-dependent charge transport mechanism. The green solid circles are the RR values obtained from other reported molecular junctions consisting of simple σ- or π-bonded molecules without MoS2 (RR = ~1). The error bars indicate the standard deviations of RR obtained from at least 100 different positions of each junction. c Contour plots of estimated RR as a function of the molecular length and barrier height for the molecular heterojunction with different numbers of MoS2 layers (NL = 1L, 2L, and 3L).
In summary, we have first implemented a molecular rectifier composed of simple molecules and 2D semiconductors. The rectifying characteristics can be implemented and further tuned by engineering band alignment between non-functional molecules and 2D semiconductors which make different transport pathways according to voltage polarities. Given that non-functional SAM-based molecular heterojunctions employing 2D semiconductors exhibit strong rectifying characteristics and that their performance can be controlled by implementing the suggested design rule, a tailored molecular rectifier based on simple σ- and π-bonded SAMs can potentially be realized.
Methods
Sample preparation and characterization
All 2D semiconductors (1L-/2L-/3L-MoS2 and 1L-WSe2) are prepared by using the typical mechanical exfoliation and transfer method. The exfoliated MoS2 and WSe2 layers are picked up by using a poly-propylene carbonate (PPC)/polydimethyl siloxane (PDMS) stamp and then mechanically transferred onto the Au/SiO2/Si substrate. The number of TMD layers is verified by optical contrast, after which AFM in non-contact mode (Park NX10, Park Systems Corp., South Korea) is used to determine the thickness of each layer of the TMDs. The Raman and PL spectra of the TMDs are obtained using a home-built spectrometer equipped with a monochromator (Andor, SOLIS 303i) and a 532 nm excitation laser with a spot diameter of 0.5 μm. The signal is collected by an objective lens (100 × NA = 0.9) and dispersed by 1200 and 300 line/mm gratings for the Raman and PL measurements. To form the densely packed non-functionalized SAMs on the Au tip, the tip is immersed in the molecular solutions (~5 mM ethanol) for several hours in a glove-box filled with nitrogen gas with less than 10 ppm O2. To remove the non-assembled residual molecules from the Au tip, the tip is repeatedly rinsed with ethanol and was blown dry using N2.
Electrical characterization
The Au tip coated with the non-functionalized SAMs is carefully placed at the bottom of the 2D semiconductor with FL = 1 nN. For the electrical measurement, the Au tip is grounded, and a voltage is applied to the bottom Au electrode. The electrical I-V characteristics are measured in stationary mode with FL = 1 nN using a DLPCA-2000 built-in current amplifier (Electro-Optical Components) at a humidity of <15%. To obtain statistically meaningful data, the electrical measurements are repeated at different junction positions for each molecular junction (at least 100 times).
Estimated number of contacted molecules
For the OPT(n) (C(n)) molecular SAMs on the Au (111) surface, the √3 × √3R30° (Wood’s notation) structure of the closed packed molecules with each tilt angle of θ = 17° (30°) which yields a grafting density No (=~4.40 (4.65) × 1018 m−2 for OPT (alkyl) SAMs) were adopted28,29. Using Hertzian elastic-contact model30 considering the Au-tip radius of ~30 nm (Supplementary Fig. 13), the net force (Pn), contact radius (a), contact area, grafting density (No), and the number of each molecular SAMs are estimated and summarized in Supplementary Table 1.
Pathway-dependent charge transport mechanism
Because tunneling through the molecular barrier is the dominant charge transport mechanism at a relatively high positive voltage (e.g., V ≈ 1.0 V), J could be extracted by applying the following tunneling equation31:
where dtot is the total tunneling width (the molecular length in this case), m is the mass of the majority carrier, and Φ is the molecular barrier height. On the other hand, at relatively high negative voltage (e.g., V = −1.0 V), charge transport could occur by both tunneling and Schottky emission across each molecular and MoS2 barrier. In that case, the transport J can be extracted by applying the following equation32:
where A* is the Richardson constant, T is the temperature, kB is the Boltzmann constant, ΦSB,eff is the effective Schottky barrier height for NL-MoS2/Au, n is the ideality factor for MoS2, β is the attenuation factor for the molecules, and dm is the molecular length. Note that both charge transport mechanisms at negative voltage could sequentially occur in the present molecular heterojunction system. J is also estimated in the low voltage regime where charge transport could have sequentially occurred via two tunnel barriers (i.e., the molecular and NL-MoS2 barriers). In such a case, \({d}_{\mathrm{tot}} \, = \, {d}_{\mathrm{m}} + {d}_{{\mathrm{MoS}}_{2}}\) and the effective Φ could be extracted by using the multi-barrier tunneling model33:
where \({d}_{\mathrm{m}} \,( {d}_{{\mathrm{MoS}}_{2}})\) is the molecular length (NL-MoS2 thickness) and \({\Phi}_{\mathrm{m}} \, ({{\Phi }}_{{\mathrm{MoS}}_{2}})\) is the molecular barrier (NL-MoS2 barrier). However, because the interfacial barrier between the molecular SAMs and NL-MoS2 can change depending on the applied voltage polarity, variation of Φ may be possible (Supplementary Fig. 11). Based on this pathway-dependent charge transport mechanism according to the voltage polarity, the electrical characteristics for the developed molecular heterojunction systems are theoretically modeled (Fig. 4 and Supplementary Fig. 12). Additional schematics of the pathway-dependent charge transport according to the voltage polarity are presented in the Supplementary Information (Supplementary Fig. 11).
References
Chen, J., Reed, M., Rawlett, A. & Tour, J. Large on-off ratios and negative differential resistance in a molecular electronic device. Science 286, 1550–1552 (1999).
Reddy, P., Jang, S.-Y., Segalman, R. A. & Majumdar, A. Thermoelectricity in molecular junctions. Science 315, 1568–1571 (2007).
van der Molen, S. J. et al. Light-controlled conductance switching of ordered metal− molecule− metal devices. Nano Lett. 9, 76–80 (2008).
Song, H. et al. Observation of molecular orbital gating. Nature 462, 1039–1043 (2009).
Capozzi, B. et al. Single-molecule diodes with high rectification ratios through environmental control. Nat. Nanotechnol. 10, 522–527 (2015).
Hayakawa, R. et al. Large magnetoresistance in single-radical molecular junctions. Nano Lett. 16, 4960–4967 (2016).
Li, Y. et al. Gate controlling of quantum interference and direct observation of anti-resonances in single molecule charge transport. Nat. Mater. 18, 357–363 (2019).
Meng, L. et al. Side-group chemical gating via reversible optical and electric control in a single molecule transistor. Nat. Commun. 10, 1450 (2019).
Díez-Pérez, I. et al. Rectification and stability of a single molecular diode with controlled orientation. Nat. Chem. 1, 635–641 (2009).
Van Dyck, C. & Ratner, M. A. Molecular rectifiers: a new design based on asymmetric anchoring moieties. Nano Lett. 15, 1577–1584 (2015).
Yuan, L., Breuer, R., Jiang, L., Schmittel, M. & Nijhuis, C. A. A molecular diode with a statistically robust rectification ratio of three orders of magnitude. Nano Lett. 15, 5506–5512 (2015).
Chen, X. et al. Molecular diodes with rectification ratios exceeding 105 driven by electrostatic interactions. Nat. Nanotechnol. 12, 797–803 (2017).
Wang, G., Kim, T.-W. & Lee, T. Electrical transport characteristics through molecular layers. J. Mater. Chem. 21, 18117–18136 (2011).
Xie, Z., Bâldea, I., Smith, C. E., Wu, Y. & Frisbie, C. D. Experimental and theoretical analysis of nanotransport in oligophenylene dithiol junctions as a function of molecular length and contact work function. ACS Nano 9, 8022–8036 (2015).
Tonndorf, P. et al. Photoluminescence emission and Raman response of monolayer MoS2, MoSe2, and WSe2. Opt. Express 21, 4908–4916 (2013).
Zhang, X. et al. Phonon and Raman scattering of two-dimensional transition metal dichalcogenides from monolayer, multilayer to bulk material. Chem. Soc. Rev. 44, 2757–2785 (2015).
Shin, J. et al. Correlational effects of the molecular-tilt configuration and the intermolecular van der Waals interaction on the charge transport in the molecular junction. Nano Lett. 18, 4322–4330 (2018).
Metzger, R. M. Unimolecular electronics. Chem. Rev. 115, 5056–5115 (2015).
Gong, C., Colombo, L., Wallace, R. M. & Cho, K. The unusual mechanism of partial Fermi level pinning at metal–MoS2 interfaces. Nano Lett. 14, 1714–1720 (2014).
Kim, C. et al. Fermi level pinning at electrical metal contacts of monolayer molybdenum dichalcogenides. ACS Nano 11, 1588–1596 (2017).
Allain, A. & Kis, A. Electron and hole mobilities in single-layer WSe2. ACS Nano 8, 7180–7185 (2014).
Guo, Y., Liu, D. & Robertson, J. Chalcogen vacancies in monolayer transition metal dichalcogenides and Fermi level pinning at contacts. Appl. Phys. Lett. 106, 173106 (2015).
Chiu, M. H. et al. Band alignment of 2D transition metal dichalcogenide heterojunctions. Adv. Funct. Mater. 27, 1603756 (2017).
Li, S.-L. et al. Thickness scaling effect on interfacial barrier and electrical contact to two-dimensional MoS2 layers. ACS Nano 8, 12836–12842 (2014).
Yoon, H. S. et al. Layer dependence and gas molecule absorption property in MoS2 Schottky diode with asymmetric metal contacts. Sci. Rep. 5, 10440 (2015).
Wager, J. F. & Robertson, J. Metal-induced gap states modeling of metal-Ge contacts with and without a silicon nitride ultrathin interfacial layer. J. Appl. Phys. 109, 094501 (2011).
Kim, G.-S. et al. Schottky barrier height engineering for electrical contacts of multilayered MoS2 transistors with reduction of metal-induced gap states. ACS Nano 12, 6292–6300 (2018).
Sabatani, E., Cohen-Boulakia, J., Bruening, M. & Rubinstein, I. Thioaromatic monolayers on gold: a new family of self-assembling monolayers. Langmuir 9, 2974–2981 (1993).
Poirier, G. & Tarlov, M. The c (4x2) superlattice of n-alkanethiol monolayers self-assembled on Au (111). Langmuir 10, 2853–2856 (1994).
Johnson, K. Contact Mechanics (Cambridge University Press, Cambridge, 1985).
Wang, W., Lee, T. & Reed, M. A. Mechanism of electron conduction in self-assembled alkanethiol monolayer devices. Phys. Rev. B 68, 035416 (2003).
Chattopadhyay, P. & Daw, A. On the current transport mechanism in a metal—insulator—semiconductor (MIS) diode. Solid State Electron. 29, 555–560 (1986).
Wang, G., Kim, T.-W., Lee, H. & Lee, T. Influence of metal-molecule contacts on decay coefficients and specific contact resistances in molecular junctions. Phys. Rev. B 76, 205320 (2007).
Acknowledgements
This work was accomplished with financial support from the National Research Foundation of Korea (grant no. NRF-2019R1A2C2003704 and 2017R1A5A1014862 (SRC Program: vdWMRC Center)), Korea University Grant, KU-KIST Research Fund, and Korea TORAY Science Foundation. Y.J. and T.L. thank the financial support from the National Creative Research Laboratory program (grant no. 2012026372).
Author information
Authors and Affiliations
Contributions
G.W. and C.-H.L. conceived the project and the idea, J.S. and S.Y. designed, carried out, and analyzed the experiments, Y.J. contributed to the temperature-dependent electrical measurement, J.S.E. contributed to the TMD sample preparation, T.-W.K. and T.L. contributed to the data analysis, and all authors analyzed the experimental results and wrote the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Shin, J., Yang, S., Jang, Y. et al. Tunable rectification in a molecular heterojunction with two-dimensional semiconductors. Nat Commun 11, 1412 (2020). https://doi.org/10.1038/s41467-020-15144-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-15144-9
This article is cited by
-
Nanoscale molecular rectifiers
Nature Reviews Chemistry (2023)
-
Non-covalent interaction-based molecular electronics with graphene electrodes
Nano Research (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.