Abstract
Optically-interfaced spins in the solid state are a promising platform for quantum technologies. A crucial component of these systems is high-fidelity, projective measurement of the spin state. Here, we demonstrate single-shot spin readout of a single rare earth ion qubit, Er3+, which is attractive for its telecom-wavelength optical transition and compatibility with silicon nanophotonic circuits. In previous work with laser-cooled atoms and ions, and solid-state defects, spin readout is accomplished using fluorescence on an optical cycling transition; however, Er3+ and other rare earth ions generally lack strong cycling transitions. We demonstrate that modifying the electromagnetic environment around the ion can increase the strength and cyclicity of the optical transition by several orders of magnitude, enabling single-shot quantum nondemolition readout of the ion’s spin with 94.6% fidelity. We use this readout to probe coherent dynamics and relaxation of the spin.
Similar content being viewed by others
Introduction
Atomic and atom-like defects in the solid state provide an optical interface to individual electronic and nuclear spin qubits1, and are used for a variety of quantum technologies. As sensors, they can probe temperature and magnetic and electric fields with nanoscale spatial resolution2,3,4. In quantum networks, spin-photon entanglement5,6,7 has enabled deterministic entanglement of remote spins8. Defect spins have also been used to demonstrate key components of quantum information processors, including quantum error correction9 and 10-qubit quantum registers with multi-qubit gates10.
These works primarily leverage the well-studied nitrogen vacancy (NV) center in diamond. However, a much broader range of defects exists that may be advantageous for particular applications. For example, the SiV−11 and SiV0 12 color centers in diamond are promising for quantum networks because of their low spectral diffusion, while color centers in silicon carbide13 may be easier to integrate with nanoscale devices. Rare earth ions are another family of defects that can offer long spin coherence14 and narrow, stable optical transitions (in the telecom band for the case of Er3+)15, and may be doped into a variety of host crystals. Several recent works have begun to probe individual rare earth ions16,17,18,19,20,21, using an optical cavity to overcome their low intrinsic photon emission rates20,21.
A key capability for atomic defects is high-fidelity spin readout using the optical transition1. Single-shot optical spin measurements have been achieved in quantum dots22 and in the NV23 and SiV−24 color centers in diamond by leveraging highly cyclic optical transitions that arise from atomic selection rules. However, cyclic optical transitions are not a universal feature of atomic defects, and are often absent in low-symmetry defects and in the presence of strain25 or spin-orbit coupling without careful alignment of the magnetic field22,24. Single-shot readout has not been achieved in atomic defects without intrinsic cycling transitions, such as rare earth ions26.
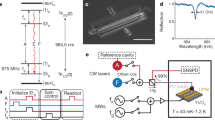
In this work, we demonstrate that tailoring the electromagnetic density of states around an atom with an optical cavity can induce highly cyclic optical transitions in an emitter that is not naturally cyclic. Using a single Er3+ ion in Y2SiO5 (YSO) coupled to a silicon nanophotonic cavity (Fig. 1a), we demonstrate a greater than 100-fold enhancement of the cyclicity: under conditions where the branching ratio of the bare ion results in a spin flip after scattering fewer than ten photons, a cavity-coupled ion can scatter over 1200. This is sufficient to realize single-shot spin readout with a fidelity of 94.6%, and to enable continuous, quantum nondemolition measurement of quantum jumps between the ground state spin sublevels. The improvement in the cyclicity arises from selective Purcell enhancement of the spin-conserving optical decay pathway (Fig. 1b), determined primarily by the alignment of the cavity polarization and the spin quantization axis defined by a magnetic field. A small additional enhancement arises from detuning of the spin-non-conserving transitions from the optical cavity, an effect that was recently used to enhance the cyclicity of a quantum dot in a nanophotonic cavity27. This generic technique opens the door to exploiting a much broader range of atomic defects for quantum technology applications, and is a particular advance for individually addressed rare earth ions.
a The experimental device is a silicon photonic crystal cavity on top of an Er3+-doped YSO crystal. Light in the cavity evanescently couples to the Er3+ ions. (inset) Definition of magnetic field angle (φ, θ); (x, y, z) refer to the (D1, D2, b) optical axes of the YSO crystal. b Without a cavity, the spin-conserving transitions A, B and spin-non-conserving transitions C, D are comparable in strength. The cavity selectively enhances A,B, resulting in highly cyclic optical transitions. c In the absence of a magnetic field, the four transitions are degenerate and give rise to a single, stable optical transition with a full width at half maximum of 6 MHz (centered at λ = 1536.48 nm). A magnetic field lifts the degeneracy. The color bar denotes the fluorescence intensity (arbitrary units). d The Zeeman splitting is strongly anisotropic, measured here by applying a 112G magnetic field at various angles φ (θ = 90∘) while driving the ion with a phase-modulated laser containing frequencies f0 ± fEOM, where f0 is the transition frequency when B = 0. The solid (dashed) line shows the predicted splitting between the A–B (C–D) transitions29.
Results
Optically addressing single Er3+ ions
Our experimental approach, following ref. 20, is based on a YSO crystal doped with a low concentration (<1 ppm) of Er3+ ions placed in close proximity to an optical cavity in a silicon photonic crystal waveguide (Fig. 1a). Assembled devices are placed inside a 3He cryostat at 0.54 K with a three-axis vector magnet. Light is coupled to the cavities using a lensed optical fiber on a three-axis translation stage. The high quality factor (6 × 104) and small mode volume of the cavity, together with the high radiative efficiency of the Er3+ optical transition, enable Purcell enhancement of the Er3+ emission rate by a factor of P = 700 (Fig. 2a). There are several hundred ions within the mode volume of the cavity, but their optical transitions are inhomogeneously broadened over a several GHz span, such that stable, single ion lines can be clearly isolated (Fig. 1c)20.
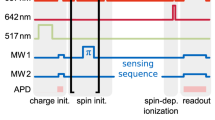
a The measurement sequence consists of alternating pulses on the A and B transitions (10 μs) followed by a fluorescence collection window (45 μs), repeating every trep = 60 μs. The fluorescence lifetime is 16.2 ± 0.2 μs, shortened from its free-space value of 11.4 ms by P = 703 ± 6 in this device. b The intensity autocorrelation g(2) is computed from the integrated fluorescence after each pulse. Odd values of n (blue points) probe the correlation between pulses driving different transitions and are anti-bunched as a result of the spin staying in the same state over many excitation cycles. g(2) decays as \({e}^{-n/{n}_{0}}\) because of optical pumping, giving the cyclicity C ≈ n0/2. In this measurement, C = 660 ± 66. g(2)(0) = 0.3 is consistent with the signal-to-background ratio of 10. c, d The cyclicity varies dramatically with the angle of the external magnetic field, but is described by a model (red line) based on the independently measured g tensors (see text). e The cyclicity decreases rapidly with the Purcell factor, demonstrated here by measurements on several ions (shown in different colors) with the detuning varied to change P. In all plots, error bars denote estimated ±1σ statistical uncertainty.
The ground and excited states of the 1.536 μm optical transition in Er3+:YSO are effective spin-1/2 manifolds, which emerge as the lowest energy states of the 16- (14-)fold degenerate 4I15/2 ground (4I13/2 excited) free-ion multiplets in the crystal field potential, respectively. In the absence of a magnetic field, the ground and excited states are two-fold degenerate, as required by Kramers’ theorem28. This degeneracy is lifted in a small magnetic field, revealing four distinct optical transitions (Fig. 1b, c). Transitions A and B conserve the spin, while C and D flip the spin.
Improving the cyclicity of the optical transitions
To probe the selection rules of the optical transition, we excite the spin-conserving A and B lines alternately (Fig. 2a). The average fluorescence following the A and B pulses is the same, since the transitions are symmetrically detuned from the cavity and the spin is on average unpolarized from continuous optical pumping by the excitation light. However, the intensity autocorrelation function, g(2)(ntrep) (where n is the offset in the number of pulses) is anti-bunched for odd-numbered pulse offsets (i.e., A–B correlations) and bunched for even offsets (i.e., A–A or B–B correlations), revealing that only one of the transitions A or B is bright at any given time, depending on the instantaneous spin state (Fig. 2b). Note that the fluorescence after each pulse is integrated before computing the autocorrelation, so g(2)(ntrep) is only defined for discrete times. Eventually, the spin relaxes and g(2) decays exponentially to 1 after an average of n0 pulses. Under the assumption (to be verified later) that the observed spin relaxation arises primarily from optical pumping between the spin sublevels, we extract the optical transition cyclicity C = n0Pex, where Pex ≈ 1/2 is the probability to excite the ion in each pulse. This value of Pex is assured by using an intense excitation pulse to saturate the ion, and is verified using the independently measured collection efficiency (Supplementary Note 3).
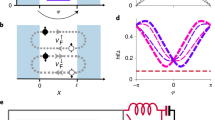
We repeat this measurement with different orientations of the magnetic field, and find that the cyclicity varies by nearly three orders of magnitude (Fig. 2c, d), with a maximum value of 1260 ± 126. This results from the changing orientation of the atomic transition dipole moment with respect to the cavity polarization, with the maximum cyclicity occurring when the spin-conserving transitions A, B are aligned to the cavity and the spin-flip transitions C, D are orthogonal to it. It can be captured by a simple model where the decay rates on each transition are proportional to the projection of an associated dipole moment d onto the cavity polarization ϵ at the position of the ion (Supplementary Note 2). For the spin conserving transition, \({\Gamma }_{{\rm{AB}}}\propto | \left\langle {\uparrow }_{{\rm{e}}}\right|{\boldsymbol{\epsilon }}\cdot {{\bf{d}}}_{| | }|{\uparrow }_{{\rm{g}}}\rangle {| }^{2}\), while ΓCD is defined analogously with d∣∣ replaced by d⊥. When the magnetic field is rotated, the spin sublevels mix such that \(\left|\uparrow (\varphi ^{\prime} ,\theta ^{\prime} )\right\rangle =\alpha \left|\uparrow (\varphi ,\theta )\right\rangle +\beta \left|\downarrow (\varphi ,\theta )\right\rangle\), with the coefficients α, β completely specified by the anisotropic g tensor describing the Zeeman shifts (Fig. 1d)29. Together with the time-reversal symmetry properties of the Kramers’ doublets, this allows the complete angular dependence of C = ΓAB/ΓCD + 1 to be described by only two parameters: ϵ ⋅ d∣∣ and ϵ ⋅ d⊥ at a single (arbitrary) reference orientation . In this model, the role of the cavity is to restrict the decay to a particular polarization, such that the decay rates are determined by a single matrix element ∣ϵ ⋅ d∣2; in free space, there is no preferred ϵ.
Since the dipole matrix elements for Er3+:YSO and the cavity field polarization at the position of the atom are not known, we treat ϵ ⋅ d∣∣ and ϵ ⋅ d⊥ as fit parameters. A fit to this model displays excellent agreement with the data, and allows the complete angle dependence of the cyclicity to be extracted from a small number of measurements. While this discussion centers on electric dipole coupling, the Er3+ transition we study has comparable electric and magnetic dipole matrix elements30, and the predicted magnetic Purcell factor for our structures is similar20, depending on the precise position of the ion. We show in the Supplementary Information that the electric and magnetic contributions have the same angular dependence and may be summed into a single term (Supplementary Note 2). We also demonstrate that the detuning of the C, D transitions from the cavity makes an additional, small contribution to the cyclicity at the highest magnetic fields used (Supplementary Note 6).
To quantify the extent to which the cyclicity is enhanced by the cavity, we study a second ion with lower Purcell factor and then lower it further by detuning the cavity. The cyclicity is observed to decrease roughly linearly with P (Fig. 2e). Based on the dependence of the cyclicity on the cavity detuning for this ion, we estimate that the cyclicity C0 of the ion alone is less than 10 (limited by the bare ion branching ratio, which may be affected by decays through intermediate crystal field levels and phonon-assisted excitation to higher excited states; see Supplementary Note 4), such that the enhancement by the cavity is greater than 100. We note that C0 has not been directly measured for Er3+:YSO.
Single-shot quantum nondemolition measurement
Next, we focus on using the cavity-enhanced cyclicity to measure the spin state. Figure 3a shows a time trace of photons recorded in a single run of the experiment, with telegraph-like switching between \(|{\downarrow }_{{\rm{g}}}\rangle\) (where transition B is bright) and \(|{\uparrow }_{{\rm{g}}}\rangle\) (where transition A is bright) clearly visible. A continuous estimation of the spin state occupation using a Bayesian estimator applied to the full measurement record31 shows clearly resolved quantum jumps between these states, demonstrating the quantum nondemolition nature of the measurement. The quantum jumps are driven by optical pumping from the measurement process itself, because of the finite cyclicity.
a Photons detected during a single run of the experiment using the sequence in Fig. 2a. The black curve shows the probability to be in \(|{\uparrow }_{{\rm{g}}}\rangle\) inferred from a Bayesian analysis, revealing quantum jumps between the spin states induced by optical pumping. b An adaptive maximum likelihood (ML) algorithm is used to perform successive single-shot spin measurements, with the result of each, independent measurement indicated by a circle [data from dashed box in a]. c Histogram of photon counts for a fixed integration window of 51 ms following initialization using a ML measurement. The horizontal axis is the difference between the number of A and B photons detected in the measurement window.
To demonstrate single-shot measurement of the spin, we use a maximum likelihood (ML) algorithm to estimate the state at time t using photon counts from times \(t^{\prime} > t\). The measurement duration is adaptive: each measurement terminates when a set fidelity threshold or time limit is reached, and a new, independent measurement is begun32. The outcome of each measurement is shown by the circles in Fig. 3b. The average measurement fidelity estimated by the ML algorithm is 94.6%, and 91% of consecutive measurements have the same outcome. The average time to complete a measurement is 20 ms, which corresponds to the average time to detect two photons. The optimum fixed measurement window is 51 ms, resulting in a slower measurement with a lower average fidelity of 91.1% (Fig. 3c).
Single Er3+ spin dynamics
Lastly, we apply these spin measurement techniques to investigate the ground state spin dynamics. We infer the intrinsic spin relaxation rate T1,dark by reducing the optical excitation rate 1/trep until the total spin lifetime \({T}_{1}=1/({T}_{{\rm{1,dark}}}^{-1}+{T}_{1,{\rm{op}}}^{-1})\), measured via g(2), saturates (Fig. 4a). T1,op = Ctrep/Pex is the optical pumping time. T1,dark increases with increasing magnetic field strength, in a manner that starkly diverges from the expected B−4 behavior of spin-lattice relaxation (Fig. 4b)28. One possible explanation is flip–flop interactions with nearby Er3+ ions33, which is consistent with the fact that T1,dark varies sharply with the magnetic field angle and is different by a factor of 20 between three ions studied (Supplementary Note 6). In this device, the average separation between magnetically equivalent Er3+ ions is estimated to be 70 nm, such that the dipole–dipole interaction strength is around 1 kHz; the flip–flop rate is likely much slower because of spectral diffusion from nearby 89Y nuclear spins.
a Spin relaxation times measured at varying repetition rates of the pulse sequence for several magnetic field amplitudes [(φ, θ) = (100, 90)°]. At low excitation rates, the spin relaxation time becomes independent of the optical excitation rate, revealing an intrinsic relaxation time T1,dark. b T1,dark varies strongly with the amplitude of the magnetic field. The dashed line indicates the expected spin-lattice relaxation rate (Supplementary Note 6)39. c Using a single-shot projective measurement to initialize the spin, we can directly measure T1,dark. This experiment is performed on a different ion (ion 3) at 112 G, where T1,dark = 45 ± 4 s is roughly five times longer than in the ion used (a, b). d Rabi oscillations can be observed between the two states using a microwave pulse of variable length (fMW = 1.76 GHz for B = 112 G). c, d The contrast is consistent with a measurement fidelity of ~95% for this ion, which enters twice through the initial and final measurements.
In Fig. 4c, we use single-shot spin measurements to directly measure T1,dark = 45 ± 4 s in a different ion. This is the longest electronic spin T1 measured for Er3+, to the best of our knowledge34. In Fig. 4d, we demonstrate high-visibility Rabi oscillations between the ground state spin sublevels, driven by a microwave magnetic field applied through a coplanar waveguide. We measure \({T}_{2}^{* }=125\pm 5\) ns (in a Ramsey experiment), and T2 = 3.3 ± 0.2 μs (Hahn echo), consistent with previous measurements of electron spin coherence in solid-state hosts with abundant nuclear spins17,35. Longer coherence times to enable storage of quantum states and the observation of coherent dynamics between interacting Er3+ ions may be achieved using dynamical decoupling. Ultimately, it will be beneficial to use alternative host crystals with lower nuclear spin content; Er3+ incorporation has been demonstrated in several candidates including CaWO4, Si, and TiO236.
Discussion
Our results demonstrate that the optical properties of atomic systems are malleable through control of their local environment. Using a photonic nanostructure, we have achieved more than two orders of magnitude improvement in the emission rate and cyclicity of a single Er3+ ion, and demonstrated single-shot readout of its spin. Realistic improvements in the quality factor of the optical cavity and photon collection efficiency η will enable another 20-fold enhancement in emission rate and spin readout with F > 0.99 in 50 μs (Q = 106 and η = 0.2; see Supplementary Note 5). These results represent a significant step towards realizing quantum networks based on single Er3+ ions. This measurement approach may also be extended to address many closely-spaced Er3+ spins in the same device by exploiting small differences in their optical transition frequencies, providing a foundation for studying strongly interacting spin systems. Finally, this technique will enable a much broader class of atomic defects to be explored for quantum technologies.
After completion of this work, became aware of a related work demonstrating single-shot spin measurements of single 171Yb3+ ions coupled to a nanophotonic cavity37 using a similar approach.
Methods
Devices fabrication
The YSO crystals used in this work were obtained from Scientific Materials, and are doped with trace concentrations of Er3+ during growth. Nanophotonic structures are fabricated from silicon-on-insulator wafers using electron beam lithography and inductively-coupled-plasma reactive ion etching (Supplementary Note 1). After undercutting the oxide in concentrated hydrofluoric acid and critical point drying, suspended devices are transferred onto the host crystal using a stamping technique20.
Experimental setup
The assembled devices are installed in a 3He cryostat with a base temperature of approximately T = 540 mK (spin dynamics are unobservable at T = 4 K, presumably because of rapid spin-lattice relaxation in the ground or excited states38). For most experiments, light is coupled into the devices using a lensed optical fiber. The measurement of Rabi oscillations in Fig. 4c uses a slightly different device geometry that incorporates a microwave coplanar waveguide approximately 125 μm from the photonic crystal. Microwave pulses are generated using a signal generator modulated by an IQ mixer driven by an arbitrary waveform generator and amplified to 21 W before entering the cryostat. A low duty cycle is used to avoid heating the sample. The optical pulses are derived from a laser stabilized to a ULE reference cavity, and shaped with a sequence of acousto-optic modulators and an electro-optic intensity modulator.
Data availability
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
References
Awschalom, D. D., Hanson, R., Wrachtrup, J. & Zhou, B. B. Quantum technologies with optically interfaced solid-state spins. Nat. Photon. 12, 516–527 (2018).
Kucsko, G. et al. Nanometre-scale thermometry in a living cell. Nature 500, 54–58 (2013).
Maletinsky, P. et al. A robust scanning diamond sensor for nanoscale imaging with single nitrogen-vacancy centres. Nat. Nanotechnol. 7, 320–324 (2012).
Dolde, F. et al. Electric-field sensing using single diamond spins. Nat. Phys. 7, 459–463 (2011).
Togan, E. et al. Quantum entanglement between an optical photon and a solid-state spin qubit. Nature 466, 730–734 (2010).
De Greve, K. et al. Quantum-dot spin-photon entanglement via frequency downconversion to telecom wavelength. Nature 491, 421–425 (2012).
Gao, W. B., Fallahi, P., Togan, E., Miguel-Sanchez, J. & Imamoglu, A. Observation of entanglement between a quantum dot spin and a single photon. Nature 491, 426–430 (2012).
Bernien, H. et al. Heralded entanglement between solid-state qubits separated by three metres. Nature 497, 86–90 (2013).
Taminiau, T. H., Cramer, J., van der Sar, T., Dobrovitski, V. V. & Hanson, R. Universal control and error correction in multi-qubit spin registers in diamond. Nat. Nanotechnol. 9, 171–176 (2014).
Bradley, C. E. et al. A 10-qubit solid-state spin register with quantum memory up to one minute. Phys. Rev. X 9, 031045 (2019).
Sipahigil, A. et al. An integrated diamond nanophotonics platform for quantum-optical networks. Science 354, 847–850 (2016).
Rose, B. C. et al. Observation of an environmentally insensitive solid-state spin defect in diamond. Science 361, 60–63 (2018).
Christle, D. J. et al. Isolated electron spins in silicon carbide with millisecond coherence times. Nat. Mater. 14, 160–163 (2014).
Zhong, M. et al. Optically addressable nuclear spins in a solid with a six-hour coherence time. Nature 517, 177–180 (2014).
Böttger, T., Thiel, C. W., Cone, R. L. & Sun, Y. Effects of magnetic field orientation on optical decoherence in Er3:Y2SiO5. Phys. Rev. B 79, 115104 (2009).
Yin, C. et al. Optical addressing of an individual erbium ion in silicon. Nature 497, 91–94 (2013).
Siyushev, P. et al. Coherent properties of single rare-earth spin qubits. Nat. Commun. 5, 3895 (2014).
Utikal, T. et al. Spectroscopic detection and state preparation of a single praseodymium ion in a crystal. Nat. Commun. 5, 3627 (2014).
Nakamura, I., Yoshihiro, T., Inagawa, H., Fujiyoshi, S. & Matsushita, M. Spectroscopy of single Pr3 ion in LaF3 crystal at 1.5 K. Sci. Rep. 4, 7364 (2014).
Dibos, A. M., Raha, M., Phenicie, C. M. & Thompson, J. D. Atomic source of single photons in the telecom band. Phys. Rev. Lett. 120, 243601 (2018).
Zhong, T. et al. Optically addressing single rare-earth ions in a nanophotonic cavity. Phys. Rev. Lett. 121, 183603 (2018).
Delteil, A., Gao, W.-b., Fallahi, P., Miguel-Sanchez, J. & Imamoğlu, A. Observation of quantum jumps of a single quantum dot spin using submicrosecond single-shot optical readout. Phys. Rev. Lett. 112, 116802 (2014).
Robledo, L. et al. High-fidelity projective read-out of a solid-state spin quantum register. Nature 477, 574–578 (2011).
Sukachev, D. D. et al. Silicon-vacancy spin qubit in diamond: a quantum memory exceeding 10 ms with single-shot state readout. Phys. Rev. Lett. 119, 223602 (2017).
Tamarat, P. et al. Spin-flip and spin-conserving optical transitions of the nitrogen-vacancy centre in diamond. N. J. Phys. 10, 045004 (2008).
Bartholomew, J. G., Ahlefeldt, R. L. & Sellars, M. J. Engineering closed optical transitions in rare-earth ion crystals. Phys. Rev. B 93, 014401 (2016).
Sun, S., Kim, H., Solomon, G. S. & Waks, E. Cavity-enhanced optical readout of a single solid-state spin. Phys. Rev. Appl 9, 054013 (2018).
Abragam, A. & Bleaney, B. Electron Paramagnetic Resonance of Transition Ions (Dover, 1986).
Sun, Y., Böttger, T., Thiel, C. W. & Cone, R. L. Magnetic g tensors for the 4I15∕2 and 4I13∕2 states of Er3+ :Y2 SiO5. Phys. Rev. B 77, 085124 (2008).
Dodson, C. M. & Zia, R. Magnetic dipole and electric quadrupole transitions in the trivalent lanthanide series: calculated emission rates and oscillator strengths. Phys. Rev. B 86, 125102 (2012).
Gammelmark, S., Mølmer, K., Alt, W., Kampschulte, T. & Meschede, D. Hidden Markov model of atomic quantum jump dynamics in an optically probed cavity. Phys. Rev. A 89, 043839 (2014).
Hume, D., Rosenband, T. & Wineland, D. High-fidelity adaptive qubit detection through repetitive quantum nondemolition measurements. Phys. Rev. Lett. 99, 120502 (2007).
Car, B., Veissier, L., Louchet-Chauvet, A., Gouët, J.-L. L. & Chanelière, T. Optical study of the anisotropic erbium spin flip-flop dynamics. Phys. Rev. B 100, 165107 (2019).
Probst, S. et al. Anisotropic rare-earth spin ensemble strongly coupled to a superconducting resonator. Phys. Rev. Lett. 110, 157001 (2013).
Petta, J. R. et al. Coherent manipulation of coupled electron spins in semiconductor quantum dots. Science 309, 2180–2184 (2005).
Phenicie, C. M. et al. Narrow optical line widths in erbium implanted in TiO2. Nano Lett. 19, 8928–8933 (2019).
Kindem, J. M. et al. Coherent control and single-shot readout of a rare-earth ion embedded in a nanophotonic cavity. Preprint at https://arxiv.org/abs/1907.12161 (2019).
Welinski, S. et al. Electron spin coherence in optically excited states of rare-earth ions for microwave to optical quantum transducers. Phys. Rev. Lett. 122, 247401 (2019).
Kurkin, I. N. & Chernov, K. P. EPR and spin-lattice relaxation of rare-earth activated centres in Y2 SiO5 single crystals. Phys. B+C. 101, 233–238 (1980).
Acknowledgements
We acknowledge helpful conversations with Charles Thiel, Nathalie de Leon and Alp Sipahigil. Support for this research was provided by the National Science Foundation (NSF, EFRI ACQUIRE program Grant No. 1640959), the Princeton Center for Complex Materials (PCCM), an NSF MRSEC (DMR-1420541), the Air Force Office of Scientific Research (Grant No. FA9550-18-1-0081), the DARPA DRINQS program (Grant No. D18AC00015), the Eric and Wendy Schmidt Transformative Technology Fund and the Princeton Catalysis Initiative. We acknowledge the use of Princeton’s Imaging and Analysis Center, which is partially supported by PCCM, as well as the Princeton Micro-Nano Fabrication Lab and Quantum Device Nanofabrication Lab facilities. C.M.P. was supported by the Department of Defense through the National Defense Science & Engineering Graduate Fellowship Program.
Author information
Authors and Affiliations
Contributions
M.R., S.C., C.M.P., S.O., A.M.D., and J.D.T. contributed to the design and execution of the experiment. M.R. and J.D.T. analyzed the data and wrote the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Matthew Sellars, and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Raha, M., Chen, S., Phenicie, C.M. et al. Optical quantum nondemolition measurement of a single rare earth ion qubit. Nat Commun 11, 1605 (2020). https://doi.org/10.1038/s41467-020-15138-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-15138-7
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.