Abstract
The glass transition temperature (Tg) is a key property that dictates the applicability of conjugated polymers. The Tg demarks the transition into a brittle glassy state, making its accurate prediction for conjugated polymers crucial for the design of soft, stretchable, or flexible electronics. Here we show that a single adjustable parameter can be used to build a relationship between the Tg and the molecular structure of 32 semiflexible (mostly conjugated) polymers that differ drastically in aromatic backbone and alkyl side chain chemistry. An effective mobility value, ζ, is calculated using an assigned atomic mobility value within each repeat unit. The only adjustable parameter in the calculation of ζ is the ratio of mobility between conjugated and non-conjugated atoms. We show that ζ correlates strongly to the Tg, and that this simple method predicts the Tg with a root-mean-square error of 13 °C for conjugated polymers with alkyl side chains.
Similar content being viewed by others
Introduction
The glass transition temperature (Tg) of conjugated polymers governs chain dynamics and mechanical properties. Below Tg, the storage moduli of conjugated polymers are on the order of one GPa, making the materials too stiff and too brittle for flexible devices1. At higher temperatures, the storage modulus decreases orders of magnitude to ~10 MPa for a semicrystalline polymer, or ~1 MPa for an entangled amorphous polymer1,2. Therefore, one of the key design requirements for soft or stretchable electronics is to ensure that Tg lies below room temperature3,4. Furthermore, solution-processing of conjugated polymers for integration into various electronic devices5,6,7 results in morphologies that are far from equilibrium and which tend to evolve with time. The kinetics of morphological evolution with processing or under operation are limited by chain diffusion or segmental motion, which depends on the temperature with respect to Tg. Annealing above Tg can lead to cold crystallization8,9, enhancement of liquid crystalline order10, or stronger phase separation with another additive or polymer11,12,13. Thus, Tg demarks embrittlement and can dictate morphological evolution in the active layer of electronic devices, thereby impacting mechanical and electrical performance.
Quantitatively predicting the glass transition temperature of conjugated polymers from the chemical structure remains a challenge. Tg appears to increase with both chain stiffness and bulkier side groups14,15,16,17, and decreases as alkyl side group length increases1, but universal molecular models that connect the Tg to a given repeat unit structure are lacking. Nevertheless, a connection between the glass transition and the local motion of atoms has been proposed. Measures of the Debye–Waller factor 〈u2〉 describe local atomic displacements and define a characteristic volume of motion18, the dynamic free volume (vf)19,20,21,22,23,24. Tg has been successfully predicted from either the structural relaxation time, which is found to be universally related to 〈u2〉, or vf, using the generalized Lindemann criteria15,19,25. Further connecting local motions to complex chemical structures could extend the predictive power of these models.
Other approaches have used data to build empirical correlations based on the quantitative structure-property relationships (QSPR) method26, group contributions approaches27, and machine learning28 to predict and match with experimentally measured Tgs of many polymers. For QSPR, each bond in the repeat unit is assigned a bond flexibility value, which is further weighted by various molecular descriptors that capture the atomic variance in mass and polarizability29,30,31. Then, a multistep linear regression analysis that trains these descriptors eventually allows a good match between predicted and experimentally measured Tg values, but also generates many parameters that are challenging to physically interpret, such as topological bond connectivity values26,31. Similarly, group contribution methods empirically assume that structural groups in the repeat unit provide weighted additive contributions to the Tg, and that the contribution from one group also depends on the presence of other nearby groups27. Using a large data set of 854 polymers, while considering 229 parameters (i.e., descriptors), a model composed of 69 dimensions can predict the Tg with a root-mean-square error of 24 °C28. In all of the aforementioned cases, these methods require at least five parameters to predict the Tg from the chemical structure. We thus propose that a simpler method, similar to the seminal work by Boyer32 and Van Krevelen27 on flexible polymers, is warranted for the design of conjugated polymers, given the large number of different backbones and side groups that are possible.
The Tg of conjugated polymers is notoriously difficult to identify, because many such materials are semicrystalline and have rigid backbones. Signatures of Tg in differential scanning calorimetry (DSC) scans are thereby suppressed33, although some unambiguous values have been summarized by Müller34. Alternatively, rheological measurements are sensitive to changes in mechanical properties, and can unambiguously locate the Tg of conjugated polymers as the peak in the loss modulus as a function of temperature8.
In this work, we obtained glass transition temperatures using rheology of various polymers, with values between −50 °C and 200 °C. We use Tgs from rheology to derive a simple correlation between Tg and the chemical structure of conjugated polymers with alkyl side chains. Altogether, we examine materials based on polyalkylthiophene, polydialkylfluorene, polyarylene, poly(p-phenylene vinylene), and donor-acceptor alternating architectures (or “push-pull” polymers), including macromolecules with linear and branched side chains. We find that an effective atomic mobility parameter is strongly correlated with Tg for all 32 polymers included in this study. The chemical structures of the various types of semiflexible polymers with different alkyl side chains are shown in Fig. 1, and their full chemical names and sources are summarized in Supplementary Note 1. We demonstrate that our universal description holds for both conjugated and non-conjugated polymers with aromatic backbones. Thus, the correlation between atomic mobility and Tg is rationalized to result from the common structural scheme of rigid aromatic backbones and flexible alkyl side chains. We expect this correlation between Tg and the effective atomic mobility to guide the design of conjugated polymers and other rigid aromatic polymers for future applications, including soft, flexible, and stretchable electronics.
Polymers that are highlighted in red belong to Group 1 (mostly thiophene-rich polymers), others belong to Group 2 (mostly phenyl-rich polymers). Full names are found in Supplementary Note 1.
Results
Measurements of glass transition temperatures
Given the rich phase behavior of conjugated polymers, dynamic mechanical analysis, such as linear shear rheometry, is a reliable and unambiguous way to identify the glass transition temperature3,8,34. Because of the dynamic nature of the glass transition response, Tg is known to be highly dependent on the probing parameters, such as the rate of heating and the frequency of mechanical oscillation. Therefore, in order to consistently compare Tgs of various conjugated polymers in this work, Tg is determined by either rheology with a heating rate of 5 °C/min and an oscillation frequency of 1 rad/s, or with differential scanning calorimetry (DSC) using a heating rate of 10 °C/min, where Tg is taken as the midpoint of the transition.
Specifically, Tg is located as the temperature that shows either the local maximum of G″ in Fig. 2, Supplementary Figs. 1–4, or a step change in the heat flow in Supplementary Figs. 5 and 6. In Fig. 2a, the local maximum of G″ at lower temperatures has been attributed to alkyl side chain relaxation, while the local maximum of G″ at higher temperatures is associated with the segmental backbone relaxation; this classification was verified by studying the dependence of interlayer spacing on the side chain length of P3ATs16,35. As the side chain length of poly(3-alkylthiophene) (P3AT) increases, the glass transition temperature of the backbone shifts to a lower temperature while that of the side chain increases. These changes in backbone and side chain Tgs have been observed previously and are attributed to “internal plasticization” of the backbone by the highly mobile alkyl side chains16. Not all conjugated polymers exhibit two Tgs, such as poly((9,9-dioctylfluorene)-2,7-diyl-alt-[4,7-bis(thiophen-5-yl)-2,1,3-benzothiadiazole]-2′,2″-diyl) (PFTBT)8. We speculate that side chain nanodomains for PFTBT are not large enough to exhibit a measurable side chain Tg due to the smaller side chain fraction than in P3ATs8. Nevertheless, backbone Tgs for other push-pull polymers, such as poly[N-9′-heptadecanyl-2,7-carbazole-alt-5,5-(4′,7′-di-2-thienyl-2′,1′,3′-benzothiadiazole)] (PCDTBT), also show an ~50 °C decrease when hexyl side chains are added to the thiophene units (Fig. 2b).
On the other hand, for a set of conjugated polymers with the same branched side chains but different backbones, the side chain Tg is found to be roughly the same while the backbone Tg changes appreciably (see Supplementary Fig. 4 and Supplementary Note 2). Additionally, the G″ peak corresponding to the glass transition for these branched side chains appears sharper than that of the backbone in Supplementary Fig. 4, in contrast to the case of regiorandom P3ATs in Fig. 2a. Clearly, Tg depends on the length and number of alkyl side chains attached to the conjugated backbone. Tg also depends modestly on the molecular weight, by ~15 °C for molecular weights between 10 and 100 kg/mol8.
Correlation between T g and side chain mass fraction
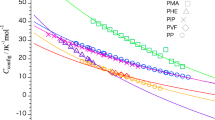
We now focus on the Tg that first demarks embrittlement upon cooling, the backbone glass transition. We first show the dependence of the backbone Tg on the alkyl side chain mass fraction, w. The value for w is directly calculated from the repeat unit structure (ignoring chain ends) in Supplementary Note 3 and is summarized in Supplementary Table 1 along with the corresponding Tg values. Figure 3 shows Tg versus w, where data can be roughly classified into two groups: structures in Group 1 are rich with thiophene rings; Group 2 structures are dominated by phenyl rings. This assignment is imperfect, but highlights potential insights. For instance, the trends for both Group 1 and Group 2 agree with many other polymer systems that have stiff backbones and increasing lengths of flexible side chains16,36,37. The suppression of Tg due to internal plasticization from flexible side chains is expected, as has been demonstrated from a generic monomer model that predicts the Tg15. In order to better quantify the difference between the two Groups in Fig. 3, the data were modeled with the Fox equation38,
by treating these polymers as nanophase separated mixtures of alkyl side chains (subscript sc) and conjugated backbones (subscript bb) with corresponding glass transition temperatures for each as Tg,sc and Tg,bb.
As shown in Table 1, both Tg,sc and Tg,bb differ significantly between Groups 1 and 2, suggesting that the side chain mass fraction alone cannot fully account for differences in the glass transition temperature of conjugated polymers. In particular, phenyl-rich backbones have a 69 K higher Tg,bb than thiophene-rich backbones even in the limit of no side chains, because different rings contribute differently to Tg, as suggested in predictions made by Dudowicz15 and experiments by Sokolov39. This finding motivates refined models connecting the chemical structure and Tg, as discussed below.
Correlation between T g and packing length
Conjugated polymers have a common structural scheme, a comb-like architecture with a stiff conjugated backbone and “flexible” alkyl side chains. Although more flexible than the backbone, alkyl side chains are rather stiff, given that a dodecyl side chain is about one Kuhn length of polyethylene40. Nevertheless, based on the general trend that the backbone Tg is higher for stiffer polymers with shorter alkyl side chains, the persistence length (lp) and the Kuhn monomer volume might be key dimensional parameters that govern the Tgs of conjugated polymers (see Supplementary Note 4). lp is determined by either light scattering or the freely rotating chain model as shown in Supplementary Fig. 7. The packing length (p), which is a ratio of the Kuhn monomer volume over the square of the Kuhn length (2lp), is then a natural candidate to be correlated with Tg. Nevertheless, as shown in Supplementary Fig. 8, the Tgs of conjugated polymers do not follow a universal relationship with the packing length or other physical chain dimensions, such as persistence length, Kuhn monomer volume, or chain thickness. Instead, we speculate that the dynamic free volume swept out by atoms on short times scales are correlated with chain and segmental motions that dictate the glass transition, which has a timescale on order of 100 s19,24,41,42.
Correlation between T g and effective atomic mobility
The rough partitioning of data shown in Fig. 3 into two groups based on two predominant moieties suggests that the value for the Tgs of conjugated polymers may be described as an interpolation between Tgs of the flexible side chains and that of conjugated cores. We thus propose a semi-empirical correlation between the backbone Tg and an effective mobility of the repeat unit, ζ, which captures the local mobility or stiffness averaged over the constituent side chain and backbone structure. We calculate ζ by summing assigned atomic mobilities ζi while excluding hydrogens (i.e., akin to the united atom model), and while ignoring the atomic heterogeneity between carbon, nitrogen, sulfur, and oxygen. Each atom that is part of a side chain (either C–C or C–O single bond) is assigned a mobility of 1, while each atom that is part of an aromatic ring or the backbone is assigned a value a (a < 1). Thus, we normalize the mobility of each atom to that of an atom within a flexible chain. We specify that each ring, thiophene or phenyl, contributes equally to the Tg by constraining ζi per atom with Eq. (2):
This contribution of aromatic rings to the Tg with respect to the contribution of flexible side chains is a fitting parameter for our model. Assigning atoms within phenyl rings a value of a then sets values for atoms within thiophene rings at 1.2a, making the total contribution of either ring to ζ to be 6a. Other atoms on the backbone that are not part of an aromatic ring (e.g., alkenyl and carbonyl groups) are assigned values of a, or the same as atoms within phenyl rings.
Using the assignments summarized in Table 2, the mobility of the repeat unit ζ is calculated by summing the mobilities of the constituent atoms while normalizing by the total number of atoms (excluding hydrogens) in the entire repeat unit according to Eq. (3) below:
where Ni is the number of atoms (excluding hydrogens) in the repeat unit belonging to a phenyl ring (Nphenyl), a thiophene ring (Nthiophene), an alkenyl or carbonyl group (Ndbl bond), and a side chain (Nflexible), while ζi represents the effective atomic mobility for the corresponding unit. Contributions of atoms linked by double bonds are added to account for weakly mobile atoms on the backbone that are not part of aromatic rings, such as the vinylene moiety in PPVs and carbonyl groups in P(NDI2OD-T2), PII-2T, and PTB7. We account for fused rings by considering them as two rings minus the missing number of atoms with mobilities of a that are needed to complete two independent rings, thereby subtracting an ζdbl bondNdbl bond term to avoid double-counting. For instance, thienothiophene in PBTTT-C14 and benzodiathiazole in PFTBT can be treated as sums of two conjugated rings minus two conjugated carbons (12a – 2a = 10a). As a consequence, calculating ζ from the chemical structure of any conjugated polymer depends on a single parameter a, which describes the dynamics of the conjugated core with respect to the side chains.
As shown in Supplementary Note 5, setting a = 0.60 in Supplementary Fig. 9 maximizes the linear correlation between Tg and ζ for the 32 polymers examined in this work. Relaxing the constraint on the same mobility per ring and introducing another adjustable parameter for the atomic mobility in a thiophene ring (different than that in a phenyl ring) does not significantly improve the strength of correlation between Tg and ζ. Therefore, we uphold our original assignment of the atomic mobility in Table 2, confirming the use of a single parameter a in the calculation of ζ from the repeat unit. The effective mobility values for all 32 aromatic polymers in this study are summarized in Supplementary Table 1. Despite the drastic differences in chemical structure, Fig. 4a shows that larger values of ζ, which correspond to more mobile polymers, have lower Tg, such that
95% confidence intervals for predictions based on Eq. (4) are also shown in Fig. 4a as dotted and dashed lines. Additionally, the direct comparison between the predicted Tg and the experimental Tg is shown in Fig. 4b, with a root-mean-square error (RMSE) of 13 °C. In the limit that all atoms are completely mobile (i.e., ζ = 1), this correlation in Fig. 4a predicts a Tg of −120 °C, which is comparable with the Tg of polyethylene43,44,45,46 and the alkyl side chain Tgs of P3HT (−100 °C), P3OT (−65 °C), and P3DDT (−50 °C)16. In the other limit, that of conjugated polymers without any side chains, the Tg of unsubstituted polythiophene (ζ = 0.72) lies reasonably close to the correlation, even though this value is determined from a weak signature in DSC (Supplementary Fig. 6). No signatures of Tg are detected for poly(p-phenylene) before degradation. Nevertheless, our model is consistent with the extrapolations to zero side chains shown in Fig. 2 and Table 1 (Tg,bb) for polyphenylene vinylene (PPV, ζ = 0.6, predicted Tg = 318 °C) and for polythiophene (ζ = 0.72, predicted Tg = 186 °C).
a General correlation between the experimentally measured glass transition temperature (Tg) and the effective mobility value (ζ) for conjugated polymers with different backbones and alkyl side chains. Solid line represents the best linear fit through all data with the coefficient of determination (R2) shown above. Dotted and dashed lines represent the 95% lower and upper prediction line (LPL and UPL), respectively. Group 1 (red squares) is composed of thiophene-rich backbones and Group 2 (blue circles) is composed of phenyl-rich backbones, as introduced in Fig. 3. b Comparison between experimental Tg and prediction by Eq. (4) for all 32 alkylated conjugated polymers, which yields a root-mean-square error (RMSE) of 13 °C.
Discussion
Given the success of our simple relationship between chemical structure and Tg, we surmise that the glass transition in these materials is mainly governed by the local dynamics of the repeat unit. For instance, although the kinked polyarylenes (PAr) have much more flexible backbone conformations than polyfluorenes and other push-pull polymers (persistence lengths of 1 nm versus ~7 nm), both PmmpP-8 and PF6 show similar effective mobility values of ζ ~0.80 and similar observed Tgs at around (94 ± 7) °C. Thus, polymers with “stiffer” backbones do not necessarily have higher Tgs. Furthermore, because evidence for two Tgs for all conjugated polymers is not always observed, we hypothesize that the success of our correlation in Fig. 4 could imply two possibilities. Perhaps microphase separation of the side chains does not affect the backbone Tg, due to a decoupling of segmental dynamics between the backbone and side chains even without microphase separation. Alternatively, all conjugated polymers studied here could exhibit microphase separation of the side chains, but perhaps not all side chain Tgs are detectable with our current metrology. In addition, the length or branching of the side chain is not directly related to the backbone Tg within the accuracy of our model, and instead contributes by varying the amount of mobile atoms. Figure 4 also includes both conjugated and non-conjugated backbones (PAr’s), altogether thereby demonstrating a powerful approach to predict the Tg of aromatic polymers.
Our correlation includes Tgs for P3HTs (both regioregular and regiorandom), PFTBTs and PCDTBTs that vary in molecular weight, and as a consequence exhibit Tgs that differ by about 15 K at most for the same polymer; these are still within the 95% prediction band (i.e., about ±26 K in this case). But, as the molecular weight (see Supplementary Note 1) becomes smaller or close to its Kuhn monomer molar mass, the packing of these short and stiff chains would be drastically different than that of a Gaussian coil in the long chain limit, which may lead to a larger deviation beyond the prediction band of our current model. As shown in Supplementary Table 1, the molecular weight of every polymer is larger than its corresponding Kuhn monomer molar mass, thereby ensuring a modest effect of molecular weight on Tg.; even when the number of Kuhn segments approaches 1, predicted values are quite accurate. In addition, crystallization can perturb the Tg by perturbing chain mobilities near crystal interfaces or chain conformations in the amorphous phase; this effect is again on the order of about 15 K for conjugated polymers8. Thus, using Tgs that are extrapolated to infinite molecular weight, and, if necessary, extrapolated to zero crystallinity, could further improve the accuracy of our model.
We also consider the case of phenyl rings at the end of side chains, which are not as common as alkyl moieties (see Supplementary Note 6). As shown in Supplementary Fig. 10a, data for polystyrene (PS) and poly[2-methoxy-5-(2′-phenylethoxy)-1,4-phenylenevinylene] (MPE-PPV) lie below the correlation. This suggests that the atoms in the terminal phenyl ring are much more mobile than those of phenyl rings on the backbone, thus increasing the average value of the atomic mobility in a phenyl ring at the end of a side chain (ζphenyl,side chain). Indeed, by increasing ζphenyl, side chain from 0.60 to 0.72, both PS and MPE-PPV collapse with the rest of the data (Supplementary Fig. 10b). Along these lines, APFO-18, which has two singly attached phenyl rings as side groups, is right on the dotted lower prediction line of Fig. 4.
Although the assignment of the atomic mobility in an aromatic ring with respect to the mobility of alkyl side chains is obtained as an empirical parameter, there is significant evidence for a connection between atomic motion and Tg. One interpretation of our atomic mobility ζ is as the average local stiffness, which has been predicted to be related to short timescale motion, the dynamic free volume, and as a consequence the Tg19,47. We can use MD simulations to compare the motion of the conjugated core and carbon atoms on the side chain next to the core, and thereby minimize the contributions of long timescale diffusion to the motion of side chains. Previous work on amorphous P3HT and P3DDT at 300 K show that the ratios of the root-mean-square displacement within 2 ns, at the thiophene ring versus the closest atom on the side chain, are 0.69 for P3HT and 0.77 for P3DDT48, which is close to the value used for the correlation shown in Fig. 4 (ζthiophene/ζflexible = 1.2a = 0.72, where a = 0.6).
The connection between atomic mobility and the Tg, perhaps through local motion, implies some limits to our correlation shown in Eq. (4) and Fig. 4. For example, using non-alkyl side chains, such as those based on siloxane, could lead to different backbone-to-side chain atomic mobility ratios. Adding flexible alkyl segments to conjugated backbones or adding stiff rings to alkyl side chains (as shown for PS and MPE-PPV) should warrant different values of a for these moieties.
In summary, we propose a simple approach to predict the glass transition temperature from the chemical structure of conjugated polymers using a single adjustable parameter. Our correlation between the average mobility of constituent atoms and Tg provides an estimate that is accurate over a wide variety of rigid, aromatic (co)polymers. The side chain mass fraction and the packing length are only correlated to Tg for a limited group of conjugated polymers with either a particular backbone unit or a specific range of chain stiffness. But, a general correlation between the Tg and the effective mobility value of the repeat unit, ζ, is observed for all 32 polymers in this work, with 0.7 ≤ ζ ≤ 0.92 showing −30 °C ≤ Tg ≤ 215 °C. In essence, ζ represents the effective number of mobile atoms in a repeat unit based on the assigned mobility values for atoms ζi belonging to different units, including a phenyl ring, an alkenyl or a carbonyl group (ζi = 0.60), a thiophene ring (0.72) on the backbone, and an alkyl group (1.0) on the side chain. As a result, this correlation between the backbone Tg and ζ predicts the Tg with a root-mean-square error of 13 °C.
If we assume the target backbone Tg for stretchable, electrically-active polymers that operate around room temperature to be ~0 °C or lower, our results imply an effective mobility value ζ of 0.89 or larger. This roughly requires at least one octyl side chain per thiophene ring or one hexadecyl side chain per phenyl ring. But, side chain crystallization is likely to occur for dodecyl or longer linear side chains, thus inhibiting stretchability. Nevertheless, our analysis shows that not every ring needs to be alkylated as in the poly(3-alkylthiophene-2,5-diyl) family, but instead side chains can be part of long branched groups on selected monomers. This architecture provides opportunities for strong π-π stacking, and could thereby promote intermolecular delocalization in materials that are rubbery at room temperature.
Methods
Materials
As denoted in the Supplementary Note 1, many of the polymers examined here were purchased from commercial sources, such as the polyalkylthiophenes with different side chain lengths (PT, P3BT, P3HT, P3OT, P3DT, and P3DDT), polydialkylfluorenes with different side chain lengths (PF6, PF8, and PF12), low bandgap polymers with branched side chains (PffBT4T-2OD, PTB7, and P(NDI2OD-T2)), and some donor-acceptor alternating copolymers (PF8BT and PF8T2). In addition, various alternating copolymers were synthesized, including PFTBT, PCDTBT, PFT6BT, PCT6BT, PDPT6BT49, and PII-2T50, using previously reported procedures. The side chains of PBTTT-C14 HH are intentionally designed with head-to-head arrangement to distort the backbone planarity and suppress the crystallization of backbones, thus allowing a more apparent glass transition response. 5,5ʹ-dibromo-3,3ʹ-ditetradecyl-2,2ʹ-dithiophene for PBTTT-C14 HH was prepared by the Grignard reaction of 2-bromo-3-tetradecyl thiophene followed by bromination. Two equivalents of 2-bromo-3-tetradecyl was reacted by using active magnesium solution in THF (purchased from Rieke Metals, LLC) and [1,3-bis(diphenylphosphino)propane]dichloronickel(II) (Ni(dppp)Cl2) (purchased from Sigma-Aldrich, Inc.) as catalyst. Unreacted 2-bromo-3-tetradecyl thiophene was removed by vacuum distillation. The product passed through a short column with hexane for further purification. For bromination, 2.2 equivalents of N-bromosuccinimide (NBS) was added by 8 portions into 3,3ʹ-ditetradecyl-2,2ʹ-dithiophene solution in chloroform/acetic acid 50:50 (v/v). PBTTT-C14 HH was prepared through Stille reaction of 5,5ʹ-dibromo-3,3ʹ-ditetradecyl-2,2ʹ-dithiophene and 2,5-Bis(trimethylstannyl)thieno[3,2-b]thiophene (purchased from Sunatech, Inc.) in toluene by using tris(dibenzylideneacetone)dipalladium(0) (Pd2(dba)3) and tri(o-tolyl)phosphine. After polymerization at 90 °C for 48 h, the product was precipitated in methanol, followed by Soxhlet extraction with methanol and acetone subsequently. Polyarylenes with different side chains (PmmpP-4, PmmpP-6, PmmpP-8, and PmmpP-10) were synthesized as previously described51. Chemical structures of conjugated polymers with clearly reported Tgs but not measured here are shown in Fig. 1 as well, including poly(p-phenylene vinylene)s (M3EH-PPV, MDMO-PPV, and MEH-PPV), TFB, PF2/6, APFO-Green9, and APFO-18. Also included are the Tgs of multiple molecular weights of PFTBT, PCDTBT, and regioregular (RR) and regiorandom (RRa) P3HT from our previous work8. Molecular weights were determined as discussed in Supplementary Note 7.
Measurement of T g by rheology and DSC
Tgs are identified using linear viscoelastic rheology, except for the completely amorphous polymers (PAs) that show clear glass transition signatures in DSC experiments and an unmoldable polymer (PT) where DSC is the only option to probe its Tg. Samples for rheology are molded under vacuum in a nitrogen-filled glove box at a temperature well above their highest reversible thermal transitions. Only ~15 mg of sample is needed to form a puck with 3 mm diameter and roughly 1 mm thickness. The mass density is estimated by weighing the puck and measuring its thickness in the rheometer as summarized in Supplementary Table 1. Rheology measurement is then carried out in a strain-controlled rotational rheometer (TA Instruments ARES-G2) under a nitrogen environment. The molded puck is loaded in the rheometer between two 3 mm-diameter aluminum parallel plates at room temperature and then annealed at 20 °C above the melting temperature or 100 °C above Tg to ensure good adhesion with the plates.
Because PTB7 does not melt below 320 °C, we determine this Tg by gluing a puck molded at 300 °C onto the rheometer plates using cyanoacrylate; this glue limits experiments to below 100 °C. In this work, Tg is located as the temperature that shows the local maximum of the loss modulus G″ during a heating scan with a rate of 5 °C/min, a frequency of 1 rad/s, and an oscillatory strain amplitude of 0.001. For conjugated polymers that exhibit two G″ peaks when G′ decreases starting on the order of 1 GPa, the higher temperature transition is labeled as the Tg of the backbone, while the lower temperature to that of the side chain. Specific examples are highlighted in the Results section to support this assignment. In this work, all Tgs refer to the backbone glass transition temperatures unless otherwise stated.
Data availability
The authors declare that the data that support the findings of this manuscript can be found in the Supplementary Information and are available free of charge on Penn State’s ScholarSphere at https://scholarsphere.psu.edu/collections/prr171z013.
References
Ferry J. D. Viscoelastic Properties of Polymers, 3rd edn (John Wiley & Sons, 1980).
Xie, R. et al. Local chain alignment via nematic ordering reduces chain entanglement in conjugated polymers. Macromolecules 51, 10271–10284 (2018).
Xie, R., Colby, R. H. & Gomez, E. D. Connecting the mechanical and conductive properties of conjugated polymers. Adv. Electron. Mater. 4, 1700356 (2018).
Qian, Z. et al. Glass transition phenomenon for conjugated polymers. Macromol. Chem. Phys. 220, 1900062 (2019).
Guo, C. et al. Photovoltaic performance of block copolymer devices is independent of the crystalline texture in the active layer. Macromolecules 49, 4599–4608 (2016).
Smith, B. H. et al. Fluorination of donor–acceptor copolymer active layers enhances charge mobilities in thin-film transistors. ACS Macro Lett. 6, 1162–1167 (2017).
Lu, C. et al. Effects of molecular structure and packing order on the stretchability of semicrystalline conjugated poly(tetrathienoacene-diketopyrrolopyrrole) polymers. Adv. Electron. Mater. 3, 1600311-n/a (2017).
Xie, R. et al. Glass transition temperature of conjugated polymers by oscillatory shear rheometry. Macromolecules 50, 5146–5154 (2017).
Vakhshouri, K. & Gomez, E. D. Effect of crystallization kinetics on microstructure and charge transport of polythiophenes. Macromol. Rapid Commun. 33, 2133–2137 (2012).
McCulloch, I. et al. Liquid-crystalline semiconducting polymers with high charge-carrier mobility. Nat. Mater. 5, 328 (2006).
Nguyen, L. H. et al. Effects of annealing on the nanomorphology and performance of poly(alkylthiophene):fullerene bulk-heterojunction solar cells. Adv. Funct. Mater. 17, 1071–1078 (2007).
Lee, J. K. et al. Processing additives for improved efficiency from bulk heterojunction solar cells. J. Am. Chem. Soc. 130, 3619–3623 (2008).
Vakhshouri, K. et al. Signatures of intracrystallite and intercrystallite limitations of charge transport in polythiophenes. Macromolecules 49, 7359–7369 (2016).
Privalko, V. P. & Lipatov, Y. S. Glass transition and chain flexibility of linear polymers. J. Macromol. Sci. B 9, 551–564 (1974).
Dudowicz, J., Freed, K. F. & Douglas, J. F. The glass transition temperature of polymer melts. J. Phys. Chem. B 109, 21285–21292 (2005).
Pankaj, S., Hempel, E. & Beiner, M. Side-chain dynamics and crystallization in a series of regiorandom poly(3-alkylthiophenes). Macromolecules 42, 716–724 (2009).
Sharma, A. et al. Probing the relationship between molecular structures, thermal transitions, and morphology in polymer semiconductors using a woven glass-mesh-based DMTA technique. Chem. Mater. 31, 6740–6749 (2019).
Starr, F. W., Sastry, S., Douglas, J. F. & Glotzer, S. C. What do we learn from the local geometry of glass-forming liquids? Phys. Rev. Lett. 89, 125501 (2002).
Douglas, J. F., Pazmino Betancourt, B. A., Tong, X. & Zhang, H. Localization model description of diffusion and structural relaxation in glass-forming Cu–Zr alloys. J. Stat. Mech. Theory Exp. 2016, 054048 (2016).
Cicerone, M. T. & Douglas, J. F. β-Relaxation governs protein stability in sugar-glass matrices. Soft Matter 8, 2983–2991 (2012).
Forrey, C. et al. Prediction and validation of diffusion coefficients in a model drug delivery system using microsecond atomistic molecular dynamics simulation and vapour sorption analysis. Soft Matter 10, 7480–7494 (2014).
Soles, C. L., Douglas, J. F. & Wu, W.-L. Dynamics of thin polymer films: Recent insights from incoherent neutron scattering. J. Polym. Sci. Part B Polym. Phys. 42, 3218–3234 (2004).
Larini, L., Ottochian, A., De Michele, C. & Leporini, D. Universal scaling between structural relaxation and vibrational dynamics in glass-forming liquids and polymers. Nat. Phys. 4, 42–45 (2008).
Pazmiño Betancourt, B. A., Hanakata, P. Z., Starr, F. W. & Douglas, J. F. Quantitative relations between cooperative motion, emergent elasticity, and free volume in model glass-forming polymer materials. Proc. Natl Acad. Sci. USA 112, 2966–2971 (2015).
Dudowicz J, Freed KF, Douglas JF. in Advances in Chemical Physics (ed. Rice, S. A.) (Wiley, 2008).
Katritzky, A. R. et al. Quantitative correlation of physical and chemical properties with chemical structure: utility for prediction. Chem. Rev. 110, 5714–5789 (2010).
Van Krevelen D. W. & Te Nijenhuis K. in Properties of Polymers 4th edn (eds. Van Krevelen, D. W. & Te Nijenhuis, K.) (Elsevier, 2009).
Kim, C., Chandrasekaran, A., Huan, T. D., Das, D. & Ramprasad, R. Polymer genome: a data-powered polymer informatics platform for property predictions. J. Phys. Chem. C 122, 17575–17585 (2018).
Schut, J. et al. Glass transition temperature prediction of polymers through the mass-per-flexible-bond principle. Polymer 48, 6115–6124 (2007).
Philippe, C., Cypcar, C. C., Véronique, L. & Bernard, W. A novel approach toward the prediction of the glass transition temperature: application of the EVM model, a designer QSPR equation for the prediction of acrylate and methacrylate polymers. J. Polym. Sci. Part A Polym. Chem. 35, 2579–2590 (1997).
Bicerano, J. Prediction Of Polymers Properties 2nd edn. (Marcel Dekker, 1996).
Boyer, R. F. The relation of transition temperatures to chemical structure in high polymers. Rubber Chem. Technol. 36, 1303–1421 (1963).
Qian, Z. et al. Challenge and solution of characterizing glass transition temperature for conjugated polymers by differential scanning calorimetry. J. Polym. Sci. Part B Polym. Phys. 57, 1635–1644 (2019).
Müller, C. On the glass transition of polymer semiconductors and its impact on polymer solar cell stability. Chem. Mater. 27, 2740–2754 (2015).
Shen, X., Duzhko, V. V. & Russell, T. P. A study on the correlation between structure and hole transport in semi-crystalline regioregular P3HT. Adv. Energy Mater. 3, 263–270 (2013).
Rogers, S. & Mandelkern, L. Glass transitions of the poly-(n-alkyl methacrylates). J. Phys. Chem. 61, 985–991 (1957).
Papadopoulos, P., Floudas, G., Chi, C. & Wegner, G. Molecular dynamics of oligofluorenes: a dielectric spectroscopy investigation. J. Chem. Phys. 120, 2368–2374 (2004).
Fox, T. G. Influence of diluent and of copolymer composition on the glass temperature of a polymer system. Bull. Am. Phys. Soc. 1, 123 (1956).
Kunal, K., Robertson, C. G., Pawlus, S., Hahn, S. F. & Sokolov, A. P. Role of chemical structure in fragility of polymers: a qualitative picture. Macromolecules 41, 7232–7238 (2008).
Rubinstein, M. & Colby, R. H. Polymer Physics (Oxford University Press, 2003).
Simmons, D. S., Cicerone, M. T., Zhong, Q., Tyagi, M. & Douglas, J. F. Generalized localization model of relaxation in glass-forming liquids. Soft Matter 8, 11455–11461 (2012).
White, R. P. & Lipson, J. E. G. Polymer free volume and its connection to the glass transition. Macromolecules 49, 3987–4007 (2016).
Lide, D. R. CRC Handbook of Chemistry and Physics. (CRC Press, 1994).
Fakirov, S. & Krasteva, B. On the glass transition temperature of polyethylene as revealed by microhardness measurements. J. Macromol. Sci. Part B 39, 297–301 (2000).
Wunderlich, B. Thermal Analysis. (Academic Press, 1990).
Brandup, J. & Immergut E. H. Polymer Handbook. (John Wiley and Sons, 1989).
Hall, R. W. & Wolynes, P. G. The aperiodic crystal picture and free energy barriers in glasses. J. Chem. Phys. 86, 2943–2948 (1987).
Zhan, P. F. et al. Side chain length affects backbone dynamics in poly(3-alkylthiophene)s. J. Polym. Sci. Pol. Phys. 56, 1193–1202 (2018).
Aplan, M. P. et al. Revealing the importance of energetic and entropic contributions to the driving force for charge photogeneration. ACS Appl. Mater. Interfaces 10, 39933–39941 (2018).
Mei, J., Kim, D. H., Ayzner, A. L., Toney, M. F. & Bao, Z. Siloxane-terminated solubilizing side chains: bringing conjugated polymer backbones closer and boosting hole mobilities in thin-film transistors. J. Am. Chem. Soc. 133, 20130–20133 (2011).
Kempe, F. et al. A simply synthesized, tough polyarylene with transient mechanochromic response. Angew. Chem. Int. Ed. 57, 997–1000 (2018).
Acknowledgements
We gratefully acknowledge financial support from the National Science Foundation under grant number DMR-1629006 and DMR-1921854. We also gratefully acknowledge Tadanori Kurosawa and Zhenan Bao for providing PII-2T.
Author information
Authors and Affiliations
Contributions
R.X., R.H.C., and E.D.G. conceived and designed the project. R.X., A.R.W., A.M.F., and A.M. performed characterization measurements and, along with M.S, C.W.P., R.H.C., and E.D.G., analyzed the data. Y.L., M.A.A., F.K., and M.S. designed and synthesized materials for this work. R.H.C. and E.D.G jointly supervised this work. R.X., R.H.C., and E.D.G wrote the manuscript. All authors discussed results and edited the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Jack Douglas and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Xie, R., Weisen, A.R., Lee, Y. et al. Glass transition temperature from the chemical structure of conjugated polymers. Nat Commun 11, 893 (2020). https://doi.org/10.1038/s41467-020-14656-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-020-14656-8
This article is cited by
-
Thermal and optical properties of P3HT:PC70BM:ZnO nanoparticles composite films
Scientific Reports (2024)
-
GMXPolymer: a generated polymerization algorithm based on GROMACS
Journal of Molecular Modeling (2024)
-
Side-Chain-Type Polyimide-Cu Complexes with Suppressed Activation Energy of Relaxation for Advanced High-Temperature Capacitor
Chinese Journal of Polymer Science (2024)
-
Cascade reaction triggering and photothermal AuNPs@MIL MOFs doped intraocular lens for enhanced posterior capsular opacification prevention
Journal of Nanobiotechnology (2023)
-
A materials physics perspective on structure–processing–function relations in blends of organic semiconductors
Nature Reviews Materials (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.