Abstract
The inability of conventional electronic architectures to efficiently solve large combinatorial problems motivates the development of novel computational hardware. There has been much effort toward developing application-specific hardware across many different fields of engineering, such as integrated circuits, memristors, and photonics. However, unleashing the potential of such architectures requires the development of algorithms which optimally exploit their fundamental properties. Here, we present the Photonic Recurrent Ising Sampler (PRIS), a heuristic method tailored for parallel architectures allowing fast and efficient sampling from distributions of arbitrary Ising problems. Since the PRIS relies on vector-to-fixed matrix multiplications, we suggest the implementation of the PRIS in photonic parallel networks, which realize these operations at an unprecedented speed. The PRIS provides sample solutions to the ground state of Ising models, by converging in probability to their associated Gibbs distribution. The PRIS also relies on intrinsic dynamic noise and eigenvalue dropout to find ground states more efficiently. Our work suggests speedups in heuristic methods via photonic implementations of the PRIS.
Similar content being viewed by others
Introduction
Heuristic methods—probabilistic algorithms with stochastic components—are a cornerstone of both numerical methods in statistical physics1 and NP-Hard optimization2. Broad classes of problems in statistical physics, such as growth patterns in clusters3, percolation4, heterogeneity in lipid membranes5, and complex networks6, can be described by heuristic methods. These methods have proven instrumental for predicting phase transitions and the critical exponents of various universality classes – families of physical systems exhibiting similar scaling properties near their critical temperature1. These heuristic algorithms have become popular, as they typically outperform exact algorithms at solving real-world problems7. Heuristic methods are usually tailored for conventional electronic hardware; however, a number of optical machines have recently been shown to solve the well-known Ising8,9 and Traveling Salesman problems10,11. For computationally demanding problems, these methods can benefit from parallelization speedups1,12, but the determination of an efficient parallelization approach is highly problem-specific1.
Half a century before the contemporary Machine Learning Renaissance13, the Little14 and then the Hopfield15,16 networks were considered as early architectures of recurrent neural networks (RNN). The latter was suggested as an algorithm to solve combinatorially hard problems, as it was shown to deterministically converge to local minima of arbitrary quadratic Hamiltonians of the form
which is the most general form of an Ising Hamiltonian in the absence of an external magnetic field17. In Eq. (1), we equivalently denote the set of spins as σ ∈ {−1, 1}N or S ∈ {0, 1}N (with σ = 2S−1), and K is a N × N real symmetric matrix.
In the context of physics, Ising models describe the interaction of many particles in terms of the coupling matrix K. These systems are observed in a particular spin configuration σ with a probability given by the Gibbs distribution \(p(\sigma )\propto \exp (-\beta {H}^{(K)}(\sigma ))\), where β = 1/(kBT), with kB the Boltzmann constant and T the temperature. At low temperature, when β → ∞, the Gibbs probability of observing the system in its ground state approaches 1, thus naturally minimizing the quadratic function in Eq. (1). As similar optimization problems are often encountered in computer science2,7, a natural idea is to engineer physical systems with dynamics governed by an equivalent Hamiltonian. Then, by sampling the physical system, one can generate candidate solutions to the optimization problem. This analogy between statistical physics and computer science has nurtured a great variety of concepts in both fields18, for instance, the analogy between neural networks and spin glasses15,19.
Many complex systems can be formulated using the Ising model20—such as ferromagnets17,21, liquid-vapor transitions22, lipid membranes5, brain functions23, random photonics24, and strongly-interacting systems in quantum chromodynamics25. From the perspective of optimization, finding the spin distribution minimizing H(K) for an arbitrary matrix K belongs to the class of NP-hard problems26.
Hopfield networks deterministically converge to a local minimum, thus making it impossible to scale such networks to deterministically find the global minimum27—thus jeopardizing any electronic16 or optical28 implementation of these algorithms. As a result, these early RNN architectures were soon superseded by heuristic (such as Metropolis-Hastings (MH)) and metaheuristic methods (such as simulated annealing (SA)29, parallel tempering30, genetic algorithms31, Tabu search32 and local-search-based algorithms33), usually tailored for conventional electronic hardware. Even still, heuristic methods struggle to solve large problems, and could benefit from nanophotonic hardware demonstrating parallel, low-energy, and high-speed computations34,35,36.
Here, we propose a photonic implementation of a passive RNN, which models the arbitrary Ising-type Hamiltonian in Eq. (1). We propose a fast and efficient heuristic method for photonic analog computing platforms, relying essentially on iterative matrix multiplications. Our heuristic approach also takes advantage of optical passivity and dynamic noise to find ground states of arbitrary Ising problems and probe their critical behaviors, yielding accurate predictions of critical exponents of the universality classes of conventional Ising models. Our algorithm presents attractive scaling properties when benchmarked against conventional algorithms, such as MH. Our findings suggest a novel approach to heuristic methods for efficient optimization and sampling by leveraging the potential of matrix-to-vector accelerators, such as parallel photonic networks34. We also hint at a broader class of (meta)heuristic algorithms derived from the PRIS, such as combined simulated annealing on the noise and eigenvalue dropout levels. Our algorithm can also be implemented in a competitive manner on fast parallel electronic hardware, such as FPGAs and ASICs.
Results
Photonic computational architecture
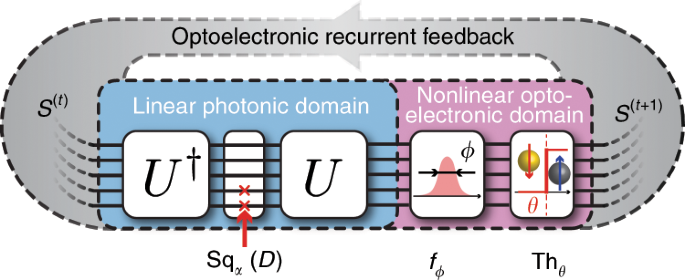
The proposed architecture of our photonic network is shown in Fig. 1. This photonic network can map arbitrary Ising Hamiltonians described by Eq. (1), with Kii = 0 (as diagonal terms only contribute to a global offset of the Hamiltonian, see Supplementary Note 1). In the following, we will refer to the eigenvalue decomposition of K as K = UDU†, where U is a unitary matrix, U† its transpose conjugate, and D a real-valued diagonal matrix. The spin state at time step t, encoded in the phase and amplitude of N parallel photonic signals S(t) ∈ {0, 1}N, first goes through a linear symmetric transformation decomposed in its eigenvalue form 2J = USqα(D)U†, where Sqα(D) is a diagonal matrix derived from D, whose design will be discussed in the next paragraphs. The signal is then fed into nonlinear optoelectronic domain, where it is perturbed by a Gaussian distribution of standard deviation ϕ (simulating noise present in the photonic implementation) and is imparted a nonlinear threshold function Thθ (Thθ(x) = 1 if x > θ, 0 otherwise). The signal is then recurrently fed back to the linear photonic domain, and the process repeats. The static unit transformation between two time steps t and t + 1 of this RNN can be summarized as
where \({\mathcal{N}}(x| \phi )\) denotes a Gaussian distribution of mean x and standard deviation ϕ. We call this algorithm, which is tailored for a photonic implementation, the Photonic Recurrent Ising Sampler (PRIS). The detailed choice of algorithm parameters is described in the Supplementary Note 2.
This simple recurrent loop can be readily implemented in the photonic domain. For example, the linear photonic interference unit can be realized with MZI networks34,37,38,39, diffractive optics40,41, ring resonator filter banks42,43,44, and free space lens-SLM-lens systems45,46; the diagonal matrix multiplication Sqα(D) can be implemented with an electro-optical absorber, a modulator or a single MZI34,47,48; the nonlinear optoelectronic unit can be implemented with an optical nonlinearity47,48,49,50,51, or analog/digital electronics52,53,54,55, for instance by converting the optical output to an analog electronic signal, and using this electronic signal to modulate the input56. The implementation of the PRIS on several photonic architectures and the influence of heterogeneities, phase bit precision, and signal to noise ratio on scaling properties are discussed in the Supplementary Note 5. In the following, we will describe the properties of an ideal PRIS and how design imperfections may affect its performance.
General theory of the PRIS dynamics
The long-time dynamics of the PRIS is described by an effective Hamiltonian HL (see refs. 19,58 and Supplementary Note 2). This effective Hamiltonian can be computed by performing the following steps. First, calculate the transition probability of a single spin from Eq. (2). Then, the transition probability from an initial spin state S(t) to the next step S(t+1) can be written as
where \(S,S^{\prime}\) denote arbitrary spin configurations. Let us emphasize that, unlike H(K)(S), the transition Hamiltonian \({H}^{(0)}\left(S| S^{\prime} \right)\) is a function of two spin distributions S and \(S^{\prime}\). Here, β = 1∕(kϕ) is analogous to the inverse temperature from statistical mechanics, where k is a constant, only depending on the noise distribution (see Supplementary Table 1). To obtain Eqs. (3), (4), we approximated the single spin transition probability by a rescaled sigmoid function and have enforced the condition θi = ∑jJij. In the Supplementary Note 2, we investigate the more general case of arbitrary threshold vectors θi and discuss the influence of the noise distribution.
One can easily verify that this transition probability obeys the triangular condition (or detailed balance condition) if J is symmetric Jij = Jji. From there, an effective Hamiltonian HL can be deduced following the procedure described by Peretto58 for distributions verifying the detailed balance condition. The effective Hamiltonian HL can be expanded, in the large noise approximation (ϕ ≫ 1, β ≪ 1), into H2:
Examining Eq. (6), we can deduce a mapping of the PRIS to the general Ising model shown in Eq. (1) since \({H}_{2}=\beta {H}^{({J}^{2})}\). We set the PRIS matrix J to be a modified square-root of the Ising matrix K by imposing the following condition on the PRIS
We add a diagonal offset term αΔ to the eigenvalue matrix D, in order to parametrize the number of eigenvalues remaining after taking the real part of the square root. Since lower eigenvalues tend to increase the energy, they can be dropped out so that the algorithm spans the eigenspace associated with higher eigenvalues. We chose to parametrize this offset as follows: \(\alpha \in {\mathbb{R}}\) is called the eigenvalue dropout level, a hyperparameter to select the number of eigenvalues remaining from the original coupling matrix K, and Δ > 0 is a diagonal offset matrix. For instance, Δ can be defined as the sum of the off-diagonal terms of the Ising coupling matrix Δii = Σj≠i∣Kij∣. The addition of Δ only results in a global offset on the Hamiltonian. The purpose of the Δ offset is to make the matrix in the square root diagonally dominant, thus symmetric positive definite, when α is large and positive. Thus, other definitions of the diagonal offset could be proposed. When α → 0, some lower eigenvalues are dropped out by taking the real part of the square root (see Supplementary Note 3); we show below that this improves the performance of the PRIS. We will specify which definition of Δ is used in our study when α ≠ 0. When choosing this definition of Sqα(D) and operating the PRIS in the large noise limit, we can implement any general Ising model (Eq. (1)) on the PRIS (Eq. (6)).
It has been noted that by setting Sqα(D) = D (i.e., the linear photonic domain matrix amounts to the Ising coupling matrix 2J = K), the free energy of the system equals the Ising free energy at any finite temperature (up to a factor of 2, thus exhibiting the same ground states) in the particular case of associative memory couplings19 with finite number of patterns and in the thermodynamic limit, thus drastically constraining the number of degrees of freedom on the couplings. This regime of operation is a direct modification of the Hopfield network, an energy-based model where the couplings between neurons is equal to the Ising coupling between spins. The essential difference between the PRIS in the configuration Sqα(D) = D and a Hopfield network is that the former relies on synchronous spin updates (all spins are updated at every step, in this so-called Little network14) while the latter relies on sequential spin updates (a single randomly picked spin is updated at every step). The former is better suited for a photonic implementation with parallel photonic networks.
In this regime of operation, the PRIS can also benefit from computational speed-ups, if implemented on a conventional architecture, for instance if the coupling matrix is sparse. However, as has been pointed out in theory19 and by our simulations (see Supplementary Note 4, Supplementary Fig. 7), some additional considerations should be taken into account in order to eliminate non-ergodic behaviors in this system. As the regime of operation described by Eq. (7) is general to any coupling, we will use it in the following demonstrations.
Finding the ground state of Ising models with the PRIS
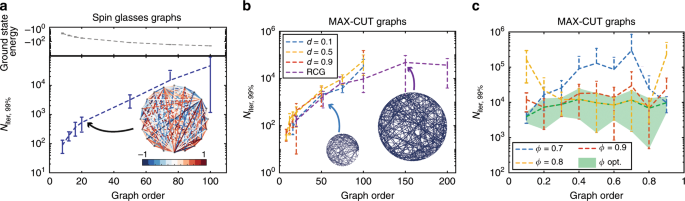
We investigate the performance of the PRIS on finding the ground state of general Ising problems Eq. (1) with two types of Ising models: MAX-CUT graphs, which can be mapped to an instance of the unweighted MAX-CUT problem9 and all-to-all spin glasses, whose connections are uniformly distributed in [−1, 1] (an example illustration of the latter is shown as an inset in Fig. 2a). Both families of models are computationally NP-hard problems26, thus their computational complexity grows exponentially with the graph order N.
(a, top) Ground state energy versus graph order of random spin glasses. A sample graph is shown as an inset in (a, bottom): a fully-connected spin glass with uniformly-distributed continuous couplings in [−1, 1]. Niter, 99% versus graph size for spin glasses (a, bottom) and MAX-CUT graphs (b). c Niter, 99% versus graph density for MAX-CUT graphs and N = 75. The graph density is defined as d = 2∣E∣∕(N(N − 1)), ∣E∣ being the number of undirected edges. RCG denotes Random Cubic Graphs, for which ∣E∣ = 3N∕2. Ground states are determined with the exact solver BiqMac57 (see Methods section). In this analysis, we set α = 0, and for each set of density and graph order we ran 10 graph instances 1000 times. The number of iterations to find the ground state is measured for each run and Niter, q is defined as the q-th quantile of the measured distribution.
The number of steps necessary to find the ground state with 99% probability, Niter, 99% is shown in Fig. 2a–b for these two types of graphs (see definition in Supplementary Note 4 and in the Methods section). As the PRIS can be implemented with high-speed parallel photonic networks, the on-chip real time of a unit step can be less than a nanosecond34,59 (and the initial setup time for a given Ising model is typically of the order of microseconds with thermal phase shifters60). In such architectures, the PRIS would thus find ground states of arbitrary Ising problems with graph orders N ~ 100 within less than a millisecond. We also show that the PRIS can be used as a heuristic ground state search algorithm in regimes where exact solvers typically fail (N ~ 1000) and benchmark its performance against MH and conventional metaheuristics (SA) (see Supplementary Note 6). Interestingly, both classical and quantum optical Ising machines have exhibited limitations in their performance related to the graph density9,61. We observe that the PRIS is roughly insensitive to the graph density, when optimizing the noise level ϕ (see Fig. 2c, shaded green area). A more comprehensive comparison should take into account the static fabrication error in integrated photonic networks34 (see also Supplementary Note 5), even though careful calibration of their control electronics can significantly reduce its impact on the computation62,63.
Influence of the noise and eigenvalue dropout levels
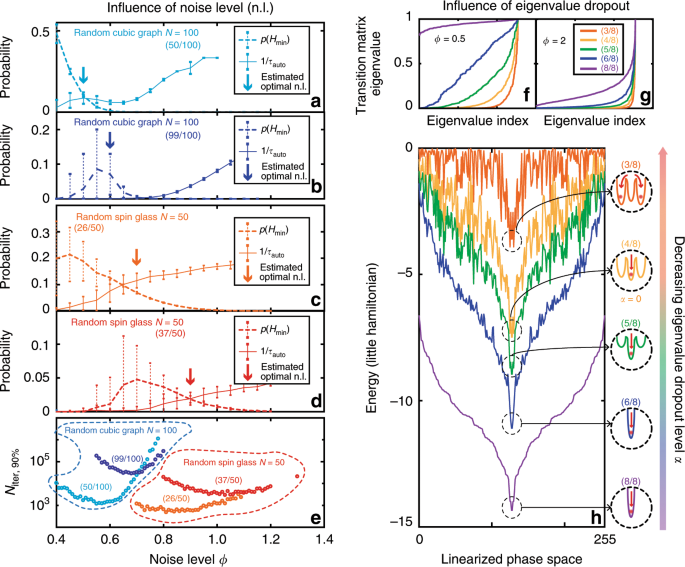
For a given Ising problem, there remain two degrees of freedom in the execution of the PRIS: the noise and eigenvalue dropout levels. The noise level ϕ determines the level of entropy in the Gibbs distribution probed by the PRIS \(p(E)\propto \exp (-\beta (E-\phi S(E)))\), where S(E) is the Boltzmann entropy associated with the energy level E. On the one hand, increasing ϕ will result in an exponential decay of the probability of finding the ground state \(p({H}_{\min },\phi )\). On the other hand, too small a noise level will not satisfy the large noise approximation HL ~ H2 and result in large autocorrelation times (as the spin state could get stuck in a local minimum of the Hamiltonian). Figure 3e demonstrates the existence of an optimal noise level ϕ, minimizing the number of iterations required to find the ground state of a given Ising problem, for various graph sizes, densities, and eigenvalue dropout levels. This optimal noise value can be approximated upon evaluation of the probability of finding the ground state \(p({H}_{\min },\phi )\) and the energy autocorrelation time \({\tau }_{{\rm{auto}}}^{E}\), as the minimum of the following heuristic
which approximates the number of iterations required to find the ground state with probability q (see Fig. 3a–e). In this expression, \({\tau }_{{\rm{eq}}}^{E}(\phi )\) is the energy equilibrium (or burn-in) time. As can be seen in Fig. 3e, decreasing α (and thus dropping more eigenvalues, with the lowest eigenvalues being dropped out first) will result in a smaller optimal noise level ϕ. Comparing the energy landscape for various eigenvalue dropout levels (Fig. 3h) confirms this statement: as α is reduced, the energy landscape is perturbed. However, for the random spin glass studied in Fig. 3f–g, the ground state remains the same down to α = 0. This hints at a general observation: as lower eigenvalues tend to increase the energy, the Ising ground state will in general be contained in the span of eigenvectors associated with higher eigenvalues (see discussion in the Supplementary Note 3). Nonetheless, the global picture is more complex, as the solution of this optimization problem should also enforce the constraint σ ∈ {−1, 1}N. We observe in our simulations that α = 0 yields a higher ground state probability and lower autocorrelation times than α > 0 for all the Ising problems we used in our benchmark. In some sparse models, the optimal value can even be α < 0 (see Supplementary Fig. 3 in the Supplementary Note 4). The eigenvalue dropout is thus a parameter that constrains the dimensionality of the ground state search.
a–d Probability of finding the ground state, and the inverse of the autocorrelation time as a function of noise level ϕ for a sample Random Cubic Graph9 (N = 00, (50/100) eigenvalues (a), (99/100) eigenvalues (b), and a sample spin glass (N = 50, (37/100) eigenvalues (c), (26/100) eigenvalues (d)). The arrows indicate the estimated optimal noise level, from Eq. (8), taking \({\tau }_{{\rm{eq}}}^{E}\) to be constant. For this study we averaged the results of 100 runs of the PRIS with random initial states with error bars representing ± σ from the mean over the 100 runs. We assumed Δii = ∑jKij. (e): Niter, 90% versus noise level ϕ for these same graphs and eigenvalue dropout levels. f–g Eigenvalues of the transition matrix of a sample spin glass (N = 8) at ϕ = 0.5 (f) and ϕ= 2 (g). h The corresponding energy is plotted for various eigenvalue dropout levels α, corresponding to less than N eigenvalues kept from the original matrix. The inset is a schematic of the relative position of the global minimum when α = 1 (with (8/8) eigenvalues) with respect to nearby local minima when α < 1. For this study we assumed Δii = ∑jKij.
The influence of eigenvalue dropout can also be understood from the perspective of the transition matrix. Figure 3f–g shows the eigenvalue distribution of the transition matrix for various noise and eigenvalue dropout levels. As the PRIS matrix eigenvalues are dropped out, the transition matrix eigenvalues become more nonuniform, as in the case of large noise (Fig. 3g). Overall, the eigenvalue dropout can be understood as a means of pushing the PRIS to operate in the large noise approximation, without perturbing the Hamiltonian in such a way that would prevent it from finding the ground state. The improved performance of the PRIS with α ~ 0 hints at the following interpretation: the perturbation of the energy landscape (which affects \(p({H}_{\min })\)) is counterbalanced by the reduction of the energy autocorrelation time induced by the eigenvalue dropout. The existence of these two degrees of freedom suggests a realm of algorithmic techniques to optimize the PRIS operation. One could suggest, for instance, setting α ≈ 0, and then performing an inverse simulated annealing of the eigenvalue dropout level to increase the dimensionality of the ground state search. This class of algorithms could rely on the development of high-speed, low-loss integrated modulators59,64,65,66.
Detecting and characterizing phase transitions with the PRIS
The existence of an effective Hamiltonian describing the PRIS dynamics Eq. (6) further suggests the ability to generate samples of the associated Gibbs distribution at any finite temperature. This is particularly interesting considering the various ways in which noise can be added in integrated photonic circuits by tuning the operating temperature, laser power, photodiode regimes of operation, etc.52,67. This alludes to the possibility of detecting phase transitions and characterizing critical exponents of universality classes, leveraging the high speed at which photonic systems can generate uncorrelated heuristic samples of the Gibbs distribution associated with Eqs. (5), (6). In this part, we operate the PRIS in the regime where the linear photonic matrix is equal to the Ising coupling matrix (Sqα(D) = D)19. This allows us to speedup the computation on a CPU by leveraging symmetry and sparsity of the coupling matrix K. We show that the regime of operation described by Eq. (7) also probes the expected phase transition (see Supplementary Note 4).
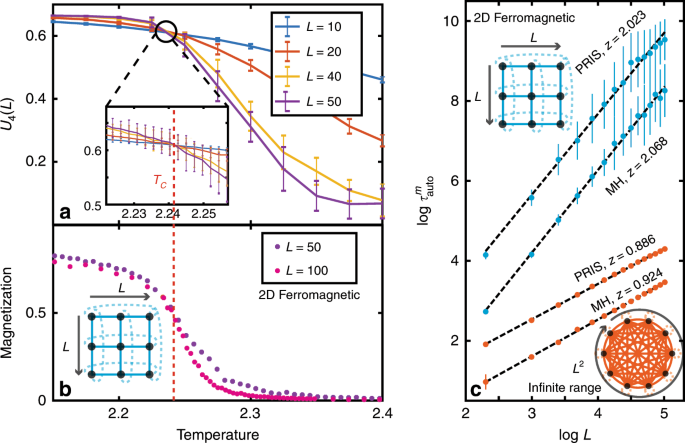
A standard way of locating the critical temperature of a system is through the use of the Binder cumulant1 \({U}_{4}(L)=1-\langle {m}^{4}\rangle /(3{\langle {m}^{2}\rangle }^{2})\), where \(m={\sum }_{i=1}^{N}{\sigma }_{i}/N\) is the magnetization and 〈.〉 denotes the ensemble average. As shown in Fig. 4a, the Binder cumulants intersect for various graph sizes L2 = N at the critical temperature of TC = 2.241 (compared to the theoretical value of 2.269 for the two-dimensional Ferromagnetic Ising model, i.e., within 1.3%). The heuristic samples generated by the PRIS can be used to compute physical observables of the modeled system, which exhibit the emblematic order-disorder phase transition of the two-dimensional Ising model1,21 (Fig. 4b). In addition, critical parameters describing the scaling of the magnetization and susceptibility at the critical temperature can be extracted from the PRIS to within 10% of the theoretical value (see Supplementary Note 4).
a Binder cumulants U4(L) for various graph sizes L on the 2D Ferromagnetic Ising model. Their intersection determines the critical temperature of the model TC (denoted by a dotted line). b Magnetization estimated from the PRIS for various L. c Scaling of the PRIS magnetization autocorrelation time for various Ising models, benchmarked versus the Metropolis-Hastings algorithm (MH). The complexity of a single time step scales like N2 = L4 for MH on a CPU and like N = L2 for the PRIS on a photonic platform. For readability, error bars in b are not shown (see Supplementary Note 4).
In Fig. 4c, we benchmark the performance of the PRIS against the well-known Metropolis-Hastings (MH) algorithm1,68,69. In the context of heuristic methods, one should compare the autocorrelation time of a given observable. The scaling of the magnetization autocorrelation time \({\tau }_{{\rm{auto}}}^{m}={\mathcal{O}}({L}^{z})={\mathcal{O}}({N}^{z/2})\) at the critical temperature is shown in Fig. 4c for two analytically-solvable models: the two-dimensional ferromagnetic and the infinite-range Ising models. Both algorithms yield autocorrelation time critical exponents close to the theoretical value (z ~ 2.1)1 for the two-dimensional Ising model. However, the PRIS seems to perform better on denser models such as the infinite-range Ising model, where it yields a smaller autocorrelation time critical exponent. More significantly, the advantage of the PRIS resides in its possible implementation with any matrix-to-vector accelerator, such as parallel photonic networks, so that the computational (time) complexity of a single step is \({\mathcal{O}}(N)\)34,38,39. Thus, the computational complexity of generating an uncorrelated sample scales like \({\mathcal{O}}({N}^{1+{z}_{{\rm{PRIS}}}/2})\) for the PRIS on a parallel architecture, while it scales like \({\mathcal{O}}({N}^{2+{z}_{{\rm{MH}}}/2})\) for a sequential implementation of MH, on a CPU for instance. Implementing the PRIS on a photonic parallel architecture also ensures that the prefactor in this order of magnitude estimate is small (and only limited by the clock rate of a single recurrent step of this high-speed network). Thus, as long as zPRIS < zMH + 2, the PRIS exhibits a clear advantage over MH implemented on a sequential architecture.
Discussion
To conclude, we have presented the PRIS, a photonic-based heuristic algorithm able to probe arbitrary Ising Gibbs distributions at various temperature levels. At low temperatures, the PRIS can find ground states of arbitrary Ising models with high probability. Our approach essentially relies on the use of matrix-to-vector product accelerators, such as photonic networks34,67, free-space optical processors28, FPGAs70, and ASICs71 (see comparison of time estimates in the Supplementary Note 5). We also perform a proof-of-concept experiment on a Xilinx Zynq UltraScale+ multiprocessor system-on-chip (MPSoC) ZCU104, an electronic board containing a parallel programmable logic unit (FPGA-Field Programmable Gate Arrays). We run the PRIS on large random spin glasses N = 100 and achieve algorithm time steps of 63 ns. This brings us closer to photonic clocks ≲1 ns, thus demonstrating that (1) the PRIS can leverage parallel architectures of various natures, electronics and photonics; (2) the potential of hybrid parallel opto-electronic implementations. Details of the FPGA implementation and numerical experiments are given in Supplementary Note 7.
Moreover, our system requires some amount of noise to perform better, which is an unusual behavior only observed in very few physical systems. For instance, neuroscientists have conjectured that this could be a feature of the brain and spiking neural networks72,73. The PRIS also performs a static transformation (and the state evolves to find the ground state). This kind of computation can rely on a fundamental property of photonics—passivity—and thus reach even higher efficiencies. Non-volatile phase-change materials integrated in silicon photonic networks could be leveraged to implement the PRIS with minimal energy costs74.
We also suggested a broader family of photonic metaheuristic algorithms which could achieve even better performance on larger graphs (see Supplementary Note 6). For instance, one could simulate annealing with photonics by reducing the system noise level (this could be achieved by leveraging quantum photodetection noise67, see discussion in Supplementary Notes 5 and 6). We believe that this class of algorithms that can be implemented on photonic networks is broader than the metaheuristics derived from MH, since one could also simulate annealing on the eigenvalue dropout level α.
The ability of the PRIS to detect phase transitions and probe critical exponents is particularly promising for the study of universality classes, as numerical simulations suffer from critical slowing down: the autocorrelation time grows exponentially at the critical point, thus making most samples too correlated to yield accurate estimates of physical observables. Our study suggests that this fundamental issue could be bypassed with the PRIS, which can generate a very large number of samples per unit time—only limited by the bandwidth of active silicon photonics components.
The experimental realization of the PRIS on a photonic platform would require additional work compared to the demonstration of deep learning with nanophotonic circuits34. The noise level can be dynamically induced by several well-known sources of noise in photonic and electronic systems52. However, attaining a low enough noise due to heterogeneities in a static architecture, and characterizing the noise level are two experimental challenges. Moreover, the PRIS requires an additional homodyne detection unit, in order to detect both the amplitude and the phase of the output signal from the linear photonic domain. Nonetheless, these experimental challenges do not impact the promising scaling properties of the PRIS, since various photonic architectures have recently been proposed34,40,45,67,75, giving a new momentum to photonic computing.
Methods
Numerical simulations
To evaluate the performance of the algorithm on several Ising problems, we simulate the execution of an ideal photonic system, performing computations without static error. The noise is artificially added after the matrix multiplication unit and follows a Gaussian distribution, as discussed above. This results in an algorithm similar to the one described in the section II of this work.
In the main text, we present the scaling performance of the PRIS as a function of the graph order. For each graph order and density, we generate 10 random samples with these properties. We then optimize the noise level (minimizing Niter, 99%) on a random sample graph and generate a total of 10 samples for each pair of graph order/density. The optimal value of ϕ is shown in Supplementary Fig. 2 in Supplementary Note 4.
For each randomly generated graph, we first compute its ground state with the online platform BiqMac57. We then make 100 measurements of the number of steps required (with a random initial state) to get to this ground state. From these 1000 runs, we define the estimate of finding the ground state of the problem with q percent probability Niter, q as the q-th quantile.
Also in the main text, we study the influence of eigenvalue dropout and of the noise level on the PRIS performance. We show that the optimal level of eigenvalue dropout is usually α < 1, and around α = 0. In some cases, it can even be α < 0 as we show in Supplementary Fig. 3 in Supplementary Note 4 where the optimal (α, ϕ) = (−0.15, 0.55) for a random cubic graph with N = 52. In addition to Fig. 3f–h from the main text showing the influence of eigenvalue dropout on a random spin glass, the influence of dropout on a random cubic graph is shown in Supplementary Fig. 4 in Supplementary Note 4. Similar observations can be made, but random cubic graphs, which show highly degenerated hamiltonian landscapes, are more robust to eigenvalue dropout. Even with α = −0.8, in the case shown in Supplementary Fig. 4 in Supplementary Note 4 the ground state remains unaffected.
Others
Further details on generalization of the theory of the PRIS dynamics, construction of the weight matrix J, numerical simulations, scaling performance of the PRIS, and comparison of the PRIS to other (meta)heuristics algorithms can be found in the Supplementary Notes 1–7.
Data availability
The data that support the plots within this paper and other findings of this study are available from the corresponding authors upon reasonable request.
Code availability
The code that supports the plots within this paper and other findings of this study are available from the corresponding authors upon reasonable request.
References
Landau, D. P. & Binder, K. A Guide to Monte Carlo Simulations in Statistical Physics (Cambridge University Press, 2009).
Hromkoviĉ, J. Algorithmics for Hard Problems: Introduction to Combinatorial Optimization, Randomization, Approximation, and Heuristics (Springer, Berlin Heidelberg, 2013).
Kardar, M., Parisi, G., Zhang, Y.-C. & Zhang, Y.-C. Dynamic scaling of growing interfaces. Phys. Rev. Lett. 56, 889–892 (1986).
Isichenko, M. B. Percolation, statistical topography, and transport in random media. Rev. Modern Phys. 64, 961–1043 (1992).
Honerkamp-Smith, A. R., Veatch, S. L. & Keller, S. L. An introduction to critical points for biophysicists; observations of compositional heterogeneity in lipid membranes. Biochim. et Biophys. Acta 1788, 53–63 (2009).
Albert, R. & Barabási, A.-L. Statistical mechanics of complex networks. Rev. Modern Phys. 74, 47–97 (2002).
Gloverand, F. & Kochenberger, G. Handbook of Metaheuristics (Springer, 2006).
Wang, Z., Marandi, A., Wen, K., Byer, R. L. & Yamamoto, Y. Coherent Ising machine based on degenerate optical parametric oscillators. Phys. Rev. A 88, 063853 (2013).
McMahon, P. L. et al. A fully programmable 100-spin coherent Ising machine with all-to-all connections. Science 354, 614–617 (2016).
Wu, K., García de Abajo, J., Soci, C., PingShum, P. & Zheludev, N. I. An optical fiber network oracle for NP-complete problems. Light Sci. Appl. 3, e147–e147 (2014).
Vázquez, M. R. et al. Optical NP problem solver on laser-written waveguide platform. Optics Express 26, 702 (2018).
Macready, W. M., Siapas, A. G. & Kauffman, S. A. Criticality and parallelism in combinatorial optimization. Science 271, 56–59 (1996).
LeCun, Y., Bengio, Y. & Hinton, G. Deep learning. Nature 521, 436–444 (2015).
Little, W. A. The existence of persistent states in the brain. Math. Biosci. 19, 101–120 (1974).
Hopfield, J. J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl Acad. Sci. USA 79, 2554–2558 (1982).
Hopfield, J. J. & Tank, D. W. “Neural” computation of decisions in optimization problems. Biol. Cybernetics 52, 141–152 (1985).
Ising, E. Beitrag zur Theorie des Ferromagnetismus. Z. Phys. 31, 253–258 (1925).
Mézard, M. & Montanari, A. Information, Physics, and Computation (Oxford University Press, 2009).
Amit, D. J., Gutfreund, H. & Sompolinsky, H. Spin-glass models of neural networks. Phys. Rev. A 32, 1007–1018 (1985).
Pelissetto, A. & Vicari, E. Critical phenomena and renormalization-group theory. Phys. Rep. 368, 549–727 (2002).
Onsager, L. Crystal statistics. I. A two-dimensional model with an order-disorder transition. Phys. Rev. 65, 117–149 (1944).
Brilliantov, N. V. Effective magnetic Hamiltonian and Ginzburg criterion for fluids. Phys. Rev. E 58, 2628–2631 (1998).
Amit, D. J. Modeling Brain Function: The World of Attractor Neural Networks (Cambridge University Press, 1989).
Ghofraniha, N. et al. Experimental evidence of replica symmetry breaking in random lasers. Nat. Commun. 6, 6058 (2015).
Halasz, M. A., Jackson, A. D., Shrock, R. E., Stephanov, M. A. & Verbaarschot, J. J. M. Phase diagram of QCD. Phys. Rev. D 58, 096007 (1998).
Barahona, F. On the computational complexity of Ising spin glass models. J. Phys. A 15, 3241–3253 (1982).
Bruck, J. & Goodman, J. W. On the power of neural networks for solving hard problems. J. Complex. 6, 129–135 (1990).
Farhat, N. H., Psaltis, D., Prata, A. & Paek, E. Optical implementation of the Hopfield model. Appl. Optics 24, 1469 (1985).
Kirkpatrick, S., Gelatt, C. D. & Vecchi, M. P. Optimization by simulated annealing. Science 220, 671–80 (1983).
Earl, D. J. & Deem, M. W. Parallel tempering: theory, applications, and new perspectives. Phys. Chem. Chemical Phys. 7, 3910 (2005).
Davis, L.D. & Mitchell, M. Handbook of Genetic Algorithms (Van Nostrand Reinhold, New York, 1991).
Glover, F. & Laguna, M. Tabu Search. in Handbook of Combinatorial Optimization, 2093–2229 (Springer, Boston, 1998).
Boros, E., Hammer, P. L. & Tavares, G. Local search heuristics for Quadratic Unconstrained Binary Optimization (QUBO). J. Heuristics 13, 99–132 (2007).
Shen, Y. et al. Deep learning with coherent nanophotonic circuits. Nat. Photon. 11, 441–446 (2017).
Silva, A. et al. Performing mathematical operations with metamaterials. Science 343, 160–163 (2014).
Koenderink, A. F., Alù, A. & Polman, A. Nanophotonics: Shrinking Light-based Technology. Science 348, 516–521.
Carolan, J. et al. Universal linear optics. Science 349, 711–716 (2015).
Reck, M., Zeilinger, A., Bernstein, H. J. & Bertani, P. Experimental realization of any discrete unitary operator. Phys. Rev. Lett. 73, 58–61 (1994).
Clements, W. R., Humphreys, P. C., Metcalf, B. J., Kolthammer, W. S. & Walsmley, I. A. Optimal design for universal multiport interferometers. Optica 3, 1460 (2016).
Lin, X. et al. All-optical machine learning using diffractive deep neural networks. Science 361, 1004–1008 (2018).
Gruber, M., Jahns, J. & Sinzinger, S. Planar-integrated optical vector-matrix multiplier. Appl. Optics 39, 5367 (2000).
Tait, A.N., Nahmias, M.A., Tian, Y., Shastri, B.J. & Prucnal, P.R. in Photonic Neuromorphic Signal Processing and Computing. 183–222 (Springer, Berlin, Heidelberg, 2014).
Tait, A. N., Nahmias, M. A., Shastri, B. J. & Prucnal, P. R. Broadcast and weight: an integrated network for scalable photonic spike processing. J. Lightwave Technol. 32, 3427–3439 (2014).
Vandoorne, K. et al. Experimental demonstration of reservoir computing on a silicon photonics chip. Nat. Commun. 5, 3541 (2014).
Saade, A. et al. Random projections through multiple optical scattering: Approximating Kernels at the speed of light. in 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 6215–6219 (IEEE, 2016).
Pierangeli, D. et al. Deep optical neural network by living tumour brain cells. Preprint at arXiv:1812.09311 (2018).
Cheng, Z., Tsang, H. K., Wang, X., Xu, K. & Xu, J.-B. In-plane optical absorption and free carrier absorption in graphene-on-silicon waveguides. IEEE J. Selected Topics Quantum Electron. 20, 43–48 (2014).
Bao, Q. et al. Monolayer graphene as a saturable absorber in a mode-locked laser. Nano Res. 4, 297–307 (2011).
Selden, A. C. Pulse transmission through a saturable absorber. Br. J. Appl. Phys. 18, 743–748 (1967).
Soljačić, M., Ibanescu, M., Johnson, S. G., Fink, Y. & Joannopoulos, J. D. Optimal bistable switching in nonlinear photonic crystals. Phys. Rev. E 66, 055601 (2002).
Schirmer, R. W. & Gaeta, A. L. Nonlinear mirror based on two-photon absorption. J. Optical Soc. Am. B 14, 2865 (1997).
Horowitz, P. & Winfield, H. The art of electronics. Chapter 8, pp 473–480 (Cambridge University Press, 2015).
Boser, B., Sackinger, E., Bromley, J., LeCun, Y. & Jackel, L. An analog neural network processor with programmable topology. IEEE J. Solid-State Circuits 26, 2017–2025 (1991).
Misra, J. & Saha, I. Artificial neural networks in hardware: a survey of two decades of progress. Neurocomputing 74, 239–255 (2010).
Vrtaric, D., Ceperic, V. & Baric, A. Area-efficient differential Gaussian circuit for dedicated hardware implementations of Gaussian function based machine learning algorithms. Neurocomputing 118, 329–333 (2013).
Williamson, I. A. D. et al. Reprogrammable electro-optic nonlinear activation functions for optical neural networks. IEEE J. Selected Topics Quant. Electronics 26, 1–12 (2019).
Rendl, F., Rinaldi, G. & Wiegele, A. Solving Max-Cut to optimality by intersecting semidefinite and polyhedral relaxations. Math. Program. 121, 307–335 (2010).
Peretto, P. Collective properties of neural networks: a statistical physics approach. Biol. Cybernetics 50, 51–62 (1984).
Lipson, M. Guiding, modulating, and emitting light on silicon-challenges and opportunities. J. Lightwave Technol. 23, 4222 (2005).
Harris, N. C. et al. Efficient, compact and low loss thermo-optic phase shifter in silicon. Optics Express 22, 10487 (2014).
Hamerly, R. et al. Experimental investigation of performance differences between coherent Ising machines and a quantum annealer. Sci. Adv. 5, eaau0823 (2019).
Miller, D. A. B. Perfect optics with imperfect components. Optica 2, 747 (2015).
Burgwal, R. et al. Using an imperfect photonic network to implement random unitaries. Optics Express 25, 28236 (2017).
Almeida, V. R., Barrios, C. A., Panepucci, R. R. & Lipson, M. All-optical control of light on a silicon chip. Nature 431, 1081–1084 (2004).
Phare, C. T., DanielLee, Y. H., Cardenas, J. & Lipson, M. Graphene electro-optic modulator with 30 GHz bandwidth. Nat. Photon. 9, 511–514 (2015).
Haffner, C. et al. Low-loss plasmon-assisted electro-optic modulator. Nature 556, 483–486 (2018).
Hamerly, R., Bernstein, L., Sludds, A., Soljačić, M. & Englund, D. Large-scale optical neural networks based on photoelectric multiplication. Phys. Rev. X 9, 021032 (2019).
Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H. & Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 21, 1087 (1953).
Hastings, W. K. Monte carlo sampling methods using Markov chains and their applications. Biometrika 57, 97–109 (1970).
Dean, J., Patterson, D. & Young, C. A new golden age in computer architecture: empowering the machine-learning revolution. IEEE Micro 38, 21–29 (2018).
Dou, Y., Vassiliadis, S., Kuzmanov, G. K. & Gaydadjiev, G. N. 64-bit floating-point FPGA matrix multiplication. in Proceedings of the 2005 ACM/SIGDA 13th international symposium on Field-programmable gate arrays-FPGA ’05, 86 (ACM Press, New York, 2005).
Knill, D. C. & Pouget, A. The Bayesian brain: the role of uncertainty in neural coding and computation. Trends Neurosci. 27, 712–719 (2004).
Maass, W. Noise as a resource for computation and learning in networks of spiking neurons. Proc. IEEE 102, 860–880 (2014).
Wang, Q. et al. Optically reconfigurable metasurfaces and photonic devices based on phase change materials. Nat. Photon. 10, 60–65 (2016).
Tait, A. N. et al. Neuromorphic photonic networks using silicon photonic weight banks. Sci. Rep. 7, 7430 (2017).
Acknowledgements
The authors would like to acknowledge Aram Harrow, Mehran Kardar, Ido Kaminer, Miriam Farber, Theodor Misiakiewicz, Manan Raval, Nicholas Rivera, Nicolas Romeo, Jamison Sloan, Can Knaut, Joe Steinmeyer, and Gim P. Hom for helpful discussions. The authors would also like to thank Angelika Wiegele (Alpen-Adria-Universität Klagenfurt) for providing solutions of the Ising models considered in this work with N ≥ 50 (computed with BiqMac57). This work was supported in part by the Semiconductor Research Corporation (SRC) under SRC contract #2016-EP-2693-B (Energy Efficient Computing with Chip-Based Photonics-MIT). This work was supported in part by the National Science Foundation (NSF) with NSF Award #CCF-1640012 (E2DCA: Type I: Collaborative Research: Energy Efficient Computing with Chip-Based Photonics). This material is based upon work supported in part by the U.S. Army Research Laboratory and the U.S. Army Research Office through the Institute for Soldier Nanotechnologies, under contract number W911NF-18-2-0048. C.Z. was financially supported by the Whiteman Fellowship. M.P. was financially supported by NSF Graduate Research Fellowship grant number 1122374.
Author information
Authors and Affiliations
Contributions
C.R.-.C., Y.S., and M.S. conceived the project. C.R.-C. and Y.S. developed the analytical models and numerical calculations, with contributions from C.Z., M.P., L.J., and T.D.; C.R.-C. and C.Z. performed the benchmarking of the PRIS on analytically solvable Ising models and large spin glasses. C.R.-C. and F.A. developed the analytics for various noise distributions. C.M., M.R.J., and C.R.-C. implemented the PRIS on FPGA. Y.S., J.D.J., D.E., and M.S. supervised the project. C.R.-C. wrote the paper with input from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare the following patent application: U.S. Patent Application No.: 16/032,737. Y.S., L.J., J.D.J., and M.S. declare individual ownership of shares in Lightelligence, a startup company developing photonic hardware for computing.
Additional information
Peer review information Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Roques-Carmes, C., Shen, Y., Zanoci, C. et al. Heuristic recurrent algorithms for photonic Ising machines. Nat Commun 11, 249 (2020). https://doi.org/10.1038/s41467-019-14096-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-14096-z
This article is cited by
-
Point convolutional neural network algorithm for Ising model ground state research based on spring vibration
Scientific Reports (2024)
-
Integrated photonic neuromorphic computing: opportunities and challenges
Nature Reviews Electrical Engineering (2024)
-
Photonic probabilistic machine learning using quantum vacuum noise
Nature Communications (2024)
-
On-demand photonic Ising machine with simplified Hamiltonian calculation by phase encoding and intensity detection
Communications Physics (2024)
-
Overdamped Ising machine with stochastic resonance phenomena in large noise condition
Nonlinear Dynamics (2024)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.