Abstract
Magnetic topological insulators (TI) provide an important material platform to explore quantum phenomena such as quantized anomalous Hall effect and Majorana modes, etc. Their successful material realization is thus essential for our fundamental understanding and potential technical revolutions. By realizing a bulk van der Waals material MnBi4Te7 with alternating septuple [MnBi2Te4] and quintuple [Bi2Te3] layers, we show that it is ferromagnetic in plane but antiferromagnetic along the c axis with an out-of-plane saturation field of ~0.22 T at 2 K. Our angle-resolved photoemission spectroscopy measurements and first-principles calculations further demonstrate that MnBi4Te7 is a Z2 antiferromagnetic TI with two types of surface states associated with the [MnBi2Te4] or [Bi2Te3] termination, respectively. Additionally, its superlattice nature may make various heterostructures of [MnBi2Te4] and [Bi2Te3] layers possible by exfoliation. Therefore, the low saturation field and the superlattice nature of MnBi4Te7 make it an ideal system to investigate rich emergent phenomena.
Similar content being viewed by others
Introduction
Magnetic topological insulators (MTIs), including Chern insulators with a Z-invariant and antiferromagnetic (AFM) topological insulators (TIs) with a Z2-invariant, provide fertile ground for the exploration of emergent quantum phenomena such as the quantum anomalous Hall (QAH) effect, Majorana modes, the topological magnetoelectric effect, the proximity effect, etc1,2. In the two-dimensional (2D) limit of ferromagnetic (FM) TIs, the QAH effect arising from chiral edge states exists under zero external magnetic fields, which has been experimentally observed in doped FM TI Cr0.15(Bi0.1Sb0.9)1.85Te3 thin films3. However, the unavoidable sample inhomogeneity in doped materials restrains the investigation of associated emergent phenomena below temperatures of hundreds of mK2. Stoichiometric MTIs are expected to have homogeneous electronic and magnetic properties, which may provide new opportunities to study the QAH effect. Recently, MnBi2Te4 was discovered to be an intrinsic AFM TI4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24. In its 2D limit, quantized Hall conductance originating from the topological protected dissipationless chiral edge states was realized in few-layer slabs15,16. However, probably because the uncompensated AFM spin configuration cannot provide enough Zeeman field to realize the band inversion in only one spin channel, to observe such a QAH effect, a high magnetic field of 12 T at 4.5 K or 6 T at 1.5 K is required to fully polarize the AFM spins into a forced FM state15.
A FM state is crucial to realize the QAH effect experimentally15; however, as we await an ideal candidate that has both TI and FM properties, an intrinsic AFM TI with low saturation fields and clean band structure where only non-trivial bands cross the Fermi level can also provide a good material platform. By this, the QAH effect may be realized with higher temperatures and reasonably low magnetic fields, which allows us to study their associated emergent phenomena at more accessible conditions. How can we realize such intrinsic AFM TIs? Recall that MnBi2Te4 crystalizing in the GeBi2Te4 structure with septuple layers (SL) of [MnBi2Te4] is an AFM material with in-plane FM and out-of-plane AFM exchange interaction. Hence, based on the SL building block, one strategy to achieve AFM with small saturation fields or even FM is to reduce the interlayer Mn-Mn exchange interaction by increasing the interlayer distance with extra spacer layers added. Structurally, SL blocks have great compatibility with [Bi2Te3] quintuple layers (QL), whose bulk form is a TI with a preserved time-reversal symmetry. As an example, GeBi4Te7 with alternating [GeBi2Te4] and [Bi2Te3] building blocks has been synthesized25. This superior compatibility provides us with flexible structural control to achieve our goal. Furthermore, not only can such superlattices manifest weak interlayer magnetic coupling, but they can also serve as natural heterostructures by exfoliation, which may enable the realization of various topological states.
The exploration of the MnTe–Bi2Te3 ternary system26 has shown that MnBi2nTe3n+1 (n = 1, 2, and 3) series exist with alternating [MnBi2Te4] and (n−1)[Bi2Te3] layers. In this work, we focus on MnBi4Te7 (n = 2) with a hexagonal superlattice crystal structure of alternate stackings of one [MnBi2Te4] SL and one [Bi2Te3] QL. Through our transport, thermodynamic, angle-resolved photoemission spectroscopy (ARPES) and density functional theory (DFT) calculations, we discovered that MnBi4Te7 is a Z2 AFM TI with an out-of-plane saturation field as low as 0.22 T at 2 K, 40 times lower than that of MnBi2Te4. Furthermore, the natural-heterostructure-like construction of MnBi4Te7 can host two distinct (001) surface states. For the [Bi2Te3] termination, clean gapped surface states are observed as has long been desired; while for the [MnBi2Te4] termination, nearly gapless surface Dirac cone is observed, similar to the case of the MnBi2Te4 compound20,21,22,23. Our finding provides a superior new material realization to explore the QAH effect, quantum spin Hall (QSH) effect and associated phenomena27.
Results
A-type antiferromagnetism in MnBi4Te7 with strong FM fluctuations and weak interlayer exchange interaction
Figure 1b shows the (00l) X-ray diffraction peaks of a piece of representative single crystal, which can be well indexed by the MnBi4Te7 crystal structure26. The Rietveld refinement of the powder X-ray diffraction pattern agrees well the MnBi4Te7 structure model26 and suggests Bi2Te3 is the only impurity inside with a molar ratio of 14% (Supplementary Fig. 1). The refined lattice parameters are a = 4.3454(5) Å, and c = 23.706(4) Å, indicating the distance between two adjacent Mn layers in MnBi4Te7 is 23.706(4) Å, much longer than the 13.8 Å of MnBi2Te4. The inset of Fig. 1b shows a picture of a MnBi4Te7 single crystal against a 1-mm scale, where the shiny cleaved ab surface can be seen.
a The view of the crystal structure of MnBi4Te7 from the [110] directions. Red arrow: Mn spins in the A-type AFM state. Blue block: edge-sharing BiTe6 octahedra; Pink block: edge-sharing MnTe6 octahedra, which are connected to the blue block via edge-sharing. J⊥ is the interlayer exchange coupling. b The (00l) X-ray diffraction peaks of the cleaved ab plane of MnBi4Te7. Inset: A piece of MnBi4Te7 against 1-mm scale. c The temperature dependent field-cooled susceptibility and inverse susceptibility taken at H = 0.1 T for H || ab and H || c. Average χ is calculated by \(\chi ^{{\mathrm{ave}}} = (2\chi ^{{\mathrm{ab}}} + \chi ^{\mathrm{c}})/3\). d and e: Full magnetic hysteresis loop of isothermal magnetization taken at various temperatures for: d H || c and e H || ab. f The temperature dependent ρxx (I || ab) and ρzz (I || c). g Transverse magnetoresistance with I || ab and H || c at various temperatures.
The magnetic properties are depicted in Fig. 1c–e. Figure 1c presents the field-cooled (FC) magnetic susceptibility data of xab (H || ab) and xc (H || c) measured at 0.1 T. The abrupt halt in the rise of xc on cooling suggests the onset of AFM ordering, similar to that seen in other vdW antiferromagnets MnBi2Te4 and CrCl3,9,28 but different from the FM one29, suggesting that long range AFM ordering takes place at 13 K. This is consistent with the specific heat measurement in Supplementary Fig. 2, where a specific heat anomaly associated with the AFM transition emerges at 13 K. As seen from Fig. 1c, fitting the inverse susceptibilities up to 80 K to the Curie-Weiss law results in Weiss temperatures of \(\theta _{\mathrm{w}}^{{\mathrm{ab}}}\) = 11.5 K, \(\theta _{\mathrm{w}}^{\mathrm{c}}\) = 12.2 K, \(\theta _{\mathrm{w}}^{{\mathrm{ave}}}\) = 11.7 K, and effective moments of \(\mu _{{\mathrm{eff}}}^{{\mathrm{ab}}}\) = 5.4μB/Mn, \(\mu _{{\mathrm{eff}}}^{\mathrm{c}}\) = 5.1μB/Mn and \(\mu _{{\mathrm{eff}}}^{{\mathrm{ave}}}\) = 5.3μB/Mn. These values indicate magnetic isotropy above TN and thus negligible single ion anisotropy in the material. Despite the fact that MnBi4Te7 is AFM below 13 K, the positive \(\theta _{\mathrm{w}}^{{\mathrm{ave}}}\) of 11.7 K suggests strong ferromagnetic (FM) exchange interactions. Recall that MnBi2Te4 has a much higher TN of 25 K and a much lower θw of 3–6 K9,18, this may indicate that the energy scales of the FM and AFM exchange interaction are much closer in MnBi4Te7. This is consistent with the fact that the extra insulating [Bi2Te3] layer reduces the interlayer exchange interaction between adjacent Mn layers as we initially designed. The AFM orders of both MnBi2Te4 and MnBi4Te7 are formed under the superexchange scenario, where the magnetic interaction between the adjacent Mn layers is mediated by the electrons of the common neighbors. Despite the long distance between the adjacent Mn layers (23.7 Å), our DFT calculation reveals an A-type AFM configuration in MnBi4Te7 with the interlayer exchange coupling about −0.15 meV/Mn, which is about one order of magnitude smaller than the counterpart of MnBi2Te4. More details are given in Supplementary Note 2.
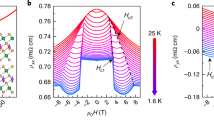
Figure 1d, e present the hysteresis loops of isothermal magnetization data for Mc(H) (H || c) and Mab(H) (H || ab), respectively. As shown in Fig. 1d, in sharp contrast to MnBi2Te4 where a spin-flop transition takes place at 3.5 T and saturates at 8 T in Mc(H)9,17,18, MnBi4Te7 undergoes a first-order spin-flip transition with hysteresis starting at a much lower field of Hf = 0.15 T. It quickly enters the forced FM state and saturates at Hc = 0.22 T. The small saturation field again indicates weaker interlayer AFM exchange interactions than in MnBi2Te4. Upon warming up to 10 K, the hysteresis area is gradually reduced to zero, but Hc remains little changed, indicating a sharp triggering of the spin-flipping between 10 K and TN. With H || ab, the saturation field is 1.0 T, indicating the c axis as the magnetic easy axis and likely Ising form. As shown in Fig. 1e, the saturation moment is 3.5μB/Mn at 7 T, which is very similar to the value of 3.6μB/Mn18 in MnBi2Te4 but smaller than the DFT calculated value of 4.6μB/Mn. The reduced Mn saturation moments in this family may arise from Mn disorders, which were observed in MnBi2Te410.
Figure 1f shows the temperature dependent in-plane (ρxx) and out-of-plane resistivity (ρzz). Above 20 K, both ρxx and ρzz decrease nearly linearly upon cooling with ρzz/ρxx~53 at 300 K (Supplementary Fig. 3), suggesting a large transport anisotropy that is consistent with its vdW nature. With further cooling, ρxx and ρzz increase slightly, which is likely caused by the enhanced scattering from spin fluctuations, a phenomenon frequently observed in low dimensional magnetic materials30,31. Then at 13 K, a sudden drop of ρxx and a sharp increase of ρzz are observed. This is in agreement with the A-type magnetic structure shown in Fig. 1a since the antiparallel alignment of Mn moments can reduce the conductivity via spin-slip scattering, while parallel alignment of the Mn moments will eliminate such scattering and thus enhance the conductivity30.
Figure 1g shows the transverse magnetoresistance (TMR), defined as MR = (ρxx(H)-ρxx(0))/ρxx(0). The main feature of the figure is the overall W shape of the TMR. The W shape becomes deeper upon warming, with the largest negative TMR of 8% appearing at 12 K, which is close to TN. Above TN, it starts to become shallower and finally transforms into an ordinary parabolic shape at 50 K. The overall W shape can be understood in the framework of FM fluctuations. Above 50 K, the lack of magnetic fluctuations leads to the parabolic TMR. Upon cooling, FM fluctuations begin to appear and become increasingly stronger with maxima around TN. As a result, the summation of the positive parabolic TMR and the negative TMR arising from the FM fluctuations under fields leads to a progressively deeper W shape of TMR upon cooling. Below TN, the FM fluctuations are reduced, but still with a strong presence, leading to the shallower W shape under field.
The spin-flip transition strongly affects the transport properties, as shown in Fig. 2. ρxx(H), ρzz(H) and ρxy(H) follow the same hysteresis as that in M(H). With H || c, the transverse magnetoresistivity of ρxx with I || ab (Fig. 2a) and the longitudinal magnetoresistivity of ρzz with I || c (Fig. 2b) slightly change between 0 T to Hf. Then up to Hc, since the system enters the forced FM state and the loss of spin scattering occurs, ρxx drops by 3.8% whereas ρzz decreases by 34%. With H || ab, up to the saturation field of 1.0 T, ρzz (Fig. 2e) decreases by 39% whereas ρxx (Fig. 2f) drops by 2.6%. Our data show that the transition from AFM to FM spin alignment along the c axis has much stronger effect on ρzz than ρxx. MnBi4Te7 displays evident anomalous Hall effect (AHE) as seen in the bottom panel of Fig. 2a. Our ρxy(H) is linear up to 9 T above 50 K (Supplementary Fig. 3), suggesting single band transport here. Using n = H/eρxy, our 50 K data corresponds to an electron carrier density of 2.84 × 1020 cm−3, similar to that of MnBi2Te417,18,32. Our Hall resistivity below 13 K can be described by \(\rho _{{\mathrm{xy}}} = R_0H + \rho _{{\mathrm{xy}}}^{\mathrm{A}}\), where the R0H is the trivial linear contribution and \(\rho _{{\mathrm{xy}}}^{\mathrm{A}}\) represents the anomalous Hall resistivity. At 2 K, \(\rho _{{\mathrm{xy}}}^{\mathrm{A}}\) is extracted to be 3.3 μΩ cm, which is half of the one in MnBi2Te417. Consequently, the anomalous Hall conductivity \(\sigma _{{\mathrm{xy}}}^{\mathrm{A}}\left( { = \rho _{{\mathrm{xy}}}^{\mathrm{A}}/\rho _{{\mathrm{xx}}}^2} \right)\) is 25.5 Ω−1 cm−1 and the anomalous Hall angle (AHA ~ \(\rho _{{\mathrm{xy}}}^{\mathrm{A}}/\rho _{{\mathrm{xx}}}\)) is ~1%.
a The field dependent magnetization M, transverse magnetoresistivity of ρxx, and Hall resistivity ρxy at 2 K with I || ab and H || c. b The longitudinal magnetoresistivity of ρzz, at 2 K with I || H || c. c The field dependent magnetization M with H || ab at 2 K. d The longitudinal magnetoresistivity of ρxx, at 2 K with I || H || ab. e The transverse magnetoresistivity of ρzz, at 2 K with I || c and H || ab.
Z2 AFM TI predicted by theoretical calculation
MnBi4Te7 crystalizes in the space group (G) P-3m1 (No. 164). By taking into account the A-type AFM, the primitive cell doubles along the c axis, rendering a magnetic space group Pc-3c1 (No. 165.96) under the Belov–Neronova–Smirnova notation33, as shown in Fig. 1a. This magnetic space group is derived from its nonmagnetic space group by adding an extra sublattice generated by an operation that combines time-reversal T with a fractional translation τ1/2. Then the full magnetic group is built as GM = G + GS, where S is a combinatory symmetry S = Tτ1/2 with τ1/2 the half translation along the c axis of the AFM primitive cell. Although the explicit T-symmetry is broken, the S-symmetry (also referred to nonsymmorphic time-reversal34) still exists in bulk MnBi4Te7. In addition, MnBi4Te7 has inversion symmetry P, while the square of the symmetry operator PS equals −1 at an arbitrary k in momentum space. Therefore, analogous to TI with T-symmetry where Kramer’s degeneracy is induced by T2 = −1, in MnBi4Te7 the existence of the PS symmetry ensures an equivalent Kramer’s degeneracy in the whole Brillion zone, and thus a Z2 topological classification.
Figure 3a shows the calculated band structure of bulk AFM MnBi4Te7 with the presence of spin–orbit coupling (SOC). The conduction band minimum is located at the Γ point, while the valence band maximum in the vicinity of Γ shows a slightly curved feature. The calculated bulk band gap is about 160 meV. The projection of band eigenstates onto the p-orbitals of Bi and Te (as indicated by the blue and red coloring) clearly indicates an inverted order between several conduction and valence bands around the Γ point, which is strong evidence of the possible nontrivial topological nature. On the other hand, the Mn-3d5 states form nearly flat bands far away from the Fermi level (Supplementary Fig. 6), indicating that the main effect of Mn is to break T-symmetry by introducing staggered Zeeman field into the low-energy Hamiltonian.
a Band structure with the projection of Bloch eigenstates onto Bi-p (blue) and Te-p (red) orbitals. SOC is included. b Evolution of Wannier charge centers (WCCs) for kz = 0, indicating a nontrivial topological invariant Z2 = 1. c Surface spectra of (010) side surface, showing a gapless Dirac cone protected by S-symmetry.
To determine the topological properties of AFM MnBi4Te7, we first apply the Fu-Kane formula35 to calculate the Z2 invariant. The topological insulator phase of AFM materials is protected by S-symmetry, under which there are only four invariant k-points forming a 2D plane in the momentum space. Thus, analogous to weak Z2 indices in nonmagnetic materials, the S-symmetry indeed protects weak Z2 topological phases in AFM materials. In AFM MnBi4Te7, four TRIM points, including Γ(0, 0, 0) and three equivalent M(π, 0, 0), need to be considered here with k τ1/2 = nπ. Due to the abovementioned band inversion at the Γ point, we find that the parities for the occupied bands at Γ are opposite to that of the other three M points, indicating a nontrivial Z2 = 1. To verify our results, we also calculate the evolution of Wannier charge centers (WCCs) using the Wilson loop approach36. As show in Fig. 3b, the largest gap function and the WCCs line cross each other an odd number of times through the evolution, confirming that MnBi4Te7 is indeed a Z2 AFM topological insulator. Compared with TIs with T-symmetry, the protection of gapless surface states in AFM TIs requires that the cleaved surface respects S-symmetry that contains translation along the c axis. Figure 3c clearly shows the gapless surface Dirac cone at the Γ point for the (010) surface, partially validating the bulk-surface correspondence of MnBi4Te7 as an AFM TI. The easy-cleaved (001) plane, where the S-symmetry is broken, are measured by ARPES and compared with our theoretical calculations, as discussed in the following.
Surface and bulk states measured by ARPES
In contrast to the recently discovered AFM TI MnBi2Te4 where only one type of surface termination exists, MnBi4Te7 can terminate on two different sub-lattice surfaces on the (001) plane, i.e., the [Bi2Te3] QL termination and the [MnBi2Te4] SL termination, resulting in different surface states. ARPES with 47 eV, linear horizontal polarized light and a small beam spot reveals two different types of E-k maps by scanning across different parts of the sample in real space, as plotted in Fig. 4d, e and Fig. 4h, i. There are several distinguishing features between the two types of surface spectra: Fig. 4h, i appear to show a gap with massive quasiparticles while Fig. 4d, e show a sharp Dirac-like crossing, possibly with a small gap. The spectra of Fig. 4d, e are reminiscent of recent high resolution ARPES spectra of the MnBi2Te4 compound20,21,22,23 that show Dirac-like spectra, and we assign these states to the [MnBi2Te4] SL termination, while we assign the other set of surface states to the [Bi2Te3] QL termination.
a–c The DFT-calculated k-E map along \({\bar{\mathrm{K}}} \leftarrow {\bar{\mathrm{\Gamma }}} \to {\bar{\mathrm{K}}}\) on the [MnBi2Te4] SL termination: a surface and bulk (S+B) spectrum, b bulk only, and c surface only. d, e The experimental ARPES spectrum on the [MnBi2Te4] SL termination obtained with 47 eV, linear horizontal light: d along Μ←Γ→Μ, e along Κ←Γ→Κ high symmetry direction. f, g The DFT-calculated k-E map along \({\bar{\mathrm{K}}} \leftarrow {\bar{\mathrm{\Gamma }}} \to {\bar{\mathrm{K}}}\) on the [Bi2Te3] QL termination: f surface and bulk (S+B) spectrum, g surface only. h, i The experimental ARPES spectrum on the [Bi2Te3] QL termination obtained with 47 eV, linear horizontal light: h along Μ←Γ→Μ, i along Κ←Γ→Κ high symmetry direction. j The EDC plot at the Γ point (blue-line cut in i) showing three main peaks corresponding to the bulk conduction band, surface conduction band, and mixed surface/bulk valence band. The green curve shows the fitted Voigt profile peaks which sum to the blue curve.
On these two terminations, symmetry operations combined with τ1/2 are not preserved. In the ideal case that the surface magnetic structure perfectly inherits the bulk property, due to the A-type out-of-plane magnetization of the Mn sublayers, the gapped surface states are described by adding an exchange term to the ordinary Rashba-type surface Hamiltonian for TI with T-symmetry, i.e., \(H_{{\mathrm{surf}}}({\mathbf{k}}) = ( {\sigma _{\mathrm{x}}k_{\mathrm{y}} - \sigma _{\mathrm{y}}k_{\mathrm{x}}} ) + m_{{\mathrm{S}}/{\mathrm{Q}}}\sigma _{\mathrm{z}}\), where σ is the Pauli matrix for spin, and mS/Q the surface exchange field that distinguishes the [MnBi2Te4] SL and [Bi2Te3] QL surfaces. Our calculation shows that the surface state terminated at the [Bi2Te3] QL has a massive Dirac cone with a surface gap around 60 meV (Fig. 4f, g), and an overall structure that agrees very well with the experimental data of Fig. 4h, i, confirming the assignment of the experimental data as arising from the [Bi2Te3] QL termination. When comparing Fig. 4i with the bulk states calculated by DFT (Fig. 4b), we can easily distinguish the surface states from the bulk states. To measure gap sizes in Fig. 4i, we extract an energy distribution curve (EDC) at the Γ point and fit it to several Voigt profiles, as shown in Fig. 4j. We find that despite the appearance of some spectral weight in the gapped region in Fig. 4i, the EDC does not show any signature of a peak in the gapped region, indicating that the surface state is gapped by ~100 meV while the bulk gap is nearly 225 meV.
The equivalent calculation on the [MnBi2Te4] SL termination is shown in Fig. 4a, c and does not agree well with the experimental data of Fig. 4d, e. While the theory shows that surface states merge with the bulk valence bands, the experiment suggests a Dirac-like structure inside the gap. By taking full account of experimental resolution functions in both momentum directions and in energy, the ARPES data are consistent with either no gap or a maximum gap size of 10 meV. More details are given in Supplementary Note 3. A similar feature, i.e., nearly gapless surface Dirac cone at the SL termination, was observed recently in MnBi2Te4 single crystals20,21,22,23, where the deviation between ARPES and DFT calculation is suggested to be due to the surface-mediated spin reconstruction at the top layers of the [MnBi2Te4] SL termination.
Figure 5a, b shows stacks of measured isoenergy surfaces for the [MnBi2Te4] SL and [Bi2Te3] QL terminations over a wide range of energies both above and below the Dirac point, while Fig. 5c shows equivalent DFT calculations for the [Bi2Te3] QL termination. The six-fold symmetric isoenergy surfaces are seen in all cases, including the hexagonal warping or snow-flake effect37. We comment that while both terminations collapse to a single resolution-limited point in k-space in the middle panels in Fig. 5a, b, this is expected whether or not there is a gapless or gapped Dirac point, due to the broad energy band width of the nearby valence and conduction bands (Fig. 4j).
Discussion
The vdW AFM TI MnBi4Te7 single crystal reported here is in fact a 1:1 superlattice composing the building blocks of AFM TI [MnBi2Te4] and T-invariant TI [Bi2Te3]. Our realization of the superlattice design has three advantages. First, as discussed above, it serves as a “buffer layer” that separates and thus effectively decreases the AFM coupling between the two neighboring [MnBi2Te4] SLs, leading to a weaker magnetic field to trigger the QAH. Second, by interlayer coupling between [Bi2Te3] QL and the adjacent [MnBi2Te4] SLs, the SOC-induced nontrivial topology of [Bi2Te3] ensures the band inversion in the 2D limit. As a result, QAH is well expected in few-layer MnBi4Te7. Third, when MnBi4Te7 is exfoliated into the 2D limit, natural heterostructures are made, which provides more 2D configurations than MnBi2Te4 or Bi2Te3 single crystal since the latter ones are only stacked by one type of building block. One can exfoliate MnBi4Te7 with designed termination and different film thickness. For example, two types of three-layer systems with distinct topological properties, [MnBi2Te4]/[Bi2Te3]/[MnBi2Te4] and [Bi2Te3]/[MnBi2Te4]/[Bi2Te3], should be easily obtained by exfoliation. Recent calculations27 show that [MnBi2Te4]/[Bi2Te3]/[MnBi2Te4] is a QAH insulator if a small magnetic field around 0.2 T is applied to stabilize the forced FM phase. On the other hand, [Bi2Te3]/[MnBi2Te4]/[Bi2Te3] is suggested to be a QSH insulator with time-reversal-symmetry breaking27 which cannot be achieved from the thin films of either MnBi2Te4 or Bi2Te3. Therefore, the 2D version exfoliated from bulk vdW TI MnBi4Te7 paves an avenue to chase the long-sought emergent properties such as QAH effect and QSH effect. As the foundation of engineering 2D heterostructures, such topological vdW materials could open up unprecedented opportunities in discovering novel fundamental physics as well as making new quantum devices38.
Methods
Sample growth and characterization
Single crystals of MnBi4Te7 were grown using self-flux11. Mn, Bi and Te elements are mixed so the molar ratio of MnTe: Bi2Te3 is 15:85. The mixtures are loaded in a 2 mL crucibles, sealed in quartz tube, heated to and held at 900 °C for 5 h. After a quick cooling to 595 °C, the mixtures are slowly cooled down to 582 °C over one to three days, where sizable single crystals are obtained after centrifuging. Although Bi2Te3 is the inevitable side product, we can differentiate MnBi4Te7 pieces by measuring their (00l) diffraction peaks. In each growth, a few sizable plate-like MnBi4Te7 single crystals with typical dimensions of 3 × 3 × 0.5 mm3 were obtained.
To confirm the phase, X-ray diffraction data were collected using a PANalytical Empyrean diffractometer (Cu Kα radiation). Samples used for powder X-ray diffraction were ground into powder inside acetone to reduce the preferred orientation. Electric resistivity and heat capacity data were measured in a Quantum Design (QD) DynaCool Physical Properties Measurement System (DynaCool PPMS). The magnetization data were measured in a QD Magnetic Properties Measurement System (QD MPMS). All magnetic data were calculated assuming the molar ratio between MnBi4Te7 and Bi2Te3 impurity is 86:14 in the sample suggested by powder X-ray refinement (Supplementary Fig. 1). Magnetic data measured for H || c were corrected with a demagnetization factor.
ARPES measurements
ARPES measurements on single crystals of MnBi4Te7 were carried out at the Advanced Light Source beamline 7.0.2 with photon energies between 40 and 55 eV with linear horizontal polarization. Single crystal samples were top-posted on the (001) surface, and cleaved in-situ in an ultra-high vacuum better than 4 × 10−11 Torr and a temperature of 15 K. ARPES spectra were taken at 12 K, slightly smaller than TN. As the cleaved terrain is expected to consist of patches of exposed [Bi2Te3] QL and [MnBi2Te4] SL, to eliminate the effect of possible QL and SL mixing on the ARPES data, we scanned a 1 mm square surface of the sample in 50 μm steps with a 50 μm beam spot and collected spectra from over 200 different spots on the sample. We looked at each spectrum, finding many regions with clear, sharp features. We also narrowed the beam spot down to 20 μm × 20 μm and scanned more finely, in 15 µm steps, in smaller regions of interest. We found that there were regions on the order of 50 × 50 μm that were spectroscopically stable, meaning the ARPES spectra were not changing from spot to spot. We then took our data with a 20 μm × 20 μm beam spot and studied the centroid of the spectroscopically stable regions, which we believe will minimize any contamination due to another surface.
First-principles calculations
We apply density functional theory (DFT) by using the projector-augmented wave (PAW) pseudopotentials39 with the exchange-correlation of Perdew–Burke–Ernzerhof (PBE) form40 and GGA + U41 approach within the Dudarev scheme42 as implemented in the Vienna ab-initio Simulation Package (VASP)43. The energy cutoff is chosen 1.5 times as large as the values recommended in relevant pseudopotentials. The U value is set to be 5 eV6. The k-points-resolved value of BZ sampling is 0.02 × 2π Å−1. The total energy minimization is performed with a tolerance of 10−6 eV. The crystal structure and atomic position are fully relaxed until the atomic force on each atom is <10−2 eV Å. SOC is included self-consistently throughout the calculations. We constructed Wannier representations44,45 by projecting the Bloch states from the DFT calculations of bulk materials onto the Mn-3d, Bi-6p, and Te-5p orbitals. The band spectra of the surface states are calculated in the tight-binding models constructed by these Wannier representations and by the iterative Green’s function technique as implemented in WannierTools package46.
Data availability
Data supporting the findings in this study are available from the corresponding authors on reasonable request.
References
Mong, R. S. K., Essin, A. M. & Moore, J. E. Antiferromagnetic topological insulators. Phys. Rev. B 81, 245209 (2010).
Tokura, Y., Yasuda, K. & Tsukazaki, A. Magnetic topological insulators. Nat. Rev. Phys. 1, 126–143 (2019).
Chang, C.-Z. et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator. Science 340, 167–170 (2013).
Hirahara, T. et al. Large-gap magnetic topological heterostructure formed by subsurface incorporation of a ferromagnetic layer. Nano Lett. 17, 3493–3500 (2017).
Hagmann, J. A. et al. Molecular beam epitaxy growth and structure of self-assembled Bi2Se3/Bi2MnSe4 multilayer heterostructures. N. J. Phys. 19, 085002 (2017).
Otrokov, M. M. et al. Highly-ordered wide bandgap materials for quantized anomalous Hall and magnetoelectric effects. 2D Mater. 4, 025082 (2017).
Gong, Y. et al. Experimental realization of an intrinsic magnetic topological insulator. Chin. Phys. Lett. 36, 076801 (2019).
Lee, D. S. et al. Crystal structure, properties and nanostructuring of a new layered chalcogenide semiconductor, Bi2MnTe4. CrystEngComm 15, 5532–5538 (2013).
Otrokov, M. M. et al. Prediction and observation of the first antiferromagnetic topological insulator. Preprint at https://arxiv.org/abs/1809.07389 (2018).
Zeugner, A. et al. Chemical aspects of the candidate antiferromagnetic topological insulator MnBi2Te4. Chem. Mater. 31, 2795–2806 (2019).
Yan, J.-Q. et al. Crystal growth and magnetic structure of MnBi2Te4. Phys. Rev. Mater. 3, 064202 (2019).
Otrokov, M. et al. Unique thickness-dependent properties of the van der Waals interlayer antiferromagnet MnBi2Te4 films. Phys. Rev. Lett. 122, 107202 (2019).
Zhang, D. et al. Topological axion states in the magnetic insulator MnBi2Te4 with the quantized magnetoelectric effect. Phys. Rev. Lett. 122, 206401 (2019).
Li, J. et al. Intrinsic magnetic topological insulators in van der Waals layered MnBi2Te4 -family materials. Sci. Adv. 5, eaaw5685 (2019).
Deng, Y. et al. Magnetic-field-induced quantized anomalous Hall effect in intrinsic magnetic topological insulator MnBi2Te4. Preprint at https://arxiv.org/abs/1904.11468 (2019).
Liu, C. et al. Quantum phase transition from axion insulator to Chern insulator in MnBi2Te4. Preprint at https://arxiv.org/abs/1905.00715 (2019).
Lee, S. H. et al. Spin scattering and noncollinear spin structure-induced intrinsic anomalous Hall effect in antiferromagnetic topological insulator MnBi2Te4. Phys. Rev. Res. 1, 012011 (2019).
Yan, J. -Q. et al. Evolution of structural, magnetic and transport properties in MnBi2-xSbxTe4. Phys. Rev. B 100, 104409 (2019).
Chen, B. et al. Intrinsic magnetic topological insulator phases in the Sb doped MnBi2Te4 bulks and thin flakes. Nat. Commun. 10, 1–8 (2019).
Hao, Y.-J. et al. Gapless surface Dirac cone in antiferromagnetic topological insulator MnBi2Te4. Phys. Rev. X 9, 041038 (2019).
Chen, Y. et al. Topological electronic structure and its temperature evolution in antiferromagnetic topological insulator MnBi2Te4. Phys. Rev. X 9, 041040 (2019).
Swatek, P. et al. Gapless Dirac surface states in the antiferromagnetic topological insulator MnBi2Te4. Preprint at https://arxiv.org/abs/1907.09596 (2019).
Li, H. et al. Dirac surface states in intrinsic magnetic topological insulators EuSn2As2 and MnBi2nTe3n+1. Phys. Rev. X 9, 041039 (2019).
Vidal, R. et al. Surface states and Rashba-type spin polarization in antiferromagnetic MnBi2Te4 (0001). Phys. Rev. B 100, 121104 (2019).
Muff, S. et al. Separating the bulk and surface n-to p-type transition in the topological insulator GeBi4-xSbxTe7. Phys. Rev. B 88, 035407 (2013).
Aliev, Z. S. et al. Novel ternary layered manganese bismuth tellurides of the MnTe-Bi2Te3 system: synthesis and crystal structure. J. Alloy. Compd. 789, 443–450 (2019).
Sun, H. et al. Rational design principles of the quantum anomalous hall effect in superlatticelike magnetic topological insulators. Phys. Rev. Lett. 123, 096401 (2019).
McGuire, M. A. et al. Magnetic behavior and spin-lattice coupling in cleavable van der Waals layered CrCl3 crystals. Phys. Rev. Materials 1, 014001 (2017).
Liu, Y. et al. Anomalous Hall effect in the van der Waals bonded ferromagnet Fe3-xGeTe2. Phys. Rev. B 97, 165415 (2018).
Masuda, H. et al. Quantum Hall effect in a bulk antiferromagnet EuMnBi2 with magnetically confined two-dimensional Dirac fermions. Sci. Adv. 2, e1501117 (2016).
Shen, B. et al. Structural distortion and incommensurate noncollinear magnetism in EuAg4As2. Preprint at https://arxiv.org/abs/1809.07317 (2018).
Cui, J. et al. Transport properties of thin flakes of the antiferromagnetic topological insulator MnBi2Te4, Phys. Rev. B 99, 155125 (2019).
Belov, N., Neronova, N. & Smirnova, T. Shubnikov groups. Kristallografiya 2, 315–325 (1957).
Hua, G. et al. Dirac semimetal in type-IV magnetic space groups. Phys. Rev. B 98, 201116 (2018).
Fu, L. & Kane, C. L. Topological insulators with inversion symmetry. Phys. Rev. B 76, 045302 (2007).
Soluyanov, A. A. & Vanderbilt, D. Computing topological invariants without inversion symmetry. Phys. Rev. B 83, 235401 (2011).
Fu, L. Hexagonal warping effects in the surface states of the topological insulator Bi2Te3. Phys. Rev. Lett. 103, 266801 (2009).
Geim, A. K. & Grigorieva, I. V. Van der Waals heterostructures. Nature 499, 419 (2013).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Anisimov, V. I., Zaanen, J. & Andersen, O. K. Band theory and Mott insulators: Hubbard U instead of Stoner I. Phys. Rev. B 44, 943 (1991).
Dudarev, S., Botton, G., Savrasov, S., Humphreys, C. & Sutton, A. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+ U study. Phys. Rev. B 57, 1505 (1998).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Mostofi, A. A. et al. An updated version ofwannier90: a tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 185, 2309–2310 (2014).
Marzari, N. & Vanderbilt, D. Maximally localized generalized Wannier functions for composite energy bands. Phys. Rev. B 56, 12847 (1997).
Wu, Q., Zhang, S., Song, H.-F., Troyer, M. & Soluyanov, A. A. WannierTools: an open-source software package for novel topological materials. Comput. Phys. Commun. 224, 405–416 (2018).
Acknowledgements
We thank Paul C. Canfield, Quansheng Wu, Suyang Xu, Filip Ronning and Chris Regan for helpful discussions, and Chris Jozwiak and Roland Koch at the Advanced Light Source for experimental help. Work at UCLA and UCSC was supported by the U.S. Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences (BES) under award number DE-SC0011978 and DE-SC0017862, respectively. Work at CU Boulder was supported by the U.S. National Science Foundation-Division of Material Research under NSF-DMR-1534734. Work at SUSTech was supported by the NSFC under Grant No. 11874195, the Guangdong Provincial Key Laboratory of Computational Science and Material Design under Grant No. 2019B030301001, “Climbing Program” Special Funds under Grant No. pdjhb0448 and Center for Computational Science and Engineering of SUSTech. H.C. acknowledges the support from U.S. DOE BES Early Career Award KC0402010 under contract no. DE-AC05- 00OR22725. This research used resources of the Advanced Light Source, which is a DOE Office of Science User Facility under contract no. DE-AC02-05CH11231.
Author information
Authors and Affiliations
Contributions
N.N. conceived the idea and organized the research. N.N., Q.L., and D.D. supervised the research. C.H., J.L., E.E., H.B., and N.N. grew the bulk single crystal and carried out X-ray and transport measurements. A.R. and C.H. performed magnetic measurements. K.G., X.Z., P.H., D.N., and D.D. carried out the ARPES measurements and data analysis. Q.L., P.L., H.S., and Y.L. performed the first-principles calculations. H.C., L.D. and C.H. carried out structure determination. N.N., Q.L., D.D., and K.G. prepared the manuscript with contributions from all authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Guang Bian and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hu, C., Gordon, K.N., Liu, P. et al. A van der Waals antiferromagnetic topological insulator with weak interlayer magnetic coupling. Nat Commun 11, 97 (2020). https://doi.org/10.1038/s41467-019-13814-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-13814-x
This article is cited by
-
Intrinsic exchange biased anomalous Hall effect in an uncompensated antiferromagnet MnBi2Te4
Nature Communications (2024)
-
Evidence of striped electronic phases in a structurally modulated superlattice
Nature (2024)
-
High Chern number van der Waals magnetic topological multilayers MnBi2Te4/hBN
npj 2D Materials and Applications (2023)
-
Quantum-metric-induced nonlinear transport in a topological antiferromagnet
Nature (2023)
-
Manipulating exchange bias in 2D magnetic heterojunction for high-performance robust memory applications
Nature Communications (2023)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.