Abstract
The relaxation of photoexcited nanosystems is a fundamental process of light–matter interaction. Depending on the couplings of the internal degrees of freedom, relaxation can be ultrafast, converting electronic energy in a few fs, or slow, if the energy is trapped in a metastable state that decouples from its environment. Here, we study helium nanodroplets excited resonantly by femtosecond extreme-ultraviolet (XUV) pulses from a seeded free-electron laser. Despite their superfluid nature, we find that helium nanodroplets in the lowest electronically excited states undergo ultrafast relaxation. By comparing experimental photoelectron spectra with time-dependent density functional theory simulations, we unravel the full relaxation pathway: Following an ultrafast interband transition, a void nanometer-sized bubble forms around the localized excitation (He\({}^{* }\)) within 1 ps. Subsequently, the bubble collapses and releases metastable He\({}^{* }\) at the droplet surface. This study highlights the high level of detail achievable in probing the photodynamics of nanosystems using tunable XUV pulses.
Similar content being viewed by others
Introduction
Understanding the ultrafast response of condensed phase nanosystems to photoexcitation is essential for many research areas, including atmospheric science1, radiation damage in biological matter2,3, light-harvesting mechanisms in natural and artificial complexes4,5, and photocatalysis6. However, the complex couplings of electronic and translational degrees of freedom often present major theoretical challenges7. In addition, the complexity of heterogeneous solid or liquid systems, as well as difficulties in preparing well-controlled samples and performing reproducible measurements, make it difficult to unravel the elementary steps in the relaxation process. In this respect, superfluid He nanodroplets are ideal model systems for studying the photodynamics in weakly-bound nanostructures, both experimentally and theoretically; He atoms have a simple electronic structure, interatomic binding is extremely weak, and the structure of He nanodroplets is homogeneous and nearly size-independent due to their superfluid nature8,9. Exploring transient phenomena associated with superfluidity is a particularly intriguing aspect of He nanodroplet spectroscopy10,11. By probing the dynamics of laser-excited molecular systems coupled to He droplets, one gains insight into the fluid dynamics, dissipation, and transport properties of a superfluid on the molecular scale12,13,14.
The properties of pure He droplets can be directly studied using electron bombardment or XUV radiation. From previous theoretical15,16 and static photoexcitation studies17,18,19,20,21,22,23, the following dynamical response to resonant absorption of an XUV photon has been inferred: The electronic excitation created in the droplet localizes on an atomic or molecular center He\({}_{n}^{* }\), \(n=1,2,\ldots\!\), within a few 100 fs24. Subsequently, a void cavity or bubble forms around He\({}_{n}^{* }\) due to Pauli repulsion between the excited electron and the surrounding ground state He atoms21, which expands up to a radius of 6.4 Å25 within about 350 fs26. Depending on how close to the droplet surface the excitation localizes, the bubble either collapses before fully forming thereby ejecting He\({}^{* }\) or He\({}_{2}^{* }\) out of the droplet, or remains in a metastable state inside the droplet21. Using laser-based high-harmonic light sources27, various ultrafast processes initiated by exciting high-lying states in the autoionization continuum of He nanodroplets have been revealed, including the emission of slow electrons22, the ejection of Rydberg atoms and excimers28,29, and ultrafast interband relaxation23. However, the dynamics of low-lying states below the autoionization threshold and in particular the bubble formation have not been probed for pure He nanodroplets, neither at the strongest absorption band associated with the atomic He\({}^{* }\) \(1s2p\) \({}^{1}P\) state (photon energy around \(h\nu =21.6\,\) eV18), nor at the lowest optically accessible \(1s2s\) \({}^{1}S\) state (\(h\nu =21.0\,\) eV18).
In the present study, we excite these lowest excited states to directly probe the relaxation dynamics of neutral pure He nanodroplets. The experiment is carried out using tunable XUV pulses generated by the seeded free-electron laser (FEL) FERMI30. The comparison of time-resolved photoelectron spectra (PES) with time-dependent density functional theory (TD-DFT) calculations reveals an ultrafast three-step relaxation process. Despite the extremely weak binding of the He atoms in the droplets and the superfluid nature thereof, energy dissipation is very efficient even for the lowest excited states; more than 1 eV of electron energy is dissipated in <1 ps due to the coupling of electronic and nanofluid nuclear degrees of freedom.
Results
Resonant two-photon ionization scheme
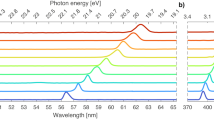
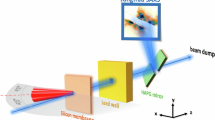
The pump-probe scheme is sketched in Fig. 1. The gray shaded area in Fig. 1a shows the absorption spectrum of He nanodroplets taken from Joppien et al.18; for reference, the He\({}^{* }\) atomic levels are given on the right-hand side of Fig. 1a. The massive broadening and shifting of the excited state is due to a repulsive interaction between the \(2p\) Rydberg electron and the \(1s\) core electrons at large interatomic distances31. The straight vertical arrows illustrate the pump (red) and probe (blue) steps, realized by one XUV pulse and one time-delayed UV pulse. The electron kinetic energy, \({T}_{{\rm{e}}}\), measured by means of electron velocity-map imaging (VMI)30,32, is represented as a black double-sided arrow. The most likely relaxation pathway for \(1s2p\) \({}^{1}P\)-excited He nanodroplets is indicated by the dotted curved arrows. The inset shows a schematic view of a He nanodroplet exposed to a pair of laser pulses, containing a localized excitation marked by (\(*\)).
a The filled area represents the absorption spectrum of He nanodroplets taken from Joppien et al.18. He atomic levels are shown on the right-hand side. b Potential curves of the singlet-excited He\({}_{2}^{* }\) dimer correlating to the \(1s2s\) \({}^{1}S\) and \(1s2p\) \({}^{1}P\) atomic states were computed as detailed in the Methods section. The vertical straight arrows indicate the pump and probe laser pulses, the dotted curved arrows indicate the droplet relaxation pathway. The double-sided arrow in (a) illustrates the electron kinetic energy \({T}_{{\rm{e}}}\).
Time-resolved photoelectron spectra
Examples of time-dependent PES measured by exciting He droplets to the \(1s2s\) \({}^{1}S\) state (\(h\nu =21.0\) eV) and on the blue edge of the \(1s2p\) \({}^{1}P\) band (\(h\nu =22.2\) eV) are shown in Fig. 2a and b, respectively. The horizontal dashed lines indicate the electron energy one would expect for direct 1+1′ ionization of He by absorption of one pump and one probe photon,
where \({E}_{{\rm{i}}}=24.6\) eV is the ionization energy of He and \(h\nu ^{\prime} =4.8\,\) eV is held fixed. The panels on the right-hand sides show the PES at selected pump-probe delays. For positive delays (XUV first, UV second), the PES mainly consist of two spectral components in both cases a) and b). A broad feature labeled ‘D’ dominates the PES at short delays \(t\ \lesssim \ 0.5\) ps, whereas a sharp peak ‘A’ becomes prominent at longer delays. The PES for each value of the pump-probe delay were fit with the sum of three Gaussian functions. The fit parameters were mildly constrained to ensure the convergence of two Gaussians to peaks ‘A’ and ‘D’, whereas the third Gaussian approximates the electron background signal. Fig. 2c and d show the amplitudes and center positions of these two peaks obtained from the fits of the PES measured at various \(h\nu\). Peak D (solid lines in Fig. 2c) rises within the first 0.5 ps delay time and then slowly decreases, accompanied by a rapid increase of peak A (dashed lines). The opposite trends of these two components indicates a redistribution of population from D to A within 0.5–2.5 ps.
The He nanodroplets contained on average \(\overline{N}=5\ \times \ 1{0}^{5}\) He atoms and were excited to their 1s2s state at the pump photon energy \(h\nu =21.0\) eV (a) and their 1s2p state at \(h\nu =22.2\) eV (b). The probe photon energy is \(h\nu ^{\prime} =4.8\) eV. The horizontal dashed lines indicate the electron energy corresponding to direct two-photon ionization of He. The panels on the right-hand sides show the electron spectra recorded at various fixed pump-probe delays. The bottom panels show the results of fitting the spectra with multiple peaks (area in (c), position in (d)).
The energy of peak D (Fig. 2d) rapidly decreases within \(t\ <\ 1\) ps, followed by a slow decrease beyond 2.5 ps. Peak A slightly shifts from 0.9 to 0.8 eV within \(t\ <\ 1\) ps and remains constant thereafter. Its linewidth is limited by the resolution of the spectrometer. The final peak position matches the electron energy expected for ionization of a He atom in the lowest excited singlet state,
where E(\(1s2s\) \({}^{1}S\)) = 20.6 eV. Therefore, we associate peak A with the ionization of a \(1s2s\) \({}^{1}S\)-excited He\({}^{* }\) which is either weakly bound to the droplet surface or ejected into vacuum. This interpretation is supported by PES measured for various He droplet sizes presented in the Supplementary Fig. 1 and discussed in Supplementary Note 1. While for larger droplets peak A appears slightly later and remains less intense in proportion to peak D, its position converges to the same final value (\(0.8\,\) eV). Consequently, peak D is assigned to a He\({}^{* }\) located further inside the He droplet such that it is energetically shifted up. This assignment is backed by the evolution of the He\({}^{+}\) and He\({}_{2}^{+}\) ion yields as a function of delay, see Supplementary Fig. 2. When exciting the He droplet to its \(1s2s\) \({}^{1}S\) state at \(h\nu =21.0\) eV (Fig. 2a), the initial position of peak D (\(1.2\,\) eV) matches the electron energy one expects based on the droplet absorption spectrum (Fig. 1a),
At higher \(h\nu\), where mainly the \(1s2s\) \({}^{1}P\) droplet state is excited (Fig. 2b), feature D corresponds to a superposition of \({}^{1}S\) and \({}^{1}P\) states which relaxes into the \({}^{1}S\) droplet state faster than the cross correlation of the two laser pulses (\(250\,\) fs FWHM) and thus cannot be fully resolved. Note that not all droplets evolve into the atomic \({}^{1}S\) state (peak A); in the final stage of relaxation, the state that converges to an energy 0.1–0.2 eV above the \({}^{1}S\) atomic value (feature D) and the atomic \({}^{1}S\) state are nearly equally populated.
Potential energy curves of the He\({}_{2}^{* }\) excimer
How can the extremely weakly bound, ultracold van der Waals He clusters induce ultrafast energy relaxation by up to 1.6 eV within 1 ps? To answer this question, we first consider the potential curves of the He\({}_{2}^{* }\) excimer correlated to the atomic \(1s2s\) \({}^{1}S\) and \(1s2p\) \({}^{1}P\) levels as the simplest model system for the excited He droplet, shown in Fig. 1b. The blue-shifted absorption profiles with respect to the atomic levels can be related to the steep upwards bending of the optically active A, D, and F states in the range of most probable interatomic distances (3.6 Å), indicated by the gray oval line. When exciting He in a nanodroplet, these diatomic states are expected to be strongly coupled to form a band-like structure. Following ultrafast intraband relaxation to the lowest state B of this manifold, the system further relaxes by internal conversion via the crossing of potential curves B and C at short interatomic distance, as illustrated by the dotted arrows. Subsequently, the local environment rearranges to accommodate the newly formed \(1s2s\) \({}^{1}S\) He\({}^{* }\) atom. On the longer timescale of the fluorescence lifetime, some of the He\({}^{* }\) stabilize by forming He\({}_{2}^{* }\) excimers19,20,33.
Time-dependent density functional theory calculations
To simulate this process for He droplets in three dimensions, we carried out TD-DFT calculations for a He\({}^{* }\) excitation in the \(1s2s\) \({}^{1}S\) state, as outlined in the Methods section. Note that this transition is forbidden in free atoms. Therefore it preferentially takes place in the surface region of the droplets where the radially-varying He density breaks the symmetry of the free He atom and makes the transition partly allowed (see Methods).
As seen in Fig. 3, the system evolves differently depending on the initial position d of He\({}^{* }\) with respect to the droplet surface. The radius of the droplet containing \(N=1000\) He atoms is \({R}_{D}\ =\ 2.2\) nm. Shown are snapshots of the He density distribution at fixed times t after He\({}^{* }\) excitation. Such snapshots for intermediate values of d are shown in Supplementary Fig. 3 and discussed in Supplementary Note 2. When He\({}^{* }\) is initially placed at the surface of the droplet (\(d=0\), left column), the surrounding region is locally compressed and forms a spherical dimple, while He\({}^{* }\) flies off within \(t\ \lesssim \ 1\) ps. This scenario resembles the dynamics of excited alkali metal atoms which initially reside in dimple states at the droplet surface34,35,36,37. When He\({}^{* }\) is initially placed deeper in the bulk of the droplet (\(d=0.7\,\) nm, right column), first a bubble forms around He\({}^{* }\), which then bursts at \(t\approx 4\) ps, thereby allowing He\({}^{* }\) to escape out of the droplet. This scenario has also been studied theoretically and experimentally for photoexcited silver atoms38 and indium atoms embedded in He nanodroplets14.
Besides visualizing the dynamics ensuing excitation of the droplet, the TD-DFT model allows us to simulate the time-dependent PES, see Methods section. Figure 4a shows the resulting electron kinetic energies \({T}_{{\rm{e}}}^{{\rm{sim}}}\) for different values of d. In the case He\({}^{* }\) is initialized close to the droplet surface (\(d=0\) and \(0.2\) nm), \({T}_{{\rm{e}}}^{{\rm{sim}}}\) rapidly drops from about 1.4 eV at \(t=0\) to the final value of \(0.8\,\) eV within \(t=250\)–500 fs due to prompt desorption of He\({}^{* }\). When He\({}^{* }\) is placed deeper inside the droplet (\(d=0.4\), \(0.7\), and \(1.2\) nm), an initial fast drop of \({T}_{{\rm{e}}}^{{\rm{sim}}}\) from 1.6 to 0.9\(-1.1\) eV is followed by a slow decrease to 0.9 eV at \(t=2\) ps.
Simulated (a) and measured (b) electron energies. The He droplets were excited to the \(1s2s\) state at \(h\nu =21.0\) eV. The dashed line in (b) is the average of the simulated curves in (a) for different initial positions of the He\({}^{* }\) excitation. The geometric weight of each curve as well as the experimental pulse cross correlation function are taken into account.
The average of all curves in Fig. 4a, weighted by the geometric factor \({({R}_{D}-d)}^{2}\), is shown in Fig. 4b as a dashed line. It nicely follows the experimental curve for the droplet feature D (red solid line in Fig. 4b) up to about 2 ps delay and eventually converges to the final value of the atomic peak A. In particular, the fast drop between 0 and 1 ps coincides with the drop of peak D energy in the experimental PES (Fig. 2d) and with the appearance of peak A as the bubble forms around He\({}^{* }\). Thereafter it slowly decreases from 0.9 to 0.8 eV as the bubble migrates to the droplet surface and eventually releases an unperturbed He\({}^{* }\). Note that the simulated curve for \(d=0.7\) nm shows an oscillatory behavior between \(t=0.4\) and 2 ps. We attribute this nearly periodic modulation of \({T}_{{\rm{e}}}\) to the oscillation of the He bubble around He\({}^{* }\). He bubble oscillations around impurity atoms (Ag and In) have also been discussed14,38.
Discussion
From the comparison of the experimental and theoretical results, we can now map out the full picture of the relaxation dynamics of excited He nanodroplets: Initiated by the excitation of the \(1s2p\) \({}^{1}P\) nanodroplet state, which is likely delocalized over several He atoms24, ultrafast interband relaxation to the \(1s2s\) \({}^{1}S\) droplet state occurs within \({<}250\,\) fs induced by curve crossings of the He\({}_{2}^{* }\) potentials (step 1). This is in line with earlier photoluminescence studies which showed that the \(1s2p\) \({}^{1}P\) droplet state mainly decays by XUV-photon emission of He\({}_{2}^{* }\) in its A state correlating to the \(1s2s\) \({}^{1}S\) state of He\({}^{* }\)19.
Further relaxation proceeds within the \(1s2s\) \({}^{1}S\) droplet band by localization of the excitation due to the local opening of a void bubble around an excited He\({}^{* }\) atom (step 2). The relaxation time associated with this step (0.5 ps) is in good agreement with the established model of bubble formation around an electron, if we assume a final bubble radius of 6.4 Å25,26. It is nearly independent of the location of He\({}^{* }\) within the droplet and of the droplet size \(\overline{N}\). This explains the weak variation of the experimental pump-probe PES when changing \(\overline{N}\).
Subsequently, the bubble migrates to the droplet surface and bursts to release a free He\({}^{* }\) (step 3). The fact that in our experiment, both free and bubble-bound He\({}^{* }\) are measured at \(t=2.5\) ps shows that the migration of the bubble to the surface is a slow process that strongly depends on the initial He\({}^{* }\) location and therefore on \(\overline{N}\). A recent study of the excited state dynamics of xenon clusters revealed electronic relaxation and the emission of free xenon atoms39. Thus, our findings appear not to be specific to He nanodroplets but of rather general relevance for weakly bound condensed phase systems. Eventually, the He\({}^{*}\) atoms that remain attached to the droplet surface further relax by forming He\({}_{2}^{* }\) as seen in time-independent measurements19,20. The latter radiatively decay to the ground state after undergoing vibrational relaxation and partly detaching from the droplet33.
The presented measurements show that it is now possible to follow the relaxation dynamics of free nanodroplets in great detail using ultrashort tunable XUV pulses. Diffractive imaging of He droplets and embedded impurities has recently attracted considerable attention40,41,42. However, direct time resolved imaging of the bubble dynamics is at the present stage challenging, given the small size of the bubbles and the expected low contrast. Further development of ultra-bright X-ray light sources is needed to enter the regime of atomic resolution in single clusters and will then deliver a wealth of detailed information. The present technique could be used for probing the photodynamics of more complex natural or synthetic nanosystems in various regimes of excitation of the valence shell43 and even inner shells44.
Methods
The experiments described were performed at the low density matter (LDM) end station of the seeded free-electron laser FERMI30.
He droplet generation
The He nanodroplets were formed by expanding He gas from a high pressure reservoir (50 bar) through a pulsed, cryogenically cooled Even-Lavie nozzle at a pulse repetition rate of \(10\,\) Hz45. The mean size of the He droplets formed in this way was controlled by changing the temperature of the nozzle in the range of 5–28 K.
Light sources
Linearly polarized XUV pulses in the photon energy range 21.0–22.2 eV were provided by the FERMI free electron laser set to the 5th harmonic of the seed laser wavelength46. The XUV pulses generated in this way have a bandwidth \({<}0.1\) eV and a temporal duration of about 100 fs FWHM. A Kirkpatrick-Baez mirror system was used to focus the FEL light to a spot size of 0.5 mm in the interaction region of the spectrometer. To minimize non-linear effects due to absorption of more than one photon per droplet the XUV pulses were strongly attenuated by a combination of a N\({}_{2}\) filled gas cell and an aluminum filter. The pulse energy in the interaction region was estimated to be 6 μJ.
The UV probe pulses (170 fs duration, 7 μJ pulse energy) were generated by frequency tripling part of the 775 nm Ti:Sa laser used to generate the seed light for the FEL. The UV pulses were focused to the same focal spot size as the XUV beam and superimposed with the XUV pulses in a quasi collinear geometry via reflection from a holey mirror. The temporal cross-correlation function was measured using two-photon ionization of He atoms via the He \(1s5p\) \({}^{1}P\) state. A Gaussian fit yields a FWHM of 250 fs.
Electron detection, data acquisition, and analysis
PES from the He nanodroplets are recorded using a VMI spectrometer, in which electrons are accelerated by electrostatic optics imaged onto a position sensitive detector consisting of a 75 mm microchannel plate and phosphor screen assembly. For each step of the pump-probe delay of 50 fs delay, VMI spectrometer images from 2000 shots were saved. A background subtraction procedure was implemented in which the bunches of He nanodroplets were periodically desynchronized from the FEL pulses so that spurious signals such as scattered light could be subtracted. The VMI spectrometer images for each delay were then summed and subsequently inverted using the pBasex routine to extract the photoelectron kinetic energy and angular distributions47.
Ab initio calculations of He–He\({}^{* }\) and He–He\({}^{+}\) potentials and transition dipole moment
The He\({}^{* }\)–He interaction potentials corresponding to 2s and 2p He atomic asymptotes were obtained at the CC3-EOM level48,49 by using the Psi4 code50. The basis set was taken from ref. 51. All the calculated potentials were corrected for basis set superposition errors by the counterpoise method of Boys and Bernardi52.
The transition dipole \({\overrightarrow{\mu }}_{2s}\) as a function of He\({}^{* }\)(2s)–He(1s) distance was evaluated at the multi-reference configuration interaction (MRCI) level using the Molpro code53,54. The active space consisted of the molecular states originating from 1s and 2s atomic states. These calculations employed the basis set given in refs. 55,56. The transition dipole induced by the inhomogeneous He density in the droplet surface region is calculated as the vector sum of dipole moments of a single He\({}^{* }\)–He pair weighted by the radial He density distribution,
We find the transition dipole moment to be peaked nearly at the He droplet radius \({r}_{0}{N}^{1/3}\), \({r}_{0}=2.22\) Å, where it takes the value \(| {\overrightarrow{\mu }}_{2s}^{{\rm{drop}}}| =0.17\) Debye.
Time-dependent density function theory
The dynamics of the excited He droplet was simulated using time-dependent density functional theory (TD-DFT) for droplets consisting of 1000 He atoms15,16, to which the dynamics of the He\({}^{* }\) atom is self-consistently coupled.
Due to the light mass of the He\({}^{* }\) “impurity”, its dynamics is followed by solving the Schrödinger equation for it, where the potential term is given by the He\({}^{* }\)-droplet interaction. The expected high velocity of the impurity makes it advantageous to use the test-particles method for solving the Schrödinger equation16,34. We obtain the excess energy transfered to the photoelectron as \({T}_{{\rm{e}}}(t)=h\nu ^{\prime} -[{U}^{+}(t)-{U}^{* }(t)]\). Here, the interaction energies of He\({}^{* }\) with its local environment in the He droplet in the (t-dependent) initial state, \({U}^{* }(t)\) is computed as
where \({\Phi }^{2}\) is the probability density of He\({}^{* }\), \(\rho\) is the ground-state He density, and \({{\mathcal{V}}}_{{\rm{He}}-{{\rm{He}}}^{* }}\) is the He–He\({}^{* }\) interaction pair potential, respectively. The interaction energy of He\({}^{+}\) with the droplet in the final state, \({U}^{+}(t)\), is obtained in the same way using the He–He\({}^{+}\) interaction potential, \({{\mathcal{V}}}_{{\rm{He}}-{{\rm{He}}}^{+}}\).
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
Code availability
The results of the simulation were obtained by adapting to the test particles approach the \({}^{4}\)He-DFT BCN-TLS computing package which is freely available at M. Pi, F. Ancilotto, F. Coppens, N. Halberstadt, A. Hernando, A. Leal, D. Mateo, R. Mayol and M. Barranco, \({}^{4}\)He-DFT BCN-TLS: A Computer Package for Simulating Structural Properties and Dynamics of Doped Liquid Helium-4 Systems, https://github.com/bcntls2016/.
References
George, C., Ammann, M., D’Anna, B., Donaldson, D. J. & Nizkorodov, S. A. Heterogeneous photochemistry in the atmosphere. Chem. Rev. 115, 4218–4258 (2015).
Barbatti, M. et al. Relaxation mechanisms of UV-photoexcited DNA and RNA nucleobases. PNAS 107, 21453–21458 (2010).
Gokhberg, K., Kolorenč, P., Kuleff, A. I. & Cederbaum, L. S. Site-and energy-selective slow-electron production through intermolecular Coulombic decay. Nature 505, 661–663 (2014).
Collini, E. et al. Coherently wired light-harvesting in photosynthetic marine algea at ambient temperature. Nature 463, 644–647 (2010).
Son, H.-J. et al. Light-harvesting and ultrafast migration in porphyrin-based metal-organic frameworks. J. Am. Chem. Soc. 135, 862–869 (2013).
Schneider, J., Bahnemann, D., Ye, J., Puma, G. L. & Dionysiou, D. D. Photocatalysis: Fundamentals and Perspectives. (The Royal Society of Chemistry, Cambridge, 2016).
Masson, A. et al. Coupled electronic and structural relaxation pathways in the postexcitation dynamics of Rydberg states of BaAr\({}_{N}\) clusters. Phys. Rev. Lett. 113, 123005 (2014).
Toennies, J. P. & Vilesov, A. F. Superfluid helium droplets: a uniquely cold nanomatrix for molecules and molecular complexes. Angew. Chem. Int. Ed. 43, 2622–2648 (2004).
Stienkemeier, F. & Lehmann, K. Spectroscopy and dynamics in helium nanodroplets. J. Phys. B 39, R127 (2006).
Benderskii, A. V., Eloranta, J., Zadoyan, R. & Apkarian, V. A. A direct interrogation of superfluidity on molecular scales. J. Chem. Phys. 117, 1201 (2002).
Grüner, B. et al. Vibrational relaxation and decoherence of Rb\({}_{2}\) attached to helium nanodroplets. Phys. Chem. Chem. Phys. 13, 6816–6826 (2011).
Brauer, N. B. et al. Critical Landau velocity in helium nanodroplets. Phys. Rev. Lett. 111, 153002 (2013).
Shepperson, B. et al. Laser-induced rotation of iodine molecules in helium nanodroplets: Revivals and breaking free. Phys. Rev. Lett. 118, 203203 (2017).
Thaler, B. et al. Femtosecond photoexcitation dynamics inside a quantum solvent. Nature Comm. 9, 4006 (2018).
Barranco, M. et al. Helium nanodroplets: an overview. J. Low Temp. Phys. 142, 1–81 (2006).
Ancilotto, F. et al. Density functional theory of doped superfluid liquid helium and nanodroplets. Int. Rev. Phys. Chem. 36, 621–707 (2017).
Fröchtenicht, R. et al. The photoionization of large pure and doped helium droplets. J. Chem. Phys. 104, 2548–2556 (1996).
Joppien, M., Karnbach, R. & Möller, T. Electronic excitations in liquid-helium: the evolution from small clusters to large droplets. Phys. Rev. Lett. 71, 2654–2657 (1993).
Karnbach, R., Joppien, M. & Möller, T. Electronic excitation, decay and photochemical processes in rare gas clusters. J. Chim. Phys. 92, 499–520 (1995).
von Haeften, K. et al. Discrete visible luminescence of helium atoms and molecules desorbing from helium clusters: The role of electronic, vibrational, and rotational energy transfer. Phys. Rev. Lett. 78, 4371–4374 (1997).
von Haeften, K., Laarmann, T., Wabnitz, H. & Möller, T. Bubble formation and decay in \({}^{3}\)He and \({}^{4}\)He clusters. Phys. Rev. Lett. 88, 233401 (2002).
Peterka, D. S., Lindinger, A., Poisson, L., Ahmed, M. & Neumark, D. M. Photoelectron imaging of helium droplets. Phys. Rev. Lett. 91, 043401 (2003).
Ziemkiewicz, M. P. et al. Femtosecond time-resolved XUV + UV photoelectron imaging of pure helium nanodroplets. J. Chem. Phys. 141, 174306 (2014).
Closser, K. D., Gessner, O. & Head-Gordon, M. Simulations of the dissociation of small helium clusters with ab initio molecular dynamics in electronically excited states. J. Chem. Phys. 140, 134306 (2014).
Hansen, J. P. & Pollock, E. L. Liquid-helium configuration around a metastable excited helium atom. Phys. Rev. A 5, 2214–2216 (1972).
Rosenblit, M. & Jortner, J. Dynamics of the formation of an electron bubble in liquid helium. Phys. Rev. Lett. 75, 4079–4082 (1995).
Ziemkiewicz, M. P., Neumark, D. M. & Gessner, O. Ultrafast electronic dynamics in helium nanodroplets. Int. Rev. Phys. Chem. 34, 239–267 (2015).
Kornilov, O. et al. Femtosecond photoelectron imaging of transient electronic states and Rydberg atom emission from electronically excited He droplets. J. Phys. Chem. 115, 7891–7900 (2011).
Bünermann, O. et al. Ultrafast probing of ejection dynamics of Rydberg atoms and molecular fragments from electronically excited helium nanodroplets. J. Chem. Phys. 137, 214302 (2012).
Lyamayev, V. et al. A modular end-station for atomic, molecular, and cluster science at the low density matter beamline of FERMI@Elettra. J. Phys. B 46, 164007 (2013).
Guberman, S. L. & Goddard, W. A. Nature of the excited states of He\({}_{2}\). Phys. Rev. A 12, 1203–1221 (1975).
Eppink, A. T. J. B. & Parker, D. H. Velocity map imaging of ions and electrons using electrostatic lenses: Application in photoelectron and photofragment ion imaging of molecular oxygen. Rev. Sci. Instrum. 68, 3477 (1997).
Buchenau, H., Toennies, J. P. & Northby, J. A. Excitation and ionization of \({}^{4}\)He clusters by electrons. J. Chem. Phys. 95, 8134–8148 (1991).
Hernando, A. et al. Desorption of alkali atoms from \({}^{4}\)He nanodroplets. Phys. Chem. Chem. Phys. 14, 3996–4010 (2012).
von Vangerow, J. et al. Desorption dynamics of heavy alkali metal atoms (Rb, Cs) off the surface of helium nanodroplets. J. Phys. Chem. A 118, 6604–6614 (2014).
von Vangerow, J. et al. Imaging excited-state dynamics of doped he nanodroplets in real-time. J. Phys. Chem. Lett. 8, 307–312 (2017).
Dozmorov, N. V. et al. Quantum dynamics of Rb atoms desorbing off the surface of He nanodroplets. Phys. Rev. A 98, 043403 (2018).
Mateo, D. et al. Translational dynamics of photoexcited atoms in \({}^{4}\)He nanodroplets: the case of silver. Phys. Chem. Chem. Phys. 15, 18388–18400 (2013).
Serdobintsev, P. Yu, Melnikov, A. S., Pastor, A. A., Timofeev, N. A. & Khodorkovskiy, M. A. Relaxation times measurement in single and multiply excited xenon clusters. J. Chem. Phys. 148, 194301 (2018).
Gomez, L. F., Loginov, E. & Vilesov, A. F. Traces of vortices in superfluid helium droplets. Phys. Rev. Lett. 108, 155302 (2012).
Langbehn, B. et al. Three-dimensional shapes of spinning helium nanodroplets,. Phys. Rev. Lett. 121, 255301 (2018).
Rupp, D. et al. Coherent diffractive imaging of single helium nanodroplets with a high harmonic generation source. Nature Comm. 8, 493 (2017).
LaForge, A. C. et al. Real-time dynamics of the formation of hydrated electrons upon irradiation of water clusters with extreme ultraviolet light. Phys. Rev. Lett. 122, 133001 (2019).
Lackner, F. et al. Direct observation of ring-opening dynamics in strong-field ionized selenophene using femtosecond inner-shell absorption spectroscopy. J. Chem. Phys. 145, 234313 (2016).
Pentlehner, D. et al. Rapidly pulsed helium droplet source. Rev. Sci. Instrum. 80, 043302 (2009).
Allaria, E. et al. Highly coherent and stable pulses from the FERMI seeded free-electron laser in the extreme ultraviolet. Nat. Photonics 6, 699 (2012).
Garcia, G. A., Nahon, L. & Powis, I. Two-dimensional charged particle image inversion using a polar basis function expansion. Rev. Sci. Instrum. 75, 4989–4996 (2004).
Koch, H., Christiansen, O., Jørgensen, P., Sanchez de Mer’as, A. M. & Helgaker, T. The CC3 model: An iterative coupled cluster approach including connected triples. J. Chem. Phys. 106, 1808–1818 (1997).
Smith, C. E., King, R. A. & Crawford, T. D. Coupled cluster excited methods including triple excitations for excited states of radicals. J. Chem. Phys. 122, 054110 (2005).
Turney, J. M. et al. Psi4: an open-source ab initio electronic structure program. J. Chem. Phys. 2, 556–565 (2012).
Fiedler, S. L. & Eloranta, J. Interaction of helium Rydberg state atoms with superfluid helium. J. Low Temp. Phys. 174, 269–283 (2014).
Boys, F. & Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 19, 553–566 (1979).
Knowles, P. J. & Werner, H.-J. Internally contracted multiconfiguration-reference configuration interaction calculations for excited states. Theor. Chim. Acta 84, 95–103 (1992).
Werner, H.-J., Knowles, P. J., Knizia, G., Manby, F. R. & Schütz, M. Molpro: a general-purpose quantum chemistry program package. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2, 242–253 (2012).
Sunil, K. K. et al. Theoretical investigation of the a \({}^{3}{\Sigma }_{u}^{+}\), a \({}^{1}{\Sigma }_{u}^{+}\), c \({}^{3}{\Sigma }_{g}^{+}\), and c \({}^{1}{\Sigma }_{g}^{+}\) potential energy curves of He2 and of He* (21S, 23S)+He scattering. J. Chem. Phys. 78, 6190–6202 (1983).
Chabalowski, C. F., Jensen, J. O., Yarkony, D. R. & Lengsfield, B. H. Theoretical study of the radiative lifetime for the spin-forbidden transition a\({}^{3}{\Sigma }^{+}\to {X}^{1}{\Sigma }_{g}^{+}\) in He2. J. Chem. Phys. 90, 2504–2512 (1989).
Acknowledgements
Funding from the Deutsche Forschungsgemeinschaft (MU 2347/8-1, STI 125/19-1, and the priority program 1840 QUTIF, the Carlsberg Foundation, National Science Foundation (DMR-1828019), Carl-Zeiss-Stiftung, Grant No. FIS2017-87801-P (AEI/FEDER, UE), and Swiss National Science Foundation (200020_162434) is gratefully acknowledged. O.G., D.M.N., and M.P.Z. were supported by the U.S. Department of Energy, Office of Basic Energy Sciences, Chemical Sciences, Geosciences and Biosciences Division, through Contract No. DE-AC02-05CH11231.
Author information
Authors and Affiliations
Contributions
M.M. and F.S. conceived the experiment. C.C., M.C., A.D., M.D., M.D.F., C.G., and O.P. implemented the experiment. M.M., A.C.L., A.C., P.O’K., C.C., M.C., M.D.F., P.F., Y.O., P.P., O.P., K.C.P., R.R., M.P.Z., and F.S. performed the measurements. M.M., A.C.L., A.C., and P.O’K. analyzed the experimental data. J.E. performed the ab initio calculations. A.H., M.P., and M.B. performed the TDDFT calculations. A.C.L., P.O’K., M.D., O.G., D.M.N., T.M., J.E., M.B., and F.S. contributed to the interpretation of the data. M.M. wrote the paper with input from all other authors.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks the anonymous reviewers for their contributions to the peer review of this work. Peer review reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mudrich, M., LaForge, A.C., Ciavardini, A. et al. Ultrafast relaxation of photoexcited superfluid He nanodroplets. Nat Commun 11, 112 (2020). https://doi.org/10.1038/s41467-019-13681-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-13681-6
This article is cited by
-
Photoelectron Spectroscopy of Coronene Molecules Embedded in Helium Nanodroplets
Journal of Low Temperature Physics (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.