Abstract
The discovery of new materials that efficiently transmit spin currents has been important for spintronics and material science. The electric insulator Gd3Ga5O12 (GGG), a standard substrate for growing magnetic films, can be a spin current generator, but has never been considered as a superior conduit for spin currents. Here we report spin current propagation in paramagnetic GGG over several microns. Surprisingly, spin transport persists up to temperatures of 100 K \(\gg\) Tg = 180 mK, the magnetic glass-like transition temperature of GGG. At 5 K and 3.5 T, we find a spin diffusion length λGGG = 1.8 ± 0.2 μm and a spin conductivity σGGG = (7.3 ± 0.3) × 104 Sm−1 that is larger than that of the record quality magnet Y3Fe5O12 (YIG). We conclude that exchange stiffness is not required for efficient spin transport, which challenges conventional models and provides new material-design strategies for spintronic devices.
Similar content being viewed by others
Introduction
According to conventional wisdom, spin currents can be carried by conduction electrons and spin waves1,2,3,4. Mobile electrons in a metal carry spin currents over distances typically less than a micron, whereas spin waves, the collective excitation of the magnetic order parameter5,6,7,8,9,10,11,12 can communicate spin information over much longer distances (Fig. 1a). In particular, the ferrimagnetic insulator Y3Fe5O12 (YIG) supports spin transport over up to a millimeter1,2.
Concepts of spin current in a ferromagnetic insulator and a paramagnetic insulator and paramagnetism of Gd3Ga5O12. a A schematic illustration of a ferromagnet, in which spins are aligned to form long-range order owing to strong exchange interaction. b A schematic illustration of a paramagnet, in which directions of localized spins are random due to thermal fluctuations. c Magnetization M as a function of the applied magnetic field B at 5 K, 100 K, and 300 K. The saturation magnetization of GGG is ∼7 μB per Gd3+ at 5 K. d The temperature dependence of the magnetization of GGG at B = 0.1 T
Gd3Ga5O12 (GGG) is an excellent substrate material for the growth of, e.g., high-quality YIG films13. Above Tg = 180 mK, it is a paramagnetic insulator (band gap of 6 eV14) with Gd3+ spin-7/2 local magnetic moments that are weakly coupled by an effective spin interaction15 Jex ~ 100 mK. Recently, the spin Seebeck effect (SSE), i.e., thermal spin current generation, was observed in GGG at low temperatures (< 20 K) and high magnetic fields16.
Here, we report long-range (500 nm) spin transport in a GGG slab (Fig. 1b) under applied magnetic fields even at much higher temperature (~100 K) than the Curie–Weiss temperature |ΘCW|, whereas at low temperatures GGG turns out to be a surprisingly good spin-conductor.
Results
Material characterization
GGG does not exhibit long-range magnetic ordering at all temperatures15 (Fig. 1d), while its field-dependent magnetization is well described by the Brillouin function. The large low-temperature saturation magnetization of ~7 μB per Gd3+ (Fig. 1c) is governed by the half-filled 4f-shell of the Gd3+ local moments.
Sample structure and measurement setup
We adopt the standard nonlocal geometry5,6,7,8,9,10,11,12 to study spin transport in a device comprised by two Pt wires separated by a distance d on top of a GGG slab (Fig. 2b and Supplementary Note 1). Here, spin currents are injected and detected via the direct and inverse spin Hall effects1,17 (SHE and ISHE), respectively (Fig. 2a). A charge current, Jc, in one Pt wire (injector) generates non-equilibrium spin accumulation μs with direction σs at the Pt/GGG interface by the SHE. When σs and the magnetization M in GGG are collinear, the interface spin-exchange interaction transfers spin angular momentum from the conduction electron spins in Pt to the local moments in GGG at the interface, thereby creating a non-equilibrium magnetization in the GGG beneath the contact that generates a spin diffusion current into the paramagnet. Some of it will reach the other Pt contact (detector) and generate a transverse voltage in Pt by means of spin pumping into Pt and the ISHE.
Observation of long-range spin transport through a paramagnetic insulator. a Schematics of spin injection (left panel) and detection (right panel) at two Pt/GGG contacts. Jc and Js denote the spatial directions of charge and spin currents, respectively. Js is injected into GGG by applying Jc via the SHE in Pt. At the detector, Js is driven in the direction normal to the interface and is converted into Jc via the ISHE in Pt. b A schematic of the experimental setups. The nonlocal device consists of two Pt wires patterned on a GGG slab. B and EISHE denote the directions of the applied magnetic field and the electric field induced by the ISHE, respectively. We apply Jc to the left Pt wire and detect the voltage L|EISHE| between the ends of the right Pt wire with length L. c The B dependence of V at \(\theta = {\mathrm{0}}\) for Pt contacts separated by d = 0.5 μm at 300 K (red plots) and 5 K (blue plots) for |B| < 4 T. d The θ and Jc dependence of V for the same device at 5 K. The left panel shows the θ dependence of V while B = 3.5 T was rotated in the z–y plane; the gray line is a cos2θ fit. The right panel shows the Jc dependence of Vmax, determined by fitting Vmaxcos2θ to the θ dependence. We subtracted a constant offset voltage Voffset from V in c and d (see Supplementary Note 2)
To our knowledge, long-range spin transport in magnets has been observed only below their Curie temperatures5,6,7,8,9,10,11,12, e.g., YIG, NiFe2O4, and α-Fe2O3, so magnetic order and spin-wave stiffness have been considered indispensable. Here, we demonstrate that a relatively weak magnetic field can be a sufficient condition for efficient spin transport, demonstrating that the dipolar interactions alone generate coherent spin waves.
Observation of long-range spin transport through paramagnetic insulator
First, we discuss the field and temperature dependence of the nonlocal detector voltage V in Pt/GGG/Pt with contacts at a distance d = 0.5 μm. We use the standard lock-in technique to rule out thermal effects (see Methods). A magnetic field B is applied at angle \(\theta = {\mathrm{0}}\) in the z–y plane (see Fig. 2b) such that the magnetization in GGG is parallel to the spin polarization σs of the SHE-induced spin accumulation in the injector.
Figure 2c shows V(B) at 300 and 5 K. Surprising is the voltage observed at low, but not ultralow temperatures that increases monotonically as a function of |B| and saturates at about 4 T. Pt/YAG/Pt, where YAG is the diamagnetic insulator Y3Al5O12, does not generate such a signal (Fig. 3b); apparently the paramagnetism of GGG (Fig. 1c) is instrumental in the effect.
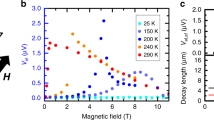
Temperature and magnetic field dependence of the nonlocal voltage signal. All experimental data were obtained by the same device (d = 0.5 μm) with a current amplitude of 100 μA. a The temperature (T) dependence of the amplitude of the maximum nonlocal voltage Vmax for Pt/GGG/Pt, Pt/TGG/Pt, and Pt/YAG/Pt obtained from a sinusoidal fit to the magnetic field angle θ dependences of V at B = 3.5 T. The error bars represent the 68% confidence level (±s.d.). The inset shows the T dependence of the magnetization M of GGG, TGG, and YAG at B = 3.5T. b, c Comparison between V for Pt/YAG/Pt, Pt/TGG/Pt, and Pt/GGG/Pt. b (c) shows the B dependences of V for Pt/YAG/Pt and Pt/TGG/Pt (Pt/GGG/Pt) at 5 K for |B| < 9 T. d, e The θ and B dependence of V for Pt/GGG/Pt at various temperatures. We varied θ by rotating the field at B = 3.5 T in the z–y plane. The field was changed from −9 T to 9 T at \(\theta = {\mathrm{0}}\) for the B dependence
We present the nonlocal voltage in Pt/GGG/Pt at 5 K as a function of the out-of-plane magnetic field angle θ and injection-current Jc as defined in Fig. 2b. The left panel of Fig. 2d shows that V at \(\left| B \right| = 3.5\; {\mathrm{T}}\) is described by \(V(\theta ) = V_{\mathrm{max}}\;{\mathrm{cos}}^2\theta\): it is maximal (Vmax) at \(\theta = {\mathrm{0}}\) and \(\theta = \pm \!{\mathrm{180}}^ \circ\) (B // y) but vanishes at \(\theta = \pm \!{\mathrm{90}}^ \circ\) (B // z) (also see Supplementary Note 2). Furthermore, V depends linearly on |Jc| (see the right panel of Fig. 2d). The same cos2θ dependence in Pt/YIG/Pt is known to be caused by the injection and detection efficiencies of the magnon spin current by the SHE and ISHE, respectively, that both scale like cosθ (refs. 5,6,7). The SHE-induced spin accumulation at the Pt injector interface, i.e., the driving force for the nonlocal magnon transport, scales linearly with Jc, and so does the nonlocal V (ref. 5). The above observations are strong evidence for spin current transport in paramagnetic GGG without long-range magnetic order.
Temperature and high-field dependence of nonlocal spin signal
Figure 3d shows the θ dependence of V at B = 3.5 T and various temperatures T. Clearly, V ~ Vmax(T)cos2θ, where Vmax(T) in Fig. 3a decreases monotonically for T > 5 K, nearly proportional to M(T) at the same B as shown in the inset to Fig. 3a. The field-induced paramagnetism therefore has an important role in the |V| generation. Surprisingly, Vmax at 3.5 T persists even at 100 K, which is two orders of magnitude larger than |ΘCW| = 2 K. The exchange interaction at those temperatures can therefore not play any role in the voltage generation. In contrast, a large paramagnetic magnetization (~μB per f.u. at 3.5 T) is still observed at 100 K, consistent with long-range spin transport carried by the field-induced paramagnetism.
At high fields, Fig. 3e shows a non-monotonic V(B, \({\mathrm{\theta }} = {\mathrm{0}}\)): At T < 30 K, V gradually decreases with field after a maximum at ~4 T, which becomes more prominent with decreasing T. A similar feature has been reported in Pt/YIG/Pt9 and interpreted in terms of the freeze-out of magnons: a Zeeman gap \(\propto B\) larger than the thermal energy \(\propto T\) critically reduces the magnon number and conductivity. It appears that thermal activation of magnetic fluctuations is required to enable a spin current in GGG as well.
Estimation of spin diffusion length
By changing the distance d between the Pt contacts, we can measure the penetration depth of an injected spin current. Vmax at 5 K, as plotted in Fig. 4a, decreases monotonously with increasing d. A similar dependence in Pt/YIG/Pt is well described by a magnon diffusion model18,19. We postulate that the observed spin transport in GGG can be described in terms of magnon diffusion of purely dipolar spin waves. As the GGG thickness of 500 μm \(\gg\) d, we cannot use a simple one-dimensional diffusion model that would predict a simple exponential decay \(V_{\mathrm{max}}(d) \sim {\mathrm{exp}}( \!\!- \!d/\lambda )\). Considering two spatial dimensions (see Supplementary Note 4) leads to:
where \(K_0(d/\lambda )\) is the modified Bessel function of the second kind, \(\lambda = \sqrt {{D\tau }}\) is the spin diffusion (relaxation) length, D is the spin diffusion constant, τ is the spin relaxation time, and C is a numerical coefficient that does not depend on d. By fitting Eq. (1) to the experimental data, we obtained λGGG = 1.82 ± 0.19 µm at \(B = {\mathrm{3}}{\mathrm{.5}}\; {\mathrm{T}}\) and \(T = 5\; {\mathrm{K}}\).
Comparison with theory. a The experimental results (blue circles) and calculations (solid red line) for Vmax in Pt/GGG/Pt as a function of the separation d between the Pt contacts and an applied current of 100 μA. We obtain Vmax by a cos2θ fit to the magnetic field angle θ dependence of V at B = 3.5 T and T = 5 K. By using Eq. (1), the spin diffusion length λGGG = 1.82 ± 0.19 µm. The error bars represent the 68% confidence level (±s.d.). b The experimental results (blue circles) and calculation (solid red line) of the B dependence of the nonlocal V for Pt/GGG/Pt for |B| < 9 T. The experimental data shown in b are the same as those shown in Fig. 3c
A long spin relaxation length in an insulator implies weak spin-lattice relaxation by spin-orbit interaction, which in GGG should be weak because the 4f-shell in Gd3+ is half-filled with zero orbital angular momentum (L = 0). We tested this scenario by a control experiment on a Pt/Tb3Ga5O12 (TGG)/Pt nonlocal device with similar geometry (d = 0.5 μm). TGG is also a paramagnetic insulator with large field-induced M at low temperatures (see the inset to Fig. 3a). However, Tb3+ ions have a finite orbital angular momentum (L = 3) and an electric quadrupole that strongly couples to the lattice20. Indeed, we could not observe any nonlocal voltage in Pt/TGG/Pt in the entire temperature range (see Fig. 3a–c). This result highlights the importance of a weak spin-lattice coupling in long-range paramagnetic spin transmission.
Modeling of nonlocal spin signal
We model the nonlocal voltages in a normal-metal (N)/paramagnetic insulator (PI)/normal-metal (N) system by the magnon diffusion equation in the PI and interface exchange interactions at the metal contacts21 with spin-charge conversion (see Supplementary Notes 3 to 6). The voltage in the Pt detector as a function of B and T reads:
where ξ(B, T) = gμBB/kB(T + |ΘCW|), g is the g-factor, μB is the Bohr magneton, kB is the Boltzmann constant, BS(x) is the Brillouin function as a function of x for spin-S, C1 and C2 are known numerical constants, S = 7/2 is the electron spin of a Gd3+ ion, gs is the effective spin conductance of the Pt/GGG interface, and σGGG is the spin conductivity in GGG. The observed V(B) is well described by Eq. (2) (see Fig. 4b). The best fit of Eq. (2) is achieved by σGGG = (7.25 ± 0.26) × 104 Sm−1 and gs = (1.82 ± 0.05) × 1011 Sm−2. We determine σGGG and gs by fitting the experimental data to a numerical (finite-element) simulation of the diffusion19 that takes the finite width of the contacts and the GGG film into account (the details are discussed in Supplementary Note 9). Surprisingly, the obtained σGGG (gs) value is at the same temperature eight (six) times larger than that of the Pt/YIG/Pt sample8 (σYIG = (0.9 ± 0.6) × 104 Sm−1 and gs = 0.3 × 1011 Sm−2 at 10 mT), which is evidence for highly efficient paramagnetic spin transport.
Discussion
The reported spin transport in GGG has not been observed nor does affect previous nonlocal experiments in YIG/GGG, conducted at room temperature5,9 or at low temperatures and low fields6,7,8, because under those conditions GGG is not magnetically active. Non-negligible contributions from GGG may appear only at low-temperature and high fields, as observed in the local SSE of a Pt/YIG/GGG junction22.
A few papers address the spin current in paramagnets16,23,24,25,26. Shiomi et al. and Wu et al. reported paramagnetic spin pumping in La2NiMnO6 and SSE in GGG and DyScO3 in their paramagnetic phases, respectively. Spin currents were observed above but close to the magnetic ordering temperature and therefore attributed to critical spin fluctuations (paramagnons). Here we find a nonlocal signal in GGG even at 100 K, much higher than |ΘCW| = 2 K in GGG (see Fig. 3a). The exchange interaction has been reported to cause spin diffusion in Heisenberg paramagnets27 at zero magnetic fields. We cannot measure a possible contribution to the spin transport by diffusion at (nearly) zero magnetic fields in our setup by the spin conductivity mismatch and the decrease of the spin diffusion length at small field (see Supplementary Note 7 and 8). However, direct spin diffusion is suppressed when the rotational symmetry is broken by anisotropy or applied magnetic fields28 (exponentially so in Heisenberg ferromagnets29). The contribution from direct magnetic dipole–dipole interactions dominates nuclear spin diffusion, but is orders of magnitude smaller than what we observe30.
A plausible mechanism is based on the long-range dipolar interaction, which becomes important when the Zeeman and thermal energies are of comparable magnitude. The paramagnetic system acquires a finite magnetization by applying magnetic field, and the dipole interaction is enhanced, especially in GGG with large Gd magnetic moments. The dipole interaction can support collective spin-wave excitations even in paramagnets that for small wave numbers are identical to those of ferromagnets (see Supplementary Discussion).
Finally, we address the large spin conductivity of GGG at low temperatures and high magnetic fields. Thermally occupied magnons with energies up to about kBT carry the spin transport. In YIG, their dispersion is dominated by the exchange interaction. Although large exchange energy corresponds to a large magnon group velocity, exchange magnons have short wave lengths, which make them sensitive to local magnetic disorder such as grain boundaries that give rise to spin-wave scattering limiting YIG’s spin conductivity. In contrast, the dipolar interaction is long-ranged and therefore less affected by (short-range) disorder. In GGG, the long-range dipole interaction dominates the excitation of spin waves for frequencies comparable to the Zeeman energy (≈ gµBB). Therefore, paramagnets with strong dipolar but weak exchange interactions, such as GGG, may provide ideal spin conductors as long as the thermal fluctuation of the magnetic moments is sufficiently suppressed by applied magnetic fields. Moreover, the large spin conductance gs indicates a strong interface exchange interaction at a metal contact to GGG.
In summary, we discovered spin transport in the Curie-like paramagnetic insulator Gd3Ga5O12 over several microns. Its transport efficiency at moderately low temperatures and high magnetic fields is even higher than that of the best magnetically ordered material YIG. Low-temperature experiments31, covering the magnetic glass-like transition temperature of GGG, may be interesting to explore the link between spin frustration and spin transport in GGG. Magnonic crystals2 can help determining the length scales that govern the observed spin transport. Since paramagnetic insulators are free from Barkhausen noise associated to magnetic domains and magnetic after-effects (aging)32 typical for ferromagnets and antiferromagnets, they are promising materials for future spintronics devices.
Methods
Sample preparation
A single-crystalline Gd3Ga5O12 (111), Y3Al5O12 (111), and Tb3Ga5O12 (111) (500 μm in thickness) were commercially obtained from CRYSTAL GmbH, Surface Pro GmbH, and MTI Corporation, respectively. For magnetization measurements, the slabs were cut into 3 mm long and 2 mm wide. For transport measurements, a nonlocal device with Pt wires was fabricated on a top of each slab by an e-beam lithography and lift-off technique. Here, the Pt wires were deposited by magnetron sputtering in a 10−1 Pa Ar atmosphere. The dimension of the Pt wire is 200 μm long, 100 nm wide, and 10 nm thick and the separation distance between the injector and detector Pt wires are ranged from 0.3 to 3.0 μm. A microscope image of a device is presented in Supplementary Fig. 1. We measured the temperature dependence of the resistance between the two Pt wires on the GGG substrate but found that the resistance of the GGG is too high to be measurable.
Magnetization measurement
The magnetization of GGG, YAG, and TGG slabs was measured using a vibrating sample magnetometer option of a quantum design physical properties measurement system (PPMS) in a temperature range from 5 K to 300 K under external magnetic fields up to 9 T.
Spin transport measurements
We measured the spin transport with a PPMS by a standard lock-in technique from 5 K to 300 K. An a.c. charge current was applied to the injector Pt wire with a Keithley 6221 and the voltage across the detector Pt wire was recorded with a lock-in amplifier (NF 5640). The typical a.c. charge current has a root-mean-square amplitude of 100 μA and a frequency of 3.423 Hz.
Data availability
The data that support the findings of this study are available from the corresponding author on request.
References
Kajiwara, Y. et al. Transmission of electrical signals by spin-wave interconversion in a magnetic insulator. Nature 464, 262–266 (2010).
Chumak, A. V., Vasyuchka, V. I., Serga, A. & Hilebrands, B. Magnon spintronics. Nat. Phys. 11, 453–461 (2015).
Jungwirth, T., Marti, X., Wadley, P. & Wunderlich, J. Antiferromagnetic spintronics. Nat. Nanotech. 11, 231–241 (2016).
Maekawa, S., Valenzuela, S. O., Saitoh, E. & Kimura, T. (eds.) Spin Current 2nd edn. (Oxford Univ. Press, 2017).
Cornelissen, L. J., Liu, J., Duine, R. A., Ben Youssef, J. & van Wees, B. J. Long-distance transport of magnon spin information in a magnetic insulator at room temperature. Nat. Phys. 11, 1022–1026 (2015).
Goennenwein, S. T. B. et al. Non-local magnetoresistance in YIG/Pt nanostructures. Appl. Phys. Lett. 107, 172405 (2015).
Vélez, S., Bedoya-Pinto, A., Yan, W., Hueso, L. & Casanova, F. Competing effects at Pt/YIG interfaces: Spin Hall magnetoresistance, magnon excitations, and magnetic frustration. Phys. Rev. B 94, 174405 (2016).
Cornelissen, L. J., Shan, J. & van Wees, B. J. Temperature dependence of the magnon spin diffusion length and magnon spin conductivity in the magnetic insulator yttrium iron garnet. Phys. Rev. B 94, 180402(R) (2016).
Cornelissen, L. J. & van Wees, B. J. Magnetic field dependence of the magnon spin diffusion length in the magnetic insulator yttrium iron garnet. Phys. Rev. B 93, 020403(R) (2016).
Cornelissen, L. J. et al. Nonlocal magnon-polaron transport in yttrium iron garnet. Phys. Rev. B 96, 104441 (2017).
Shan, J. et al. Nonlocal magnon spin transport in NiFe2O4 thin films. Appl. Phys. Lett. 110, 132406 (2017).
Lebrun, R. et al. Tunable long-distance spin transport in a crystalline antiferromagnetic iron oxide. Nature 561, 222–225 (2018).
Sun, Y. et al. Growth and ferromagnetic resonance properties of nanometer-thick yttrium iron garnet films. Appl. Phys. Lett. 101, 152405 (2012).
Ghimire, K., Haneef, H. F., Collins, R. W. & Podraza, N. J. Optical properties of single-crystal Gd3Ga5O12 from the infrared to ultraviolet. Phys. Status Solidi B 252, 2191–2198 (2015).
Schiffer, P. et al. Frustration induced spin freezing in a site-ordered magnet: gadolinium gallium garnet. Phys. Rev. Lett. 74, 2379 (1995).
Wu, S. M., Pearson, J. E. & Bhattacharya, A. Paramagnetic spin Seebeck effect. Phys. Rev. Lett. 114, 186602 (2015).
Saitoh, E., Ueda, M., Miyajima, H. & Tatara, G. Conversion of spin current into charge current at room temperature: Inverse spin-Hall effect. Appl. Phys. Lett. 88, 182509 (2006).
Rezende, S. et al. Magnon spin-current theory for the longitudinal spin-Seebeck effect. Phys. Rev. B 89, 014416 (2014).
Cornelissen, L. J., Peters, K. J. H., Bauer, G. E. W., Duine, R. A. & van Wees, B. J. Magnon spin transport driven by the magnon chemical potential in a magnetic insulator. Phys. Rev. B 94, 014412 (2016).
Bierig, R. W., Weber, M. J. & Warshaw, S. I. Paramagnetic resonance and relaxation of trivalent rare-earth ions in calcium fluoride. II. spin-lattice relaxation. Phys. Rev. 134, A1504 (1964).
Takahashi, S., Saitoh, E. & Maekawa, S. Spin current through a normal-metal/insulating-ferromagnet junction. J. Phys. Conf. Ser. 200, 062030 (2010).
Kikkawa, T. et al. Magnon polarons in the spin Seebeck effect. Phys. Rev. Lett. 117, 207203 (2016).
Shiomi, Y. & Saitoh, E. Paramagnetic spin pumping. Phys. Rev. Lett. 113, 266602 (2014).
Wang, H., Cu, C., Hammel, P. C. & Yang, F. Spin transport in antiferromagnetic insulators mediated by magnetic correlations. Phys. Rev. B 91, 220410(R) (2015).
Hirobe, D. et al. One-dimensional spinon spin currents. Nat. Phys. 13, 30–34 (2016).
Okamoto, S. Spin injection and spin transport in paramagnetic insulators. Phys. Rev. B 93, 064421 (2016).
Bennett, H. S. & Martin, P. C. Spin diffusion in the Heisenberg paramagnet. Phys. Rev. 138, A608 (1965).
Lovesey, S. W. & Loveluck, J. M. Wavelength-dependent fluctuations in classical paramagnets in a magnetic field. II. Dynamical properties. J. Phys. C: Solid State Phys. 9, 3659 (1976).
Balucani, U., Vaia, R., Federighi, A. & Tognetti, V. Longitudinal spin fluctuations in Heisenberg ferromagnets: the hydrodynamic regime. Nuovo Cim. D. 9, 1403–1432 (1987).
Bloembergen, N. On the interaction of nuclear spins in a crystalline lattice. Physica 15, 386–426 (1949).
Liu, C. et al. Probing short-range magnetic order in a geometrically frustrated magnet by means of the spin Seebeck effect. Phys. Rev. B 98, 060415(R) (2018).
Hohler, B. & Kronmüller, H. Magnetic after-effects in ferromagnetic materials. J. Magn. Magn. Mater. 19, 267–274 (1980).
Acknowledgements
We thank S. Maekawa, J. Barker, R. Iguchi, T. Niizeki, and D. Hirobe for discussions, and R. Yahiro for experimental help. This work is a part of the research program of ERATO Spin Quantum Rectification Project (No. JPMJER1402) from JST, the Grant-in-Aid for Scientific Research on Innovative Area Nano Spin Conversion Science (Nos. JP26103005 and JP26103006), the Grant-in-Aid for Scientific Research (S) (No. JP19H05600), Grant-in-Aid for Research Activity Start-up (Nos. JP18H05841 and JP18H05845), 19H006450 from JSPS KAKENHI, JSPS Core-to-Core program the International Research Center for New-Concept Spintronics Devices, World Premier International Research Center Initiative (WPI) from MEXT, Japan, Netherlands Organization for Scientific Research (NWO), and NanoLab NL. K.O. acknowledges support from GP-Spin at Tohoku University.
Author information
Authors and Affiliations
Contributions
K.O. designed the experiment, fabricated the samples, collected all of the data. S.T. formulated the theoretical model. K.O. and S.T. analyzed the data. S.T. and K.O. estimated the parameters. L.J.C. and J.S. carried out the numerical simulation. T.K., B.J.v.W., G.E.W.B., and E.S. developed the explanation of the experimental results. E.S. supervised the project. K.O., S.T., L.J.C., J.S., S.D., T.K., G.E.W.B, B.J.v.W, and E.S. discussed the results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Oyanagi, K., Takahashi, S., Cornelissen, L.J. et al. Spin transport in insulators without exchange stiffness. Nat Commun 10, 4740 (2019). https://doi.org/10.1038/s41467-019-12749-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-12749-7
This article is cited by
-
Triplon current generation in solids
Nature Communications (2021)
-
Dynamical Spin Conductivity of the Heisenberg Antiferromagnetic Checkerboard Lattice
Brazilian Journal of Physics (2021)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.