Abstract
In many species, the offspring of related parents suffer reduced reproductive success, a phenomenon known as inbreeding depression. In humans, the importance of this effect has remained unclear, partly because reproduction between close relatives is both rare and frequently associated with confounding social factors. Here, using genomic inbreeding coefficients (FROH) for >1.4 million individuals, we show that FROH is significantly associated (p < 0.0005) with apparently deleterious changes in 32 out of 100 traits analysed. These changes are associated with runs of homozygosity (ROH), but not with common variant homozygosity, suggesting that genetic variants associated with inbreeding depression are predominantly rare. The effect on fertility is striking: FROH equivalent to the offspring of first cousins is associated with a 55% decrease [95% CI 44–66%] in the odds of having children. Finally, the effects of FROH are confirmed within full-sibling pairs, where the variation in FROH is independent of all environmental confounding.
Similar content being viewed by others
Introduction
Given the pervasive impact of purifying selection on all populations, it is expected that genetic variants with large deleterious effects on evolutionary fitness will be both rare and recessive1. However, precisely because they are rare, most of these variants have yet to be identified and their recessive impact on the global burden of disease is poorly understood. This is of particular importance for the nearly one billion people living in populations where consanguineous marriages are common2, and the burden of genetic disease is thought to be disproportionately due to increased homozygosity of rare, recessive variants3,4,5. Although individual recessive variants are difficult to identify, the net directional effect of all recessive variants on phenotypes can be quantified by studying the effect of inbreeding6, which gives rise to autozygosity (homozygosity due to inheritance of an allele identical-by-descent).
Levels of autozygosity are low in most of the cohorts with genome-wide data7,8 and consequently very large samples are required to study the phenotypic impact of inbreeding9. Here, we meta-analyse results from 119 independent cohorts to quantify the effect of inbreeding on 45 commonly measured complex traits of biomedical or evolutionary importance, and supplement these with analysis of 55 more rarely measured traits included in UK Biobank10.
Continuous segments of homozygous alleles, or runs of homozygosity (ROH), arise when identical-by-descent haplotypes are inherited down both sides of a family. The fraction of each autosomal genome in ROH > 1.5 Mb (FROH) correlates well with pedigree-based estimates of inbreeding11.We estimate FROH using standard methods and software6,12 for a total of 1,401,776 individuals in 234 uniform sub-cohorts. The traits measured in each cohort vary according to original study purpose, but together cover a comprehensive range of human phenotypes (Fig. 1, Supplementary Data 7). The five most frequently contributed traits (height, weight, body mass index, systolic and diastolic blood pressure) are measured in >1,000,000 individuals; a further 16 traits are measured >500,000 times.
Census of complex traits. Sample sizes are given for analyses of 57 representative phenotypes, arranged into 16 groups covering major organ systems and disease risk factors. HDL high-density lipoprotein, LDL low-density lipoprotein, hs-CRP high-sensitivity C-reactive protein, TNF-alpha tumour necrosis factor alpha, FEV1 forced expiratory volume in one second, FVC forced vital capacity, eGFR estimated glomerular filtration rate
We find that FROH is significantly associated with apparently deleterious changes in 32 out of 100 traits analysed. Increased FROH is associated with reduced reproductive success (decreased number and likelihood of having children, older age at first sex and first birth, decreased number of sexual partners), as well as reduced risk-taking behaviour (alcohol intake, ever-smoked, self-reported risk taking) and increased disease risk (self-reported overall health and risk factors including grip strength and heart rate). We show that the observed effects are predominantly associated with rare (not common) variants and, for a subset of traits, differ between men and women. Finally, we introduce a within-siblings method, which confirms that social confounding of FROH is modest for most traits. We therefore conclude that inbreeding depression influences a broad range of human phenotypes through the action of rare, recessive variants.
Results
Cohort characteristics
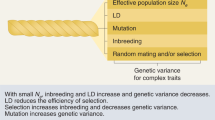
As expected, cohorts with different demographic histories varied widely in mean FROH. The within-cohort standard deviation of FROH is strongly correlated with the mean (Pearson’s r = 0.82; Supplementary Fig. 3), and the most homozygous cohorts provide up to 100 times greater per-sample statistical power than cosmopolitan European-ancestry cohorts (Supplementary Data 5). To categorise cohorts, we plotted mean FROH against FIS (Fig. 2). FIS measures inbreeding as reflected by non-random mating in the most recent generation, and is calculated as the mean individual departure from Hardy–Weinberg equilibrium (FSNP; see Methods). Cohorts with high rates of consanguinity lie near the FROH = FIS line, since most excess SNP homozygosity is caused by ROH. In contrast, cohorts with small effective population sizes, such as the Amish and Hutterite isolates of North America, have high average FROH, often despite avoidance of mating with known relatives, since identical-by-descent haplotypes are carried by many couples, due to a restricted number of possible ancestors.
Mean FROH and FIS for 234 ROHgen sub-cohorts. Each cohort is represented by a circle whose area is proportional to the approximate statistical power (\(N\sigma _{F_{{\mathrm{ROH}}}}^2\)) contributed to estimates of \(\beta _{F_{{\mathrm{ROH}}}}\). Mean FROH can be considered as an estimate of total inbreeding relative to an unknown base generation, approximately tens of generations past. FIS measures inbreeding in the current generation, with FIS = 0 indicating random mating, FIS > 0 indicating consanguinity, and FIS < 0 inbreeding avoidance46. In cohorts along the y-axis, such as the Polynesians and the Anabaptist isolates, autozygosity is primarily caused by small effective population size rather than preferential consanguineous unions. In contrast, in cohorts along the dotted unity line, all excess SNP homozygosity is accounted for by ROH, as expected of consanguinity within a large effective population. A small number of cohorts along the x-axis, such as Hispanic and mixed-race groups, show excess SNP homozygosity without elevated mean FROH, indicating population genetic structuring, caused for instance by admixture and known as the Wahlund effect. A few notable cohorts are labelled. BBJ Biobank Japan, BiB Born in Bradford, UKB UK Biobank, MESA Multiethnic Study of Atherosclerosis, TCGS Tehran Cardiometabolic Genetic Study
Traits affected by F ROH
To estimate the effect of inbreeding on each of the 100 phenotypes studied, trait values were regressed on FROH within each cohort, taking account of covariates including age, sex, principal components of ancestry and, in family studies, a genomic relationship matrix (GRM) (Supplementary Data 3). Cross-cohort effect size estimates were then obtained by fixed-effect, inverse variance-weighted meta-analysis of the within-cohort estimates (Supplementary Data 10). Twenty-seven out of 79 quantitative traits and 5 out of 21 binary traits reach experiment-wise significance (0.05/100 or p < 0.0005; Fig. 3a, b). Among these are replications of the previously reported effects on reduction in height13, forced expiratory lung volume in one second, cognition and education attained6. We find that the 32 phenotypes affected by inbreeding can be grouped into five broader categories: reproductive success, risky behaviours, cognitive ability, body size, and health.
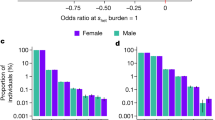
Scope of inbreeding depression. a Effect of FROH on 25 quantitative traits. To facilitate comparison between traits, effect estimates are presented in units of within-sex standard deviations. Traits shown here reached Bonferroni-corrected significance of p = 0.0005 (=0.05/100 traits). Sample sizes, within-sex standard deviations, and effect estimates in measurement units are shown in Supplementary Data 9. FEV1 forced expiratory volume in one second. Traits are grouped by type. b Effect of FROH on eight binary traits with associated p values. Effect estimates are reported as ln(Odds-Ratio) for the offspring of first cousins, for which E(FROH) = 0.0625. Self-declared infertility is shown for information, although this trait does not reach Bonferroni corrected significant (\({\mathrm{{OR}}}_{0.0625}\) = 2.6 ± 1.1, p = 0.0006). Numbers of cases and controls and effect estimates for all binary traits are shown in Supplementary Data 10. c Sex-specificity of ROH effects. The effect of FROH in men versus that in women is shown for 13 traits for which there was evidence of significant differences in the effects between sexes. For 11 of these 13 traits the magnitude of effect is greater in men than in women. Traits such as liver enzymes levels (alanine transaminase, gamma-glutamyl transferase) show sex-specific effects of opposite sign (positive in women, negative in men), which cancel out in the overall analysis. BMI body mass index, LDL low-density lipoprotein. All errors bars represent 95% confidence intervals
Despite the greater individual control over reproduction in the modern era, due to contraception and fertility treatments, we find that increased FROH has significant negative effects on five traits closely related to fertility. For example, an increase of 0.0625 in FROH (equivalent to the difference between the offspring of first cousins and those of unrelated parents) is associated with having 0.10 fewer children [β0.0625 = −0.10 ± 0.03 95% confidence interval (CI), p = 1.8 × 10−10]. This effect is due to increased FROH being associated with reduced odds of having any children (OR0.0625 = 0.65 ± 0.04, p = 1.7 × 10−32) as opposed to fewer children among parents (β0.0625 = 0.007 ± 0.03, p = 0.66). Since autozygosity also decreases the likelihood of having children in the subset of individuals who are, or have been, married, (OR0.0625 = 0.71 ± 0.09, p = 3.8 × 10−8) it appears that the cause is a reduced ability or desire to have children, rather than reduced opportunity. Consistent with this interpretation, we observe no significant effect on the likelihood of marriage (OR0.0625 = 0.94 ± 0.07, p = 0.12) (Fig. 3b). All effect size, odds ratios and 95% CI are stated as the difference between FROH = 0 and FROH = 0.0625.
The effects on fertility may be partly explained by the effect of FROH on a second group of traits, which capture risky or addictive behaviour. Increased FROH is associated with later age at first sex (β0.0625 = 0.83 ± 0.19 years, p = 5.8 × 10−17) and fewer sexual partners (β0.0625 = −1.38 ± 0.38, p = 2.0 × 10−12) but also reduced alcohol consumption (β0.0625 = −0.66 ± 0.12 units per week, p = 1.3 × 10−22), decreased likelihood of smoking (OR0.0625 = 0.79 ± 0.05, p = 5.9 × 10−13), and a lower probability of being a self-declared risk-taker (OR0.0625 = 0.84 ± 0.06, p = 3.4×10−5) or exceeding the speed limit on a motorway (p = 4.0 × 10−8). Conservative beliefs are likely to affect these traits, and are known to be confounded with FROH in some populations14, however, fitting religious participation as a covariate in UKB reduces, but does not eliminate the reported effects (Supplementary Fig. 10b, Supplementary Data 20). Similarly, fitting educational attainment as an additional covariate reduces 16 of 25 significant effect estimates, but actually increases 9, including age at first sex and number of children (Supplementary Fig. 10a, Supplementary Data 20). This is because reduced educational attainment is associated with earlier age at first sex and increased number of children, which makes it an unlikely confounder for the effects of FROH, which are in the opposite directions.
A third group of traits relates to cognitive ability. As previously reported, increased autozygosity is associated with decreased general cognitive ability, g6,15 and reduced educational attainment6. Here, we also observe an increase in reaction time (β0.0625 = 11.6 ± 3.9 ms, p = 6.5 × 10−9), a correlate of general cognitive ability (Fig. 3a, Supplementary Data 10).
A fourth group relates to body size. We replicate previously reported decreases in height and forced expiratory volume6 (Supplementary Data 21) and we find that increased FROH is correlated with a reduction in weight (β0.0625 = 0.86 ± 0.12 kg, p = 3.4 × 10−28) and an increase in the waist to hip ratio (β0.0625 = 0.004 ± 0.001, p = 1.4 × 10−11).
The remaining effects are loosely related to health and frailty; higher FROH individuals report significantly lower overall health and slower walking pace, have reduced grip strength (β0.0625 = −1.24 ± 0.19 kg, p = 6.9 × 10−24), accelerated self-reported facial ageing, and poorer eyesight and hearing. Increased FROH is also associated with faster heart rate (β0.0625 = 0.56 ± 0.24 bpm, p = 5.9 × 10−6), lower haemoglobin (β0.0625 = 0.81 ± 0.24 gL−1, p = 1.6 × 10−11), lymphocyte percentage, and total cholesterol (β0.0625 = −0.05 ± 0.015 mmol L−1, p = 5.2 × 10−10).
Sex-specific effects of F ROH
Intriguingly, for a minority of traits (13/100), the effect of FROH differs between men and women (Fig. 3c, Supplementary Data 12). For example, men who are the offspring of first cousins have 0.10 mmol L−1 [95% CI 0.08–0.12] lower total cholesterol on average, while there is no significant effect in women; LDL shows a similar pattern. More generally, for these traits, the effect in men is often of greater magnitude than the effect in women, perhaps reflecting differing relationships between phenotype and fitness.
Associations most likely caused by rare, recessive variants
The use of ROH to estimate inbreeding coefficients is relatively new in inbreeding research11,16,17,18,19. Earlier frequency-based estimators such as FSNP and FGRM20, made use of excess marker homozygosity21,22,23 and did not require physical maps. We performed both univariate and multivariate regressions to evaluate the effectiveness of FROH against these measures. The correlations between them range from 0.13 to 0.99 and are strongest in cohorts with high average inbreeding (Supplementary Data 6, Supplementary Fig. 6). Significantly, univariate regressions of traits on both FSNP and FGRM show attenuated effect estimates relative to FROH (Supplementary Data 13). This attenuation is greatest in low autozygosity cohorts, suggesting that FROH is a better estimator of excess homozygosity at the causal loci (Fig. 4c).
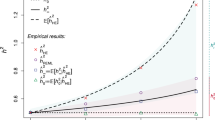
Inbreeding depression caused by ROH. a Effect of different ROH lengths on height, compared with the effect of SNP homozygosity outside of ROH. The effects of shorter (<5 Mb) and longer (>5 Mb) ROH per unit length are similar and strongly negative, whereas the effect of homozygosity outside ROH is much weaker. The pattern is similar for other traits (Supplementary Fig. 11a; Supplementary Data 14). b \({\boldsymbol{F}}_{{\mathbf{ROH}}}\) is more strongly associated than \({\boldsymbol{F}}_{{\mathbf{GRM}}}\) in a bivariate model of height. Meta-analysed effect estimates, and 95% confidence intervals, are shown for a bivariate model of height (\({\mathrm{{Height}}}\sim F_{{\mathrm{ROH}}} + F_{{\mathrm{GRM}}}\)). The reduction in height is more strongly associated with \(F_{{\mathrm{ROH}}}\) than \(F_{{\mathrm{GRM}}}\), as predicted if the causal variants are in weak LD with the common SNPs used to calculate \(F_{{\mathrm{GRM}}}\) (Supplementary Note 5). The pattern is similar for other traits (Supplementary Fig. 15a, b; Supplementary Data 22). c FROH is a lower variance estimator of the inbreeding coefficient than FGRM. The ratio of \(\beta _{F_{{\mathrm{GRM}}}}:\beta _{F_{{\mathrm{ROH}}}}\) is plotted against \(\frac{{{\mathrm{{var}}}(F_{{\mathrm{ROH}}})}}{{{\mathrm{{var}}}(F_{{\mathrm{GRM}}})}}\) for all traits in all cohorts. When the variation of \(F_{{\mathrm{GRM}}}\) which is independent of \(F_{{\mathrm{ROH}}}\) has no effect on traits, \(\hat \beta _{F_{{\mathrm{GRM}}}}\) is downwardly biased by a factor of \(\frac{{{\mathrm{{var}}}(F_{{\mathrm{ROH}}})}}{{{\mathrm{{var}}}(F_{{\mathrm{GRM}}})}}\) (Supplementary Note 4). A linear maximum likelihood fit, shown in red, has a gradient consistent with unity [1.01; 95% CI 0.84–1.18], as expected when the difference between \(F_{{\mathrm{GRM}}}\) and \(F_{{\mathrm{ROH}}}\) is not informative about the excess homozygosity at causal variants (Supplementary Note 5). d FROH is a better predictor of rare variant homozygosity than FGRM. The excess homozygosities of SNPs, extracted from UK Biobank imputed genotypes, were calculated at seven discrete minor allele frequencies (\(F_{{\mathrm{MAF}}}\)), and regressed on two estimators of inbreeding in a bivariate statistical model (see Supplementary Note 5). The homozygosity of common SNPs is better predicted by \(F_{{\mathrm{GRM}}}\), but rare variant homozygosity is better predicted by \(F_{{\mathrm{ROH}}}\). The results from real data (Fig. 4b, Supplementary Figs 15a, b and Supplementary Data 22) are consistent with those simulated here, if the causal variants are predominantly rare. All errors bars represent 95% confidence intervals
To explore this further, we fit bivariate models with FROH and FGRM as explanatory variables. For all 32 traits that were significant in the univariate analysis, we find that \(\widehat \beta _{F_{\mathrm{ROH}}|F_{\mathrm{GRM}}}\) is of greater magnitude than \(\widehat \beta _{F{\mathrm{GRM}}|F{\mathrm{ROH}}}\)in the conditional analysis (Fig. 4b, Supplementary Data 22). This suggests that inbreeding depression is predominantly caused by rare, recessive variants made homozygous in ROH, and not by the chance homozygosity of variants in strong LD with common SNPs (Fig. 4d, Supplementary Note 5). We also find that ROH of different lengths have similar effects per unit length (Fig. 4a, Supplementary Fig. 11a), consistent with their having a causal effect on traits and not with confounding by socioeconomic or other factors, as shorter ROH arise from deep in the pedigree are thus less correlated with recent consanguinity.
Quantifying the scope of social confounding
Previous studies have highlighted the potential for FROH to be confounded by non-genetic factors6,24. We therefore estimated the effect of FROH within various groups, between which confounding might be expected either to differ, or not be present at all.
For example, the effect of FROH on height is consistent across seven major continental ancestry groups (Supplementary Fig. 1, Supplementary Data 18), despite differing attitudes towards consanguinity, and consequently different burdens and origins of ROH. Similarly, grouping cohorts into consanguineous, more cosmopolitan, admixed and those with homozygosity due to ancient founder effects also shows consistent effects (Supplementary Fig. 2, Supplementary Data 19). Equally, categorising samples into bins of increasing FROH shows a dose-dependent response of the study traits with increased FROH (Supplementary Data 17 and Fig. 5a, b show the response for height and ever having children; Supplementary Figs 9a–f for all significant traits). The proportionality of these effects is consistent with a genetic cause, while it is difficult to envisage a confounder proportionally associated across the entire range of observed FROH. In particular, the highest FROH group (FROH > 0.18), equivalent to the offspring of first-degree relatives, are found to be, on average, 3.4 [95% CI 2.5–4.3] cm shorter and 3.1 [95% CI 2.5–3.7] times more likely to be childless than an FROH = 0 individual.
Evidence ROH effects are un-confounded. a Linear decrease in height with increasing FROH. Average heights (in metres) is plotted in bins of increasing FROH. The limits of each bin are shown by red dotted lines, and correspond to the offspring of increasing degree unions left-to-right. The overall estimate of \(\beta _{F_{{\mathrm{ROH}}}}\) is shown as a solid black line. Subjects with kinship equal to offspring of full-sibling or parent–child unions are significantly shorter than those of avuncular or half-sibling unions who in turn are significantly shorter than those of first-cousin unions. b Linear decrease in odds of ever having children with increasing FROH. Linear model approximations of ln(Odds-Ratio) for ever having children (1 = parous, 0 = childless) are plotted in bins of increasing FROH. A strong relationship is evident, extending beyond the offspring of first cousins. c ROH effects are consistent in adoptees. The ratios of effect estimates, \(\beta _{F_{{\mathrm{ROH}}}}\), between adoptees and all individuals are presented by trait. All traits are directionally consistent and overall show a strongly significant difference from zero (average = 0.78, 95% CI 0.56–1.00, p = 2 × 10−12). FEV1 forced expiratory volume in one second. d ROH effects are consistent in full siblings. The ratios of effect estimates within full siblings to effects in all individuals (\(\beta _{F_{{\mathrm{ROH}}\_{\mathrm{wSibs}}}}:\beta _{F_{{\mathrm{ROH}}}}\)) are presented by trait. Twenty-three of 29 estimates are directionally consistent and overall show a significant difference from zero (average = 0.78, 95% CI 0.53–1.04, p = 7 × 10−10). BMI body mass index. All errors bars represent 95% confidence intervals
Next, we estimated \(\beta_{{F}_{\rm{ROH}}}\) for 7153 self-declared adopted individuals in UK Biobank, whose genotype is less likely to be confounded by cultural factors associated with the relatedness of their biological parents. For all 26 significant traits measured in this cohort, effect estimates are directionally consistent with the meta-analysis and 3 (height, walking pace and hearing acuity) reach replication significance (p < 0.004). In addition, a meta-analysis of the ratio \(\widehat \beta _{F_{{\mathrm{ROH}}\_{\mathrm{ADOPTEE}}}}:\widehat \beta _{F_{\mathrm{ROH}}}\) across all traits differs significantly from zero (Fig. 5c; average = 0.78, 95% CI 0.56–1.00, p = 2 × 10−12).
Finally, the effect of FROH was estimated in up to 118,773 individuals in sibships (full-sibling pairs, trios, etc.: \(\widehat \beta _{F_{\mathrm{ROH}\_{\mathrm{w{Sibs}}}}}\)). FROH differences between siblings are caused entirely by Mendelian segregation, and are thus independent of any reasonable model of confounding. The variation of FROH among siblings is a small fraction of the population-wide variation11 (Supplementary Data 5); nevertheless, 23 out of 29 estimates of \(\widehat \beta _{F_{{\mathrm{ROH}}\_{\mathrm{wSibs}}}}\) are directionally consistent with \(\widehat \beta _{F_{\mathrm{ROH}}}\), and two (self-reported overall health and ever having children) reach replication significance. A meta-analysis of the ratio \(\widehat \beta _{F_{{\mathrm{ROH}}\_{\mathrm{wSibs}}}}:\widehat \beta _{F_{\mathrm{ROH}}}\) for all traits is significantly greater than zero (Fig. 5d; average = 0.78, 95% CI 0.53–1.04, p = 7 × 10−10), indicating a substantial fraction of these effects is genetic in origin. However, for both adoptees and siblings, the point estimates are less than one, suggesting that non-genetic factors probably contribute a small, but significant, fraction of the observed effects.
Discussion
Our results reveal inbreeding depression to be broad in scope, influencing both complex traits related to evolutionary fitness and others where the pattern of selection is less clear. While studies of couples show optimal fertility for those with distant kinship25,26, fewer have examined reproductive success as a function of individual inbreeding. Those that did are orders of magnitude smaller in size than the present study, suffer the attendant drawbacks of pedigree analysis, and have found mixed results27,28,29. Our genomic approach also reveals that in addition to socio-demographic factors and individual choice, recessive genetic effects have a significant influence on whether individuals reproduce. The discordant effects on fertility and education demonstrate that this is not just a result of genetic correlations between the two domains30.
The effects we see on fertility might be partially mediated through a hitherto unknown effect of autozygosity on decreasing the prevalence of risk-taking behaviours. Significant effects of autozygosity are observed for self-reported risk taking, speeding on motorways, alcohol and smoking behaviour, age at first sexual intercourse and number of sexual partners. Independent evidence for a shared genetic architecture between risk-taking and fertility traits comes from analysis of genetic correlations using LD-score regression in UKB (Supplementary Table 1). The core fertility traits, ever had children and number of children, are strongly genetically correlated (rG = 0.93; p < 10−100). Genetic correlations with ever-smoking and self-reported risk-taking are lower, but also significant: 0.23–0.27, p < 10−10. Age at first sex is strongly genetically correlated both with the fertility traits, (rG = 0.53–0.57), and number of sexual partners, ever-smoking and risk-taking30 (rG = 0.42–0.60).
Reproductive traits are understandable targets of natural selection, as might be walking speed, grip strength, overall health, and visual and auditory acuity. While we cannot completely exclude reverse causality, whereby a less risk-taking, more conservative, personality is associated with greater likelihood of consanguineous marriage, we note that the effects are consistent for ROH < 5 Mb, which are less confounded with mate choice, due to their more distant pedigree origins (Supplementary Fig. 11a). This group of traits also shows similar evidence for un-confounded effects in the analysis of adoptees and full siblings (Fig. 5c, d; Supplementary Data 16) and the signals remained after correcting for religious activity or education.
On the other hand, for some traits that we expected to be influenced by ROH, we observed no effect. For example, birth weight is considered a key component of evolutionary fitness in mammals, and is influenced by genomic homozygosity in deer31; however, no material effect is apparent here (Supplementary Data 10). Furthermore, in one case, ROH appear to provide a beneficial effect: increasing FROH significantly decreases total and LDL-cholesterol in men, and may thus be cardio-protective in this regard.
Our multivariate models show that homozygosity at common SNPs outside of ROH has little influence on traits, and that the effect rather comes from ROH over 1.5 Mb in length. This suggests that genetic variants causing inbreeding depression are almost entirely rare, consistent with the dominance hypothesis1. The alternative hypothesis of overdominance, whereby positive selection on heterozygotes has brought alleles to intermediate frequencies, would predict that more common homozygous SNPs outside long ROH would also confer an effect. The differential provides evidence in humans that rare recessive mutations underlie the quantitative effects of inbreeding depression.
Previous studies have shown that associations observed between FROH and traits do not prove a causal relationship14,24. Traditional Genome-wide Association Studies (GWAS) can infer causality because, in the absence of population structure, genetic variants (SNPs) are randomly distributed between, and within, different social groups. However, this assumption does not hold in studies of inbreeding depression, where, even within a genetically homogeneous population, social groups may have differing attitudes towards consanguinity, and therefore different average FROH and, potentially, different average trait values. We therefore present a number of analyses that discount social confounding as a major factor in our results. Firstly, we show that the effects are consistent across diverse populations, including those where ROH burden is driven by founder effects rather than cultural practices regarding marriage. Effects are also consistent across a 20-fold range of FROH: from low levels, likely unknown to the subject, to extremely high levels only seen in the offspring of first-degree relatives. Secondly, we show that the effects of ROH are consistent in direction and magnitude among adopted individuals, and also for short ROH which are not informative about parental relatedness. Finally, we introduce a within-siblings method, independent of all confounders, that confirms a genetic explanation for most of the observed effects. Variation in FROH between siblings is caused entirely by random Mendelian segregation; we show that higher FROH siblings experience poorer overall health and lower reproductive success, as well as other changes consistent with population-wide estimates. Nevertheless, average effect sizes from both adoptees and siblings are 20% smaller than population-wide estimates, confirming the importance of accounting for social confounding in future studies of human inbreeding depression.
Our results reveal five large groups of phenotypes sensitive to inbreeding depression, including some known to be closely linked to evolutionary fitness, but also others where the connection is, with current knowledge, more surprising. The effects are mediated by ROH rather than homozygosity of common SNPs, causally implicating rare recessive variants rather than overdominance as the most important underlying mechanism. Identification of these recessive variants will be challenging, but analysis of regional ROH and in particular using whole-genome sequences in large cohorts with sufficient variance in autozygosity will be the first step. Founder populations or those which prefer consanguineous marriage will provide the most power to understand this fundamental phenomenon.
see Supplementary Data.
Methods
Overview
Our initial aim was to estimate the effect of FROH on 45 quantitative traits and to assess whether any of these effects differed significantly from zero. Previous work7,11 has shown that inbreeding coefficients are low in most human populations, and that very large samples are required to reliably estimate the genetic effects of inbreeding13. To maximise sample size, a collaborative consortium (ROHgen6) was established, and research groups administering cohorts with SNP chip genotyping were invited to participate. To ensure that all participants performed uniform and repeatable analyses, a semi-automated software pipeline was developed and executed locally by each research group. This software pipeline required cohorts to provide only quality-controlled genotypes (in plink binary format) and standardised phenotypes (in plain-text) and used standard software (R, PLINK12,32, KING33) to perform the analyses described below. Results from each cohort were returned to the central ROHgen analysts for meta-analysis.
During the initial meta-analysis, genotypes were released for >500,000 samples from the richly phenotyped UK Biobank (UKB)10. It was therefore decided to add a further 34 quantitative phenotypes and 21 binary traits to the ROHgen analysis. Many of these additional traits were unique to UKB, although 7 were also available in a subset of ROHgen cohorts willing to run additional analyses. In total, the effect of FROH was tested on 100 traits and therefore experiment-wise significance was defined as 5 × 10−4 (=0.05/100).
Cohort recruitment
In total, 119 independent, genetic epidemiological study cohorts were contributed to ROHgen. Of these, 118 were studies of adults and contributed multiple phenotypes, while 1 was a study of children and contributed only birth weight. To minimise any potential confounding or bias caused by within-study heterogeneity, studies were split into single-ethnicity sub-cohorts wherever applicable. Each sub-cohort was required to use only one genotyping array and be of uniform ancestry and case-status. For example, if a study contained multiple distinct ethnicities, sub-cohorts of each ancestry were created and analysed separately. At minimum, ancestry was defined on a sub-continental scale (i.e. European, African, East Asian, South Asian, West Asian, Japanese, and Hispanic were always analysed separately) but more precise separation was used when deemed necessary, for example, in cohorts with large representation of Ashkenazi Jews. In case-control studies of disease, separate sub-cohorts were created for cases and controls and phenotypes associated with disease status were not analysed in the case cohort: for example, fasting plasma glucose was not analysed in Type 2 diabetes case cohorts. Occasionally, cohorts had been genotyped on different SNP genotyping microarrays and these were also separated into sub-cohorts. There was one exception (deCODE) to the single microarray rule, where the intersection between all arrays used exceeded 150,000 SNPs. In this cohort the genotype data from all arrays was merged since the correspondence between FROH for the individual arrays and FROH the intersection dataset was found to be very strong (\(\beta _{{\mathrm{merged}},{\mathrm{hap}}}\) = 0.98, r2 = 0.98; \(\beta _{{\mathrm{merged}},{\mathrm{omni}}}\) = 0.97, r2=0.97). Dividing studies using these criteria yielded 234 sub-cohorts. Details of phenotypes contributed by each cohort are available in Supplementary Data 4.
Ethical approval
Data from 119 independent genetic epidemiology studies were included. All subjects gave written informed consent for broad-ranging health and genetic research and all studies were approved by the relevant research ethics committees or boards. PubMed references are given for each study in Supplementary Data 2.
Genotyping
All samples were genotyped on high-density (minimum 250,000 markers), genome-wide SNP microarrays supplied by Illumina or Affymetrix. Genotyping arrays with highly variable genomic coverage (such as Exome chip, Metabochip, or Immunochip) were judged unsuitable for the ROH calling algorithm and were not permitted. Imputed genotypes were also not permitted; only called genotypes in PLINK binary format were accepted. Each study applied their own GWAS quality controls before additional checks were made in the common analysis pipeline: SNPs with >3% missingness or MAF <5% were removed, as were individuals with >3% missing data. Only autosomal genotypes were used for the analyses reported here. Additional, cohort-specific, genotyping information is available in Supplementary Data 2.
Phenotyping
In total, results are reported for 79 quantitative traits and 21 binary traits. These traits were chosen to represent different domains of health and reproductive success, with consideration given to presumed data availability. Many of these traits have been the subject of existing genome-wide association meta-analyses (GWAMA), and phenotype modelling, such as inclusion of relevant covariates, was copied from the relevant consortia (GIANT for anthropometry, EGG for birth weight, ICBP for blood pressures, MAGIC for glycaemic traits, CHARGE-Cognitive, -Inflammation & -Haemostasis working groups for cognitive function, CRP, fibrinogen, CHARGE-CKDgen for eGFR, CHARGE-ReproGen for ages at menarche and menopause, Blood Cell & HaemGen for haematology, GUGC for urate, RRgen, PRIMA, QRS & QT-IGC for electrocardiography, GLGC for classical lipids, CREAM for spherical equivalent refraction, Spirometa for lung function traits, and SSGAC for educational attainment and number of children ever born). Further information about individual phenotype modelling is available in Supplementary Note 1 and Supplementary Data 8.
ROH calling
Runs of homozygosity (ROH) of >1.5 Mb in length were identified using published methods6,11. In summary, SNPs with minor allele frequencies below 5% were removed, before continuous ROH SNPs were identified using PLINK with the following parameters: homozyg-window-snp 50; homozyg-snp 50; homozyg-kb 1500; homozyg-gap 1000; homozyg-density 50; homozyg-window-missing 5; homozyg-window-het 1. No linkage disequilibrium pruning was performed. These parameters have been previously shown to call ROH that correspond to autozygous segments in which all SNPs (including those not present on the chip) are homozygous-by-descent, not chance arrangements of independent homozygous SNPs, and inbreeding coefficient estimates calculated by this method (FROH) correlate well with pedigree-based estimates (FPED)11. Moreover, they have also been shown to be robust to array choice6.
Calculating estimators of F
For each sample, two estimates of the inbreeding coefficient (F) were calculated, FROH and FSNP. We also calculated three additional measures of homozygosity: FROH<5Mb, FROH>5Mb and FSNP_outsideROH.
FROH is the fraction of each genome in ROH >1.5 Mb. For example, in a sample for which PLINK had identified n ROH of length li (in Mb), i ϵ {1..n}, then FROH was then calculated as
where FROH<5Mb and FROH>5Mb are the genomic fractions in ROH of length >5 Mb, and in ROH of length <5 Mb (but >1.5 Mb), respectively, and the length of the autosomal genome is estimated at 3 gigabases (Gb). It follows from this definition that
Single-point inbreeding coefficients can also be estimated from individual SNP homozygosity without any reference to a genetic map. For comparison with FROH, a method of moments estimate of inbreeding coefficient was calculated34, referred to here as FSNP, and implemented in PLINK by the command–het.
where O(HOM) is the observed number of homozygous SNPs, E(HOM) is the expected number of homozygous SNPs, i.e. \(\mathop {\sum}\nolimits_{i = 1}^N {\left( {1 - 2p_iq_i} \right)}\), and N is the total number of non-missing genotyped SNPs.
FROH and FSNP are strongly correlated, especially in cohorts with significant inbreeding, since both are estimates of F. To clarify the conditional effects of FROH and FSNP, an additional measure of homozygosity,FSNPoutsideROH, was calculated to describe the SNP homozygosity observed outside ROH.
where
And NSNP_ROH is the number of homozygous SNPs found in ROH. Note that:
A further single point estimator of the inbreeding coefficient, described by Yang et al.20 as \(\widehat F^{{\mathrm{{III}}}}\), is implemented in PLINK by the parameter –ibc (Fhat3) and was also calculated for all samples.
where N is the number of SNPs, pi is the reference allele frequency of the ith SNP in the sample population and xi is the number of copies of the reference allele.
Effect size estimates for quantitative traits
In each cohort of n samples, for each of the quantitative traits measured in that cohort, trait values were modelled by
where y is a vector (n × 1) of measured trait values, \(\beta_{{F}_{\rm{ROH}}}\) is the unknown scalar effect of FROH on the trait, FROH is a known vector (n × 1) of individual FROH, b is a vector (m × 1) of unknown fixed covariate effects (including a mean, μ), X in a known design matrix (n × m) for the fixed effects, and ε is an unknown vector (n × 1) of residuals.
The m fixed covariates included in each model were chosen with reference to the leading GWAMA consortium for that trait and are detailed in Supplementary Data 8. For all traits, these covariates included: age (and/or year of birth), sex, and at least the first 10 principal components of the genomic relatedness matrix (GRM). Where necessary, additional adjustments were made for study site, medications, and other relevant covariates (Supplementary Data 3).
For reasons of computational efficiency, it was decided to solve Eq. (10) in two steps. In the first step, the trait (y) was regressed on all fixed covariates to obtain the maximum likelihood solution of the model:
All subsequent analyses were performed using the vector of trait residuals ε′, which may be considered as the trait values corrected for all known covariates.
In cohorts with a high degree of relatedness, mixed-modelling was used to correct for family structure, although, because ROH are not narrow-sense heritable, this was considered less essential than in Genome-Wide Association Studies. Equation (11) becomes
where u is an unknown vector (n × 1) of polygenic effects with multivariate normal distribution of mean 0 and covariance matrix σg2A, where A is the genomic relationship matrix (GRM). In these related cohorts, a GRM was calculated using PLINK v1.9 and Grammar+ residuals of Eq. (12) were estimated using GenABEL35. These Grammar+ residuals (ε′) were used in subsequent analyses.
To estimate \(\beta_{{F}_{\rm{ROH}}}\) for each trait, trait residuals were regressed on FROH to obtain the maximum likelihood (ML) solution of the model
The sex-specific estimates of \(\beta_{{F}_{\rm{ROH}}}\) (Supplementary Data 12) were obtained from Eq. (13) applied to the relevant sex.
For all traits, a corresponding estimates of \(\beta_{{F}_{\rm{SNP}}}\) and \(\beta_{\rm{F}_{\rm{GRM}}}\) were obtained from the models
and the effects of different ROH lengths and of SNP homozygosity (Fig. 4b) were obtained from the model
Effect size estimates for binary traits
Binary traits were analysed by two methods. The primary estimates of \(\beta_{{F}_{\rm{ROH}}}\) (Fig. 3b and Supplementary Data 10) were obtained from full logistic models:
where g() is the link function (logit), and where FROH and all applicable covariates (Supplementary Datas 3, 8) were fitted simultaneously. Mixed modelling for family structure was not attempted in the logistic models since an accepted method was not apparent.
For all subsequent results, y was scaled by \(1/\sigma _y^2\) and analysed by linear models, as for quantitative traits, including mixed-modelling where appropriate for family studies. This method of estimating binary traits with simple linear models gives asymptotically unbiased estimates of \(\beta_{{F}_{\rm{ROH}}}\) and se(\(\beta_{{F}_{\rm{ROH}}}\)) on the ln(Odds-Ratio) scale36. For all significant binary traits, a comparison of \(\widehat \beta _{F_{\mathrm{ROH}}}\) from the full model with \(\widehat \beta _{F_{\mathrm{ROH}}}\) from the linear model approximation is presented in Supplementary Fig. 8.
To give \(\widehat \beta _{F_{\mathrm{ROH}}}\) a more tangible interpretation, effect estimates are frequently quoted in the text as β0.0625, i.e. the estimated effect in the offspring of first cousins, where 6.25% of the genome is expected to be autozygous.
Religiosity and educational attainment as additional covariates
To assess the importance of potential social confounders, proxy measures of socio-economic status and religiosity were separately included in Eq. (13) as additional covariates. The modified effect estimates (\(\widehat {\beta \prime }_{F_{\mathrm{ROH}}}\)) were tested for significance (Supplementary Data 20) and compared to the uncorrected estimates (\(\beta_{{F}_{\rm{ROH}}}\)) (Supplementary Fig. 10a, b).
Since Educational Attainment (EA) was measured in many cohorts, this was chosen as the most suitable proxy for socio-economic status. However, since FROH is known to affect EA directly6 any change in \(\beta_{{F}_{\rm{ROH}}}\) when conditioning on EA cannot be assumed to be entirely due to environmental confounding.
The analysis of religiosity was only carried out in UKB, where a rough proxy was available. Although no direct questions about religious beliefs were included, participants were asked about their leisure activities. In response to the question Which of the following do you attend once a week or more often? (You can select more than one), 15.6% of UKB participants selected Religious Group from one of the seven options offered. In the models described, religiosity was coded as 1 for those who selected Religious Group and 0 for those who did not. Although this is likely to be an imperfect measure of actual religious belief it is currently the best available in a large dataset.
Assortative mating
Humans are known to mate assortatively for a number of traits including height and cognition37, and so we sought to investigate if this could influence our results, for example, by the trait extremes being more genetically similar and thus the offspring more homozygous. We see no evidence for an effect of assortative mating on autozygosity, however. Firstly, a polygenic risk score for height (see Supplementary Note 1), which explains 18.7% of the phenotypic variance in height, was not associated with FROH (p = 0.77; Supplementary Fig. 5). Secondly, linear relationships between traits and autozygosity extend out to very high FROH individuals (Supplementary Figs. 9a–f). Samples in the highest FROH group are offspring of genetically similar parents, very likely first or second degree relatives and, for example, the height of these samples is on average 3.4 cm [95% CI 2.5–4.3] shorter than the population mean. Assortative mating would suggest this height deficit has been inherited from genetically shorter parents, but this would require an implausibly strong relationship between short stature and a propensity to marry a very close relative. Thirdly, the sex-specific effects we observe could only be explained by assortative mating if the additive heritability of these traits also differed by gender.
Average trait values in groups of similar F ROH
In each cohort individuals were allocated to one of ten groups of similar FROH. The bounds of these groups were the same for all cohorts, specifically {0, 0.002, 0.0041, 0.0067, 0.0108, 0.0186, 0.0333, 0.06, 0.10, 0.18 and 1.0}. Within each group the mean trait residual (ε′) and mean FROH were calculated, along with their associated standard errors. Within each cohort the expectation of ε′ is zero at the mean FROH, however as mean FROH varies between cohorts (Fig. 2, Supplementary Data 5) it was necessary to express ε′ relative to a common FROH before meta-analysis. Hence, for this analysis only, the trait residuals (ε′) were expressed relative to the FROH = 0 intercept, i.e. by subtracting μ from Eq. (13).
Effect of F ROH within adoptees
We compared \(\beta_{{{F}_{\rm{ROH}\_{\rm{ADOPTEE}}}}}\) to cross-cohort \(\beta_{{F}_{\rm{ROH}}}\), not that from UKB alone, as we consider the latter to be a noisy estimate of the former; estimates in UKB are consistent with those from meta-analysis.
Effect of F ROH within full-sibling families
In a subset of cohorts, with substantial numbers of related individuals, further analyses were performed to investigate the effect of FROH within full-sibling families. In each of these cohorts, all second-degree, or closer, relatives were identified using KING (parameters:–related–degree 2). Full-siblings were then selected as relative pairs with genomic kinship >0.175 and IBS0 >0.001. This definition includes monozygotic twins, who were intentionally considered as part of full-sibling families. Although monozygotic twins are expected to have identical FROH, they may not have identical trait values, and including additional trait measurements decreases the sampling error of the within-family variance estimate, hence increasing statistical power. Dizygotic twins were also included.
For each individual (j) with identified siblings, the values of FROH and trait residual (ε′) were calculated relative to their family mean (and called FjROH_wSibs and εjwSibs, respectively), i.e. for individual j with n full-siblings Sk where k ϵ {1..n}
The effect of FROH within-full-siblings (\(\beta_{{F}_{\rm{ROH}}\_{\rm{wSibes}}}\)) was estimated by linear regression of εwSibs on FROH_wSibs.
Importantly, the variation of FROH within full-siblings is entirely caused by differences in Mendelian segregation, and is therefore completely independent of all possible confounders. Hence, the effect estimates obtained by this method are estimates of the genetic effects of FROH, unbiased by any possible confounder. Since confounding by social factors is a major concern in this field, methods that can definitively exclude this possibility are of critical importance.
Between-cohort meta-analysis
As is typical in genome-wide association meta-analyses (GWAMA), genetic effects were estimated within single-ethnicity sub-cohorts, and meta-analysis of the within-cohort effect sizes was used to combine results38. This established method eliminates any potential confounding caused by between-cohort associations between FROH and traits.
Each cohort returned estimates and standard errors of: \(\beta_{{F}_{\rm{ROH}}}\), \(\beta_{{F}_{\rm{SNP}}},\beta_{{F}_{\rm{ROH} > {\rm{Mb}}}},\beta_{{F}_{\rm{ROH} < {\rm{Mb}}}},\beta_{{F}\_{\rm{outsideROH}}}, \beta_{{F}_{\rm{ROH}\_{\rm{wSibs}}}}\), as well as trait means (\(\overline {\varepsilon \prime }\)) and standard errors within each of 10 FROH bins. The between-cohort mean of each of these 16 estimates was then determined by fixed-effect, inverse-variance meta-analysis using the R package metafor39. Results shown in Figs. 3–5 are meta-analysed averages of the within-cohort effects.
The meta-analysis was also run for various subsets of cohorts, stratified by ancestry as defined in Supplementary Data 18. Meta-analysis estimates from these groupings are shown in Supplementary Fig. 1.
Median and 95% CI of a ratio
In the analyses of adoptees (Fig. 5c), siblings (Fig. 5d) and potential confounders (Supplementary Figs. 10a, b) we wished to compare the effect estimates (\(\beta_{{F}_{\rm{ROH}}}\)) from two different methods across a wide range of traits. The units of \(\beta_{{F}_{\rm{ROH}}}\) differ by trait so, to allow comparison across all traits, the unitless ratio of effect size estimates was calculated (for example \(\beta_{{F}_{\rm{ROH}\_{\rm{wSibs}}}}\): \(\beta_{{F}_{\rm{ROH}}}\)). Figure 5c, d and Supplementary Figs. 10a, b show the medians and 95% CI of these ratios. These were determined empirically by bootstrap since, although formulae exist for the mean and standard error of a ratio40, the assumption of normality is violated when \(\beta_{{F}_{\rm{ROH}}}\)/se(\(\beta_{{F}_{\rm{ROH}}}\)) is not large.
Genetic correlations in UK Biobank
Genetic correlations were calculated using LD-Score Regression41, implemented in LDSC v1.0.0 (https://github.com/bulik/ldsc). Summary statistics were parsed using default parameters in the LDSC ‘munge_sumstats.py’ script, extracting only variants present in the HapMap 3 reference panel.
Accuracy of F ROH measures of inbreeding effects
A recent paper suggested that ROH may overestimate inbreeding effects by as much as 162%42; however, this could only be the case if FROH underestimates excess homozygosity at the causal loci by at least 162%. We do not believe this to be the case since the maximum FROH measured in many cohorts is around 0.25 (the expectation in the offspring off first-degree relatives), and the effect size estimates from these samples are consistent with the overall estimates (Fig. 5c, d and Supplementary Fig. 9a–f). We note that Yengo et al. applied the ROH calling parameters used here to imputed data. These parameters have been validated for called genotype data6 but not, to our knowledge, for the higher SNP density and error rate of imputed data (see also Supplementary Note 4). The simple method for detecting ROH used here was well suited to our study, since it could be easily implemented on over one million samples, and most of the variation in FROH is caused by easily-identified long ROH.43,44,45
Reporting summary
Further information on research design is available in the Nature Research Reporting Summary linked to this article.
Data availability
The meta-analysed data which support these findings are available as Supplementary Data files. Cohort-level summary statistics underlying all figures and tables are available in a publicly accessible dataset (https://doi.org/10.6084/m9.figshare.9731087). In the majority of cases we do not have consent to share individual-level data, although for UK Biobank this is available on request from https://www.ukbiobank.ac.uk/.
References
Charlesworth, D. & Willis, J. H. The genetics of inbreeding depression. Nat.Rev. Genet. 10, 783–796 (2009).
Bittles, A. H. & Black, M. L. Consanguinity, human evolution, and complex diseases. Proc. Natl Acad. Sci. 107, 1779–1786 (2010).
Nakatsuka, N. et al. The promise of discovering population-specific disease-associated genes in South Asia. Nat. Genet. 49, 1403–1407 (2017).
Narasimhan, V. M. et al. Health and population effects of rare gene knockouts in adult humans with related parents. Science 352, 474–477 (2016).
Saleheen, D. et al. Human knockouts and phenotypic analysis in a cohort with a high rate of consanguinity. Nature 544, 235–239 (2017).
Joshi, P. K. et al. Directional dominance on stature and cognition in diverse human populations. Nature 523, 459–462 (2015).
Kirin, M. et al. Genomic runs of homozygosity record population history and consanguinity. PLoS ONE 5, e13996 (2010).
Pemberton, T. J. et al. Genomic patterns of homozygosity in worldwide human populations. Am. J. Hum. Genet. 91, 275–292 (2012).
Ceballos, F. C., Joshi, P. K., Clark, D. W., Ramsay, M. & Wilson, J. F. Runs of homozygosity: windows into population history and trait architecture. Nat. Rev. Genet. 19, 220–234 (2018).
Sudlow, C. et al. UK Biobank: an open access resource for identifying the causes of a wide range of complex diseases of middle and old age. PLoS Med. 12, e1001779 (2015).
McQuillan, R. et al. Runs of homozygosity in European populations. Am. J. Hum Genet. 83, 359–372 (2008).
Purcell, S. & Chang, C. PLINK 1.9. www.cog-genomics.org/plink/1.9/.
McQuillan, R. et al. Evidence of inbreeding depression on human height. PLoS Genet. 8, e1002655 (2012).
Abdellaoui, A. et al. Association between autozygosity and major depression: stratification due to religious assortment. Behav. Genet. 43, 455–467 (2013).
Bashi, J. Effects of inbreeding on cognitive performance. Nature 266, 440–442 (1977).
Broman, K. W. & Weber, J. L. Long homozygous chromosomal segments in reference families from the centre d’Etude du polymorphisme humain. Am. J. Hum. Genet. 65, 1493–1500 (1999).
Gibson, J., Morton, N. E. & Collins, A. Extended tracts of homozygosity in outbred human populations. Hum. Mol.Genet. 15, 789–795 (2006).
Lencz, T. et al. Runs of homozygosity reveal highly penetrant recessive loci in schizophrenia. Proc.Natl. Acad. Sci. USA. 104, 19942–19947 (2007).
Keller, M. C., Visscher, P. M. & Goddard, M. E. Quantification of inbreeding due to distant ancestors and its detection using dense single nucleotide polymorphism data. Genetics 189, 237–249 (2011).
Yang, J., Lee, S. H., Goddard, M. E. & Visscher, P. M. GCTA: a tool for genome-wide complex trait analysis. Am. J. Hum. Genet. 88, 76–82 (2011).
Coulson, T., Albon, S., Jon, S. & Pemberton, J. Microsatellite loci reveal sex-dependent responses to inbreeding and outbreeding in Red Deer calves. Evolution 53, 1951–1960 (1999).
Slate, J. & Pemberton, J. M. Comparing molecular measures for detecting inbreeding depression. J.Evolutionary Biology 15, 20–31 (2002).
Campbell, H. et al. Effects of genome-wide heterozygosity on a range of biomedically relevant human quantitative traits. Hum. Mol. Genet. 16, 233–241 (2007).
Abdellaoui, A. et al. Educational attainment influences levels of homozygosity through migration and assortative mating. PLoS ONE 10, e0118935 (2015).
Helgason, A., Pálsson, S., Guobjartsson, D. F., Kristjánsson, P. & Stefánsson, K. An association between the kinship and fertility of human couples. Science 319, 813–816 (2008).
Bittles, A. H., Grant, J. C., Sullivan, S. G. & Hussain, R. Does inbreeding lead to decreased human fertility? Ann. Hum. Biol. 29, 111–130 (2002).
Alvarez, G., Ceballos, F. C. & Berra, T. M. Darwin was right: inbreeding depression on male fertility in the Darwin family. Biol. J.Linn.Soc. 114, 474–483 (2015).
Ober, C., Hyslop, T. & Hauck, W. W. Inbreeding effects on fertility in humans: evidence for reproductive compensation. Am. J. Hum. Genet. 64, 225–231 (1999).
Robert, A., Toupance, B., Tremblay, M. & Heyer, E. Impact of inbreeding on fertility in a pre-industrial population. Eur. J. Hum. Genet. 17, 673–681 (2009).
Day, F. R. et al. Physical and neuro-behavioural determinants of reproductive onset and success Europe PMC Funders Group. Nat. Genet. 48, 617–623 (2016).
Huisman, J., Kruuk, L. E. B., Ellis, P. A., Clutton-Brock, T. & Pemberton, J. M. Inbreeding depression across the lifespan in a wild mammal population. Proc.Natl. Acad. Sci. 113, 3585–3590 (2016).
Chang, C. C. et al. Second-generation PLINK: rising to the challenge of larger and richer datasets. GigaScience 4, 7 (2015).
Manichaikul, A. et al. Robust relationship inference in genome-wide association studies. Bioinformatics 26, 2867–2873 (2010).
Wright, S. Genetics of populations. Encyclopedia Britannica Vol. 10, 111-A-D-112 (1948).
Belonogova, N. M., Svishcheva, G. R., van Duijn, C. M., Aulchenko, Y. S. & Axenovich, T. I. Region-based association analysis of human quantitative traits in related individuals. PLoS ONE 8, e65395 (2013).
Cook, J. P., Mahajan, A. & Morris, A. P. Guidance for the utility of linear models in meta-analysis of genetic association studies of binary phenotypes. Eur. J. Hum. Genet. 25, 240–245 (2017).
Buss, D. The Evolution of Desire: Strategies of Human Mating. Vol. 15 (Basic Books, 2003).
Okbay, A. et al. Genome-wide association study identifies 74 loci associated with educational attainment. Nature 533, 539–542 (2016).
Viechtbauer, W. Conducting meta-analyses in R with the metafor Package. J. Stat. Softw. 36, 1–48 (2010).
Fieller, E. C. Some problems in interval estimation. J. R. Stat. Soc. Ser. B 16, 175–185 (1954).
Bulik-Sullivan, B. et al. An atlas of genetic correlations across human diseases and traits. Nat. Genet. 47, 1236–1241 (2015).
Yengo, L. et al. Detection and quantification of inbreeding depression for complex traits from SNP data. Proc. Natl. Acad. Sci. 114, 8602–8607 (2017).
Kardos, M., Nietlisbach, P. & Hedrick, P. W. How should we compare different genomic estimates of the strength of inbreeding depression? Proc. Natl. Acad. Sci. USA 115, E2492–E2493 (2018).
Gazal, S. et al. Inbreeding coefficient estimation with dense SNP data: comparison of strategies and application to HapMap III. Hum. Hered. 77, 49–62 (2014).
Johnson, E. C., Evans, L. M. & Keller, M. C. Relationships between estimated autozygosity and complex traits in the UK Biobank. PLoS Genet. 14, e1007556 (2018).
Keller, L. F. & Waller, D. M. Inbreeding effects in wild populations. Trends Ecol. Evol. 17, 230–241 (2002).
Acknowledgements
This paper is the work of the ROHgen consortium. We thank the Sigma T2D Consortium, whose members are detailed in Supplementary Note 3. We thank the UK Biobank Resource, approved under application 19655; we acknowledge funding from the UK Medical Research Council Human Genetics Unit and MRC Doctoral Training Programme in Precision Medicine. We also thank Neil Robertson, Wellcome Trust Centre for Human Genetics, Oxford, for use of his author details management software, Authorial. Finally, we thank all the participants, researchers and funders of ROHgen cohorts. Cohort-specific acknowledgements are in Supplementary Data 2; personal acknowledgements and disclosures are in Supplementary Note 2. We thank Rachel Edwards for administrative assistance.
Author information
Authors and Affiliations
Contributions
Directed consortium: T.E., P.K.J. and J.F.W. Central analyst: D.W.C., Y.O., N. Pirastu and P.K.J. Cohort PI: C.A.A.-S., M.L.A., T.A., F.A., E.B., G.J.d.B., E.P.B., S. Chanock, Y.-D.I.C., Z.C., R.M.v.D., M.S.D., N.D., P.E., B.I.F., C.A. Haiman, D.A.v.H., I.H., M.A.I., P.J., T. Kessler, K.-T.K., D.P.V.d.K., W.-P.K., J. Kuusisto, C.L., D.A.L., L.L., T.A.M., Y. Murakami, K.K.O., L.O., O.P., N. Poulter, P.P.P., L.Q.-M., K.R., D.C.R., S.S.R., P.M.R., L.J.S., P.J.S., W.H.-H.S., A. Stanton, J.M.S., L. Straker, T.T.-L., J.H.V., V.V., Y.X.W., N.J.W., C.S.Y., J.-M.Y., F.W.A., S.J.L.B., D.M.B., D.A.B., L.H.v.d.B., S.I.B., D.B., C. Bouchard, M.J.C., J.C.C., G.R.C., C.-Y.C., M. Ciullo, M. Cornelis, D. Cusi, G.D.-S., I.D., C.M.v.D., D.E., J. Erdmann, J.G.E., E.E., M.K.E., B.F., M.F., A.F., Y.F., P. Gasparini, C. Gieger, C. Gonzalez, S.F.A.G., L.R.G., L.G., V.G., U.G., A. Hamsten, P.v.d.H., C.-K.H., H. Hochner, S.C.H., V.W.V.J., Å.J., J.B.J., J.W.J., J.J., J. Kaprio, S.L.K., F.K., M. Kumari, M. Laakso, M. Laudes, W.L., N.G.M., W. März, G. Matullo, M.I.M., T.R.M., A. Metspalu, B.F.M., K.L.M., G.W.M., D.M.-K., P.B.M., K.E.N., C.O., A.J.O., C. Palmer, G.G.P., E.P., C.E.P., L.P., M. Pirastu, D.J.P., D.P., B.M.P., C.R., J.I.R., I.R., D.K.S., R.S., H. Schunkert, A.R.S., N. Small, E.-S.T., N.J.T., D.T., T.T., P.V., D.R.W., T.-Y.W., J.W., A.B.Z., M. Perola, P.K.M., A.G.U., J.S.K., D.I.C., R.J.F.L., N.F., C.H., J.R.B.P., T.E., K. Stefansson, M. Kubo, J.F.W. Cohort analyst: D.W.C., Y.O., K.H.S.M., D.M., I.G., H.M., K.L., J.H.Z., P.D., R.R., C. Schurmann, X.G., F. Giulianini, W. Zhang, C.M.-G., R.K., Y.B., T.M.B., C. Baumbach, G.B., M.J.B., M. Brumat, J.-F.C., D.L.C., D.A.E., C.F., H.G., M. Germain, S.D.G., H.G.d.H., S.E.H., E.H., A.H.-C., C.I., I.E.J., Y.J., T. Kacprowski, T. Karlsson, M.E.K., S.A.L., R.L.-G., A. Mahajan, W. Meng, M.E.M., P.J.v.d.M., M.Munz, T.N., T.P., G. Prasad, R.B.P., T.D.S.P., F. Rizzi, E.S., B.R.S., D.S., L. Skotte, A.V.S., A.v.d.S., C.N.S., R.J.S., S.M.T., S.T., C.T., N.V., C.V., L.W., H.R.W., R.E.W., L.R.Y., J. Yao, N.A.Y., W. Zhao, A.A.A., S.A., M. Akiyama, M. Alver, G. Chen, M. Cocca, M.P.C., G. Cugliari, F.R.D., G.E.D., G.G., A.G., M. Gögele, M. Graff, E.G.-H., A. Halevy, D.A.v.H., J.H., Y.K., M. Kanai, N.D.K., M. Loh, S.L., Y.L., J’a.L., N.M., X.W.M., M. Mezzavilla, A. Moore, H.M.-M., M.A.N., C.A.R., A.R., D.R., M.S.-L., W.R.S., B.S., J.v.S., S.S., S.R.S., T.T.S., A. Tillander, E.V., L. Zeng, N.A., L. Benjamin, L.F.B., J.P.B., J.A.B., S. Carmi, G.R.C., M. Cornelis, D. Cusi, R.D., D.E., J.D.F., M.F., S.F., P. Goyette, S.C.H., Å.J., S.W.v.d.L., J. Lahti, R.A.L., S.E.M., K.E.N., J.R.O’c., E.P., L.P., J.D.R., F. Rivadeneira, C.R., R.A.S., X.S., J.A.S., C.A.W., J. Yang, L.Y., D.I.C., N.F., R.G.W., J.R.B.P., T.E., A. Helgason. Provided data: Y.O., C. Schurmann, W. Zhang, C.M.-G., Y.B., A.M.D., K.R.v.E., C.F., H.G., M.E.K., K. Matsuda, R.B.P., F. Rizzi, E.S., M.C.S., A.V.S., S.M.T., N.V., A.A.A., C.A.A.-S., M.L.A., M.A.A., A.R.B., E.B., J.B.B., G.J.d.B., E.P.B., L. Broer, H.C., S. Chanock, M.-L.C., G. Chen, Y.-D.I.C., Y.-F.C., J.C., M.S.D., K.D., M.D., A.P.D., N.D., S.S.E., J. Elliott, R.E., J.F.F., K.F., B.I.F., M. Gögele, M.O.G., S.G., D.F.G., K.G., B.G., Y.G., S.P.H., C.A. Haiman, T.B.H., M. Hedayati, M. Hirata, I.H., C.A. Hsiung, Y.-J.H., M.A.I., A.J., P.J., Y.K., C.C.K., W.-P.K., I.K., B.K.K., J. Kuusisto, L.J.L., D.A.L., I.-T.L., W.-J.L., M.M.L., J. Liu, S.J.L., R.M., A.W.M., P.M., G. Másson, C.M., T. Meitinger, L.M., I.Y.M., Y. Momozawa, T.A.M., A.C.M., T. Muka, A.D.M., R.d.M., J.C.M., M.A.N., M.N., M.J.N., I.M.N., L.O., S.P., G. Pálsson, J.S.P., C. Pattaro, A.P., O.P., N. Poulter, L.Q.-M., K.R., S.R., D.C.R., W.v.R., F.J.A.v.R., C. Sabanayagam, C.F.S., V.S., K. Sandow, B.S.-K., P.J.S., W.H.-H.S., Y. Shi, S.R.S., J.K.S., J.R.S., B.H.S., A. Stanton, L. Stefansdottir, L. Straker, P.S., G.S., M.A.S., A.M.T., K.D.T., N.T., Y.-C.T., G.T., U.T., R.P.T., T.T.-L., I.T., S.V., J.H.V., V.V., U.V., E.V., S.M.W., M.W., G.S.W., S.W., C.S.Y., J.-M.Y., L. Zhang, J.Z., S.J.L.B., D.M.B., S.I.B., A.C., M.J.C., D. Cesarini, J.C.C., G.R.C., M. Cornelis, D. Cusi, G.D.-S., I.D., R.D., D.E., J. Erdmann, J.G.E., E.E., M.K.E., B.F., M.F., Y.F., P. Gasparini, C. Gonzalez, S.F.A.G., L.G., V.G., C.-K.H., A.A.H., H. Hochner, H. Huikuri, S.C.H., V.W.V.J., P.L.D.J., M.J., J.W.J., J. Kaprio, S.L.K., M. Laakso, S.W.v.d.L., J.Lahti, W.L., N.G.M., G. Matullo, B.F.M., K.L.M., G.W.M., P.B.M., D.R.N., A.J.O., W.P., C. Palmer, C.E.P., L.P., P.A.P., T.J.P., D.J.P., D.P., B.M.P., J.D.R., F. Rivadeneira, C.R., J.I.R., I.R., D.K.S., N. Sattar, H. Schunkert, A. Teumer, N.J.T., T.T., D.R.W., J.B.W., C.W., J.W., A.B.Z., M. Perola, P.K.M., A.G.U., J.S.K., D.I.C., L.F., C.S.H., C.H., R.G.W., T.E. Contributed to manuscript: D.W.C., C. Schurmann, S.E.H., S.M.T., E.P.B., J.C., A.P.D., X.G., S.P.H., D.A.v.H., P.J., W.-P.K., D.A.L., S.J.L., A.P., J.M.S., A.M.T., J.-M.Y., J.Z., I.D., R.D., Y.F., J.W.J., C.R., J.I.R., M.Perola, R.J.F.L., P.K.J., J.F.W. Wrote manuscript: D.W.C. and J.F.W.
Corresponding author
Ethics declarations
Competing interests
M.L.A. is an employee of Genentech, a member of The Roche Group. D.A.L. has received support from several national and international government and charity funders, as well as Roche Diagnostics and Medtronic for work unrelated to this publication. M.I.M.: The views expressed in this article are those of the author(s) and not necessarily those of the NHS, the NIHR, or the Department of Health. He has served on advisory panels for Pfizer, NovoNordisk, Zoe Global; has received honoraria from Merck, Pfizer, NovoNordisk and Eli Lilly; has stock options in Zoe Global; has received research funding from Abbvie, Astra Zeneca, Boehringer Ingelheim, Eli Lilly, Janssen, Merck, NovoNordisk, Pfizer, Roche, Sanofi Aventis, Servier & Takeda. As of June 2019, M.Mc.C. is an employee of Genentech, and holds stock in Roche. T. Muka is now working as medical specialist at Novo Nordisk. O.P. is owner of Gen-info Ltd. Gen‐info Ltd provided support in the form of salaries and financial gains for author O.P., but did not have any additional role in selection of the journal or preparation of this manuscript. N. Poulter received financial support from several pharmaceutical companies which manufacture either blood pressure lowering or lipid lowering agents, or both, and consultancy fees. V.S. has participated in a congress trip sponsored By Novo Nordisk. P.J.S. has received research awards from Pfizer Inc. M.J.C. is Chief Scientist for Genomics England, a UK government company. B.M.P. serves on the DSMB of a clinical trial funded by Zoll LifeCor and on the Steering Committee of the Yale Open Data Access Project funded by Johnson & Johnson. A.R.S. is an employee of Regeneron Pharmaceutical Inc. The remaining authors declare no competing interests.
Additional information
Peer review information Nature Communications thanks Jun Li, Matthew Robinson and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Clark, D.W., Okada, Y., Moore, K.H.S. et al. Associations of autozygosity with a broad range of human phenotypes. Nat Commun 10, 4957 (2019). https://doi.org/10.1038/s41467-019-12283-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-019-12283-6
This article is cited by
-
Multilocus pathogenic variants contribute to intrafamilial clinical heterogeneity: a retrospective study of sibling pairs with neurodevelopmental disorders
BMC Medical Genomics (2024)
-
Assessment of inbreeding depression on morphometric traits among North Indian population cohorts
Discover Public Health (2024)
-
Requiem for Heterosis as a Cause of the Flynn Effect: Positive Combined Effects of Numbers and Lengths of Homozygosity Runs on Offspring-Parent Differences in Educational Attainment
Evolutionary Psychological Science (2024)
-
The coefficients of inbreeding revealed by ROH study among inbred individuals belonging to each type of the first cousin marriage: A preliminary report from North India
Genes & Genomics (2023)
-
Ancestry-related distribution of Runs of homozygosity and functional variants in Qatari population
BMC Genomic Data (2022)
Comments
By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.